Abstract
Detailed analysis of a band diagram of a photonic crystal (PhC) slab prepared on a nano-diamond layer is presented. Even though the PhC is structurally imperfect, the existence of leaky modes, determined both theoretically and experimentally in the broad spectral region, implies that an efficient light interaction with a material periodicity occurs in the sample. It is shown that the luminescence emission spectrum of a light source placed directly on the PhC surface can be modified by employing the optical modes of the studied structure. We stress also the impact of intrinsic optical losses of the nano-diamond on this modification.
Similar content being viewed by others
Introduction
Photonic crystal (PhC) slabs are structures of finite height which are periodically patterned in the dielectric constant in two dimensions1,2. Light can be guided in these structures, however, compared to uncorrugated (smooth) slabs, guided modes can also occur due to the band folding at the Brillouin zone (BZ) edges above the air light line and thus can radiate out from the structure3,4. These radiative modes are then called guided resonances5 or leaky modes. The physical mechanism of the light extraction can be easily understood by considering the Bragg diffraction of the guided modes on the periodic structure. Inversely, light of a suitable wavelength and an incident angle can be coupled into the structure. This effect can be utilized to experimentally determine the leaky mode band diagram of the structure from transmission and/or reflection measurements6,7,8. When the external spectrally broad light is incident on the periodic structure, it is diffracted into forward and backward direction and waves with the particular wavelengths propagating under suitable angles of incidence can couple to leaky modes of the PhC (defined by the parameters of the structure) and can be guided in the layer. When propagating in the plane of the PhC, they are again diffracted into forward (in the direction of the incident beam) and backward direction and radiate out from the structure—thus the name leaky modes. The zeroth order transmitted wave is exactly out of the phase (π-shifted) with respect to the modes outcoupled in the forward direction leading into the destructive interference and thus into the deep minima in the transmission efficiency9. Symetrically, maxima will occur at the spectral position of leaky modes in the reflection spectra. Due to the Fano-like shape of these resonances, minima in transmission can be slightly spectrally shifted with respect to the maxima in reflection10.
Here we present a detailed study of the leaky modes of a nanocrystalline diamond (NCD) PhC slab by investigating polarization resolved photonic band diagrams determined from experiment and simulation. We use an illustrative description of the symmetry based coupling to leaky modes by correlating their energy profiles with the band diagram. Next, the PhC effect on the photoluminescence (PL) of quantum dots (QDs) placed on the surface of the PhC slab is studied, indicating the ability to modify the shape of the PL spectrum and shift the PL emission maximum to a different energy driven by the dimensions of the PhC and at the same time to filter part of light emitted from the QDs. In order to obtain this effect, the PL emission spectrum of the QDs must spectrally overlap with the leaky modes of the PhC. These effects can be utilized, e.g. to manipulate the photonic properties or to enhance the sensitivity of diamond-based sensors.
Results
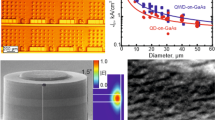
The measurements were realized on a NCD layer with periodically textured surface in two dimensions (Fig. 1(a)). NCD columns with the diameter d ~ 280 nm and the height of 135 ± 15 nm were ordered into the square lattice with the lattice constant a ~ 350 nm (as obtained from the SEM measurements). The total height of the layer with the columns was 420 ± 15 nm. The layer was seated on the transparent quartz substrate allowing to perform transmission measurements with negligible losses in the substrate. Details of the preparation process and positive results on enhanced extraction efficiency of the intrinsic diamond PL from the PhC were published elsewhere11,12. Sample dimensions, namely column diameter, stated here differ slightly from those published in11,12 due to more precise and accurate SEM measurement performed with a conductive polymer.
SEM image and the transmission measurement setup.
(a) 45° angle-view SEM image of the PhC sample. (b) Transmission measurement setup. Either S- or P-polarized collimated light is incident at the angle θ along the Γ–X or Γ–M crystal directions, respectively. Only the NCD layer with patterned surface without a substrate is shown.
The measurements were performed with the S- (electric field perpendicular to the plane of incidence) and P- (electric field in the the plane of incidence) polarized light incident along the Γ–X and Γ–M crystal directions using the setup sketched in Fig. 1(b). Each polarization couple to different leaky modes based on their mutual symmetry. As it follows from the discussion above, relatively deep minima occur in transmission spectra at the position of leaky modes. The measured transmission curves were converted into 2D maps forming photonic band diagrams of leaky modes in angle-wavelength representation (Fig. 2(a) and (c) for the S- and P-polarized incident light, respectively). In parallel with these experiments, photonic band diagrams of leaky modes were also numerically calculated using the Rigorous Coupled Wave Analysis technique. The PhC dimensions were slightly adjusted within their detection error in order to obtain the best spectral coincidence of the simulated and measured leaky resonances at the normal incidence and at another arbitrary incident angle. As it is apparent from the comparison of the simulated (Fig. 2(b) and (d)) and measured (Fig. 2(a) and (c)) band diagrams, excellent qualitative and even quantitative agreement in a broad spectral range was obtained between the experiment and theory using the following geometrical dimensions a = 350 nm, d = 280 nm, total height 425 nm, column height 150 nm. Nevertheless, small differences occur due to the following. First, the refractive index dispersion and optical losses in the diamond were not included in the simulation and only a real constant value of refractive index n = 2.41 was used. Second, simulation does not take into account the structural imperfection of the columns of the real structure. And third, the computed photonic band diagrams show also spectrally very narrow features which are unresolved in the measured spectra due to the limited spectral resolution of the detection system.
The computed photonic band diagram plotted in Fig. 3(a) includes all the leaky modes of the structure and is zoomed around the first TE (transverse electric) and TM (transverse magnetic) resonance at the Γ point. Here the TE mode is the mode of which the component of the electric field parallel with the sample plane and perpendicular to the mode propagation direction carries most of its energy. In case of the mode propagating in the x-direction, it is Ey component. On the other hand, energy of the TM mode propagating in the x-direction is stored comparably in both, Ex component—parallel to the mode propagation direction—and Ez component—perpendicular to the sample plane. Leaky bands, marked either by letter S or P based on light polarization that excited them, are visible in the zoomed band diagram. The general shape of the band diagram is similar to that obtained simply by folding the guided modes bands of the uncorrugated waveguide into the irreducible BZ considering the square lattice symmetry12. However, we can distinguish some differences—fourfold degeneracy splitting at the Γ point5; splitting of bands which are doubly degenerate in case of the band-folded diagram (in our case, e.g., two parallel nearly horizontal TE bands in the Γ–X direction marked by the black circle created due to splitting of doubly degenerate band based on the polarization). The similar effect of bands degeneracy lifting was computed using perturbative approach for the PhC slab with thin 2D grating13 and measured in reflection spectra of 2D PhC slab7.
Zoomed-in computed photonic band diagram and the electric field profiles of the modes.
(a) Zoom into the normalized sum of the S- and P-polarized calculated photonic band diagrams. Demonstration of polarization dependent band splitting. (b) Distribution of the Ey electric field component of the lowest TE leaky mode having the similar symmetry as the S-polarized incident light. Coordinate system is shown in Fig. 1(b). (c) Distribution of the Ex and Ez electric field components of the lowest TM leaky mode having the similar symmetry as the P-polarized incident light.
The reason for the different S- and P-polarized coupling can be understood by investigating the electric field profile of the modes with respect to the field profile of the source. Here it is demonstrated on the two energetically lowest leaky bands in the Γ–X direction, marked by black points in Fig. 3(a), the left one excited by the S- and the right one excited by the P-polarized light.
The only non-zero component of the electric field of S-polarized light is vector Ey pointing into y-direction (Fig. 1(b)) and thus the incident light can couple only to the Ey component of the leaky mode. Moreover, this source is odd with respect to the mirror plane y = 0 meaning that it can excite only mode having the same odd symmetry in Ey, i.e., mode that under mirror reflection through the plane y = 0 becomes its own opposite. This behaviour is demonstrated in Fig. 3(b) where the computed electric field distribution is plotted for the TE leaky mode with air wavelength of 815 nm. The field pattern is displayed for the TE mode relevant electric field component Ey in two distinct planes— on the left, the plane cutting the sample vertically through the middle of the columns in the Γ–X direction (plane y = 0) and on the right, the plane parallel to the sample and going through the middle of uncorrugated diamond layer (z = 0, borders of the columns are depicted in order to give an idea of the mode wavelength with respect to the lattice constant a). The mode is propagating in the x-direction and its wavefronts can be clearly recognized in both Ey field patterns. Most important is the fact that this mode is odd with respect to the mirror plane y = 0 (as can be determined from Fig. 3(b)—right) and thus can be excited with the S-polarized light source.
On the other hand, the electric field of the P-polarized light have the electric field components pointing into x- and z-direction, both possessing even symmetry with respect to the mirror plane y = 0, i.e., invariant under mirror reflection through the plane y = 0. The electric field distribution of the lowest TM mode with the air wavelength of 815 nm is plotted for the Ex and Ez electric field components in Fig. 3(c) in the same manner as in case of the TE mode. The mode possesses the similar symmetry with respect to the mirror plane y = 0 as the P-polarized light source and thus the external incident light with this polarization can couple into the mode.
Also the higher order modes will be either even or odd with respect to the mirror plane y = 0 and, as it follows from the discussion above, they will be excited either with P- or S-polarized light, respectively.
A short video of the normally incident light being coupled into the TE leaky mode of the 2D PhC slab was created in order to give a better insight into the physics involved. The video is part of Supplementary Information.
The effect of the material periodicity of the NCD PhC slab on luminescence of quantum dots on its surface was investigated using silicon nanocrystals (SiNCs). Their PL emission spectrum overlaps with spectrally broad leaky modes of the PhC. Powder of the SiNCs (preparation details in Ref. 14) consisting of small Si clusters was drop-casted on the diamond PhC forming a very thin layer (< 20 nm thick). The SiNCs were excited by an external laser source (355 nm, 8 ns pulses) from a non-resonant angle. (If the laser were coupled resonantly into the structure, the excitation field in the vicinity of the PhC would be strongly enhanced, which would cause burning of the NCs.) The detection of PL from the SiNCs was performed using two different detection setups, either through the substrate (like during the transmission measurements—setup 1) or directly from the front side of the sample (setup 2), i.e. from the side where the SiNCs were placed, in the direction normal to the PhC plane (θ = 0°) with the solid detection angle of ~ 1°.
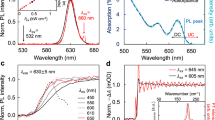
The signals measured in setups 1 and 2 are plotted in Fig. 4 in comparison with the typical spectrum of the SiNCs drop-casted on a thick quartz substrate (thus not modulated by the Fabry–Pérot interferences). All curves in Fig. 4 are normalized to the signal maximum in order to show the PhC impact on the shape of the PL spectra. Moreover, the non-normalized spectra cannot be displayed due to the fact that distribution of the SiNCs on the sample surface was not homogeneous.
Photonic crystal effect on PL of the QDs (SiNCs) on the PhC surface.
PL detected from behind (setup 1) and from the front side of the sample (setup 2) compared to the typical SiNCs spectrum is plotted. All spectra are normalized to the maximum. The black arrows indicate spectral position of leaky resonances.
The PL spectrum detected through the substrate (setup 1) shows strong resonant dips at the spectral positions of leaky modes (~750 nm, ~625 nm, ~530 nm) because part of the light emitted from the SiNCs, heading towards the substrate, is partly coupled to the leaky modes of the structure and interacts with the periodic material modulation in a very similar way as the incident light during transmission measurements does. On the other hand, PL spectrum detected directly from the top of the SiNCs on the PhC surface (setup 2) exhibit peaks at the wavelengths of the leaky modes causing the change of the spectral shape of the typical PL signal. The overall maximum of the signal is up-shifted to the ~ 625 nm and other broad peaks arise at around 750 and 530 nm. The mechanism causing the change of the PL spectrum is very similar to the effect which causes maxima in the PhC reflection spectrum at spectral position of leaky modes as explained in Introduction. However, as it is in more detail explained below, due to the existence of absorption and scattering mechanisms in nano-diamond, the resonance at 625 nm is in the setup 2 PL less pronounced than in the setup 1 PL (Fig. 4).
The influence of optical losses on the transmission and reflection spectra is demonstrated by computing the spectra for the case of normal light incidence on the PhC sample surface. The losses are simulated such that the imaginary part κ of the refractive index is set to be positive. The results of the simulation for the case of κ = 0, 0.001, 0.01 are plotted in Fig. 5. Also the absorption defined as 1–transmission–reflection efficiency is plotted. Obviously, the absorption is zero for the case of κ = 0 (Fig. 5(a)) and resonances can be recognized at the spectral position of leaky modes—Fano-like shaped maxima in the reflection and minima in the transmission spectra. In the case of κ = 0.001 (Fig. 5(b)), the presence of the absorption mechanism causes noticeable reduction of the reflected intensity at the position of the resonance, however, the transmission efficiency changes only negligibly. This is the reason why the resonances in the PL spectrum of the SiNCs on the PhC surface are less pronounced if the detection is performed from the front of the sample (i.e., reflection-like measurement) than when the detection applies from behind of the sample (i.e., transmission-like measurement). In the case of very high losses (κ = 0.01—Fig. 5(c)), the shape of reflection spectrum changes dramatically compared to the case with no or low losses and such a sample is not suitable to manipulate the PL. Losses due to light absorption in diamond defects present in our sample are comparable to the case of κ = 0.001. However, additional losses are present due to light scattering on imperfections of the sample surface and scattering on the NCD grains of which the layer is composed. Taking into account the latter, our experiment corresponds to the regime between the κ = 0.001 and κ = 0.01. The above discussion suggests that it is very important to design dimensions and improve the quality of the final PhC such that the losses are minimized which is the goal of our future study.
The PhC effect on the PL spectrum of the SiNCs is even more evident when the setup 1 PL spectrum is normalized by the typical shape of PL spectrum of the SiNCs as plotted in Fig. 6(a) together with the computed and measured transmission spectra for the zero angle of incidence (θ = 0°). Three main effects can be recognized in this graph. First, due to losses in the real sample, the leaky resonance minima (e.g. at 750 nm) in measured transmission spectrum are shallower than in the simulated one. Second, introducing the SiNCs into voids of the sample causes the change of the PhC properties which leads to slight spectral shift of the minima in the PL signal with respect to the measured transmission minima. However, the shift is very low which suggests that the photonic properties of the PhC were only negligibly affected by the presence of the SiNCs, most probably due to very low density of nanocrystals. Third, due to the fact that not all light emitted by the SiNCs is coupled to the PhC, the dips in the red curve in Fig. 6(a) are less pronounced than those in the gray or black curve. Normalized angle-resolved PL spectra detected from behind of the sample and showing the strong interaction of light emitted from the SiNCs with the PhC, are shown in Fig. 6(b). The detection was performed through the substrate and the detection fiber was rotated along the Γ–X crystal direction with the sample being fixed. The detection was not polarization resolved. The spectra were normalized by the spectrum of the SiNCs on thick quartz substrate in order to obtain reasonable contrast between minima and maxima in the signal. Minima occur in the PL spectra due to light coupling into the leaky modes and it is evident that these minima follow very well the photonic bands of the ‘pure’ PhC sample (compare with Fig. 2(a) and (c)).
Normal-incidence spectra comparison and the angle-resolved normalized setup 1 PL.
(a) Comparison of the measured and computed transmission spectra measured at normal incidence to the PhC plane (θ = 0°) with the PL spectrum measured in the setup 1 and normalized by the typical SiNCs spectrum. (b) Angle-resolved PL spectra of the SiNCs on the PhC surface detected along the Γ–X direction and normalized by the typical spectrum of the SiNCs.
The absolute comparison of the signal intensity detected from the SiNCs within the PhC and from the SiNCs on the unpatterned NCD layer (which surrounded the PhC) cannot be done due to the fact that distribution of the SiNCs on the surface of the sample was not homogeneous. However, the above discussion indirectly proves that the PL of the SiNCs on the PhC surface detected from the front side of sample (setup 2) must be in principle enhanced compared to the PL of the SiNCs outside the PhC (provided the NCs are uniformly distributed over the sample) due to the fact that part of the light directed towards the substrate is redirected upwards through interaction with the PhC. Such a PL enhancement mechanism can be applied in biosensing in case a very low concentration of quantum dots as probes must be used.
Discussion
We have experimentally and theoretically characterized photonic properties of the nano-diamond PhC slab seated on the quartz substrate. Excellent agreement between the theory and experiment was obtained for the leaky modes band diagrams for different polarizations and crystal directions which proves that our structure, even though not structurally perfect, exhibits good photonic properties. However, the principal limitation is represented by optical losses owing to the fact that the layer is composed of diamond grains having surface and volume defects. We also verified the ability of the PhC sample to interact with the quantum dots drop-casted on its surface. 2D-periodic pattern allowed to manipulate light emitted from the SiNCs due to the overlap of their emission spectrum with the leaky modes of the structure. As the spectral position of the leaky modes is controlled by dimensions of the PhC, our results can be generalized to light source with an arbitrary emission wavelength. Thanks to the fact that diamond is very hard and sustainable material, sample is not damaged even after few years and maintains its photonic properties. It can also be cleaned very effectively from the species deposited on its surface. Therefore one sample can be used in combination with different light sources if their spectrum overlaps with the PhC leaky modes. Even the combination of light sources emitting different colours could be used simultaneously, if the spectral position of leaky modes was tuned carefully. To conclude, our results open the possibility to manipulate the shape of the PL spectrum of an arbitrary light source and also to shift its PL maximum to a different energy within some reasonable interval around the original maximum.
Methods
Sample preparation
The NCD layer was grown from a diamond powder by microwave plasma-assisted chemical vapour deposition on the quartz substrate (for details see Ref. 15). 2D periodic structure was fabricated employing electron beam litography on the NCD layer coated with electron sensitive polymer. On a periodic matrix prepared in the polymer, a nickel layer was evaporated and processed by lift-off strategy to form a masking matrix. Afterwards, a plasma etching was applied leading into a periodically ordered diamond columns. In the end, the nickel layer was removed (for details see Ref. 11).
Transmission measurements
Transmission measurements were performed with the sample placed on a motorized rotational stage. The rotational stage was computer controlled and allowed to obtain transmission spectrum for the precise angle with relatively small step of 0.3°. The collimated light beam was incident on the sample at the angle θ which was varied from 0° up to 25.2° along the Γ–X and Γ–M crystal directions (see the setup sketched in Fig. 1(b)).
Photonic band diagram and mode profiles simulations
Photonic band diagrams of leaky modes were obtained from the transmission curves at different angles. Transmission curves were computed by using the commercial software package DiffractMOD based on Rigorous Coupled Wave Analysis technique and developed by the RSoft Design Group. Also the reflection and absorption curves were obtained with this method. The electric field profiles of the leaky modes were computed using a conjugate gradient plane-wave expansion method implemented in the MIT Photonic-Bands (MPB) package16.
References
Joannopoulous, J. D., Johnson, S. G., Winn, J. N. & Meade, R. D. Photonic Crystals: Molding the Flow of Light (Princeton University Press, Princeton, 2008).
Johnson, S. G., Fan, S., Villeneuve, P. R., Joannopoulos, J. D. & Kolodziejski, L. A. Guided modes in photonic crystal slabs. Phys. Rev. B 60, 5751–5758 (1999).
Wierer, J. J., David, A. & Megens, M. M. III-nitride photonic-crystal light-emitting diodes with high extraction effciency. Nature Photon. 3, 163–169 (2009).
Wiesmann, C., Bergenek, K., Linder, N. & Schwarz, U. T. Photonic crystal LEDs – designing light extraction. Laser & Photon. Rev. 3, 262–286 (2009).
Fan, S. & Joannopoulos, J. D. Analysis of guided resonances in photonic crystal slabs. Phys. Rev. B 65, 235112 (2002).
Astratov, V. N. et al. Photonic band-structure effects in the reflectivity of periodically patterned waveguides. Phys. Rev. B 60, R16255–R16258 (1999).
Pacradouni, V. et al. Photonic band structure of dielectric membranes periodically textured in two dimensions. Phys. Rev. B 62, 4204–4207 (2000).
Ganesh, N. et al. Enhanced fluorescence emission from quantum dots on a photonic crystal surface. Nature Nanotech. 2, 515–520 (2007).
Rosenblatt, D., Sharon, A. & Friesem, A. A. Resonant grating waveguide structures. IEEE J. Quantum Electron. 33, 2038–2059 (1997).
Rybin, M. V. et al. Bragg scattering induces Fano resonance in photonic crystals. Phot. Nano. Fund. Appl. 8, 86–93 (2010).
Ondič, L. et al. Effective extraction of photoluminescence from a diamond layer with a photonic crystal. ACS Nano 5, 346–350 (2011).
Ondič, L. et al. Enhanced photoluminescence extraction efficiency from a diamond photonic crystal via leaky modes. New J. Phys. 13, 063005 (2011).
Paddon, P. & Young, J. F. Two-dimensional vector-coupled-mode theory for textured planar waveguides. Phys. Rev. B 61, 2090–2101 (2000).
Dohnalová, K. et al. White-emitting oxidized silicon nanocrystals: Discontinuity in spectral development with reducing size. J. Appl. Phys. 107, 053102 (2010).
Kromka, A. et al. Formation of continuous nanocrystalline diamond layers on glass and silicon at low temperatures. Chem. Vap. Deposition 14, 181–186 (2008).
Johnson, S. G. & Joannopoulos, J. D. Block-iterative frequency-domain methods for Maxwell’s equations in a planewave basis. Opt. Express 8, 173–190 (2001).
Acknowledgements
This work was supported by the GAAV (Grants No. IAA101120804, KJB100100903, M100100902), GAUK (Grants No. 73910 and SVV-2012-265306), GACR (Grants No. P205/10/0046 and P108/11/0794).
Author information
Authors and Affiliations
Contributions
L.O. performed the experiments. O.B., M.V. and A.K. designed and prepared the sample. L.O. and J.Č. performed simulations. L.O. and I.P. analysed the data and wrote the article. All authors discussed and reviewed the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Video 1
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/
About this article
Cite this article
Ondič, L., Babchenko, O., Varga, M. et al. Diamond photonic crystal slab: Leaky modes and modified photoluminescence emission of surface-deposited quantum dots. Sci Rep 2, 914 (2012). https://doi.org/10.1038/srep00914
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00914
This article is cited by
-
Machine learning classification for field distributions of photonic modes
Communications Physics (2018)
-
Silicon nanocrystal-based photonic crystal slabs with broadband and efficient directional light emission
Scientific Reports (2017)
-
A programmable nanoreplica molding for the fabrication of nanophotonic devices
Scientific Reports (2016)
-
Photonic crystal traps THz waves
Nature Photonics (2014)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.