Introduction

Precise timekeeping, dissemination and synchronisation have been some of the most important technological tasks for several centuries1,2. No later than Harrison's time, it was realised that precise time-keeping devices (chronometer) having the same stable frequency and precisely synchronised can have important applications in navigation. In modern times, satellite-based global positioning and navigation systems such as the GPS use the same principle. Here, the entire system shares one common clock frequency and one common, highly synchronised system time. The entire system's time is often synchronised at the nanosecond accuracy level.

With the advances in modern atomic timekeeping technology such as optical clocks3,4, ultra-high precision frequency dissemination and time synchronisation technology have become even more important. Sometimes, the dissemination of frequency alone is sufficient for applications such as the comparison of atomic frequency standards between different research laboratories5,6 and the comparison of definitions of relevant physical constants (e.g., metre, candela and ampere). Throughout the past decade, different frequency dissemination schemes based on fibre links have been proposed and demonstrated, including optical frequency dissemination7,8,9,10,11,12, microwave frequency dissemination13,14,15,16,17,18, optical frequency comb dissemination19,20 and the recently reported all-digital radio-frequency dissemination21.

More often, one will need to know the exact time delay between these remote locations to precisely synchronise the clocks. This is the case and the basic requirement for a global navigation satellite system (GNSS)22, very long baseline interferometry (VLBI)23 and the Deep Space Network24. Occasionally, timing dissemination alone can also fulfil some applications and different time dissemination schemes have also been proposed and demonstrated25,26. This type of synchronisation, however, can cause problems over longer times. For example, if two clocks are left running alone after an initial synchronisation, over a period of free-running time τ, they will show a timing uncertainty relative to each other, often proportional to . In other words, the errors will accumulate over time.

In this report, we demonstrate a continuous, precise time and frequency synchronisation system based on the conventional fibre communication network. At the time of submitting this paper, the system has been operating continuously for over four months. By precisely transferring a “local” clock's frequency to a “remote” location, we ensure that the clock rates at the two locations are identical, i.e., the two sites' clocks run at the same rate. Furthermore, by precisely measuring the time delay of the pulsed clock signals' transit between the two locations, we can synchronise these clocks. The method described in this paper can improve the precision of clock synchronisation by 20,000 times over that using satellites and 4,000 times (in one day) over that achievable using the best commercially available hydrogen maser. It may find important applications in radio astronomy, such as in VLBI.

Results

Precise frequency transfer and time synchronisation

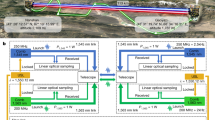
Figure 1(a) outlines the principle of the time and frequency synchronisation system that we have developed. First, the reference frequency from an atomic clock that is to be transferred is boosted to a higher frequency (which leads to a higher signal-to-noise ratio for compensation) using a phase-locking method and is converted to squared-wave timing pulses using a synthesised clock generator. Light from two lasers with different wavelengths carrying the frequency and timing signals are transferred from the local to remote site via the same fibre link. Two wavelength division multiplexers (WDM) are used to combine and separate the modulated laser light at the local and remote sites. Subsequently, part of the laser light carrying the frequency modulation is amplified and sent back via the same fibre. The additional phase noise induced by fibre transmission is then detected and compensated by a phase noise compensation system at the local site, as shown schematically in Figure 1(b). The transfer delay fluctuation is compensated by a similar time delay compensation system, as shown schematically in Figure 1(c). At the remote site, the frequency and timing signals are detected and recovered by two fast photo-detectors. The frequency modulation signal is used to phase-lock the slaved oscillator, which supplies the frequency reference for the slaved clock and the received timing signal is used to synchronise the slaved clock's time to that of the local site.

Figure 1
figure 1

Accurate time and frequency synchronisation system.

(a) The principle of the time and frequency synchronisation system. At the “remote” site, a slaved oscillator is phase locked to the received frequency signal from the “local” site, reproducing the frequency and phase of the oscillator. (b) The phase noise compensation system for frequency dissemination. (c) The time-delay compensation system for time synchronisation.

Full size image

We have performed the experimental demonstration via an urban telecommunication fibre link network connecting Tsinghua University (THU) and the National Institute of Metrology of China (NIM), both in Beijing. The one-way fibre length is 40 km and for convenience, we connect the two parallel 40 km fibre links at the NIM site. Consequently, the local and remote sites of the 80 km fibre link are both placed in the same THU laboratory. Figure 1(b) shows a schematic of the experimental system. The basic concept of the phase noise compensation method depends on detecting the round-trip phase noise of the fibre link and then subtracting half the phase noise from the transmitting signal at the sending (local) site. This way, the frequency and the phase of the “local” site's oscillator are precisely reproduced at the “remote” end. At the “local” site, a stable oscillator containing a voltage-controlled crystal oscillator (VCXO) and a phase-locked dielectric resonant oscillator (PDRO) generates a signal that can be expressed as . Without considering its amplitude, this signal is used as the source of frequency dissemination. In addition, three more oscillators at different frequencies, whose signals can be expressed as , and , are employed and phase-locked to an atomic clock. These ancillary signals satisfy the following conditions:

where ξ is a fixed phase difference. Among them, is the frequency signal to disseminate or to be reproduced at the “remote” site. V1 and V2 are two assistant frequency references used to generate the error signal for feedback control of the phase of V0. When working properly, the signal V0 is sent to the “remote” site and a return signal is sent back. With the assistance of two more signals V1 and V2, its phase is locked to the reference signal Vr, exactly reproducing its frequency and phase at the “remote” site (for details, see the “methods” section).

In the experiment, the microwave signal V0 is used to modulate the amplitude of the light from a 1547 nm, single-mode laser source consisting of an electro-absorption modulated diode laser (EADL), an erbium-doped fibre amplifier (EDFA) and a polarisation scrambler. The modulated optical signal, whose power is lower than the stimulated Brillouin scattering threshold of the 80 km fibre link, is combined with the 1555 nm light from the time delay compensation system by a WDM and then coupled into the 80 km fibre link through an optical circulator. At the “remote” site, after separation from the 1555 nm light by another WDM, the received light is detected by a fast photo-detector, FPD1. The converted signal is used to lock the phase of a slaved oscillator, which can be represented as , where φp is the phase accumulated from the 80 km fibre transmission. To stabilise this phase, a portion of the received light is transmitted back to the “local” site via another optical circulator and detected by a fast photo-detector, FPD2. This way, an oscillatory signal containing twice the phase noise of the fibre transmission, , is obtained at the local site. Through a series of electronic operations, an error signal Ve proportional to the phase difference is obtained. Using this error signal to control V0 will ensure that . Hence, the slaved oscillator reproduces the frequency and phase of the reference oscillator of the local site.

Figure 2(a) shows the measured fractional frequency stability of this fibre dissemination link. The blue line is the result when the fibre link is running freely. It has a stability of 2.4×10−12/s and 1.2×10−14/day. The dark line is the result when the fibre-induced phase noise is actively compensated with a 200 Hz locking bandwidth and the locking bandwidth is mainly determined by the length of the fibre link and the associated electronics. The dissemination stability is improved to 7×10−15/s and 4.5×10−19/day. For comparison, we also show the typical frequency stability (red line) of a commercial active hydrogen maser (H-maser)27. We can clearly see that the phase noise of the compensated frequency dissemination system is much smaller than that of the H-maser itself. More importantly, through active compensation, the stability σy(τ) of the frequency dissemination system shows the typical phase-lock system's time dependence at a rate proportional to 1/τ after a 100 s latency. As shown in Figure 2(b), after 100 s, the phase error between the “local” oscillator and its remote replica is always maintained at the 50 femtosecond level. For comparison, we also show the accumulated time/frequency error for a typical, time-keeping hydrogen maser. Because its fractional frequency stability typically improves at a rate proportional to , the cumulative timing error between two hydrogen masers after initial synchronisation will be approximately 200 ps after one day. The method we have demonstrated here makes a significant improvement in time synchronisation accuracy.

Figure 2
figure 2

Measured stability of the frequency dissemination system.

(a) The measured fractional frequency stability. The blue line is the result of an 80 km free running fibre link, the black line shows the result with phase noise compensation and the red line is the frequency stability of the H-maser used for comparison. (b) The accumulated time (phase) error between the oscillators. The dark line is the accumulated time error between the “remote” and “local” oscillators linked by the 80 km fibre link with compensation. The red line is the accumulated time error between two H-masers.

Full size image

Precision time-delay measurement

Now, with the two remote sites' clock frequencies synchronised, we have ensured that the two sites' clocks beat at the same rate. To synchronise clocks at these remote sites, one will also need to know precisely the time delay of the transmission. Furthermore, because this time delay varies with the equivalent length of the transmission channel, it will need to be compensated for. Figure 1(c) outlines the schematic set-up of this time delay compensation system. A timing signal is generated by a synthesised clock generator (SCG). It generates an output pulse signal with an 80 ps rise and fall time, at a random jitter below 1 ps and at a rate of 500 Hz. This timing signal first goes through a controllable delay (resolution 5 ps) and then modulates 1555 nm laser light. Similar to the method of frequency transfer, the modulated 1555 nm light is sent from the local to remote site along the same 80 km fibre link and partially reflected back. After detection at the local site, a time interval counter (TIC) is used to continuously measure the round-trip delay and gives the delay time T averaged over every 50 measurement samples. Through an iterative algorithm, it gives the error of the single-trip delay Δt and uses it to feedback control a delay generator to compensate for the transfer delay between the “local” and “remote” sites. Using this method, a feedback loop with a 10 Hz locking bandwidth is realised; the result is shown in Figure 3. As shown, the averaged forward transfer delay is maintained at 400,086,216±50 ps between 1 s and 6×104 s. With the stable transfer delay, a slaved clock is then synchronised to that of the local site to an accuracy level of ±50 ps. Currently, the accuracy of the transfer delay measurement and control is mainly limited by the electric noise (jitter) of the equipment, such as the TIC and delay generator used in the experiment. However, in principle, the accuracy of time synchronisation between two remote clocks can be improved to the femtosecond level. One method for achieving this is to rely on the phase of the signals. For example, it is possible to ensure that the accuracy of the “coarse” synchronisation (using pulsed signals) is within half of the wavelength of the frequency transfer. Subsequently, the pulses will be used only to identify the appropriate cycle of the sinusoidal signal. The actual, “fine” synchronisation can rely on the zero-crossing point of the frequency signal. We note that currently the 50 ps accuracy demonstrated here may be sufficient for most applications. Experiments demonstrating finer synchronisation are underway.

Figure 3
figure 3

Measured transfer delay of time-dissemination system.

(a) The transfer delay of the free-running fibre link, showing a fluctuation of approximately 3.2 ns. (b) The time dissemination delay of the compensated fibre link, showing instability below 50 ps. The inset shows the Allan deviation derived from the experimental results.

Full size image

Discussion

In this study, we have demonstrated a highly precise time and frequency synchronisation method via a conventional telecommunication fibre network. We use a simple radio-frequency, amplitude modulation to transfer the frequency and timing signal of an atomic frequency standard. Compared to experiments in which highly precise optical carrier frequencies are transferred7,8,9,10,11,12, the present method is much simpler and hence more reliable. In addition, it is very robust and has been running continuously for several months at the time of writing this report. The precision achieved here is shown to be approximately 20,000 times better than that of using satellites and 4,000 times (1 day) better than that achievable using the best commercially available atomic clocks, which are based on the hydrogen maser. Now, we discuss the feasibility of extending the range of the fibre link to several thousand kilometres and its potential applications to VLBI.

First, having a modular structure, the transfer method can be extended in segments, with relay modules housed in fibre telecommunication relay stations. If N segments are employed, then the overall uncertainty increases only sub-linearly with the overall segment number. Here, σ is the error caused by each segment. This slow increase in cumulative error makes it possible to extend the method over several thousands of kilometres without a significant degradation in accuracy. Secondly, we note that VLBI depends heavily on synchronising remote clocks23 and various relativistic effects have to be carefully considered22. These effects, for example, gravitational frequency shift28, depend on accurately knowing the gravitational potential and other conditions of the local clock. However, clock synchronisation using electromagnetic waves (Einstein synchronisation as demonstrated in this paper) is much simpler and more accurate and does not feature this complication. The clock rate synchronisation method and time delay measurement described in this paper are independent of the gravitational potential at the receiver's location. Therefore, it is hoped that the method demonstrated here will be useful to the radio astronomy community.

Methods

Error signal generation

To generate the error signal used for feedback control, the frequency and phase of the signal, V0, a series of operations are made at the “local” site. We first mix down the signals V1 and V0 to obtain . Then, by mixing signals V2 and V4, we obtain . Subsequently, by mixing these two intermediate signals, Ve1 and Ve2, we obtain the following error signal: . This signal, Ve, is then used for the phase-locked loop (PLL) to feedback-control the phase of V0. Hence, we obtain ω0 = ωr and . Here, for the convenience of discussion, we can neglect the fixed phase difference ξ. By closing the phase-locked loop, the received microwave signal at the “remote” site therefore becomes , exactly reproducing the frequency and phase of the reference frequency standard at the “local” site.

In the present experiment, the microwave frequency used for dissemination is chosen to be 9.1 GHz and the corresponding settings of the main and ancillary oscillators are ωr = 9100 MHz, ω1 = 9095 MHz, ω2 = 9105 MHz and ω0 = 9100 MHz, respectively. These frequencies are chosen for experimental convenience and are by no means unique; moreover, they only need to satisfy the conditions presented in Eq. (1).

Iterative generation of time-delay Δt

To maintain a constant time difference, C, between the “local” and “remote” sites during time dissemination, a variable time delay Δti is added during the i-th compensation cycle. During this cycle, the uncompensated transfer delay from the local to remote site, ti, the compensating value Δti and Ti, the total round-trip delay including the compensation value, satisfy the condition Ti = 2ti+Δti−1, where i = 1,2,3… indicates the cycle number. Furthermore, we have ti+Δti = C. Using these two equations, an iterative algorithm can be obtained to generate the compensating value for the next control cycle. During the experiment, because the controlled delay box cannot give a negative delay value, we preset an initial delay value Δt0 = 20,000 ps for the controlled delay box, which is larger than the range of fluctuation. The value t1 = 400,066,216 ps is the instantaneous single-trip delay value when the locking loop is started. We set C = t1+Δt0 = 400,086,216 ps for the dissemination delay and subsequently maintain this value to within ±50 ps during the experiment. The method assumes that the fibre-link's length fluctuation varies much more slowly than the 0.8 ms two-way transit time and the experimental results confirm this assumption.