Abstract
Many dynamical systems, both natural and artificial, are stimulated by time dependent external signals, somehow processing the information contained therein. We demonstrate how to quantify the different modes in which information can be processed by such systems and combine them to define the computational capacity of a dynamical system. This is bounded by the number of linearly independent state variables of the dynamical system, equaling it if the system obeys the fading memory condition. It can be interpreted as the total number of linearly independent functions of its stimuli the system can compute. Our theory combines concepts from machine learning (reservoir computing), system modeling, stochastic processes and functional analysis. We illustrate our theory by numerical simulations for the logistic map, a recurrent neural network and a two-dimensional reaction diffusion system, uncovering universal trade-offs between the non-linearity of the computation and the system's short-term memory.
Similar content being viewed by others
Introduction
Many dynamical systems, both natural and artificial, are driven by external input signals and can be seen as performing non-trivial, real-time computations of these signals. The aim of this work is to study the online information processing that takes place within these dynamical systems. The importance of this question is underlined by the multitude of examples from nature and engineering which fall into this category. These include the activation patterns of biological neural circuits to sensory input streams1, the dynamics of many classes of artificial neural network models used in artificial intelligence (including the whole field of “reservoir computing”2,3,4,5 as well as its recent implementation using time delay systems6,7,8) and systems of interacting chemicals, such as those found within a cell, that display intra-cellular control mechanisms in response to external stimuli9. Recent insight in robotics has demonstrated that the control of animal and robot locomotion can greatly be simplified by exploiting the physical body's response to its environment10,11. Additional systems to which our theory could apply are population dynamics responding to, e.g., changes in food supply, ecosystems responding to external signals such as global climate changes and the spread of information in social network graphs. All of these exemplary systems display completely different physical implementations.
We present a general framework that allows to compare the computational properties of a broad class of dynamical systems. We are able to characterize the information processing that takes place within these systems in a way which is independent of their physical realization, using a quantitive measure. It is normalized appropriately such that completely different systems can be compared and it allows us to characterize different computational regimes (linear vs. non-linear; long vs. short memory).
Some initial steps in this direction are provided by the linear memory capacity introduced in12 (later theoretically extended to linear systems in discrete time13 and continuous time systems14 and using Fischer information15). Although it has been argued that short-term memory of a neural system is crucial for the brain to perform useful computation on sensory input streams15,16, it is our belief that the general paradigm underlying the brain's computation cannot solely rely on maximizing linear memory. The neural circuits have to compute complex non-linear and spatio-temporal functions of the inputs. Prior models focusing on linear memory capacity in essence assumed the dynamic system to only implement memory, while the complex non-linear mapping is off-loaded to an unspecified read-out mechanism. We propose to endow the dynamic system with all the required computational capacity and use only simple linear read-out functions. The capacity measures we introduce are therefore of great interest since they quantify all the information processing that takes place within the dynamical system and don't introduce an artificial separation between linear and non-linear information processing.
One of the startling results of this work with potentially far reaching consequences is that all dynamical systems, provided they obey the condition of having a fading memory17 and have linearly independent internal variables, have in principle the same total normalized capacity to process information. The ability to carry out useful information processing is therefore an almost universal characteristic of dynamical systems. This result provides theoretical justification for the widely used paradigm of reservoir computing with a linear readout layer2,3,4; indeed it confirms that such systems can be universal for computation of time invariant functions with fading memory.
We illustrate the versatility of our approach by using numerical simulations on three very different dynamical systems: the logistic map, a recurrent neural circuit and a two-dimensional reaction diffusion system. These examples allow us to uncover the (potentially universal) trade-off between memory depth and non-linear computations performed by the dynamic system itself. We also discuss how the influence of noise decreases the computation capacity of a dynamical system.
Results
Dynamical systems
The dynamical systems we consider are observed in discrete time  . They are described by internal variables xj(t), j ∈ J, being the set of indices of all internal variables. The set J may be finite or (enumerably or continuously) infinite.
. They are described by internal variables xj(t), j ∈ J, being the set of indices of all internal variables. The set J may be finite or (enumerably or continuously) infinite.
The internal variables are driven by external signals u(t) ∈ UK which can have arbitrary dimensionality. Typical examples for the set U include a discrete set, or subsets of  such as the unit interval or the whole real line
such as the unit interval or the whole real line  . When studying a dynamical system, we do not necessarily have access to all the dynamical variables x(t). This corresponds to experimental situations where many variables may not be measurable and is also the case if the number of dynamical variables |J| is infinite. We therefore assume that we can only access the instantaneous state of the system through a finite number N of the internal variables: xi(t), i = 1, …, N. Note that we use the term internal variables throughout the paper for easy of notation. The theory however also holds if we cannot directly observe the internal states, but only have access to them via N observation functions. An important special case is when the dynamical system comprises a finite number |J| = N of dynamical variables and we have access to all of them.
. When studying a dynamical system, we do not necessarily have access to all the dynamical variables x(t). This corresponds to experimental situations where many variables may not be measurable and is also the case if the number of dynamical variables |J| is infinite. We therefore assume that we can only access the instantaneous state of the system through a finite number N of the internal variables: xi(t), i = 1, …, N. Note that we use the term internal variables throughout the paper for easy of notation. The theory however also holds if we cannot directly observe the internal states, but only have access to them via N observation functions. An important special case is when the dynamical system comprises a finite number |J| = N of dynamical variables and we have access to all of them.
The system evolves according to an evolution equation of the form:

with Tj the mapping from input and previous state to the j'th current state. We denote a dynamical system with the evolution law eq. (1) by the capital letter X.
In order to evaluate the performance of the system in a standardized way and to make analytical derivations tractable, we will take the inputs u(t) to be independent and identically drawn from some probability distribution p(u). It should be noted that in many, if not all, real world situations the inputs are not i.i.d. Most of the theory should also hold for the non-i.i.d. case, but this significantly complicates the construction of a basis for the Hilbert space defined in Definition 5. However our aim is to characterize the dynamical system itself. By taking the inputs to be i.i.d. we eliminate as much as possible any observed structure originating from the inputs, so that any measured structure will be due to the dynamical system itself. The distribution p(u) can be chosen according to what is most relevant for the dynamical system under study.
In order to study this dynamical system experimentally, we proceed as follows. First the system is initialized in an arbitrary initial state at a time -T′ and is driven for T′ time steps with a sequence of i.i.d. inputs drawn from the distribution p(u). This to ensure that potential initial transients have died out. Next, we drive the system for T timesteps with inputs from the same distribution. During this later phase we record both the values of the inputs u(t) and of the state variables x(t) which will be used to get insight into how information is processed by the dynamical system.
Capacity for reconstructing a function of the inputs
We will denote by u–h(t) = (u(t – h + 1), …, u(t)) the sequence of h previous inputs up to time t. It follows that u–∞(t) = (…, u(t – 2), u(t – 1), u(t)) is the left infinite sequence of all previous inputs up to time t. We will often consider functions of a finite number h, or an infinite number of time-steps (the latter corresponding to the limit T, T′ → ∞). We often wish to refer to a sequence of inputs without referring to the time at which they act, in which case we denote by u–h = (u–h+1, …, u0) ∈ Uh a sequence of h inputs and by u–∞ = (…, u–2, u–1, u0) ∈ U∞ a left infinite sequence of inputs.
Consider a function on sequences of h inputs

Given the recorded inputs u(t), it induces a time dependent function z(t) = z(u–h(t)).
A central quantity in our analysis will be the capacity to reconstruct the function z from the state of a dynamical system using a linear estimator. We introduce this notion as follows. Consider a linear estimator constructed from the observed data

We measure the quality of the estimator by the Mean Square Error (MSE):

where here and throughout we denote by a subscript T quantities that are generated from the measured data. We are interested in the estimator which minimizes the MSE.
Definition 1
The Capacity for the dynamical system X to reconstruct the function z is

where  .
.
The notion of capacity can also be interpreted from the point of view of computation. In this approach, one wishes to use the dynamical system to compute the function z(u–h) and to this end one uses, following the ideas introduced in reservoir computing2,3,4, the simple linear readout eq. (3). The capacity C[X, z] measures how successful the dynamical system is at computing z. Note that this capacity is essentially the same measure that was introduced in12 when z(t) = u(t – l) is a linear function of one of the past inputs. The main difference with the notation of12 is the treatment of a possible bias term in eq. (3). This corresponds to writing  and is equivalent to introducing an additional observation function xN+1(t) = 1 which is time independent. In what follows we do not introduce such a bias term, as this makes the statement of the results simpler. We discuss the relation between the two approaches in the supplementary material.
and is equivalent to introducing an additional observation function xN+1(t) = 1 which is time independent. In what follows we do not introduce such a bias term, as this makes the statement of the results simpler. We discuss the relation between the two approaches in the supplementary material.
We note several properties of the capacity:
Proposition 2
For any function z(t) and any set of recorded data x(t), t = 1, …, T the capacity can be expressed as

where  denotes the time average of a set of data and
denotes the time average of a set of data and  denotes the inverse of the matrix 〈xixj〉T. If 〈xixj〉T does not have maximum rank, then
denotes the inverse of the matrix 〈xixj〉T. If 〈xixj〉T does not have maximum rank, then  is zero on the kernel of 〈xixj〉T and equal to its inverse on the complementary subspace and
is zero on the kernel of 〈xixj〉T and equal to its inverse on the complementary subspace and
Proposition 3
For any function z and any set of recorded data, the capacity is normalized according to:

where CT [X, z] = 0 if the dynamical system is unable to even partially reconstruct the function z and CT = 1 if perfect reconstruction of z is possible (that is if there is a linear combination of the observation functions xi(t) that equals z(t)).
Note that CT [X, z] depends on a single set of recorded data. The computed value of the capacity is therefore affected by statistical fluctuations: if one repeats the experiment one will get a slightly different value. This must be taken into account, particularly when interpreting very small values of the capacity CT. We discuss this issue in the supplementary material.
The capacity is based on simple linear estimators  . For this reason the capacity characterizes properties of the dynamical system itself, rather than the properties of the estimator. Consider for instance the case where z[u–h] = u–3 is the input 3 time steps in the past. Because the estimator is a linear combination of the states xi(t) of the dynamical system xi at time t, a nonzero capacity for this function indicates that the dynamical system can store information in a linear subspace of x(t) about the previous inputs for at least 3 time steps. Consider now the case where z[u–h] = u–2u–3 is a nonlinear function of the previous inputs (in this case the product of the inputs 2 and 3 time steps in the past). Then a nonzero capacity for this function indicates that the dynamical system both has memory and is capable of nonlinear transformations on the inputs, since the dynamical system is the only place where a nonlinear transformation can occur. We therefore say that if CT (X, z) > 0, the dynamical system X can, with capacity C(X, z), approximate the function z.
. For this reason the capacity characterizes properties of the dynamical system itself, rather than the properties of the estimator. Consider for instance the case where z[u–h] = u–3 is the input 3 time steps in the past. Because the estimator is a linear combination of the states xi(t) of the dynamical system xi at time t, a nonzero capacity for this function indicates that the dynamical system can store information in a linear subspace of x(t) about the previous inputs for at least 3 time steps. Consider now the case where z[u–h] = u–2u–3 is a nonlinear function of the previous inputs (in this case the product of the inputs 2 and 3 time steps in the past). Then a nonzero capacity for this function indicates that the dynamical system both has memory and is capable of nonlinear transformations on the inputs, since the dynamical system is the only place where a nonlinear transformation can occur. We therefore say that if CT (X, z) > 0, the dynamical system X can, with capacity C(X, z), approximate the function z.
In summary, by studying the capacity for different functions we can learn about the information processing capability of the dynamical system itself. Because the capacity is normalized to 1, we can compare the capacity for reconstructing the function z for different dynamical systems.
Maximum capacity of a dynamical system
Consider two functions z and z′ and the associated capacities CT [X, z] and CT [X, z′]. If the functions z and z′ are close to each other, then we expect the capacities to also be close to each other. On the other hand if z and z′ are sufficiently distinct, then the two capacities will be giving us independent information about the information processing capability of the dynamical system. To further exploit the notion of capacity for reconstructing functions z, we therefore need to introduce a distance on the space of functions  . This distance should tell us when different capacities are giving us independent information about the dynamical system.
. This distance should tell us when different capacities are giving us independent information about the dynamical system.
To introduce this distance, we note that the probability distribution p(u) on the space of inputs and associated notion of integrability, provide us with an inner product, distance and norm on the space of functions  , where
, where  , is the expectation taken with respect to the measure p(u) on Uh. We define the Hilbert space
, is the expectation taken with respect to the measure p(u) on Uh. We define the Hilbert space  as the space of functions
as the space of functions  with bounded norm
with bounded norm  (this is technically known as the weighted L2 space). In the following we suppose that
(this is technically known as the weighted L2 space). In the following we suppose that  and hence
and hence  , is separable, i.e., that it has a finite or denumerable basis.
, is separable, i.e., that it has a finite or denumerable basis.
The following theorem is one of our main results. It shows that if functions z and z′ in  are orthogonal, then the corresponding capacities CT [X, z] and CT [X, z′] measure independent properties of the dynamical system and furthermore the sum of the capacities for orthogonal state variables cannot exceed the number N of output functions of the dynamical system.
are orthogonal, then the corresponding capacities CT [X, z] and CT [X, z′] measure independent properties of the dynamical system and furthermore the sum of the capacities for orthogonal state variables cannot exceed the number N of output functions of the dynamical system.
Theorem 4
Consider a dynamical system as described above with N output functions xi(t) and choose a positive integer  . Consider any finite set YL = {y1, …, yL} of size |YL| = L of orthogonal functions in
. Consider any finite set YL = {y1, …, yL} of size |YL| = L of orthogonal functions in  ,
,  , l, l′ = 1, …, L. We furthermore require that the fourth moment of the y1 is finite
, l, l′ = 1, …, L. We furthermore require that the fourth moment of the y1 is finite  . Then, in the limit of an infinite data set T → ∞, the sum of the capacities for these functions is bounded by the number N of output functions (independently of h, of the set YL, or of its size |YL| = L):
. Then, in the limit of an infinite data set T → ∞, the sum of the capacities for these functions is bounded by the number N of output functions (independently of h, of the set YL, or of its size |YL| = L):

The fact that the right hand side in eq. (8) depends only on the number of output functions N implies that we can compare sums of capacities, for the same sets of functions YL, but for completely different dynamical systems.
Fading Memory
In order to characterize when equality is attained in Theorem 4 we introduce the notion of fading memory Hilbert space and fading memory dynamical system:
Definition 5
Hilbert space of fading memory functions. The Hilbert space  of fading memory functions is defined as the limit of Cauchy sequences in
of fading memory functions is defined as the limit of Cauchy sequences in  , as h increases, as follows:
, as h increases, as follows:
-
1
If
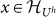 , then
, then 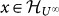 and
and 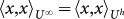 .
. -
2
Consider a sequence
 ,
, 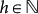 , then the limit limh→∞ xh exists and is in
, then the limit limh→∞ xh exists and is in 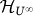 if for all
if for all  > 0, there exits
> 0, there exits 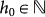 , such that for all h, h′ > h0,
, such that for all h, h′ > h0, 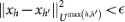 .
. -
3
Conversely, all
 are the limit of a sequence of the type given in 2.
are the limit of a sequence of the type given in 2. -
4
The scalar product of x,
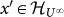 is given by
is given by 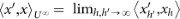 , where xh → x and
, where xh → x and  are any two Cauchy sequences that converge to x and x′ according to 2) above.
are any two Cauchy sequences that converge to x and x′ according to 2) above.
In the supplementary information we prove that  indeed constitutes a Hilbert space and that it has a denumerable basis if
indeed constitutes a Hilbert space and that it has a denumerable basis if  is separable.
is separable.
Definition 6
Fading Memory Dynamical System17. Consider a dynamical system given by the recurrence x(t) = T(x(t – 1), u(t)) with some initial conditions x(–T′) and suppose that one has access to a finite number of internal variables xi(t), i = 1, …,N. This dynamical system has fading memory if, for all  > 0 , there exists a positive integer
> 0 , there exists a positive integer  , such that for all h > h0, for all initial conditions x0 and for all sufficiently long initialization time T′ > h, the variables xi(t) at any time t ≥ 0 are well approximated by the functions
, such that for all h > h0, for all initial conditions x0 and for all sufficiently long initialization time T′ > h, the variables xi(t) at any time t ≥ 0 are well approximated by the functions  :
:

where the expectation is taken over the t + T′ previous inputs.
When the dynamical system has fading memory, its output functions xi(t) can be identified with vectors in the Hilbert space of fading memory functions. Indeed the convergence condition eq. (9) in the definition of fading memory dynamical systems is precisely the condition that the functions  have a limit in
have a limit in  . We can thus identify
. We can thus identify  , where
, where  .
.
The following result states that if the dynamical system has fading memory and if the dynamical variables xi, i = 1, …,N, are linearly independent (their correlation matrix has full rank) and if the function yl constitute a complete orthonormal basis of the fading memory Hilbert space  , then one has equality in Theorem 4:
, then one has equality in Theorem 4:
Theorem 7
Consider a dynamical system with fading memory as described above with N accessible variables xi(t). Because the dynamical system has fading memory, we can identify the output functions with functions xi(u–∞) in  . Consider an increasing family of orthogonal functions in
. Consider an increasing family of orthogonal functions in  with
with  if L′ ≥ L and
if L′ ≥ L and  ,
,  , l, l′ = 1, …,L , such that in the limit L → ∞, the sets YL tends towards a complete orthogonal set of functions in
, l, l′ = 1, …,L , such that in the limit L → ∞, the sets YL tends towards a complete orthogonal set of functions in  . Suppose that the readout functions xi(u–∞) and the basis functions y1(u–∞) have finite fourth order moment:
. Suppose that the readout functions xi(u–∞) and the basis functions y1(u–∞) have finite fourth order moment:  . Consider the limit of an infinite data set T → ∞ and infinite initialization time T′ → ∞. Suppose the correlation matrix
. Consider the limit of an infinite data set T → ∞ and infinite initialization time T′ → ∞. Suppose the correlation matrix  has rank N. Then the sum of the capacities for the sets YL tends towards the number N of output functions:
has rank N. Then the sum of the capacities for the sets YL tends towards the number N of output functions:

This result tells us that under the non-strict conditions of Theorem 7 (fading memory and linearly independent internal variables), all dynamical systems driven by an external input and comprising N linearly independent internal variables have the same ability to carry out computation on the inputs, at least as measured using the capacities. Some systems may carry out more interesting computations than others, but at the fundamental level the amount of computation carried out by the different systems is equivalent.
Connections with other areas
There is a close connection between the sum of capacities for orthogonal functions  and system modeling and in particular Wiener series representation of dynamical systems18,19. Indeed suppose that one wishes to model the dynamical system with variables xi (which for simplicity of the argument we suppose to belong to
and system modeling and in particular Wiener series representation of dynamical systems18,19. Indeed suppose that one wishes to model the dynamical system with variables xi (which for simplicity of the argument we suppose to belong to  ) by linear combinations of the finite set of orthonormal functions
) by linear combinations of the finite set of orthonormal functions  , l = 1, …,L. The best such approximation is
, l = 1, …,L. The best such approximation is  and we can write:
and we can write:  where the errors Δi are orthogonal to the yl. We can then write the sum of the capacities as
where the errors Δi are orthogonal to the yl. We can then write the sum of the capacities as

That is, the extent to which the sum of the capacities for a finite set of orthogonal functions saturates the bound given in Theorem 7 is proportional to how well the dynamical system can be modeled by the linear combinations of these functions. This connection between the degree to which dynamical systems can be used for computation and system modeling has to our knowledge not been noted before.
Reservoir computing was one of the main inspirations for the present work and is closely connected to it. We shed new light on it and in particular on the question raised in2 of characterizing the combinations of dynamical systems and output layer that have universal computing power on time invariant functions with fading memory. In2 it was shown that the system has universal computing power if the dynamical system has the point-wise separation property (a weak constraint) and if the readout layer has the approximation property (a strong constraint). Here we consider simple readout layers which are linear functions of the internal states of the dynamical system, see eq. (3). Our work shows that the combination of a dynamical system and a linear output layer has universal computing power on time invariant functions with fading memory if, in the limit N → ∞, the set of internal states xi, i = 1, …,N, spans all of the Hilbert space  of fading memory functions. This provides a new class of systems which have universal computing power on time dependent inputs. In particular it provides theoretical justification for the widely used paradigm of reservoir computing with linear readout layer20,3,21, by proving that such systems can be universal.
of fading memory functions. This provides a new class of systems which have universal computing power on time dependent inputs. In particular it provides theoretical justification for the widely used paradigm of reservoir computing with linear readout layer20,3,21, by proving that such systems can be universal.
Applications
To illustrate our theory, we have chosen driven versions of three (simulated) dynamical systems. The first is the well-known logistic map22, governed by the equation

with u(t) the input,  and
and  a piecewise linear saturation function, i.e.,
a piecewise linear saturation function, i.e.,

to ensure that 0 ≤ v (t) ≤ 1. The parameter ι can be used to scale the strength with which the system is driven. When not driven, this system becomes unstable for ρ > 3.
The second system is an echo-state network (ESN)20, which can be thought of as a simplified model of a random recurrent neural network. ESNs are very successful at processing time dependent information3,21. The N internal variables xi(t), i = 1 … N, evolve according to the following equation

where the coefficients wij and vi are independently chosen at random from the uniform distribution on the interval [–1, +1] and the matrix wij is then rescaled such that its maximal singular value equals 1. The parameters ρ and ι, called the feedback gain and input gain respectively, can be varied. It was shown in20,23 that, if the maximal singular value of the weight matrix W = [wij] equals one, ESN are guaranteed to have fading memory whenever ρ < 1. In the absence of input, they are unstable for ρ > 1. Because of the saturating nature of the tanh nonlinearity, driving an ESN effectively stabilizes the system dynamics24. In this work we took an ESN with N = 50 variables. A single instantiation of the coefficients wij and vi was used for all calculations presented below.
The last system is a driven version of the continuous-time continuous space two-dimensional Gray-Scott reaction diffusion (RD) system25,26, a one-dimensional version of which was used in9 in a machine learning context. This system consists of two reagents, A and B, which have concentrations axy(τ) and bxy(τ) at spatial coordinates (x, y) and at (continuous-valued) time τ. The reaction kinetics of the undriven system are described by the following differential equations:

Reagents A and B diffuse through the system with diffusion constants da and db, respectively. A is converted into B at rate  . B cannot be converted back into A. A is supplied to the system through a semipermeable membrane, one side of which is kept at a fixed (normalised) concentration of 1.0. The rate with which A is fed to the system is proportional to the concentration difference accross the membrane with a rate constant f (the feed rate). B is eliminated from the system through a semipermeable membrane at a rate proportional to its concentration (the outside concentration is set to 0.0), with rate constant f + k. To drive the system with input signal u (t), we first convert it to continuous time as follows: u (τ) = u (t) , tTS ≤ τ < (t + 1) TS, for a given value the sampling period TS. This signal is then used to modulate the concentration of A outside the membrane:
. B cannot be converted back into A. A is supplied to the system through a semipermeable membrane, one side of which is kept at a fixed (normalised) concentration of 1.0. The rate with which A is fed to the system is proportional to the concentration difference accross the membrane with a rate constant f (the feed rate). B is eliminated from the system through a semipermeable membrane at a rate proportional to its concentration (the outside concentration is set to 0.0), with rate constant f + k. To drive the system with input signal u (t), we first convert it to continuous time as follows: u (τ) = u (t) , tTS ≤ τ < (t + 1) TS, for a given value the sampling period TS. This signal is then used to modulate the concentration of A outside the membrane:

In order to break the spatial symmetry of the system, the modulation strength wxy is randomized accross the system. The concentration of A is observed at N discrete positions (25 in our experiments) by taking one sample per sampling period TS. In our numerical experiments, we keep all parameters da, db, f, k, ι and wxy constant and explore the behavior of the systems as TS is varied. Further details about the RD system are given in the supplementary material.
Total capacity
We now apply our theoretical results to the study of these three dynamical systems. We first choose the probability distribution over the inputs p(u) and the complete orthonormal set of functions yl. We take p(u) to be the uniform distribution over the interval [–1, +1]. As corresponding basis we use finite products of normalized Legendre polynomials for each time step:

where  , di ≥ 0, is the normalized Legendre polynomial of degree di. The normalized Legendre polynomial of degree 0 is a constant,
, di ≥ 0, is the normalized Legendre polynomial of degree di. The normalized Legendre polynomial of degree 0 is a constant,  . The index l ≡ {di} therefore corresponds to the set of di, only a finite number of which are non zero. We do not evaluate the capacity when {di} is the all zero string, i.e., at least one of the di must be non zero (see supplementary material for details of the expressions used). Other natural choices for the probability distributions p(u) and the set of orthonormal functions (which will not be studied here) are for instance inputs drawn from a standard normal distribution and a basis of products of Hermite polynomials, or uniformly distributed inputs with a basis of products of trigonometric functions.
. The index l ≡ {di} therefore corresponds to the set of di, only a finite number of which are non zero. We do not evaluate the capacity when {di} is the all zero string, i.e., at least one of the di must be non zero (see supplementary material for details of the expressions used). Other natural choices for the probability distributions p(u) and the set of orthonormal functions (which will not be studied here) are for instance inputs drawn from a standard normal distribution and a basis of products of Hermite polynomials, or uniformly distributed inputs with a basis of products of trigonometric functions.
Each of the dynamical systems in our experiments were simulated. After an initialization period the inputs and outputs were recorded for a duration T = 106 time steps. When using finite data, one must take care not to overestimate the capacities. According to the procedure outlined in the supplementary material, we set to zero all capacities for which  and therefore use in our analysis the truncated capacities
and therefore use in our analysis the truncated capacities  where θ is the Heaviside function. The value of
where θ is the Heaviside function. The value of  is taken to be
is taken to be  = 1.7 10–4 for ESN,
= 1.7 10–4 for ESN,  = 1.1 10–4 for RD system and
= 1.1 10–4 for RD system and  = 2.2 10–5 for the logistic map (see supplementary material for the rationale behind these choices of
= 2.2 10–5 for the logistic map (see supplementary material for the rationale behind these choices of  ). We have carefully checked that the values we obtain for
). We have carefully checked that the values we obtain for  are reliable.
are reliable.
According to the above theorems, for fading memory systems with linearly independent state variables, the sum of all capacities  should equal the number of independent observed variables N. To test this, in Figure 1 we plot the sum of the measured capacities
should equal the number of independent observed variables N. To test this, in Figure 1 we plot the sum of the measured capacities

as a function of the parameter ρ for logistic map and ESN and for three values of the input scaling parameter ι. For very small input scaling, the capacity CTOT remains close to N up to the bifurcation point of the undriven system and then drops off rapidly. As the input scaling increases, the loss of capacity becomes less abrupt, but its onset shifts to lower values. We attribute this to two effects which act in opposite ways. On the one hand, when the input strength increases, the response of the system to the input becomes more and more nonlinear and is not well approximated by a polynomial with coefficients <  . As a consequence CTOT underestimates the total capacity. On the other hand driving these systems on average stabilizes their dynamics24 and this effect increases with the input amplitude ι. Therefore the transition to instability becomes less abrupt for larger values of ρ.
. As a consequence CTOT underestimates the total capacity. On the other hand driving these systems on average stabilizes their dynamics24 and this effect increases with the input amplitude ι. Therefore the transition to instability becomes less abrupt for larger values of ρ.
The measured capacities  contain much additional information about how the dynamical systems process their inputs. To illustrate this, we have selected a parameter that changes the degree of nonlinearity for each system: the input scaling parameter ι for the ESN and logistic map and the sampling period TS for the RD system and studied how the capacities change as a function of these parameters. In Figure 2 we show the breakdown of the total capacity according to the degree
contain much additional information about how the dynamical systems process their inputs. To illustrate this, we have selected a parameter that changes the degree of nonlinearity for each system: the input scaling parameter ι for the ESN and logistic map and the sampling period TS for the RD system and studied how the capacities change as a function of these parameters. In Figure 2 we show the breakdown of the total capacity according to the degree  of the individual basis functions. The figure illustrates how, by increasing ι or TS, the information processing that takes place in these systems becomes increasingly non-linear. It also shows that these systems process information in inequivalent ways. For instance from the figure it appears that, contrary to the other systems, the ESN is essentially incapable of computing basis functions of even degree when the input is unbiased (we attribute this to the fact that the tanh appearing in the ESN is an odd function).
of the individual basis functions. The figure illustrates how, by increasing ι or TS, the information processing that takes place in these systems becomes increasingly non-linear. It also shows that these systems process information in inequivalent ways. For instance from the figure it appears that, contrary to the other systems, the ESN is essentially incapable of computing basis functions of even degree when the input is unbiased (we attribute this to the fact that the tanh appearing in the ESN is an odd function).
Breakdown of total measured capacity according to the degree  of the basis function as a function of the parameter ι for ESN and logistic map and Ts for RD system.
of the basis function as a function of the parameter ι for ESN and logistic map and Ts for RD system.
The values of ρ (0.95 for ESN and 2.5 for logistic map) were chosen close to the edge of stability, a region in which the most useful processing often occurs 27. The scale bar indicates the degree of the polynomial. Capacities for polynomials up to degree 9 were measured, but the higher degree contributions are too small to appear in the plots. Note how, when the parameters ι and TS increase, the systems become increasingly nonlinear. Due to the fact that the hyperbolic tangent is an odd function and the input is unbiased, the capacities for the ESN essentially vanish for even degrees.
Memory vs. non-linearity trade-off
Further insight into the different ways dynamical systems can process information is obtained by noting that the measured capacities rescaled by the number of observed signals,  , constitute a (possibly sub-normalised because of underestimation or failure of the fading memory property) probability distribution over the basis functions. This enables one to compute quantities which summarize how information is processed in the dynamical systems and compare between systems. We first (following12) consider the linear memory capacity (the fraction of the total capacity associated to linear functions):
, constitute a (possibly sub-normalised because of underestimation or failure of the fading memory property) probability distribution over the basis functions. This enables one to compute quantities which summarize how information is processed in the dynamical systems and compare between systems. We first (following12) consider the linear memory capacity (the fraction of the total capacity associated to linear functions):

where the delta function is equal to 1 iff. its argument is zero and otherwise is equal to 0. Conversely, the non-linearity of the dynamical system is defined by associating to each Legendre polynomial  in eq. (12) the corresponding degree di and to products of Legendre polynomials the sums of the corresponding degrees, i.e., the total degree of the basis function, to obtain
in eq. (12) the corresponding degree di and to products of Legendre polynomials the sums of the corresponding degrees, i.e., the total degree of the basis function, to obtain

In Figure 3 we plot how these quantities evolve for the three dynamical systems as a function of the chosen parameters ι and TS. Unsurprisingly the linearity L and non-linearity NL are complementary, when the first decreases the second increases. We interpret this as a fundamental tradeoff in the way dynamical systems process information: on one end of the scale they store the information but then are linear, while on the other end they immediately process the input in a highly non-linear way, but then have small linear memory.
Influence of noise on the computation in dynamical systems
Real life systems are often affected by noise. The capacities enable one to quantify how the presence of noise decreases the computational power of a dynamical system. Here we model noise by assuming that there are two i.i.d. inputs u and v, representing the signal and the noise respectively. The aim is to carry out computation on u. The presence of the unwanted noise v will degrade the performances. The origin of this degradation can be understood as follows. We can define the Hilbert space  of fading memory functions of u−∞, as well as the Hilbert space
of fading memory functions of u−∞, as well as the Hilbert space  of fading memory functions of v–∞. The dynamical system belongs to the tensor product of these two spaces
of fading memory functions of v–∞. The dynamical system belongs to the tensor product of these two spaces  and a basis of the full space is given by all possible products of basis functions for each space. It is only over the full space that Theorem 7 holds and that the capacities will sum to N. However since v is unknown, the capacities which are measurable are those which depend only on u. The corresponding basis functions project onto a subspace and therefore these capacities will not sum to N. Furthermore, we expect that the more non-linear the system, the larger the fraction of the total capacity which will lie outside the subspace
and a basis of the full space is given by all possible products of basis functions for each space. It is only over the full space that Theorem 7 holds and that the capacities will sum to N. However since v is unknown, the capacities which are measurable are those which depend only on u. The corresponding basis functions project onto a subspace and therefore these capacities will not sum to N. Furthermore, we expect that the more non-linear the system, the larger the fraction of the total capacity which will lie outside the subspace  . This is illustrated in Figure 4 (left panel). We also consider in Figure 4 (right panel) the case where there are K input signals of equal strength and the aim is to carry out computation on only one of them.
. This is illustrated in Figure 4 (left panel). We also consider in Figure 4 (right panel) the case where there are K input signals of equal strength and the aim is to carry out computation on only one of them.
Decrease of total capacity CTOT due to noise, for an ESN with ρ = 0.95, for different values of ι, corresponding to varying degree of nonlinearity.
In the left panel there are two i.i.d. inputs, the signal u and the noise v. The horizontal axis is the input signal to noise ratio in dB ( ). The fraction of the total capacity which is usable increases when the SNR increases and decreases when the system becomes more non-linear (increasing ι). In the right panel there are a varying number K of i.i.d. inputs with equal power, the total power being kept constant as K varies. The capacity for computing functions of a single input in the presence of multiple inputs is plotted. The black line indicates the situation for a strictly linear system, where the capacity for a single input should equal N/K.
). The fraction of the total capacity which is usable increases when the SNR increases and decreases when the system becomes more non-linear (increasing ι). In the right panel there are a varying number K of i.i.d. inputs with equal power, the total power being kept constant as K varies. The capacity for computing functions of a single input in the presence of multiple inputs is plotted. The black line indicates the situation for a strictly linear system, where the capacity for a single input should equal N/K.
Discussion
In the present work we introduce a framework for quantifying the information processing capacity of a broad class of input driven dynamical systems, independently of their implementation. Aside from the fundamental result that under general conditions dynamical systems of the same dimensionality have globally the same computational capacity, our framework also allows testing of hypotheses about these systems.
We have already outlined several insights about the influence of system parameters on the kind of computation carried out by the dynamical system, but the potential implications go much further. While previous work on memory capacities12,13,14,15 seemed to indicate that non-linear networks tend to have bad (linear) memory properties and are thus unsuitable for long-term memory tasks, we now conclude that information is not lost inside these networks but merely transformed in various non-linear ways. This implies that non-linear mappings with memory in dynamical systems are not only realisable with linear systems providing the memory followed by a non-linear observation function, but that it is possible to find a system that inherently implements the desired mappings. Moreover, our framework allows an a-priori evaluation of the suitability of a given system to provide a desired functional mapping, e.g., required for a class of applications.
When considering sequences that are not i.i.d. (as is the case for most real-world data), the construction of an orthonormal function basis, although it exists in theory, is often not feasible. From this perspective, the upper bound on total capacity is largely a theoretical insight. However, by using either an over-complete set of functions or an orthonormal but incomplete set, a lot of useful information about the way a system processes a given type of input data or about the type of processing required for a given task can still be gained.
An avenue for further research with high potential would be to extend the current framework such that the systems can be adapted or even constructed so as to provide certain functional mappings. Also, a study of the effects of coupling several of these systems with known computational properties on the global capacity of the whole would be very interesting in the context of larger real-world dynamical systems.
The framework is applicable under rather loose conditions and thus to a variety of dynamical systems representative of realistic physical processes. It is for instance now possible to give a complete description of the functional mappings realised by neuronal networks, as well as the influence of network structure and even homeostatic and synaptic plasticity on the realised functional mappings. The application of the proposed measures to models for different neural substrates such as the hippocampus or prefrontal cortex could further elucidate their roles in the brain. Additionally, it allows for instance to evaluate the suitability of the physical embodiment of dynamical systems such as robots to inherently perform computation, thus creating an opportunity for simplifying their controller systems. Finally, it provides a novel way to approach systems which are not generally considered to explicitly perform computation, such as intra-cellular chemical reactions or social networks, potentially yielding entirely new insights into information processing and propagation in these systems.
References
Arbib, M. (Ed.) The handbook of brain theory and neural networks, second edition. The MIT Press, Cambridge MA (2003).
Maass, W., Natschläger, T. & Markram, H. Real-time computing without stable states: a new framework for neural computation based on perturbations. Neural Comp. 14, 2531–2560 (2002).
Jaeger, H. & Haas, H. Harnessing nonlinearity: predicting chaotic systems and saving energy in wireless communication. Science 304, 78–80 (2004).
Verstraeten, D., Schrauwen, B., D'Haene, M. & Stroobandt, D. An experimental unification of reservoir computing methods. Neural Networks 20, 391–403 (2007).
Vandoorne, K. et al. Toward optical signal processing using Photonic Reservoir Computing. Optics Express 16(15), 11182–11192 (2008).
Appeltant, L. et al. Information processing using a single dynamical node as complex system. Nat. Commun. 2, 468–472 (2011).
Paquot, Y. et al. Optoelectronic Reservoir Computing. Nat. Sci. Rep. In press (2011).
Larger, L. et al. Photonic information processing beyond Turing: an optoelectronic implementation of reservoir computing. Optics Express 20(3), 3241–3249 (2012).
Dale, K. & Husbands, P. The evolution of Reaction-Diffusion Controllers for Minimally Cognitive Agents. Artificial Life 16, 1–19 (2010).
Pfeifer, R., Iida, F. & Bongard, J. C. New Robotics: Design Principles for Intelligent Systems. Artificial Life 11, 1–2 (2005).
Hauser, H., Ijspeert, A. J., Füchslin, R. M., Pfeifer, R. & Maass, W. Towards a theoretical foundation for morphological computation with compliant bodies. Biol. Cyber. 105, 355–370 (2011).
Jaeger, H. Short Term Memory in Echo State Networks. Fraunhofer Institute for Autonomous Intelligent Systems, Tech. rep. 152 (2002).
White, O., Lee, D. & Sompolinsky, H. Short-term memory in orthogonal neural networks. Phys. Rev. Lett. 92(14), 148102 (2002).
Hermans, M. & Schrauwen, B. Memory in linear recurrent neural networks in continuous time. Neural Networks 23(3), 341–355 (2010).
Gangulia, S., Huhc, D. & Sompolinsky, H. Memory traces in dynamical systems. Proc. Natl. Acad. Sci. USA 105, 18970–18975 (2008).
Buonomano, D. & Maass, W. State-dependent computations: Spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 10(2), 113–125 (2009).
Boyd, S. & Chua, L. Fading memory and the problem of approximating nonlinear operators with Volterra series. IEEE Trans. Circuits Syst. 32, 1150–1161 (1985).
Wiener, N. Nonlinear Problems in Random Theory. John Wiley, New York (1958).
Lee, Y. W. & Schetzen, M. Measurement of the Wiener kernels of a nonlinear system by cross-correlation. Int. J. Control 2, 237–254 (1965).
Jaeger, H. The “echo state” approach to analysing and training recurrent neural networks. Fraunhofer Institute for Autonomous Intelligent Systems, Tech. rep. 148 (2001).
Lukosevicius, M. & Jaeger, H. Reservoir computing approaches to recurrent neural network training. Comp. Sci. Rev. 3, 127–149 (2009).
May, R. M. Simple mathematical models with very complicated dynamics. Nature 261, 459–467 (1976).
Buehner, M. & Young, P. A tighter bound for the echo state property. IEEE Trans. Neural Netw. 17, 820–824 (2006).
Ozturk, M. C., Xu, D. & Principe, J. C. Analysis and Design of Echo State Networks. Neural Comp. 19, 111–138 (2006).
Gray, P. & Scott, S. K. Sustained oscillations and other exotic patterns of behavior in isothermal reactions. J. Phys. Chem. 89, 22–32 (1985).
Pearson, J. Complex patterns in a simple system. Science 261, 189–192 (1993).
Langton, C. G. Computation at the edge of chaos. Physica D 42, 12–37 (1990).
Acknowledgements
The authors acknowledge financial support by the IAP project Photonics@be (Belgian Science Policy Office) and the FP7 funded AMARSi EU project under grant agreement FP7-248311.
Author information
Authors and Affiliations
Contributions
J.D., B.S. and S.M. designed research, J.D., D.V. and S.M. performed research, all authors analyzed data and wrote the paper.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary material: Information processing capacity of dynamical systems
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Dambre, J., Verstraeten, D., Schrauwen, B. et al. Information Processing Capacity of Dynamical Systems. Sci Rep 2, 514 (2012). https://doi.org/10.1038/srep00514
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00514
This article is cited by
-
Harnessing synthetic active particles for physical reservoir computing
Nature Communications (2024)
-
Interface-type tunable oxygen ion dynamics for physical reservoir computing
Nature Communications (2023)
-
A novel approach to minimal reservoir computing
Scientific Reports (2023)
-
A refined information processing capacity metric allows an in-depth analysis of memory and nonlinearity trade-offs in neurocomputational systems
Scientific Reports (2023)
-
Information Processing Capacity of Spin-Based Quantum Reservoir Computing Systems
Cognitive Computation (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.




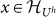 , then
, then 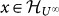 and
and 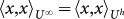 .
.  ,
, 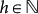 , then the limit limh→∞ xh exists and is in
, then the limit limh→∞ xh exists and is in 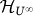 if for all
if for all  > 0, there exits
> 0, there exits 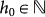 , such that for all h, h′ > h0,
, such that for all h, h′ > h0, 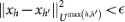 .
.  are the limit of a sequence of the type given in 2.
are the limit of a sequence of the type given in 2. 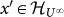 is given by
is given by 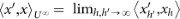 , where xh → x and
, where xh → x and  are any two Cauchy sequences that converge to x and x′ according to 2) above.
are any two Cauchy sequences that converge to x and x′ according to 2) above. 


