Introduction

The liquid-to-solid transition is characterized by the spontaneous breaking of both positional and orientational symmetry, but how this happens microscopically is still a matter of debate1,2,3,4,5,6. Most approaches, like classical nucleation theory (CNT) or density functional theories (DFT)7,8, assume that the crystallization process is primarily controlled by positional ordering, with the liquid regarded as a spatially uniform background where nucleation can occur at any location with an equal probability. However experiments9,10,11 and simulations12,13,14,15 have recently started to point out deviations from the classical picture of crystallization, suggesting that this process could be more complex than previously thought.

We argue that for understanding the origin of such deviations it may be crucial to recognize the role of thermally excited fluctuations in driving the transition from the liquid phase to the crystal phase. Fluctuation effects were first identified in globular proteins and colloidal systems close to a metastable critical point, where crystallization starts with the formation of amorphous high-density aggregates and is followed by the actual nucleation event occurring within these fluctuations16,17,18,19,20: the two-step nucleation scenario. These studies revealed that the coupling between critical concentration fluctuations and density ordering (crystallization) plays a key role in nucleation. Even for a single component liquid, experiments9,10,11 and simulations12,14 have recently showed the importance of density fluctuations in the initial stage of crystallization, which leads to the formation of precursors. Since the two-step nucleation scenario looks valid far20 or even in absence14 of a critical point, it has been suggested that this scenario (in which density fluctuations foreshadow structural ordering) could indeed be a general nucleation mechanism. Independently from the aforementioned two-step scenario, recent simulation works13,21 have pointed out the importance of another type of fluctuations occurring in the supercooled liquid phase: spontaneous critical-like fluctuations of bond orientational order22,23. While the density order parameter (and in general translational order) is a measure of the relative spacing between the neighbouring particles, bond orientational order expresses instead the relative orientation of the (geometrical) bonds between a particle and its neighbouring particles. In both scenarios, thermal fluctuations promote the formation of crystal precursors, i.e. preordered regions which trigger the nucleation process. However, since density and bond orientational ordering proceed simultaneously in the process of crystal nucleation, it has remained elusive how these order parameters are coupled and whether any of the two plays a primary role.

In the present work we will investigate precursors in models of colloidal systems in order to elucidate the microscopic mechanism of crystal formation. We use here the word precursor as a short term for denoting the region of the liquid's free energy basin where nucleation is more likely to occur. We will first rule out the possibility of a two-step process involving densification as the first step towards crystallization. We will show instead that the nucleation process proceeds with the crystalline structures emerging first at liquid-like densities, a process akin to what was reported by some studies of nucleation in molecular systems24,25. By examining the crystallization process in the two dimensional order-parameter space of density and orientational order, we will show that precursor regions are not characterized by locally denser regions, but by locally bond-oriented regions and we will present a novel microscopic explanation of this mechanism. We will show that these precursor regions not only act as seeds of the nucleation process, but also determine the particular polymorph which is to be nucleated from them. This new concept implies that polymorphism is already a property of the metastable liquid state.

It is interesting to note that regions of high bond orientational order have also been identified as responsible for the highly heterogeneous dynamics in deeply supercooled liquids and could be linked to a growing structural length at the origin of the glass transition22,26. A study of the microscopic properties controlling the crystallization of the liquid is thus of utmost importance not only in elucidating the pathway to crystallization, but potentially also to explain how crystallization can be avoided. In this context, we will show that our two-order parameter description provides a thermodynamic justification of Frank's hypothesis27 that icosahedral clusters of particles act as inhibitors of crystallization.

In this Article we concentrate on the homogeneous nucleation process for the simplest nontrivial model of a liquid, hard spheres of diameter σ, by means of computer simulations. This system is ideal for studying crystallization and has already provided tremendous contributions to our basic understanding of crystal nucleation28,29,30. In Supplementary Information we extend the generality of our study by applying the same concepts to very different classes of materials, in particular systems governed by ultrasoft potentials (like polymeric materials) and tetrahedrally coordinated potentials (like water).

Results

Let us start by introducing the order parameters used in this study. We will describe here their basic properties, while for the exact mathematical definition we refer to the Methods section. We will always adopt a microscopic approach, by studying local order parameters (defined at a particle level). Since the liquid-to-solid transition is characterized by both translational and orientational symmetry breaking, we wish to monitor both properties during the crystallization process. A good order parameter for translational order, which expresses the relative spacing between particles in the system, is of course the local density ρi. This is easily computed by means of Voronoi diagrams, which assign to each particle a local volume vi = 1/ρi. To describe orientational order, which expresses the relative orientation between the neighbours around each particle, we use the spherical harmonics analysis introduced by Steinhardt et al.31. We thus define our bond orientational order parameter as q6(i), which is a rotationally invariant scalar defined for each particle i. A closely related order parameter is Q6(i), which is obtained by coarse-graining q6(i) over its neighbours. The importance of Q6 lies in the fact that it is a good order parameter to detect precursor regions, as we will show later. Finally, to address the question whether crystal nuclei emerge from dense precursors, we need an order parameter that distinguishes disordered configurations from crystal-like ones. We call this order parameter S (as for structure): for particle i it goes from a value close to 0 in the liquid-state to a value close to 12 (as the number of neighbours in a close-packed structure) in the crystal state.

Composition of crystals during nucleation and growth

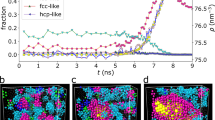
We begin by following 50 spontaneous crystallization events from the metastable state at reduced pressure βpσ3 = 17, where β = 1/kBT and σ is the hard-spheres diameter. Under these conditions nuclei form and dissolve repeatedly, until the appearance of a nucleus which grows over the critical size and eventually spans the whole system. For each configuration we identify crystal particles following the criteria pioneered by Frenkel and co-workers28 (see Methods) and identify individual clusters via a cluster algorithm. Figure 1a shows the average number of particles with local bcc, hcp or fcc coordination within the crystal nuclei, as a function of their size. The vertical dashed line in Fig. 1a, which indicates the average size of the critical nucleus () obtained from umbrella sampling simulations (see Supplementary Information), separates the nucleation and growth regime. Within clusters of size smaller than nc, (66 ± 1)% of the particles are in local fcc coordination. This is markedly different from the ratio for random stacking of hcp and fcc hexagonal planes, nfcc/nhcp ~ 1, which is predicted from the very small bulk free energy difference (around 0.1% of the thermal energy in favour of fcc) between fcc and hcp phases32,33. This behaviour of hard spheres, also pointed out in earlier studies including both experiments2,29,34,35,36 and simulations37,38,39, remains to our knowledge still unexplained and we will show in the following a mechanism which accounts for this unbalance. The inset of Fig. 1a shows the average density of the crystalline particles as a function of the nucleus size. All crystalline phases form at an average number density of ~ 1.06σ−3, higher than the metastable liquid density of ~ 1.02σ−3. The presence of a jump is of course expected for the averaged order parameters (both ρ and q6) at a first-order phase transition. More surprisingly instead, the density at which the smallest crystals start forming is still very far from the bulk density of the stable crystal . Thus the nucleation of the solid phase happens under conditions very far from the bulk solid. As the crystal grows, both the densities of the fcc and hcp phases gradually increase, whereas bcc particles are unable to pack efficiently and hence do not contribute to the cluster growth. Here we note that a bulk bcc crystal is in fact mechanically unstable in hard spheres (meaning that a bulk bcc crystal will immediately transform into a mixture of fcc and hcp crystals).

Figure 1
figure 1

Composition and radial profiles for crystalline nuclei averaged over many independent trajectories at βpσ3 = 17.

(a) Relation between cluster size and polymorphs. Average number of particles for bcc (circles), hcp (diamonds) and fcc (squares) polymorphs as a function of the total crystal size (n). The dashed line grows as the volume, ~ n, whereas the dashed-dotted line grows as the surface, ~ n2/3. The vertical dashed line indicates the critical nucleus size nc, which separates the nucleation regime (the tint blue colour region) and the growth regime. The inset shows the average density of particles belonging to the different polymorphs and the continuous line the average density of the liquid phase. Also shown are two examples of snapshots of crystal nuclei from the computer simulations, at sizes n = 40 (left) and n = 220 (right). The particles are coloured according to the following code: fcc (red), hcp (green) and bcc (blue). (b) Average density profiles as a function of the distance r from the centre of mass of the nucleus. Lines are density profiles for nuclei of sizes between n = 5 and n = 205 (plotted every Δn = 20 with the order given by the arrow); each density profile is averaged over nuclei of sizes n ± 5. Crystals are nucleated at conditions very far from the bulk value, indicated by the dashed horizontal line. The inset shows the density difference Δρ between the centre of the nucleus and the liquid density, as a function of the normalized nucleus size (R/Rcritical). (c) Comparison between the density profile (ρ(r) black line) and the structural order parameter profile (S(r) red line) for the critical nucleus (size n = 80). Both profiles are normalized to be unity in the fcc crystal state and zero in the liquid phase. The inset shows the (S,ρ)-map for nuclei of different sizes (the same as in the panel b). The continuous line is the classical behaviour, while simulation results show that nuclei form in S-ordered precursors and not locally denser precursors.

Full size image

Now we turn to the order parameter profiles of crystal nuclei. Figure 1b shows the averaged radial profiles of ρ(r) for different sizes of the nucleus (indicated by the arrow). The density profiles gradually increase as the nucleus becomes bigger, but still do not reach the bulk values even for sizes much larger than the critical nucleus size. This is in stark contrast to the prediction of classical nucleation theory (CNT), according to which critical nuclei share the same thermodynamic properties of the bulk solid phase. Such deviations from CNT was predicted by non-classical approaches24,40,41,42. Contrary to a two-step scenario, where densification foreshadows structuring14,20, we find no such an indication, as shown in the inset of Fig. 1b, where the density gap Δρ between the nucleus and the liquid phase is displayed for different radii R/Rcritical (normalized to the value of the critical radius). The density of the nucleus grows continuously from the liquid, with an almost linear relationship between Δρ and the nucleus size R.

Figure 1c shows both the density radial profile ρ(r) and the profile of the structural order parameter S(r) for critical nuclei (n ~ 80). Both profiles are normalized as to be unity in the pure fcc crystal and zero in the bulk liquid phase. Going from the liquid phase (r = ∞) to the centre of the nucleus (r = 0) we see that the nucleus first develops some structural order at liquid-like densities and only later does the density increase as well. At the centre of the nucleus both the structural order parameter and the density are far from their bulk values, but density is lagging behind the development of structural order. The inset shows the (S,ρ)-map for nuclei of different sizes. The continuous line is the classical behaviour, while simulation points always fall in the region of structured precursors and not locally denser precursors. We note that the gradual increase of structural order is rather similar to that reported in Ref.24, where the structural order profile grows both its height and range simultaneously. It may be worth noting that the result in Ref.24 is derived from a one-order-parameter DFT model, where a perfect decoupling of structural order from density is implicitly assumed. The introduction of a coupling between density and structural order in the same type of model leads instead to the saturation of both structural and density order at the first stages of nucleation17,40. This is an interesting point to be studied since, as described later, our results suggest indeed a weak coupling between the two types of order parameters. In relation to this, we also note that translational order in DFT is not the same as bond orientational order: the former is specific to solid-type fluctuations, but the latter can be linked to both liquid-type and solid-type fluctuations.

In conclusion we have found no signs of the two-step process involving enrichment at constant size and then growth, contrary to some theoretical predictions14,20,42. We rather find that the density increase is foreshadowed by the prestucturing of the nucleus. This lagging of densification behind structuring is similar to the results of previous nucleation studies in Lennard-Jones systems8,17,25,40, but with the difference that in these studies both density and structural order are already saturated to the equilibrium values when the nucleus size slightly exceeds the critical size, whereas not in our case (see Fig. 1b and c). Moreover the prestructuring prior to densification has always been ascribed to the low compressibility of the liquid phase (see, e.g., Ref.8). In the next section we will show instead that density fluctuations in the liquid and crystal phase overlap to a large extent and that the prestructuring of the nucleus is rather due to the development of orientational order, as the true first step towards crystallization.

Interplay between density and bond orientational order

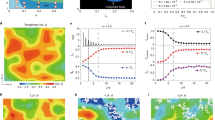
To explain the nucleation pattern unveiled in the previous section, we will address the question of how density (ρ) and orientational order (q6) are coupled. In Fig. 2a we display (ρ,q6)-maps for the metastable liquid (before the appearance of the critical nucleus) at different pressures. We average separately for particles identified as liquid (liquid branch, dashed line) and crystal (crystal branch, lines with symbols) (see also Fig. S1b in Supplementary Information). By comparing the relative position of the two branches in the (ρ, q6)-map it is easy to spot the regions of stability of each phase: the stable branch lies below the metastable branch, having higher orientational order at fixed density (or conversely, the stable phase can reach the same degree of orientational order at lower packing). Let us start by examining the system at reduced pressure βpσ3 = 11. This pressure is just below the melting pressure, which is βpσ3 = 11.5443. As shown in Fig. 2a, the liquid branch is always located below the crystal branch and it is thus the stable branch for all values of q6 and ρ. This result is of course the expected one, since we are before the melting line. What is surprising is that we are able to determine the relative position of the system with respect to the melting line by simply looking at its (ρ, q6) map, without resorting to free energy calculations. And again as expected, as we increase the pressure a crossover between the two branches appears, with the crystal branch gaining stability. For clarity we will focus on the curves at βpσ3 = 17, which is the same pressure at which we obtained our Fig. 1. At low ρ and q6 the liquid branch is the stable one. The crystal branch remains metastable until it reaches a plateau of constant ρ, where the crossover with the liquid branch occurs. The value of this plateau is ρ = 1.06σ−3 which is exactly the average density of the onset of crystal formation which we determined in the inset of Fig. 1a. After this plateau the crystal phase thus becomes the stable phase. This means that in the metastable liquid, particles which reach (because of thermal fluctuations) values of q6 and ρ bigger than the crossover values are in local coordination shells that are transforming from liquid to crystal-like. The reason why this process occurs at constant density is clear if we consider the fact that these particles are already embedded in regions of high orientational order. This means that their neighbours are already highly ordered and by means of small local rearrangements are able to attain the symmetry of the crystal (in practice crossing the threshold which we use to identify crystal particles). We show an example of such a microscopic process in the snapshots in Fig. 2a, where small local rearrangements (white arrows) cause a change of the coordination around the central particle from liquid-like (blue) to crystal-like (red), without changing the local density but by increasing significantly the orientational order.

Figure 2
figure 2

Roles of density and bond orientational order in crystal nucleation.

(a) Relation between density (ρ) and bond orientational order (q6) in the metastable liquid for different pressures, βpσ3 = 11, 14, 17. Dashed lines are averages over particles in liquid-like environments, whereas full lines+symbols are averages over those in crystal-like environments. For each pressure, the stable phase is given by the lowest line. For βpσ3 = 11, which is just below the melting pressure βpσ3 = 11.54, the liquid line is always stable against the crystal line. But as the pressure is increased the crystal line crosses the liquid line to become the stable phase. The transition from liquid-like to crystal-like happens at constant density and can be rationalized by the small cage rearrangements (as seen in the snapshots) which are sufficient to promote the transition with very little density change. At higher densities a second crossover occurs and the liquid branch becomes stable again against the crystal-like branch. (b) Probability density for the structural order parameter S in the (Q6, ρ) plane. The number of connected neighbours grows continuously from 0 to 12 from the liquid to the crystal phase. Contour lines are almost parallel to the ρ axis signalling that crystallization is promoted mostly by bond orientational order. Regions of high ρ contain particles in a range of environments from liquid-like to crystal-like, which means that density fluctuations alone are not sufficient to promote crystallization.

Full size image

If we now follow the curve at higher q6 and ρ a surprising result emerges: a second crossover between the crystal and liquid branches makes the liquid branch stable again. The density of this crossover is ρ = 1.107σ−3, which corresponds to a volume packing of (which is also the conventional value which marks the beginning of the glassy state in hard spheres30). This second crossover tells us that at very high q6 and ρ the crystal phase becomes unfavoured again. Note that these are purely static results, not affected by the underlying dynamics. By using bond orientational analysis (see Supplementary Information), the structures responsible for the stability of the liquid branch at high density are easily identified as particles embedded in icosahedral environments. Icosahedral particles belonging to the liquid branch can attain higher densities than the corresponding crystal structures, but due to their fivefold symmetry are not able to attain long range translational order. The second crossover in the (ρ, q6) map tells us thus that crystals have a stability window, which is limited at low densities by disordered configurations (larger configurational entropy of liquid particles) and at high density by clusters with icosahedral structure. We have thus shown that icosahedral particles act as inhibitor to crystallization, as was recently observed in both experiments44,45 and simulations46. This is consistent with a scenario that glass-forming ability is controlled by frustration against crystallization, or the presence of low free-energy local configurations incompatible with the crystal symmetry in a liquid23,26,47,48,49.

We have seen that the crystallization process is driven by the development of orientational order, which explains the prestructuring of the nuclei at liquid-like densities. Precursor regions are thus easily identified by bond orientational order alone. The one disadvantage of q6 is that it also reveals the signal from icosahedral environments of particles. To locate crystal precursors, an effective strategy is to spatially coarse-grain q613,50, thus enhancing the signal from coherent regions (crystal-like) and suppressing it in disordered or icosahedral-like regions. This is the order parameter called Q6, which grows continuously from the liquid branch to the crystal branch. In Fig. 2b we plot, for the metastable liquid (prior to the appearance of the critical nuclei) at pressure βpσ3 = 17, a map in the (Q6, ρ) plane of the structural order parameter S. S(i) quantifies how many first-shell neighbours of particle i have similar local environments: for a disordered liquid we expect S to be null, whereas for a bulk close-packed crystal to be 12, i.e. all neighbours share the same environment. As we can see from Fig. 2b the structural order parameter grows ‘continuously’ from low Q6 to high Q6 values. Contour lines are almost parallel to the ρ axis, meaning that density is only weakly coupled to the increase of crystalline structure. In other words, high density regions encompass all possible values of the S, while high Q6 regions are always the most crystalline. So precursor regions are exclusively controlled by the coarse-grained orientational order parameter and density fluctuations are not sufficient to promote crystallization.

Polymorph selection

Crystals repeatedly appear, grow and melt as represented by the fluctuations in the bond orientational order parameter Q6. Since crystal nuclei appear from regions of high bond orientational order, the study of such regions should provide important information on the forming nuclei. In particular we will show that not only the precursor regions act as seed for crystal growth, but they also determine which polymorph will be nucleated from them. To do so we use the order parameters W4 and W6, which are very useful in the detection of polymorphs. We report their exact definition in the Methods section and just report here their basic properties. W6 is a good order parameter to distinguish between bcc crystals and close-packed crystals (hcp and/or fcc), since it is positive in the former whereas negative for the latter. W4 is instead good to distinguish between fcc crystals (for which it has negative values) and hcp crystals (for which it has positive values). Figure 3a shows the probability distribution for the order parameter W4 in liquid regions having Q6 higher than a fixed threshold, . The W4 distribution was obtained by considering only liquid particles (crystal particles are not included in the histogram) in the metastable state (before the critical nucleus is formed) and the threshold values are always within the liquid distribution. While the metastable liquid has on average a symmetrical distribution around W4 = 0, Fig. 3a reveals that the high Q6 regions have a predominant contribution from negative values of W4, which correspond to the fcc symmetry. Similar histograms are obtained if instead of thresholds one uses small Q6 intervals centered at progressively high values of Q6 (always within the liquid distribution).

Figure 3
figure 3

Mechanism of polymorph selection.

(a) Order parameter W4 for liquid particles having Q6 > 0.25, 0.26, 0.27, 0.28, 0.29, 0.30, 0.31, 0.32 (the order is given by the arrow). As Q6 increases, the regions of high structural order in the liquid are characterized by a growing population of fcc-like clusters. (b) Order parameter W6 for liquid particles having Q6 > 0.27, 0.28, 0.29, 0.30, 0.31, 0.32. As Q6 increases, the distributions move to lower and negative values of W6, thus showing no preference for the bcc symmetry (W6 > 0). Ordering seen in the pair correlation function. (c) Pair distribution function, g(r), for liquid particles having Q6 > 0.25, 0.28, 0.30, 0.32 (the order is given by the arrows). The y axis has been split to display the first maximum of g(r) (the corresponding x scale is on the top axis). Regions of high Q6 clearly show an enhanced shoulder in the second peak of the pair distribution function, which is a precursor to crystallization. (d) Two-body excess entropy s2 (continuous line), calculated for liquid particles with ; the dashed and dotted-dashed lines are instead calculated for liquid particles having W4 < 0 and W4 > 0 respectively. fcc-like particles (W4 < 0) in regions of high Q6 are thus favoured for crystallization over hcp-like particle (W4 > 0).

Full size image

Since we have shown that crystals form from particles of high Q6, the following scenario emerges for the nucleation of hard-sphere crystals: the supercooled liquid develops regions of high orientational order (Fig. 2b), whose symmetry favours the nucleation of the fcc phase (Fig. 3a). Figure 3b plots the probability distribution for the order parameter W6, showing that indeed the regions of high Q6 display no preference for the bcc symmetry (characterized by W6 > 0). Figure 3c displays the radial distribution function, g(r), for the same high Q6 regions. Notably, higher Q6 regions show an enhancement of the shoulder in the second peak of the pair distribution function, which is known to be a structural precursor to the freezing transition51. The fact that regions of high Q6 are more prone to crystallization can also be seen in Fig. 3d, where the two-body excess entropy52,53, s2, is plotted for different values of the threshold . It is known that the two-body excess entropy forms the dominant contribution to the excess entropy, of the order of 85 – 90% in simple monoatomic liquids. Its value is s2 = −6.8 for the metastable liquid and for the bulk crystal. The inset shows that the s2 value indeed rapidly decreases for increasing values of the threshold . Moreover, the dashed and dotted-dashed lines display the values of s2 calculated for particles having W4 < 0 (fcc-like) and W4 > 0 (hcp-like) respectively, demonstrating that there is a large difference in the configurational entropy (at the two-particle level) between particles having fcc and hcp symmetry, the former ones being strongly favoured towards crystallization (the difference between the s2 value of hcp and fcc-like particles is of the order of 1%). This implies that although fcc and hcp have the same free energy in bulk, small clusters of fcc symmetry have a lower free energy (lower configurational, but higher correlational entropy) than those of hcp symmetry.

Discussions

In this Article we have studied the process of crystallization from the perspective of both local translational and bond orientational order. Crystallization has so far been described by translational ordering of the density field. However, our study clearly indicates that symmetry selection due to packing constraint or directional bonding (like in water, see Supplementary Information), which is represented by bond orientational order, plays a key role in the crystallization process. It is bond orientational order and neither density nor translational order that triggers crystal nucleation. Structuring before densification was also reported in Refs.18,25 for molecular liquids, in which the range of the interaction is longer than the size of the constitutive particles. A recent result54 also found structuring prior to densification for flat hard-sphere crystal interfaces. For molecular liquids, the DFT approach showed that the density of the critical nucleus might deviate significantly from the bulk phases and that the compactification of the nuclei has to be accompanied by an increase of their local structure (i.e. lattice periodicity). This nucleation mechanism is often ascribed to the low compressibility of the liquid, which favours structuring prior to densification upon nucleation8. Contrary to this scenario, our results suggest that this behaviour is a consequence of the weak coupling between density fluctuations and bond-order fluctuations, with the latter driving the crystallization process. In other words, it is due to the fact that nuclei form in precursors of high orientational order, where small displacements can considerably increase the order with very little density change (see the pictures in Fig. 2a). The increase in the structural order parameter is thus inherited from a well defined region of the metastable liquid phase space, characterized by having high orientational order. Note that high density regions are not necessarily characterized by high orientational order and thus they alone cannot trigger the nucleation process. The existence of these regions of high density and low orientational order suggests that it is not the low compressibility of the liquid which is responsible for the coupling between density and orientational order.

Moreover we found that regions of high bond orientational order within the metastable liquid not only act as crystal precursors but can also determine which particular crystal polymorph will nucleate from them, even when precritical nuclei (which naturally populate the metastable phase) are disregarded from the analysis. Since the large population of subcritical embryos belongs to the same metastable free energy basin of the liquid (as can be seen for example in Fig. 2b), it is natural to expect that the emergence of polymorphism will be a continuous process starting in the liquid phase. Polymorphism develops together with bond orientational order, highlighting the role of precursor regions in the polymorph selection process. A liquid has orientationally ordered precursor regions which can exist in a variety of crystal symmetries, according to some high-dimensional probability distribution. For hard spheres, the projections of this probability distribution along some reaction coordinates are reported in Fig. 3 and show that precursor regions with the fcc-symmetry are more abundant than hcp-symmetry regions. So if a nucleation event occurs in any of these regions, the crystal environment will reflect the symmetry of the precursor, or the symmetry favoured in a liquid. For hard spheres, the preference towards fcc was pointed out in earlier studies, both experiments2,29,34,35,36 and simulations37,38,39 and can be explained classically neither by Ostwald's step rule nor by the Alexander-McTague scenario55. While correctly pointing to the relevance of metastable states, Ostwald's rule cannot be literally applied to predict the outcome of a nucleation process. Instead, we have shown that the relative abundance of one polymorph over the other depends directly on the liquid-state precursor's composition. This may be related to the scenario proposed by Stranski and Totomanow56, where the embryos that form most readily are those with the lowest free energy barrier to nucleation. Our results suggest that the physical mechanism behind this rule is a matching of bond orientational symmetry between precursor regions and crystals, which leads to the reduction of the free barrier for nucleation (the interfacial energy). To give a more quantitative account of this scenario, we also calculated the pair correlation entropy of precursor regions (Fig. 3), showing indeed an imbalance between the different crystal symmetries. We confirm that this scenario of crystallization and the resulting selection mechanism of polymorphs are also valid for soft spheres (the Gaussian Core model)57 and water (see Supplementary Information). These results could help clarifying the mechanism behind the interplay between crystallization and liquid polymorphism which was recently found for both water58 and silicon59.

Our two-dimensional analysis also unveiled a density range of stability of the crystals which continuously form in the metastable liquid. This range of stability is limited at low densities by the usual disordered liquid configurations and at high densities by fivefold arrangements of particles. This result, obtained from purely static arguments, provides a thermodynamic justification of Frank's hypothesis27 that icosahedral clusters of particles act as inhibitors of crystallization. This finding may enhance our understanding of the nature of a supercooled metastable liquid state and crystallization, possibly shedding light on the interplay between crystallization and vitrification60. Liquid and crystal often have very different densities, due to the translational order of the latter. However, our study reveals that bond orientational order is the first step in the pathway from the liquid to the crystal state and a disconnection of this link by competing orientational orderings or random disorder may be responsible for the avoidance of crystallization, i.e. vitrification (see Fig. 2a and Refs.23,26).

Methods

We study the crystallization process in a system of N = 4000 monodisperse hard spheres of diameter σ by means of isothermal-isobaric (NPT) Monte Carlo simulations. Lengths are given in units of the particle diameter σ and pressure in units of kBT/σ3, where kBT = 1. We place the spheres randomly in a simulation box at packing fraction η = 0.5352 and equilibrate the system at reduced pressure βpσ3 = 17.0. At this pressure the liquid is metastable with respect to crystallization, with a difference in chemical potential between the liquid and solid state of β|Δµ| = 0.54. As shown in39 the free energy barrier between the metastable liquid phase and the crystal phase is and the size of the critical nucleus is . Under this conditions crystallization is a rare event, for which not only long trajectories can be obtained for the supercooled liquid, but also enough nucleation events can be observed spontaneously.

To identify crystal particles we use the local bond-order analysis introduced by Steinhardt et al.31. One first introduces a (2l + 1) dimensional complex vector (ql), which is defined for each particle i as , where l is a free integer parameter, m is an integer that runs from m = −l to m = l, Ylm are the spherical harmonics, is the vector from particle i to particle j and the sum goes over all neighbouring particles Nb(i) of particle i. Since for hard spheres it is known that the stable crystals are the close packed structures we can impose Nb(i) = 12, i.e. we consider only the 12 nearest neighbours (a procedure which is density independent and greatly improves the statistics). From the vectors ql one can construct different invariants and our bond orientational order parameter is one of them, specifically . The vectors ql have been proven to be useful also to identify crystal particles within the liquid. This procedure, first applied to study nucleation by Frenkel and co-workers28, consists of comparing the orientational environments of two neighbouring particles via a scalar product . If the scalar product between two neighbours exceeds 0.7 then the two particles are deemed connected. We then identify particle i as being within a crystal if it is connected with at least 7 neighbours and otherwise within a liquid. The structural order parameter, S(i), of a particle i (which we employed in Fig. 1c and Fig. 2b) simply expresses the number of connected neighbours in a continuous way, i.e. .

To distinguish between the different crystal polymorphs we employ the spatially averaged local bond order parameters introduced in Ref.50. We first define the quantities . Given the previous definition, one can construct the rotationally invariant quantities

and

where the term in parentheses is the Wigner 3 − j symbol (which is different from zero only when m1 + m2 + m3 = 0).

More details about these analyses are given in Supplementary Information.