Introduction

To date, one of the best examples of weak gravity modifications of quantum mechanics is the experiment of Colella, Overhauser and Werner1,2. In that experiment, the interference pattern of a beam of neutrons, split into two legs that travel at different heights in the Earth's gravitational field, was observed. Another possible observable effect that has been discussed in the literature is the decoherence of matter waves through coupling to a fluctuating metric3,4. To obtain a consistent description of experimental findings, it was shown that the Hamiltonian must consist of two parts, the usual kinetic term and a gravitational term. This forms the basis of a sub-class of semi-classical Einstein equations, known as Newton-Schrödinger Hamiltonians5,6.

Here we follow a simplified approach and take the metric tensor to be of the isotropic form: . Under weak gravity, , where ηµν is the Minkowski metric of flat space and is the perturbation given in terms of the potential . In our model, the metric is assumed static. We need then to address the quantum mechanical treatment of the electron. The approach we use is to generalize the standard Hilbert-Schrödinger formalism to curved space-time represented in terms of a metric that depends continuously on the coordinates. In other words, we do not concern ourselves with the quantized nature of the gravitational field itself. This semiclassical approach seems reasonable for weak gravity due to an external source that is not coupled to the motion of the particles under consideration. The generalization of the Klein Gordon equation to curved space-time is done by introducing the covariant derivatives in the Laplacian operator7:

where g = −det(gµν), m is the electron mass, c the speed of light and ψ the electron wavefunction. Upon promoting the metric to an operator status, we construct the Hermitian covariant momentum operator8 as . Extracting the −p0c term from (1) yields the non-relativistic Hamiltonian as

where latin indices are used for the spatial components (with p≡pa), while greek letters are used for 4-vectors. Finally the effect of an external electromagnetic field A(i.e., the probe field in a Thomson scattering experiment) is introduced into the Hamiltonian (2) via a gauge transformation p→p−eA, where e is the electron charge.

The specific form of the coefficients h0 and h1 depends on the chosen metric and limited by the requirement that the Ricci curvature should be zero or second order in the acceleration. In the weak gravity limit we can expand the metric coefficients in terms of exponentials, such that and , where the Rindler metric1 applies for ξ = 0 and the Schwarzschild metric for ξ = −1. The exponential factors in the metric coefficients are associated with a localized gravity. In order to emulate a gravitational-like field in the laboratory we use the principle of conform equivalence whereby the system (electron plus probe field) is equivalently described by a space-time metric which yields the same dynamical behavior. In a terrestrial laboratory, such a metric should not affect the electromagnetic field and the only non-trivial metric with this property is the variable mass metric (h0 = h1).

Results

Let's consider the case of an electron oscillating in the field produced by the superposition of two laser beams with orthogonal polarizations, with vector potential A = A0 + A1 and A0 · A1 = 0. We take A0 to be a strong low-frequency optical laser field in which the motion of the electron can be treated classically, such that , with ω0 the field frequency. Let the field component A1 be a relatively weak perturbative high frequency (x ray) laser field, the effects of which on the electron are treated quantum-mechanically. Hence, , with ω1 ≫ ω0. We can decompose the canonical momentum as , where and v0 = |v0| is the velocity of the electron due to the optical laser field only, which yields that the energy of the electron as . Replacing γ0 with a function of the space-time coordinates alone puts this equation in a form that is conform equivalent to a general relativistic Hamiltonian with metric given by , with acceleration . This transformation can be achieved for a single electron by replacing γ0 with the first integral of the equation of motion in the field A0. What that we have obtained in this way corresponds to the variable mass metric model (ξ = 1), so called because the Hamiltonian form for the energy is the same as that for a particle in Minkowski space-time whose mass varies proportionally to h0 = h1. For a system of many electrons, we assume that the effective extent of the system is small compared with the amplitude of the motion. This means either the electrons occupy a small region or the probed region is small. The underlying idea that dynamical processes confined to one (space) dimension can affect the other dimensions via a distorsion of the metric is not new and has appeared in extended versions of general relativity such as Kaluza-Klein9,10.

Scattering of x-ray photons by electrons accelerated in the field of an optical laser

Our goal is to design an experiment where it may be possible to test some aspects of general relativity in the laboratory by emulating the variable mass metric through the acceleration of electrons in an intense optical laser field (which corresponds to the field A0) and by probing them by scattering of x ray photons (given by the field A1). Thanks to the development of chirped pulse amplification of optical laser light11, state-of-art laser systems can now achieve focused intensities , thus being able to accelerate the electron to unprecedented values:

This poses as an ideal tool to study weak gravity models12,13,14. For the field A1 let's take instead the one generated with a fourth generation source, or Free Electron Laser (FEL)15. Without loss of generality, for the rest of the paper we will replace p1 by p and A1 by A.

For the present, we assume that the scattering takes place on a sufficiently short timescale () and is confined to a region of FEL spot in which the acceleration field is relatively homogeneous. Accordingly, a can be considered to be constant. More importantly, in an accelerated frame, the conservation of particles does not always hold. Indeed, the most prominent manifestation of quantum gravity is that black holes radiate energy at the universal temperature - the Hawking temperature16. This is a quite general fact, not confined to black holes. As shown by Davies, Unruh and Fulling17,18,19, an observer in a uniformly accelerated frame experiences the surrounding vacuum as filled with thermal radiation with temperature K (kB is the Boltzmann constant). However, when mc2, , the change in the number of electrons and x ray photons will be negligible (a restatement of the fact that we are still in the weak field limit, well below the Schwinger limit).

As it is customary, we regard the scattering part of the Hamiltonian to be determined solely by the A† · A term. Indeed, for an ensemble of weakly-coupled free electrons (e.g., an ideal electron gas) the polarization contribution from second order terms involving p · A terms can be neglected. This is particularly true to the scattering of x rays if the FEL photon energy is much higher than the plasma frequency of the electron gas20. Thus the effective interaction Hamiltonian for the scattering of radiation from an ensemble of electrons in a local gravitational field and confined in a volume is

where ρ(r) is the electron density operator and is the Jacobian of the induced metric on the 3-dimensional spatial manifold. We use a second quantized representation for the electromagnetic field,

where is the annihilation operator for a photon in a state of wavenumber k, frequency ω, polarization and is the vacuum permittivity. Such a representation follows directly from Eq. (1) with the variable mass metric when m = 0. Since the variable mass metric only affects particles with a finite rest mass, photons are unaffected by it. We note that in the weak gravity limit, when pair creation is negligible, the vacuum state remains unchanged and the Bogolubov transformation is not required. Consequently the standard representation of the electromagnetic field in Minkowski space-time is applicable.

Calculation of the differential cross section

The double differential scattering cross section for the x ray photons is given in the Born approximation as:

where β (α) refers to the initial (final) electron state, ω = ωi − ωf is the change in x ray photon frequency due to scattering and q = ki − kf the corresponding change in photon wavenumber, the initial (final) polarization and is the density of final states. N is the total number of electrons in the scattering volume. We then obtain (see supplementary information):

where re is the classical electron radius and is the density-density (Van Hove) correlation function21, for particles undergoing collective acceleration a. The coefficient λ depends on the choice of the metric and for the variable mass metric defined above yields λ = 2 (see supplementary information). Eq. (7) is formally identical to the formula describing the scattering of photons from an ensemble of electrons in the absence of a gravitational (or acceleration) field21. The effect of acceleration, however, is to introduce an imaginary component into the scattering wavenumber. The density-density correlation (or dynamical form factor) function is given by21

where , is the spatial Fourier transform of the density operator and 〈…〉 denotes a time average over the scattering process. We also note that Eq. (8) is written in the less common time-symmetric form21, which is more appropriate to non-equilibrium systems. This preserves the reality of the density-density correlation function for any value of k and ω, which is an essential requirement since the differential cross section represents an experimental observable (i.e., the number of scattered photons).

The next step in the evaluation of Eq. (8) is to write the position operator for the j-th electron as rj(t) = rj0(t) + R(t), where rj0 represents the background thermal motion of each electron and R is the superimposed collective motion induced by the optical laser pulse. Without loss of generality, let us assume that we probe the ensemble at the time when all the electrons are at the peak of the laser acceleration (we denote this time as t = 0) and hence, for small times R(t) = at2/2, which can be substituted into Eq. (8). In the case of uniform acceleration, during which the motion of the electrons is assumed to be non-relativistic and ignoring a constant normalization factor, we readily obtain (details provided in the supplementary information)

where S0(q, ω) is the usual equilibrium structure factor calculated at t = 0, with q = Re(k). We notice that for a → 0 we have S(k, ω) = S0(q, ω) as expected.

The case of a dilute electron gas

In order to estimate the relative importance of the acceleration correction to the structure factor, let us consider the case of a weakly interacting electron gas in thermal equilibrium at the temperature T. In this case S0(q, ω) takes a simple Gaussian profile21 and from Eq. (9) we obtain

where,

Eq. (10) also implies that the outgoing photon carries an uncertainty in energy expressed as and is consistent with the energy uncertainty imposed by the motion of the electrons being non-relativistic. Eqs. (7) and (10) are the main result of our work. They show that the scattering of photons from an ensemble of accelerated electrons is seen as if those electrons are in thermal equilibrium at an effective temperature Teff, which depends on the acceleration. Moreover, this effective temperature scales with the metric parameter, λ (or ξ), providing, for the first time, a direct way to determine the validity of the models of quantum mechanics in curved space-time and the specific details of the coupling between classical and quantized fields. Previous work done by solving a generalized form of the Dirac equation in curved space-time has also shown that the metric can have observable effects22. In fact, it was suggested that energy levels shifts in atoms could arise from the local curvature, although at scales not currently achievable in a laboratory.

Discussion

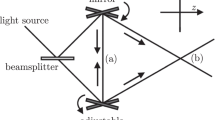
Let us now consider the implication of Eq. (10) in a scattering experiment as laid out in Figure 1. To limit velocity dispersion between the high intensity optical laser and the FEL, the thermal electrons are generated in a ~0.2 mm long channel by ionization of an under-dense low atomic number gas jet (Figure 1), driven by focussing a high energy (~100 J) long-pulse (~1 ns) laser beam. The electron densities will be in excess of ~ 1019 cm−3 and temperatures ~200 eV23. We will now assess the feasibility of measuring the effective temperature within current facilities. We write q2 ≈ 2(ω1/c)2(1 − µ), where µ is the cosine of the scattering angle (µ ≈ 0.96 for 15° scattering angle). In practical units,

Assuming that the acceleration field is produced with an optical laser with intensity I ~ 1019 W/cm2 and the thermal electrons (at T ~ 200 eV) are probed with ω1 ~ 0.5 keV x ray photons in forward scattering geometry (see Figure 1), we get Teff − T ~ 300 eV. This is readily within our experimental capabilities owing to the recent development of Thomson scattering in the x ray regime24,25. Simple estimates indicate that, with ~ 1013 photons/pulse in the FEL beam, we should expect > 40 photons/shot detected. A few shots would then be sufficient for obtaining high quality spectra24.

Figure 1
figure 1

Proposed experimental setup.

A high-energy laser excites a pulsed gas jet creating a plasma with electron density ~ 1019 cm-3. A high-intensity CPA optical laser beam then accelerates the electrons while the FEL probes them with synchronized x ray pulses in a collinear geometry.

Full size image

Ideally, we would perform the experiment to probe electrons scattering from the point of maximum acceleration and zero velocity, which sets the pulse duration of the FEL to less than a femtosecond. Recent developments in free electron laser operations have indeed shown that such short pulse duration in the x ray regime is possible26. At present, the temporal synchronization of optical and x ray pulses has been demonstrated at the few fs level27, but work to reduce it below to ~1 fs is underway28. Limitation in the pulse duration and temporal synchronization would also introduce a superimposed chirp in the scattered light due to the varying Doppler shift of electrons at high velocity and modest acceleration. Since the electrons will oscillate primarily along the direction of the optical laser polarization, this effect can be removed in the measured spectrum by choosing the geometry of the experiment such that the scattering wavenumber, q, is perpendicular to the polarization axis, as shown in Figure 1.

While a high power laser, an FEL, as well as a long pulse high-energy laser beam are not currently available on a single end-station, suggestions for such a facility have been already put forward both at the Linac Coherent Light Source (LCLS) in Stanford (CA) and at the European XFEL in Desy (Germany). Indeed, the scientific case described in this letter is very compelling and our estimates indicate that a direct test of the semiclassical theory of quantum mechanics in curved space-time will become possible.