Abstract
The 2011 Tohoku-oki (Mw 9.1) earthquake is so far the best-observed megathrust rupture, which allowed the collection of unprecedented offshore data. The joint inversion of tsunami waveforms (DART buoys, bottom pressure sensors, coastal wave gauges and GPS-buoys) and static geodetic data (onshore GPS, seafloor displacements obtained by a GPS/acoustic combination technique), allows us to retrieve the slip distribution on a non-planar fault. We show that the inclusion of near-source data is necessary to image the details of slip pattern (maximum slip ~48 m, up to ~35 m close to the Japan trench), which generated the large and shallow seafloor coseismic deformations and the devastating inundation of the Japanese coast. We investigate the relation between the spatial distribution of previously inferred interseismic coupling and coseismic slip and we highlight the importance of seafloor geodetic measurements to constrain the interseismic coupling, which is one of the key-elements for long-term earthquake and tsunami hazard assessment.
Similar content being viewed by others
Introduction
A giant interplate earthquake of magnitude Mw 9.1 occurred on March 11, 2011 at 05:46 UTC (Japan Meteorological Agency, JMA) off the Tohoku coast (Japan) with epicentre at 142.68°E 38.19°N1, at the interface between the Pacific and Okhotsk plates (Fig. 1a). It generated a huge tsunami that devastated the eastern coasts of the Honshu Island and locally inundated up to 5 km inland killing more than 15,000 people2. It also caused a severe nuclear accident at the Fukushima nuclear power plant, whose effects are still under investigation.
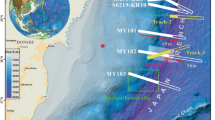
Location map of the 11 March 2011 Mw 9.1 Tohoku-oki earthquake.
a) Red star indicates the epicentre position1. Red and white “beach ball” represents the focal mechanism of this earthquake1. Red triangles indicate the DART stations used in the inversion; b) Yellow, pink and cyan shadow zones are approximated rupture areas of the 869 Jogan, 1896 and 1933 Sanriku-oki earthquakes respectively39. Cyan circles indicate GPS stations onshore, magenta circles the geodetic seafloor observation sites15,16, red triangles the bottom pressure sensors and GPS-buoys (Table S3 in Supplementary Information). White arrow indicates the approximate convergence direction of the Pacific plate (estimated velocity of 9.2 cm/yr54).
Seismological, geodetic and marine observational networks provided unprecedented high-quality recordings of the 2011 Tohoku-oki earthquake. More important, this is the first megathrust event that allowed the collection of offshore near-field data recorded very close to the causative source and to the trench. Tsunami waves were recorded by coastal wave gauges3, GPS-buoys4 and bottom pressure sensors5,6,7,8 close to the Japanese coast off Iwate, Miyagi and Fukushima Prefectures2,9,10,11,12,13 and by Deep-ocean Assessment and Report Tsunami (DART) buoys14 in the open Pacific Ocean, whereas several seafloor instruments measured the coseismic deformation in the shallowest part of the Okhotsk plate15,16; up to 31 m of horizontal coseismic displacement were measured in the epicentral zone by a GPS/acoustic combination technique15,16.
Tsunami waveforms and onshore geodetic data (e.g. GPS, InSAR) are often used to retrieve the slip distribution of great subduction earthquakes17,18,19. Tsunami data improve the resolution on the offshore portion of the subduction interface, whereas onshore geodetic data well resolve the slip distribution on the landward portion of the fault plane. Their combined use thus helps to constrain the slip on the entire fault20,21. In the case of the 2011 Tohoku-oki event the presence of near-source offshore instruments yields a more robust picture of the rupture2,9,10,11,12,13,22,23,24, with important implications both for long-term seismic and tsunami hazard assessment and tsunami warning11,25.
The relation between interseismic coupling (plate convergence fraction that is not accommodated by aseismic sliding) and coseismic slip has been recently studied by many authors and for different great subduction earthquakes19,26,27,28,29,30,31,32. Zones of possible future large earthquakes are those where stress accumulates during the interseismic period26,27,33 and they can be likely identified by mapping the degree of plate coupling. Highly coupled zones will eventually rupture in future earthquakes34 making the estimation of plate coupling a key ingredient in long-term seismic and tsunami hazard assessment. However, even assuming that the imaged coupling remains constant in time, forecasting which parts of the fault will rupture during the next seismic event is still an open issue, since this depends on the fault zone mechanical conditions determined by local heterogeneous pre-stress and frictional properties controlling the dynamic rupture evolution. For example, ruptures in large earthquakes are likely to nucleate in coupled zones but they may propagate also in relatively uncoupled portions of the fault plane extending all the way to the trench35. Large historical tsunamigenic events already occurred in the past off Tohoku (Fig.1b), such as the megathrust earthquakes in 869 (Jogan36,37) and in 1896 (Sanriku38) and an outer-rise event in 1933 (Sanriku39,40). Some authors argue that the 1896 Sanriku earthquake has been characterized by very shallow rupture with destructive effects locally similar to 2011 event. Most of the models of the 2011 Tohoku-oki earthquake slip distribution obtained up to now inverting tsunami, seismic and geodetic data agree in imaging the rupture as characterized by extremely high slip values concentrated in a relatively small area, with the rupture extending up to the trench for most slip models2,9,10,12,13,22,23,24,31,41,42,43,44,45,46,47,48,49.
Models of interseismic coupling obtained inverting onshore geodetic measurements of the interseismic deformation before the 2011 earthquake26,27,50 showed a large locked portion of the subduction zone offshore the Tohoku region. These models then could have suggested the occurrence of a giant megathrust event, even if they feature a relatively low coupling in the shallowest portion of the subduction zone near the trench. This last result can be due to the limited resolution of onshore geodetic data on the shallowest portion of the plate interface near the trench31. This bias can be removed by using data recorded in the very near-field by seafloor instruments that revealed to be very effective to measure the plate motion offshore13,22,23,24,51,52. In other words, the amount of strain accumulation on the shallow part of the megathrust might be better imaged by means of seafloor near-trench observations.
In this study, we perform a joint inversion using tsunami waveforms (DART buoys, bottom pressure sensors, coastal wave gauges and GPS-buoys, Fig. 1) and geodetic data (GPS onshore and seafloor displacements obtained by a GPS/acoustic combination technique15,16, Fig. 1b), to infer the slip distribution of the 2011 Tohoku-oki earthquake. We use realistic fault geometry with variable strike and dip and extend our fault model up to the trench (Table S1 in Supplementary Information). We then discuss the results in the context of long-term earthquake and tsunami hazard assessment along subduction zones, highlighting the importance of very near-source data25.
Results
We solve the inverse problem using a global search technique (the simulated annealing53) following previous studies that used this approach for inverting different geophysical data sets19,21. The resolving power of different combinations of geodetic and tsunami data used here is evaluated with several synthetic checkerboard tests (Fig. S3 in Supplementary Information). The main result emerging from our study is that the use of seafloor observations significantly increases the control on the offshore slip pattern (Figs. S3b,c in Supplementary Information) and that the joint inversion of the whole data set provides a sufficiently homogeneous resolution on the entire fault plane (Fig. S3e in Supplementary Information). The solution of the inverse problem is inherently non-unique and therefore, instead of showing the best fitting model, we compute and show the average slip model calculated over the ensemble of models that satisfactorily fits the data19,21. This will be done for each synthetic test as well as for each of the inversions for the 2011 Tohoku-oki earthquake presented below. The reported model errors (Fig. S6, Tables S2 in Supplementary Information for the slip distribution of the Tohoku-oki earthquake) are the standard deviations of the marginal distributions of the model parameter (slip value).
2011 Tohoku-oki slip distribution
The joint inversion of the whole geodetic and tsunami data sets shows that the rupture area with slip > 10 m extends over a region of about 250×180 km from about 36.5°N to 39.5°N and it is characterized by a main patch of slip (Fig. 2) located up-dip from the hypocenter (~143°E, 38°N), that features a peak slip of about 48 m at a depth of ~13 km (Fig. 2, Table S2 in Supplementary Information). The rupture extends eastward up to the trench with slip values of about 35 m and westward approximately near the Fukushima and Ibaraki regions at a depth of 25 km with slip values close to 10 m (Fig. 2, Table S2 in Supplementary Information).
2011 Tohoku-oki slip model.
Slip distribution for the 2011 Tohoku-oki earthquake obtained from the joint inversion of tsunami and geodetic data. Orange arrows represent the slip direction (rake, Table S2 in Supplementary Information). Thin black contours above the fault plane indicate the interseismic coupling (from 10% to 100%, at 10% intervals) along the megathrust50. Black arrow indicates the approximate convergence direction of the Pacific plate (estimated velocity of 9.2 cm/yr54). Red star as of Figure 1.
The average rake angle on the rupture area is about 91° consistently with the Pacific-Okhotsk plates relative motion54 (Fig. 2). The estimated seismic moment is M0 = 5.28×1022 Nm (using a depth dependent rigidity model55) corresponding to a magnitude Mw = 9.1. The main features of the slip pattern imaged by means of the joint inversion (large and shallow slip up-dip from the hypocenter) are consistent with the results obtained using other kind of geophysical data sets (seismic42,43,49, strong motion47, tsunami2,9 and geodetic data22,45,46, or in several joint inversions10,13,23,24,44,48) at least as regards the long-wavelength rupture features56,57,58, with some differences due to the resolution of each data set and/or fault parameterization.
The predicted tsunami waveforms show a generally good agreement with the observed records (Fig. 3c). Some discrepancies might suggest a more complex rupture history24,41,42,43,45,47,48,49,56,58. In this study, we indeed assume a circular rupture front propagating with a velocity of 1 km/s relying on seismic estimates48,59 because several performed tests (not shown) demonstrated that the data set used here does not allow a robust retrieval of rupture velocity. The overall slip pattern is consistent with the observations indicating a tsunami with two distinct phases. The two pressure gauges TM1-2 and most of the GPS-buoys recorded, after a flatter initiation likely due to rupture of a relatively deep patch12, a shorter period tsunami wave, with a maximum amplitude up to 5–6 meters (Fig. 3c), a dramatic anticipation of the devastating tsunami effects observed along Iwate, Miyagi and Fukushima Prefectures11. The very large slip (up to ~35 m) at shallow depths featured by the model appears sufficient to explain the impulsive character of the Tohoku tsunami12, though with a second order lack of peak amplitude (10% on the average), e.g. at TM1 and TM2 or at DART 21418. The horizontal coseismic displacements at GPS stations are well reproduced, whereas there is some local discrepancy between predicted and observed vertical displacements, which could be due to inaccuracies in the fault position or dip and to the homogeneous half space approximation, as rigidity contrasts may be important for modelling GPS60.
Comparison between observed and predicted data sets.
Comparison between observed (black) and predicted a) horizontal and b) vertical displacements at GPS (red) and geodetic seafloor observation sites (magenta); c) Comparison between the observed (black) and predicted (red) tsunami waveforms; peak value (predicted/observed) in meters is indicated for each station.
The large horizontal displacement (up to 31 m) seen in the offshore geodetic observations used in this work (Figs. 3a,b), including those relatively close to the trench, are predicted satisfactorily. However, even closer to the trench, there are two further sea bottom displacement measurements61 (Fig. S2 in Supplementary Information), indicating a greater horizontal displacement (up to ~70 m), which our model would largely underestimate. We do not attempt to include these data in the inversion for several reasons. We use relatively large subfaults in the elastic homogeneous half space approximation. Then, we are not able to model the inherently 3D fine scale structure of the trench region, with additional complexities such as rigidity contrasts, possible inelastic processes13, the eventual dislocation on a normal branching fault61,62 with a likely consequent extensional regime of the sedimentary wedge, or the eventual contribution of the submarine mass failure evidenced by recent bathymetric surveys63,64. We thus consider our model an accurate and robust long wavelength image of the slip on most of the fault, while it will need a refinement in a narrow band in the trench region, even with the aim to assess the relative importance of additional tsunamigenic mechanisms.
Interseismic coupling and coseismic slip during the Tohoku-oki earthquake
Our model (Fig. 2) suggests that the nucleation of the Tohoku-oki earthquake occurred within a strongly coupled zone (between 70 and 80 %). The overall rupture zone conversely has a limited overlap with the coupling itself, consistently with the results of other studies31. Slip distribution is more elongated in the SW-NE direction and its centroid is displaced toward the trench, featuring up to ~35 meters of slip from about 38°N to 39°N in a zone of relatively low to zero coupling (< 30%). Whether this rupture propagated in a relatively uncoupled zone or, alternatively, the coupling is poorly resolved and higher than expected close to the trench is a matter hard to address. It has been suggested that a classical elastic back-slip accumulation model may not be sufficient to explain the shallow rupture propagation for great subduction earthquakes65. However, the onshore GPS data cannot fully resolve the coupling distribution in the trench region31. This is also shown by our resolution tests (Fig. S3b in Supplementary Information), which further demonstrate that using the seafloor instruments increases the resolution of the offshore slip pattern (Figs. S3b,c in Supplementary Information). We therefore extend this result to the interseismic coupling and we suggest that, using offshore geodetic measurements collected during the interseismic period, would allow us to better constrain the spatial distribution of coupling25.
This can be further investigated by inverting the different geodetic data sets of the Tohoku-oki earthquake. The slip model resulting from the inversion of only the onshore GPS data features a main slip patch concentrated around the hypocenter and a maximum slip amplitude of ~25 meters at a depth of ~25 km (Fig. 4a), consistently to other GPS inversions66,67. This slip model is also correlated to the coupling distribution. However, whereas the horizontal displacements at the GPS onshore stations are very well reproduced (Figs. S4a,b in Supplementary Information), the model is not suitable to explain the large coseismic deformations measured offshore15,16 (Figs. S4a,b in Supplementary Information) and the observed tsunami is dramatically underestimated (Fig. S4c in Supplementary Information). On the other hand, inverting also seafloor coseismic displacements obtained by a GPS/acoustic combination technique15,16 we obtain a shallower (about 15 km of depth) primary patch of slip (Fig. 4b) with larger slip amplitude (~46 meters) at about 38°N and both the inland and offshore horizontal geodetic displacements are well matched (Figs. S5a,b in Supplementary Information). Therefore near-source seafloor instruments are essential to retrieve information about the slip offshore and GPS on land alone are not able to resolve. Even so, the impulsive tsunami component in the near-source (GPS-buoys and TMs) is underestimated (Fig. S5c in Supplementary Information). The present configuration of geodetic data has a sufficient control of the macroscopic (long-wavelength) offshore slip pattern, but can predict only the far-field tsunami (Fig. S5c in Supplementary Information), since the details of coseismic slip pattern are not retrieved. It thus appears also evident the primary role of offshore tsunami data (TMs and GPS buoys) to constrain some features of the slip distribution (Figs. 2,3) which cannot be well resolved by a few offshore geodetic data. This result is also consistent with those of the resolution tests in Supplementary Information (Figs. S3c,d,e). Near source tsunameters are also very important for tsunami warning as their records can be accessible in real-time, more easily than seafloor geodetic measurements, supporting their planned intensive deployment and their integration into the existing Japanese tsunami warning system11,68.
Geodetic Slip models.
a) Slip distribution for the 2011 Tohoku-oki earthquake obtained from the inversion of GPS onshore only. Cyan circles within the upper left inset indicate GPS stations onshore used in the inversion; b) Slip distribution for the 2011 Tohoku-oki earthquake obtained by inverting the whole geodetic data set. Cyan circles within the upper left inset indicate GPS stations onshore, magenta circles the geodetic seafloor observation sites, both used in the inversion. Thin black contours and red star as of Figure 2.
The increase of near-trench resolution determined by offshore geodetic data (as shown in this study for the slip distribution), would extend to the estimation of interseismic coupling if offshore geodetic instruments were used for estimating displacement rates during the interseismic period and of course deployment of additional instruments would further increase the accuracy of coupling estimation. Actually, some previous studies in Japan69,70, though based only on single-point measurements, already showed the potentiality of offshore geodetic instruments. In particular, these coupling estimations are fairly consistent along strike direction with recent coupling distributions50, showing a decrease of coupling departing from Miyagi toward Fukushima. Conversely, coupling off Miyagi is found to increase in the updip direction at least up to a depth of about 20 km on the fault plane and in contrast with the deeper maximum coupling estimated by onshore measurements. This is analogous to our finding that the centroid of the slip distribution moves updip when using also offshore data (Fig. 4). However, getting a comprehensive image of the secular seafloor movement would require a significant improvement of observational capability and continuous measurements52 which would in turn improve our understanding of the physical processes generating megathrust earthquakes and associated tsunamis, as well as our ability to define tsunami scenarios for hazard assessment.
Discussion
The slip distribution of the 2011 Tohoku-oki earthquake is characterized by extremely high slip values (up to ~48 meters) concentrated, despite of the great magnitude (Mw 9.1), in a relatively small area, with the rupture extending with high slip values (~35 meters) up to the trench.
Our findings, resulting from a joint inversion of geodetic and tsunami data, account for the huge tsunami ensuing from the earthquake and most of the very large and shallow coseismic deformation associated to this seismic event. A possible further contribution from the frontal wedge deformation or secondary faults will be further investigated using additional data and by means of more sophisticated models (e.g. finite elements models) in order to take into account the three-dimensional geometrical and rheological complexities.
We have analyzed the different resolving power of geodetic and tsunami data, stressing the importance to use offshore instruments in the very near-field of the source area to recover a robust picture of the rupture, which will yield important implications for long-term seismic and tsunami hazard assessment. Seafloor instruments, measuring the deformations along the megathrust, should be used to better estimate the interseismic plate coupling, which is a key element to infer the tectonic strain accumulation. Our results strongly support the implementation of offshore monitoring networks along subduction zones, along with near-source tsunameters which would significantly improve existing tsunami early warning systems.
Methods
Tsunami Data
The tsunami generated by Tohoku-oki earthquake was recorded by many coastal wave gauges3 and GPS-buoys4 (provided by Nationwide Ocean Wave information network for Ports and Harbours, NOWPHAS) positioned at ~20 km off the coast. Tsunami waves were recorded also by ocean bottom pressure sensors of Japan Agency for Marine-Earth Science and Technology (JAMSTEC) Kushiro-Tokachi and Muroto cabled observatories5,6, JMA Tokai and Boso cabled observatories7, Earthquake Research Institute (ERI), University of Tokyo, Sanriku cabled observatory8 and by DART buoys9 in the open Pacific Ocean (acquired by National Oceanic and Atmospheric Administration, NOAA and by Russian Far Eastern Regional Hydrometeorological Research Institute, RFERHRI). We use a subset of these data that allows maximizing the azimuthal coverage around the earthquake source (Fig. 1). We remove the tidal component from each waveform following a procedure based on robust LOWESS71. Tsunami waveforms at bottom pressure sensors TM1 and TM2 (ERI) are digitized from the figure in the website http://outreach.eri.u-tokyo.ac.jp/eqvolc/201103_tohoku/eng/#sealevel.
Geodetic Data
Coseismic deformations associated to Tohoku-oki event were measured by the GPS stations distributed along the Honshu Island. Geospatial Information Authority (GSI) of Japan has provided all original GPS Earth Observation Network (GEONET) RINEX data. To extract the three components of the coseismic offsets, we process the data with GIPSY-OASIS software (https://gipsy-oasis.jpl.nasa.gov/) and Jet Propulsion Laboratory (JPL) flinnR orbit and clock products. We use the kinematic precise point positioning strategy72 with ambiguity resolution73. Coseismic displacements are calculated as a simple difference of the position estimates averaged over 15 minutes before and after the mainshock excluding the first 5 minutes during the most intense ground shaking. We use also the coseismic displacements measured at several location on the seafloor off the coasts of Tohoku region and obtained by means of a GPS/acoustic technique15,16 as difference between the positions observed before and after the 2011 Tohoku-oki earthquake15,16.
Fault Geometry
We build a fault model consistent with the megathrust geometry74 and the Japan trench location, taking into account the variability of strike and dip along the surface. Dip values range from 6° to 22° according to the fault depth increase (from 4 to ~66 km, Fig. S1 in Supplementary Information). After using the software SEAGRID (http://woodshole.er.usgs.gov/operations/modeling/seagrid/seagrid.html) to create a curvilinear orthogonal grid above the plate surface, we obtain a fault area parameterized with 189 quadrangular subfaults with a size of ~25×25 km (Fig. S1 and Table S1 in Supplementary Information).
Green's Functions
To obtain an accurate coverage of the fault surface we divide it into quadrilaterals (our subfaults) and we then further divide each quadrilateral into two triangles. The Green's function for geodetic stations and the vertical seawater displacement then result as the linear combination of the coseismic displacement analytically computed in a homogeneous elastic half space75 for each pair of triangles forming a quadrilateral.
We model the tsunami Green's functions for each subfault by using the nonlinear dispersive wave model NEOWAVE76,77 for the tsunami propagation. A wet-dry moving boundary is applied at the coastline and full wave transmission at the open sea. Equations are solved numerically by means of a semi-implicit finite difference technique on a staggered grid. The nonlinear shallow water equations include a non-hydrostatic pressure term and a vertical momentum equation in order to take into account the tsunami generation from seafloor deformation and the weakly dispersive behaviour of the tsunami wave propagation.
The bathymetric grid for the computational domain (Fig. 1a) has 1 arc min of spatial resolution and it was provided by Hydrographic and Oceanographic Department (HOD) of the Japan Coast Guard.
Inversion
We infer the coseismic slip distribution following the method of linear superposition of Green's functions and solving the inverse problem using a particular implementation of the Simulated Annealing technique, the Heath Bath algorithm53,78.
The adopted misfit function is different for tsunami and geodetic data. On one hand, for tsunami data we use a function that has been demonstrated to be sensitive to both amplitude and phase matching of the time series79. On the other hand, the cost function for the geodetic data set is a standard L2 norm. We insert two extra terms in the cost function to minimize the seismic moment and to add smoothing constraints to the slip distribution. This pair of factors is selected from a number of possible pairs as the one that maximizes the factor values without degrading the fit to data.
We assign larger weights at TMs and DARTs (Table S3 in Supplementary Information) because the former are positioned above the source, whereas the latter are the only ones ensuring azimuthal coverage to the east of the source area. The weights at the remaining tsunami stations are assigned basing on their spatial/azimuthal density around the fault surface. We set also a larger weight for seafloor geodetic observations with respect to the GPS stations (a seafloor observation weights five times a GPS data) because of their better control on the slip offshore (Figs. S3b,c in Supplementary Information). In addition, in order to avoid an unbalancing between the behaviour of different cost functions used for different data sets during the simulated annealing, distinct weights are assigned to the entire tsunami and geodetic data sets, ending up with a relative weight of 1.2 of geodetic over tsunami data. Since this procedure is not straightforward, resolution tests, further than being used to evaluate the different data resolving power, are also a guide for optimizing fine-tuning of intra- and inter-data set weights through a trial and error approach.
More detailed explanation of the inversion method is given in the Supplementary Information.
References
Chu, R. et al. Initiation of the great Mw 9.0 Tohoku–Oki earthquake. .Earth Planet. Sci. Lett., 308, 277–283, 10.1016/j.epsl.2011.06.031 (2011).
Fujii, Y., Satake, K., Sakai, S., Shinohara, M. & Kanazawa, T. Tsunami source of the 2011 off the Pacific coast of Tohoku, Japan earthquake. .Earth, Planets and Space 63, 815–820, 10.5047/eps.2011.06.010 (2011).
Nagai, T. Development and Improvement of the Japanese coastal wave observation network (NOWPHAS). .J. Jpn. Soc. Civil. Eng. no. 609 (VI-41), 1–14, in Japanese (1998).
Kato, T. et al. Tsunami due to the 2004 September 5th off the Kii Peninsula earthquake, Japan, recorded by a new GPS buoy. .Earth, Planets Space 57, 279–301 (2005).
Momma, H. et al. Monitoring System for Submarine Earthquakes and Deep Sea Environment. .Proc. MTS/IEEE OCEANS '97 2, 1453–1459 (1997).
Hirata, K. et al. Real-time geophysical measurements on the deep seafloor using submarine cable in the southern Kurile subduction zone. .IEEE J. Ocean Eng. 27, 170–181 (2002).
Fujisawa, I., Tateyama, S. & Fujisaki, J. Permanent ocean-bottom earthquake and tsunami observation system off the Boso Peninsula. .Weath. Serv. Bull. 53, 127–166, in Japanese (1986).
Kanazawa, T. & Hasegawa, A. Ocean-bottom observatory for earthquakes and tsunami off Sanriku, north-east Japan using submarine cable. .International Workshop on Scientific Use of Submarine Cables, Comm. For Sci. Use of Submarine Cables, Okinawa, Japan (1997).
Saito, T., Ito, Y., Inazu, D. & Hino, R. Tsunami source of the 2011 Tohoku-Oki earthquake, Japan: Inversion analysis based on dispersive tsunami simulations. .Geophys. Res. Lett. 38, L00G19, 10.1029/2011GL049089 (2011).
Yamazaki, Y., Lay, T., Cheung, K. F., Yue,, H. & Kanamori, H. Modeling near-field tsunami observations to improve finite-fault slip models for the 11 March 2011 Tohoku earthquake. .Geophys. Res. Lett. 38, L00G15, 10.1029/2011GL049130 (2011).
Tsushima, H. et al. Near-field tsunami forecasting using offshore tsunami data from the 2011 off the Pacific coast of Tohoku Earthquake. .Earth, Planets and Space 63, 821–826, 10.5047/eps.2011.06.052 (2011).
Maeda, T., Furumura, T., Sakai, K. & Shinohara, S. Significant tsunami observed at the ocean-bottom pressare gauges at 2011 Off the Pacific Coast of Tohoku Earthquake. .Earth, Planets and Space 63, 803–808, 10.5047/eps.2011.06.005 (2011).
Yokota, Y. et al. Joint inversion of strong motion, teleseismic, geodetic and tsunami datasets for the rupture process of the 2011 Tohoku earthquake. .Geophys. Res. Lett. 38, L00GL21, 10.1029/2011GL050098 (2011).
González, F. I. et al. The NTHMP tsunameter network. .Nat. Hazards 35, 25–39, 10.1007/s11069-004-2402-4 (2005).
Sato, M. et al. Displacement Above the Hypocenter of the 2011 Tohoku-Oki Earthquake. .Science 332, 1395, 10.1126/science.1207401 (2011).
Kido, M., Osada, Y., Fujimoto, H., Hino, R. & Ito, Y. Trench-normal variation in observed seafloor displacements associated with the 2011 Tohoku-Oki earthquake. .Geophys. Res. Lett. 38, L24303, 10.1029/2011GL050057 (2011).
Satake, K. Inversion of tsunami waveforms for the estimation of a fault heterogeneity: method and numerical experiments. .J. Phys. Earth. 35, 241–254 (1987).
Vigny, C. et al. The 2010 Mw 8.8 Maule Megathrust Earthquake of Central Chile, Monitored by GPS. .Science 332, 1417–1421, 10.1126/science.1204132 (2011).
Lorito, S. et al. Limited overlap between the seismic gap and coseismic slip of the great 2010 Chile earthquake. .Nat. Geosci. 4, 173–177, 10.1038/ngeo1073 (2011).
Satake, K. Depth Distribution of Coseismic Slip along the Nankai Trough, Japan, from Joint Inversion of Geodetic and Tsunami Data. .J. Geophys. Res. 98, 4553–4565 (1993).
Romano, F., Piatanesi, A., Lorito, S. & Hirata, K. Slip distribution of the 2003 Tokachi-oki Mw 8.1 earthquake from joint inversion of tsunami waveforms and geodetic data. .J. Geophys. Res. 115, B11313, 10.1029/2009JB006665 (2010).
Pollitz, F. F., Bürgmann, R. & Banerjee, P. Geodetic slip model of the 2011 M9.0 Tohoku earthquake. .Geophys. Res. Lett. 38, L00G08, 10.1029/2011GL048632 (2011).
Koketsu, K. et al. A unified source model for the 2011 Tohoku earthquake. .Earth Planet. Sci. Lett. 310, 480–487, 10.1016/j.epsl.2011.09.009 (2011).
Lee, S. J., Huang, B. S., Ando, M., Chiu, H. C. & Wang, J. H. Evidence of large scale repeating slip during the 2011 Tohoku-Oki earthquake. .Geophys. Res. Lett. 38, L19306, 10.1029/2011GL049580 (2011).
Newman, A. Hidden depths. .Nature 474, 441–443, 10.1038/474441a (2011).
Nishimura, T. et al. Temporal change of interplate coupling in northeastern Japan during 1995-2002 estimated from continuous GPS observations. .Geophysical Journal International 157, 901–916, 10.1111/j.1365-246X.2004.02159.x (2004).
Hashimoto, C., Akemi, N., Sagiya, T. & Matsu'ura, M. Interplate seismogenic zones along the Kuril-Japan trench inferred from GPS data inversion. .Nat. Geosci. 2, 141–144, 10.1038/ngeo421 (2009).
McCloskey, J., Nalbant, S. S. & Steacy, S. Indonesian earthquake: Earthquake risk from co-seismic stress. .Nature 434, 291, 10.1038/434291 (2005).
Konca, A. O. et al. Partial rupture of a locked patch of the Sumatra megathrust during the 2007 earthquake sequence. .Nature 456, 631–635, 10.1038/nature07572 (2008).
Moreno, M., Rosenau, M. & Oncken, O. 2010 Maule earthquake slip correlates with pre-seismic locking of Andean subduction zone. .Nature 467, 198–202, doi:10.1038/nature09349 (2010).
Loveless, J. P. & Meade, B. J. Spatial correlation of interseismic coupling and coseismic rupture extent of the 2011 MW = 9.0 Tohoku-oki earthquake. .Geophys. Res. Lett. 38, L17306, 10.1029/2011GL048561 (2011).
Moreno, M. et al. Heterogeneous plate locking in the South-Central Chile subduction zone: Building up the next great earthquake. .Earth Planet. Sci. Lett. 305, 413–424, 10.1016/j.epsl.2011.03.025 (2011).
Savage, J. C. A Dislocation Model of Strain Accumulation and Release at a Subduction Zone. .J. Geophys. Res. 88, 4984–4996 (1983).
Lay, T. & Kanamori, H. An asperity model of great earthquake sequences. .Earthquake Prediction - An International Review, AGU Geophys. Mono.: Washington, D.C., p. 579–592 (1981).
Faulkner, D. R., Mitchell, T. M., Behnsen, J., Hirose, T. & Shimamoto, T. Stuck in the mud? Earthquake nucleation and propagation through accretionary forearcs. .Geophys. Res. Lett. 38, L18303, 10.1029/2011GL048552 (2011).
Satake, K., Namegaya, Y. & Yamaki, S. Numerical simulation of the AD 869 Jogan tsunami in Ishinomaki and Sendai plains (in Japanese with English abstract). .Ann. Rep. Active Fault Paleoearthquake Res. 8, 71–89 (2008).
Minoura, K., Imamura, F., Sugawara, D., Kono, Y. & Iwashita, T. The 869 Jogan tsunami deposit and recurrence interval of large-scale tsunami on the Pacific coast of northeast Japan. .Journal of Natural Disaster Science 23, 2, 83–88 (2001).
Tanioka, Y. & Satake, K. Tsunami generation by horizontal displacement of ocean bottom. .Geophys. Res. Lett. 23, 8, 861–864, 10.1029/96GL00736 (1996).
Kanamori, H., Miyazawa, M. & Mori, J. Investigation of the earthquake sequence off Miyagi prefecture with historical seismograms. .Earth, Planets and Space 58, 1533–1541 (2006).
Sawai, Y. et al. Marine incursions of the past 1500 years and evidence of tsunamis at Suijin-numa, a coastal lake facing the Japan Trench. .The Holocene 18, 517–528 (2008).
Ide, S., Baltay, A. & Beroza, G. C. Shallow Dynamic Overshoot and Energetic Deep Rupture in the 2011 Mw 9.0 Tohoku-Oki Earthquake. .Science 10.1126/science.1207020 (2011).
Lay, T., Ammon, C. J., Kanamori, H., Xue, L. & Kim, M. J. Possibile large near-trench slip during the great 2011 Tohoku (Mw9.0) earthquake. .Earth, Planets and Space 63, 687–692, 10.5047/eps.2011.05.033 (2011).
Ammon, C., Lay, T., Kanamori, H. & Cleveland, M. “A rupture model of the great 2011 Tohoku earthquake”. .Earth, Planets and Space 63, 693–696, 10.5047/eps.2011.05.015 (2011).
Simons, M., et al. The 2011 Magnitude 9.0 Tohoku-Oki Earthquake: Mosaicking the Megathrust from Seconds to Centuries. .Science 332, 6036, 1421–1425, 10.1126/science.1206731 (2011).
Yue, H. & Lay, T. Inversion of high-rate (1 sps) GPS data for rupture process of the 11 March 2011 Tohoku earthquake (Mw 9.1). .Geophys. Res. Lett. 38, L00G09, 10.1029/2011GL048700 (2011).
Ito, T., Ozawa, K., Watanabe, T. & Sagiya, T. Slip distribution of the 2011 Tohoku earthquake inferred from geodetic data. .Earth, Planets and Space 63, 627–630, 10.5047/eps.2011.06.023 (2011).
Suzuki, W., Aoi, S., Sekiguchi, H. & Kunugi, T. Rupture process of the 2011 Tohoku-Oki mega-thrust earthquake (M9.0) inverted from strong-motion data. .Geophys. Res. Lett. 38, L00G16, 10.1029/2011GL049136 (2011).
Yoshida, Y., Ueno, H., Muto, D. & Aoki, S. Source process of the 2011 off the Pacific coast of Tohoku Earthquake with the combination of teleseismic and strong motion data. .Earth, Planets and Space 63, 565–569, 10.5047/eps.2011.05.011 (2011).
Yagi, Y. & Fukahata, Y. Rupture process of the 2011 Tohoku-oki earthquake and absolute elastic strain release. .Geophys. Res. Lett. 38, L19307, 10.1029/2011GL048701 (2011).
Loveless, J. P. & Meade, B. J. Geodetic imaging of plate motions, slip rates and partitioning of deformation in Japan. .J. Geophys. Res. 115, B02410, 10.1029/2008JB006248 (2010).
Gagnon, K., Chadwell, C. D. & Norabuena, E. Measuring the onset of locking in the Peru–Chile trench with GPS and acoustic measurements. .Nature 434, 10.1038/nature03412 (2005).
Fujita, M. et al. GPS/Acoustic seafloor geodetic observation: method of data analysis and its application. .Earth Planets Space 58, 265–275 (2006).
Rothman, D. Automatic estimation of large residual statics corrections. .Geophysics 51, 332–346, 10.1190/1.1442092 (1986).
DeMets, C., Gordon, R. G. & Argus, D. F. Geologically current plate motions. .Geophysical Journal International 181, 1–80, 10.1111/j.1365-246X.2009.04491.x (2010).
Huang, Z., Zhao, D. & Wang, L. Seismic heterogeneity and anisotropy of the Honshu arc from the Japan Trench to the Japan Sea. .Geophysical Journal International 184, 1428–1444, 10.111/j.1365-246X.2011.04934.x (2011).
Meng, L., Inbal, A. & Ampuero, J.-P. A window into the complexity of the dynamic rupture of the 2011 Mw 9 Tohoku-Oki earthquake. .Geophys. Res. Lett. 38, L00G07, 10.1029/2011GL048118 (2011).
Yao, H., Gerstoft, P., Shearer, P. M. & Mecklenbräuker, C. Compressive sensing of the Tohoku-Oki Mw 9.0 earthquake: Frequency-dependent rupture modes. .Geophys. Res. Lett. 38, L20310, 10.1029/2011GL049223 (2011).
Koper, K. D., Hutko, A. R. & Lay, T. Along-dip variation of teleseismic short-period radiation from the 11 March 2011 Tohoku earthquake (Mw 9.0). .Geophys. Res. Lett. 38, L21309, 10.1029/2011GL049689 (2011).
Lay, T. & Kanamori, H. Insights from the great 2011 Japan earthquake. .Phys. Today 64(12), 33–39, 10.1063/PT.3.1361 (2011).
Hoechner, A., Babeyko, A. Y. & Sobolev, S. V. Enhanced GPS inversion technique applied to the 2004 Sumatra earthquake and tsunami. .Geophys. Res. Lett. 35, L08310, 10.1029/2007GL033133 (2008).
Ito, Y. et al. Frontal wedge deformation near the source region of the 2011 Tohoku-Oki earthquake. .Geophys. Res. Lett. 38, L0OG05, 10.1029/2011GL048355 (2011).
Tsuji, T. et al. Potential Tsunamigenic Faults of the 2011 Tohoku Earthquake. Earth, Planets and Space 63, 831–834, 10.5047/eps.2011.05.028 (2011).
Fujiwara, T. et al. The 2011 Tohoku-Oki Earthquake: Displacement Reaching the Trench Axis. .Science 334, 6060, 1240, doi:10.1126/science.1211554 (2011).
Kawamura, K., Sasaki, T., Kanamatsu, T., Sakaguchi, A. & Ogawa, Y. Large submarine landslides in the Japan Trench: A new scenario for additional tsunami generation. .Geophys. Res. Lett. 39, L05308, 10.1029/2011GL050661 (2012).
Wang, D. & Mori, J. Frequency-dependent energy radiation and fault coupling for the 2010 Mw8.8 Maule, Chile and 2011 Mw9.0 Tohoku, Japan, earthquakes. .Geophys. Res. Lett. 38, L22308, 1029/2011/GL049652 (2011).
Ozawa, S. et al. Coseismic and postseismic slip of the 2011 magnitude-9 Tohoku-Oki earthquake. .Nature 475, 373–376, 10.1038/nature10227 (2011).
Ohzono, M., Iinuma, T., Ohta, Y. & Miura, S. Coseismic slip distribution of the 2011 off the Pacific coast of Tohoku Earthquake (M9.0) estimated based on GPS data – Was the asperity in Miyagi-oki ruptured? .Earth, Planets and Space 63, 643–648, 10.5047/eps.2011.06.013 (2011).
Monastersky, R. Tsunami forecasting: The next wave. .Nature 483, 144–146, 10.1038/483144a (2012).
Matsumoto, Y. et al. Weal interplate coupling beneath the subduction zone off Fukushima, NE Japan, inferred from GPS/acoustic seafloor geodetic observation. .Earth, Planets and Space 60, e9-e12 (2008).
Sato, M. et al. Restoration of interplate locking after the 2005 Off-Miyagi Prefecture earthquake, detected by GPS/acoustic seafloor geodetic observation. .Geophys. Res. Lett. 38, L01312, 10.1029/2010GL045689 (2011).
Barbosa, S. M., Fernandes, M. J. & Silva, M. E. Nonlinear sea level trends from European tide gauge records. .Annales Geophysicae 22, 1465–1472 (2004).
Zumberge, J. F., Heflin, M. B., Jefferson, D. C., Watkins, M. M. & Webb, F. H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. .J. Geophys. Res. 102, 5005–5017, 10.1029/96JB03860 (1997).
Bertiger, W. et al. Single receiver phase ambiguity resolution with GPS data. .J. Geodesy 84, 327–337, 10.1007/s00190-010-0371-9 (2010).
Hayes, G. P. &, Wald, D. J. Advancing techniques to constrain the geometry of the seismic rupture plane on subduction interfaces a priori: Higher-order functional fits. .Geochem. Geophys. Geosyst. 10, Q09006, 10.1029/2009GC002633 (2009).
Meade, B. J. Algorithms for the calculation of exact displacements, strains and stresses for triangular dislocation elements in a uniform elastic half space. .Comput. Geosci. 33, 1064–1075, 10.1016/j.cageo.2006.12.003 (2007).
Yamazaki, Y., Kowalik, Z. & Cheung, K. F. Depth-integrated, non-hydrostatic model for wave breaking. .Int. J. Numer. Meth. Fluids 61, 473–497, 10.1002/fld.1952 (2009).
Yamazaki, Y., Cheung, K. F. & Kowalik, Z. Depth-integrated, non-hydrostatic model with grid nesting for tsunami generation, propagation and run-up. .Int. J. Numer. Meth. Fluids 67, 2081–2107, 10.1002/fld.2485 (2011).
Sen, M. & Stoffa, P. L. Nonlinear one-dimensional seismic waveform inversion using simulated annealing. .Geophysics 56, 1624–1638, 10.1190/1.1442973 (1991).
Spudich, P. & Miller, D. P. Seismic site effects and the spatial interpolation of earthquake seismograms: results using aftershocks of the 1986 North Palm Springs, California, earthquake. .Bull. Seismol. Soc. Am. 80, 6, 1504–1532, (1990).
Acknowledgements
We acknowledge Mariko Sato and Motoyuki Kido for providing geodetic seafloor measurements. We wish to thank all of the data providers who made this study possible and in particular JMA (stations Boso and Tokai), NOWPHAS (coastal wave gauges and GPS-buoys), JAMSTEC (stations KPGs and MPGs), ERI at the University of Tokyo (stations TMs), NOAA (DART 21413, 21418, 21419), RFERHR (DART 21401) and GEONET (GPS data) which managed to promptly release data in the aftermath of the earthquake. We particularly thank CASPUR's staff (http://www.caspur.it/en/) for providing computing resources necessary to perform tsunami simulations. We acknowledge useful information received by Yoshihiro Ito, Masahiro Yamamoto and Brendan Meade. Some Figures were drawn with Generic Mapping Tools (http://gmt.soest.hawaii.edu/).
Author information
Authors and Affiliations
Contributions
F.R., A.P. and S.L. were involved in all of the phases of this study. N.D. processed and analysed GPS data and contributed to paper writing. K.H. contributed to analysing tsunami data, to result interpretation and paper writing. S.A. contributed to model GPS data and paper writing. Y.Y. wrote the tsunami modelling numerical code and supervised the modelling of tsunami data. M.C. promoted the experiment, contributed to result interpretation and paper writing.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Electronic supplementary material
Supplementary Information
Supplementary Information
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareALike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
Romano, F., Piatanesi, A., Lorito, S. et al. Clues from joint inversion of tsunami and geodetic data of the 2011 Tohoku-oki earthquake. Sci Rep 2, 385 (2012). https://doi.org/10.1038/srep00385
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00385
This article is cited by
-
Early forecasting of tsunami inundation from tsunami and geodetic observation data with convolutional neural networks
Nature Communications (2021)
-
Frequency-dependent amplification of the Sanriku tsunamis in Ryori Bay
Earth, Planets and Space (2020)
-
Modeling coastal tsunami hazard from submarine mass failures: effect of slide rheology, experimental validation, and case studies off the US East Coast
Natural Hazards (2017)
-
Preceding seismic activity and slow slip events in the source area of the 2011 Mw 9.0 Tohoku-Oki earthquake: a review
Geoscience Letters (2015)
-
Quantification of Tsunami Bathymetry Effect on Finite Fault Slip Inversion
Pure and Applied Geophysics (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.