Abstract
Gold nanoparticles (GNPs) are being proposed as contrast agents to enhance X-ray imaging and radiotherapy, seeking to take advantage of the increased X-ray absorption of gold compared to soft tissue. However, there is a great discrepancy between physically predicted increases in X-ray energy deposition and experimentally observed increases in cell killing. In this work, we present the first calculations which take into account the structure of energy deposition in the nanoscale vicinity of GNPs and relate this to biological outcomes and show for the first time good agreement with experimentally observed cell killing by the combination of X-rays and GNPs. These results are not only relevant to radiotherapy, but also have implications for applications of heavy atom nanoparticles in biological settings or where human exposure is possible because the localised energy deposition high-lighted by these results may cause complex DNA damage, leading to mutation and carcinogenesis.
Similar content being viewed by others
Introduction
The goal of radiotherapy is to provide tumour control by killing cancerous cells using ionising radiation while simultaneously sparing surrounding tissues. Since the fraction of cells which survive an exposure to radiation is typically expressed as  , where S is the surviving fraction, α and β are properties of the cell line and D is the dose of radiation delivered (in terms of energy per unit mass), this requires delivering high doses to tumour volumes while minimising those to surrounding healthy tissues.
, where S is the surviving fraction, α and β are properties of the cell line and D is the dose of radiation delivered (in terms of energy per unit mass), this requires delivering high doses to tumour volumes while minimising those to surrounding healthy tissues.
In current medical practice, this is typically achieved through spatially shaping dose around the tumour through the use of multiple modulated radiation fields, such as in Intensity Modulated Radiation Therapy (IMRT)1. However, the dose ratio achievable between a tumour and surrounding healthy tissues is typically limited by their very similar X-ray absorption characteristics.
While beam delivery methods are continually being refined to improve the quality of the conformation of dose delivery to tumours, alternative methods to improve the discrimination between tumours and healthy tissue are being considered. One such method which has received increasing interest in recent years is the use of heavy atom contrast agents. Heavier elements increase the dose delivered to surrounding tissues due to their greater mass energy absorption coefficients and can thus potentially improve the contrast between healthy and cancerous cells if they can be preferentially delivered to tumours.
Gold nanoparticles (GNPs) have been of particular interest for this application, as they combine a high mass attenuation coefficient and bio-compatibility, which has led to them being used as a contrast agent in X-ray imaging2,3. In addition, it has been shown that these particles are preferentially taken up into tumours in mice and that this leads to an improvement in tumour control following radiotherapy4.
Numerous theoretical studies have been carried out investigating the viability of GNP contrast agents and have shown that the dose to tissue volumes can be significantly increased by the addition of GNP due to their greater X-ray absorption5,6,7. Concentrations on the order of 1% by mass have been suggested to increase the dose deposited by up to a factor of two, which suggests considerable potential for increasing cell killing through the selective delivery of gold nanoparticles.
The capability of contrast agents to sensitise cells to radiation has also been verified experimentally. Significant increases in DNA damage and cell killing in vitro and improved tumour control in vivo have been observed for GNPs8,9,10 as well as for molecular agents containing heavy atoms (e.g. cis-platinates11).
However, there is a disconnect between the theoretically predicted increases in cell killing and experimentally observed results. While most theoretical studies suggest that GNP concentrations on the order of 1% combined with keV X-rays would be necessary to generate significant increases in cell killing, experimental studies have observed enhancement of the effects of radiation at GNP concentrations which are orders of magnitude smaller. Resolving this discrepancy is important, not only for the use of GNPs as future therapeutic agents, but also to quantify carcinogenic risks associated with heavy atom nanoparticles in other applications, whether following a deliberate radiation exposure in imaging, or interaction with background radiation.
Most theoretical work on contrast agents has focused on a macroscopic view of dose, averaging effects over volumes much larger than a single cell. This approach is fundamentally flawed, however, as it neglects the significant dose inhomogeneity on the nanoscale which is caused by the introduction of a contrast agent. This effect has been experimentally verified in a plasmid system with GNPs12. Few studies have taken this effect into account, often neglecting either the discrete nanoparticle nature of the gold or not relating these inhomogeneities directly to cell survival.
This work addresses this deficiency by calculating dose distributions on the nanoscale in the vicinity of a GNP and using a model for cell survival which can take these inhomogeneities into account to generate new predictions for the effects of GNPs on radiotherapy.
Monte Carlo calculations were used to predict the dose distribution around GNPs on the nanometre scale. The results of these calculations show very high degrees of dose localisation and demonstrate the importance of Auger electrons created following ionisations near the nanoparticle's surface. From these dose distributions, the resultant biological effect is predicted within the framework of the Local Effect Model13,14, a model originally devised to describe the high levels of damage seen in charged particle therapies by accounting for dose inhomogeneities found along heavy ion tracks. The implications of this model for the effects of energy and GNP size on their radio-sensitising properties are explored and finally a direct comparison (with no adjustable parameters) with experimental results is presented which shows that these predictions are in excellent agreement with experimentally measured survival for cells exposed to radiation in the presence of GNPs.
Results
As a first step to evaluating the effects of nanoscale dose deposition in the radio-enhancing effects of GNPs, Monte Carlo simulations were carried out to quantify the degree of dose inhomogeneity introduced by presence of a GNP. These simulations calculated the response of a single GNP suspended in water to monoenergetic X-ray radiation for a series of nanoparticle sizes (2 to 50 nm in diameter) and energies (20 to 150 keV).
The models recorded the rate at which ionising events occurred in the GNP, the spectrum of secondary particles and the distribution of energy which was deposited in the vicinity of the GNP following an ionising event.
One striking result was the very low rate of ionising events in the GNPs - for example, when a 20 nm GNP was exposed to 100 keV X-rays, approximately 0.001 ionisations were recorded per Gy (J/kg) deposited in the surrounding water volume. This value is in line with what would be expected based on the mass attenuation coefficient of gold. However, this rate means that, for doses typically used in radiotherapy, over 99% of the nanoparticles present in a system would not contribute to the dose-modifying effects. This highlights the limitations of averaging the dose-modifying effect over large volumes containing many GNPs, as instead of a relatively homogeneous distribution of additional dose spread over all GNPs, little or no effect would be seen near most GNPs, with dramatic spikes in dose in the vicinity of the few which do see ionising events.
For all combinations of nanoparticle size and X-ray energy considered in this work, the rate of ionising events per nanoparticle as a function of dose was found to be well described by considering the ratio of the ionisation cross-sections of gold and water and the mass of the nanoparticle. As a result, the ionisation rate scales strongly with both incident photon energy and particle size in the range of conditions described in this work.
Following an ionising event in gold, a number of low-energy secondary electrons are produced. These will include a photo- or Compton electron with relatively high energy, followed by a shower of Auger electrons with much lower energies (all with energies ⪅10 keV, with many at energies <1 keV), which are emitted as electrons in the ionised gold atom reorganise themselves to fill the vacancy caused by the ionisation. These electrons are responsible for much of the additional energy deposited due to the presence of GNPs and an example of the resulting energy distribution can be seen in Figure 1.
Average energy deposit in the vicinity of a 20 nm gold nanoparticle after a single ionising event by a 40 keV photon.
Energy deposition is here scored in keV in concentric shells around the nanoparticle, broken down into contributions from electrons produced by different processes. In the vicinity of the nanoparticle, Auger electrons produce the dominant contribution, but this falls off rapidly as low-energy electrons are stopped, leaving only the contribution of energetic L-shell Auger electrons beyond 200 nm. Compton electrons are not plotted due to their low number, but are typically roughly 1% of the contribution of the photoelectrons.
While in most cases the energetic photo- or Compton electron carries away most of the energy from the incident photon, the high energy of this particle means it has a very long range in the surrounding water volume, leading to little of its energy being deposited in the vicinity of the GNP. By contrast, the low-energy Auger electrons have much shorter ranges and so deposit much more of their energy near the nanoparticle. As a result of this much denser ionisation, they are the dominant source of dose until several hundred nanometres from the nanoparticle's surface.
The dominance of the Auger electrons has significant implications for the distribution of energy which is deposited in the vicinity of the GNP. The spectrum of Auger electrons which is generated following an ionising event does not depend on the energy of the ionising particle, but rather on the shell from which the initial photo- or Compton electron was ejected. As a result, the dose deposited in the immediate vicinity of a GNP varies only weakly with the energy of the incident photon and any enhancement which is dominated by this inhomogeneity would have an energy dependence very different to that suggested by simple mass energy absorption considerations.
In addition, because the Auger electrons which dominate the short-range dose are generated at very low energies, the location at which the ionising event occurs in the GNP is very significant. Low-energy Auger electrons have even shorter ranges in gold than in water - on the order of a few nanometres. Thus, while events which occur on the surface of the nanoparticle tend to emit the full spectrum of Auger electrons, only highly energetic particles escape following events which occur within the bulk of the nanoparticle, as illustrated in Figure 2. As a result, the majority of low-energy electrons which escape from the nanoparticle and the corresponding elevated short-range doses, are primarily the contribution of events which occur within a thin shell at the nanoparticle's surface.
Comparison of track structure of ionising events either on the surface (solid lines) or in the bulk (dashed lines) of a 20 nm spherical gold nanoparticle, plotted both in 3D (plot a) and as a 2D projection (plot b).
Here, an incident 50 keV photon (green tracks) interacts with the gold nanoparticle and ejects a number of electrons (red tracks). For the event which occurs in the bulk, the majority of low-energy electrons are stopped immediately in the nanoparticle, allowing only the most energetic and sparsely ionising electrons to escape. By contrast, the surface event also produces a very large shower of low energy electrons who deposit their energy very densely in the vicinity of the nanoparticle, leading to high doses and many ionising events in a small volume.
The magnitude of this effect is illustrated in Figure 3. As noted above, an ionising event in a gold atom generates a photo- or Compton electron together with a shower of a dozen or more Auger electrons as resulting inner shell vacancies are filled. However, these electrons must escape the GNP before they can potentially cause damage to a surrounding cell and this is not guaranteed due to their strong absorption within the gold. Figure 3 shows the probability of different numbers of electrons being emitted following an ionising event in gold at different depths.
Probability of different numbers of electrons being emitted from a GNP following an ionisation by a 50 keV photon, as a function of the distance from the ionising event to the nanoparticle surface.
All ionising events in gold typically produce a large number of secondary Auger electrons, but many of these electrons are emitted at low energies and cannot escape because they are stopped in the GNP bulk. At distances a few nanometres within the GNP, a broad distribution of electron yields can be seen, as most Auger electrons can escape following ionisations near the surface. By contrast, at points further from the surface, the distribution is sharply peaked, with only one or two electrons generated following most ionising events.
It can be seen that the distribution is sharply peaked at long distances to the surface (10 nm or more) with 75% of ionisations leading to the emission of only one or two electrons from the GNP. This is the result of the vast majority of lower-energy secondary electrons being stopped within the GNP before they reach the surface, with only the highly energetic photoelectron and potentially an L-shell Auger electron escaping. By contrast, at the surface of the GNP the distribution of electron yield is very broad, with 10 or more electrons being emitted following more than 5% of events, which indicates the majority of the electrons produced Auger cascade can potentially escape the GNP at such depths.
From the variation of electron yield with depth as seen in Figure 3, it can be seen that the surface layer which potentially emits large numbers of Auger electrons is only a few nanometres thick. Thus, it would appear that for many GNP a relatively small layer near the surface has a much greater influence on the dose inhomogeneity seen in GNP-enhanced therapies than the core, even when the core may be substantially larger.
Figure 4 plots the dose deposited following a single ionisation in nanoparticles of various sizes, calculated by dividing energy deposits of the type illustrated in Figure 1 by the mass of the corresponding water shell at each distance. This supports the above observations about the effects a small shell on the GNP surface, showing that smaller nanoparticles deposit larger doses in their vicinity due to their greater surface:volume ratio, with 2 nm nanoparticles depositing between 2 and 3 times more energy than larger nanoparticles at short ranges (<200 nm). This size effect diminishes at longer ranges, as dose deposited far from the nanoparticle is the result of photoelectrons and energetic Auger electrons, which reliably escape from all sizes of nanoparticle.
Average radial doses which are deposited following a single ionising event from 40 keV primary radiation in gold nanoparticles of a variety of sizes.
These doses are calculated by scoring the energy deposited to the water volume in concentric shells around the nanoparticle and dividing these values by the mass of the water shell. Two features are particularly striking - firstly, areas in the vicinity of the nanoparticle (< 50 nm) see extremely large doses following a typical ionising event. Secondly, small nanoparticles deposit more dose in their local area than larger ones, due to the greater relative contribution from the outer layer of the nanoparticle. The scale and distribution of these doses are broadly similar to those seen in charged particle therapies in the vicinity of a track, which suggests the possible applicability of the local effect model as a way to analyse these results.
Figure 4 also illustrates the dramatic variation in dose near the nanoparticle, with doses on the order of thousands of Gy deposited in the vicinity of the nanoparticle following a single ionising event. This combination of extremely high doses and extremely small volumes is relatively uncommon in X-ray radiotherapy, as the incident radiation is typically very sparsely ionising.
By contrast, distributions of this sort are regularly seen around particle tracks in charged particles therapies, such as heavy ion therapy. This is potentially very significant, as charged particles are known to kill significantly more cells for a given dose deposit than a corresponding dose of X-rays, a concept that is typically quantified as a Relative Biological Effectiveness (RBE). The RBE is defined as the ratio of doses required to lead to the same level of cell killing comparing a sparsely ionising benchmark (X-rays) to a more densely ionising radiation source.
The hypothesis that the high degree of dose localisation near GNPs is responsible for the large dose enhancements observed experimentally can be tested by applying a predictive framework which has been successful in accounting for the biological effects of dose inhomogeneity in heavy ion therapy. To quantify this effect, the Local Effect Model (LEM)13,14 has been applied to the inhomogeneous dose distributions around GNPs to determine what additional cell killing results from this effect.
In the LEM, instead of calculating the cell killing based on a dose averaged over the entire cell, the probability of damage occurring at each point within a cell is calculated based on the local dose at that point and a survival probability is calculated based on the average level of damage throughout the cell. This model can be applied to the dose distributions around GNP to provide predictions of biological effectiveness.
One of the assumptions of the LEM is that the response of a cell to a given microscopic dose deposited by densely ionising radiation is related to how the cell would respond to a uniform dose of sparsely ionising radiation. As a result, the predictions of the LEM are closely related to the cell line under consideration and as a result a specific example cell line must be considered to calculate predictions of enhancement. For this work, MDA-MB-231 breast cancer cells have been chosen, as they have been extensively studied in conjunction with GNPs10 and their radiation response in the absence of gold has been shown to be characterised by the parameters α = 0.019 ± 0.025, β = 0.052 ± 0.007.
The LEM was applied to the dose distributions generated for a series of combinations of GNP size and X-ray energy as outlined in the methods and the resulting predicted RBEs for MDA-MB-231 breast cancer cells are plotted in Figure 5. These results show that, for all combinations of particle size and photon energy, taking into account the dose inhomogeneity in the vicinity of GNPs using the LEM leads to predicted RBEs which are several times greater than those predicted by the change in macroscopic dose alone.
Predicted relative biological effectiveness (RBE) of irradiations of MDA-231 cells (survival parameters α = 0.019 ± 0.025, β = 0.052 ± 0.00710) in the presence of 500 µg/mL of gold nanoparticles for a variety of nanoparticle sizes exposed to 40 keV X-rays (a) and 20 nm nanoparticles exposed to a variety of energies (b).
These values were calculated either through as the modification in average dose through the addition of the GNPs (circles), or using the Local Effect Model (squares). The change in macroscopic dose is small, on the order of a few %, in good agreement with the ratio of energy absorption coefficients between gold and water (dotted line). By contrast, the LEM predicts significantly higher effectiveness in all conditions, with strong dependencies on both nanoparticle diameter and incident photon energy. Increasing nanoparticle diameter significantly reduces the RBE, which can be understood as the result of increasing numbers of low-energy electrons being trapped inside the nanoparticle and not contributing to dose in the water volume. The dashed line is an empirical fit, as described in the text. The variation with energy was found to be well described by assuming that each ionising event in a gold nanoparticle contributes a fixed additional probability of a lethal event in a cell, which was characterised by a single empirical fitting parameter, taken to be constant at all energies. Good agreement with modelled values was seen at all points, except immediately above gold's K-edge in plot b, where a significant increase in RBE is observed. This is the result of the majority of the photoelectrons which result from K-shell events being produced at relatively low energies (<5 keV), causing them to contribute much more significantly to short-range dose inhomogeneities than at other energies which are distant from absorption edges.
This increase in effectiveness is in qualitative agreement with experimental results, suggesting that these dose inhomogeneities may be responsible for some or all of the large enhancements which are observed experimentally. These results also suggest that significant variation in enhancement would be observed as a function of both nanoparticle size and incident photon energy.
Figure 5a shows that the RBE decreases significantly as nanoparticle size increases. This is unsurprising, given the above observations about the significant contribution of short-range electrons to dose inhomogeneities in this system. Analytic predictions of how the dose inhomogeneity and RBE vary with particle diameter from first principles are not feasible, due to the complex variation of the emitted electron spectrum with nanoparticle size. However, a relatively simple empirical prediction of the form  where d is the nanoparticle diameter and A, d0 and n are fitting parameters was found to give very good agreement with the data.
where d is the nanoparticle diameter and A, d0 and n are fitting parameters was found to give very good agreement with the data.
This model was chosen based on observations that the large dose enhancements derived from the short-range, low-energy Auger electrons. When d is vanishingly small, all such electrons escape, giving a maximum increase in RBE of A. As d increases, the proportion of the electrons which escape decreases and at large d only a relatively thin shell at the surface emits electrons. This means that the yield of electrons from large nanoparticles would be expected to be proportional to d0/d, where d0 is the thickness of the shell which emits low-energy electrons. However, because the electrons do not have a single well-defined range, the Auger electron emitting shell does not have a clear cut-off. As a result, the yield of low-energy electrons (and thus RBE) will not follow the above relationship exactly, a fact which is incorporated by the addition of a power scaling term, n. When the above relation was fitted to the data in Figure 5a, values of A = 1.6 ± 0.2, d0 = 3.6 ± 1.0 and n = 0.94 ± 0.05 were obtained and the resulting curve is plotted as the dashed line.
The fitted values for d0 and n are in broad agreement with what would be predicted from the other results presented in this work. As noted in the discussion of Figure 3, low-energy electrons are predominately produced from a shell a few nanometres in depth, in agreement with the value of d0. Similarly, the asymptotic behaviour for large d of enhancement being proportional to d0/d is also present, with n taking a value close to 1.
Figure 5b shows a variation of RBE with energy which differs significantly from the ratio of mass energy absorption coefficients that is typically used when describing GNP-enhanced radiotherapy15,5,7. By applying the LEM, it can be seen that there is an additional increase in RBE which was found to generally be proportional to the rate of ionising events in gold. Again, this is in line with above observations, in particular the fact that the enhancement is dominated by the effects of the Auger cascade. This means that, as each ionising event in gold leads to a single Auger cascade, whose form is independent of the incident particle energy, it is only the number of these ionising events which determines the additional enhancement, independent of any other factors.
An exception to this relationship can be seen just above gold's K-edge at 80.7 keV, where the incident photons had just enough energy to free electrons from the most tightly bound shell in gold. At energies just slightly above this edge, the photoelectrons produced by such an interaction have low energies, comparable to those of the Auger electrons and as a result contribute significantly to the short-range dose inhomogeneity and the associated increase in RBE. However, this effect is very strongly dependent on energy, disappearing almost entirely by 85 keV and so is unlikely to prove significant for practical applications of GNP-enhanced radiotherapy.
A fitting function was chosen that described the behaviour of the RBE away from absorption edges, based on the assumption that macroscopic dose and short-range dose are independent, which took the form  . Here, ρ is the concentration of GNP expressed as a fraction of the total mass of the target volume, µen is the mass energy absorption coefficient of the indicated material, Rioni [E] is the number of ionisations which would occur in gold at unit density per Gy deposited in the surrounding water and B is an empirical fitting constant.
. Here, ρ is the concentration of GNP expressed as a fraction of the total mass of the target volume, µen is the mass energy absorption coefficient of the indicated material, Rioni [E] is the number of ionisations which would occur in gold at unit density per Gy deposited in the surrounding water and B is an empirical fitting constant.
In this expression, the first term in the brackets describes the simple macroscopic dose enhancement, which has been used extensively elsewhere, while the second term is related to the additional enhancement which would be seen due to the dose inhomogeneities which follow individual ionising events. When B was fitted to the observed data, a value of B = (2.55 ± 0.14) × 10−15 was obtained, which can be viewed as the probability of damage following a single ionisation in a 20 nm GNP within a cell. The resulting curve is plotted alongside the data in Figure 5b and shows good agreement over the whole energy range.
The above results can be combined into a single expression for RBE by noting that the rate of ionisation is independent of nanoparticle size as they are all effectively transparent to X-rays at these energies and that the additional enhancement resulting from the Auger cascade is independent of photon energy. These can then be combined into an expression of the form  . This mirrors the form of the above expression for the energy dependence, but the empirical constant B has now been replaced by a new function,
. This mirrors the form of the above expression for the energy dependence, but the empirical constant B has now been replaced by a new function,  , to represent the variation of induced dose inhomogeneity with dose as seen in Figure 5a. The value of C was empirically fitted to the data and found to be C = (1.50 ± 0.08) × 10−14 for this data. This function would be expected to hold true for all combinations of nanoparticle size and energy where the conditions are broadly similar to the results presented in this paper - that is, GNP small enough to be effectively transparent to X-rays and incident particles whose energies are such that their interactions with gold are dominated by the photoelectric effect.
, to represent the variation of induced dose inhomogeneity with dose as seen in Figure 5a. The value of C was empirically fitted to the data and found to be C = (1.50 ± 0.08) × 10−14 for this data. This function would be expected to hold true for all combinations of nanoparticle size and energy where the conditions are broadly similar to the results presented in this paper - that is, GNP small enough to be effectively transparent to X-rays and incident particles whose energies are such that their interactions with gold are dominated by the photoelectric effect.
As these predictions are in good qualitative agreement with experimental results, the model was also tested against a real data set to evaluate its quantitative agreement. A previously published work10 has shown the radio-sensitising effects of 500 µg/mL of 1.9 nm GNPs on MDA-MB-231 cells exposed X-rays from a 160 kVp source and are used here as a test data set.
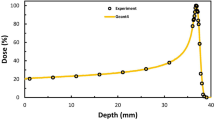
These results are illustrated in Figure 6. Points are the experimentally observed cell survival data, for cells exposed to varying doses either in the absence (squares) or presence (circles) of gold. The solid line is a linear-quadratic survival curve which was fitted empirically to the radiation response of the cells in the absence of gold and used to determined α and β values for the MDA cells, as required for the LEM. Based on these values and calculated microscopic dose distributions for 1.9 nm GNPs exposed to 160 kVp X-rays, predictions were generated for the survival of the MDA cells in the presence of 500 µg/mL of 1.9 nm GNPs as a function of X-ray dose, which is plotted as the dashed line. It can be seen that this line is in excellent agreement with the experimentally observed survival for cells exposed to GNP, suggesting that this model has good predictive power and is clearly in better agreement than the change in macroscopic dose, which only suggests an increase in effect of approximately 5% for this system.
Experimentally observed cell survival for MDA-231 cells exposed to 160 kVp X-rays with (circles) and without (squares) exposure to 500 µg/mL of 1.9 nm gold nanoparticles, taken from10.
In the original analysis, this data was fitted using a conventional linear-quadratic model, to determine if a radiosensitising effect was observed. Here, the data is used to investigate whether the model presented in this work is capable of accurately quantifying the sensitising effects of GNPs. To that end, only the control data was fitted to directly using a linear quadratic, which gave α = 0.019 ± 0.025, β = 0.052 ± 0.007 (solid line). These parameters were used, together with modelled microscopic dose in the vicinity of a 1.9 nm GNP exposed to 160 kVp X-rays, in the Local Effect Model to predict the behaviour of the cells which were exposed to gold nanoparticles, without reference to the experimentally observed results. These theoretical predictions are plotted as the dashed line. The agreement is very good, substantially better than simple energy absorption considerations which predict an increase in damage of just 5% for this gold concentration, which suggests that the microscopic dose in the vicinity of GNPs is a significant contribution to experimentally observed GNP dose enhancement.
These results not only suggest a change in the magnitude of damage, but also the shape of the cell survival curve. In the macroscopic dose model, contrast agents are believed to simply change the dose deposited in the system, increasing D to some new value D′ = εD, where ε > 1. If cell survival curves are plotted against the dose which is delivered to the control cells, this causes cells with GNPs to appear to have modified α and β values. The macroscopic model would predict that these would be αAu = εα and βAu = ε 2 β. However, since in the LEM the short-range energy deposition associated with each ionising event in gold increases the chance of a lethal event by some fixed amount and the number of ionising events is directly proportional to dose, the additional enhancement manifests itself as a linear function of dose. As a result, the LEM predicts much greater increases in the α value in the fitted parameters than would be predicted by simply comparing absolute changes in cell killing.
These predictions about the varying form of the dose response are in excellent agreement with the results in Figure 6, as well as other work published on GNP dose enhancement which has identified significant increases in α (and little or no change in β) in cell lines which are sensitised by GNPs9,10,16.
Discussion
The excellent agreement shown in Figure 6 between the model's predictions and observed cell survival in GNP-enhanced radiotherapy indicates that nanoscale dose deposition near heavy atom dopants must be considered when predicting the effect of heavy atoms on biological systems exposed to ionising radiation. Additionally the agreement shows the wider applicability of the LEM, as it gave rise to accurate predictions outside the domain of heavy ion therapy.
It can be seen that the approach presented in this work predicts sensitising effects at concentrations much smaller than those which macroscopic dose considerations suggest are necessary and provides for the first time good agreement between predictions of enhancement made from physical principles and experimentally observed results. The scale and nature of this effect as several important implications, most importantly for the use of nanoparticle contrast agents in radiotherapy, where the lower concentrations required make contrast-enhanced therapies a more promising treatment modality.
However, this sensitising effect may be detrimental for other applications of heavy atom nanoparticles17,18,19,20,21,22, particularly in imaging. Calculations of risk associated with radiation exposure incorporate a weighting factor (wR)23, typically related to the type and energy of incident radiation. wR is large for protons and heavy ions due to their highly localised dose distributions, which means even small radiation doses cause complex DNA damage, potentially leading to carcinogenesis. A similar effect may occur in the vicinity of a heavy atom nanoparticle following an ionising event, meaning their presence will necessitate an increase in wR for other types of radiation, whether resulting from background radiation, or deliberate exposures during imaging. The exact scale of this effect must be evaluated, as it poses a significant challenge for the evaluation of the long-term environmental impact of nanoparticles.
This model of GNP dose enhancement also offers several possible avenues for future development. For example, the dominance of short-range effects highlights the importance of the sub-cellular uptake and localisation. While in this work a homogeneous nanoparticle distribution was assumed and agreed well with the effects of 1.9 nm GNPs in MDA-MB-231 cells, uptake and distribution depend on the type of cell and the contrast agent being considered, differing greatly even between different sizes of GNP24. Similarly, the observed enhancement varies significantly between different cell lines, suggesting that the observed enhancement depends significantly on the biological distribution of the GNPs within the cell9. These observations highlight the importance of improved understanding of sub-cellular localisation of these contrast agents, as agents which see an inhomogeneous distribution may see a decreased efficacy, as GNPs which are localised far from sensitive areas within the cell would be less likely to lead to cell death.
However, this also indicates the potential for improved control over sub-cellular localisation to dramatically improve the effectiveness of contrast agent enhanced therapies, as a relatively small number of well-targeted particles could potentially lead to a significant concentration within the cell nucleus and a correspondingly large RBE. Additionally, the relative inactivity of the core of the nanoparticle is of potential interest to approaches which seek to optimise nanoparticle properties by combining cores and coatings of different materials25,26, as this could potentially be achieved without compromising the dose-enhancing properties of the surface.
Methods
Simulations
Simulations of the dose deposited around a GNP following exposure to X-rays were carried out using the Geant427 Monte Carlo toolkit (version 4.9.3), using with the Geant4-DNA extensions28 to provide sufficient resolution of track structure in the water volume.
The simulation geometry consisted of a single gold nanoparticle (whose size could be varied at runtime), placed at the centre of a cube of water with sides of 200 µm. Simulations were carried out with nanoparticles ranging in diameter from 2 to 50 nm. The large size of the water volume relative to the GNP allowed for sufficient dose buildup to occur by the time the beam reached the particle, allowing for effects of secondary particles to be taken into account. Energy deposits in the water volume surrounding the GNP were recorded according to position and size, broken down by the time of particle which deposited the energy (primary photon, photoelectron, Auger electron, etc).
Irradiations were carried out with a variety of types of X-ray spectra. Monoenergetic X-ray beams ranging from 20 to 150 keV were modelled, together with the simulated output of a 160 kVp X-ray source (to provide comparison with the experimental setup used to produce the data illustrated in Figure 6). In all cases, an X-ray exposure uniformly irradiating a single face of the water volume was simulated.
The number of primary events required to give acceptable statistics for each combination varied based on nanoparticle size and primary energy. This ranged from a low of 1.04 × 108 events (for 20 keV photons on a 20 nm nanoparticle) up to 2.16 × 109 particles for 150 keV photons on a 20 nm nanoparticle.
Local Effect Model
In normal cell-survival analysis, the fraction of cells which survive an exposure to ionising radiation is given by a linear-quadratic response,  , where α and β are characteristics of the cell line and D is the mean dose delivered to the entire volume containing the cells. This dose is typically calculated on a macroscopic scale, averaged over a volume containing a very large number of cells.
, where α and β are characteristics of the cell line and D is the mean dose delivered to the entire volume containing the cells. This dose is typically calculated on a macroscopic scale, averaged over a volume containing a very large number of cells.
This approach works well for sparsely ionising radiation such as the X-rays which are typically used in radiotherapy. However, if an equal dose D is delivered to a cell population using densely ionising radiation such as heavy ions, significantly more cells are killed. This increase in killing is referred to as the Relative Biological Effectiveness (RBE) and is defined by RBE = DX /DI , where DX is a dose of X-ray radiation and DI is the dose of densely ionising radiation which leads to the same level of cell killing.
While the RBE can be empirically determined from cell survival experiments, considerable effort has also been put into explaining it from a theoretical basis. One such approach which seeks to do this is the Local Effect Model (LEM). A brief description is presented below - more comprehensive descriptions and verification of the LEM can be found elsewhere13.
Instead of considering the cell-killing effects of an average macroscopic dose as described above, the LEM considers the probability of damage occuring at each point in a cell based on the dose at that point alone and calculates a surviving fraction based on the sum probability of damage occurring over the whole cell.
The LEM describes the damage which occurs to cells in terms of “lethal lesions”, which can be described in the case of a uniform dose as S(D) = e−N(D), where N(D) is the number of lethal lesions induced by a homogeneous dose D. Thus, for sparsely ionising radiation, it can be seen that N(D) = −log(S[D]) = αD + βD2, by applying the linear-quadratic survival, as above.
However, for inhomogeneous radiation, the number of lesions induced is calculated based off the local dose at each point and then integrated over the whole cell volume, giving  where Dr is the local dose delivered at point r and dV/V is the corresponding volume fraction which sees that dose. Once the total number of lesions within a cell, Ntot , is calculated, the survival probability is then given by
where Dr is the local dose delivered at point r and dV/V is the corresponding volume fraction which sees that dose. Once the total number of lesions within a cell, Ntot , is calculated, the survival probability is then given by  . It can be seen that this simplifies to the standard survival curve in the case of a uniform dose, but inhomogeneous doses can cause greater levels of damage due to the quadratic term in the dose response.
. It can be seen that this simplifies to the standard survival curve in the case of a uniform dose, but inhomogeneous doses can cause greater levels of damage due to the quadratic term in the dose response.
While the LEM is typically applied to heavy ion therapies, it can be applied to any system where the dose distribution can be calculated, such as the GNP-radiation interaction described in this work.
To calculate the LEM-predicted survival for a given system, a radial dose distribution was generated in Geant4 for the corresponding combination of GNP size and X-ray energy. This provides values for the short-range dose contribution which results from an ionising event in a GNP and would be predicted to be highly inhomogeneous with dose. Since this only described the volume affected by a single ionising event, the volume associated with each dose must be scaled to describe the fraction of the total volume which sees that dose, which is a function of the GNP density, gold ionisation rate at that energy and the total dose deposited.
Once the rapidly-varying component of the dose distribution has been calculated, this can be added to the effectively uniform background dose level which is delivered by X-rays which do not interact with GNPs to give the full dose volume distribution for a given combination of X-ray energy and GNP size. This can then be applied to the function above to calculate the local damage at each point in the volume and thus Ntot and SLEM .
The RBE has been used to characterise the varying effects of GNP enhancement at different energies. As the exact dose-modifying effects of GNP vary as a function of energy, this was considered by comparison to the survival at 2 Gy of X-ray dose. That is, RBE = 2/DAu , where DAu is the dose at which the LEM predicts that cells irradiated in the presence of GNPs would have equal survival to those exposed to 2 Gy of X-rays in the absence of gold.
From the above model, it is clear that the effects of the LEM depend on the α and β radiation response parameters in the absence of GNPs. For the results presented in this work, these were taken to be α = 0.019 ± 0.025 and β = 0.052 ± 0.007, which correspond to MDA-MB-231 breast cancer cells, whose radiation response in the presence of GNPs has previously been investigated10.
Radial Dose Calculations
The dose distribution in the GNP-water system is typically calculated by scoring energy deposits in concentric shells centered on the gold nanoparticle and dividing these deposits by the mass of the shell12,29 and this method was used to illustrate the distributions shown in Figures 1 and 4. However, this calculation is slightly misleading, as energy deposits spread from the location of the ionising event (as seen in Figure 2), rather than the nanoparticle centre. As a result, calculations of dose which centre on the nanoparticle tend to slightly underestimate the dose, by considering energy deposits spread over a larger than is actually the case.
To address this, the dose distributions used to the LEM were scored in concentric shells centered on the individual ionising events in the GNP, rather than the nanoparticle itself. Scoring in this way does not significantly affect the conclusions derived from Figures 1 or 4, but does somewhat increase the RBE predictions obtained for larger nanoparticles, by approximately 10%.
Cell Survival Data
The effects of GNP on cell survival following radiation exposure was investigated using a clonogenic cell survival assay. MDA-MB-231 breast cancer cells were exposed to X-ray doses from a 160 kVp source, ranging from 0 to 6 Gy, having been incubated either in normal cell growth media or cell growth media containing 500 µg/mL of 1.9 nm gold nanoparticles for 24 hours prior to irradiation. The surviving fraction was calculated by comparing the number of live cells after these exposures to the number of live cells in the unirradiated control samples.
Further details on the clonogenic assay and the experimental conditions can be found elsewhere10.
In the original publication, the data was analysed by fitting linear-quadratic survival curves of the form  . This showed an increase in α and β due to the sensitising properties of the GNPs. In this work, the effects of adding the gold were modelled by simulating the local dose deposited in the vicinity of a 2 nm GNP following exposure to 160 kVp X-rays and predicting the surviving fraction at each dose for a 500 µg/mL concentration of GNPs in cells whose α and β values were taken to be equal to that of the MDA-MB-231 cells which were irradiated in the absence of GNPs. This theoretically predicted curve is plotted through the with-gold data in Figure 6.
. This showed an increase in α and β due to the sensitising properties of the GNPs. In this work, the effects of adding the gold were modelled by simulating the local dose deposited in the vicinity of a 2 nm GNP following exposure to 160 kVp X-rays and predicting the surviving fraction at each dose for a 500 µg/mL concentration of GNPs in cells whose α and β values were taken to be equal to that of the MDA-MB-231 cells which were irradiated in the absence of GNPs. This theoretically predicted curve is plotted through the with-gold data in Figure 6.
Change history
18 April 2013
A correction has been published and is appended to both the HTML and PDF versions of this paper. The error has not been fixed in the paper.
References
Webb, S. The physical basis of IMRT and inverse planning. Brit. J. Radiol. 76, 678–689 (2003).
Hainfeld, J. F., Slatkin, D. N., Focella, T. M. & Smilowitz, H. M. Gold nanoparticles: a new X-ray contrast agent. Brit. J. Radiol. 79, 248–53 (2006).
Cai, Q.-Y. et al. Colloidal gold nanoparticles as a blood-pool contrast agent for X-ray computed tomography in mice. Invest. Radiol. 42, 797–806 (2007).
Hainfeld, J. F., Dilmanian, F. A., Slatkin, D. N. & Smilowitz, H. M. Radiotherapy enhancement with gold nanoparticles. J. Pharm. Pharmacol. 60, 977–85 (2008).
Cho, S. Estimation of tumour dose enhancement due to gold nanoparticles during typical radiation treatments: a preliminary Monte Carlo study. Phys. Med. Biol. 50, N163 (2005).
Robar, J. L. Generation and modelling of megavoltage photon beams for contrast-enhanced radiation therapy. Phys. Med. Biol. 51, 5487–504 (2006).
McMahon, S. J., Mendenhall, M. H., Jain, S. & Currell, F. Radiotherapy in the presence of contrast agents: a general figure of merit and its application to gold nanoparticles. Phys. Med. Biol. 53, 5635–51 (2008).
Brun, E., Sanche, L. & Sicard-Roselli, C. Parameters governing gold nanoparticle X-ray radiosensitization of DNA in solution. Colloid Surface. B 72, 128–134 (2009).
Butterworth, K. T. et al. Evaluation of cytotoxicity and radiation enhancement using 1.9 nm gold particles: potential application for cancer therapy. Nanotechnology 21, 295101 (2010).
Jain, S. et al. Cell specific radiosensitization by gold nanoparticles at megavoltage radiation energies. Int. J. Radiat. Oncol. 79, 531–539 (2011).
Rousseau, J. et al. Enhanced survival and cure of F98 glioma-bearing rats following intracerebral delivery of carboplatin in combination with photon irradiation. Clin. Cancer Res. 13, 5195–201 (2007).
Carter, J. D., Cheng, N. N., Qu, Y., Suarez, G. D. & Guo, T. Nanoscale energy deposition by X-ray absorbing nanostructures. J. Phys. Chem. B 111, 11622–5 (2007).
Scholz, M. & Kraft, G. Calculation of heavy ion inactivation probabilities based on track structure, x ray sensitivity and target size. Radiat. Prot. Dosim. 52, 29–33 (1994).
Elsässer, T. & Scholz, M. Cluster effects within the local effect model. Radiat. Res. 167, 319–29 (2007).
Robar, J. L., Riccio, S. A. & Martin, M. A. Tumour dose enhancement using modified megavoltage photon beams and contrast media. Phys. Med. Biol. 47, 2433–49 (2002).
Chithrani, D. et al. Gold Nanoparticles as Radiation Sensitizers in Cancer Therapy. Radiat. Res. 173, 719–728 (2010).
Campbell, C. T. & Claussen, M. The Active Site in Nanoparticle Gold Catalysis. Science 306, 234–235 (2004).
Storhoff, J. J., Lucas, A. D., Garimella, V., Bao, Y. P. & Müller, U. R. Homogeneous detection of unamplified genomic DNA sequences based on colorimetric scatter of gold nanoparticle probes. Nat. Biotechnol. 22, 883–7 (2004).
Liu, J. & Lu, Y. Preparation of aptamer-linked gold nanoparticle purple aggregates for colorimetric sensing of analytes. Nat. Protoc. 1, 246–52 (2006).
Peer, D. et al. Nanocarriers as an emerging platform for cancer therapy. Nat. Nanotechnol. 2, 751–60 (2007).
Park, S. Y. et al. DNA-programmable nanoparticle crystallization. Nature 451, 553–6 (2008).
Turner, M. et al. Selective oxidation with dioxygen by gold nanoparticle catalysts derived from 55-atom clusters. Nature 454, 981–3 (2008).
ICRP. ICRP Publication 92: Relative Biological Effectiveness (RBE), Quality Factor (Q) and Radiation Weighting Factor (wR) (Elsevier, Oxford, 2003).
Chithrani, B. D., Ghazani, A. A. & Chan, W. C. W. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Lett. 6, 662–8 (2006).
Lin, J. Gold-Coated Iron (Fe@Au) Nanoparticles: Synthesis, Characterization and Magnetic Field-Induced Self-Assembly. J. Solid State Chem. 159, 26–31 (2001).
Chen, M., Yamamuro, S., Farrell, D. & Majetich, S. A. Gold-coated iron nanoparticles for biomedical applications. J. Appl. Phys. 93, 7551 (2003).
Agostinelli, S. et al. Geant4 - a simulation toolkit. Nucl. Instrum. Methods Phys. Res., Sect. A 506, 250–303 (2003).
Chauvie, S., Francis, Z., Guatelli, S., Incerti, S. & Mascialino, B. Geant4 physics processes for microdosimetry simulation: design foundation and implementation of the first set of models. IEEE Trans. Nucl. Sci. 54, 2619 (2006).
Jones, B. L., Krishnan, S. & Cho, S. H. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Med. Phys. 37, 3809 (2010).
Acknowledgements
This work was supported by a Cancer Research UK grant (Grant No. C1278/A9901)
Author information
Authors and Affiliations
Contributions
S.J.M. proposed use of the LEM which he implemented along with the Monte Carlo calculations and drafted the manuscript, all under the supervision of F.J.C who proposed alpha's role in testing the model and the wider carcinogenic implications. S.J., J.C. and K.T.B. performed cell survival experiments, including the results shown in Figure 6, under the direction of D.H. and K.P. W.H., M.M. and G.S. performed additional experiments, planned by F.J.C., which informed the development of this model. G.D. performed TEM studies which informed ideas about the uptake of GNPs. A.H. performed dosimetric measurements and provided input on clinical implications, along with S.J. and J.O. All authors contributed extensively to discussions about this work and in reviewing the manuscript.
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/
About this article
Cite this article
McMahon, S., Hyland, W., Muir, M. et al. Biological consequences of nanoscale energy deposition near irradiated heavy atom nanoparticles. Sci Rep 1, 18 (2011). https://doi.org/10.1038/srep00018
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/srep00018
This article is cited by
-
The effect of nanoparticle coating on biological, chemical and biophysical parameters influencing radiosensitization in nanoparticle-aided radiation therapy
BMC Chemistry (2023)
-
Gold Nanoparticles Enhancing Generation of ROS for Cs-137 Radiotherapy
Nanoscale Research Letters (2022)
-
Improve the cytotoxic effects of megavoltage radiation treatment by Fe3O4@Cus–PEG nanoparticles as a novel radiosensitizer in colorectal cancer cells
Cancer Nanotechnology (2022)
-
Radiation dose enhancement using gold nanoparticles with a diamond linear accelerator target: a multiple cell type analysis
Scientific Reports (2022)
-
Breaking photoswitch activation depth limit using ionising radiation stimuli adapted to clinical application
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.