Abstract
Multi-regional input-output (MRIO) models are one of the most widely used approaches to analyse the economic interdependence between different regions. We utilised the latest socioeconomic datasets to compile a Chinese MRIO table for 2012 based on the modified gravity model. The MRIO table provides inter-regional and inter-sectoral economic flows among 30 economic sectors in China’s 30 regions for 2012. This is the first MRIO table to reflect China’s economic development pattern after the 2008 global financial crisis. The Chinese MRIO table can be used to analyse the production and consumption structure of provincial economies and the inter-regional trade pattern within China, as well as function as a tool for both national and regional economic planning. The Chinese MRIO table also provides a foundation for extensive research on environmental impacts by linking industrial and regional output to energy use, carbon emissions, environmental pollutants, and satellite accounts.
Design Type(s) | source-based data transformation objective |
Measurement Type(s) | Socioeconomic Factors |
Technology Type(s) | computational modeling technique |
Factor Type(s) | geographic location |
Sample Characteristic(s) | Municipality of Beijing • Municipality of Tianjin • Hebei Province • Shanxi Province • Inner Mongolia Autonomous Region • Liaoning Province • Jilin Province • Heilongjiang Province • Municipality of Shanghai • Jiangsu Province • Zhejiang Province • Anhui Province • Fujian Province • Jiangxi Province • Shandong Province • Henan Province • Hubei Province • Hunan Province • Guangdong Province • Guangxi Zhuang Autonomous Region • Hainan Province • Municipality of Chongqing • Sichuan Province • Guizhou Province • Yunnan Province • Shaanxi Province • Gansu Province • Qinghai Province • Ningxia Hui Autonomous Region • Xinjiang Autonomous Region |
Machine-accessible metadata file describing the reported data (ISA-Tab format)
Similar content being viewed by others
Background & Summary
Although China is usually viewed as a homogenous entity in socioeconomic analysis, it is a vast country with great variations in economic development patterns, resource endowments, population density, and lifestyle. For example, the per capita gross domestic production (GDP) in Beijing, the capital of China, was more than four times the value for Gansu, a poor province in western China. China has entered a new phase of economic development since the 2008 global financial crisis – a “new normal” – in which its economic development model has changed greatly. The domestic trade patterns among different provinces might have changed because the economy is growing faster in western China than in eastern China.
Multi-regional input-output (MRIO) models are one of the most widely used approaches to analyse the economic interdependence between different regions. Because of data availability, most of the available MRIO models demonstrate inter-country economic relationships, such as the Global Trade Analysis Project (GTAP)1, World Input-Output Database (WIOD)2, Organisation for Economic Co-operation and Development Inter-Country Input-Output (OECD-ICIO)3, and EORA MRIO4. Some researchers have compiled Chinese MRIO tables based on provincial input-output tables. Zhang and Qi integrated China into eight regions and compiled MRIO tables for these eight regions for 2002 and 2007 (ref. 5). Liu et al. compiled MRIO table for China’s 30 provinces and 30 economic sectors for 2007 (ref. 6) and 20107. The 2007 MRIO table has been used to analyse energy use8,9, carbon emissions10, air pollutants11 and water consumption12,13 embodied in trade among China’s 30 provinces. The 2010 MRIO table is the latest available version and was compiled based on the 2007 MRIO table and provincial extended input-output tables for 2010. Since only 17 Chinese provinces provide extended input-output tables for 2010, the extended input-output tables of the remaining 13 regions were compiled based on their 2007 bench-mark tables14. Therefore, the 2010 MRIO table is not as accurate as the 2007 MRIO table and cannot fully reflect the changes in China’s economic structure after the 2008 global financial crisis. The Chinese government released surveyed input-output tables at the provincial level for 2012. Based on these provincial input-output tables, we compiled the Chinese MRIO table for 2012 for 30 regions (excluding Hong Kong, Macao, Taiwan, and Tibet).
In the 2012 MRIO table, there are 30 economic sectors in each region. Final use is divided into five categories, including rural household consumption, urban household consumption, government consumption, fixed capital formation, and changes in inventories (Table 1). Value added is divided into four categories, including compensation of employees, net taxes on production, depreciation of fixed capital, and operating surplus (Table 2). Exports from each region are divided into international and domestic exports, and imports to each region are divided into international and domestic imports (Table 3).
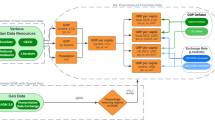
The Chinese MRIO table can be used to analyse provincial economies within China, as a tool for both national and regional economic planning. The table demonstrates the trade pattern among different sectors and different regions. Figure 1 demonstrates the inter-sector dependence of 30 economic sectors in China. The Chinese MRIO table can also be used to assess the economic impacts of events along supply chains and can identify economically related industry clusters. The Chinese MRIO table for 2012 can be used to estimate the changes in China’s economic development patterns by integrating the available MRIO tables for 2007 and 2010.
The names of sectors 1 to 30 can be found in Table 4. The rows demonstrate the distribution of a sector’s output throughout the economy, while the columns describe the inputs required by a sector to produce its output. The colour corresponds to the inter-sector transfer, from the largest one in red to the smallest one in blue (see scale). Based on the Chinese MRIO table, we can also analyse the inter-sector transfers at the provincial level.
In addition, the Chinese MRIO table can be used to perform environmentally extended input-output analysis (EEIOA) by adding additional columns, such as energy use, carbon emissions, water consumption, and air pollutants15,16. For example, the data on energy inputs to each sector and each region can be applied to assess the carbon emissions embodied in the trade among 30 sectors and 30 regions. The data on China’s air pollutants can be obtained from the Multi-resolution Emission Inventory for China (MEIC)17. Further, the data on China’s energy consumption and carbon emissions at national and provincial levels can be downloaded freely from the China Emission Accounts and Datasets (CEADs, www.ceads.net) and are also presented in our previous paper published in Scientific Data18.
Methods
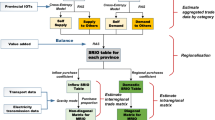
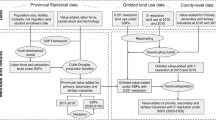
We compiled an MRIO database for China’s 26 provinces and 4 cities; Hong Kong, Macao, Taiwan, and Tibet were excluded due to data unavailability. The Chinese MRIO table was compiled based on the input-output tables (IOTs) for 30 Chinese provinces that are published by the National Statistics Bureau. The IOTs demonstrate the economic linkages among 42 economic sectors at the provincial level. All provincial IOTs were aggregated into 30 sectors (see Table 4 for the concordance of sectors) because there are 30 sectors in the Chinese MRIO tables for both 2007 and 2010. We aim to build a time-series MRIO table database for China. It must be stated that the aggregation of sectors might result in bias in the input-output analysis. For example, Su and Ang19 indicated that sector aggregation affected the results of CO2 emissions embodied in trade in the environmental input–output analysis framework. In addition, Lenzen20 showed that both aggregation and disaggregation resulted in bias in the input-output analysis of environmental issues.
Transfer provincial competitive IOTs into non-competitive IOTs.
IOTs can be divided into two categories according to the ways in which imports are treated, i.e., competitive and non-competitive IOTs. In competitive IOTs, imports are aggregated into a single column vector in the final use, and there is no distinction between imported input and domestically produced input. In non-competitive IOTs, the intermediate input is divided into domestic intermediate input and imported intermediate input, and the final use is divided into domestic final use and imported final use. The non-competitive IOTs are needed to compile the Chinese MRIO table. However, the original provincial IOTs are competitive IOTs.
As imports of commodities are treated as competitive imports in original provincial IOTs, the imports are also accounted for in the intermediate transactions and final demand transaction21. The impact of the domestic economy of an exogenous demand cannot be distinguished. It is necessary to transfer competitive imports into non-competitive imports in the compilation process. There are normally two approximation procedures to estimate the matrix of domestic transactions and interindustry imports. Method one is to assume that the layout of the matrix of competitive imports is the same as the domestic intermediate matrix, which implies that no imports are consumed directly in the final demand. Method two considers the final demand and assumes that the proportion of imports in intermediate commodities is the same as that in the final demand. In this study, we adopt the latter method by assuming that every economic sector and final use category uses imports in the same proportions16,22. Therefore, the matrix of competitive imports can be derived from the vector of competitive imports through multiplication by the proportion mentioned above. In the provincial competitive IOTs, the total output of a province can be expressed as
where O is the total output, A is the direct requirements matrix, F is the final use, and M is the imports. The share of import in the supply of goods to each sector is
where si is the share of import in the supply of goods to sector i, oi is the total output of sector i, and mi is the import of sector i. The new requirements matrix (Ad) and final use (Fd) in which only domestic goods are included are derived by
where L is a vector with all elements equal to 1, and indicates that the vector is diagonalised. In this way, the import is removed from the intermediate use and final use and becomes a new column vector (including the import for intermediate use and final use) in the IOTs. In the new non-competitive IOTs, the total output of a province is expressed as
Modified gravity model to compile the MRIO
We use the gravity model and modify it with interactions among different regions for the same sector23,24. There are two main reasons to adopt the gravity model for estimating interregional trade flows. First, the gravity model is the most appropriate approach on the basis of available Chinese data. The approaches to construct MRIO tables can be identified as survey and non-survey approaches. The survey-based approach identifies interregional trade flows from a collection of primary data by surveys of industries and final consumers, while non-survey techniques estimate interregional trade flows from single-regional input-output tables by various modification techniques25. The gravity model has become the mainstream non-survey tool to estimate the interregional trade flows, not only for its simplicity, but also because of the fewer data requirements. The feasibility and reliability of this approach have been proven in many studies26. Other approaches are based mainly on location quotients, i.e., a type of estimation that involves scaling down. Location quotients are frequently used to estimate the interregional trade coefficients. The method is often criticised for its reliability25. Moreover, there are usually more data requirements for other non-survey approaches, such as the mathematical programming model developed by Canning and Wang27 and the computable general equilibrium (CGE) model28. Second, the MRIO table is also used to build a time-series MRIO table database for China. The MRIO tables for 2007 and 2010 were both constructed using the gravity model6,7. To maintain methodological consistency, we chose the gravity model to compile the 2012 MRIO table.
In the standard gravity model, the interregional trade flows are specified as a function of the total regional outflows, total regional inflows, and transfer cost, which is usually proxied by a distance function. The gravity model is
where is the trade flows of sector i from region r to region s, eβ0 is the constant of proportionality, is the total outflows of sector i from region r, is the total inflows of sector i to region s, drs is the distance between region r and region s (we use the distance between the capital cities of the two provinces in the study), β1 and β2 are weights assigned to the masses of origin and destination, respectively, and β3 is the distance decay parameter. The above equation can be transformed into
and further into
where Y is the logarithm of the trade flows of product i between regions, Ln is a vector with all elements equal to 1, X1 and X2 are the logarithm of the total outflows from origin regions and total inflows to destination regions, respectively, and X3 is the logarithm of the distance between two regions. The equation can be solved using multiple regression.
There are different interregional competition and cooperation relationships for different sectors. The industrial supply chains in some sectors are shorter, and there may be competitive relationships among different regions for these sectors, such as agriculture, food processing and textiles. In comparison, the industrial supply chains in other sectors are longer, and there may be more cooperative relationships among different regions for these sectors, such as machinery and chemicals. To reflect interregional competition and cooperation in our analysis, we introduce the concept of impact coefficients among different regions for the same sector. The impact coefficient for one sector is obtained by
where is the impact coefficient between regions g and h for sector i, and are the location entropy of sector i in regions g and h, respectively, and n is the number of regions. The impact coefficients indicate that stronger interactions for sector i occur between regions g and h if the location entropy of the sector in both regions is higher. The impact coefficient equation indicates that when g≠h, and a higher value indicates stronger interactions. In addition, when g=h.
We also introduce the concept of impact exponents among different regions for the same sector. It is assumed that if a larger proportion of one sector’s output is used for its own intermediate inputs, then interregional cooperation exists for the sector. The impact exponent for one sector is obtained by
where θi is the impact exponent for sector i, δi is the proportion of the total output of sector i that it uses as its own intermediate inputs, and is the average value of δi. If θi>0, there are competitive relationships for sector i; otherwise, there are cooperative relationships for sector i.
We use the impact coefficients and impact exponents to modify the interregional trade flows that are obtained by the standard gravity model. The formula is
where Y′ represents the modified trade flows of sector i and represents the trade flows, which are obtained by the standard gravity model.
The initial trade flow matrix produced above does not meet the “double sum constraints”, in which the row and column totals match the known values in the 2012 IOTs. The RAS approach is used to adjust the trade flow matrix to ensure agreement with the summed constraints29. The RAS approach tends to preserve the structure of the initial matrix as much as possible with a minimum number of necessary changes to restore the row and column sums to the known values26.
Adjustment according to the Chinese national IOT
In addition to the provincial IOTs, China also published a national IOT for 2012. There are great gaps between the national IOT and provincial IOTs. The sum of the total output of the 30 provinces in the provincial IOTs is 7% higher than the national total output in the national IOT. The total amount in the national IOT is assumed to be more accurate, while provincial IOTs more closely represent the economic structure at the provincial level. Therefore, we use the national IOT to adjust the total amount of output, value added, and international export and import in the MRIO, which is compiled based on provincial IOTs. Then, the adjusted MRIO table is balanced by the RAS approach.
where , , , and are the adjusted output, value added, and international export and import for sector i, respectively. oi, vi, ei, and mi are original output, value added, and international export and import for sector i, respectively, which are obtained from the MRIO table compiled using the modified gravity model. , , , and are the output, value added, and international export and import for sector i, respectively, which are obtained from China’s national IOT.
Data Records
The Chinese MRIO table for 2012 is stored as an excel document, and the codes are stored as a word document (Data Citation 1). The Chinese MRIO table has three main parts (Table 5). First, the top left part is a 900×900 matrix, which is the intermediate monetary flows among 30 regions and 30 sectors. Second, the top right part is a 900×150 matrix, which is the final use of 30 regions and 5 final use categories, including rural household consumption, urban household consumption, government consumption, fixed capital formation, and changes in inventories. The bottom left is a 4×900 matrix, which is the value added of 30 regions and 30 sectors. The value added is divided into compensation of employees, net taxes on production, depreciation of fixed capital, and operating surplus. In addition, international export is demonstrated as a 900×1 column vector, while international import is divided into import used as intermediate use (1×900 row vector) and import used as final use (1×150 row vector). The total output column vector is equal to the transposition of the total input row vector.
Technical Validation
The Chinese MRIO table is compiled using the modified gravity model. The multiple regression impacts the quality of the MRIO table. The regression results for 30 economic sectors are shown in Table 6. It can be observed that the goodness of fit (R2) for most sectors is greater than 0.4, except for metal mining and petroleum and gas. The R2 value for the textile sector exceeds 0.8.
The RAS approach is used to adjust the trade flow matrix to ensure agreement with the “double sum constraints”. There is a 900×1 column vector that reflects the balance error in the Chinese MRIO table. The balance error in the table is caused mainly by the balance error in the provincial IO tables and the gap between total inflows and outflows at the provincial level. The proportions of error in the total output for most sectors are within ±5%, which is close to the values in the Chinese MRIO tables for 2007 and 2010 (refs 6,7).
China also published a national single-region input-output (SRIO) table for 2012 in addition to the provincial IOTs. We compared the sector dependence between the MRIO and SRIO tables (Table 7). It can be observed that the proportions of other sectors' input relative to the total intermediate input for each sector are similar in the two tables. Most of the differences are within ±15%. The largest difference is 22%, i.e., for gas and water production and supply.
The structure of intermediate use, final use, exports, imports, and output is critical for the quality of the MRIO table. We compared the structure of the Chinese MRIO table and other four widely used global MRIO tables that include China, i.e., the Global Trade Analysis Project (GTAP)1, World Input-Output Database (WIOD)2, Organisation for Economic Co-operation and Development Inter-Country Input-Output (OECD-ICIO)3, and EORA4. With respect to the Chinese MRIO table, the proportions of intermediate use, final use, and export in the total output are 61, 31, and 7%, respectively. The largest proportion of intermediate use is 64% in EORA, while the smallest proportion is 58% in GTAP (Fig. 2a). In the Chinese MRIO table, 79.6% of China’s imports are used for intermediate use, while the remaining 20.4% are used for final use. The largest proportion of imports for intermediate use is 80.2% in GTAP, while the smallest proportion is 73.9% in OECD-ICIO (Fig. 2b).
(a) compares the structure of intermediate use, final use, and exports. (b) compares the structure of imports for intermediate and final use. The intermediate use and final use exclude imports, so the summation of intermediate use, final use, and exports is equal to the total output. Data sources: Global Trade Analysis Project (GTAP)1, World Input-Output Database (WIOD)2, Organisation for Economic Co-operation and Development Inter-Country Input-Output (OECD-ICIO)3, and EORA4.
Additional information
How to cite this article: Mi, Z. et al. A multi-regional input-output table mapping China's economic outputs and interdependencies in 2012. Sci. Data 5:180155 doi: 10.1038/sdata.2018.155 (2018).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
References
Aguiar, A., Narayanan, B. & McDougall, R. An overview of the GTAP 9 data base. J. Glob. Econ. Anal. 1, 181–208 https://doi.org/10.21642/JGEA.010103AF (2016).
Timmer, M. P., Dietzenbacher, E., Los, B., Stehrer, R. & Vries, G. J. An illustrated user guide to the world input–output database: the case of global automotive production. Rev. Int. Econ. 23, 575–605 https://doi.org/10.1111/roie.12178 (2015).
Yamano, N. OECD inter-country input–output model and policy implications in: Uncovering Value Added in Trade: New Approaches to Analyzing Global Value Chains (ed. Xing, Y. World Scientific, 2016).
Lenzen, M., Kanemoto, K., Moran, D. & Geschke, A. Mapping the structure of the world economy. Environ. Sci. Technol. 46, 8374–8381 https://doi.org/10.1021/es300171x (2012).
Zhang, Y. & Qi, S. China Multi-Regional Input-Output Models: 2002 and 2007. (China Statistics Press, 2012).
Liu, W. et al. Theory and Practice of Compiling China 30-Province Inter-Regional Input-Output Table of 2007 (China Statistics Press, 2012).
Liu, W., Tang, Z., Chen, J. & Yang, B. China 30-Province Inter-Regional Input-Output Table of 2010 (China Statistics Press, 2014).
Zhang, B., Chen, Z. M., Xia, X. H., Xu, X. Y. & Chen, Y. B. The impact of domestic trade on China's regional energy uses: A multi-regional input–output modeling. Energy Policy 63, 1169–1181 https://doi.org/10.1016/j.enpol.2013.08.062 (2013).
Zhang, Y. et al. Multi-regional input–output model and ecological network analysis for regional embodied energy accounting in China. Energy Policy 86, 651–663 https://doi.org/10.1016/j.enpol.2015.08.014 (2015).
Feng, K. et al. Outsourcing CO2 within China. Proc. Natl. Acad. Sci. USA 110, 11654–11659 https://doi.org/10.1073/pnas.1219918110 (2013).
Li, Y. et al. Interprovincial reliance for improving air quality in China: a case study on black carbon aerosol. Environ. Sci. Technol. 50, 4118–4126 https://doi.org/10.1021/acs.est.5b05989 (2016).
Zhang, C. & Anadon, L. D. A multi-regional input–output analysis of domestic virtual water trade and provincial water footprint in China. Ecol. Econ. 100, 159–172 https://doi.org/10.1016/j.ecolecon.2014.02.006 (2014).
Zhang, C. & Anadon, L. D. Life cycle water use of energy production and its environmental impacts in China. Environ. Sci. Technol. 47, 14459–14467 https://doi.org/10.1021/es402556x (2013).
Sun, X., Li, J., Qiao, H. & Zhang, B. Energy implications of China's regional development: New insights from multi-regional input-output analysis. Appl. Energy 196, 118–131 https://doi.org/10.1016/j.apenergy.2016.12.088 (2017).
Mi, Z. et al. Socioeconomic impact assessment of China's CO2 emissions peak prior to 2030. J. Clean Prod. 142, 2227–2236 https://doi.org/10.1016/j.jclepro.2016.11.055 (2017).
Mi, Z. et al. Consumption-based emission accounting for Chinese cities. Appl. Energy 184, 1073–1081 https://doi.org/10.1016/j.apenergy.2016.06.094 (2016).
MEIC. National CO2 emissions. Multi-resolution Emission Inventory for China http://www.meicmodel.org/index.html (2018).
Shan, Y. et al. China CO2 emission accounts 1997–2015. Sci. Data 5, 170201 https://doi.org/10.1038/sdata.2017.201 (2018).
Su, B. & Ang, B. W. Input–output analysis of CO2 emissions embodied in trade: The effects of spatial aggregation. Ecol. Econ. 70, 10–18 https://doi.org/10.1016/j.ecolecon.2010.08.016 (2010).
Lenzen, M. Aggregation versus disaggregation in input–output analysis of the environment. Econ. Syst. Res. 23, 73–89 https://doi.org/10.1080/09535314.2010.548793 (2011).
Mi, Z. et al. Pattern changes in determinants of Chinese emissions. Environ. Res. Lett. 12, 074003 https://doi.org/10.1088/1748-9326/aa69cf (2017).
Weber, C. L., Peters, G. P., Guan, D. & Hubacek, K. The contribution of Chinese exports to climate change. Energy Policy 36, 3572–3577 https://doi.org/10.1016/j.enpol.2008.06.009 (2008).
Leontief, W. & Strout, A. Multiregional input-output analysis in: Structural Interdependence and Economic Development (ed. Barna, T. McMillan, 1963).
Liu, W., Li, X., Liu, H., Tang, Z. & Guan, D. Estimating inter-regional trade flows in China: A sector-specific statistical model. J. Geogr. Sci. 25, 1247–1263 https://doi.org/10.1007/s11442-015-1231-6 (2015).
Bonfiglio, A. & Chelli, F. Assessing the behaviour of non-survey methods for constructing regional input–output tables through a Monte Carlo simulation. Econ. Syst. Res. 20, 243–258 https://doi.org/10.1080/09535310802344315 (2008).
Miller, R. E. & Blair, P. D. Input-Output Analysis: Foundations and Extensions (Cambridge University Press, 2009).
Canning, P. & Wang, Z. A flexible mathematical programming model to estimate interregional input–output accounts. J. Reg. Sci. 45, 539–563 https://doi.org/10.1111/j.0022-4146.2005.00383.x (2005).
Hulu, E. & Hewings, G. J. The development and use of interregional input‐output models for Indonesia under conditions of limited information. Rev. Urban Reg. Dev. Stud. 5, 135–153 https://doi.org/10.1111/j.1467-940X.1993.tb00127.x (1993).
Jackson, R. & Murray, A. Alternative input-output matrix updating formulations. Econ. Syst. Res. 16, 135–148 https://doi.org/10.1080/0953531042000219268 (2004).
Data Citations
Mi, Z. et al. Figshare https://doi.org/10.6084/m9.figshare.c.4064285 (2018)
Acknowledgements
This study was supported by the National Key R&D Program of China (2016YFA0602604, 2016YFA0602603), the Natural Science Foundation of China (41629501, 71761137001), Chinese Academy of Engineering (2017-ZD-15-07), the UK Economic and Social Research Council (ES/L016028/1), the Natural Environment Research Council (NE/N00714X/1 and NE/P019900/1) and the British Academy Grant (AF150310).
Author information
Authors and Affiliations
Contributions
Z.M. led the project and prepared the manuscript. D.G. designed the research. Z.M. and J.M. compiled the Chinese multi-regional input-output table for 2012. All authors (Z.M., J.M., H.Z., Y.S., Y.-M.W., and D.G.) participated in the collection of data and the revision of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
ISA-Tab metadata
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ The Creative Commons Public Domain Dedication waiver http://creativecommons.org/publicdomain/zero/1.0/ applies to the metadata files made available in this article.
About this article
Cite this article
Mi, Z., Meng, J., Zheng, H. et al. A multi-regional input-output table mapping China's economic outputs and interdependencies in 2012. Sci Data 5, 180155 (2018). https://doi.org/10.1038/sdata.2018.155
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/sdata.2018.155
This article is cited by
-
An interregional environmental assessment framework: revisiting environmental Kuznets curve in China
Environmental Science and Pollution Research (2024)
-
Reality check and determinants of carbon emission flow in the context of global trade: Indonesia being the centric studied country
Environment, Development and Sustainability (2023)
-
Influence and optimization of regional enterprise spatial structure change on regional economic pattern under artificial intelligence
Soft Computing (2023)
-
A bibliometric review on carbon accounting in social science during 1997–2020
Environmental Science and Pollution Research (2022)
-
A general equilibrium assessment of COVID-19's labor productivity impacts on china's regional economies
Journal of Productivity Analysis (2022)