The effect of co-location on human communication networks

Abstract

The ability to rewire ties in communication networks is vital for large-scale human cooperation and the spread of new ideas. We show that lack of researcher co-location during the COVID-19 lockdown caused the loss of more than 4,800 weak ties—ties between distant parts of the social system that enable the flow of novel information—over 18 months in the email network of a large North American university. Furthermore, we find that the reintroduction of partial co-location through a hybrid work mode led to a partial regeneration of weak ties. We quantify the effect of co-location in forming ties through a model based on physical proximity, which is able to reproduce all empirical observations. Results indicate that employees who are not co-located are less likely to form ties, weakening the spread of information in the workplace. Such findings could contribute to a better understanding of the spatiotemporal dynamics of human communication networks and help organizations that are moving towards the implementation of hybrid work policies to evaluate the minimum amount of in-person interaction necessary for a productive work environment.

Main

The ability to establish and leverage communication networks to share information and collaboratively accomplish sophisticated tasks is a distinguishing feature of humans¹. While the ability to form social ties with others was originally developed when individuals were in close proximity, technological improvements have allowed increasingly remote forms of communication and collaboration, that now include tele- and video-conferencing, email and chats². These changes reinvigorated longstanding debates about the extent to which social relationships are predicated upon physical proximity³. While earlier studies in sociology and organizational science discuss the role of spatial propinquity in producing interpersonal ties^4,5, the causal mechanisms through which co-location affects social networks remain understudied^6,7,8,9.

Addressing this question is all the more relevant today. First, in planning the transition towards the post-COVID-19-pandemic ‘new normal’, institutions and policy-makers world-wide are wondering about the best way to reshape work environments following COVID-19^10,11,12,13. Second, the massive shift to remote work during the past two years has produced a trove of big data that promises to elucidate what happens when we remove physical presence as a main conduit of communication¹⁴. While recent work has started to highlight changes in the communication networks of information workers due to mandatory remote work, the data were collected across several campuses in the continental USA—making it difficult to link these network changes to a lack of physical proximity¹⁵. Hence, the following question remains open: what is the effect of co-location on human communication networks?

In this study, we explore the mechanism via which the complete removal and subsequent partial reintroduction of physical co-location at a large North American university—the MIT campus—affects the structure of its digital communication network. We find that, despite the robustness of many network measures to the shift to remote work, physical co-location plays a crucial role in the formation of weak ties.

Since Mark Granovetter’s seminal work in 1973¹⁶, weak ties have been identified as fundamental microscopic structures that enable the spread of ideas and opportunities in social networks. Our hypothesis is that weak ties form due to chance encounters in and around the office, so removing the possibility for chance encounters should affect the formation of weak ties. By hindering new weak tie formation, the removal of physical co-location leads to increased redundancy in email networks—more information is spread between fewer people. Put differently, physical proximity is vital for updating the people with whom we communicate over time. This is in line with earlier work on the notion of propinquity, used to denote the tendency to form connections among proximate individuals³. Propinquity can be modeled with a modification of the link-central preferential attachment model, which includes a co-location factor τ, accurately reproducing the dynamics of formation and stability of weak ties caused by long-term removal and partial reintroduction of physical co-location on the MIT campus.

Results

Forming the daily email network

We build and analyze a large email network of research workers at MIT in Cambridge, MA. Despite the wide-scale adoption of synchronous video-conferencing technology, email remains a universal mode of digital communication used by researchers to exchange information and organize meetings. To study changes in communication behavior due to fully remote work, we study the email habits of 2,834 MIT faculty and postdocs over 18 months starting on 26 December 2019. Each researcher belongs to a ‘research unit’, which describes their campus affiliation (see Supplementary Information for a complete list—the partition of the MIT research community into research units is in general finer than the partition into departments). During March 2020 MIT started implementing COVID-19 contingency plans, which led to a progressive decrease in campus attendance and culminated on Monday 23 March 2020 with the halting of in-person research activities. For each day, the number of emails sent between each pair of (anonymized) individuals is determined exactly for >66% pairs of individuals from randomized, aggregated data and used to form the edge weights of an undirected network. For the remaining pairs we estimate the number of emails sent using non-negative matrix factorization (Methods).

Robustness of network metrics to the remote work transition

Our initial analysis did not show many changes in the network: directly comparing connected components and the number of intra-/inter-research unit connections in the email network in February 2020 and February 2021 using a paired test on the logarithms of these network metrics (Methods) highlights few significant differences (Fig. 1a). However, due to the seasonal nature of academic work, paired testing comparing only February is not sufficient to estimate the short- and cumulative long-term effects of fully remote working on the communication network.

Fig. 1: Robustness of global network topology in daily reciprocated email networks.

a, The change from the beginning of the spring 2020 semester (weekdays between 5 February and 5 March 2020) to the spring 2021 semester (weekdays between 17 February and 19 March 2021) in the number of users in the largest component, the number of components, the number of connections (edges) between users who are in the same research unit and the number of connections (edges) between users in distinct research units. 95% confidence intervals (CIs) from two-sided z test on the coefficients of a generalized least squares model fit to the log difference in means (n = 16 d for all variables). Full results are in Supplementary Tables 1–4. b, Predicted cumulative change in network metrics compared with a synthetic counterfactual from 23 March 2020 to 15 July 2021. Posterior predictive intervals with 95% coverage computed using Bayesian structural time series (n_pre = 8 weeks, n_post = 72 weeks). Fitted values/intervals use the mean as the measure of central tendency.

Source data

To provide a statistically robust estimation of long-term effects, we design a methodology based on the Bayesian structural time series approach. The approach is based on the construction of a synthetic counterfactual time series from a covariate unaffected by the treatment. A well constructed synthetic counterfactual can capture fluctuations in the time series of interest due to seasonality and confounding factors other than the treatment. If the predictive power of the covariate wanes over time (which can happen because, for example, the model is only fit on data before the treatment is applied), then the width of the posterior predictive interval around the synthetic counterfactual will increase over time, representing our increased uncertainty about the distant future. As the treatment in this case corresponds to the termination of campus access for researchers, we use email data from weekends, when most researchers were not entering the office, to construct our counterfactual (Methods). When studying these cumulative effects, there are also no significant differences in the number of intra-/inter-research unit connections, the number of connected components or the size of the giant component due to remote work (Fig. 1b). A detailed plot highlighting the evolution of the uncertainty of the Bayesian structural time series model over time can be found in Supplementary Information. The fact that the sign (loss versus gain) of the change in network metrics such as connected components, inter-unit connections and size of giant component differs between Fig. 1a and Fig. 1b is indicative of the fact that choosing a single month in 2020 and 2021 for comparison does not accurately capture cumulative effects.

Weak-tie formation is impeded by remote work

To study the effect of remote work on the sorts of connection that might arise from serendipitous encounters on campus, we investigate the structure of weak ties in the email network. Because local bridges can be identified knowing only the topology of a social network, Granovetter suggested using the notion of a local bridge as an accessible proxy for the notion of a weak tie¹⁶ (see Supplementary Information for detailed definitions). To check that our results are robust to alternative definitions of weak ties, we repeat our analysis (obtaining very similar results) using low-contact-frequency ties in Supplementary Information. Figure 2a provides an illustration of the way in which chance encounters lead to the formation of new local bridges.

Fig. 2: Changes in weak ties in the MIT email network after the shift to remote work.

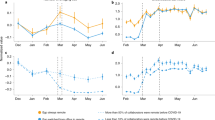
a, A candidate mechanism for local bridge formation in a social network which requires co-location. b, A drop of 55.70 (6.2%) in the number of local bridges (weak ties) after 23 March 2020 (P = 0.002, 95% CI [−91.627, −19.774]). There is a drop of −38.03 (38.7%) in the mean number of new (not previously seen) weak ties appearing each weekday after 23 March 2020 (P < 0.001, 95% CI [−53.38, −22.68]). ***P < 0.001, **0.001 ≤ P < 0.01. Statistics represent the results of a two-sided z test corresponding to a local polynomial RDD (n_pre = 42 d, n_post = 188 d). c, There is a cumulative loss of 5,110 weak ties throughout an entire year (P < 0.001, 95% posterior predictive interval [−4,957, −5,267]) and a non-significant loss of 2,930 new weak ties (P = 0.241, 95% posterior predictive interval [−11,588, 5,730]). Posterior predictive intervals computed using Bayesian structural time series (n_pre = 8 weeks, n_post = 72 weeks). d, The number of weak ties that become strong (become embedded in triangles) or are churned (dropped from the network) in a 30 d rolling window. Fitted values/intervals use the mean as the measure of central tendency.

Source data

The removal of physical co-location (as a consequence of mandatory fully remote work) caused an immediate and persistent drop in the number of weak ties formed in the MIT email network. Figure 2b shows the causal effect of a lack of co-location estimated with a piecewise polynomial regression discontinuity design (RDD) on both the number of weak ties and the number of new (not previously seen) weak ties. There is a statistically significant 6.2% drop in the number of weak ties and a 38.7% drop in the number of new weak ties coinciding with the sudden absence of co-location. Because we study a fixed population of users, as we see more ties the number of new weak ties will naturally decrease—thus the downward trend of new weak ties is expected. However, the significant jump discontinuity on 23 March 2020 indicates that the absence of physical co-location is negatively associated with the ability to form new weak ties. The decrease in the addition of new weak ties hints at a stagnation effect—researchers are not updating their pool of weak ties as often as would be expected.

Not only is the drop in weak ties sudden and statistically significant at the onset of the transition to full remote working, but it is also cumulatively significant over the course of more than one year. Using Bayesian structural time series to estimate the cumulative effect of a lack of co-location, we see in Fig. 2c a significant predicted loss of more than 5,100 weak ties from 23 March 2020 until 15 July 2021 due to remote work—approximately 1.8 ties per person in the 2,834 researchers we study. Thus we find that remote work leads to a long-lasting, statistically significant drop in weak ties. Figure 2c also shows a non-significant cumulative drop in the number of new weak ties formed in the network—we explain this phenomenon in detail in the following section.

Finally, we identify a striking difference in the mechanism via which local bridges disappear due to remote work: in the short term through the end of the spring 2020 semester, local bridges become embedded in triangles, while in the long term they are dropped from the network (Fig. 2d). We also confirm in Supplementary Information that ego networks become more stagnant in the absence of co-location—the social contacts of researchers become more similar from week to week after remote work. Specifically, by computing the intersection over union of the edges in the daily reciprocated email networks on day d and day d + 7, we see a lasting, significant increase in the stability of network edges from week to week after remote work (Supplementary Fig. 1h).

Weak-tie formation and physical proximity

As people are more likely to meet by chance on campus if their offices are nearby⁹, we expect to observe more consistent changes in the formation of new weak ties for co-located MIT personnel. For each week we predict the mean value of the dependent variable (weak ties between researchers in a fixed distance range) during business days. We use the mean of weekend values as our covariate for the Bayesian structural time series approach with treatment on 23 March 2020 outlined previously. To have a consistent measure of distance across all days in the data, we use distance between the campus offices of researchers rather than the distance between their active work environments—during the shift to remote work the distance between researchers’ campus offices does not change. We use four distance thresholds: 0 m (researchers working in the same laboratory), 0–150 m (close/nearby researchers in distinct laboratories), 150–650 m (researchers at medium distance) and >650 m (far-away researchers). The distribution of distances between researcher offices can be found in Supplementary Information.

Using Bayesian structural time series with a synthetic counterfactual constructed from weekend email network data, we find an immediate and lasting drop in the number of new weak ties between researchers in distinct but nearby research laboratories (Fig. 3b). This is in line with our expectation that propinquity contributes to weak-tie formation. Given this decrease, it may seem surprising that there is an increase in the number of new weak ties between researchers in the same laboratory (Fig. 3b). However, Yang et al.¹⁵ discovered an increase in the use of asynchronous communication (for example email) after the COVID-19 pandemic. A plausible explanation for the increase in new weak ties between researchers in the same laboratory is that after the shift to remote work email was used to schedule one-on-one meetings or ask small questions between same-laboratory researchers that formerly would have been scheduled or asked in person. Figure 3c,d shows a non-significant decrease in the number of new weak ties formed between researchers in distinct laboratories at medium and far distances. This is also compatible with our intuition, as we do not expect researchers who work far away from one another to have many chance encounters even when working in person.

Fig. 3: Formation of new weak ties stratified by distance.

a, The estimated effect between researchers in the same laboratory. b, The estimated effect between researchers in distinct laboratories within 150 m. c, The estimated effect between researchers in distinct laboratories between 150 and 650 m. d, The estimated effect between researchers in distinct laboratories further apart than 650 m. Shaded regions represent 95% posterior predictive intervals computed using Bayesian structural time series with a synthetic counterfactual constructed from weekend data (n_pre = 8 weeks, n_post = 72 weeks for all panels). Fitted values/intervals use the mean as the measure of central tendency.

Source data

The effect of hybrid work on the formation of weak ties

MIT reopened its campus for the fall 2021 semester starting on 8 September 2021. However, following MIT recommendation many research laboratories adopted a hybrid mode of work with researchers only physically present for (at most) three out of five business days each week, implying that the chance of serendipitous encounters was still lower than before the COVID-19 pandemic. Furthermore, limitations on the number of people allowed to eat together at a time and ongoing restrictions to international travel prevented departments from hosting large-scale events where researchers might typically mix. To estimate the causal effect of the end of remote work, we calculate a synthetic counterfactual for 2021 weekday email data from 2020 weekday email data (Methods).

The percentage of new weak ties at close distances is higher than expected in fall 2021 given the percentage at close distances in fall 2020 (Fig. 4a), with no significant differences observed at other distance thresholds. The number of weak ties rises more sharply than expected on 8 September 2020 (Fig. 4b) given the rise at the beginning of the fall 2020 semester. Despite this, the total number of new weak ties is lower than or similar to the predicted value after hybrid work (Fig. 4b). Taken together, the results of Fig. 4 hint at the partial but incomplete success of the hybrid work model in allowing researchers to once more form new weak ties with other proximal researchers.

Fig. 4: The effect of reintroducing co-location between researchers.

a, The predicted cumulative change due to hybrid work in the percentage of new weak ties between researchers in the same laboratory, researchers in distinct laboratories at distance less than 150 m, researchers in distinct laboratories at distance between 150 m and 650 m, and researchers in distinct laboratories at distance larger than 650 m. 95% posterior predictive intervals computed using Bayesian structural time series (n_pre = 29 d, n_post = 35 d). b, An RDD on the difference between the numbers of weak ties in September 2020 and September 2021 using a two-sided z test (effect = 67.5, P = 0.022, 95% CI [9.740, 125.266], n_pre = 34 d, n_post = 26 d). *0.01 ≤ P < 0.05. c, The changes in the total number of new ties between researchers at the distance thresholds detailed above with 95% posterior predictive intervals computed using Bayesian structural time series. Fitted values/intervals use the mean as the measure of central tendency.

Source data

Modeling the effect of distance on tie formation

Our empirical results are consistent with the existence of some kind of mechanism via which co-location promotes weak-tie formation. Here we seek to address the following question: given a collection of potential communicating pairs of researchers, how can we choose which pairs of researchers communicate each weekday to accurately capture the topological structure and temporal dynamics of real world networks?

Previous work has identified at least four factors relevant to tie formation^17,18,19: focal closure, triadic closure, link-centric preferential attachment and physical co-location. Figure 5 gives a diagrammatic depiction of these four factors. However, determining a simple functional form via which these factors combine to govern the evolution of a dynamic communication network is still an open problem. Here we describe a simple network evolution model via which co-location multiplicatively scales the effect of homophily to determine which pairs of people communicate on a given day (see Methods for details). We simulate the formation of email networks on weekdays by creating an edge memory dictionary from the last two weeks of February 2020, then generating new graphs each day using our model. Previous work on the effect of distance on tie formation has primarily focused on distance and homophily as separate, additive factors that both contribute positively to tie formation^3,20,21. However, bringing people with clashing personalities close together is more likely to make them enemies than friends and hence unlikely to make them contact one another via email. For this reason we view co-location as a multiplicative factor that scales the effects of homophily to form new ties. See Supplementary Information for an ablation study of our model together with a discussion of other random graph models.

Fig. 5: Illustration of model mechanisms.

In our tie choice model the probability of two people interacting depends on four key mechanisms: co-location, whether the two belong to the same research unit, whether the two have a mutual connection, and their pattern of past communication.

Our goal is to reproduce the dynamics of weak-tie formation in networks with a simple network evolution model. To reproduce the qualitative features observed in the data, we set the τ for each pair of individuals to 0 (corresponding to no physical co-location) starting from 23 March 2020 then back to 1 on 8 September 2021. Upon the removal of co-location, our model produces a drop in the number of weak ties (Fig. 6a) and new weak ties (Fig. 6b), which is qualitatively similar to what we observe in the empirical data. It also reproduces the increase in edge stability (Fig. 6c), as well as the robustness of long-distance ties to a sudden absence of co-location (Fig. 6d). Here the weekly periodicity is measured as the intersection over union of the edge sets of the networks on days d and d − 7. By looking at the number of weak ties, the clustering coefficient and the week to week periodicity (Fig. 6a,b) produced by our model after 8 September 2021, we see that our model predicts that complete reintroduction of co-location results in a complete recovery of weak ties. The signs of the logarithm of the distance interaction coefficients allow us to identify the following potential mechanism for the drop in weak ties: two researchers are more likely to form new weak ties when they are co-located. To further confirm this hypothesis, we have simulated a scenario without the sudden transition to fully remote work modeled through the change in the value of the physical co-location variable on 23 March 2020. The results, reported in Supplementary Information, show no observable drop in weak ties, providing further evidence in support of our explanatory hypothesis.

Fig. 6: A tie choice model in which distance multiplicatively scales the effects of homophily.

The output of our model when artificially setting office distances to a large fixed constant after 23 March 2020, then returning researcher offices to their initial positions on 8 September 2021. ***P < 0.001. a, A simulated drop in the number of local bridges on 23 March 2020 (effect = −65.2, P < 0.001, 95% CI [−76.109, −54.316], n_pre = 42, n_post = 238) followed by an increase in the fall (effect = 51.9, P < 0.001, 95% CI [42.091, 61.693], n_pre = 129, n_post = 38). b, The number of new weak ties entering the network (effect = −47.0, P < 0.001, 95% CI [−60.566, −33.510], n_pre = 42, n_post = 238). All statistics are two-sided z tests. c, The weekly periodicity and daily clustering coefficient. IOU is intersection over union. d, The number of simulated weak ties between users in distinct research units first appearing between 4 February 4 and 23 March 2020 versus between 23 March 2020 and 22 May 2020. Fitted values/intervals use the mean as the measure of central tendency.

Source data

Discussion

Several sociologists have argued that the lack of connections during the COVID-19 pandemic negatively impacted mental and physical well-being as well as innovation, collaboration and creativity^22,23. However, the mechanism via which such effects have occurred has yet to be explicitly identified. As businesses and universities make crucial decisions about the amount of in-person work after the COVID-19 pandemic, understanding the lasting effects of remote work on research communities is of paramount importance.

Our study shows that the transition to fully remote work on the MIT campus—with consequent complete removal of physical co-location between co-workers—had notable effects on the email communication network: while some common topological features were preserved, the formation of weak ties was hindered, causing weak-tie deterioration and network stagnation in the long term. Employees who are not co-located are less likely to form ties, weakening the spread of information in the network^24,25,26. The mechanism of weak-tie formation can be successfully reproduced using a link formation model through which co-location multiplicatively scales the effects of homophily between researchers.

Our findings have implications for the design of future research campuses and work environments, as well as for the development of new virtual technologies that seek to recreate interactions that happen in physical offices. Today it is of the utmost importance to identify what is the ‘minimum amount’ of in-presence work that enables the formation of weak ties, so that individual and societal benefits related to remote work can be preserved without impacting the generation of new ideas and innovation in general. While previous studies have documented the effects of reduced in-person collaboration in the short term¹⁵, we show that the shift to remote communication produces a long-lasting impact on the formation of local bridges in collaborative networks, with effects accumulating over time. Expanding on the existing methodology, we demonstrate that paired testing estimates, conventionally used to evaluate the short-term effects of stay-at-home restrictions, do not accurately represent the long-term changes in the social network. We provide an alternative estimation strategy that produces more robust inference about the long-term effects.

We also would like to highlight several important considerations on our causal inference strategy. We use the Bayesian structural time-series method to estimate the long-term effects of the mandatory shift to remote work by constructing a counterfactual prediction of weekday email exchanges using weekend email data. The validity of our methodology is supported by three main arguments. First, at a weekly level, weekend email exchanges are sufficiently predictive of the weekday emails due to common unobserved seasonality and the fact that work communication tends to spill over into weekends. Second, even if weekend email exchanges are affected by the shift to mandatory remote work, this is not due to changes in co-location of researchers since people typically do not come to the office on weekends. Finally, while there are other potential pandemic-related confounding factors such as changes in childcare that could a priori contribute to changes in the MIT email network, it is reasonable to expect such confounding factors to be distributed independently of the distance between researcher offices. Thus, by stratifying connections by the distance between researcher offices, we directly attribute the observed loss in new weak-tie formation to a lack of co-location. Still, our approach is not without its limitations. In particular, the predictive power of the weekend email exchanges is limited by the fact that we only observe the network for three months before intervention and could benefit from adding data for previous years.

Our results suggest that the loss of social connections that otherwise spontaneously emerge in shared spaces can not be immediately restored by simply returning to offices. When designing work-from-home policies, firms and organizations should consider ways to promote serendipitous interactions across organizational units if they want to retain efficient discovery and transmission of novel information. Still, our initial findings on the hybrid work model that followed the reintroduction of partial in-person collaboration at MIT show a slight recovery in the number of weak ties—especially between researchers who are once again co-located. This hints at the possibility of establishing a work balance trade-off by combining in-person and remote interactions among colleagues, which could inform the transition to a hybrid, post-COVID-19 new normal.

Methods

Ethical review

This research was reviewed and classified as exempt by the Massachusetts institute of Technology (MIT) Committee on the Use of Humans as Experimental Subjects (MIT’s institutional review board), because the research was secondary use research involving the use of de-identified data.

Data preprocessing

Data were analyzed using Python 3.7.9, NumPy 1.21.5, pandas 1.1.5, statsmodels 0.12.1, OSMnx 1.0.1, python-flint 0.3.0, SciPy 1.6.0 and GeoPandas 0.8.1.

We start with a fixed set of anonymized researchers ${{{\mathcal{R}}}}$ (research staff, faculty and postdocs) from 112 different research units. As required by MIT staff for privacy reasons, these researchers are grouped via ten random partitions (no researchers are shared between the groups in a partition) of ${{{\mathcal{R}}}}$, ${{{{\mathcal{R}}}}}_{i}={\coprod }_{j}{G}_{j}^{i}$, 1 ≤ i ≤ 10. We describe below how to estimate individual-level data from aggregated data, which was necessary to ensure that the studied users were active through the entire time period of interest. Each group G_jⁱ contains at least five researchers, and all researchers in G_j belong to the same research unit. Let ${g}_{ij}\in {{{\mathcal{R}}}}$ denote the collection of researchers in G_jⁱ. For a pair of groups G_jⁱ, G_kⁱ and a day d, our data contain the sum W_jkⁱ of all emails sent between groups j and k for randomization i:

$${W}_{jk}^{i}=\mathop{\sum}\limits_{{g}_{ij}\in {G}_{j}^{i}}\mathop{\sum}\limits_{{g}_{ik}\in {G}_{k}^{i}}{{{{\rm{emails}}}}}_{d}({g}_{ij},{g}_{ik}).$$

(1)

For each research unit U, let ${{{{\mathcal{R}}}}}^{U}$ denote the collection of researchers in the research unit. Because each group contains only researchers from a single research unit, each equation (1) is a sum over researchers from at most two research units. Grouping the equations (1) by pairs of research units U, V on each day d we obtain a collection of constrained linear systems of Diophantine equations,

$${W}_{V}^{U}={A}_{V}^{U}{\mathbf x}_{V}^{U}$$

(2)

$${\mathbf x}_{V}^{U}\ge 0$$

(3)

where ${\mathbf{x}}_V^U$ is the column vector whose entries are emails_d(g_ij, g_ik), 1 ≤ i ≤ 10, ${g}_{ij}\in {{{{\mathcal{R}}}}}^{U}$, ${g}_{jk}\in {{{{\mathcal{R}}}}}^{V}$ and $A_V^U$ is the matrix of coefficients of the equations (1). Each of these linear systems is guaranteed to have at least one solution (the actual number of emails sent), but may be underdetermined. If there is a unique solution, we use the Hermite normal form²⁷ of $A_V^U$ to find it. If the system is underdetermined, we use non-negative matrix factorization²⁸ with an ℓ¹ penalty to quickly estimate a sparse non-negative solution, as the algorithms that compute exact sparse integer solutions are slow. This procedure yields an estimate for each day d and each pair $u,v\in {{{\mathcal{R}}}}$ of emails_d(u, v). In Supplementary Information we show that our approximate solutions are very close to true solutions.

Network formation

To rule out changes in the data due to departures from the university or new hires, we ensure that each user sent at least one email over the university network before the end of the 2020 spring semester and at least one email after 20 May 2021. We denote this set of active users by ${{{\mathcal{A}}}}$.

We are missing data from 23 December 2020 and 19–21 January 2021; because these days are during the winter holiday at MIT this does not heavily affect our analysis. For each of the remaining 562 days from 26 December 2019 through 15 July 2021, we obtain a weighted, undirected network whose nodes represent (anonymized) individuals. Fix a day d; for each user u in ${{{\mathcal{A}}}}$, let Nb_d(u) denote the number of people whom u emailed on day d. For a pair of users $u,v\in {{{\mathcal{A}}}}$, let emails_d(u, v) denote the number of emails sent (estimated as in the previous section) from u to v on day d. To rule out massmails, let ${{{{\mathcal{A}}}}}_{d}\subseteq {{{\mathcal{A}}}}$ be the subset

$${{{{\mathcal{A}}}}}_{d}=\{u\in {{{\mathcal{A}}}}| 1\le {{{\rm{Nb}}}}(u) < 100\}.$$

Define a weighted, undirected network N_d with nodes ${{{{\mathcal{A}}}}}_{d}$. For two nodes u, v, there is an edge (u, v) if emails(u, v) ≥ 1 and emails(v, u) ≥ 1. The weight of the edge is defined to be min(emails_d(u, v), emails_d(v, u)). Although the email data are partially estimated due to randomization and aggregation, for >66% of the edges with non-zero weight in the estimated network N_d we were able to recover the true number of emails sent. If we include all edges between users contributing to a non-zero weight edge in at least one random aggregation of the network (but which may have weight zero in the estimated network), >99.9% of edges have the ground truth number of emails. When building the undirected network N_d, we consider four possible time windows during which emails can be reciprocated: the same day (daily), within 5 business days (weekly), within 10 business days (biweekly) or within 21 business days (monthly). For results on weekly, biweekly and monthly networks see Supplementary Information. Previous studies have found that more than 90% of emails are replied to on the same day that they are sent, with more than half being replied to within 47 min (ref. ²⁹). Requiring emails to be reciprocated the same day hides interactions between users who typically respond slowly to emails; however, it is useful for filtering out massmails, observing sharp discontinuities in the data and increasing the power of hypothesis tests. Allowing longer periods of reciprocation captures weaker ties missed in the daily reciprocated email network, but we are forced to sacrifice some statistical power either to autocorrelation or lower sample size; additionally, the networks become more saturated, destroying some topological features of interest. Examples of daily, weekly, biweekly and monthly email networks are reported in Supplementary Information.

To examine whether this hybrid mode of work returned tie formation to prepandemic levels, we first restrict ourselves to a collection of 2,206 researchers who sent at least five emails after September 2021 and before May 2020, then proceed as above to form networks from 23 December 2020 to 31 October 2021. We choose a stricter requirement for inclusion in the network than previously, as we observe many users becoming inactive starting in summer 2021.

When comparing February 2020 with February 2021, we pair the days in the two months as follows: the first Tuesday of the MIT semester in February 2020 is paired with the first Tuesday of the MIT semester in February 2021, and so on. For each pair of days (d₂₀₂₀ⁱ, d₂₀₂₁ⁱ), we consider the set of users ${{{{\mathcal{A}}}}}_{{d}_{2020}^{i}}\cap {{{{\mathcal{A}}}}}_{{d}_{2021}^{i}}$ who were active on both days and, as above, form a pair of undirected networks (G₂₀₂₀ⁱ, G₂₀₂₁ⁱ) whose edges (u, v) correspond to reciprocated emails on d₂₀₂₀ⁱ (for G₂₀₂₀ⁱ) or d₂₀₂₁ⁱ (for G₂₀₂₁ⁱ). Directly comparing these networks allows us to completely remove the effects of seasonality or any difference in makeup of active users in February 2020 and February 2021.

Link-centric preferential attachment

The goal of our model is not to serve as a tool for prediction, but to understand the mechanism via which distance impacts link formation. Through experimentation, we found that using link-centric preferential attachment alone to propagate a dynamic network produced daily networks that had too many local bridges. Thus we use a two-step approach, which first produces an intermediate network using link-centric preferential attachment, then adds edges in a way that increases the clustering coefficient of the network. This is analogous to the reverse of the Watts–Strogatz method³⁰, where the intermediate network has high clustering coefficient and local bridges are added afterwards.

Our link formation model has the following parameters.

• P, the periodicity of the model. P controls how much the graph on day d looks like the graph on day d − 7. In other words, the higher the value of P, the closer the dynamic network is to being 7-periodic (or 5-periodic if weekends are removed).

• O, the tendency to connect with old links. The higher the value of O, the more likely it is that a given link will connect with a previous partner rather than someone new. This is one of the standard parameters from a vanilla link-centric preferential attachment model, and this parameter decays exponentially in the number of days between contact: O = c e^−d, where c is a constant and d is the number of days since the link last appeared.

• N, the tendency to reach out to new people. This is typically the complement of O in vanilla link-centric attachment models (we have more parameters than the standard two).

• D, the tendency to connect with people in the same department.

• F, the tendency to be introduced to a mutual friend.

The parameters O, N and P rely on a memory dictionary, which stores the days on which a given edge has appeared. For all of the above parameters {P, O, N, D, F}, we include interaction terms

$$\{{C}_{P},{C}_{O},{C}_{N},{C}_{D},{C}_{F}\}$$

controlling the extent to which co-location amplifies or dampens the effect. For example, from the empirical data we conclude that co-location should dampen periodicity while amplifying the probability of reaching out to new partners.

Let $e=(u,v)\in {{{\mathcal{A}}}}\times {{{\mathcal{A}}}}$ be a pair of nodes. For each parameter Q ∈ {P, O, N, D, F} let ${{\mathbb{1}}}_{Q}$ denote the associated indicator variable. Specifically,

$$\begin{array}{ll}{{\mathbb{1}}}_{P}(e)=&\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,u,v\,{{{\rm{connected}}}}\,7\,{{{\rm{d}}}}\,{{{\rm{in}}}}\,{{{\rm{the}}}}\,{{{\rm{past}}}}\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.\\ {{\mathbb{1}}}_{N}(e)=&\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,u,v\,{{{\rm{have}}}}\,{{{\rm{never}}}}\,{{{\rm{connected}}}}\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.\\ {{\mathbb{1}}}_{O}(e,{d}_{\mathrm{c}})=&\left\{\begin{array}{ll}\mathop{\sum}\limits_{{d}_{\mathrm{p}}}{\mathrm{e}}^{-({d}_{\mathrm{c}}-{d}_{\mathrm{p}})/562}\quad &{{{\rm{if}}}}\,u,v\,{{{\rm{have}}}}\,{{{\rm{previously}}}}\,{{{\rm{connected}}}}\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.\\ {{\mathbb{1}}}_{D}(e)=&\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,u,v\,{{{\rm{are}}}}\,{{{\rm{in}}}}\,{{{\rm{the}}}}\,{{{\rm{same}}}}\,{{{\rm{research}}}}\,{{{\rm{unit}}}}\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.\\ \tau (e)=&\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,u,v\,{{{\rm{have}}}}\,{{{\rm{offices}}}}\,{{{\rm{within}}}}\,150\,{{{\rm{m}}}}\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.\end{array}$$

where d_c is the current day, and d_p are the past days on which the tie e was present in the network. The 150 m cutoff is chosen on the basis of the empirical results.

Consider the set E of all edges that appear on at least one day in the empirical data. Note that the use of E rather than the set of all possible edges makes this model unsuitable for prediction tasks. On each day d, we start by adding an edge e ∈ E to the random network G₁^d with probability

$$\begin{array}{ll}{p}_{e}\propto \tau (e)\mathop{\sum}\limits_{Q\in \{P,O,N,D\}}{C}_{Q}{{\mathbb{1}}}_{Q}(e)Q\\ +(1-\tau (e))\mathop{\sum}\limits_{Q\in \{P,O,N,D\}}\frac{1}{{C}_{Q}}{{\mathbb{1}}}_{Q}(e)Q.\end{array}$$

If C_Q > 1 then co-location amplifies the effect of parameter Q, while if C_Q < 1 it dampens the effect. In total, in the first step we add ε₁ edges to G₁^d, where ${\varepsilon }_{1} \sim {{{\mathcal{N}}}}(1000,10)$.

In the second step, we add the parameter F,

$${{\mathbb{1}}}_{F}(e)=\left\{\begin{array}{ll}1\quad &{{{\rm{if}}}}\,{d}_{{G}_{1}}(u,v)=2\\ 0\quad &{{{\rm{otherwise}}}}\end{array}\right.$$

where G₁^d is the random network constructed in step 1, and d_G is the usual (unweighted) shortest path distance in the graph G. In words, ${{\mathbb{1}}}_{F}(e)=1$ if adding e will close a triangle in the network. A new edge e is added to the network in step two with probability

$$\begin{array}{ll}{p}_{e}\propto \tau (e)\mathop{\sum}\limits_{Q\in \{P,O,N,D,F\}}{C}_{Q}{{\mathbb{1}}}_{Q}(e)Q\\ +(1-\tau (e))\mathop{\sum}\limits_{Q\in \{P,O,N,D,F\}}\frac{1}{{C}_{Q}}{{\mathbb{1}}}_{Q}(e)Q.\end{array}$$

In total we add ε₂ edges to G₁^d in the second step, where ${\varepsilon }_{2} \sim {{{\mathcal{N}}}}(500,10)$. including the parameter F has the effect of increasing the expected number of triangles in the random graph, and hence reducing the percentage of edges that are local bridges.

With parameters fixed, we proceed to form networks one day at a time, adding the edges from the current network to a memory dictionary after formation. To model the effect of remote work, for each day d after 23 March 2020, we set the distance between researcher offices to be a fixed constant larger than 650 m (all other parameters remain fixed). For parameter values we set

$$\begin{array}{lllll}P=80{,}000&N=2{,}000&O=1&D=90{,}000&F=200{,}000\\ {C}_{P}=\frac{2}{3}&{C}_{N}=2&{C}_{O}=1&{C}_{D}=\frac{10}{11}&{C}_{F}=\frac{2}{3}.\end{array}$$

Regression discontinuity

Figure 2a,b (respectively Fig. 4c) shows the drop in weak-tie and new weak-tie formation (respectively increase in weak ties) due to the policy change on 23 March 2020. We used RDDs^31,32,33 to estimate the causal impact of the policy change. RDDs are a classic, quasiexperimental procedure for estimating treatment effects in observational studies. In an RDD, treatment assignment is determined by an assignment variable rather than through randomization.

For an RDD to be valid, we need only assume that the response is continuous with the assignment variable near the cutoff and that subjects cannot precisely manipulate the assignment variable^32,33. Figures 2a,b and 4c show that the responses (weak ties and new weak ties) are continuous with the assignment variable time, albeit observed with noise. The assignment variable, time, is not precisely manipulable by subjects since the announced policy was not known far in advance. Furthermore, there would be little reason to manipulate assignment since subjects are free to send emails at the same rate before and after the policy change.

In Fig. 2a and Fig. 4c, we model the weekly mean number of weak ties with the discontinuous linear regression

$$Y=\alpha +\eta D+{\beta }_{2}D(X-c)+\epsilon$$

(4)

where c is the cutoff date (either 23 March 2020 or 8 September 2021) and D is the binary variable

$$D=\left\{\begin{array}{ll}1\quad &X\ge c\\ 0\quad &X < c\end{array}\right.$$

that indicates if the date X is before or after the policy change date c. The error term ϵ is assumed to be heteroskedastic white noise. The coefficient η is the impact of the policy and measures the gap between the two sides of the regression. We estimate η and the other coefficients with generalized least squares with AR(n) structured covariance matrix with n = 5 and report the value of $\hat{\eta }$ and its P value in Fig. 2. We use heteroskedasticity-robust estimators for standard errors, so that in total standard errors are robust to autocorrelation (from the AR(5) generalized least squares) and heteroskedasticity³⁴.

In Fig. 2a, we assumed a discontinuous order-one polynomial trend line because the data did not display any apparent higher-order nonlinear behavior. The data were subset to 3 January 2020 to 1 October 2020, to semilocalize our regression around the discontinuity, which reduces bias in $\hat{\eta }$ (ref. ³³), and to avoid influence from the two outlying regions (before 3 January 2020 and during December 2020). These outliers correspond to winter break at MIT and represent a natural and expected decrease in weak ties not due to the policy change.

In Fig. 2b, we similarly model the rate of new weak-tie formation over time. We assumed a second-order discontinuous polynomial trend (equation (5)) due to the observed parabolic behavior before the cutoff point. Using the same notation as in equation (4), our linear regression is given by

$$Y=\alpha +\eta D+{\beta }_{1}(X-c)+{\beta }_{2}{(X-c)}^{2}+{\beta }_{3}D(X-c)+{\beta }_{4}D{(X-c)}^{2}+\epsilon .$$

(5)

The coefficient η is, again, the causal impact of the policy change. We report the value of $\widehat{\eta }$ and its P value in Fig. 2.

Bayesian structural time series

We stress that, when using Bayesian methods, reported CIs are credible intervals of the predicted dependent variable (also called posterior predictive intervals), and P values are posterior tail probabilities. Bayesian structural time series combines a state-space model for time-series data and Bayesian model averaging for parameter selection and estimation³⁵.

As a state-space model, Bayesian structural time series combines three components of state: a local linear trend,

$$\begin{array}{ll}{\mu }_{t+1}&={\mu }_{t}+{\delta }_{t}+{\eta }_{\mu ,t}\\ {\delta }_{t+1}&={\delta }_{t}+{\eta }_{\delta ,t},\end{array}$$

with ${\eta }_{\mu ,t} \sim {{{\mathcal{N}}}}(0,{\sigma }_{\mu }^{2})$, ${\eta }_{\delta ,t} \sim {{{\mathcal{N}}}}(0,{\sigma }_{\delta }^{2})$; a seasonality component,

$${\gamma }_{t+1}=-\mathop{\sum }\limits_{s=0}^{S-2}{\gamma }_{t-s}+{\eta }_{\gamma ,t}$$

with S the number of seasons and η_γ,t again an independent error; and (static) covariates, which are predictive of the time series in question before the intervention,

$${Z}_{t}={\beta }^{\mathrm{T}}{{{{\bf{x}}}}}_{t}.$$

For the local linear trend and seasonality components, we use the default priors of the CausalImpact library:

$$\frac{1}{\sigma } \sim {{{\mathcal{G}}}}(1{0}^{-2},1{0}^{-2}{s}_{y}^{2})\qquad {s}_{y}^{2}=\mathop{\sum}\limits_{t}\frac{{({y}_{t}-\overline{y})}^{2}}{n-1}$$

where ${{{\mathcal{G}}}}(-,-)$ denotes a gamma distribution. For the covariates (the weekend data), in general a spike-and-slab prior is used with the spike defined by

$$p(\xi )=\mathop{\prod }\limits_{i=1}^{J}{\pi }_{j}^{{\xi }_{j}}{(1-{\pi }_{j})}^{\left.1-{\xi }_{j}\right)}$$

with π_j initialized to $\frac{M}{J}$ where M is the expected model size. The slab part of the spike-and-slab prior is

$$\begin{array}{ll}{\beta }_{\xi }| {\sigma }_{\epsilon }^{2} \sim {{{\mathcal{N}}}}{(0,{\sigma }_{\epsilon }^{2}{({{{\Sigma }}}_{\xi })}^{-1})}^{-1}\\ \frac{1}{{\sigma }_{\epsilon }^{2}} \sim {{{\mathcal{G}}}}\left(\frac{{\nu }_{\epsilon }}{2},\frac{{s}_{\epsilon }}{2}\right)\\ {{{\Sigma }}}^{-1}=\frac{1}{n}\left\{\frac{1}{2}{X}^{T}X+\frac{1}{2}{{{\mathrm{diag}}}}({X}^{\mathrm{T}}X)\right\}\end{array}$$

where X is the covariate data. Because we include only one covariate (the weekly minimum) the spike-and-slab prior collapses to just a normal-inverse Gamma distribution. We use 1,000 iterations of Markov chain Monte Carlo to compute posterior predictive distributions.

Consider the binary variable X(r, d) defined by

$$X(r,d)=\left\{\begin{array}{ll}1\quad &{{{\rm{researcher}}}}\,r\,{{{\rm{is}}}}\,{{{\rm{in}}}}\,{{{\rm{their}}}}\,{{{\rm{office}}}}\,{{{\rm{on}}}}\,{{{\rm{day}}}}\,d\\ 0\quad &{{{\rm{otherwise}}}}.\end{array}\right.$$

For us, ‘treatment’ consists of setting X(r, d) to zero for d after 23 March 2020 by not permitting researchers to enter their campus offices. The time series whose counterfactual we want to estimate is the weekday maximum of the network measure while the covariate is the weekend minimum. As most employees are not physically present in their office on weekends, X(r, d) = 0 for most r when d is a weekend so that the treatment has little effect. We verify this assumption by looking at the number of distinct MAC (media access control) addresses connected to routers in on-campus research laboratories on the weekday and weekend (Supplementary Information).

When studying the effect of hybrid work, we construct a counterfactual using weekday email data spanning 22 July 2020 through 14 October 2020 as a covariate for email data spanning 28 July 2021 through 20 October 2021, aligning so that the starts of the fall 2020 and fall 2021 semesters coincide. We also remove Memorial Day (a university holiday) from both the 2020 and 2021 data.

Reporting summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.