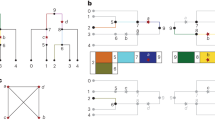
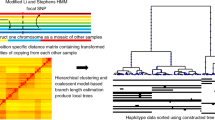
Abstract
Because haplotype information is of widespread interest in biomedical applications, effort has been put into their reconstruction. Here, we propose an efficient method, called haploSep, that is able to accurately infer major haplotypes and their frequencies just from multiple samples of allele frequency data. Even the accuracy of experimentally obtained allele frequencies can be improved by re-estimating them from our reconstructed haplotypes. From a methodological point of view, we model our problem as a multivariate regression problem where both the design matrix and the coefficient matrix are unknown. Compared to other methods, haploSep is very fast, with linear computational complexity in the haplotype length. We illustrate our method on simulated and real data focusing on experimental evolution and microbial data.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$99.00 per year
only $8.25 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
In the ‘Drosophila simulans’ section, we used published data11,58. We obtained allele frequency data and sequences of founder haplotypes from the authors (N. Barghi and C. Schlötterer). In the ‘Longshanks experiment in mice’ section, we used time-series data from the experiment described by Castro et al.40 (only partially published so far). We obtained the allele frequency data for the considered region from the authors (F. Chan, L. Hiramatsu and N. Barton). In the ‘Caenorhabditis elegans’ section, we used published data from Noble and others39. The raw data are available from NCBI SRA under BioProject PRJNA381203. We obtained allele frequency data and genotypes from the authors (L. Noble and H. Teotónio). In the ‘HIV’ section, we used published data from Zanini and others21. The data are available at https://hiv.biozentrum.unibas.ch/data/. Source data are provided with this paper.
Code availability
All our code is written in R. Our software, simulation functions and examples are available from https://github.com/MartaPelizzola/haploSep. Our code is also available in our Code Ocean repository59, where we also provide code to generate Figs. 1–5.
References
Tewhey, R., Bansal, V., Torkamani, A., Topol, E. J. & Schork, N. J. The importance of phase information for human genomics. Nat. Rev. Genet. 12, 215–223 (2011).
Marchini, J., Howie, B., Myers, S., McVean, G. & Donnelly, P. A new multipoint method for genome-wide association studies by imputation of genotypes. Nat. Genet. 39, 906–913 (2007).
Tishkoff, S. A. et al. Global patterns of linkage disequilibrium at the CD4 locus and modern human origins. Science 271, 1380–1387 (1996).
Sabeti, P. C. et al. Detecting recent positive selection in the human genome from haplotype structure. Nature 419, 832–837 (2002).
Garud, N. R., Good, B. H., Hallatschek, O. & Pollard, K. S. Evolutionary dynamics of bacteria in the gut microbiome within and across hosts. PLoS Biol. 17, e3000102 (2019).
Feng, Q. et al. Gut microbiome development along the colorectal adenoma–carcinoma sequence. Nat. Commun. 6, 6528 (2015).
Wang, J. et al. A metagenome-wide association study of gut microbiota in type 2 diabetes. Nature 490, 55–60 (2012).
The 1000 Genomes Project Consortium A global reference for human genetic variation. Nature 526, 68–74 (2015).
Burke, M. K. et al. Genome-wide analysis of a long-term evolution experiment with Drosophila. Nature 467, 587–590 (2010).
Illingworth, C. J., Parts, L., Schiffels, S., Liti, G. & Mustonen, V. Quantifying selection acting on a complex trait using allele frequency time series data. Mol. Biol. Evol. 29, 1187–1197 (2012).
Barghi, N. et al. Genetic redundancy fuels polygenic adaptation in Drosophila. PLoS Biol. 17, e3000128 (2019).
Futschik, A. & Schlötterer, C. The next generation of molecular markers from massively parallel sequencing of pooled DNA samples. Genetics 186, 207–218 (2010).
Schlötterer, C., Tobler, R., Kofler, R. & Nolte, V. Sequencing pools of individuals—mining genome-wide polymorphism data without big funding. Nat. Rev. Genet. 15, 749–763 (2014).
Turner, T. L., Stewart, A. D., Fields, A. T., Rice, W. R. & Tarone, A. M. Population-based resequencing of experimentally evolved populations reveals the genetic basis of body size variation in Drosophila melanogaster. PLoS Genet. 7, e1001336 (2011).
Savolainen, O., Lascoux, M. & Merilä, J. Ecological genomics of local adaptation. Nat. Rev. Genet. 14, 807–820 (2013).
Michalak, P., Kang, L., Schou, M. F., Garner, H. R. & Loeschcke, V. Genomic signatures of experimental adaptive radiation in Drosophila. Mol. Ecol. 28, 600–614 (2019).
Karasov, T., Messer, P. W. & Petrov, D. A. Evidence that adaptation in Drosophila is not limited by mutation at single sites. PLoS Genet. 6, e1000924 (2010).
Burke, M. K. How does adaptation sweep through the genome? Insights from long-term selection experiments. Proc. R. Soc. B Biol. Sci. 279, 5029–5038 (2012).
Meier, J. et al. Haplotype tagging reveals parallel formation of hybrid races in two butterfly species. Preprint at bioRxiv https://doi.org/10.1101/2020.05.25.113688 (2020).
Jones, F. C. et al. The genomic basis of adaptive evolution in threespine sticklebacks. Nature 484, 55–61 (2012).
Zanini, F. et al. Population genomics of intrapatient HIV-1 evolution. eLife 4, e11282 (2015).
Sudderuddin, H. et al. Longitudinal within-host evolution of HIV Nef-mediated CD4, HLA and SERINC5 downregulation activity: a case study. Retrovirology 17, 3 (2020).
Franssen, S. U., Barton, N. H. & Schlötterer, C. Reconstruction of haplotype-blocks selected during experimental evolution. Mol. Biol. Evol. 34, 174–184 (2017).
Otte, K. A. & Schlötterer, C. Detecting selected haplotype blocks in evolve and resequence experiments. Mol. Ecol. Resour. 21, 93–109 (2021).
Excoffier, L. & Slatkin, M. Maximum-likelihood estimation of molecular haplotype frequencies in a diploid population. Mol. Biol. Evol. 12, 921–927 (1995).
Pirinen, M. Estimating population haplotype frequencies from pooled SNP data using incomplete database information. Bioinformatics 25, 3296–3302 (2009).
Gasbarra, D., Kulathinal, S., Pirinen, M. & Sillanpää, M. J. Estimating haplotype frequencies by combining data from large DNA pools with database information. IEEE/ACM Trans. Comput. Biol. Bioinform. 8, 36–44 (2011).
Long, Q. et al. PoolHap: inferring haplotype frequencies from pooled samples by next generation sequencing. PLoS ONE 6, e15292 (2011).
Kessner, D., Turner, T. L. & Novembre, J. Maximum likelihood estimation of frequencies of known haplotypes from pooled sequence data. Mol. Biol. Evol. 30, 1145–1158 (2013).
Cao, C.-C. & Sun, X. Accurate estimation of haplotype frequency from pooled sequencing data and cost-effective identification of rare haplotype carriers by overlapping pool sequencing. Bioinformatics 31, 515–522 (2015).
Pulido-Tamayo, S. et al. Frequency-based haplotype reconstruction from deep sequencing data of bacterial populations. Nucleic Acids Res. 43, e105 (2015).
Cao, C. et al. Reconstruction of microbial haplotypes by integration of statistical and physical linkage in scaffolding. Mol. Biol. Evol. https://doi.org/10.1093/molbev/msab037 (2021).
Knyazev, S. et al. CliqueSNV: an efficient noise reduction technique for accurate assembly of viral variants from NGS data. Preprint at bioRxiv https://doi.org/10.1101/264242 (2018).
Lu, Y. & Zhou, H. H. Statistical and computational guarantees of Lloyd’s algorithm and its variants. Preprint at https://arxiv.org/pdf/1612.02099.pdf (2016).
Kawecki, T. J. et al. Experimental evolution. Trends Ecol. Evol. 27, 547–560 (2012).
Long, A., Liti, G., Luptak, A. & Tenaillon, O. Elucidating the molecular architecture of adaptation via evolve and resequence experiments. Nat. Rev. Genet. 16, 567–582 (2015).
Schlötterer, C., Kofler, R., Versace, E., Tobler, R. & Franssen, S. U. Combining experimental evolution with next-generation sequencing: a powerful tool to study adaptation from standing genetic variation. Heredity 114, 431–440 (2015).
Tilk, S. et al. Accurate allele frequencies from ultra-low coverage pool-seq samples in evolve-and-resequence experiments. G3 9, 4159–4168 (2019).
Noble, L. M., Rockman, M. V. & Teotónio, H. Gene-level quantitative trait mapping in Caenorhabditis elegans. G3 11, jkaa061 (2021).
Castro, J. P. et al. An integrative genomic analysis of the Longshanks selection experiment for longer limbs in mice. eLife 8, e42014 (2019).
Spitzer, K., Pelizzola, M. & Futschik, A. Modifying the chi-square and the CMH test for population genetic inference: adapting to overdispersion. Ann. Appl. Stat. 14, 202–220 (2020).
Marchini, M. et al. Impacts of genetic correlation on the independent evolution of body mass and skeletal size in mammals. BMC Evol. Biol. 14, 258 (2014).
Noble, L. M. et al. Polygenicity and epistasis underlie fitness-proximal traits in the Caenorhabditis elegans multiparental experimental evolution (CeMEE) panel. Genetics 207, 1663–1685 (2017).
Ahn, S., Ke, Z. & Vikalo, H. Viral quasispecies reconstruction via tensor factorization with successive read removal. Bioinformatics 34, i23–i31 (2018).
Zhang, K., Deng, M., Chen, T., Waterman, M. S. & Sun, F. A dynamic programming algorithm for haplotype block partitioning. Proc. Natl Acad. Sci. USA 99, 7335–7339 (2002).
Indap, A. R., Marth, G. T., Struble, C. A., Tonellato, P. & Olivier, M. Analysis of concordance of different haplotype block partitioning algorithms. BMC Bioinformatics 6, 303 (2005).
Barter, R. L. & Yu, B. Superheat: an R package for creating beautiful and extendable heatmaps for visualizing complex data. J. Comput. Graph. Stat. 27, 910–922 (2018).
Behr, M. & Munk, A. Identifiability for blind source separation of multiple finite alphabet linear mixtures. IEEE Trans. Information Theory 63, 5506–5517 (2017).
Behr, M., Holmes, C. & Munk, A. Multiscale blind source separation. Ann. Stat. 46, 711–744 (2018).
Behr, M. & Munk, A. Minimax estimation in linear models with unknown design over finite alphabets. Preprint at https://arxiv.org/pdf/1711.04145.pdf (2020).
Diamantaras, K. I. A clustering approach for the blind separation of multiple finite alphabet sequences from a single linear mixtureAuthor links open overlay panel. Signal Process. 86, 877–891 (2006).
Gavish, M. & Donoho, D. L. The optimal hard threshold for singular values is 4/√3. IEEE Trans. Inform. Theory 60, 5040–5053 (2014).
Efron, B. Bootstrap methods: another look at the jackknife. Ann. Stat. 7, 1–26 (1979).
Waples, R. S. A generalized approach for estimating effective population size from temporal changes in allele frequency. Genetics 121, 379–391 (1989).
Jónás, A., Taus, T., Kosiol, C., Schlötterer, C. & Futschik, A. Estimating the effective population size from temporal allele frequency changes in experimental evolution. Genetics 204, 723–735 (2016).
Haller, B. C. & Messer, P. W. SLiM 3: forward genetic simulations beyond the Wright–Fisher model. Mol. Biol. Evol. 36, 632–637 (2019).
Homer, N. DWGSIM: whole genome simulator for next-generation sequencing (GitHub Repository, 2010).
Barghi, N. et al. Data from:Genetic redundancy fuels polygenic adaptation in Drosophila. Dryad Digital Repository https://doi.org/10.5061/dryad.rr137kn
Pelizzola, M., Behr, M., Li, H., Munk, A. & Futschik, A. Code from: Multiple haplotype reconstruction from Allele frequency data (Code Ocean Capsule, 2021); https://doi.org/10.24433/CO.2948466.v2
Acknowledgements
We are grateful to the laboratories of N. Barton, C. Schlötterer and H. Teotonio for providing us with their experimental data. We also thank Q. Long, L. Mak and C. Cao for helping us with using PoolHapX. M.P. and A.F. acknowledge support of the Austrian Science Fund (FWF; DK W1225-B20). M.B. was supported by the Deutsche Forschungsgemeinschaft (DFG; German Research Foundation) Postdoctoral Fellowship BE 6805/1-1. M.B. acknowledges funding via DFG-GRK 2088. This work benefited from a research stay that was partially supported by the Simons Foundation and by Mathematisches Forschungsinstitut Oberwolfach. A.M. and M.B. acknowledge support via DFG-SFB 803 Z02. H.L. is funded and A.M. is supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy—EXC 2067/1-390729940.
Author information
Authors and Affiliations
Contributions
A.F. and A.M. conceived the project. M.P., M.B., H.L. and A.F. contributed to the design of the research and wrote the manuscript. M.P., M.B. and H.L. wrote the code for software, simulations and data analysis. All authors read and approved the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Computational Science thanks the anonymous reviewers for their contribution to the peer review of this work. Fernando Chirigati was the primary editor on this article and managed its editorial process and peer review in collaboration with the rest of the editorial team.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary sections 1–13 and Figs. 1–37.
Source data
Source Data Fig. 1
Statistical source data.
Source Data Fig. 2
Statistical source data.
Source Data Fig. 3
Statistical source data.
Source Data Fig. 4
Statistical source data.
Source Data Fig. 5
Statistical source data.
Rights and permissions
About this article
Cite this article
Pelizzola, M., Behr, M., Li, H. et al. Multiple haplotype reconstruction from allele frequency data. Nat Comput Sci 1, 262–271 (2021). https://doi.org/10.1038/s43588-021-00056-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s43588-021-00056-5
This article is cited by
-
Haplotype based testing for a better understanding of the selective architecture
BMC Bioinformatics (2023)