Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Accelerating computational modeling and design of high-entropy alloys

Nature Computational Science volume 1, pages 54–61 (2021)Cite this article

Subjects

A preprint version of the article is available at arXiv.

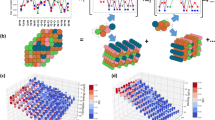
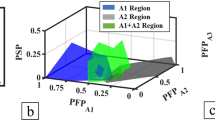
Abstract

High-entropy alloys, with N elements and compositions {cν = 1,N} in competing crystal structures, have large design spaces for unique chemical and mechanical properties. Here, to enable computational design, we use a metaheuristic hybrid Cuckoo search (CS) to construct alloy configurational models on the fly that have targeted atomic site and pair probabilities on arbitrary crystal lattices, given by supercell random approximates (SCRAPs) with S sites. Our Hybrid CS permits efficient global solutions for large, discrete combinatorial optimization that scale linearly in a number of parallel processors, and linearly in sites S for SCRAPs. For example, a four-element, 128-site SCRAP is found in seconds—a more than 13,000-fold reduction over current strategies. Our method thus enables computational alloy design that is currently impractical. We qualify the models and showcase application to real alloys with targeted atomic short-range order. Being problem-agnostic, our Hybrid CS offers potential applications in diverse fields.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Hybrid CS-optimized 250-atom cell for a bcc equiatomic ABCDE solid-solution alloy with zero SRO for three neighbor shells around each atom.
Fig. 2: Hybrid CS and CS function values versus iterations (objective evaluations) to reach the optimum for six functions.
Fig. 3: Hybrid CS performance.
Fig. 4: Hybrid CS versus MC-only optimization for a 54-atom bcc SCRAP.
Fig. 5: Eform versus SRO for Cu0.75Au0.25 in 108-site SCRAP.
Fig. 6: SCRAPs results for refractory bcc TaNbMo, TaNbMoW and TaNbMoWV.

Similar content being viewed by others

Data availability

Supporting data for all data plotted in the Figs. 1–6 (as well as Supplementary Figs. 1–4) are available as source data in spreadsheets, in the Supplementary Information (see additional information) and at Code Ocean50 and https://github.com/DuaneDJohnson/Hybrid-Cuckoo-Search/. Source data are provided with this paper.

Code availability

Interactive open-source codes are available via Code Ocean for Hybrid-CS SCRAPs50 and for Hybrid CS for 1D functions51. For open-source codes (and data) for Hybrid CS SCRAPs or 1D functions, see https://github.com/DuaneDJohnson/Hybrid-Cuckoo-Search/.

References

  1. Yeh, J. W. et al. Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303 (2004).

    Article  Google Scholar 

  2. Cantor, B., Chang, I. T. H., Knight, P. & Vincent, A. J. B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 375–377, 213–218 (2004).

    Article  Google Scholar 

  3. Senkov, O. N., Miller, J., Miracle, D. & Woodward, C. Accelerated exploration of multi-principal element alloys with solid solution phases. Nat. Commun. 6, 6529 (2015).

    Article  Google Scholar 

  4. George, E. P., Raabe, D. & Ritchie, R. O. High-entropy alloys. Nat. Rev. Mater. 4, 515–534 (2019).

    Article  Google Scholar 

  5. Gao, M.C., Yeh, J-W., Liaw, P. K., Zhang, Y. (Ed.), High-Entropy Alloys: Fundamentals and Applications, 1st ed., Springer Inter. Publishing, Switzerland, 2016, pp. 333–366.

  6. Singh, P., Smirnov, A. V. & Johnson, D. D. Atomic short-range order and incipient long-range order in high-entropy alloys. Phys. Rev. B 91, 224204 (2015).

    Article  Google Scholar 

  7. Singh, P. et al. Design of high-strength refractory complex solid-solution alloys. npj Comput. Mater 4, 16 (2018).

    Article  Google Scholar 

  8. Miracle, D. B. & Senkov, O. N. A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511 (2017).

    Article  Google Scholar 

  9. Zhang, Y. et al. Influence of chemical disorder on energy dissipation and defect evolution in concentrated solid solution alloys. Nat. Commun. 6, 8736 (2015).

    Article  Google Scholar 

  10. Singh, P. et al. Vacancy-mediated complex phase selection in high entropy alloys. Acta Mater. 194, 540–546 (2020).

    Article  Google Scholar 

  11. Karati, A. et al. Ti2NiCoSnSb—a new half-Heusler type high-entropy alloy showing simultaneous increase in Seebeck coefficient and electrical conductivity for thermoelectric applications. Sci. Rep. 9, 5331 (2019).

    Article  Google Scholar 

  12. Ding, Q. et al. Tuning element distribution, structure and properties by composition in high-entropy alloys. Nature 574, 223–227 (2019).

    Article  Google Scholar 

  13. Li, Z., Pradeep, K. G., Deng, Y., Raabe, D. & Tasan, C. C. Metastable high-entropy dual-phase alloys overcome the strength-ductility trade-off. Nature 534, 227–230 (2016).

    Article  Google Scholar 

  14. Zhang, R. et al. Short-range order and its impact on the CrCoNi medium-entropy alloy. Nature 581, 283–287 (2020).

    Article  Google Scholar 

  15. Singh, P., Smirnov, A. V. & Johnson, D. D. Ta-Nb-Mo-W refractory high-entropy alloys: anomalous ordering behavior and its intriguing electronic origin. Phys. Rev. Mater. 2, 055004 (2018).

    Article  Google Scholar 

  16. Yang, X. S. & Deb, S. Cuckoo search via Lévy flights. In Proc. World Congress on Nature and Biologically Inspired Computing 210–214 (IEEE, 2009).

  17. Yang, X. S. & Deb, S. Engineering optimisation by Cuckoo Search. Int. J. Math. Model. Numer. Optim. 1, 330–343 (2010).

    MATH  Google Scholar 

  18. Back, T., Fogel, D. & Michalewicz, Z. Handbook of Evolutionary Computation (Oxford Univ. Press, 1996).

  19. Yang, X. S. Engineering Optimization: An Introduction with Metaheuristic Applications (Wiley, 2010).

  20. Yang, X. S., Koziel, S. & Leifsson, L. Computational optimization, modelling and simulation: recent trends and challenges. Procedia Comput. Sci. 18, 855–860 (2013).

    Article  Google Scholar 

  21. Blum, C. & Roli, A. Metaheuristics in combinatorial optimization: overview and conceptual comparison. ACM Comput. Surv. 35, 268–308 (2003).

    Article  Google Scholar 

  22. Ashlock, D. Evolutionary Computation for Modeling and Optimization 1st edn (Springer, 2016).

  23. Kirkpatrick, S., Gelatt, C. D. Jr & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).

    Article  MathSciNet  Google Scholar 

  24. Holland, J. H. Adaptation in Natural and Artificial Systems 1st edn (MIT Press, 1992).

  25. Kennedy, J. & Eberhart, R. Particle swarm optimization. In Proc. ICNN’95 International Conference on Neural Networks Vol. 4, 1942–1948 (IEEE, 1995).

  26. Dorigo, M., Maniezzo, V. & Colorni, A. Ant system: optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. B Cybern. 26, 29–41 (1996).

    Google Scholar 

  27. Yang, X. S. Bat algorithm for multi-objective optimisation. Int. J. Bio-Inspired Comput. 3, 267–274 (2011).

    Article  Google Scholar 

  28. Sharma, A., Singh, R., Liaw, P. K. & Balasubramanian, G. Cuckoo searching optimal composition of multicomponent alloys by molecular simulations. Scrip. Mater. 130, 292–296 (2017).

    Article  Google Scholar 

  29. Cowley, J. M. An approximate theory of order in alloys. Phys. Rev. 77, 669–675 (1950).

    Article  Google Scholar 

  30. Moss, S. C. X-ray measurement of short-range order in Cu3Au. J. Appl. Phys. 35, 3547–3553 (1964).

    Article  Google Scholar 

  31. Gutowski, M. Lévy flights as an underlying mechanism for global optimization algorithms. Preprint at https://arxiv.org/pdf/math-ph/0106003.pdf (2001).

  32. Johnson, D. D. in Computation of Diffuse Intensities in Alloys, Characterization of Materials (ed. Kaufmann, E.) 346–375 (Wiley, 2012).

  33. Van de Walle, A. et al. Efficient stochastic generation of special quasirandom structures. Calphad 42, 13–18 (2013).

    Article  Google Scholar 

  34. Johnson, D. D., Nicholson, D. M., Pinski, F. J., Gyorffy, B. L. & Stocks, G. M. Density-functional theory for random alloys: total energy within the coherent-potential approximation. Phys. Rev. Lett. 56, 2088–2091 (1986).

    Article  Google Scholar 

  35. Alam, A. & Johnson, D. D. Structural properties and stability of (meta)stable ordered, partially ordered, and disordered Al–Li alloy phases. Phys. Rev. B 85, 1441202 (2012).

    Article  Google Scholar 

  36. Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).

    Article  Google Scholar 

  37. Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid–metal/amorphous–semiconductor transition in germanium. Phys. Rev. B 49, 14251–14269 (1994).

    Article  Google Scholar 

  38. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1994).

    Article  Google Scholar 

  39. Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).

    Article  MathSciNet  Google Scholar 

  40. Orr, R. L. Heats of formation of solid Au–Cu alloys. Acta Metall. 8, 489–493 (1960).

    Article  Google Scholar 

  41. Flinn, P. A., McManus, G. M. & Rayne, J. A. Elastic constants of ordered and disordered Cu3Au from 4.2 to 300 °K. J. Phys. Chem. Solids 15, 189–195 (1960).

    Article  Google Scholar 

  42. Smallmann, R. E. & Nagan, A. H. W. Modern Physical Metallurgy 3rd edn (Butterworths, 1970).

  43. Togo, A. & Tanaka, I. First-principles phonon calculations in materials science. Scrip. Mater. 108, 1–5 (2015).

    Article  Google Scholar 

  44. Yeh, J.-W. Alloy design strategies and future trends in high-entropy alloys. JOM 65, 1759–1771 (2013).

    Article  Google Scholar 

  45. Sohn, S. S. et al. Ultrastrong medium-entropy single-phase alloys designed via severe lattice distortion. Adv. Mater. 31, 1807142 (2019).

    Article  Google Scholar 

  46. Pinski, F. J. et al. Origins of compositional order in NiPt alloys. Phys. Rev. Lett. 66, 766–769 (1991).

    Article  Google Scholar 

  47. Ceguerra, A. V. et al. Short-range order in multicomponent materials. Acta Crystallogr. A 68, 547–560 (2012).

    Article  Google Scholar 

  48. Zunger, A., Wei, S.-H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353–356 (1990).

    Article  Google Scholar 

  49. Song, H. et al. Local lattice distortion in high-entropy alloys. Phys. Rev. Mater. 1, 023404 (2017).

    Article  Google Scholar 

  50. Singh, R., Sharma, A., Singh, P., Balasubramanian, G. & Johnson, D. D. SCRAPs: a multicomponent alloy structure design tool; https://doi.org/10.24433/CO.0000024.v1

  51. Singh, R., Sharma, A., Singh, P., Balasubramanian, G. & Johnson, D. D. Hybrid-CS code for 1D test functions; https://doi.org/10.24433/CO.6419254.v1

Download references

Acknowledgements

R.S. was supported in part by D.D.J.’s F. Wendell Miller Professorship at ISU. Work at Ames Laboratory (by R.S., A.S., P.S. and D.D.J.) was funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science & Engineering Division. Ames Laboratory is operated for the US DOE by Iowa State University under contract no. DE-AC02-07CH11358. G.B. was funded by the National Science Foundation through award no. 1944040.

Author information

Authors and Affiliations

  1. Mechanical Engineering, Iowa State University, Ames, IA, USA

    Rahul Singh & Aayush Sharma

  2. Ames Laboratory, US Department of Energy, Iowa State University, Ames, IA, USA

    Prashant Singh & Duane D. Johnson

  3. Mechanical Engineering & Mechanics, Lehigh University, Bethlehem, PA, USA

    Ganesh Balasubramanian

  4. Materials Science & Engineering, Iowa State University, Ames, IA, USA

    Duane D. Johnson

Authors
  1. Rahul Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aayush Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Prashant Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ganesh Balasubramanian
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Duane D. Johnson
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

D.D.J. proposed and supervised the project. R.S. wrote the SCRAPs generation code using the hybrid CS algorithm. R.S. and A.S. did initial testing. D.D.J. developed the linear-scaling parallel algorithm and scaling analysis. P.S. and R.S. implemented SCRAPs optimization with parallelization and catalogged timings. P.S. completed DFT and phonon calculations, and performed analysis with D.D.J. P.S. got the code running on Code Ocean. R.S., A.S., P.S. and G.B. drafted the initial manuscript, then D.D.J. prepared the final manuscript with approval from all the authors.

Corresponding author

Correspondence to Duane D. Johnson.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Fernando Chirigati was the primary editor on this Article and managed its editorial process and peer review in collaboration with the rest of the editorial team. Nature Computational Science thanks the anonymous reviewers for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Singh, R., Sharma, A., Singh, P. et al. Accelerating computational modeling and design of high-entropy alloys. Nat Comput Sci 1, 54–61 (2021). https://doi.org/10.1038/s43588-020-00006-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s43588-020-00006-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing