Abstract
In recent years, network analysis has been applied to identify and analyse patterns of statistical association in multivariate psychological data. In these approaches, network nodes represent variables in a data set, and edges represent pairwise conditional associations between variables in the data, while conditioning on the remaining variables. This Primer provides an anatomy of these techniques, describes the current state of the art and discusses open problems. We identify relevant data structures in which network analysis may be applied: cross-sectional data, repeated measures and intensive longitudinal data. We then discuss the estimation of network structures in each of these cases, as well as assessment techniques to evaluate network robustness and replicability. Successful applications of the technique in different research areas are highlighted. Finally, we discuss limitations and challenges for future research.
Similar content being viewed by others
Introduction
In many scientific fields, researchers study phenomena best characterized at the systems level1. To understand such phenomena, it is often insufficient to focus on the way individual components of a system operate. Instead, one must also study the organization of the system’s components, which can be represented in a network2. The value of analysing the structure of a system in this way has been underscored by the advent of network science, which has delivered important insights into diverse sets of phenomena studied across the sciences3,4. This Primer discusses methodology to apply this line of reasoning to the statistical analysis of multivariate data.
Network approaches involve the identification of system components (network nodes) and the relations among them (links between nodes). Well-known examples include semantic networks (in which concepts are connected through shared meanings5), social networks (in which people are connected through acquaintance6) and neural networks (in which neurons are connected through axons7). After nodes and links are identified, and a network has been constructed, one can study its topology using descriptive tools of network science8. For instance, one can describe the global topology of a network (such as a small-world network or random graph9) or the position of individual nodes within the network (for example, by assessing node centrality10). These analyses are often carried out with the goal of relating structural features of the network to system dynamics4,11.
Network representations have a long history as research tools in statistics, where they encode important information concerning the joint probability distribution of a set of variables12. For instance, in graphical models, unconnected nodes are conditionally independent given all or a subset of other nodes in the network12; in causal models, graphical criteria are used to determine whether parameters in an estimated causal model are identified13; and in structural equation models, path-tracing rules on network representations are used to determine the value of empirical correlations implied by the model14.
In this Primer, we present network analysis of multivariate data as a method that combines both multivariate statistics and network science to investigate the structure of relationships in multivariate data. This approach identifies network nodes with variables and links between nodes and describes them with statistical parameters that connect these variables (for example, partial correlations). Statistical models are used to assess the parameters that define the links in the network, in a process known as network structure estimation. Then, using a process of network description, the resulting network is characterized using the tools of network science15,16,17. Here, we refer to this combined procedure of network structure estimation and network description as psychometric network analysis (Fig. 1).
Joint probability distribution of multivariate data characterized in terms of conditional associations and independencies. Conditional independencies translate into disconnected nodes; conditional associations translate into links between nodes, typically weighted by the strength of the association. The resulting structure is subsequently described and analysed as a network.
Network approaches to multivariate data can be used to advance several different goals. First, they can be used to explore the structure of high-dimensional data in the absence of strong prior theory on how variables are related. In these analyses, psychometric network analysis complements existing techniques for the exploratory analysis of psychological data, such as exploratory factor analysis (which aims to represent shared variance due to a small number of latent variables) and multidimensional scaling (which aims to represent similarity relations between objects in a low-dimensional metric space). The unique focus of psychometric network analysis is on the patterns of pairwise conditional dependencies that are present in the data. Second, network representations can be used to communicate multivariate patterns of dependency effectively, because they offer powerful visualizations of patterns of statistical association. Third, network models can be used to generate causal hypotheses, as they represent statistical structures that may offer clues to causal dynamics; for instance, networks that represent conditional independence relations form a gateway that connects correlations to causal relations13,18,19.
Here, we review these functions of network analysis in the context of three types of application in psychological science, illustrating them with examples taken from personality, attitude research and mental health.
Experimentation
The schematic workflow of psychometric network analysis as discussed in this paper is represented in Fig. 2. Typically, one starts with a research question that dictates a data collection scheme, which includes cross-sectional designs, time-series designs and panel designs. Psychometric network analysis begins with node selection, a choice primarily driven by substantive rather than methodological considerations. The core of the psychometric network analysis methodology then lies in the steps of network structure estimation, network description and network stability analysis. Importantly, inferences drawn from the output of network analytic methods require both substantive domain knowledge and general methodological considerations regarding the stability and robustness of the estimated network in order to optimally inform scientific inference.
The heart of the psychometric network analysis methodology described lies in the steps of network structure estimation (to construct the network), network description (to characterize the network) and network stability analysis (to assess the robustness of results). These steps are informed by substantive research questions and data collection procedures. Output of the network approaches combines with general methodological considerations and domain-specific knowledge to support scientific inference.
Network approaches to multivariate data are based on generic statistical procedures and thus invite applications to many types of data. The approaches discussed in this paper, however, have been developed and typically used in the context of psychometric variables such as responses to questionnaire items, symptom ratings and cognitive test scores20, possibly extended with background variables such as age and gender21, genetic information22, physiological markers23, medical conditions24, experimental interventions25 and anticipated downstream effects26. Accordingly, the nodes we discuss will ordinarily represent items and tests.
The majority of network modelling approaches use conditional associations to define the network structure prevalent in a set of variables20,27. A conditional association between two variables holds when these variables are probabilistically dependent, conditional on all other variables in the data. Which measure of conditional association to use depends on the structure of the data; for instance, for multivariate normal data, partial correlations would be indicated, whereas for binary data, logistic regression coefficients may be used. The strength of this conditional association is typically represented in the network as an edge weight that describes the connection between two nodes. If the association between two variables can be explained by other variables in the network, so that their conditional association vanishes when these other variables are controlled for, then the corresponding nodes are disconnected in the network representation.
The description of the joint probability distribution of a set of variables in terms of pairwise statistical interactions is a graphical model12 known as the pairwise Markov random field (PMRF)27. Versions of the PMRF are known under several other names as well in the statistical literature; see refs28,29 for an overview of the relations between relevant statistical models. Many network modelling approaches attempt to estimate the PMRF, typically using existing statistical methodologies such as significance testing30, cross-validation31, information filtering32 and regularized estimation16,33,34,35,36. Because of its prominence in the literature, this Primer is limited to network approaches that use the PMRF, although it should be noted that other approaches to the analysis of multivariate data exist, including models based on zero-order associations37, self-reported causal relations between variables38,39 and relative importance of variables40.
Because, in typical multivariate data, a substantive subset of associations between variables vanishes upon conditioning, applications of network modelling generally return non-trivial topological structures and the description of such structures is an important goal of psychometric network analysis. For instance, the extent to which network nodes are connected and the network’s general topology are of interest, as well as the position of individual nodes in that structure. Thus, psychometric network analysis typically involves interpreting the output of statistical estimation procedures, for example an estimated PMRF, as the input for network description techniques taken from network science (Fig. 1).
Types of data
Network models always operate on associations among sets of variables, but such associations can be extracted from many different experimental and quasi-experimental designs. We focus on three designs that represent typical data environments in social science where psychometric network analysis can be relevant: cross-sectional networks, longitudinal networks of panel data and time-series networks (Fig. 3).
Cross-sectional data
In applications to cross-sectional data, networks are representations of the conditional associations between variables measured at a single time point in a large sample (T = 1, N = large). In this case, the associations between variables are driven by individual differences, which renders such networks useful for studying the psychometric structure of psychological tests29. In the cross-sectional data example used here, we are interested in the empirical relations among personality and personal goals. We analyse a data set in which three levels of personality structure are assessed via questionnaires, using network models to investigate empirical relations among these elements and personal goals. Our illustrative personality data set features 432 observations and 39 variables of interest41.
We represent network structures as they arise at different levels of aggregation42 at which personality can be described. These can be higher-order traits, such as conscientiousness; facets, such as orderliness, industriousness and impulse control43; or even specific single items, such as prudent, reflective and disciplined (items of impulse control44) that allow for a finer distinction of personality characteristics below facets (see ref.45 for an example). The objective of psychometric network analysis, in this case, would be to offer insight into the multivariate pattern of conditional dependencies that characterize the joint distribution of these variables at these different levels of aggregation (Box 1).
When cross-sectional data are analysed through network estimation and interpreted via network description, is it important to keep in mind that resulting topologies represent structures that describe differences between individuals, and that these are not necessarily isomorphic to processes or mechanisms that characterize the individuals who make up the data. That is, inter-individual differences do not necessarily translate to intra-individual processes46,47. If one is interested solely in the structure of individual differences, cross-sectional data are adequate, but research into intra-individual dynamics ideally complements such data sources with panel data or time series.
Panel data
In network applications to longitudinal data (also referred to as panel data), a limited set of repeated measurements characterize both the association structure of variables at a given time point and the way these conditional dependencies’ change over time (N > T). Such measures can illuminate the structure of individual differences and intra-individual change in parallel.
In our example for network approaches to panel data, we use repeated assessments of emotions and beliefs towards Bill Clinton as represented in longitudinal panel data of the American National Election Studies (ANES) between 1992 and 1996. We aim to model consistency, stability and extremity of attitudes towards Bill Clinton during the time that he transitioned from governor of Arkansas to president of the United States. The network theory of attitudes (Box 2) formalizes changes in attitude importance as network temperature, for example, increasing or decreasing interdependence between attitude elements. In the panel data example, network analyses can assist in modelling temperature changes in the interdependence of attitude elements towards BillClinton.
Time-series data
Networks as applied to time-series data of one or multiple persons characterize multivariate dependencies between time series of variables that are assessed intra-individually (T = large, N ≥ 1). Such networks are most often applied in situations where one seeks insight into the dynamic structure of systems. For instance, in the social and clinical sciences, recent years have witnessed a surge of daily diary studies and ecological momentary assessment, conducted via smartphones and designed to study such dynamic structures. Studies typically measure experiences — such as mood states, symptoms, cognitions and behaviours — at the moment they occur48,49. In such cases, network analyses can assist in interpreting intensive longitudinal data by offering insightful characterizations of the multivariate pattern of dynamics.
In the time-series data example used here, we leverage data gathered during the onset of the COVID-19 pandemic to investigate the impact of reduced social contact due to lockdown measures on the mental health of students enrolled at Leiden University in the Netherlands. In this ecological momentary assessment study, students were followed daily for 2 weeks, assessing momentary social contact as well as current stress, anxiety and depression 4 times per day via a smartphone application50. In this situation, a network model can be fitted to these data to investigate to what degree social contact variables influence mental health variables over the course of hours and days. Because, in this case, multiple individuals were assessed multiple times, the design is mixed; in such situations, it is often profitable to use a statistical multilevel approach27,51, in which the repeated observations are treated as nested in the individuals. This explicitly separates individual differences from time dynamics52.
Results
In a PMRF, the joint likelihood of multivariate data is modelled through the use of pairwise conditional associations, leading to a network representation that is undirected. There are several benefits to the PMRF that make this particular network representation important. First, the PMRF encodes conditional independence relations (in terms of absent links between nodes), which form an important gateway to identify candidate data-generating mechanisms29,53,54. However, the PMRF does not require an a priori commitment to any particular data-generating mechanism (unlike directed acyclic graph estimation or latent variable modelling, for example). Because PMRFs do not place strong assumptions on the structure of the generating model but do hold clues to causal structure through conditional independencies, they are well suited to exploratory analyses (see also Limitations and optimizations). In addition, estimated PMRFs often describe the data successfully with only a subset of the possible parameters (for example, using sparse network structures), which leads to more insightful network visualizations. Finally, a priori commitments invariably lead to problems of underdetermination, because many structurally different models will produce indistinguishable data, which is known as statistical equivalence. By contrast, the PMRF is uniquely identified, so there are no two equivalent PMRFs with different parameters that fit the data equally well.
If data are continuous, a popular type of PMRF is the Gaussian graphical model (also known as a partial correlation network) in which edges are parameterized as partial correlation coefficients55,56. If data are binary, a popular PMRF developed to estimate the Ising model can be used, in which edges are parameterized as log-linear relationships16,29,36. The Ising model and the Gaussian graphical model can be combined in mixed graphical models, in which edges are parameterized as regression coefficients from generalized linear regression models57. Mixed graphical models represent the most general approach to PMRF estimation and also allow for the inclusion of categorical and count variables.
Cross-sectional data
The PMRF can readily be estimated from cross-sectional data, in which case it can be reasonably assumed that all cases or rows in the data set — which usually represent people — are independent. This assumption is violated, however, in panel data and time-series designs, in which an individual case is not a person but, rather, a single measurement moment of one of the persons in the sample. In this case, violations of independence occur in two ways: temporal dependencies are introduced owing to the temporal aspect of data gathering (for example, a person who feels sad at 12:00 might still feel sad at 15:00), and responses from the same person may correlate more strongly with one another than responses between different persons (for example, a person might feel, on average, very sad in all responses). Thus, whereas cross-sectional data can use independence assumptions that allow for the application of population-sample logic, time-series data require a model to deal with the dependence between data points.
Time-series data
To address time dependencies, PMRFs may be extended with temporal effects that represent regressions on the previous time point in a single-person case. These temporal effects may, for instance, be estimated through the application of a vector autoregressive model. The structure of the associations that remain after taking temporal effects into account can also be represented in a PMRF. This network is typically designated as the contemporaneous network. Thus, in contrast to the case of cross-sectional networks, the application of network modelling to multivariate time series returns separate network structures to characterize the dependence relation describing associations that link variables through time, and associations that link variables after these temporal effects have been taken into account. These networks have a distinct function in the interpretation of results. The temporal network can be read in terms of carry-over effects at the timescale defined by the spacing between repeated measures, where the temporal ordering can also assist causal interpretation. The contemporaneous network will include associations that are due to effects that occur at different timescales rather than those defined by the spacing between repeated measurements. Note that, just as cross-sectional networks, time-series networks almost always represent correlational data; interpretation of such networks in causal terms is never straightforward.
Panel data
In panel data or N >1 time-series settings, multilevel modelling can differentiate between within-person and between-person variance In addition to the temporal and contemporaneous networks (both of which represent within-person information), one then obtains a third structure of associations that can be characterized as a PMRF. This third structure represents the conditional associations between the long-term averages of the time series between people. This structure, similar to that of cross-sectional networks, represents associations driven by individual differences and is known as the between-persons network. Thus, in the cross-sectional case one obtains one network (the PMRF of the association between individual differences), in the time-series case one obtains two networks (the directed temporal network of vector autoregressive coefficients and the undirected contemporaneous network of the regression residuals) and for multiple time series and panel data one obtains three networks (temporal and contemporaneous networks driven by intra-individual processes and the between-persons network driven by individual differences). In addition, one may use multiple time series to identify network structures that are (in)variant over individuals58 or that define subgroups59.
Edge selection
Methods of edge selection are based on general statistical theory as applied to the estimation of conditional associations. Three methods are featured in the literature. First, approaches based on model selection through fit indices can be used. For example, regularized estimation procedures16,33 lead to models that balance parsimony and fit, in the sense that they aim to only include edges that improve the fit of the network model to data (for instance, by minimizing the extended Bayesian information criterion35). Second, null hypothesis testing procedures are used to evaluate each individual edge for statistical significance30; if desired, this process can be specialized to deal with multiple testing, through Bonferroni correction or false discovery rate approaches, for example. Last, cross-validation approaches can be used. In these approaches, the network model is chosen based on its performance in out of sample prediction, such as in k-fold cross-validation31.
Network description
Once a network structure is estimated, network description tools from network science can be applied to investigate the topology of PMRF networks3,60.
Global topologies that are particularly important revolve around the distinction between sparse versus dense networks. In sparse networks, few (if any) edges are present relative to the total number of possible edges. In dense networks, the converse holds, and relatively many edges are present. This distinction is important for two reasons. First, optimal estimation procedures may depend on sparsity, for example regularization-based approaches can be expected to perform well if data are generated from a sparse network, but may not work well in dense networks. Second, in sparse networks the importance of individual nodes is typically more pronounced, because in dense networks all nodes tend to feature a similar large number of edges. Further analyses can be used to investigate the global topology of the network structure in greater detail; for example, Dalege et al.61 investigate small-world features9 of attitude networks and Blanken et al.62 use clique percolation methodology to assess the structure of psychopathology networks. Although network visualizations are typically based on aesthetic principles — for example, by using force-based algorithms63 — recently, techniques have been proposed to visualize networks based on multidimensional scaling64. These techniques allow node placement to mirror the strength of conditional associations in the PRMF, so that more strongly connected nodes are placed in closer vicinity to each other.
Local topological properties of networks feature attributes of particular nodes or sets of nodes. For example, measures of centrality can be used to investigate the position of nodes in the network. The most commonly used centrality metrics are node strength, which sums the absolute edge weights of edges per node; closeness, which quantifies the distance between the node and all other nodes by averaging the shortest path lengths to all other nodes; and betweenness, which quantifies how often a node lies on the shortest path connecting any two other nodes65. These metrics are directly adapted from social network analysis, and can be used to assess the position of variables in the network representation constructed by the researchers. Strength conveys how strongly the relevant variable is conditionally associated with other variables in the network, on average. However, note that closeness and betweenness treat association as distances, which can be problematic. More recently, new measures have been introduced, specifically designed for the analysis of PMRF structures. Expected influence is a measure of centrality that takes the sign of edge weights into account66; this can be appropriate when variables have a non-arbitrary coding, such as when the high values of all variables indicate more psychopathology. Predictability quantifies how much variance in a node is explained by its neighbours54, which can be used to assess the extent to which the network structure predicts node states. Further extensions to the characterization of networks and nodes in terms of network science involve participation coefficients, minimal spanning trees and clique percolation as proposed by Letina et al.67 and Blanken et al.62. Finally, the shortest paths between nodes may yield insight into the strongest predictive pathways, and clustering in the network may yield insight into potential underlying unobserved causes and the dimensionality of the system68.
Applications
Although network approaches as discussed here draw on insights from statistics and network theory, the specific combination of techniques discussed in this paper has its roots in psychometric modelling in psychological contexts. This section discusses three areas in which this approach has been particularly successful. First, the domain of personality research, where network models have been applied to describe the interaction between stable behavioural patterns that characterize an individual. Second, the domain of attitude research, in which networks have been designed to model the interaction between attitude elements (feelings, thoughts and behaviours) to explain phenomena such as polarization. Last, the domain of mental health research, where networks have been used to represent disorders as systems of interacting symptoms and to represent key concepts such as vulnerability and resilience.
Personality research
Personality researchers are interested in examining the processes characterizing personality traits69. One type of these processes is motivational: research shows that traits such as conscientiousness or extraversion can be considered as means to achieve specific goals, for example getting tasks done and having fun, which have been identified as goals relevant for conscientiousness and extraversion, respectively70. Psychometric network analysis of personality traits and motivational goals combined offers a novel way to explore relations among relatively stable dispositions. Personality networks can represent personality at different levels of abstraction, from higher-order traits to facets to specific items. One could wonder which abstraction level should be preferred. The answer requires balancing simplicity and accuracy of predictions and of explanations. Focusing on a level that is too abstract might result in losing important details, whereas adding elements beyond necessary could result in noisy estimates and, thus, faulty conclusions. An approach that can help is out of sample predictability71. We illustrate this by reanalysing data from Costantini et al.41 (Study 3) that include 9 goals identified as relevant for conscientiousness and 30 items from an adjective-based measure of conscientiousness that assess three main facets: industriousness, impulse control and orderliness44.
Data and analysis
In this sample (N = 432) we explored how well we could predict goals using a tenfold cross-validation approach72. The networks depicted in Fig. 4 represent Gaussian graphical models estimated with the qgraph R package15, using graphical lasso regularization. The lambda parameter for graphical lasso was selected through the extended Bayesian information criterion (γ = 0.5 (ref.33)). We varied the level of representation of the personality dimensions from general (single trait) to specific (3 facets) to molecular (30 items) and explored the relationships between personality and 9 goal scores.
Network of relationships between motivational goals (yellow) and conscientiousness at the level of the trait (panel a), its facets (panel b) and items (panel c). Blue edges represent positive connections and red edges represent negative connections; thicker edges represent stronger relationships. Relationships between personality and goals are emphasized with saturated colours. *Items reverse-scored before entering network estimation. d | Strength centrality for each goal in each network.
The results depicted in Fig. 4a suggest that some goals are positively associated and some negatively associated with an overall conscientiousness score. Two goals, personal realization (node 3) and be safe (node 7), do not show direct connections to the trait. However, this network does not consider several ways in which one can be conscientious. Some people can be more organized, others can be more controlled and yet others can be more industrious43. The facet-level network (Fig. 4b) shows that most goals are related to a specific subset of one or two of the three facets, thus characterizing more clearly specific portions of the trait. At this level, personal realization (node 3) is positively related to industriousness but negatively connected to the remaining facets, something that would not have been apparent had we considered the trait level exclusively. At the item level (Fig. 4c), connections appear generally consistent with those emerging at the facet level, albeit with some exceptions. For example, avoid or manage things you do not care about (node 6) shows relations with items of orderliness, whereas no such connection emerged at the facet level.
Results
Figure 4d shows strength centrality estimates for all nodes in the three networks. Irrespective of the abstraction level considered, the most central goal was do something well, avoid mistakes (node 4). The centrality of node 4 is due to connections to other goals, rather than to its connections to conscientiousness. Such connections suggest that node 4 might serve as a means for several other goals. For example, one could speculate that doing things well might be important in the pursuit of more abstract goals, such as personal realization (node 3) or having control (node 2) (see ref.72 for a discussion of the abstractness of these goals).
Results show that the trait level is never the best level for prediction and that some goals are best predicted at the item level and others at the facet level (Table 1), albeit in one case (goal 16) the trait level performed better than the item level. In general, specific levels might be useful if one is mainly interested in examining which elements of the personality system drive the association with a criterion73 or if one is purely interested in prediction. In our example, the item level performed, on average, slightly better than the facet level in terms of prediction, although this was not the case for all goals (see also ref.74). A preference for more abstract levels sometimes amounts to sacrificing a small portion of prediction in exchange for a noticeable gain in theoretical simplicity. Furthermore, using abstract predictors can sometimes assuage multicollinearity. At the same time, abstracting too much can lump together concepts that are better understood separately. There is no ultimate answer to the selection of the best abstraction level in personality as it heavily depends on the questions being asked and the data available. In general, the facet level might often provide a good balance between specificity and simplicity75,76.
Attitude research
Social psychologists are interested in how beliefs and attitudes can change over time. We illustrate the use of networks to improve our understanding of these processes with a study of attitudes towards Bill Clinton in the United States in the early 1990s. Based on the network theory of attitudes (Box 2) one expects that temperature should decrease throughout the years, because Bill Clinton was probably more on individuals’ minds when he was president than before he was president. We investigate changes in the network structure of these attitudes in the years before and during his presidency and whether the temperature of the attitude network changes. In this example, we estimate temperature using variations in how strongly correlated the attitude elements are at the different time points. Temperature of attitude networks can, however, also be measured by several proxies, such as how much attention individuals direct towards a given issue and how important they judge the issue.
Data and analysis
We use data from the open access repository of the ANES between 1992 and 1996 including beliefs and emotions towards Bill Clinton. For this example, the presented data have been previously reported77,78. Beliefs were assessed using a four-point scale ranging from describes Bill Clinton extremely well to not at all. Emotions were assessed using a dichotomous scale with answer options of yes, have felt and no, never felt. Dichotomizing the belief questions, we fit an Ising model with increasing constraints representing their hypotheses to this longitudinal assessment of beliefs and emotions in the American electorate. We investigate the impact on the fit of the model of constraining edges between nodes to be equal across time points, constraining the external fields to be equal across time points and constraining the temperature (the entropy of the system) to be equal across time points. Additionally, we tested whether a dense network (all nodes are connected) or a sparse network (at least some edges are absent) fits the data best. After estimating the network, we applied the walktrap algorithm to the network to detect different communities, such as, for example, sets of highly interconnected nodes68,79. The walktrap algorithm makes use of random walks to detect communities. If random walks between two nodes are sufficiently short, these two nodes are assigned to the same community.
Results
The results show a sparse network with a stable network structure, where edges do not differ between time points (Fig. 5). The model with varying external information and temperature fitted the data best. Figure 5a shows the estimated network at the four time points. The attitude network is connected: every attitude element is at least indirectly connected to every other attitude element. As can be seen, negative emotions of feeling afraid and angry are strongly connected to each other, as are positive emotions of feeling hope and pride. Within the beliefs, believing that Bill Clinton gets things done and provides strong leadership are closely connected. The belief that he cares about people is closely connected to the positive emotions. The walktrap algorithm detected two communities: one large community that contains all beliefs and the positive emotions; and one smaller community that contains the negative emotions. This indicates that positive emotions are more closely related to (positive) beliefs than positive and negative emotions are related to each other.
a | Estimated attitude network towards Bill Clinton. Colour of nodes corresponds to communities detected by the walktrap algorithm. Blue edges indicate positive connections between attitude elements and red edges indicate negative connections; width of the edges corresponds to strength of connection. b | Change in temperature throughout time. c | Histograms for overall attitude towards Bill Clinton in each year.
Figure 5b shows changes in temperature throughout the years. As can be expected from the network theory of attitudes (Box 2), the temperature of the attitude network generally decreased throughout the years, with the sharpest drop before the election in 1996 revealing an increase in the specificity of respondents’ attitudes towards Clinton. This implies that attitude elements became more consistent over time, resulting in more polarized attitudes. The increase in temperature between 1993 and 1994, however, is somewhat surprising.
Figure 5c shows the distribution of the overall attitude, separately measured on a scale ranging from 0 to 100, with higher numbers indicating more favourable attitudes. Based on the decreasing temperature of the attitude networks, a corresponding increase in the extremity of these distributions is to be expected. This is exactly what was found; the variance of the distributions increased in a somewhat similar fashion as the temperature of the attitude network decreased. The increase in the variance between 1993 and 1994 was the only exception.
Mental health research
Mental health research and practice rest on reportable symptoms and observable signs. Therapists interviewing patients will ask questions about subjective symptoms as well as assess signs of behavioural distress (such as agitated hand-wringing and crying). The challenge for both mental health researchers and therapists is to determine the cause of the person’s constellation of signs and symptoms. Therapists, moreover, have the additional charge of using this information to devise an appropriate course of treatment. The network theory of psychopathology80,81 suggests that mental disorders are best understood as clusters of symptoms sufficiently unified by causal relations among those symptoms that support induction, explanation, prediction and control82,83 (Box 3). Signs and symptoms are constitutive of disorder, not the result of an unobservable common cause. We illustrate this with an example study of social interaction and its relations to mental health variables in a student sample during the COVID-19 pandemic.
Data and analysis
Researchers have devised an ecological momentary assessment study following 80 students (mean age = 20.38 years, standard deviation = 3.68, range = 18–48 years; n = 60 female, n = 19 male, n = 1 other) from Leiden University for 2 weeks in their daily lives50. With 19 different nationalities represented, this sample is highly international. Most students are single (n = 50), one–third of the students are currently employed and about 1 in 5 students report prior mental health problems. In this study, participants are asked about the extent of their worry, sadness, irritability and other subjective phenomenological experiences four times per day via a smartphone application. We use multilevel vector autoregressive modelling to assess the contemporaneous and temporal associations among problems related to generalized anxiety and depression. As a reminder, the contemporaneous network covers relations within the same 3-h assessment window, and the temporal network lag – 1 relations between one 3-h window and the next.
Results
The resulting networks can be used to inform our understanding of how the modelled variables evolve over time (Fig. 6). In this application, the model suggests that the cognitive symptom worry and the affective symptom nervous exhibit a strong contemporaneous association but do not exhibit a conditional dependence relation in temporal analyses, indicating that the relation between these items may be limited to a 3-h time interval. Similarly, we can clarify the paths by which external factors, such as social interaction, predict and are predicted by mental health. For example, the contemporaneous association between offline social interaction (nodes 8) and worry (node 3) occurs via feelings of loneliness (node 7), information which could be used in the generation of hypotheses about the causal relationships among these symptoms. It is also notable that different types of social interaction are differentially associated with loneliness. Offline social interaction is conditionally associated with lower levels of loneliness, whereas online social interaction is associated with higher levels of loneliness. The temporal associations further inform our understanding of these relationships. Difficulty envisioning the future and difficulty relaxing predict online social interaction, and online social interaction predicts subsequent difficulty relaxing. This illustrates how psychometric network analysis of time series naturally leads to more detailed hypotheses about the system under study; do note that this use of network analysis is exploratory and that generated hypotheses require independent testing, ideally through research that utilizes experimental interventions.
Contemporaneous network (left) of conditional associations between variables obtained after controlling for temporal effects in the temporal network (right); latter represents carry-over effects from one time point to the next. Blue edges indicate positive connections and red edges indicate negative connections; width of edges corresponds to strength of connection.
Network analyses not only equip researchers to investigate the associations among symptoms but also provide a novel framework for conceptualizing treatment. There are at least two potential ways one can intervene on a system, such as that depicted in Fig. 6. First, we can lower the mean level of a node by diminishing its frequency or severity. For example, we could intervene on the online social interaction node, hoping, based on the contemporaneous relations, that it might promote offline social interaction, alleviate loneliness and, in turn, foster less worry, more optimism and greater interest and pleasure. However, even if initially successful, merely intervening on a node may be insufficient, leaving the person vulnerable to relapse, as the structure of the network remains intact. If pessimism and an inability to relax are, indeed, encouraging online social interaction, then when our intervention on this node ceases, the problem may return, erasing our treatment gains. Accordingly, instead of targeting a specific node (or symptom), we may target the link between symptoms, thereby changing the structure of the network. For example, rather than aiming to reduce online social interaction in general, we could specifically target the tendency to engage in online social interaction when the person experiences pessimism or difficulty relaxing, thereby eliminating the temporal association between these symptoms and online social interaction and disrupting the network.
Reproducibility and data deposition
A challenge posed by the estimation of PMRFs from multivariate data is that estimation error and sampling variation need to be taken into account when interpreting the network model. For example, networks estimated from two different groups of people may look different visually but this difference may be due to sampling variation. Several statistical methods have been proposed for assessing the stability and accuracy of estimated parameters as well as to compare network models of different groups. For many statistical estimators, data resampling techniques such as bootstrapping and permutation tests have been developed for this purpose17,84.
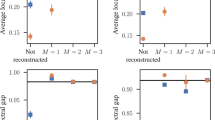
Standard approaches to robustness analyses involve three targets: individual edge weight estimates, differences between edges in the network and topological metrics defined on the network structure, such as node centrality. The robustness of edge weight estimates can be assessed by constructing intervals that reflect the sensitivity of edge weight estimates to sampling error, such as confidence intervals, credibility intervals and bootstrapped intervals (Fig. 7a). The robustness of differences between edge weights can be assessed by investigating to what degree the bootstrapped intervals for the relevant coefficients overlap (Fig. 7b). The robustness of network properties such as node centrality can be investigated through a case-dropping bootstrap, in which progressively fewer cases are sampled from the original data set to obtain subsamples; the correlation between centrality measures in these subsamples and the total sample is plotted as a function of the size of the subsamples (Fig. 7c). Various approaches are available to assess these forms of robustness, including approaches based on bootstrapping17 and Bayesian statistics85.
a | Sample value (red line), bootstrapped 95% intervals (shaded area) and average bootstrapped value (blue line) of edge weights. b | Whether the 95% bootstrapped interval of the differences between any two edges includes the value zero (grey squares) or not (dark squares) gives an indication of whether two edges are different from each other17. Diagonal visualizes magnitude of original edge; red indicates negative values, blue indicates positive values and colour saturation indicates absolute values (more saturated the colour, stronger the edge). c | Results of case-dropping bootstrap analysis showing average correlation between strength centrality estimated in the full sample and strength estimated on a random subsample, retaining only a certain portion of cases (from 90% to 10%). Shaded area indicates 95% bootstrapped confidence intervals of correlation estimates. Higher values indicate better stability of centrality estimates17.
The generalizability of network structures can be assessed by comparing results in different samples. This is typically assessed by examining the similarity of network structures across samples. A formal test for the invariance of networks has been developed to assess the null hypothesis that the networks are identical at the level of the population from which individuals have been sampled84 and Bayesian analyses86 can also be used to assess invariance of networks. Finally, moderated network analysis87 and multi-group analysis have been introduced as methods for statistically comparing groups88. To gain more insight into the degree to which pairwise associations correspond across networks, the correlation between edge weights in different groups can be inspected.
It should be emphasized that, owing to sampling variability, one should not ordinarily expect to reproduce the network completely, and that the degree to which the network structure replicates depends on several factors, including the network architecture itself80,89. For this reason, network analysts have developed tools to compute the expected reproducibility of network structure estimation results27. Figure 8 displays the expected replicability of one of the personality networks reported above that one should expect, if the estimated networks were the true networks, using different sample sizes. For instance, from this analysis it is apparent that the item-level network should be expected to replicate less strongly than the facet-level and trait-level networks.
ReplicationSimulator generates multiple data sets from an estimated network to assess expected sensitivity (probability of including edges given that they are, in fact, present in the generating network) and specificity (probability of leaving out edges given that they are, in fact, absent in the generating network) as well as expected correlation between edge weights for two replication data sets generated from the network.
In addition to sampling variability, network structures can be affected by random measurement error. The effects of measurement error differ depending on the type of network estimated. In cross-sectional networks, ignoring measurement error typically leads to an underestimation of network density. If the strength of edges is associated with the network structure itself, this may lead to an artificial magnification of network structure. In longitudinal and time-series networks, however, measurement error can also lead to spurious edges90. One way to deal with measurement error is to utilize latent variable modelling; in this case, the network model is augmented with a measurement model that relates multiple observables to a single latent node, and the PMRF is estimated at the level of these latent nodes27.
To improve standardization and reproducibility, recent research explicates minimal shared norms in reporting psychological network analyses91. For methods sections of scientific papers, such norms include information on subsample and variable selection, the presence of deterministic relations between variables and skip structures that may distort the network, the estimation methods used as well as any additional specifications (such as thresholding, regularization, parameter settings), how the accuracy and stability of edge estimates were assessed and, finally, the statistical software and packages used, including their versions (Table 2).
In terms of results, current norms recommend reporting the final sample size after handling missing data, plotting and visualization choices and the accuracy and stability checks of any network model, in light of the research question of the researcher. If the research questions concern centrality estimates, case-drop bootstrap results would be reported, for example. Many reporting routines are dependent on the specific research goals of the researcher and different analysis routines result in different reporting choices. Burger et al.91 elaborate on these routines and further discuss important considerations for network analysis and potential sources of misinterpretation of network structures.
Limitations and optimizations
Network structure estimation
Although many network structures are now estimable through standard software, some limitations still remain. First, although treatments of dichotomous, unordered categorical and continuous data and their combinations are well developed57, treatments of ordinal data are still suboptimal. Ongoing research is developing approaches for such data, which are common in the social sciences92,93. Second, estimation routines have traditionally used nodewise regularized regression16 or the graphical lasso33. Although these techniques return visually attractive networks, statistically they are most appropriate when networks can be expected to be sparse35,36. Non-regularized estimation approaches based on model selection provide an important alternative, as research suggests that they can outperform regularized approaches in several situations94,95. Third, many network modelling techniques handle missing data suboptimally, for example through list-wise deletion. Emerging estimation frameworks use alternative approaches, which allow for better missing data handling, for instance through full-information maximum likelihood88,96.
Interpretation
The fact that, in psychometric network models, edges are not observed but estimated necessitates the evaluation of sampling variance, which requires extensions. First, current techniques for edge selection do not guarantee that unselected edges are statistically indistinguishable from zero or that evidence for their absence is strong. Relatedly, many current estimation methods do not produce standard errors or confidence intervals around edge weight estimates, as the sampling distributions of regularized regression coefficients are unwieldy. This limits the interpretation of individual edges. In non-regularized networks, significance tests can be used, but this practice is not based on model selection and therefore inherits problems inherent in significance testing. New Bayesian approaches address these challenges, as they can quantify evidence for or against edge inclusion97.
Second, network structures depend on which variables are included. Nodes that are highly central in one network may therefore be peripheral in another. In addition, if important nodes are missing, this can affect the structure of the network; for instance, it may lead to increased edge strengths among nodes that represent effects of an omitted common cause98. If nodes are essentially duplicates of each other — for example, if two nodes have topological overlap — this will influence the network architecture as well99,100. Thus, network interpretation depends on a judicious choice of which variables to include in the network, and more research is needed to develop theoretical frameworks to guide these choices.
Third, centrality metrics have been suggested to reflect the importance of nodes to the system that the network represents33 and early literature interpreted nodes with high centrality as more plausible targets for intervention101. However, recent work has highlighted situations where centrality is not a good proxy for causal influence102,103, and for certain networks, peripheral nodes may be more important in determining system behaviour104. In addition, in some areas such as psychopathology, interactions may occur at different timescales, which complicates the relation between association structure and causal dynamics. This has rendered the use of centrality measures a topic of debate, with some papers arguing that, because psychometric network models do not specify dynamics or flow, centrality metrics should not be interpreted in terms of causal dynamics at all. In addition, centrality metrics that concatenate paths between nodes (such as closeness and betweenness) are based on (absolute) conditional associations; these do not represent physical distances — they violate transitivity — and should not be interpreted as such. Finally, although network software indexes many types of centrality, including closeness, betweenness, degree, strength, eigenvalue and expected influence, there are no clear guidelines on which interpretations are licensed by each of these105, so more research is needed to investigate the relation between theoretical properties of possible generating models and empirical estimates of centrality106.
Causal inference
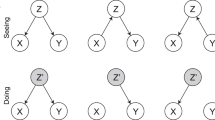
The constituent parts of PMRFs are purely statistical associations, so that direct causal inference based on network structures is not justified. Although the PMRF itself is typically unique — there are no alternative PMRFs that will generate the same set of joint probability distributions — the correspondence between the PMRF and generative causal systems is one to many: edges between nodes may arise owing to directed causal effects or feedback loops, but also owing to unobserved common causes107, conditioning on common effects102,108 and various other structures (Fig. 9). As is the case for causal inference in general, causal inference based on PMRFs requires the statistical structure to be augmented by substantively backed assumptions53. This motivates the articulation of strong network theories in addition to the development of network models, as for instance have been devised for intelligence109,110, attitudes61,111 and certain mental disorders112.
Current directions in network estimation may assist in causal inference by developing better methodologies. For example, causal search algorithms may be effective in identifying a particular causal model in certain cases18,113,114,115. In addition, inclusion of interventions in network structures may facilitate causal interpretation25,116,117. Alternatively, researchers may revert to non-causal interpretation of network structures. In such cases, marginal associations can be preferred over conditional associations if the goal is purely to describe the patterns of association. For example, Schwaba et al.118 opted to model a network of correlations rather than partial correlations, because of the descriptive nature of their goal.
Confirmatory testing
Most applications of network analysis use exploratory techniques to estimate network structures20. However, advances in network estimation allow one to constrain parameters (such as edge weights) to a specific value, constrain edges to have the same edge weight as each other or constrain edge weights to be equal across different groups88,119. The ability to test these constraints adds confirmatory data analysis approaches to the network analytic toolbox120. The psychonetrics R package121 is an example of an implementation that allows for confirmatory testing of network constraints. There are also Bayesian implementations available for testing constraints in networks that can be used to test whether an edge is positive, negative or null, and to test order constraints on edge weights85.
One way of arriving at network hypotheses is on the basis of exploratory network analyses. For example, an initial data set may be used to estimate a network model exploratively. In the next step, all of the estimated zeros are included as constraints in a network model that is fitted to a new data set122. Similarly, one can use an exploratively estimated network to formulate different hypotheses about the order of the strengths of edge weights and test these hypotheses against each other using Bayes factors123. A second way of arriving at network hypotheses is from substantive theory about the phenomena being modelled, from which network structures implied by the theory can be deduced124. To test substantive hypotheses, future methodological research should provide tools that can help researchers express substantive hypotheses in constraints on network structures, which can subsequently be tested using confirmatory models.
Outlook
Network models are suited to estimate and represent patterns of conditional associations without requiring strong a priori assumptions on the generating model, which renders them well suited to exploratory data analysis and visualization of dependency patterns in multivariate data. As statistical analysis methods, the software routines for estimating, visualizing and analysing networks enhance existing exploratory data analysis methods, as they focus specifically on the patterns of pairwise conditional associations between variables. The resulting network representation of conditional associations between variables, as encoded in the PMRF, may be of interest in its own right, but can also function as a gateway that allows the researcher to assess the plausibility of different generating models that may produce the relevant conditional associations. This assessment may include latent variable models29 and directed acyclic graphs115 in addition to explanations based on network theories80,123.
Because network models for multivariate data explicitly represent pairwise interactions between components in a system, they form a natural bridge from data analysis to theory formation based on network science principles3. In this respect, networks not only accommodate the multivariate architecture of systems but also offer a toolbox to develop formal theories of the dynamical processes that form and maintain them61,124. One successful example of such an approach is the mutualism model of intelligence125, which proposes an explanation of the positive correlations between intelligence tests based on network concepts. This explanation quantifies how the structure of the cognitive network impacts the dynamic processes taking place in it. This model has been extended to explain various empirical phenomena reported in the intelligence literature126,127. Similar developments have taken place in clinical psychology112,128 and attitude research78, as featured in the current paper.
The combination of network representations in data analytics and theory formation is remarkably fruitful in forging connections between different fields and research programmes. One important connection is that between the study of inter-individual differences and intra-individual mechanisms. More than half a century ago, Cronbach famously diagnosed psychological science to be a deeply divided discipline129. With one camp of psychological scientists concerned with mechanistic explanations and another camp primarily focused on the study of individual differences, that dichotomy is still prevailing. Some argue that in order to overcome this division, psychological scientists should rethink their widespread practice of detaching statistical practice from substantive theory130,131,132. One reason for this detachment, however, has been the long-standing lack of an intuitive modelling framework that facilitates both theory construction and process-based computations and simulation, so that it can connect the two disciplines129. But this gap is exactly what makes network approaches fall on fertile soil. Networks readily accommodate the multivariate architecture of psychological systems and also offer a toolbox to develop formal theories of the dynamical processes that act on them. In this manner, models of intra-individual dynamics can serve as explanations of systems of inter-individual differences, bridging the gap between intra-individual and inter-individual modelling129.
Network models are not only useful to create bridges from data analysis to theory formation but also to connect different scientific disciplines to each other. In recent years, network science and associated complex systems approaches have led to an active interdisciplinary research area in which researchers from many fields collaborate. Network approaches in psychology, as discussed here, have similarly broadened the horizon of relevant candidate methodologies relevant to psychological research questions; for instance, it is remarkable that the first network model fitted to psychopathology data16 was based on modelling approaches developed to study atomic spins133,134, whereas subsequent studies into the research dynamics of psychopathology135 investigated sudden transitions using methodology developed in ecology136 and, finally, recent studies of interventions in such networks are based on control theory137. Clearly, network representations create a situation where scientists with different disciplinary backgrounds find a common vocabulary.
This common vocabulary creates tantalizing possibilities for building bridges between research areas — particularly in cases where the systems studied are plausibly constituted by networks operating at different levels, such as human behaviour. For instance, largely independent of one another, neuroscience and psychology have both developed research traditions rooted in network science. With network models of the brain based on neuroimaging studies and network models of psychological responses, the bigger picture might no longer be obstructed by disciplinary fences138,139. This promise is by no means limited to psychology and its subdisciplines; the network fever is spanning many disciplines, such as physics, ecology and biology. In fact, the best cited network papers are concerned with universal network characteristics that can advance interdisciplinary theory and modelling9,140. We have only begun to chart the connections between disciplines that deal with complex networks, and we hope that network approaches to multivariate data can play a productive role in this respect.
Code availability
Code and data used in sample analyses are available from https://github.com/DennyBorsboom/NatureMethodsPrimer_NetworkAnalysis.
Change history
21 February 2022
A Correction to this paper has been published: https://doi.org/10.1038/s43586-022-00101-1
References
Meadows, D. H. Thinking in Systems: A Primer (Chelsea Green, 2008). This text is the most convincing to motivate systems thinking throughout the sciences.
Barabási, A. L. The network takeover. Nat. Phys. 8, 14–16 (2012).
Newman, M. E. J. Networks: An Introduction (Oxford University Press, 2010). This text is an ideal introduction to network science and the associated mathematical modelling techniques.
Newman, M. E. J., Barabási, A. L. E. & Watts, D. J. The Structure and Dynamics of Networks (Princeton University Press, 2006).
Richens, R. H. Preprogramming for mechanical translation. Mech. Transl. Comput. Ling. 3, 20–25 (1956).
Milgram, S. The small world problem. Psychol. Today 2, 60–67 (1967).
Ramón y Cajal, S. The Croonian Lecture: la fine structure des centres nerveux. Proc. R. Soc. Lond. 55, 444–468 (1894).
Newman, M. E. & Clauset, A. Structure and inference in annotated networks. Nat.Commun. 7, 1–11 (2016).
Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998). This article kickstarts the growth of network science in the past few decades.
Bavelas, A. A mathematical model for group structures. Appl. Anthropol. 7, 16–30 (1948).
Kolaczyk, E. D. Statistical Analysis of Network Data: Methods and Models (Springer, 2009). This text is an authoritative overview of statistical models for network analysis.
Cox, D. R. & Wermuth, N. Multivariate Dependencies: Models, Analysis and Interpretation Vol. 67 (CRC, 1996).
Pearl, J. Causality: Models, Reasoning, and Inference (Cambridge University Press, 2000). This crucial book makes the connection between conditional independence patterns and causal structures.
Wright, S. Correlation and causation. J. Agric. Res. 20, 557–585 (1921).
Epskamp, S., Cramer, A. O., Waldorp, L. J., Schmittmann, V. D. & Borsboom, D. qgraph: network visualizations of relationships in psychometric data. J. Stat. Softw. 48, 1–18 (2012).
Van Borkulo, C. D. et al. A new method for constructing networks from binary data. Sci. Rep. 4, 1–10 (2014). This paper is the first application of regularized network modelling in psychopathology.
Epskamp, S., Borsboom, D. & Fried, E. I. Estimating psychological networks and their accuracy: a tutorial paper. Behav. Res. Methods 50, 195–212 (2018). This article introduces robustness analysis for network modelling.
Spirtes, P., Glymour, C. N., Scheines, R. & Heckerman, D. Causation, prediction, and search (MIT Press, 2000).
Haslbeck, J., Ryan, O., Robinaugh, D., Waldorp, L. & Borsboom, D. Modeling psychopathology: from data models to formal theories. Psychol. Methods https://doi.org/10.31234/osf.io/jgm7f (2021).
Robinaugh, D. J., Hoekstra, R. H., Toner, E. R. & Borsboom, D. The network approach to psychopathology: a review of the literature 2008–2018 and an agenda for future research. Psychol. Med. 50, 353–366 (2020).
Deserno, M. K., Borsboom, D., Begeer, S. & Geurts, H. M. Multicausal systems ask for multicausal approaches: a network perspective on subjective well-being in individuals with autism spectrum disorder. Autism 21, 960–971 (2017).
Isvoranu, A. M. et al. Toward incorporating genetic risk scores into symptom networks of psychosis. Psychol. Med. 50, 636–643 (2020).
Fried, E. et al. Using network analysis to examine links between individual depressive symptoms, inflammatory markers, and covariates. Psychol. Med. 16, 2682–2690 (2019).
Isvoranu, A. M. et al. Extended network analysis: from psychopathology to chronic illness. BMC Psychiatry 21, 1–9 (2021).
Blanken, T. F. et al. Introducing network intervention analysis to investigate sequential, symptom-specific treatment effects: a demonstration in co-occurring insomnia and depression. Psychother. Psychosom. 88, 52–54 (2019).
Blanken, T. F., Borsboom, D., Penninx, B. W. & Van Someren, E. J. Network outcome analysis identifies difficulty initiating sleep as a primary target for prevention of depression: a 6-year prospective study. Sleep 43, zsz288 (2020).
Epskamp, S. Psychometric network models from time series and panel data. Psychometrika 85, 206–231 (2020). This article systematizes psychometric network models for longitudinal data.
Kindermann, R. P. & Snell, J. L. On the relation between Markov random fields and social networks. J. Math. Sociol. 7, 1–13 (1980).
Marsman, M. et al. An introduction to network psychometrics: relating Ising network models to item response theory models. Multivar. Behav. Res. 53, 15–35 (2018). This article establishes systematic links between network models and latent variable analysis.
Williams, D. R. & Rast, P. Back to the basics: rethinking partial correlation network methodology. Br. J. Math. Stat. Psychol. 73, 187–212 (2020).
Haslbeck, J. M. & Waldorp, L. J. How well do network models predict observations? On the importance of predictability in network models. Behav. Res. Methods 50, 853–861 (2018).
Christensen, A. P., Kenett, Y. N., Aste, T., Silvia, P. J. & Kwapil, T. R. Network structure of the Wisconsin Schizotypy Scales — short forms: examining psychometric network filtering approaches. Behav. Res. Methods 50, 2531–2550 (2018).
Epskamp, S. & Fried, E. I. A tutorial on regularized partial correlation networks. Psychol. Med. 23, 617 (2018).
Costantini, G. et al. Stability and variability of personality networks. A tutorial on recent developments in network psychometrics. Pers. Individ. Differ. 136, 68–78 (2019).
Barber, R. F. & Drton, M. High-dimensional Ising model selection with Bayesian information criteria. Electron. J. Stat. 9, 567–607 (2015).
Ravikumar, P., Wainwright, M. J., Raskutti, G. & Yu, B. High-dimensional covariance estimation by minimizing ℓ1-penalized log-determinant divergence. Electron. J. Stat. 5, 935–980 (2011). This seminal article presents regularized estimation of network structure.
Borsboom, D. & Cramer, A. O. Network analysis: an integrative approach to the structure of psychopathology. Annu. Rev. Clin. Psychol. 9, 91–121 (2013).
Frewen, P. A., Allen, S. L., Lanius, R. A. & Neufeld, R. W. Perceived causal relations: novel methodology for assessing client attributions about causal associations between variables including symptoms and functional impairment. Assessment 19, 480–493 (2012).
Deserno, M. K. et al. Highways to happiness for autistic adults? Perceived causal relations among clinicians. PLoS ONE 15, e0243298 (2020).
Robinaugh, D. J., LeBlanc, N. J., Vuletich, H. A. & McNally, R. J. Network analysis of persistent complex bereavement disorder in conjugally bereaved adults. J. Abnorm. Psychol. 123, 510–522 (2014).
Costantini, G., Saraulli, D. & Perugini, M. Uncovering the motivational core of traits: the case of conscientiousness. Eur. J. Pers. 34, 1073–1094 (2020).
Deserno, M. K., Borsboom, D., Begeer, S. & Geurts, H. M. Relating ASD symptoms to well-being: moving across different construct levels. Psychol. Med. 48, 1179–1189 (2018).
Roberts, B. W., Lejuez, C., Krueger, R. F., Richards, J. M. & Hill, P. L. What is conscientiousness and how can it be assessed? Dev. Psychol. 50, 1315–1330 (2014).
Costantini, G. et al. Development of indirect measures of conscientiousness: combining a facets approach and network analysis. Eur. J. Pers. 29, 548–567 (2015).
Mõttus, R., Kandler, C., Bleidorn, W., Riemann, R. & McCrae, R. R. Personality traits below facets: the consensual validity, longitudinal stability, heritability, and utility of personality nuances. J. Pers. Soc. Psychol. 112, 474–490 (2017).
Molenaar, P. C. A manifesto on psychology as idiographic science: bringing the person back into scientific psychology, this time forever. Measurement 2, 201–218 (2004). This article establishes the need for time-series modelling of psychometric data.
Hamaker, E. L., Kuiper, R. M. & Grasman, R. P. A critique of the cross-lagged panel model. Psychol. Methods 20, 102–116 (2015). This article demonstrates the need to separate between-subject from within-subject structures in the analysis of longitudinal data.
aan het Rot, M., Hogenelst, K. & Schoevers, R. A. Mood disorders in everyday life: a systematic review of experience sampling and ecological momentary assessment studies. Clin. Psychol. Rev. 32, 510–523 (2012).
Moskowitz, D. S. & Young, S. N. Ecological momentary assessment: what it is and why it is a method of the future in clinical psychopharmacology. J. Psychiatry Neurosci. 31, 13 (2006).
Fried, E. I., Papanikolaou, F. & Epskamp, S. (2021). Mental health and social contact during the COVID-19 pandemic: an ecological momentary assessment study. Clin. Psychol. Sci. https://doi.org/10.1177/21677026211017839 (2021).
Bringmann, L. F. et al. A network approach to psychopathology: new insights into clinical longitudinal data. PLoS ONE 8, e60188 (2013). This article introduces multilevel time-series modelling in the context of psychopathology networks.
Hamaker, E. L., Ceulemans, E., Grasman, R. P. P. P. & Tuerlinckx, F. Modeling affect dynamics: state of the art and future challenges. Emot. Rev. 7, 316–322 (2015).
Pearl, J. Causal inference. Causality: objectives and assessment. Proc. Mac. Learn. Res. 6, 39–58 (2010).
Spirtes, P., Glymour, C. N., Scheines, R. & Heckerman, D. Causation, Prediction, and Search (MIT Press, 2000).
Chen, B., Pearl, J. & Kline, R. Graphical tools for linear path models. Psychometrika 4, R432 (2018).
Roverato, A. & Castelo, R. The networked partial correlation and its application to the analysis of genetic interactions. J. R. Stat. Soc. 66, 647–665 (2017).
Haslbeck, J. & Waldorp, L. J. mgm: estimating time-varying mixed graphical models in high-dimensional data. Preprint at https://arxiv.org/abs/1510.06871 (2020). This article generalizes the network model to mixed data types.
Gates, K. M. & Molenaar, P. C. M. Group search algorithm recovers effective connectivity maps for individuals in homogeneous and heterogeneous samples. NeuroImage 63, 310–319 (2012).
Gates, K. M., Lane, S. T., Varangis, E., Giovanello, K. & Guskiewicz, K. Unsupervised classification during time-series model building. Multivar. Behav. Res. 52, 129–148 (2017).
Barabasi, A. L. Network Science (Cambridge University Press, 2018). This text is an authoritative overview of network science.
Dalege, J. et al. Toward a formalized account of attitudes: the causal attitude network (CAN) model. Psychol. Rev. 123, 2 (2016).
Blanken, T. F. et al. The role of stabilizing and communicating symptoms given overlapping communities in psychopathology networks. Sci. Rep. 8, 1–8 (2018).
Fruchterman, T. M. & Reingold, E. M. Graph drawing by force-directed placement. Software Pract. Exper. 21, 1129–1164 (1991).
Jones, P. J., Mair, P. & McNally, R. J. Visualizing psychological networks: a tutorial in R. Front. Psychol. 9, 1742 (2018).
Opsahl, T., Agneessens, F. & Skvoretz, J. Node centrality in weighted networks: generalizing degree and shortest paths. Soc. Netw. 32, 245–251 (2010). This article generalizes network metrics to weighted networks as intensively used in current network approaches to multivariate data.
Robinaugh, D. J., Millner, A. J. & McNally, R. J. Identifying highly influential nodes in the complicated grief network. J. Abnorm. Psychol. 125, 747 (2016).
Letina, S., Blanken, T. F., Deserno, M. K. & Borsboom, D. Expanding network analysis tools in psychological networks: minimal spanning trees, participation coefficients, and motif analysis applied to a network of 26 psychological attributes. Complexity https://doi.org/10.1155/2019/9424605 (2019).
Golino, H. F. & Epskamp, S. Exploratory graph analysis: a new approach for estimating the number of dimensions in psychological research. PLoS ONE 12, e0174035 (2017).
Baumert, A. et al. Integrating personality structure, personality process, and personality development. Eur. J. Pers. 31, 503–528 (2017).
McCabe, K. O. & Fleeson, W. Are traits useful? Explaining trait manifestations as tools in the pursuit of goals. J. Pers. Soc. Psychol. 110, 287–301 (2016).
Yarkoni, T. & Westfall, J. Choosing prediction over explanation in psychology: lessons from machine learning. Perspect. Psychol. Sci. 12, 1100–1122 (2017).
Costantini, G., Perugini, M. & Mõttus, R. A framework for testing causality in personality research. Eur. J. Pers. 32, 254–268 (2018).
Mõttus, R. Towards more rigorous personality trait—outcome research. Eur. J. Pers. 30, 292–303 (2016).
Mõttus, R. et al. Descriptive, predictive and explanatory personality research: different goals, different approaches, but a shared need to move beyond the Big Few traits. Eur. J. Pers. 34, 1175–1201 (2020).
Paunonen, S. V. & Ashton, M. C. Big five factors and facets and the prediction of behavior. J. Pers. Soc. Psychol. 81, 524 (2001).
Paunonen, S. V. & Ashton, M. C. On the prediction of academic performance with personality traits: a replication study. J. Res. Pers. 47, 778–781 (2013).
Dalege, J., Borsboom, D., van Harreveld, F., Waldorp, L. J. & van der Maas, H. L. Network structure explains the impact of attitudes on voting decisions. Sci. Rep. 7, 1–11 (2017).
Dalege, J., Borsboom, D., van Harreveld, F. & van der Maas, H. L. A network perspective on attitude strength: testing the connectivity hypothesis. Soc. Psychol. Personal. Sci. 10, 746–756 (2019).
Pons, P. & Latapy, M. Computing communities in large networks using random walks. J. Graph. Algorithms Appl. 10, 191–218 (2006).
Borsboom, D. A network theory of mental disorders. World Psychiatry 16, 5–13 (2017).
McNally, R. Network analysis of psychopathology: controversies and challenges. Annu. Rev. Clin. Psychol. 17, 31–53 (2020). This paper is a state-of-the-art overview of the status of network analysis in psychopathology.
Kendler, K. S., Zachar, P. & Craver, C. What kinds of things are psychiatric disorders? Psychol. Med. 41, 1143–1150 (2011).
Held, B. S. The distinction between psychological kinds and natural kinds revisited: can updated natural-kind theory help clinical psychological science and beyond meet psychology’s philosophical challenges? Rev. Gen. Psychol. 21, 82–94 (2017).
Van Borkulo, C. D., et al. Comparing network structures on three aspects: a permutation test (preprint). https://doi.org/10.13140/RG.2.2.29455.38569 (2017).
Williams, D. R. & Mulder, J. Bayesian hypothesis testing for Gaussian graphical models: conditional independence and order constraints. J. Math. Psychol. 99, 102441 (2020). This article introduces Bayesian approaches to hypothesis testing in network models.
Williams, D. R., Piironen, J., Vehtari, A. & Rast, P. Bayesian estimation of Gaussian graphical models with predictive covariance selection. Preprint at https://arxiv.org/abs/1801.05725 (2018).
Haslbeck, J. M., Borsboom, D. & Waldorp, L. J. Moderated network models. Multivariate Behav. Res. 56, 256–287 (2019).
Epskamp, S., Isvoranu, A. M. & Cheung, M. Meta-analytic Gaussian network aggregation. Psychometrika https://doi.org/10.1007/s11336-021-09764-3 (2021).
Williams, D. R. Learning to live with sampling variability: expected replicability in partial correlation networks. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/fb4sa (2020).
Schuurman, N. K. & Hamaker, E. L. Measurement error and person-specific reliability in multilevel autoregressive modeling. Psych. Methods 24, 70 (2019).
Burger, J. et al. Reporting standards for psychological network analyses in cross-sectional data. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/4y9nz (2020).
Isvoranu, A. & Epskamp, S. Continuous and ordered categorical data in network psychometrics: which estimation method to choose? deriving guidelines for applied researchers. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/mbycn (2021).
Johal, S. K. & Rhemtulla, M. Comparing estimation methods for psychometric networks with ordinal data. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/ej2gn (2021).
Williams, D. R., Rhemtulla, M., Wysocki, A. C. & Rast, P. On nonregularized estimation of psychological networks. Multivariate Behav. Res. 54, 719–750 (2019).
Wysocki, A. C. & Rhemtulla, M. On penalty parameter selection for estimating network models. Multivariate Behav. Res. 56, 288–302 (2019).
Mansueto, A. C., Wiers, R., van Weert, J., Schouten, B. C. & Epskamp, S. Investigating the feasibility of idiographic network models. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/hgcz6 (2020).
Williams, D. R., Briganti, G., Linkowski, P. & Mulder, J. On accepting the null hypothesis of conditional independence in partial correlation networks: a Bayesian analysis. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/7uhx8 (2021).
Hallquist, M. N., Wright, A. G. & Molenaar, P. C. Problems with centrality measures in psychopathology symptom networks: why network psychometrics cannot escape psychometric theory. Multivariate Behav. Res. 56, 199–223 (2019).
Christensen, A. P., Golino, H. & Silvia, P. J. A psychometric network perspective on the validity and validation of personality trait questionnaires. Eur. J. Pers. 34, 1095–1108 (2020).
Fried, E. I. & Cramer, A. O. Moving forward: challenges and directions for psychopathological network theory and methodology. Perspect. Psychol. Sci. 12, 999–1020 (2017).
Rhemtulla, M. et al. Network analysis of substance abuse and dependence symptoms. Drug Alcohol. Depend. 161, 230–237 (2016).
Dablander, F. & Hinne, M. Node centrality measures are a poor substitute for causal inference. Sci. Rep. 9, 1–13 (2019).
Spiller, T. R. et al. On the validity of the centrality hypothesis in cross-sectional between-subject networks of psychopathology. BMC Med. 18, 1–14 (2020).
Quax, R., Apolloni, A. & Sloot, P. M. The diminishing role of hubs in dynamical processes on complex networks. J. R. Soc. Interface 10, 20130568 (2013).
Bringmann, L. F. et al. What do centrality measures measure in psychological networks? J. Abnorm. Psychol. 128, 892 (2019).
Borgatti, S. P. Centrality and network flow. Soc. Netw. 27, 55–71 (2005).
Rohrer, J. M. Thinking clearly about correlations and causation: graphical causal models for observational data. Adv. Methods Pract. Psychol. Sci. 1, 27–42 (2018).
de Ron, J., Fried, E. I. & Epskamp, S. Psychological networks in clinical populations: investigating the consequences of Berkson’s bias. Psychol. Med. 51, 168–176 (2021).
Kan, K. J., van der Maas, H. L. & Levine, S. Z. Extending psychometric network analysis: empirical evidence against g in favor of mutualism? Intelligence 73, 52–62 (2019).
Kievit, R. A. et al. Mutualistic coupling between vocabulary and reasoning supports cognitive development during late adolescence and early adulthood. Psychol. Sci. 28, 1419–1431 (2017).
Dalege, J., Borsboom, D., van Harreveld, F. & van der Maas, H. L. The attitudinal entropy (AE) framework as a general theory of individual attitudes. Psychol. Inq. 29, 175–193 (2018). This article develops the network theory of attitudes.
Robinaugh, D. et al. Advancing the network theory of mental disorders: a computational model of panic disorder. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/km37w (2020). This article is the first to augment symptom network models with substantively plausible formalized theory.
Scutari, M. Learning Bayesian networks with the bnlearn R package. J. Stat. Softw. 35, 1–22 (2010).
Colombo, D. & Maathuis, M. H. Order-independent constraint-based causal structure learning. J. Mach. Learn. Res. 15, 3741–3782 (2014).
Ryan, O., Bringmann, L. F. & Schuurman, N. K. The challenge of generating causal hypotheses using network models. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/ryg69 (2020).
Kossakowski, J. J., Gordijn, M. C. M., Harriette, R. & Waldorp, L. J. Applying a dynamical systems model and network theory to major depressive disorder. Front. Psychol. 10, 1762 (2019).
Mooij, J. M., Magliacane, S. & Claassen, T. Joint causal inference from multiple contexts. J. Mach. Learn. Res. 21, 1–108 (2020).
Schwaba, T., Rhemtulla, M., Hopwood, C. J. & Bleidorn, W. A facet atlas: visualizing networks that describe the blends, cores, and peripheries of personality structure. PLoS ONE 15, e0236893 (2020).
Drton, M. & Richardson, T. S. in Proceedings of the 20th Conference on Uncertainty in Artificial Intelligence (UAI ‘04) 130–137 (AUAI Press, 2004).
Epskamp, S., Rhemtulla, M. & Borsboom, D. Generalized network psychometrics: combining network and latent variable models. Psychometrika 82, 904–927 (2017).
Epskamp, S. Psychonetrics: structural equation modeling and confirmatory network analysis. Psychonetrics http://psychonetrics.org/ (2020).
Kan, K. J., de Jonge, H., van der Maas, H. L., Levine, S. Z. & Epskamp, S. How to compare psychometric factor and network models. J. Intell. 8, 35 (2020).
Rodriguez, J. E., Williams, D. R., Rast, P. & Mulder, J. On formalizing theoretical expectations: Bayesian testing of central structures in psychological networks. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/zw7pf (2020).
Cramer, A. O., Waldorp, L. J., Van Der Maas, H. L. & Borsboom, D. Comorbidity: a network perspective. Behav. Brain Sci. 33, 137 (2010).
Van Der Maas, H. L. et al. A dynamical model of general intelligence: the positive manifold of intelligence by mutualism. Psychol. Rev. 113, 842 (2006). This article contains the first articulation of a network model to account for patterns of individual differences in psychology.
Savi, A. O., Marsman, M., van der Maas, H. L. & Maris, G. K. The wiring of intelligence. Perspect. Psychol. Sci. 14, 1034–1061 (2019).
Van Der Maas, H. L., Kan, K. J., Marsman, M. & Stevenson, C. E. Network models for cognitive development and intelligence. J. Intell. 5, 16 (2017).
Cramer, A. O. et al. Major depression as a complex dynamic system. PloS ONE 11, e0167490 (2019).
Cronbach, L. J. [1957]. The two disciplines of scientific psychology. Am. Psychol. 12, 671 (2016).
Gigerenzer, G. Personal reflections on theory and psychology. Theor. Psychol. 20, 733–743 (2010).
Wood, D., Gardner, M. H. & Harms, P. D. How functionalist and process approaches to behavior can explain trait covariation. Psychol. Rev. 122, 84 (2015).
Borsboom, D., van der Maas, H. L., Dalege, J., Kievit, R. A. & Haig, B. D. Theory construction methodology: a practical framework for building theories in psychology. Perspect. Psychol. Sci. 16, 756–766 (2021).
Lenz, W. Beitrag zum Verständnis der magnetischen Erscheinungen in festen Körpern [German]. Physikalische Z. 21, 613–615 (1920).
Ising, E. Beitrag zur theorie des ferromagnetismus [German]. Z. für Phys. 31, 253–258 (1925).
Wichers, M., Groot, P. C. & Psychosystems, E. S. M., EWS Group. Critical slowing down as a personalized early warning signal for depression. Psychother. Psychosom. 85, 114–116 (2016). This article is the first to investigate early warnings in psychopathology transitions.
Scheffer, M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009). This crucial article articulates the link between complex systems, sudden transitions and early warning signals in time series.
Henry, T. R., Robinaugh, D. & Fried, E. I. On the control of psychological networks. (preprint). PsyArXiv https://doi.org/10.31234/osf.io/7vpz2 (2021).
Brooks, D. et al. The multilayer network approach in the study of personality neuroscience. Brain Sci. 10, 915 (2020).
Bathelt, J., Geurts, H. M. & Borsboom, D. More than the sum of its parts: merging network psychometrics and network neuroscience with application in autism. Preprint at bioRxiv https://doi.org/10.1101/2020.11.17.386276 (2020).
Liljeros, F., Edling, C. R., Amaral, L. A. N., Stanley, H. E. & Åberg, Y. The web of human sexual contacts. Nature 411, 907–908 (2001).
R Core Team. R: A Language and Environment for Statistical Computing (R Foundation for Statistical Computing, 2020).
McCrae, R. R. & Costa, P. T. Jr. in Sage Handbook of Personality Theory and Assessment Vol. 1 273–294 (Sage, 2008).
Ashton, M. C. & Lee, K. Objections to the HEXACO model of personality structure—and why those objections fail. Eur. J. Pers. 34, 492–510 (2020).
Cramer, A. O. J. et al. Dimensions of normal personality as networks in search of equilibrium: you can’t like parties if you don’t like people. Eur. J. Pers. 26, 414–431 (2012).
Goldberg, L. R. et al. The international personality item pool and the future of public-domain personality measures. J. Res. Pers. 40, 84–96 (2006).
McNally, R. J. What is Mental Illness? (Belknap Press of Harvard University Press, 2011).
Borsboom, D. Psychometric perspectives on diagnostic systems. J. Clin. Psychol. 64, 1089–1108 (2008).
Acknowledgements
D.J.R.’s work on this manuscript was supported by a National Institute of Mental Health (NIMH) Career Development Award (K23-MH113805). M.K.D.’s work was supported by a Rubicon fellowship of the Netherlands Organization for Scientific Research (NWO) (no. 019.191SG.005). D.B.’s work was supported by European Research Council Consolidator Grant 647209. M.P. and G.C.’s work was supported by European Union’s Horizon 2020 research and innovation programme (grant no. 952464). E.I.F. is supported by funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant no. 949059). S.E. is supported by NWO Veni (grant number 016-195-261). C.D.v.B.’s work was supported by European Research Council Consolidator Grant 647209, granted to D.B. J.D.’s work was supported by an EU Horizon 2020 Marie Curie Global Fellowship (no. 889682). The content is solely the responsibility of the authors and does not necessarily represent the views of the funding agencies.
Author information
Authors and Affiliations
Contributions
Introduction (D.B. and M.K.D.); Experimentation (D.B., M.K.D., E.I.F. and C.D.v.B.); Results (D.B., M.K.D., S.E., A.-M.I. and L.J.W.); Applications (D.B., M.K.D., E.I.F., R.J.M., D.J.R., M.P., J.D. and G.C.); Reproducibility and data deposition (D.B., M.K.D. and G.C.); Limitations and optimizations (D.B., M.K.D., M.R., R.v.B. and A.C.W.); Outlook (D.B. and M.K.D.); Overview of the Primer (D.B. and M.K.D.).
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information
Nature Reviews Methods Primers thanks D. Hevey, S. Letina, M. Southward and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Related links
International Personality Item Pool: https://ipip.ori.org/
IPIP-Big Five Factor Markers open data: https://openpsychometrics.org/_rawdata/IPIP-FFM-data-8Nov2018.zip
Glossary
- Node centrality
-
A generic term that subsumes a family of measures that aim to assess how central a node is in a network topology, such as node strength, betweenness and closeness.
- Network structure estimation
-
The application of statistical models to assess the structure of pairwise (conditional) associations in multivariate data.
- Network description
-
Characterization of the global network topology and the position of individual nodes in that topology.
- Psychometric network analysis
-
The analysis of multivariate psychometric data using network structure estimation and network description.
- Node selection
-
The choice of which variables will function as nodes in the network model.
- Network stability analysis
-
The assessment of estimation precision and robustness to sampling error of psychometric networks.
- Conditional association
-
A statistical association between two variables that does not vanish when taking into account other variables that may explain the association.
- Edge weight
-
In psychometric network analysis, edge weights typically are parameter estimates that represent the strength of the conditional association between nodes.
- Pairwise Markov random field
-
(PMRF). An undirected network that represents variables as nodes and conditional associations as edges, in which unconnected nodes are conditionally independent.
- Topological structures
-
A generic term to characterize networks in terms of their global topology, for instance in terms of density or architecture.
- Conscientiousness
-
A term used in personality research to designate the propensity to be self-controlled, responsible, hardworking and orderly and to follow rules. In most models of human personality, conscientiousness is considered a high-order factor.
- Facets
-
Specific traits subsumed by a factor in hierarchically organized models of personality. For instance, orderliness and industriousness are facets of conscientiousness.
- Network temperature
-
A parameter of network models that controls the entropy of node state patterns. A network with low temperature will allow only node states that align, such that positively connected nodes must be in the same state and negatively connected nodes must be in the opposite state, whereas a network with high temperature will allow more random patterns of activation.
- Ecological momentary assessment
-
Daily diary methodology to measure psychological states and behaviours in the moment, for instance by using ambulatory assessment devices such as mobile phones to administer questionnaires that probe how the person feels or what the person does at that specific point in time.
- Underdetermination
-
The problem that explanatory models often are not identifiable from the data.
- Mixed graphical models
-
Models for relations between variables of continuous and discrete type based on conditional associations.
- Contemporaneous network
-
A network that represents within-person conditional associations between variables within the same time point. Contemporaneous networks are often estimated after conditioning on effects of the previous time point, as expressed in a time-series model.
- Edge selection
-
A method to determine which edges of a mixed graphical model are to be included and excluded.
- Polarization
-
A social process that leads to higher prevalence of more extreme attitudes in a population, leading to a bimodal population distribution, with only strong supporters and opponents, rather than a normal distribution in which most people obtain a middle position.
- Lambda parameter
-
A regularization parameter to determine edge inclusion/exclusion that obtains a nominal false positive rate.
- Estimation error
-
The amount by which an estimate differs from the target value.
- Nodewise regularized regression
-
An algorithm to obtain a network in which each node, in turn, is used as the dependent variable in a penalized regression function to identify which other nodes are connected to the relevant node.
- Non-regularized estimation approaches
-
Approaches that do not use a penalized likelihood function in network structure estimation but rely on different methodologies for edge selection, such as null hypothesis testing or Bayesian approaches.
- Topological overlap
-
A concept that expresses the degree to which two nodes have the same position in the network topology. Two nodes with high topological overlap have very similar connections to other nodes.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Borsboom, D., Deserno, M.K., Rhemtulla, M. et al. Network analysis of multivariate data in psychological science. Nat Rev Methods Primers 1, 58 (2021). https://doi.org/10.1038/s43586-021-00055-w
Accepted:
Published:
DOI: https://doi.org/10.1038/s43586-021-00055-w
This article is cited by
-
New psychometric evidence from the Revised Mental Health Inventory (R-MHI-5) in Peruvian adolescents from a network psychometrics approach
BMC Psychology (2024)
-
eHealth tools use and mental health: a cross-sectional network analysis in a representative sample
Scientific Reports (2024)
-
Dynamic predictors of COVID-19 vaccination uptake and their interconnections over two years in Hong Kong
Nature Communications (2024)
-
Psychological flexibility and cognitive-affective processes in young adults’ daily lives
Scientific Reports (2024)
-
Network analysis of anxiety and depressive symptoms during the COVID-19 pandemic in older adults in the United Kingdom
Scientific Reports (2024)