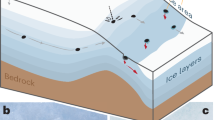
Abstract
The parameters allowing for near-trench megathrust ruptures are debated and commonly involve the presence of site-dependent tectonic factors (e.g. rough subducting topography, amount of sediments), implying the need for direct geophysical observations. Here we use seismic imaging techniques to explore the mechanisms triggering shallow ruptures in the Rivera subduction zone, along the non-accretionary Jalisco-Colima continental margin, W Mexico, where three large (Mw~8) tsunamigenic megathrust earthquakes occurred in the last century. The seismic image reveals large interplate topographic variations morphologically alike to incoming trench-parallel ridges seaward of the study area. Ridge subduction only occurs along the southern non-accretionary margin of the Rivera system, where past earthquakes released large near-trench coseismic energy, indicating that subducting ridges enhance interplate coupling. Subducting ridges uplift the margin, causing upper-plate fracturing and low rigidity areas. Such elastic structure quantitatively explains the dynamics of slow and tsunamigenic ruptures in the past. We conclude that ridge subduction beneath the Jalisco-Colima continental margin promotes shallow seismogenesis and explains the large tsunamigenic potential of the area.
Similar content being viewed by others
Introduction
Rough subducting topography is invoked to explain shallow megathrust seismogenesis1,2,3,4. Particularly, in subduction systems with sediment-starved trenches5, the subducting topography plays an important role in determining interplate coupling and defining upper-plate tectonism6. In turn, upper-plate tectonics and the distribution of fracturing with depth determine the depth distribution of upper-plate elastic rock properties, key in controlling, to a large extent, the dynamic behaviour of megathrust earthquakes7. Yet, the linkage between upper-plate elastic structure and subducting topography, and its role in shallow tsunamigenic ruptures have not been quantified. Here we focus on the Mexican Pacific coast, offshore Jalisco and Colima, which is defined by the subduction of the Rivera oceanic plate beneath the North American (NA) plate with a convergence rate that increases from 1.5–2 cm yr−1 near Puerto Vallarta in the north to 3.5–4.4 cm yr−1 in the south8 (Fig. 1a). From north to south, the upper plate of this subduction system exhibits two different tectonic regimes. From the northernmost region of the Middle America Trench (MAT) to 19.2°N latitude, the continental margin is controlled by a subduction-accretion regime as evidenced by a well-developed accretionary prism observed from seismic images9,10. South of 19.2°N, the margin is highly eroded and non-accretionary, and it is characterised by several slope failure scars visible from bathymetry11 (Fig. 2c). Upper-plate submersible observations along this southern region provide evidence of episodic tectonic subsidence during the Neogene supporting that subduction-erosion controls upper-plate tectonics in this section of the12.
a Regional map of the Rivera subduction zone depicting the study area (red box), and the location of the seismic line TS02 (this study) and TS06b10. Blue arrows are convergence vectors in cm yr−1 from ref. 8. NW-SE seamounts chains are marked in the figure with black arrows. The Rivera Fracture Zone (FZ) sets the boundary between the Rivera plate, and the Pacific and Cocos oceanic plates. MAT Middle America Trench. b Close-up of the study area showing the presence of bending-related faulting and trench-parallel oceanic ridges in the outer rise. The epicentre and distribution of the 1995 Colima-Jalisco earthquake are shown in the figure18, together with the associated aftershock distribution19. Yellow dots along seismic line TS02 are ocean-bottom seismometers.
a Average P-wave velocity model of the 500 Monte Carlo inversions, and average interplate geometry with error bounds (red band). Red dots are ocean-bottom seismometers. b Standard deviation model of velocities associated with the Monte Carlo analysis. The red band is the same average interplate geometry with error bounds as in (a). c Close-up of the margin showing the location of line TS02 and the presence of margin scars (black arrows), indicating past slope failure events. The red arrow indicates the position of the interplate high retrieved at 15 km along our model (a). Orange dots depict aftershocks of the 1995 Colima-Jalisco earthquake from ref. 19. d Along-dip topographic profiles of the outer rise extracted from the black box in (c) compared with the inverted interplate high (red line). Black arrows show the location of oceanic ridges on the outer rise.
Tectonic regime variations along the margin correlate with along-strike topographic variations of the incoming Rivera plate (Fig. 1). Subduction accretion along the margin occurs in a region facing a comparatively smoother incoming oceanic Rivera plate, characterised by localised NW-SE trending seamount chains seemingly formed at the Pacific-Rivera Rise, and NNW-SSE trending normal faulting related to the bending of the incoming plate13 (Fig. 1b). In its southern region, the incoming Rivera plate features a rougher topography (Fig. 1) represented by sharp NW-SE trending ridges extending through the diffuse plate boundary between the Rivera and Cocos oceanic plates (Fig. 1b). According to plate reconstructions and magnetic lineaments, these ridges were not generated at the Pacific-Rivera Rise (Fig. 1), but formed during the northward propagation of the East Pacific Rise (EPR) at 1.7 Ma, segmented from the main EPR by the Rivera Fracture Zone at 0.95 Ma, and finally incorporated in the Rivera plate motion14,15,16.
Interplate seismicity in the southern subduction system is characterised by large (Mw ~8) shallow and tsunamigenic megathrust earthquakes, such as the two events in 1932 (Ms 7.8 and 8.0)17, and the Mw 8, 1995 Colima-Jalisco earthquake18,19. These events generated devastating tsunami waves indicating that the rupture reached the shallow portion of the plate interface20 (Fig. 1). In some cases, even buried megathrust aftershocks seem to have triggered localised tsunamis that are either explained by submarine landslides21 or hypothetical splay faulting22. In particular, the 1995 event released one-third of the total seismic moment near the trench18, producing the largest fault displacement at 10–15 km from the trench (Fig. 1b), and unusual near-trench aftershock activity (Fig. 1b)19. The shallow seismogenic character of this region was tentatively attributed to the lack of sediments with high pore pressure19, but the absence of geophysical observations yields large unknowns regarding the main contributing factors controlling the generation of large and shallow tsunamigenic coseismic slip. Here, we use spatially coincident 2D multichannel seismic (MCS) and wide-angle seismic (WAS) data acquired during the TSUJAL experiment in 201423 to investigate the shallow tectonic and elastic structure of the margin, and its role in the generation of shallow tsunamigenic megathrust ruptures (Fig. 1).
Results
Velocity structure and interplate topography
We apply seismic imaging techniques to obtain a 2D P-wave velocity (Vp) model of the upper plate and the geometry of the interplate (Fig. 2), and a spatially coincident pre-stack depth migrated (PSDM) seismic section of the first 20 km of the margin (Fig. 3) (Methods; Supplementary Figs. 1–6). From top to bottom, the velocity structure of the upper plate is characterised by <1-km-thick sedimentary layer with Vp < 2.5 km s−1 ± 0.1 km s−1 (Fig. 2a, b). Beneath, the sediment-basement boundary is defined by a sharp (1–2 s−1) velocity contrast (Fig. 2a). Overall, basement velocity increases downdip, as observed in subduction zones worldwide7, reaching maximum values of 5.0–5.5 km s−1 consistent with the presence of plutonic rocks as evidenced by seabed rock sampling12 (Fig. 2a). The toe of the upper plate (<20 km from the trench) is characterised by Vp < 4.5 km s−1 (Fig. 2a) and a prominent low-velocity anomaly (Vp < 4.0 ± 0.15-0.1 km s−1) at 15 km from the trench (Fig. 2a). The low-velocity body coincides with a highly fractured media observed in the PSDM image (Fig. 3) and spatially correlates with a prominent interplate high that defines a 2-km-high ~5 km-wide body (Fig. 2a). The interplate reflector is resolved as a ~8.5° SE-dipping irregular interface, and its topographic variations are within the range of our tomographic resolution (Methods; Supplementary Figs. 5, 7). Overall, the structure of the shallow subduction zone inferred here shows a more heterogeneous upper-plate velocity structure than previous forward models derived from land stations installed >60 km away from the trench11.
a Pre-stack depth migrated section of profile TS02 showing the geometry of the interplate (white dots), the top of the basement (blue dots), and the presence of the subducting ridge at 14−15 km from the trench. Red circles are ocean-bottom seismometers, and the blue arrow points to reverse polarity reflectors. Black arrows indicate normal faulting. b Same PSDM section as in (a) overlapped with P-wave velocity values from the 2D tomographic model in Fig. 2a. The inverted interplate reflector is also included in the figure and matches with the location of the interplate interpreted in (a).
The interplay between subducting ridges, upper and lower plate tectonics and margin erosion
The combination of the tomographic model with the PSDM image (Fig. 3) shows that interplate topographic variations relate to the relief of the incoming oceanic plate. A comparison between the inverted interplate reflector with the incoming bathymetry of the Rivera Plate (Fig. 2d) shows that the subducting topographic high is morphologically (height and width) comparable to the incoming oceanic ridges of the Rivera plate. Based on these results, and the lack of seamount chains in the southern portion of the Rivera plate (Fig. 1a), we interpret the subducted topography as a trench-parallel ridge subducting beneath the NA plate. This interpretation is consistent with the hypothesis that the ancient EPR fabric, observed in the outer rise (Fig. 1b), is subducting16.
Our geophysical results show that upper-plate tectonics is highly dependent on the subducted oceanic relief. This way, the upper plate features pervasive normal faulting and localised top of the basement depression at the wake of the subducted ridge indicating the collapse of upper-plate material (CDP4000-4500, Fig. 3a), while it is locally uplifted and highly fractured atop the ridge. Collapsing upper-plate material may seal upper-plate fractures previously generated by the subducting ridge and enhance compaction. Such a hypothesis would explain the higher upper-plate basement velocity in the wake of the ridge than above it (Fig. 3b). The complex network of fractures atop the ridge may prevent the amount of uplifting to be equivalent to the height of the subducted topography. Yet, margin uplifting is enough to increase the dip of the slope towards the trench from 5° to 14° (Fig. 3). Slope oversteepening is proposed to be the precursor for slope failure through submarine landslides and control margin erosion elsewhere along the MAT24. Consistent with this, at the same distance from the trench that we observe slope oversteepening, bathymetric data show several NW-SE trending margin scars towards the north and south of our seismic line (Fig. 2c), indicating the occurrence of past slope failure events.
The two-dimensional upper-plate deformation pattern observed here has been reported in Central and South America subduction zones and is mostly attributed to seamount subduction6,25,26. However, modelling results demonstrate that the three-dimensional structural pattern depends on the shape and size of the subducting body27,28. The erosive pattern associated with isolated subducting seamount causes localised basal erosion of the upper plate and localised embayment of the margin6,27,28, a structural framework somewhat different from that observed here. In the study area, margin erosion occurs over hundreds of kilometres along the trench axis, indicating that upper-plate basal erosion occurs similarly along strike, supporting the existence of subducting trench-parallel elongated ridges.
The subduction of rough-spreading fabric has contributed to the erosion of margins worldwide29,30. In some regions, the roughness of the lower plate is enhanced by the presence of bending-related faulting13. In northern Chile, the topographic roughness of the lower plate is enhanced by bending-related faulting oblique to the spreading fabric, as it induces up to 800 m of vertical seafloor displacement29. In our study area, the rough-spreading fabric and the bending-related faulting appear to have the same NW-SE trend in the southern region of the Rivera plate (Fig. 1b). Thus, it is likely that such faulting modifies the topography of the spreading fabric, increasing the roughness of the incoming plate, particularly near the trench as observed in Alaska30, where the subduction of trench-parallel rough subducting fabric enhances interplate seismicity.
Discussion
The presence of subducting ridges beneath the continental margin carries important implications for interplate coupling, shallow seismogenesis and earthquake dynamic properties.
Implications for interplate coupling
Rough subducting seafloor influences interplate coupling28,31,32. Conceptual models of seamount subduction propose that the uplift of the upper plate increases normal stress, enhancing the coupling between plates33,34. Yet, these models did not take into account the complex pattern of fractures that are generated atop the subducted feature. Alternative models predict that interplate coupling is reduced by this network of upper-plate fractures32, promoting stable sliding and preventing the accumulation of elastic energy. Yet, numerical simulations reveal that overpressure builds up landward of the subducting roughness28,35, favouring hydrofracturing and pore fluid drainage26, which in turn, increases effective stress and interplate coupling36, promoting the occurrence of confined ruptures landward of the subducted seamount. Supporting this scenario, the PSDM section reveals reverse polarity reflections within the subducting sediments trenchward of the subducted ridge, indicating the presence of overpressured pore fluids (CDP4000-5000; Fig. 3). Yet, reverse polarity reflectors are not observed landward of the ridge in subducting sediments, indicating that fluid drainage may have occurred as a result of hydrofracturing. We hypothesise that fluids may have escaped upwards through the complex network of fractures atop the ridge. The presence of fluid-bearing fractures would contribute to reducing upper-plate seismic velocities atop the ridge, and thus explain our tomographic results.
The presence of comparatively higher coupling landward of the rough subducting oceanic fabric is also supported by the rupture pattern of past earthquakes in the area. Analogue modelling shows that the rupture generated by rough subducting topography is controlled by its spatial extent and shape31. Considering that oceanic ridges converge trench parallel beneath the margin in the southern subduction system8, stress accumulation would occur along-strike rather than being localised as in the case of isolated seamounts28, resulting in a set of NW-SE-elongated asperities. Finite-fault inversion results of the 1995 earthquake show that coseismic slip released near the trench (Fig. 1) followed a trench-parallel patchy distribution18,37 (Fig. 1b), consistent with the presence of trench-parallel asperities along the interplate. Similarly, the distribution of aftershocks of the 1995 Colima-Jalisco Earthquake shows several events in the leading flank of the subducting ridge19 (Fig. 2c), supporting the presence of overpressured areas. Based on these aspects, we propose that the rough subducting topography of the southern Rivera Plate contributes to expel pore fluids from subducing sediments landward of subducted ridges, enhancing interplate coupling, and promoting the formation of a pattern of trench-parallel shallow asperities.
Subducting ridges determine upper-plate elastic properties
Megathrust earthquakes offshore Colima-Jalisco exhibited a depth-dependent dynamic behaviour22,37. In particular, the 1995 Colima-Jalisco event displayed the largest slip and slowest propagation in the shallow region, with rupture velocity ranging between 1.0–1.5 km s−1 in the first 10–12 km from the trench37. In addition, the event was characterised by a discrepancy between the surface wave magnitude (Ms 7.4) and the seismic moment magnitude (Mw 8)18,19, implying a depletion in high frequencies. Such dynamic behaviour is characteristic of shallow megathrust earthquakes38, including tsunami earthquakes39, and largely explained by the trenchward decrease in rigidity of rocks overlying the fault7,40,41. Thus, to understand the dynamic behaviour of shallow events in the area we calculate the distribution of upper-plate rigidity along our seismic line using the Vp tomographic model (Methods). Upper-plate tectonics and the distribution of elastic properties along our line are intimately related to the subducting oceanic topography (Figs. 3, 4). Our results show that intense fracturing atop the ridge causes comparatively lower rigidity areas in the upper plate (Fig. 4b). In addition to this local variation, the overall depth distribution of rigidity of rocks overlying the interplate decreases trenchward. Rigidity drops from ~30 GPa at 20 km depth to 2–5 GPa at the trench, in agreement with the global depth-distribution of rigidity derived from upper-plate tomographic models7 (Fig. 4a), and thus, favouring the enhancement of coseismic slip trenchward. Further, assuming that rupture velocity is within 70 and 90% of the S-wave velocity of rocks overlying the fault7,40,42, the low Vs estimated through the first 12 km of the fault implies that earthquakes propagate at velocities ~1.0 km s−1 (Fig. 4c), consistent with estimates of rupture velocity of the 1995 earthquake in the shallow megathrust37. In summary, the elastic structure of the margin promotes shallow ruptures with large slip, long duration, and consequently a depletion in high frequencies. A pattern that explains the dynamic behaviour of past shallow events in the study area.
a Rigidity at the base of the upper plate as a function of upper-plate thickness along our model (grey circles) compared with the global depth distribution from ref. 7. b Rigidity (Blue band) at the base of the upper plate as a function of distance from the trench compared with the relative topography of the interplate (red band). The latter was obtained by removing the landward dipping trend of the interplate and calculating the difference between the inverted reflector and a 7°-landward-dipping flat reflector. The thickness of each curve depicts the range of uncertainty derived from Monte Carlo inversion. c Vs (white dots) and the corresponding rupture velocity (Vr; grey band) at the base of the upper plate as a function of distance from the trench. Vr is calculated assuming that earthquakes propagate between 70 and 80% of Vs43. The upper and lower bounds of the grey band correspond to 80 and 70% of the model Vs, respectively. The red solid line depicts the average value of Vr within a 12-km-wide window.
Conclusions
Our results show that rough subducting topography beneath non-accretionary margins not only controls upper-plate tectonics and margin erosion but also upper-plate elastic structure, setting ideal conditions for large near-trench slip and slow ruptures. In the study area, the shallow distribution of slip of the 1995 Colima-Jalisco earthquake suggests that, rather than acting as barriers32,43, subducting ridges may act as unstable asperities, assisting deeper ruptures in reaching shallower regions of the fault, and propagating laterally along the shallow non-accretionary portion of the margin. Such seismogenic behaviour likely prevails along the entire portion of the Colima-Jalisco margin affected by the subduction of rough ancient EPR fabric, exposing more than a hundred kilometres of continental margin to shallow seismogenesis and associated tsunamigenesis. Overall, our study shows that quantifying the impacts of subducting topography on upper-plate rigidity through joint tomography of MCS and WAS data may help to explain the large tsunamigenic potential of other non-accretionary margins globally.
Methods
Seismic data acquisition and processing
Wide-angle seismic (WAS) and multichannel seismic (MCS) data used in this study were collected during the TSUJAL survey (2014) along the upper-plate segment of transect TS0223 (Supplementary Figs. 1, 2). WAS data were recorded by 4 ocean-bottom seismometers (OBS) (Supplementary Fig. 1), and data processing involved instrument relocation on the seafloor, band pass filtering (3–7; 20–25 Hz), deconvolution and a wiener shaping filter that increased the signal-to-noise ratio at far offsets (>80 km offset). The WAS source was generated with 14 air guns towed at 15 m depth that released a total volume of 6800 cubic inches every 120 s along the line. MCS data were recorded with a 6-km-long hydrophone streamer deployed at 10 m depth that included 468 active channels (5850 m length) separated 12.5 m apart. CMP distance is 6.25 m and allows a CMP nominal fold of 58–59 traces. The MCS sources consisted of an array of 12 guns divided into four subarrays of three guns that released a total volume of 3540 cubic inches. The source was towed at 8 m depth and the shooting interval was every 50 m. MCS processing has been adapted to image the deep geometry of the interplate megathrust, whose depths range between 5–9 km. A preliminary post-stack time migration has been obtained with a model derived from velocity analyses to identify the most striking structures. A pre-stack depth migration was subsequently carried out using the interval velocity model obtained in the tomographic OBS model derived from a coincident wide-angle profile (Supplementary Fig. 2). This step requires a special pre-processing flow to improve the noise suppression and the multiple removals to reveal the deeper structures. Noise suppression includes removing burst and attenuating noise without affecting the spectrum of the remaining record (TFDN), deghosting and debubbling the signal, and removing coherent noise to increase the resolution ratio via predictive deconvolution (44 ms prediction gap, and 360 ms operator length). Removing multiple includes the use of prediction of multiples following SRME strategies (RadexPro software). We use the tomographic velocity model obtained from OBS and MCS data as starting model to perform a Pre-stack depth migration with pre-computed travel-times calculated by a Kirchhoff eikonal equation approach in the common-offset domain, well suited for moderately complex geology settings handling steep dips imaging, prior to testing the aperture, the dip limits and the anti-alias filter (PRoMAX software).
Travel-time picking
We have picked travel-times of P-waves refracted through the upper-plate, or PgC seismic phases, from OBS records and MCS shot gathers (Supplementary Figs. 1, 3). We have applied the downward continuation method44 to shot gathers located between 15 and 40 km of profile distance from the trench to retrieve PgC first arrivals masked by reflected phases in the original gathers (Supplementary Fig. 4). We picked one gather every 200 m, and within each gather one trace every 200 m. Testing denser picking interval increase the computational cost without significant tomographic improvement. This way, a total of 7239 PgC travel-times were manually picked. We have also included in the inversion MCS travel-times of P-waves reflected at the interplate, or PiP phases, identified in CDP gathers (Supplementary Fig. 3). We used the stack section in Supplementary Fig. 3a to guide the manual picking of CDP gathers. We resorted the picking geometry from CDP to shot gathers and selected one shot every 400 m, yielding a total of 1053 PiP travel-times. Such decimation was selected on the basis of several tests and it provides the best balance between tomographic resolution and computational cost. Travel-time uncertainty was set on the basis of the S/N ratio of the trace 250 ms before and after the selected travel pick as proposed by ref. 45. This way, pick uncertainty of PgC travel-times from WAS data ranges between 20 and 90 ms, while PiP and PgC travel-times from MCS data is 40 ms.
Combined MCS and WAS joint refraction and reflection travel-time tomography
We have jointly inverted PgC and PiP travel-times using the modified joint refraction and reflection travel-time inversion code TOMO2D46,47. This modified version allows the source to be outside the irregular velocity mesh, which enables the inversion of travel-times recorded with streamer geometry48. The velocity grid is parametrised as a set of nodes hanging from the seafloor with a regular horizontal spacing of 100 m and a variable one in the vertical direction, with node spacing increasing from 25 m at the top of the grid to 0.5 km at the bottom of it. Regularisation parameters are defined by a set of correlation lengths (CL) that vary from top to bottom of the grid. In the horizontal direction CL increase from 1 km at the top to 5 km at the bottom of the grid, while vertical correlation lengths increase from 0.5 at the top to 1 km at the bottom of the grid. The horizontal correlation length for the reflector is 0.8 km. Damping and additional smoothing constraints are also set to stabilise the inversion. The inversion was performed following a Monte Carlo (MC) uncertainty analysis (Fig. 2a, b, and Supplementary Fig. 5). We created a set of 500 MC realisations each realisation consisting of the randomly generated 1D velocity model, an initial landward dipping interplate reflector, and a noisy travel-time dataset. Each velocity model was generated by randomly varying by 10 % the velocity of the reference 1D model in Supplementary Fig. 5a. Initial reflectors were randomly generated with landward dips between 5° and 15° (Supplementary Fig. 5a). Finally, the 500 noisy travel-time datasets were generated by adding random Gaussian noise to each manually selected travel-time. The range of noise is set on the basis of picking uncertainty. The initial uncertainty of Vp and interplate depth is shown in Supplementary Fig. 5b, while the random distribution is depicted by initial travel-time residuals in Supplementary Fig. 5d. After inverting the 500 MC realisations the overall root mean square (RMS) decreases from 350 to 65 ms after 15 iterations each (Supplementary Figs. 5d, 6). The final average velocity model reproduces first order variations of the upper-plate velocity structure and geometry of the interplate reflector as shown in Fig. 3. Small inconsistencies between the PSDM section and the tomographic result are due to the inherent limitation of travel-time tomography in resolving small-scale velocity variations. We use the average velocity model for the final interpretation (Fig. 2a), while we take the final standard deviation as a proxy of the model parameter uncertainty49 (Fig. 2b). Integration of MCS PiP and PgC travel-times increases the amount of inverted travel-time information by an order of magnitude respect WAS data. This yields a denser ray coverage of the upper plate, and thus, lowers velocity and reflector geometry uncertainties, particularly in the first 20 km from the trench (Supplementary Fig. 5c). This way, velocity and interplate location uncertainty are lowest (<0.2 km s−1) in the first 20 km from the trench (Fig. 2c). At a further distance from the trench the upper plate is mostly covered by PiP rays and few PgC rays from WAS data (Supplementary Fig. 5c). As a result, velocity and interplate geometry uncertainty increases (>0.2 km s−1) because of the inherent velocity-depth trade-off of near-vertical reflections (Fig. 2c). Additional larger velocity uncertainty (>0.4 km s−1) is associated with sharp velocity contrasts at the top of the basement, but only imply a ~10% variation of the average velocity (5.0–5.5 km s−1), yielding a similar outcome and interpretation.
Resolution test
we have tested the sensitivity of our travel-times and tomographic method to retrieve the velocity and interplate topographic variations observed in the final model (Fig. 2). We have built a true model based on the final solution (Supplementary Fig. 7a). We calculated the set of synthetic travel-times and added random Gaussian noise on the basis of the picking uncertainty as in the MC approach. The set of synthetic noisy travel-times were inverted using the same 1D reference velocity model as in the MC approach and a straight 7° landward dipping interplate reflector. The retrieved tomographic model has an RMS of ~70 ms, showing a similar velocity structure and interplate geometry than the true model, particularly in the first 20 km from the trench (Supplementary Fig. 7b). Velocity differences are overall >0.25 km s−1 in the first 20 km from the trench, with some local differences of 0.5 km s−1 landward of the subducting ridge at 14–16 km from the trench (Supplementary Fig. 7c, d). Larger velocity differences (>0.5 km s−1) are also observed at further offsets than ~30 km from the trench and deeper than 4 km depth (Supplementary Fig. 7c, 7d), consistent with larger uncertainties. Regarding the reflector geometry, we are able to retrieve the true interplate geometry with minor variations up to ~25 km from the trench (Supplementary Fig. 7c, d). At further offsets, we are not able to rely on our results given the increasing velocity-depth trade-off of reflections.
Elastic parameters calculation
To calculate rigidity (µ) at the base of the upper plate we first converted the final Vp model into density (ρ) and Vs using empirical relationships between Vp-Vs and Vp- ρ from ref. 50. In particular, we used the Nafe-Drake curve (Eq. 1 in ref. 50) to estimate ρ, while we used eq 6 in ref. 50 to derive Vs. Both relationships are valid for Vp between 1.5 and 8–8.5 km s−1, and valid for a suite of crustal rock types that includes plutonic rocks such as those sampled in the study area (i.e., granodiorites12). Rigidity was then calculated as:
Finally, to extract rigidity profiles in Fig. 4a, b, we averaged rigidity values within 0.5 km above the interplate reflector.
Data availability
Raw ocean-bottom seismometer can be found here: https://doi.org/10.6084/m9.figshare.21388122. The Multichannel PSDM seismic section can be found here: https://doi.org/10.6084/m9.figshare.21388107.v1.
Code availability
Travel-time tomography was performed using a modified version of TOMO2D48,49, available upon request to the corresponding author. Multichannel seismic data were processed with commercial software RadEXPro (https://radexpro.com/).
References
McIntosh, K. D. et al. In The Seismogenic Zone of Subduction Thrust Faults: Part III (eds Dixon, T. H. & Moore, J. C.) Ch. 9 (Columbia Univ. Press, 2007).
Sallarès, V. et al. Overriding plate structure of the Nicaragua convergent margin: relationship to the seismogenic zone of the 1992 tsunami earthquake. Geochem. Geophys. Geosyst. 14, 3436–3461 (2013).
Polet, J. & Kanamori, H. Shallow subduction zone earthquakes and their tsunamigenic potential. Geophys. J. Int. 142, 684–702 (2000).
Bell, R. et al. Hikurangi margin tsunami earthquake generated by slow seismic rupture over a subducted seamount. Earth Planet. Sci. Lett. 397, 1–9 (2014).
Geersen, J. Sediment-starved trenches and rough subducting plates are conducive to tsunami earthquakes. Tectonophysics 762, 28–44 (2019).
Ranero, C. R. & von Huene, R. Subduction erosion along the Middle America convergent margin. Nature 404, 748–752 (2000).
Sallarès, V. & Ranero, C. R. Upper-plate rigidity determines depth-varying rupture behaviour of megathrust earthquakes. Nature 576, 96–101 (2000).
Urías Espinosa, J. et al. Multibeam bathymetric survey of the Ipala Submarine Canyon, Jalisco, Mexico (20° N): the southern boundary of the Banderas forearc block? Tectonophysics 671, 249–263 (2016).
Bartolomé, R. et al. Imaging the seismic crustal structure of the western Mexican margin between 19° N and 21° N. Pure Appl. Geophys. 168, 1373–1389 (2011).
Bartolomé, R. et al. Multichannel seismic imaging of the Rivera Plate subduction at the seismogenic Jalisco Block area (Western Mexican margin). Pure Appl. Geophys. 173, 3575–3594 (2016).
Núñez, D. et al. Seismic structure of the southern Rivera plate and Jalisco block subduction zone. Seismol. Res. Lett. 90, 1756–1766 (2019).
Mercier de Lépinay, B. et al. Large Neogene subsidence event along the middle America Trench off Mexico (18 N–19 N): evidence from submersible observations. Geology 25, 387–390 (1997).
Ranero, C. R., Morgan, J. P., McIntosh, K. & Reichert, C. Bending-related faulting and mantle serpentinization at the Middle America trench. Nature 425, 367–373 (2003).
Bandy, W. L. & Hilde, T. W. C. In Cenozoic Tectonics and Volcanism of Mexico (ed. Delgado‐Granados, H., Aguirre‐Díaz, G., & Stock, J. M.) (Geological Society of America, 2000).
Peláez Gaviria, J. R., Mortera Gutiérrez, C. A., Bandy, W. L. & Michaud, F. Morphology and magnetic survey of the Rivera-Cocos plate boundary of Colima, Mexico. Geofís. Int. 52, 73–85 (2013).
Michaud, F. et al. Did the East Pacific rise subduct beneath the North America plate (western Mexico)? Geo-Mar. Lett. 20, 168–173 (2001).
Singh, S. K., Ponce, L. & Nishenko, S. P. The great Jalisco, Mexico, earthquakes of 1932: subduction of the Rivera plate. Bull. Seismol. Soc. Am. 75, 1301–1313 (1985).
Mendoza, C. & Hartzell, S. Fault-slip distribution of the 1995 Colima-Jalisco, Mexico, earthquake. Bull. Seismol. Soc. Am. 89, 1338–1344 (1999).
Pacheco, J. et al. The October 9, 1995 Colima-Jalisco, Mexico Earthquake (Mw 8): an aftershock study and a comparison of this earthquake with those of 1932. Geophys. Res. Lett. https://doi.org/10.1029/97GL02070 (1997).
Castillo‐Aja, R. & Ramírez‐Herrera, M. T. Updated tsunami catalog for the Jalisco‐Colima coast, Mexico, using data from historical archives. Seismol. Res. Lett. 88, 144–158 (2017).
Corona, N. & Ramírez-Herrera, M. T. Did an underwater landslide trigger the June 22, 1932 tsunami off the Pacific coast of Mexico? Pure Appl. Geophys. 172, 3573–3587 (2015).
Okal, E. A. & Borrero, J. C. The ‘tsunami earthquake’of 1932 June 22 in Manzanillo, Mexico: seismological study and tsunami simulations. Geophys. J. Int. 187, 1443–1459 (2011).
Núñez‐Cornú, F. J. et al. Geophysical studies across Rivera plate and Jalisco block, Mexico: TsuJal project. Seismol. Res. Lett. 87, 59–72 (2016).
Harders, R., Ranero, C. R., Weinrebe, W., & Behrmann, J. H. Submarine slope failures along the convergent continental margin of the Middle America Trench. Geochem. Geophys. Geosyst. https://doi.org/10.1029/2010GC003401 (2011).
Geersen, J., Ranero, C. R., Barckhausen, U. & Reichert, C. Subducting seamounts control interplate coupling and seismic rupture in the 2014 Iquique earthquake area. Nat. Commun. 6, 1–6 (2015).
Marcaillou, B. et al. Seamount subduction at the North-Ecuadorian convergent margin: effects on structures, inter-seismic coupling and seismogenesis. Earth Planet. Sci. Lett. 433, 146–158 (2016).
Dominguez, S., Lallemand, S. E., Malavieille, J. & von Huene, R. Upper plate deformation associated with seamount subduction. Tectonophysics 293, 207–224 (1998).
Ruh, J. B., Sallarès, V., Ranero, C. R. & Gerya, T. Crustal deformation dynamics and stress evolution during seamount subduction: high‐resolution 3‐D numerical modeling. J. Geophys. Res. Solid Earth 121, 6880–6902 (2016).
Geersen, J. et al. Active tectonics of the North Chilean marine forearc and adjacent oceanic Nazca Plate. Tectonics 37, 4194–4211 (2018).
Shillington, D. J. et al. Link between plate fabric, hydration and subduction zone seismicity in Alaska. Nat. Geosci. 8, 961–964 (2015).
Van Rijsingen, E., Funiciello, F., Corbi, F. & Lallemand, S. Rough subducting seafloor reduces interseismic coupling and mega‐earthquake occurrence: Insights from analogue models. Geophys. Res. Lett. 46, 3124–3132 (2019).
Wang, K. & Bilek, S. L. Do subducting seamounts generate or stop large earthquakes? Geology 39, 819–822 (2011).
Cloos, M. Thrust-type subduction-zone earthquakes and seamount asperities: a physical model for seismic rupture. Geology 20, 601–604 (1992).
Scholz, C. H. & Small, C. The effect of seamount subduction on seismic coupling. Geology 25, 487–490 (1997).
Martinez‐Loriente, S. et al. Influence of incoming plate relief on overriding plate deformation and earthquake Nucleation: Cocos Ridge subduction (Costa Rica). Tectonics 38, 4360–4377 (2019).
Sun, T., Saffer, D. & Ellis, S. Mechanical and hydrological effects of seamount subduction on megathrust stress and slip. Nat. Geosci. 13, 249–255 (2020).
Hjörleifsdóttir, V. et al. Was the 9 October 1995 Mw 8 Jalisco, Mexico, earthquake a near‐trench event? J. Geophys. Res. Solid Earth 123, 8907–8925 (2018).
Lay, T. et al. Depth-varying rupture properties of subduction zone megathrust faults. J. Geophys. Res. 117, B04311 (2012).
Kanamori, H. Mechanism of tsunami earthquakes. Phys. Earth Planet. Inter. 6, 346–359 (1972).
Prada, M. et al. The influence of depth-varying elastic properties of the upper plate on megathrust earthquake rupture dynamics and tsunamigenesis. J. Geophys. Res. Solid Earth 126, e2021JB022328 (2021).
Sallarès, V. et al. Large slip, long duration, and moderate shaking of the Nicaragua 1992 tsunami earthquake caused by low near-trench rock rigidity. Sci. Adv. 7, eabg8659 (2021).
Bilek, S. L. & Lay, T. Rigidity variations with depth along interplate megathrust faults in subduction zones. Nature 400, 443–446 (1999).
Kodaira, S. et al. Subducted seamount imaged in the rupture zone of the 1946 Nankaido earthquake. Science 289, 104–106 (2000).
Gras, C. et al. Full-waveform inversion of short-offset, band-limited seismic data in the Alboran Basin (SE Iberia). Solid Earth 10, 1833–1855 (2019).
Zelt, C. A. & Forsyth, D. A. Modeling wide-angle seismic data for crustal structure: southeastern Grenville Province. J. Geophys. Res. 99, 11687–11704 (1994).
Korenaga, J. et al. Crustal structure of the southeast Greenland margin from joint refraction and reflection seismic tomography. J. Geophys. Res. 105, 21591–21614 (2000).
Meléndez, A., Korenaga, J., Sallarès, V., Miniussi, A. & Ranero, C. R. TOMO3D: 3-D joint refraction and reflection traveltime tomography parallel code for active-source seismic data—Synthetic test. Geophys. J. Int. 203, 158–174 (2015).
Merino, I., Prada, M., Ranero, C. R., Sallarès, V. & Calahorrano, A. The structure of the continentocean transition in the Gulf of Lions from joint refraction and reflection travel-time tomography. J. Geophys. Res. Solid Earth 126, e2021JB021711 (2021).
Tarantola, A. Inverse ProblemTheory: Methods for Data Fitting and Model Parameter Estimation (Elsevier, 1987).
Brocher, T. M. Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bull. Seismol. Soc. Am. 95, 2081–2092 (2005).
Acknowledgements
We acknowledge the Captain and crew of the RRS James Cook, the seismic UTM-CSIC technical team and Luis Ansorena for their professional work, and the officers and crew of the AMR Holzinger (Secretaría de Marina, Mexico) and CABO/UNAM J-GAP2013 Cruise (BO El Puma, Mexico) which made possible the success of the TSUJAL cruise. We thank Dr. Carlos A.Q. Mortera Gutiérrez of the Ocean Mapping Lab (LUCO), UNAM for his help during the OBS recovery. We are grateful to Valentí Sallarès for fruitful discussions that helped to improve the manuscript. We thank the editor Luca Dal Zilio, Sean Gulick and two anonymous reviewers for their constructive review. M. Prada has been partially funded by the Beatriu de Pinós postdoctoral programme of the Government of Catalonia’s Secretariat for Universities and Research of the Ministry of Economy and Knowledge (Ref # 2017BP00170). M. Prada has had funding support from the ’Severo Ochoa Centre of Excellence’ accreditation (CEX2019-000928-S) of the Spanish Research Agency (AEI). We gratefully acknowledge financial support from MINECO (Spain) through the TSUJAL project (CGL2011-29474-C02-01), and from Mexico through CONACYT–FOMIXJAL 2008–96567 (2009); CONACYT– FOMIXJAL 2008–96539 (2009); CONACYT–FOMIXJAL 2010–149245 (2011); CONACyT-FOMIXJal (2012-08-189963), and partial funding from UNAM DGAPA Grant #IN115513-3. We also acknowledge the support of the Mexican Instituto Oceanográfico del Pacífico in Manzanillo, Secretaría de Defensa Nacional, Unidad Municipal de Proteccion Civil y Bomberos (Puerto Vallarta), Unidad Estatal de Proteccion Civil y Bomberos (Nayarit State), Unidad Municipal de Proteccion Civil y Bomberos (Jalisco State), Reserva de la Biosfera (Islas Marías) CONANP- SEMARNAT, Organo Desconcentrado de Prevención y Readaptación Social de la SEGOB, and Secretaría de Relaciones Exteriores. This work was carried out within the Grup de Recerca de la Generalitat de Catalunya B-CSI (2017 SGR 1662).
Author information
Authors and Affiliations
Contributions
M.P. contributed to the conceptualisation, data acquisition, led the writing of the paper, conducted the tomographic model and made all figures except for Supplementary Fig. 2. R.B. contributed to the conceptualisation, the writing, made Supplementary Fig. 2, processed the multichannel seismic data, computed the PSDM section, obtained funding and led the offshore TSUJAL experiment. C.G. developed the Downward Continuation code and assisted the first authors during its application. W.L.B. contributed to the text and data acquisition. J.J. D. help with the implementation of the TSUJAL experiment.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth & Environment thanks Sean Gulick and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Primary Handling Editors: Luca Dal Zilio and Joe Aslin. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Prada, M., Bartolomé, R., Gras, C. et al. Trench-parallel ridge subduction controls upper-plate structure and shallow megathrust seismogenesis along the Jalisco-Colima margin, Mexico. Commun Earth Environ 4, 53 (2023). https://doi.org/10.1038/s43247-023-00705-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-023-00705-9
This article is cited by
-
Tsunami deposits highlight high-magnitude earthquake potential in the Guerrero seismic gap Mexico
Communications Earth & Environment (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.