Introduction

Vertical crustal motions are fundamental to the creation of topography, development of sedimentary basins, and the rock cycle1,2. Rapid vertical-displacement rates (mm year−1) are often driven by tectonic processes such as crustal thickening in Tibet3 and Taiwan4,5,6, strike-slip deformation along the San Andreas fault7,8, lithospheric thinning in Central Anatolia9 and D’Entrecasteaux island of Papua New Guinea10, and deflections due to changes in surface or subsurface mass loads in Hawaii11 and Antarctica12. Mass redistribution by erosion and sedimentation amplifies vertical crustal motions13 and is important for understanding interactions between tectonic and surface processes involved in mountain building and continental growth14. Among these settings, extreme rates (>10 mm year−1) of long-term (>105–107 years) rock uplift are seldom detected15. Many studies rely on thermochronology16 and petrology-geochemistry17 to assess long-term vertical movements of crustal materials, but these methods are limited by the requirement of suitable minerals, geothermal gradient, temperature, and duration needed to thermally reset thermochronometers. Assumptions of ancient topography and thermal structure are often essential for use of thermochronologic methods to estimate long-term rock uplift18, but it is difficult to constrain these quantities in rapidly growing orogens constructed of unmetamorphosed rocks. Thus, the rates, timescales, and structural controls on vertical motions of shallow crust in active mountain belts remain poorly understood.

Stratigraphic study of inverted syn-orogenic sedimentary basins provides a powerful tool with which to document rapid subsidence and uplift of unmetamorphosed near-surface rocks in zones of mountain building at tectonically active plate margins2. Integrated paleomagnetic and biostratigraphic analysis can yield extremely high resolution [e.g., ± 5–20 thousand years (kyr)] for dating stratigraphic intervals7, and thus, remarkably high-fidelity estimates for rates of vertical crustal motions and tectonic processes. We applied this technique to investigate stratigraphic records of the Coastal Range in eastern Taiwan, which reveal a history of extremely rapid vertical crustal oscillations during accretion of volcanic-arc crust to a continent.

The island of Taiwan has emerged since late Miocene time through active collision between the Luzon island arc on the Philippine Sea plate and the Chinese continental margin of the Eurasian plate19 (Fig. 1). Rapid (~82 mm year−1) oblique convergence20 between the two plates induces rapid exhumation and denudation21, and some studies infer that collision has propagated southward through time22,23,24. Other studies of the metamorphic core (Central Range) and western foreland basin suggest that collision was geologically simultaneous from north to south, with pulses of accelerated exhumation from ~0.1 to 2–4 mm year−1 at 2.0–1.5 million years ago (Ma) and then to 4–8 mm year−1 at ~0.5 Ma25,26. These accelerations correspond to tectonic reorganizations of the overriding Philippine Sea plate27,28 that drive exhumation of high-pressure metamorphosed Miocene arc crust-bearing mélange (Yuli Belt) from >35 km crustal depth5,29,30,31,32 and rapid Quaternary emergence of the unmetamorphosed arc crust in the Coastal Range4.

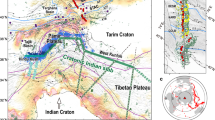
Fig. 1: The Coastal Range of eastern Taiwan.
figure 1

a Regional tectonic configuration5,28 (inset), simplified geological map of the Coastal Range34 and analyzed stratigraphic sections (blue boxes), including Hsiukuluan river (HKL), Wulou river (WL), Fungfu (FF), and Fungpin (FP) sections in the north, and Bieh river (BC), Madagida river (MDJ), and Sanshian river (SSS) sections in the south. b Millennial rates of marine terrace uplift and river incision, compiled by Lai et al.99 c Geodetic rates of vertical deformation measured during 2000–200849. Negative values mean subsidence.

Full size image

The Coastal Range contains a thick succession of Plio-Pleistocene orogen-derived marine flysch, conglomerate (Fanshuliao and Paliwan formations), and olistostromes (Lichi Mélange) that rest unconformably on Miocene volcanic arc basement (Tuluanshan Formation, ca. 15–6 Ma) (Fig. 2)33,34. The basal unconformity (ca. 6–4 Ma) is a broad erosive surface discontinuously capped by thin shallow-marine limestone (Kangkou Limestone, 5.6–3.5 Ma) and limestone-clast-bearing epiclastic deposits (Biehchi Epiclastic Unit, 5–3.5 Ma) that are directly overlain by uncemented deep-water flysch34,35. These relations record slow uplift, erosion, and intermittent sedimentation on arc basement near sea level, followed by rapid subsidence that created accommodation space for thick basin-filling sediment6,33. Basin inversion and uplift must have occurred in the last roughly 1 million years based on observation of the tilted youngest marine flysch and creation of modern Coastal Range topography4. Yet, the timing and rates of these processes remain unclear. Thermochronology and petrological methods are not suitable for solving this problem because of the short duration of burial and very low paleo-geothermal gradient revealed by clay mineralogy (~14 °C km−1)36 and no post-depositional resetting of fission-track detrital thermochronometers37. Early studies used calcareous nannoplankton data38,39 and simplified lithostratigraphic columns to derive a range of subsidence rates (0.8–5 mm year−1) and minimum uplift rate (5.9–7.5 mm year−1) with unknown spatial variability4,6. Many of these studies are now outdated and pre-date recent advances in paleomagnetism and microfossil studies34,40,41,42,43.

Fig. 2: Stratigraphy of the Coastal Range.
figure 2

Locations of studied sections are shown in Fig. 1. GPTS Geomagnetic polarity timescale. FAD First appearance datums of index microfossils. Tls Tuluanshan Formation; k Kangkou Limestone. See details of stratigraphic correlation in Supplementary Figs. 1, 2.

Full size image

To document the timing, magnitude, and rates of vertical crustal motions in the Coastal Range of eastern Taiwan, we compiled geologic and magneto-biostratigraphic data to date and accurately reconstruct two composite stratigraphic columns in the northern and southern Coastal Range (Figs. 1, 2). This includes our published data from the southern Coastal Range34 (Supplementary Fig. 1) and new detailed geologic mapping, paleomagnetic measurements, and microfossil identifications of planktonic foraminifera and calcareous nannoplankton in the northern Coastal Range (Supplementary Figs. 2–6; Supplementary Data 1–2). The foraminifera data provide improved paleobathymetry estimates (Supplementary Fig. 7, Supplementary Data 3), and compiled magneto-biostratigraphy constrains depositional age (Fig. 3a). Dense sampling of microfossils and paleomagnetic sites yields high temporal resolution (~1–15 kyr) and high accuracy (2–43 kyr) of age controls that surpass other geologic dating methods (Supplementary Data 4). Because the youngest inverted sediment is consolidated and lithified, we have to account for deposits that accumulated above the top of our measured sections and subsequently were removed by erosion. Porosity-effective stress of sandstone and vitrinite reflectance data indicate that ca. 0.45–1.95 km of strata was eroded off the youngest deposits preserved in our measured sections44. Due to uncertain variability of compaction history and geothermal structure, we used a conservative thickness of 0.5–1.0 km for eroded sediments to reconstruct the deepest subsidence prior to onset of structural inversion (Fig. 3a).

Fig. 3: Sediment-accumulation rates and subsidence-uplift histories of the Coastal Range.
figure 3

a Stratigraphic age models for the Coastal Range. b, c Geohistory curves of the northern and southern Coastal Range. Symbols and color-fill style follow Fig. 3a. Asterisk in each curve is the reconstructed depth using youngest sediment eroded from top of section. Error bars represent one standard error of the mean. See details of data and calculation results in Supplementary Data 4.

Full size image

Using high-fidelity constraints on stratigraphy and paleobathymetry, updated eustatic sea level curve (Supplementary Fig. 7), and porosity-depth functions for relevant sediment types (Supplementary Fig. 8), we conducted a modern 1-D backstripping analysis45 to progressively remove decompacted sediment and correct paleo-water depth along two composite sections. This allowed us to reconstruct the history of subsidence and uplift of arc basement in the north and south (Fig. 3b, c). See details in the “Methods” section.

Results and discussion

Subsidence-uplift histories of Taiwan's Coastal Range

Our results reveal that >5.48–6.51 km of preserved orogen-derived sediment accumulated between ~3.39 and 0.77 Ma, with a minor increase in sedimentation rate at ~2.0 Ma (Fig. 3a). Volcanic-arc basement subsided to depths of 6.53–7.78 km below modern sea level at rates of 2.26 mm year−1 in the north and 3.24 mm year−1 in the south, with tectonic forces and sediment loads making subequal contributions to the total subsidence (Fig. 3b, c). The age of youngest, now-eroded sediment is estimated to be ~0.61–0.50 Ma, providing a reasonable age estimate for the end of subsidence and onset of structural inversion (Fig. 3a). Since the folded basal unconformity and underlying volcanic basement rocks are exposed well above sea level, the difference between present-day heights of antiformal peaks and the reconstructed depth of arc basement at the end of deposition (0.82–0.77 Ma for the youngest preserved sediment; 0.61–0.50 Ma at the top of eroded sediment) provide a conservative estimate for the amount of vertical displacement during basin inversion. To exhume the volcanic-arc basement to present elevations of the Coastal Range (0–1.33 km in the north, 0–1.68 km in the south) requires extremely rapid rock uplift rates of at least 8.89–14.39 mm year−1 in the north and 10.43–14.24 mm year−1 in the south (Fig. 3b, c; Supplementary Data 4).

The minor increase in sedimentation rate at ~2.0 Ma and onset of basin inversion at ~0.8–0.5 Ma are coeval with proposed episodes of accelerated rock exhumation in the metamorphic Central Range to the west26 (Figs. 3a, 4a). Post-0.5 Ma uplift rates of ca. 9–14 mm year−1 represent the lower bound of long-term average exhumation rates in the Coastal Range. These rates are intermediate between spatially variable millennial uplift rates measured in coastal marine terraces (2.3–11.8 mm year−1)46,47 and fluvial incision rates (15.1–27.3 mm year−1) measured near the western major oblique thrust fault (Longitudinal Valley fault)48 (Fig. 1b). Notably, millennial uplift rates in the northern Coastal Range (2.3–4.7 mm year−1)46,47 are considerably slower than our calculated long-term exhumation rates (~9–14 mm year−1), and geodetic data49 reveal subsidence at rates locally up to ~23.5 mm year−1 in the north (Fig. 1b, c). This implies that the northern part of inverted arc crust may have entered a new subsidence stage very recently.

Fig. 4: Conceptual model for the history of vertical motions (blue arrows) of the Philippine Sea plate arc crust in the past ~6 Ma.
figure 4

a Forebulge uplift and foredeep subsidence occur on the Luzon arc crust during 6–0.5 Ma, in response to eastward migrating orogenic load33,34. b Post-0.5 Ma rapid uplift due to transpressional deformation and isostatic rebound of the overriding plate4,5,59. c Representative structural cross-section in the modern Coastal Range34,57. Blue lines mark major boundary faults. LVF Longitudinal Valley fault; CRF Central Range fault.

Full size image

Taken together, the stratigraphic record in the Coastal Range reveals two short cycles of up-and-down crustal motions (Fig. 3b, c). Coeval histories of uplift and subsidence in the north and south support an interpretation of simultaneous crustal dynamics along the collisional suture25,26,28, in contrast to southward-propagating growth of the Taiwan orogen inferred in some models22,23,24. These findings indicate the need for a revised tectonic interpretation to explain the observed rapid vertical oscillations of arc crust in this active arc-continent suture zone.

Drivers of rapid crustal oscillations during oceanic arc accretion

We infer that the first cycle of uplift (~6–3.4 Ma) and subsidence (~3.4–0.5 Ma) of volcanic basement was driven by early flexure and loading of accreting Luzon arc crust. This interpretation is supported by recent results showing that Plio-Pleistocene sediments (Lichi Mélange, Fanshuliao and Paliwan formations) formed on – and were derived from – an east-dipping submarine paleoslope at the steep western margin of the basin34,50. These sediments onlap the westward-inclined basal unconformity on top of Miocene arc basement (Tuluanshan Formation) and display lateral facies changes that record eastward progradation of coarse deposits into the basin34. These observations are best explained by basinward migration of the depocenter in response to eastward migration of a thrust-bounded submarine slope at the retrowedge orogenic front (Fig. 4a). Thus, the first stage of vertical crustal oscillation in the Coastal Range (slow uplift) is interpreted as a signal of forebulge uplift. This stage was followed by subsidence in an evolving retrowedge foredeep basin driven by eastward migration of a flexural wave6,33. These processes took place during development of the prowedge foreland basin in western Taiwan starting ~6.5–5 Ma25,51.

The absence of transgressive deposits at the basal unconformity between shallow-marine limestone (5.6–3.5 Ma) and overlying deep-marine flysch (~3.4–3.1 Ma) requires a sudden increase in water depth at ~3.5 Ma (Fig. 3b, c). This abrupt subsidence likely resulted from local extensional faulting52,53 in the upper dilating crust of a migrating flexural forebulge54, and may be in part related to an increase in orogenic load on the Philippine Sea plate due to accelerated topographic growth in the retrowedge at 3.2 ± 0.6 Ma55. Lithospheric bending of the Philippine Sea plate induced by northward subduction at the Ryukyu trench56 may have also influenced vertical displacements in the accreting arc crust. However, this hypothesis predicts southward migration (relative to the Coastal Range) of vertical-displacement signals, but the observed cycles of uplift and subsidence occurred simultaneously in northern and southern Coastal Range transects (Fig. 3b, c). Therefore, we suggest that northward subduction at the Ryukyu-trench exerted little or no influence on vertical crustal motions during ~6–0.5 Ma basin evolution.

Post-0.5 Ma extremely rapid uplift and basin inversion created the modern topography of the Coastal Range in a small doubly-vergent structural wedge during an abrupt change to wrench-style transpressional deformation34,57 (Fig. 4b, c). While rapid vertical displacements are observed in other oblique-convergent settings7,8, it is unusual to document large-scale exhumation at rates >10 mm year−1 driven solely by upper-crustal deformation. Isostatic adjustments to changes in lithospheric structure provide a mechanism that can explain this behavior58. A tectonic load on the Philippine Sea plate may have been suddenly released when forearc lithosphere was broken and subducted at the collisional suture zone59,60,61. Downward extraction of lithospheric fragments may have caused rapid exhumation of the overriding plate crust near the suture62,63, which may be partially responsible for the post-0.5 Ma uplift of metamorphosed (Yuli Belt) and unmetamorphosed (Coastal Range) arc crust in eastern Taiwan (Fig. 4b, c)5,34,64. Isostatic compensation by erosional unloading may also have contributed to the creation of topography65,66, but its role remains unclear. It is possible that we have underestimated post-0.5 Ma long-term uplift rates in the northern Coastal Range, because present-day topography in the north may currently be influenced by the modern subsidence stage. This youngest and ongoing subsidence likely is driven by northward convergence and reversed subduction polarity of the Philippine Sea plate at the Ryukyu trench67,68 (Fig. 1).

This study reveals a history of extremely rapid vertical oscillations (up-and-down cycles) of near-surface rocks in only ~3 Myr during active accretion of island arc crust to a growing continental margin (Fig. 3). Our results highlight the short-lived episodic nature of arc-continent collision69 and challenge ideas about long timescales that are often invoked for the rise and fall of mountainous topography by coupled tectonic and surface processes (106–107 years)70. We find that growth of topography to form an eroding steep mountain range directly on the footprint of a formerly subsiding marine basin can be accomplished in only ~500–800 kyr. This study shows that the change of direction in vertical motion, and transformation of a subsiding basin to an eroding mountainous source, can occur very quickly to drive extremely rapid rock cycling and mixing at this and other collisional plate boundaries34. Because arc collision and accretion are recognized as a fundamental process in the growth of continental crust71, our results suggest that extremely rapid vertical crustal motions may be characteristic of deformation in arc-continent suture zones through geologic time72.

Existing methods of thermochronology, petrology, and geochemistry provide a useful record of crustal burial and exhumation in these settings, but they cannot detect such short rapid vertical trajectories in shallow unmetamorphosed crust. Integrated magneto-biostratigraphy and basin subsidence analysis thus offers an important tool for documenting high-resolution histories of vertical crustal motions in tectonically active systems. This approach spans a crucial time gap that needs to be bridged to better understand dynamic feedbacks among long-term geologic (tectonic) processes and shorter timescale impacts such as climate change and landscape response1,70,73.

Methods

Geological mapping and lithostratigraphy

Detailed geological mapping for this study targeted excellent exposures in road cuts and riverbanks of the Coastal Range (Fig. 1). Marker beds (pebbly mudstone and tuffaceous turbidite) and fault zones were carefully mapped across the study area (Supplementary Figs. 3–4). We also compiled information from previously published geological maps74,75,76,77,78,79,80,81. Lithostratigraphic descriptions in type sections of the southern Coastal Range [Bieh river (BC), Madagida river (MDJ), and Sanshian river (SSS) sections] are from Lai et al.34 (Supplementary Fig. 1). New results in the northern Coastal Range [Hsiukuluan river (HKL), Wulou river (WL), Fungfu (FF), and Fungpin (FP) sections] are compiled in Supplementary Fig. 2. We produced composite columns for the northern and southern Coastal Range (Fig. 2) through correlations based on marker beds and the first appearance datums (FAD) of index fossils (Supplementary Figs. 1, 2) and aided by construction of a balanced geological cross-section (Supplementary Fig. 5). This approach assumes that the thickness (i.e., rock volume) of each unit does not change substantially across the local structures (faults and folds).

Magnetostratigraphy

In the southern Coastal Range, we adapted results and interpretations of paleomagnetic chrons from previous published studies34,42,79,80 (Supplementary Fig. 1). In the northern Coastal Range, we compiled published paleomagnetism data40,41 along with new data from samples collected in coherent strata from continuous sections (Paliwan Formation) for Hsiukuluan river (HKL), Wulou river (WL), and Fungpin (FP) sections, avoiding chaotic mass-transport deposits (slump beds, olistoliths) (Supplementary Figs. 2–4). Paleomagnetic samples were collected using a standard (22 mm diameter) drill core from fresh mudstone exposures, and remanent magnetization was measured with a 2G three-axis cryogenic magnetometer. To remove viscous remanent component of overprinting magnetic signals, we applied stepwise thermal demagnetization (THD, from room temperature up to 800 °C) or alternating-field demagnetization (AFD, from 0 up to 80 mT) to most samples. We applied a combination of THD and AFD (e.g., THD to 360 °C followed by AFD procedure) in cases of some specimens that became thermally unstable at higher temperatures. Through these procedures, we obtained reliable measurements of primary remanent component of the paleomagnetic declination and inclination from Zijderveld-type diagrams at each site (Supplementary Fig. 6). We derived mean paleomagnetic directions by restoring the perturbations of regional folds (bedding dip) (Supplementary Data 1). The age values and their uncertainty ranges of magnetic reversals follow the most recent global geomagnetic polarity timescale82,83.

Calcareous nanoplanktons and planktonic foraminifera biostratigraphy

In the southern Coastal Range, we adapted results and age interpretations from previously published studies34,42,79,80 (Supplementary Fig. 1). In the northern Coastal Range, we digitized and manually georeferenced unpublished calcareous nannoplankton fossil charts (Supplementary Data 2) and sample localities (Supplementary Figs. 3, 4) from original notes and field maps of previous works by W.-R. Chi38,84 (Supplementary Fig. 2). For planktonic foraminifera biostratigraphy, we compiled published data of index fossils85,86,87,88 and collected five new samples in Fungfu (FF) and Fungpin (FP) sections (Supplementary Figs. 2, 4; Supplementary Data 2). Samples were collected from fresh intact exposures of mudstone, and we used 63 μm sieve to extract proper size foraminifera for identification.

Interpretation of depositional ages is based primarily on the first appearance datum (FAD) for index fossils due to the potential of fossil reworking, which is commonly reported in turbidite-dominated deposits of the Coastal Range34,38,89 and confirmed by our work. Age values and uncertainties are based on recent compilations for the Indo-Pacific region90,91 (Fig. 2).

Paleobathymetry

When abundance data of both benthic and planktic foraminifera are available, one can empirically estimate the paleobathymetry (W) of the marine sediment through a regression relating planktic percentage (%Ps) to modern water depth92,93. The planktic percentage (%Ps) is defined as:

$$\begin{array}{c}{ \% P}_{s}=100\cdot \frac{P}{P\,+\,B\,-\,S\,-\,O}\end{array}$$
(1)

where P is the number of in situ planktic specimens; B is the number of benthic specimens; S is the number of stress-marker benthic specimens that are more sensitive to other environmental factors (e.g., oxygen level) rather than water depth (in the genera Bolivina, Bulimina, Chilostomella, Fursenkoina, Globobulimina, Uvigerina s.s.); O is the number of organically cemented benthic specimens and reworked fossils. Once (%Ps) is calculated, the paleobathymetry (W) can be estimated through this logistic function:

$$\begin{array}{c}W={{\exp }}\left[{{\alpha }}+\frac{1}{\beta }{{{{{\rm{ln}}}}}}\left(\frac{{ \% P}_{s}}{100\,-\,{ \% P}_{s}}\right)\right]-0.1\end{array}$$
(2)

where α and \(\beta\) are empirical constants from modern settings. Despite the lack of modern offshore constraints near Taiwan, we adapted α = 1.45 ± 0.080 and \(\beta\) = 5.23 ± 0.042 (means ± standard errors) regressed from modern analog of 0–4500 m water depth in subtropical Pacific near New Zealand by Hayward et al.92.

We converted qualitative (in ordinal scale) abundance data of from Chang85,86,87 (V: > 50 specimens; A: 21-50 specimens; C: 11–20 specimens; F: 6-10 specimens; R: < 6 specimens; ?: unsurely identified; D: reworked fossils) into quantitative (ratio) scale with ranges of uncertainty (V = 75 ± 25; A = 35 ± 15; C = 15 ± 5; F = 7 ± 3; R = 3 ± 2; ? = 1 ± 1; excluding reworked fossils) to constrain parameters P, B, and S. Parameter O is assumed to be zero because we have excluded reworked fossils. We then used Eq. (2) to calculate the paleobathymetry (W) and its uncertainty (standard error) through Gaussian error propagation at each sample site of Chang78,79,80 along studied sections [Fungfu (FF), Fungpin (FP), Bieh river (BC), Madagida river (MDJ), and Sanshian river (SSS) sections] (Supplementary Data 3).

Fossil abundance data are sometimes absent [e.g., data of Hsiukuluan river (HKL) and Wulou river (WL) sections from Chang and Chen88] or paleobathymetry cannot be calculated using the planktic-percentage method (e.g., %Ps = 0 or 100). In these cases, we used an alternative method from Hohenegger94, which relies solely on the presence/absence of the benthic species and their modern water depth distributions. The basic function of this method can be written as

$$\begin{array}{c}W=\mathop{\sum }\limits_{n=1}^{m}{l}_{n}{{d}_{n}}^{-1}/\mathop{\sum }\limits_{n=1}^{m}{{d}_{n}}^{-1}\end{array}$$
(3)

where \({l}_{n}\) and \({d}_{n}\) are the location parameter (i.e., mean water depth) and its dispersion (water depth range) of the nth benthic species, respectively; m is the total amount of benthic species that are considered. This method is based on the idea that species with narrower present-day depth distribution could yield more information about the paleobathymetry of the sediment than species adapted to live in a wide range of water depth. We collected constraints of the minimum and maximum distributed water depths of different benthic species or genera (ωmin and ωmax respectively) from publications to date (see cited data in Supplementary Data 3). We then derived the geometric mean (\({l}_{n}=\sqrt{{\omega }_{{\max }}\cdot {\omega }_{{\min }}}\)) and range (\({d}_{n}={\omega }_{{\max }}-{\omega }_{{\min }}\)) of water depth for each species or genus, and calculated the paleobathymetry (W) through Eq. (3). The uncertainty of paleobathymetry (\({\sigma }_{w}\)) can be estimated as below:

$$\begin{array}{c}{\sigma }_{w}=\sqrt{\mathop{\sum }\limits_{n=1}^{m}{\left({l}_{n}-W\right)}^{2}{{d}_{n}}^{-1}/\mathop{\sum }\limits_{n=1}^{m}{{d}_{n}}^{-1}}\end{array}$$
(4)

Lastly, we projected these sample locations along the composite stratigraphic columns to determine changes in paleobathymetry through time (Supplementary Figs. 1, 2, and 7).

Age models and quality of age measurements

Age constraints (paleomagnetic reversals and first appearance datums of index fossils) and their measured present-day stratigraphic heights (before correcting effects of compaction) on the composite sections (Fig. 2) are used to conducted linear regressions between thickness and age (Supplementary Data 4). We visually determine data trends and group data to be fitted in different regression lines (Fig. 3a). These linear models are then used to predict (using extrapolation and interpolation) depositional ages of the section boundaries (base of section, top of preserved section, top of reconstructed section) and paleobathymetry samples (Supplementary Data 3–4).

The resolution of our dating with these integrated magneto-biostratigraphy methods is expected to be as good as the precision [~1–15 thousand years (kyr)] of each astronomically-calibrated age of paleomagnetic reversal83 and first appearance datum (FAD) for index fossils90, once they are accurately placed in the stratigraphic sections. The stratigraphic position of each age-control datum was determined using the two sample sites that define a magnetic polarity reversal or the first appearance of an index fossil. The stratigraphic thickness between two bounding paleomagnetic sample sites mostly lies between 8 to 288 m, except a poor constraint (828 m) at reversal between polarity chrons C2An1.n and C1r.2r (Gauss-Matuyama boundary) near the base of Fungfu (FF) section in the northern Coastal Range (Fig. 2; Supplementary Figs. 1, 2). Using the mean sediment-accumulation rates calculated from height-age linear regressions, the uncertainty (accuracy) for most of our age measurements is estimated to be ± 2–43 kyr (0.1–2%) from targeted age values [±~507 kyr (~10%) for the Gauss–Matuyama boundary in the FF section] (Supplementary Data 4). This demonstrates remarkably high-resolution and high-fidelity controls on depositional ages and associated vertical subsidence and uplift rates.

Subsidence analysis: decompaction and backstripping

We used established numerical methods of basin geohistory analysis45 that correct for loss of pore space during progressive burial and compaction of sediment through time to reconstruct of subsidence history of the sedimentary basin. Stratigraphic thickness, corrected for the effects of compaction and sea level, is therefore used to track the depth of the basement top through time95. This approach assumes that the pore spaces are interconnected (i.e., no overpressure), and the sediment porosity [\({{\varnothing }}({{{{{\rm{z}}}}}})\)] varies as an exponential function of depth (z):

$$\begin{array}{c}{{\varnothing }}\left(z\right)={{\varnothing }}\left(0\right)\cdot {{{{{{\rm{e}}}}}}}^{-z/C}\end{array}$$
(5)

where C is a decay constant that varies with lithology. We calculated global average porosity-depth functions from previous publications95,96 to estimate initial porosity [\({{\varnothing }}\left(0\right)\)], decay constant (C), and uncertainties (standard errors) for sandy, muddy, and mean marine sediments (Supplementary Fig. 8; Supplementary Data 4). We assumed that basement rocks below the basal unconformity (i.e., Kangkou Limestone, Tuluanshan Formation) have not compacted. This assumption is supported by the presence of calcite-cemented Miocene volcaniclastic sandstones beneath the unconformity that are directly overlain by uncemented mudstones and sandstones above the contact33,34, showing that rocks beneath the unconformity were cemented prior to deep post-Miocene basin subsidence. Rocks beneath the unconformity may be subject to minor, inconsiderable amounts of compaction that do not affect the results of our subsidence analysis.

For N stratigraphic units, the present-day thickness (\({T}_{0}\)) of each unit was buried at a depth of \({D}_{0}\) when the youngest sediment deposited prior to structural tilting and erosion. There are 14 preserved units (N = 14) in both northern and southern Coastal Range. Stratigraphic positions of all age boundaries are presented in Supplementary Data 4. Uncertainties of \({T}_{0}\) of preserved units (unit 1–14) are limited by the stratal thickness between the two bounding samples that confine the magnetic reversals or the first appearance datums (FAD) of index fossils (Supplementary Figs. 1,2; Supplementary Data 4). The uppermost preserved sediment at the top of unit 1 is consolidated and lithified, which means that there must have been a considerable thickness of strata (called unit 0 in this study) above preserved unit 1 that was subsequently removed by erosion during post-0.5 Ma uplift. Porosity-effective stress of the sandstone44 and compiled vitrinite reflectance97 data yield an estimated range of eroded thickness of ca. 2.2–3.7 km above marker bed tuff Tp12 near the top of the Madagida river (MDJ) section (Supplementary Fig. 1). This implies ca. 0.45–1.95 km sediment that was deposited above unit 1 and has since been removed. For simplicity, we assumed a conservative thickness range of 0.75 ± 0.25 km for the unpreserved unit 0 in both the north and south composite sections, and we used it to reconstruct the top of section prior to structural inversion (Fig. 3; Supplementary Data 4).

To calculate the thickness of each unit at some earlier time (i.e., decompacted thickness, \({T}_{i}\)), when the unit was buried only to a depth of \({D}_{i}\), we can use the mass-balance equation:

$$\begin{array}{c}{\int }_{{D}_{i}}^{{{D}_{i}+{T}_{i}}}\left[1-{{{\varnothing }}}_{i}\left(z\right)\right]{{{{{{\rm{d}}}}}}z}=\,{\int }_{{D}_{0}}^{{{D}_{0}+{T}_{0}}}\left[1-{{{\varnothing }}}_{i}\left(z\right)\right]{{{{{{\rm{d}}}}}}z}\end{array}$$
(6)

where the \({{{\varnothing }}}_{i}\left(z\right)\) is the porosity of unit i (i = 0, 1, 2,…, N) at depth z. This approach assumes the volume of sediment grains within the unit does not change. The quantity \(\left[1-{{{\varnothing }}}_{i}\left(z\right)\right]\) represents the volume of sediment grains (per unit volume of the strata) at any level within the unit. After integrating Eq. (5), Eq. (6) is rearranged to iteratively solve \({T}_{i}\):

$$\begin{array}{c}\Longrightarrow {T}_{i}=\mathop{\sum }\limits_{k\,=\,1}^{M}{F}_{i}^{k}\cdot \left[{\varphi }_{1}\cdot {{{{{{\rm{e}}}}}}}^{-{T}_{i}/{C}_{i}^{k}}+{\varphi }_{2}\right]\end{array}$$
(7)

with \(\left\{\begin{array}{c}{\varphi }_{1}=-{C}_{i}^{k}\cdot {{{\varnothing }}}_{i}^{k}\left(0\right)\cdot {{{{{{\rm{e}}}}}}}^{-{D}_{i}/{C}_{i}^{k}}\hfill\\ {\varphi }_{2}=-{\varphi }_{1}+{T}_{0}+{C}_{i}^{k}\cdot {{{\varnothing }}}_{i}^{k}\left(0\right)\cdot {{{{{{\rm{e}}}}}}}^{-{D}_{0}/{C}_{i}^{k}}\cdot \left[{{{{{{\rm{e}}}}}}}^{-{D}_{0}/{C}_{i}^{k}}-1\right]\end{array}\right.\)where \({F}_{i}^{k}\) is the fraction of lithology k (k = 1, 2,…, M) in unit i. There are three types of lithology (M = 3) determined in this study. The fraction of sand (k = 1), mud (k = 2), and pebbly mudstone (k = 3) was measured in all sections (Supplementary Figs. 1, 2; Supplementary Data 4). We assumed that unit 0 contains subequal fractions of sand and mud (\({F}_{0}^{1}=0.5\); \({F}_{0}^{2}=0.5\); \({F}_{0}^{3}=0\)). The initial porosity [\({\varnothing }_{i}^{k}\)(0)] and decay constant (\({C}_{i}^{k}\)) for sandy, muddy, and mean marine sediments were applied respectively (Supplementary Fig. 8). After repeating Eqs. (6) and (7) for each unit from top to the base of section, we computed the sum of decompacted unit thickness (\({\epsilon }_{i}\)) at the time when unit i finished deposition:

$$\begin{array}{c}{\epsilon }_{i}=\mathop{\sum }\limits_{i\,=\,0}^{N}{T}_{i}\end{array}$$
(8)

These procedures [Eqs. (6–8)] account for the effects of removing incrementally older units from the top and allow the section to expand as underlying units are unloaded.

To evaluate the amounts of total subsidence (i.e., the true depth of the basement, \({{{{{{\rm{\sigma }}}}}}}_{i}\)) at the end of unit i deposition, we need to correct the magnitude of paleo-water depth by assuming the basin was filled with water to sea level:

$$\begin{array}{c}{{{{{{\rm{\sigma }}}}}}}_{i}={\epsilon }_{i}+{W}_{i}-{\Delta }_{i}\end{array}$$
(9)

where \({W}_{i}\) and \({\Delta }_{i}\) are the paleobathymetry and sea level relative to modern datum at the time of unit i finishing deposition. We combined means and standard errors of available paleobathymetry estimates (Supplementary Data 3) with reconstructed global sea level from Miller et al.98 using age constraints in each section (within the range of age uncertainty with extra ± 0.2 Myr and ± 0.01 Myr for paleobathymetry and relative sea level respectively) as the values of \({W}_{i}\) and \({\Delta }_{i}\) at each unit boundary (Supplementary Fig. 7; Supplementary Data 4). Paleobathymetry constraint was not available for the reconstructed unit 0 above the preserved strata. In this case, we assumed the paleobathymetry of reconstructed basin top (at the end of unit 0 deposition, \({W}_{0}\)) and its uncertainty range as a half of the \({W}_{1}\) value at the top of preserved strata [\({W}_{0}={W}_{1}/2\pm {W}_{1}/2\)] because basin inversion in the Coastal Range possibly began between the ends of unit 1 and unit 0 (Fig. 3; Supplementary Fig. 7).

Since the folded basal unconformity and underlying volcanic basement rocks are exposed well above sea level (Fig. 4c), we can calculate the minimum and the best-estimated long-term rock exhumation rates using the decompacted depth of basement at depositional ends of unit 1 and unit 0 (\({{{{{{\rm{\sigma }}}}}}}_{1}\) and \({{{{{{\rm{\sigma }}}}}}}_{0}\)) to the present-day elevations of the antiformal peaks in northern and southern Coastal Range (0–1.33 km and 0–1.68 km, respectively) (Fig. 3).

We further estimated the amount of subsidence that was contributed by tectonic forces (so-called “tectonic subsidence,” \({\zeta }_{i}\)) at the end of unit i deposition by removing effects of paleo-water depth and local (Airy) isostatic response to applied sediment loads:

$$\begin{array}{c}{\zeta }_{i}={\epsilon }_{i}\frac{\left({\rho }_{a}-{\bar{{\rho }_{s}}}^{i}\right)}{\left({\rho }_{a}-{\rho }_{w}\right)}+{W}_{i}-{\Delta }_{i}\frac{{\rho }_{a}}{\left({\rho }_{a}-{\rho }_{w}\right)}\end{array}$$
(10)

where \({\rho }_{w}\) is the density of marine water (\({\rho }_{w}=1025\,{{\mbox{kg}}}\,{{{\mbox{m}}}}^{{{\mbox{-}}}3}\)); \({\rho }_{a}\) is the density of asthenospheric mantle (\({\rho }_{a}=3300\,{{\mbox{kg}}}\,{{{\mbox{m}}}}^{{{\mbox{-}}}3}\)). \({\bar{{\rho }_{s}}}^{i}\) is the average (integral) density of the unit i with various lithologies k at each time frame of sedimentation:

$$\begin{array}{c}{\bar{{\rho }_{s}}}^{i}=\left(\mathop{\sum }\limits_{i\,=\,0}^{N}\mathop{\sum }\limits_{k\,=\,1}^{M}{F}_{i}^{k}\cdot {\Omega }_{i}^{k}\right)/{\epsilon }_{i}\end{array}$$
(11)

\({\Omega }_{i}^{k}\) represents the average (integral) 1-D mass of unit i for given lithology k at some earlier time, assuming the pore spaces were filled by marine water,

$${\Omega }_{i}^{k} ={{\int}_{{D}_{i}}^{{{{D}_{i}+{T}_{i}}}}}\left\{{{{\varnothing }}}_{i}^{k}\left(z\right)\cdot {\rho }_{w}+\left[1-{{{\varnothing }}}_{i}^{k}\left(z\right)\right]\cdot {({\rho }_{g})}_{k}\right\}{{{{{{\rm{d}}}}}}z}\\ ={({\rho }_{g})}_{k}\cdot {T}_{i}+\left[{\rho }_{w}-{({\rho }_{g})}_{k}\right]\cdot {C}_{i}^{k}\cdot {{{\varnothing }}}_{i}^{k}\left(0\right)\cdot {{{{{{\rm{e}}}}}}}^{-{D}_{i}/{C}_{i}^{k}}\cdot \left[1-{{{{{{\rm{e}}}}}}}^{-{T}_{i}/{C}_{i}^{k}}\right]$$
(12)

where \({({\rho }_{g})}_{k}\) represents the averaged density of sediment grain for each lithology k in unit i. We applied the means and standard errors of the grain densities for sandy, muddy, and mean marine sediments (for pebbly mudstone) respectively from previously published data95 (Supplementary Fig. 8; Supplementary Data 4).

Uncertainties of all input parameters were considered in the analysis. Thus, we were able to estimate the uncertainties of calculated tectonic subsidence (\({\zeta }_{i}\)) and decompacted total subsidence (\({{{{{{\rm{\sigma }}}}}}}_{i}\)) through Gaussian error propagation or delta method (Supplementary Data 4). Throughout the analysis, we found that the primary source of error is the present-day (non-decompacted) thickness of each unit (\({T}_{0}\)), followed by uncertainties in paleobathymetry estimates (\({W}_{i}\)).

Lastly, we plotted the subsidence history (i.e., geohistory) diagrams for northern and southern composite sections, which show changes in depth of basement [i.e., decompacted total subsidence (\({{{{{{\rm{\sigma }}}}}}}_{i}\))] and calculated corresponding amount of tectonic subsidence (\({\zeta }_{i}\)) through time (Fig. 3b, c). The amount of total subsidence prior to decompaction correction was also plotted as a standard convention. The position of basement top at the beginning of subsidence for each composite section was reconstructed by projecting along the oldest segment of subsidence curve to the sea level (0 km). This indicates the end of formation of the basal unconformity6,33, which is characterized by a broad erosive surface that formed near sea level and is capped by discontinuous thin (ca. 50–200 m) deposits of shallow-marine limestone (Kangkou Limestone, from 5.57–4.37 Ma to 4.31–3.47 Ma) and limestone-clast bearing epiclastic rocks (Biehchi Epiclastic Unit, from 5.53–4.31 Ma to 3.82–3.35 Ma)34,35 (Supplementary Figs. 1, 2).