Isotopic variability in tropical cyclone precipitation is controlled by Rayleigh distillation and cloud microphysics

Abstract

Tropical cyclones produce rainfall with extremely negative isotope values (δ¹⁸O and δ²H), but the controls on isotopic fractionation during tropical cyclones are poorly understood. Here we studied the isotopic composition of rainfall at sites across central Texas during Hurricane Harvey (2017) to better understand these processes. Rainfall δ¹⁸O trend towards more negative values as a result of Rayleigh distillation of precipitation-generating airmasses as they travel towards the center of the storm. Superimposed on these gradual changes are abrupt isotopic shifts with exceptionally low deuterium excess values. These appear to be controlled by microphysical processes associated with the passage of spiral rainbands over the sampling locations. Isotope-enabled climate modeling suggests that it may be possible to identify the signature of tropical cyclones from annually resolved isotopic proxy records, but will depend on the size of the storm and the proximity of the site to the core of the storm system.

Introduction

Tropical cyclones (TCs) are known to produce precipitation with extremely negative stable isotopic delta values (i.e., δ¹⁸O and δ²H) compared with other tropical rainfall sources^1,2,3,4. The exceptionally depleted isotopic signatures of TCs provide a potentially valuable indicator of past storm activity that may be recorded in high-resolution archives of climate (e.g., speleothems, tree rings, corals, etc.)^5,6. However, recent studies of modern rainfall from Central America have demonstrated that anomalously positive stable isotope values in tropical precipitation can occur under a variety of conditions, complicating the interpretation of isotope-based TC reconstructions^4,7. And while a number of studies over the past few decades have tried to characterize how rainwater stable isotopes change during TCs, and to identify hurricane events in proxy records, there remain questions about the mechanisms driving these changes and whether they are large enough to be recorded in even annually-resolved proxy records.

For example, previous studies have observed that rainwater isotopic values from TCs are spatiotemporally heterogeneous. A consistent observation in many studies of TCs is that there is a systematic depletion of heavy isotopes in rainfall radially inward towards the center of the storm, with exceptionally negative delta values only occurring in areas close to the eyewall^2,3,8,9. What causes this spatial isotopic pattern remains a subject of debate. One process suggested to account for the isotopic change is the effect of higher vertical rainout efficiency associated with higher and thicker clouds near the eyewall^2,3. Other studies have attributed these changes to post-condensation isotopic exchange between falling rain and ambient vapor^3,10 or re-evaporation of falling precipitation⁹ at the edge of TCs or the uptake of isotopically enriched moisture from nearby warm surface ocean waters⁴.

A few studies have examined high-frequency variability in TC rainfall during individual storm events and have observed large swings in the isotopic composition of precipitation on hourly timescales^4,11. For example, a study of Tropical Cyclone Ita displayed rapid swings of δ¹⁸O in both rainwater and vapor by up to ~10‰ associated with the passage of spiral rainbands¹¹. An organized spiral rainband exhibits a somewhat similar cross-band structure to squall line mesoscale convective systems (MCS), with updrafts on the inner side of the band and downdrafts on the outer side^12,13. However, unlike in an MCS, where updrafts (downdrafts) lead to convective (stratiform) precipitation with relatively enriched (depleted) isotopic values^{4,14,15,16,17}, spiral rainbands associated with TCs consist of predominantly stratiform precipitation¹². The mechanisms controlling stable isotope variability during the passage of these rainbands have not been investigated.

Here, we examine the evolution of δ¹⁸O, δ²H, and d-excess values of precipitation (hereafter δ¹⁸O_p, δ²H_p, d-excess_p) during Hurricane Harvey (2017) using 10 min to sub-daily rainwater collection from Austin (30.3°N, 97.7°W), San Antonio (29.6°N, 98.6°W), and Houston (30.1°N, 95.4°W). Hurricane Harvey was a record-setting TC in US history in terms of both total rainfall and the affected area, with an economic impact second only to Hurricane Katrina (2005)¹⁸. Although the eye of Hurricane Harvey did not pass directly over our sampling locations, its spiral rainbands produced 2–3 days of rainfall over all three sites, allowing us to capture both long-term trends and high-frequency changes in precipitation isotope values and to evaluate the causes of these variations.

Results and discussion

The evolution of Harvey and weather conditions in southeastern Texas

Hurricane Harvey was spawned from a large convective mass off the west coast of Africa on August 12, 2017 which later developed into a tropical depression on August 17. It made landfall on August 25 at 2200 Central Daylight Time (CDT) over southeastern Texas as a Category 4 hurricane (Fig. 1a). Harvey rapidly weakened as it migrated northwestward over land between August 26 and August 27. In the early morning of August 27, the synoptic condition steered Harvey back southeastward, and Harvey moved back offshore in the early morning of August 28. Harvey eventually made its way back onto land in Cameron County, Louisiana as it was migrating northeastward while dissipating¹⁸.

Fig. 1: Evolution of Hurricane Harvey and δ¹⁸O_p.

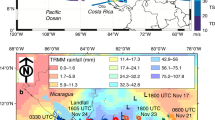
a Total precipitation between August 25 and September 2, 2017 (shadings). The glowing curve indicates the track of Hurricane Harvey. The storm symbols on the curve indicate the hurricane intensity, with the adjacent time stamps indicating the time of each stage. The storm symbols are explained in the legend; T.D. Tropical Depression; T.S. Tropical Storm. The stars indicate the rainwater sampling sites. b Violin plots showing the distribution of δ¹⁸O_p values at the three sites. c Timeseries of δ¹⁸O_p at Austin, San Antonio, and Houston. Time is reported in CDT.

The Austin Camp Mabry weather station recorded a total of 8 inches of precipitation during Hurricane Harvey¹⁸. Rainfall started around 0000 CDT August 26th and lasted until 0900 CDT August 28th, with the maximum precipitation rate occurring between 0700 and 0800 CDT August 26th (Supplementary Fig. 1). Ground-level relative humidity increased rapidly from 75 to 100% as rainfall started, which then briefly dropped to 85% after the first major rainband moved away from Austin at 1200 CDT August 26th before it quickly returned to 97%. Relative humidity remained over 90% until the morning of August 28th (Supplementary Fig. 1). The recorded temperature was relatively stable during the storm, ranging from 21 to 24 °C (Supplementary Fig. 1).

The San Antonio International Airport weather station recorded a total of 1.9 inches of precipitation during Hurricane Harvey¹⁸. Intermittent small patches of rainfall started in the afternoon of August 25th. The main storm event occurred from 0500 CDT August 26th to 1500 CDT August 27th. During the main storm, the ground-level relative humidity was constantly at around 90%, and temperature ranged from 23 to 24 °C (Supplementary Fig. 2).

The Houston George Bush Intercontinental Airport weather station recorded a total of 31.3 inches of precipitation during Hurricane Harvey¹⁸. The historically high rainfall amount in the Houston metro area was partially due to a weak stationary front during August 26–28th, which enhanced surface convergence and uplift, with moisture inflow in the eastern side of Harvey continuously delivering warm humid air from the Gulf of Mexico. The recorded ground-level relative humidity was fluctuating between 90 and 100%, and the surface temperature gradually decreased from 26 °C at the onset to 22 °C near the end (Supplementary Fig. 3).

Isotopic composition of Hurricane Harvey rainwater

Over the period of rainwater collection, the mean hourly δ¹⁸O_p values in Austin (−9.6 ± 3.35‰, 1σ, n = 50) and San Antonio (−9.86 ± 3.47‰, 1σ, n = 29) are similar, and the mean δ¹⁸O_p value in Houston is slightly higher (−8.37 ± 1.74‰, 1σ, n = 14) (Fig. 1b, Supplementary Data 1). These values are substantially more negative than the long-term average August δ¹⁸O_p (−3.4 ± 3.4‰) and mean annual δ¹⁸O_p (−4.3 ± 1.1‰) of rainfall collected in central Texas^16,19,20. The timeseries of rainfall δ¹⁸O_p at all three sites display a trend towards more negative values as the storm progressed (Fig. 1c). In Austin and San Antonio, δ¹⁸O_p decreased by over 12‰ between August 26, 0000 CDT and August 28, 0000 CDT, whereas the trend is more subtle in Houston, with a change of only ca. 6‰ between the onset and the end of the storm. At the Austin sampling location, δ¹⁸O_p values also display a return to relatively enriched values towards the end of the storm, which is not evident at the other sites.

The hourly Austin and San Antonio datasets also display high-frequency shifts in δ¹⁸O_p that are superimposed on the long-term trends (Fig. 1c). This high-frequency variability is further supported by our parallel 10-min resolution sampling at Austin, which shows changes that are consistent with our hourly data set (Supplementary Fig. 1). There is an apparent lead-lag phase relationship between the records in Austin and San Antonio, with the San Antonio δ¹⁸O_p lagging the Austin δ¹⁸O_p by approximately 2 h (Supplementary Fig. 4), suggesting that the high-frequency variability at the two sites is related.

In Austin, our data show that these high-frequency shifts in δ¹⁸O_p are accompanied by large negative shifts in d-excess of up to −15‰ during the first half of the storm (August 26, Supplementary Fig. 1). After midnight on August 27 d-excess values remained largely positive for the remainder of the storm. The evolution of d-excess_p from our parallel 10 min d-excess_p data agrees with the hourly data, showing large negative shifts during this interval of collection at 10 min-resolution (Supplementary Fig. 1). However, the d-excess_p data from San Antonio do not show exceptionally negative values (Supplementary Fig. 2), except for the first sample, which was collected during a brief period of precipitation under the influence of the periphery of the storm, where strong evaporation likely occurred. While we do not observe high-frequency changes in d-excess_p from San Antonio, there was a period of relatively low d-excess_p values between the morning of August 26 and the midnight August 27. The San Antonio d-excess_p rose back to near 10‰ on August 27 before it dropped again during the final stage of the storm. At Houston, d-excess_p values remained stable, near 10‰ but given the low resolution (several hours) sampling at that site, we cannot evaluate whether high-frequency shifts in isotopic values may have occurred there (Supplementary Fig. 3).

3-day trend in δ¹⁸O_p controlled by upstream rainout

The long-term trend of Hurricane Harvey rainfall δ¹⁸O_p in time and space shows a strong dependence on the relative distance to the hurricane eye, with delta values across all three sites decreasing as the eye approached (Figs. 2a, 3a). This observation is consistent with previous TC isotope studies, and was previously attributed to several factors including higher cloud tops near the eyewall³, diffusive isotopic exchange between falling droplets and the ambient vapor³, and post-condensation re-evaporation of falling droplets⁹. While the isotopic ratios were overall more deleted in the proximity of the eyewall at all three sites, the most depleted values observed in Austin and San Antonio occurred several hours after the closest point to the eyewall was reached (Fig. 2a). At San Antonio, δ¹⁸O_p values did not increase as Harvey migrated away, and at Austin δ¹⁸O_p only increased in the latest portion of the storm as the precipitation rate fell off dramatically. This asymmetry of the isotope-eyewall distance relationship evident in the Harvey dataset suggests that a more complex mechanism is needed to explain the long-term trends in the isotopic value of precipitation. Furthermore, similar to what has previously been observed in other TCs⁴, there is no significant correlation between the stable isotope data from Hurricane Harvey and environmental parameters, such as temperature, precipitation amount, wind speed, and relative humidity at ground level (Supplementary Fig. 1), indicating that the long-term spatiotemporal pattern of TC δ¹⁸O_p was not driven by instantaneous changes in local environmental conditions.

Fig. 2: Spatiotemporal characteristics of δ¹⁸O_p of Hurricane Harvey.

a Evolution of δ¹⁸O in space relative to the center of Hurricane Harvey (open circles color-coded by δ¹⁸O_p values). The black arrows indicate the directions of relative displacement of the sampling sites, assuming the hurricane eye was stationary. b–e Snapshots of MRMS radar reflectivity at different times. The purple line indicates the track position for Hurricane Harvey (Black and Zelinsky, 2018). The red storm symbols indicate the instant positions of the hurricane eye. The black stars indicate our sites of rainwater collection.

Fig. 3: Spatiotemporal evolution of δ¹⁸O_p controlled by the upstream rainout amount.

Scatter plots of a δ¹⁸O_p vs. Distance to the eye, b distance to the eye vs. Upstream rainout, and c δ¹⁸O vs. Upstream rainout. Blue, green, and brown dots indicate data collected from Austin, Houston, and San Antonio, respectively. The r and p values reported in the figures include data from all three sites. d Comparison of 5 km-height backward trajectories reaching Austin at the onset of the storm (turquoise, 8/26 0000 CDT), at the time when the location was at the closest point to the eye (dark blue, 8/27 0100 CDT), and at the end of the storm (light blue, 8/28 0900 CDT), showing more swirly travel history of moisture when the eye was closer.

Backward trajectories of airmasses are often used to assess the impact of moisture origin and transport history on the isotopic composition of rainfall. Although previous studies show that changes in moisture source can partially account for seasonal variability of rainwater isotopic composition in central Texas^16,19,21, it is unlikely to be the case here on such short timescales. Our analysis shows that during Hurricane Harvey, moisture delivered to our sites was primarily derived from a relatively small area (25–29°N, 90–94°W) in the Gulf of Mexico, with little change throughout the sampling period (Supplementary Fig. 5). Thus, we can simplify our interpretation by assuming that the initial isotopic value of the moisture supplied to Hurricane Harvey remained largely unchanged. Tracking the meteorological conditions along Lagrangian back trajectories of airmasses, we find that δ¹⁸O_p is most strongly correlated with total precipitation occurring along a 72 h backward trajectory (i.e., upstream rainout) (Fig. 3c). This indicates that the long-term trend of the isotopic value of hurricane rainfall reflects integrated upstream processes associated with Rayleigh distillation of water vapor via rainfall that previously fell rather than local rainfall. There is also a strong correlation between the upstream rainout and distance to the hurricane eye (Fig. 3b), with higher upstream rainout of water vapor for airmasses near the eyewall than airmasses near the edge of the storm. We hypothesize that this relationship could account for the observed spatiotemporal patterns in δ¹⁸O_p values of hurricane rainfall (Fig. 3a). Modeled back trajectories show that near the eyewall, airmasses had a longer transport history, orbiting around the hurricane eye, during which continuous rainout could have enhanced the isotopic depletion of the residual water vapor (Fig. 3d). In contrast, water vapor near the edge of the storm was transported more directly from the adjacent regions or from the ocean, which had not experienced extensive rainout, and therefore, produced precipitation with less negative δ¹⁸O_p values (Fig. 3d). The upstream rainfall control could also account for the delayed return of δ¹⁸O_p to more positive values observed in the Austin and San Antonio records. At these sites, upstream rainout remained elevated even after the closest point relative to the hurricane eye was reached because of the development of a weak stationary front in the eastern sector of the hurricane, which led to intense rainfall upwind of Austin and San Antonio and isotopic depletion over these sites (Supplementary Figs. 1 and 2).

In order to determine whether this upstream rainout effect is a fundamental process controlling isotopic fractionation in TCs, we also examined this effect in published high-resolution TC isotope studies. We find that the Chinese records of Typhoons Haitang, Meigi, and Soudelor⁹, and the Central American records of Hurricane Irma and Hurricane Otto^4,7 also exhibit significant negative correlations between upstream rainout and δ¹⁸O_p (Supplementary Table 1), similar to our findings for Hurricane Harvey. This indicates that the upstream rainout could be a widely applicable control on the spatiotemporal variability in TCs. However, we also find that some typhoons from southeastern China exhibit strong correlations between δ¹⁸O_p and relative humidity, suggesting that post-condensation evaporation may play a more important role in some storms^9,11. We find that the correlations between δ¹⁸O_p and upstream rainout generally tend to be stronger when relative humidity is higher (Supplementary Fig. 6). We hypothesize that variations in relative humidity were larger during drier TCs, and as a result, local effects associated with evaporative fractionation dominated the isotopic evolution of precipitation from these storms. Hurricane Irma appears to be an exception in that it shows relatively low relative humidity during the event and yet a significant correlation between δ¹⁸O_p and upstream rainout. We recognize that the backward trajectory analysis depends on the meteorological data input, as well as the models that generated these meteorological data. Thus, uncertainties might arise from the relatively low resolution of the global meteorological datasets used in the trajectory analysis (40 km resolution EDAS Contiguous US dataset for Hurricane Harvey; 1° × 1° resolution GDAS global dataset for other TCs; see “Methods” section for details) and any uncertainties associated with the parameterization of the climate models used to simulate them. Future studies that have access to improved meteorological input or with coupled vapor-rainwater isotope analyses may help to improve our understanding of the relative importance of humidity, upstream rainout, or other processes in driving isotopic changes in TCs.

High-frequency isotopic changes associated with spiral rainbands

The rapid (~1–3 h) shifts in the δ¹⁸O_p data from Austin and San Antonio appear to be associated with the passage of individual spiral rainbands (Fig. 2b–e, and 4a). In Austin, our record shows an initial positive shift in δ¹⁸O_p upon the arrival of each rainband, followed by a transition to more negative δ¹⁸O_p values as the rainband passes over the sampling location (e.g., 0700−0800 and 1400−1700 on August 26, 0000−0300 on August 27). Previous studies have attributed such high-frequency isotopic variability in TC to varying precipitation types, where stratiform precipitation produces more isotopically depleted rainfall than does convective precipitation^4,11. However, this is not likely the cause here. Although spiral rainbands of TC bear some structural similarity to a squall line MCS, with large anvil stratiform clouds expanding towards the outer side and weak convective precipitation forming from updrafts on the inner side, the dynamics controlling the two systems are different¹². If the changes in precipitation type were the dominant isotopic control, we would expect to see a negative shift in δ¹⁸O_p as the downdraft-dominated outer side of rainbands reached the site first, followed by a positive shift in δ¹⁸O_p associated with the subsequent updraft^22,23, opposite to what we observe (Fig. 4a). Instead, we suggest that the rapid decrease in δ¹⁸O_p values were driven by the local rainout effect during the passage of rainbands, which is supported by a weak but significant correlation between the time-derivative of δ¹⁸O_p change and hourly precipitation amount (r = −0.39, p < 0.01) in Austin. However, it is less clear what drives the initial positive shift in δ¹⁸O_p preceding the decrease within a rainband.

Fig. 4: High-frequency shifts in δ¹⁸O_p and d-excess_p strongly associated with rainbands and vertical air motions.

a Evolution of δ¹⁸O_p (blue curve), d-excess_p (red curve) in comparison with rainfall intensity (black curve) in Austin. Peaks in rain rate portray the passage of several individual spiral rainbands over Austin. Rain rate data is from the 2 min MRMS dataset⁴⁰. b Vertical velocity over Austin. Negative (positive) values indicate ascending (descending) motions. c Relative humidity over Austin. Vertical velocity and relative humidity data are from the ERA5 global reanalysis²⁸.

The observation that positive spikes in δ¹⁸O_p upon the arrival of each rainband were accompanied by large negative shifts in d-excess (Fig. 4a) suggests that these changes could be driven by kinetic isotopic fractionation rather than equilibrium condensation, which would yield d-excess values near +10‰. Negative d-excess values in rainwater are commonly interpreted as a sign of post-condensation re-evaporation because of the faster diffusion rate of HDO relative to H₂¹⁸O; re-evaporation causes the preferential escape of lighter isotopologues from liquid water, increasing δ¹⁸O_p values and decreasing d-excess values^24,25. However, using previously reported effective fractionation factors^26,27 we estimate that at least 50% of the falling droplets would need to be re-evaporated in order for re-evaporation to account for such negative d-excess_p values. Because ground-level relative humidity remained near saturation throughout our sampling campaign and these shifts occurred as precipitation was intensifying (Supplementary Fig. 1), extensive re-evaporation is unlikely. Similarly, although we observe a dip in relative humidity associated with a pause in rainfall at around 1200 CDT on August 26th, negative d-excess_p shifts were not present during this interval (Supplementary Fig. 1). Together, these observations suggest that increased evaporation associated with transient decreases in relative humidity cannot account for the spikes of exceptionally negative d-excess_p in the Austin data.

Using ERA5 hourly reanalysis data (0.25° × 0.25°)²⁸, we investigate the relationship between rainband mesoscale circulation and the rapid changes in d-excess_p and propose that it is related to the microphysics of condensation. Our results show that as rainbands arrived, these shifts in d-excess_p were accompanied by moderate ascending air motion, which could be responsible for the delivery of supercooled liquid water to the mid-troposphere (Fig. 4b). Support for this comes from the greater-than-100% relative humidity at 500 mbar (Fig. 4c). These environmental conditions are favorable for the Wegener–Bergeron–Findeisen (WBF) condensation process, in which vapor, ice, and supercooled liquid water coexist. In the WBF scenario, vapor is sub-saturated relative to liquid water but is supersaturated relative to ice, causing water molecules to evaporate from liquid water and deposit on ice condensate²⁹. Both of these processes are associated with kinetic isotopic fractionation. At such low temperatures, the effective fractionation between vapor and liquid is larger than between vapor and ice³⁰. The net result is that the WBF process would concentrate heavy isotopologues in the vapor phase, causing increased δ¹⁸O_vapor and decreased d-excess_vapor^31,32,33. The subsequent condensation of ice from such vapor would result in progressively more positive δ¹⁸O_p and negative d-excess_p values. Our parallel 10 min d-excess_p data shows a similar range of variation during this interval while exhibiting an incoherent evolution over time, which may indicate spatial heterogeneities associated with these microphysical processes (Supplementary Fig. 1). A single column convection model suggests that such changes in δ¹⁸O_vapor and d-excess_vapor can only occur when the WBF process is considered, though the magnitude of the signal is strongly dependent on parameterization³¹. Furthermore, in an idealized storm, isotopic fractionation associated with the WBF process would occur at the anvil detrainment level of a convective system where the convective clouds decay to stratiform clouds³¹, which is consistent with the observation that the strongly negative d-excess occurred when rainfall was transitioning from the stratiform side of the rainband to the weak/dying convective (Fig. 5). The subsequent decrease in δ¹⁸O_p and the return of d-excess_p values to near 10‰ as each rainband passes over indicates that the WBF process no longer plays a role once this narrow transition zone of the rainband passes, and that the hourly-scale changes in δ¹⁸O_p are dominated by local rainout effects.

Fig. 5: Schematics of a possible mechanism for the exceptionally large and coupled shifts in δ¹⁸O_p and d-excess_p.

a Spatial anatomy of two spiral rainbands at August 26th 0700 CDT and August 26th 1400 CDT, respectively, overlying MRMS radar images in Fig. 2b, c. Pink (purple) shading indicates stratiform (convective) rainfall. Purple shading with dashed outlines indicates decaying convective rainfall. The red storm symbols indicate the hurricane eye. The black stars indicate Austin, TX. b A schematic illustrating the mesoscale dynamics responsible for the WBF process and high-frequency isotopic shifts. The upper diagram highlights positive shifts in δ¹⁸O_p (blue curve) and negative shifts in d-excess_p (red curve) upon the arrival of two rainbands (black curve). The lower schematic generalizes the vertical structure of these two rainbands, showing the coexisting three phases of water in the region where stratiform rainfall transitions into convective rainfall, which is favorable for the WBF condensation. Light gray shading: the cross-section of a spiral rainband. Dark gray shading: regions of high reflectivity. Broad arrows: mesoscale circulations.

Although WBF condensation can produce condensate with very negative d-excess values, one remaining question is whether the isotopic signals of WBF condensation are preserved as raindrops fall to the ground-level. Post-condensation processes, including re-evaporation and diffusive exchanges during the fall of droplets, could alter the original isotopic composition^34,35, thus masking the original signal of condensation. Re-evaporation would further lower d-excess_p values, whereas diffusive exchanges would combine the d-excess of ambient vapor and droplets¹⁴, in this case making d-excess_p more positive. Figure 4c shows that there are a few pockets of relatively dry air with relative humidity of 70–90% in the lower troposphere at around 700 mbar, associated with the lingering drying effect of the downdrafts (Fig. 4b). We do find that the periods with negative d-excess_p occur when the lower troposphere is relatively dry. However, the converse is not true: there are multiple periods within the storm when the lower troposphere is dry but precipitation does not show anomalously negative d-excess_p values (e.g., August 26th 3:00, August 28th 0:00 and after). We thus hypothesize that a dry lower troposphere may limit diffusive exchange such that d-excess_p values remain negative, but these high frequency shifts are accounted for mainly by the microphysics of condensation.

We explore two options to explain the observation that δ¹⁸O_p values from San Antonio show hourly variations that are similar to those observed in Austin but with a smaller magnitude and a lag of approximately two hours (Fig. 1c; Supplementary Fig. 4). We hypothesize that this lead-lag relationship can be explained by either the counterclockwise moisture transport from Austin to San Antonio (with a distance of 70 miles and wind speed of 35 miles per hour) or the slow east-to-west migration of rainbands that drives hourly isotopic variations through local rainout processes. The smaller magnitude of the shifts in δ¹⁸O_p at San Antonio compared with Austin might be due to either a dilution effect during the moisture transport or a substantially weaker local rainout effect associated with lighter rainfall when rainbands passed by San Antonio. However, the large negative spikes in d-excess_p are absent in the San Antonio dataset; instead, there is only a slight decrease of ~3‰ in d-excess_p values between 0900−2200 CDT on August 26 (Supplementary Fig. 2). One possible explanation could be that as the processes driving these exceptionally negative d-excess values are microphysical, vapor d-excess values in the atmosphere are heterogeneous, and these spurious signals are homogenized or dispersed during the moisture transport from Austin to San Antonio. Alternatively, as the rainbands migrated to San Antonio, the shift to a predominance of light stratiform rainfall and less well-defined rainbands was unable to sustain extensive WRF condensation, and as a result, did not produce large negative spikes in d-excess. If there were isotope measurements from localities to the east of San Antonio, which would not have been impacted by downstream moisture from Austin, it would allow us to separate the impact of these two mechanisms. Therefore, future studies should consider sampling high-resolution rainwater at multiple sites to better understand the local vs. upstream processes in controlling high-frequency isotopic variations.

Implications for paleo TC reconstructions

Our data show that the rainwater δ¹⁸O_p values of Hurricane Harvey were substantially more negative than the mean annual and mean August δ¹⁸O_p values in this region. However, whether it could produce a significant anomaly in the annually integrated rainwater isotopic values, which might be recorded in high-resolution paleoclimate records, is less clear. To assess the relative isotopic impact of Hurricane Harvey on annually-averaged precipitation isotope values (i.e., Δδ¹⁸O), we compare the mean annual δ¹⁸O_p with and without Hurricane Harvey using the SWING2 isotope-model data³⁶ and the gridded Hurricane Harvey δ¹⁸O_p (see the “Methods” section).

As expected, our calculations demonstrate that hurricane Harvey generated isotopically depleted rainfall over a large region of the southern US (Fig. 6a). However, the total impact of Harvey on the annual isotope signal depends on the δ¹⁸O value of the storm, the amount of precipitation that fell during the storm, and the mean annual rainfall occurring in a given location. Based on the ensemble mean of SWING2 models, the mean annual precipitation at Austin, San Antonio, and Houston are approximately 900, 850, and 1100 mm per year, respectively; the mean annual δ¹⁸O_p are −5.3‰, −5.3‰, and −4.7‰, respectively. We calculate that Hurricane Harvey dumped 171, 53, and 758 mm of precipitation at these three sites, with amount-weighted mean δ¹⁸O_p values of −9.7‰, −9.7‰ and −8.0‰, respectively. Taken together, Hurricane Harvey would shift the annual mean isotopic values by −0.7‰, −0.3‰, and −1.3‰ in Austin, San Antonio, and Houston, respectively. In the core region of Hurricane Harvey precipitation over southeastern Texas, we calculate that the isotopic value of mean annual rainfall is shifted by up to −2‰ due to the incorporation of highly depleted rainfall during the hurricane event (Fig. 6b). This shift exceeds 2σ of annual δ¹⁸O_p in this region and should be evident in high-resolution proxy datasets³⁷. However, over San Antonio and the Mississippi Valley, the total precipitation that fell during Harvey is small relative to the mean annual precipitation, such that it is unlikely to produce an anomaly that is likely to be visible in an annually integrated proxy record (|Δδ¹⁸O_p|< 0.3‰; Fig. 6b). Thus, while the isotopic signature of large TC events can be significant, particularly in semi-arid regions, the anomaly will be relatively restricted spatially to the region associated with the core of the cyclone-induced rainfall anomaly. Furthermore, these calculations highlight the need for proxy records with annual or higher resolution when attempting to reconstruct hurricanes; in records with longer temporal averaging, the hurricane signature will be even more muted. In addition, the preservation potential of such a signal is proxy-specific and is subject to factors such as variability in soil moisture and surface- and groundwater hydrology associated with a given proxy^38,39. To further constrain the robustness and limitation of the isotope approach as a paleotempestology proxy, proxy-specific studies in the future are needed which will focus on how well TC signals are preserved in different proxy systems.

Fig. 6: Isotopic impact of Hurricane Harvey on mean annual rainfall.

a Estimated δ¹⁸O_p values in Hurricane Harvey rainfall (shadings; see the “Methods” section). The contours indicate mean annual precipitation (unit: mm) across this region estimated using the multi-model ensemble mean of SWING2 models. b The difference between the mean annual δ¹⁸O_p precipitation with and without Hurricane Harvey (Δδ¹⁸O_annual). The stars indicate the rainwater sampling sites in this study.

Conclusions

In this study, we investigate the mechanisms of isotopic variability during Hurricane Harvey (2017) using rainwater collected in Austin, San Antonio, and Houston. We demonstrate that event-long trends in rainfall δ¹⁸O values are predominantly controlled by upstream rainout and Rayleigh distillation along the moisture transport pathway. Since moisture near the hurricane eye generally had experienced more rainout, the upstream rainout control explains the observation of previous studies that the δ¹⁸O_p values are consistently more negative near the eyewall. In our compilation of existing TC isotope data, upstream rainout shows a strong correlation with δ¹⁸O_p in the majority of these TCs, suggesting that upstream rainout is the control on the low-frequency isotopic variability during most TCs. However, our analysis using a compilation of existing isotope data of tropical cyclone precipitation also suggests that when the relative humidity is low, isotopic changes due to re-evaporation could potentially dominate the isotopic signals in collected rainwater. Our data also exhibit relatively large high-frequency shifts in the hourly δ¹⁸O_p and d-excess_p values during the storm. While local rainout in rainbands explains the negative shifts in δ¹⁸O_p as rainbands passed by, the positive shifts in δ¹⁸O_p and negative shifts in d-excess_p that preceded them could be best accounted for by microphysical condensation processes associated with the WBF condensation. Lastly, we estimated the impact of Hurricane Harvey on annually integrated isotopic values of precipitation in order to assess whether water isotope-based approaches can be used to study paleotempestology. While a TC like Hurricane Harvey can produce a large amount of isotopically depleted rainwater over a relatively large region, whether the signal can be detected in annually resolved biogeological archives depends on the isotopic values of the storm, the total precipitation amount from the storm, and the mean annual precipitation amount. Thus, we suggest that caution should be exercised when employing the isotopic method to study paleotempestology.

Methods

Sample collection and isotope measurement

Rainwater samples were collected hourly in Austin (30.30°N, 97.73°W, n = 50) and San Antonio (29.58°N, 98.62°W, n = 29), and sub-daily in Houston (30.08°N, 95.35°W, n = 14). To collect, a bucket was placed ~1 m above ground in an uncovered area. The collected rainwater was transferred to a 2 ml glass vial using a clean glass pipette and the vial was capped immediately after collection. Minimal headspace was allowed in glass vials in order to avoid evaporation. The glass vials were stored in a refrigerator at 4 °C before isotope analysis. The buckets were emptied and wiped dry before being used again. Two buckets were used to alternate between hourly collection. In addition, we also collected a total of 119 rainwater samples in Austin at 10 min resolution on August 26 using another set of exactly the same apparatus, which yielded consistent results with hour parallel hourly sampling (Supplementary Fig. 1). In Houston, the first two samples were collected from a nearby creek because the hazardous weather condition prevented us from setting up the collection system. We use these two samples to approximate the integrated rainwater isotopic composition.

The isotope (δ¹⁸O and δ²H) measurements of rainwater samples from Austin and Houston were performed on a Picarro L2130‐i Liquid Water Analyzer at the University of Texas at Austin¹⁶. The isotope measurements of samples from San Antonio were measured using a Picarro L2130-i Water Isotope Analyzer at the University of Texas at San Antonio. Each sample was injected ten times with autosamplers and was analyzed using High Precision mode. The first two injections were discarded in order to remove the isotopic memory effects of the instrument. The average of the remaining eight measurements is reported here. A standard (δ¹⁸O = −0.23‰, δ²H = −5.01‰) calibrated against IAEA Water Standards GISP, SLAP, and VSMOW2 was inserted in the beginning, the middle, and the end of each run to correct for the intercept of the calibration equation of the instrument. Three additional in‐stock water samples of known isotope composition (δ18O = −6.58‰, −8.61‰, and −9.31‰, respectively; δ²H = −43.34‰, −59.34‰, and −63.03‰, respectively) were analyzed as check standards along with each run to verify the adjusted calibration. The analytical precision is better than 0.1‰ for δ¹⁸O and 1‰ for δ²H. δ¹⁸O and δ²H are reported in per mil (‰) relative to the standard Vienna Standard Mean Ocean Water (VSMOW). The delta notion of isotopic values is defined as:

$${{{{{{\rm{\delta }}}}}}}^{18}{{{{{{\rm{O}}}}}}}=[({\,}^{18}{{{{{{\rm{O}}}}}}/}^{16}{{{{{{\rm{O}}}}}}})_{{{{{{\rm{Sample}}}}}}}{/}({\,}^{18}{{{{{{\rm{O}}}}}}/}^{16}{{{{{{\rm{O}}}}}}})_{{{{{{\rm{VSMOW}}}}}}}-1]\times {10}^{3}{\, \% }_{0}$$

(1)

$${{{{{{\rm{\delta }}}}}}}^{2}{{{{{{\rm{H}}}}}}}=[({\,}^{2}{{{{{{\rm{H}}}}}}/}^{1}{{{{{{\rm{H}}}}}}})_{{{{{{\rm{Sample}}}}}}}{/}({\,}^{2}{{{{{{\rm{H}}}}}}/}^{1}{{{{{{\rm{H}}}}}}})_{{{{{{\rm{VSMOW}}}}}}}-1]\times 10^{3}{\, \% }_{0}$$

(2)

and the deuterium-excess (d-excess) measuring the relative enrichment of deuterium and ¹⁸O is defined as:

$${{{{{\rm{d}}}}}}{\mbox{-}}{{{{{\rm{excess}}}}}}={{{{{{\rm{\delta }}}}}}}^{2}{{{{{\rm{H}}}}}}{\,-\,}8\times {{{{{{\rm{\delta }}}}}}}^{18}{{{{{\rm{O}}}}}}$$

(3)

Meteorological data

The Multi-Radar/Multi-Sensor System (MRMS) was used to estimate the precipitation rate and precipitation type during Hurricane Harvey. MRMS ingests the US National Weather Service WSR-88D doppler radar network and Canadian radar network, along with commercial and US Terminal Doppler Weather Radar, providing 0.01° × 0.01° fields of precipitation rate and precipitation type at 2 min resolution⁴⁰. MRMS’s precipitation type data separate convective and stratiform precipitation following the algorithm described in⁴¹. To calculate the precipitation rates at our sites, we calculated the averages of precipitation rates in three 0.1° × 0.1° boxes centered around our Austin, San Antonio, and Houston sampling locations, respectively.

We also used the hourly observational weather data from the Austin Camp Mabry weather station, San Antonio International Airport weather station, and Houston George Bush Intercontinental Airport weather station. The hourly precipitation measured at these stations is consistent with the radar-derived rainfall. Here, we used the weather station data to assess the impacts of temperature, relative humidity, surface pressure, and wind speed on rainwater isotopic ratios.

HYSPLIT backward trajectory modeling

In order to evaluate the influence of moisture transport history, we performed backward trajectory analyses using the Hybrid Single-Particle Lagrangian Integrated Trajectory (HYSPLIT) model software⁴². A Python-based function PySPLIT⁴³ was used to operate the HYSPLIT software which mass-generates trajectories in batches. We used the 40 km Eta Data Assimilation System (EDAS) data covering the Contiguous US as the meteorological data input. For other TCs considered in this study that occurred outside of the Contiguous US, we used the 1° resolution Global Data Assimilation System (GDAS) data, which has global coverage. The results yielded from these two datasets for Hurricane Harvey exhibit a strong correlation with each other (r = 0.47, p = 0.0005), suggesting a relatively small impact of using different datasets for the sake of our analysis. 72 h backward trajectories were generated hourly throughout each event, with end elevation being 500, 1000, 2000, …, 8000, 9000 m above the ground.

HYSPLIT reports meteorological parameters alongside the spatial location (latitude, longitude, elevation) of airmass at a certain point. We calculated the rainout along trajectory by summing the total precipitation amount along each trajectory. To account for moisture in the entire air column, we calculated the weighted mean values of upstream rainout based on the specific humidity at each level:

$${{{{{{\rm{UR}}}}}}}_{\left({{{{{\rm{t}}}}}}\right)}=\frac{\mathop{\sum }\limits_{l=1}^{10}{q}_{(t,l)}\mathop{\sum }\limits_{n=1}^{72}{P}_{(t,l,n)}}{\mathop{\sum }\limits_{l=1}^{10}{q}_{(t,l)}}$$

(4)

where UR is the vertically specific humidity-weighted 72 h total upstream rainout, q is the specific humidity at a certain altitude, P is the hourly precipitation amount at a certain upstream location. t indicates the time at the sampling site. l indicates the altitude at the sampling site, including 10 levels (500, 1000, 2000, …, 9000 m above ground level). n indicates the number of hours prior to the arrival of the vapor at our sampling location.

SWING2

To compare the isotopic data from Hurricane Harvey to mean annual precipitation isotopic values, we used the ensemble mean of the Stable Water Isotope Intercomparison Group Phase 2 (SWING2) model data, which reports precipitation and isotopic composition of precipitation modeled by a set of different isotope-enabled general circulation models³⁶. The ensemble of these model simulations accurately reproduces the precipitation amount across this region, and the modeled isotopic ratios are comparable to the previously reported rainwater isotope data in central Texas^16,19.

Computing the annual isotopic anomaly associated with Harvey

To assess the potential isotopic signature of Hurricane Harvey that might be seen in an annually integrated paleoclimate stable isotope record, we first calculated the temporal evolution of rainfall δ¹⁸O values at each grid cell based on the migration of the hurricane eye and a transfer function based on the relationship between δ¹⁸O and distance to the eye (Fig. 3a). The event-integrated mean isotopic values at each grid cell were calculated through amount-weighting the hourly δ¹⁸O values by the gridded hourly precipitation data from the North American Land Data Assimilation System (NLDAlS)⁴⁴. We recognize that this reproduction of spatial rainwater δ¹⁸O values of Hurricane Harvey (Fig. 6a) may not necessarily be accurate since the relative distance to the eye is not a mechanistic control on isotopic values, as we discussed in the earlier text. This δ¹⁸O_p map for Hurricane Harvey likely underestimated the true isotopic depletion at the later stage when the system shifted northeastward into the Mississippi Valley, where the oceanic moisture source was cut off from the storm. Therefore, we think this approach could provide a conservative estimate of Harvey δ¹⁸O_p, which is valuable for assessing the isotopic impact of the hurricane.

To assess the relative isotopic impact of Hurricane Harvey on annually averaged precipitation isotope values, we combined the SWING2 climatological isotope values and our gridded Harvey δ¹⁸O_p values. We first calculated a gridded map of amount-weighted mean annual δ¹⁸O_p (δ¹⁸O_annual). We then compared the mean annual δ¹⁸O_p with and without Hurricane Harvey, which allows us to quantify the annually integrated stable isotope anomaly (Δδ¹⁸O_annual) value associated with the Hurricane Harvey storm event (Fig. 6b).

$$\triangle {{{{{{\rm{\delta }}}}}}}^{18}{{{{{{\rm{O}}}}}}}_{{{{{{\rm{annual}}}}}}}=\frac{{{{{{{\rm{\delta }}}}}}}^{18}{{{{{{\rm{O}}}}}}}_{{{{{{\rm{annual}}}}}}}\times \,{P}_{{{{{{\rm{annual}}}}}}}+{{{{{{\rm{\delta }}}}}}}^{18}{{{{{{\rm{O}}}}}}}_{{{{{{\rm{Harvey}}}}}}}\times {P}_{{{{{{\rm{Harvey}}}}}}}\,}{{P}_{{{{{{\rm{annual}}}}}}}+{P}_{{{{{{\rm{Harvey}}}}}}}}-{{{{{{\rm{\delta }}}}}}}^{18}{{{{{{\rm{O}}}}}}}_{{{{{{\rm{annual}}}}}}}$$

(5)

where δ¹⁸O_annual is the amount-weighted mean annual δ¹⁸O_p at each grid, P_annual is the mean annual precipitation amount at each grid, δ¹⁸O_Harvey is the amount-weighted mean δ¹⁸O_p from Hurricane Harvey at each grid, and P_Harvey is the total precipitation amount from Hurricane Harvey at each grid.