Introduction

Wind-driven ocean general circulation, organized by 100–1000-km gyres and 10–100-km mesoscale eddies, transfers its energy mostly to larger scale, arresting the downscale energy cascade to smaller scale where it can be dissipated to heat. Assuming stationarity, the power input to general circulation by the winds at ~1 TW must be dissipated at the same rate1,2. Using theories and numerical models, potentially important energy sinks have been proposed along the major ocean currents close to the bottom boundary3,4,5,6,7,8,9,10,11,12,13. A geostrophic current over the topography can radiate lee waves extracting energy from the general circulation to turbulent dissipation, which is estimated to account for the global energy sink as large as 0.15–0.23  TW3. Observations found elevated eddy diffusivity near the bottom over the horizontal distance of 2000–3000 km across the Antarctic Circumpolar Current flowing over the rough topography13. However, because the radiated lee waves can be reabsorbed into the large-scale circulation14, how far this elevation continues away from the topographic features toward the downstream is unclear. Recent in situ observations in the Southern Ocean reported the lee waves propagating in the Drake Passage over the rough topography, consistent with the linear internal-wave theory3, although the depth-integrated energy dissipation rates are two orders of magnitude smaller than the vertical internal-wave energy flux15, implying that a large fraction of lee wave energy is not dissipated locally.

On the other hand, recent high-resolution numerical studies have revealed that the Gulf Stream6 and the California Undercurrent5,7 flowing over the continental slope can alter the sign of the Ertel’s potential vorticity (PV) on their anticyclonic side, leading to a submesoscale inertial–symmetric instability and associated inevitable forward energy cascade and dissipation16. These processes are found to form widespread submesocale coherent vorticities10, which are considered to play a very important role in transporting matters5. The global energy sink caused by this mechanism is estimated to be 0.01–0.1 TW6. In the Southern Ocean, several observational studies showed that an abyssal boundary current flowing along the continental slope can turn the sign of PV11,12, which coincides with the strong turbulence11. This instability can be expected not only along the continental slope but also for other regions of the world ocean, where the subinertial surface currents and the undercurrents encounter steep bottom slopes of isolated seamounts or islands. Indeed, this is the case for the Kuroshio because throughout its path it flows through a chain of islands and over numerous ridges and seamounts, such as the I-Lan Ridge east of Taiwan, the Tokara Strait south of Kyushu, Japan, and the Izu-Ogasawara Ridge south of Tokyo17. However, whether this turbulence generation mechanism through the submesoscale flows near the bottom can really be important remains unclear due to the lack of sufficient observational evidence11,12. The negative PV generated over the steep slopes of the seamounts in the strong subinertial currents such as the Kuroshio could form streaks of mixing hotspots. If this is the case, the enhanced turbulence may continue farther downstream fueled by both lateral and vertical geostrophic shear18 than that induced locally by lee waves alone.

Regardless of the mechanisms, the strong turbulence caused by the flow over the topography can induce vertical mixing of water and tracers, including nutrients that are required for phytoplankton growth and CO2 uptake19. Because the dark subsurface layers of the Kuroshio are nutrient rich20,21,22,23, similar to the Gulf Stream24,25, subsurface mixing along the path of the Kuroshio can inject nutrients to sunlit surface layers. Recent microstructure observations in the Tokara Strait upstream Kuroshio region show very strong turbulent kinetic energy (TKE) dissipation rates >O(10–7 W kg–1)26,27. Using a tow-yo microstructure profiler, it has been shown that the strong turbulent layers form banded coherent structures clearly associated with the high vertical wavenumber near-inertial internal waves27,28. Although the near-inertial internal waves can be generated mostly by winds29, it is not clear why and how the vertical wavenumber and amplitude of the near-inertial waves seen in this region are so large. One of the several hypotheses is that the disturbances, including lee waves generated by the Kuroshio over topographic features, trigger inertial oscillations in the bottom layers4,30,31, which can radiate near-inertial waves vertically in the stratified layers above and below.

In this study, turbulence data and fine scale density and velocity data obtained from three different cruises in the Kuroshio flowing through the Tokara Strait using a tow-yo microstructure profiler were analyzed. One of the surveys was conducted in November 2017 along the Kuroshio from its upstream to the downstream across the entire Tokara Strait. Two additional tow-yo surveys were also carried out in June 2018 and November 2019 focusing the region near the Hirase submarine rise in the Tokara Strait. In addition to the in situ observations, high-resolution numerical simulations were conducted to elucidate the detailed mechanisms responsible for the observed strong turbulence, reproducing the observed flow fields. Objectives of this study are to quantify the turbulent mixing intensity along the Kuroshio over the long distance across the Tokara Strait, to elucidate whether and how the PV affects the observed turbulent mixing, and to understand the cause of the high vertical wave number near-inertial internal waves and their interaction with the submesoscale flows in the Tokara Strait.

Results

Near-inertial internal waves

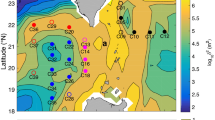
In this study, an intensive set of tow-yo microstructure surveys was conducted during November 12–21, 2017 along the Kuroshio axis from the upstream to the downstream side across the Tokara Strait (Fig. 1f). Isopycnal depressions and jumps are seen while the Kuroshio passes over the steep seamounts, which are suggestive of lee waves (Fig. 1b, c). The steepness parameter εs = Nh/U, where N is the buoyancy frequency and h the height of the seamount is ~2–4 with U ~1 m s–1, N ~10–2 s–1, and h ~200–400 m, suggesting that lee waves could be highly nonlinear and likely to break into turbulence4. The vertical shear of the horizontal current measured using a shipboard Acoustic Doppler Current Profiler (ADCP) reveals that the high vertical wavenumber shear nearly along the isopycnal is clearly amplified near the seamounts in the Tokara Strait (Fig. 1) by a factor of five in its variance (Supplementary Fig. S1a–e). The angles of these shear layers are much closer to that of a ray path with a near-inertial frequency than that with a M2 semi-diurnal tidal frequency (Fig. 1c and Supplementary Fig. S2). Hodographs of the vertical shear show anticlockwise and clockwise rotations with depth (Supplementary Fig. S3a, b), suggesting that the high vertical wavenumber shear is associated with upward and downward propagating near-inertial internal waves (Supplementary Fig. S3c, d). The ADCP observations near the seamounts reveal that the vertical shear of this highly complex flow is dominated by the near-inertial waves.

Fig. 1: Back-rotated shear (s–1) measured by shipboard ADCP during the November 2017 cruise.
figure 1

Back-rotated shear (s–1) for (a) Leg a, (b) Leg b, (c) Leg c, (d) Leg d, and (e) Leg e along the Kuroshio axis. Contours indicate isopycnals. The internal-wave ray paths computed assuming quiescent condition are shown in (c) for a near-inertial internal wave with frequency 1.05f as cyan lines and M2 internal tide as a black line. Seamount topography in the Tokara Strait is shown as black in (b, c). Location of the five legs of the transect observations is shown in (f); contours are average sea surface height (m) during the observations (available from Copernicus Marine Environment Monitoring Service, http://marine.copernicus.eu) and color shading shows bottom topography (m). Topography data are ETOPO1 blended with the 500-m mesh data available from the Japan Oceanographic Data Center, https://www.jodc.go.jp/jodcweb/. The map is created with MATLAB R2019b Mapping Toolbox.

Full size image

100-km-wide 100–1000-fold enhanced turbulence

Considering the typical TKE dissipation rates ε in the open water thermocline ~O(10−10 W kg−1), the tow-yo microstructure data near the seamounts in the Tokara Strait show 100–1000-fold enhancements of the ε with the values, 10−8–10−7 W kg−1 (Fig. 2b, c and Supplementary Fig. S1l, m). Some of these elevated dissipation rates coincide with the large-amplitude near-inertial internal waves (Fig. 1b, c). It should be noted that the lateral extent of the strong turbulent layer is very large, over 100 km across the Tokara Strait, with a vertical thickness >200 m (Fig. 2b, c). In Leg d, which is ~150 km further downstream from Leg c in the Tokara Strait (Fig. 1f), the subsurface dissipation rates and amplitudes of internal-wave shear still show relatively large values (Figs. 1d and  2d and Supplementary Fig. S1d, n). The average dissipation rates in upper 100 m are >O(10–7 W kg–1) over 65 km and >O(10–8 W kg–1) over 100 km in the Tokara Strait (Supplementary Fig. S1l, m). Using the Osborn method32, the average vertical eddy diffusivity below 100 m depth is O(10–4–10–3 m2 s–1), which is also 10–100 times larger than the typical background values ~O(10–5 m2 s–1) (Supplementary Fig. S1q, r). The lateral scale of the very strong turbulent layer of ~100 km is much greater than that of the lee waves of ~5–10 km. The turbulent eddy turnover time scale \({t}_{l}={\left({L}^{2}/\epsilon \right)}^{1/3}\,\) is estimated to be 30–80 min, assuming the largest turbulent eddy scale L ~100 m and a range of observed ε ~10–7–10–6 W kg–1. With advection by the Kuroshio at U ~1 m s–1, the turbulence would persist only a few kilometers downstream, so this is inconsistent with the observed long persisting turbulence of ~100 km.

Fig. 2: Measured turbulent kinetic energy dissipation rates.
figure 2

Turbulent kinetic energy dissipation rates ε (log10 W kg–1) for (a) Leg a, (b) Leg b, (c) Leg c, (d) Leg d, and (e) Leg e. Contours represent isopycnals as in Fig. 1. Seamount topography in the Tokara Strait is shown as black in (b, c).

Full size image

Modeling of the Kuroshio over seamounts

To investigate the detailed mechanisms of large-scale turbulence and near-inertial waves in the Tokara Strait, a nested high lateral resolution (~500 m) Regional Oceanic Modeling System (ROMS)33 was employed with climatological surface forcing and no tidal forcing. The model reproduces a realistic amplitude and path of the Kuroshio in the Tokara Strait (Supplementary Fig. S4). When the modeled Kuroshio flows over seamounts in the Tokara Strait, isopycnal displacements occur similar to the observations (Fig. 3c). Interestingly, the modeled vertical shear is amplified near the seamounts and dominated by coherent bands of high vertical wavenumber shear, which lie coherently along the isopycnal direction (Fig. 3b, c). Further, the amplitude and vertical wavenumber of the modeled shear are consistent with the observations (Fig. 1b, c). The Lagrangian frequency spectra computed to avoid Doppler smearing suggest that the frequency of the waves is near inertial (Supplementary Fig. S5). Wind energy flux into the inertial oscillation is very small during the observations and is not enhanced when the observations near seamounts (Legs b and c) were conducted (Supplementary Fig. S6), where the elevated amplitudes of the near-inertial internal waves were observed (Fig. 1b, c). Accordingly, these model results without tidal forcing suggest that the Kuroshio over the seamounts in the Tokara Strait is the most likely source of the large-amplitude near-inertial waves of high vertical wavenumber. The modeled PV shows the von Karman-like vortex street after having streaks of negative and positive values along the stream over a 50-km width originating from the northeastern and southwestern slopes of the seamounts, respectively, in the Kuroshio in the regions near the in situ observation lines (Fig. 3a, d, e). These model results still hold even when realistic tidal forcing is considered (Supplementary Figs. S7 and S8e–h). Although the model cannot resolve the inertial–symmetric instability5,6,7,8,9,34 and associated secondary Kelvin–Helmholtz (K-H) instability16, the modeled streaks of negative PV near the observation sites would explain why the turbulence in the observations is strong and long persisting (Supplementary Fig. S9).

Fig. 3: Model vertical shear and potential vorticity.
figure 3

Model results after 20 days are shown for (a) plan view of the potential vorticity at 200 m depth (10–8 m–1 s–1), for (b, c) vertical sections of the vertical shear of zonal velocity (s–1), and (d, e) vertical sections of the potential vorticity (10–8 m–1 s–1). The vertical sections shown in (b, e) are along the blue line in (a), and those in (c, d) are along the red line in (a). Contours in (a) are sea surface height (m) and contours in (b–e) represent isopycnals at every 0.5 kg m–3. Model topography is shown as black in (b–e). The boundary of black shapes indicates 200-m isobath in (a). The box with the dashed black line represents the region of the observation during June 2018 shown in Figs. 4–6, and the white–black lines indicate the ship tracks for Leg b and Leg c in observation of November 2017 shown in Figs. 1 and 2.

Full size image

The ADCP Richardson number Ri during the November 2017 cruise shows values as low as Ri ~1 (Supplementary Fig. S10), where the strong turbulence is observed in Legs b–e (Fig. 2b–e). Because PV2D is negative when f/(f + vx) > N2/(vz)2 (see “Methods”), the Ri ~ 1 corresponds to PV ~ 0 in the case without the lateral shear, supporting the above speculation that strong long-persisting turbulence is fueled by the negative PV.

Observations of negative PV

The model results suggest that the generation of the negative PV at the northeastern bottom slope of the seamounts in the upstream Kuroshio is a plausible source of the strong turbulence observed over the large lateral scale ~O(100 km) caused by inertial–symmetric instability5,6,7,8,9,34 and associated secondary K-H instability16. However, a critical evidence that the negative PV is related with the strong turbulence has not been established by the observations presented thus far. To fill this gap, the ADCP and tow-yo microstructure observations were repeated in June 2018 near the Hirase submarine rise in the Tokara Strait (Figs. 3a and 4). The observations show that the absolute vorticity (Fig. 4) and the two-dimensional PV2D (see “Methods”) become negative on the northeastern lee of the seamount (Fig. 5a, b), which are clearly correlated with the very large turbulent dissipation rates of >O(10−6 W kg−1) (Fig. 5c, d). There are some exceptional data of large turbulent dissipation rates even with positive PV2D on the southwestern side, where large cyclonic vorticity is formed (Figs. 4 and 5c). The coarse resolution ADCP-8-m Richardson number Ri shows relatively low values in this region (Supplementary Fig. S11), suggesting that vertical shear could be strong enough to trigger K-H-type shear instability, while PV stays positive with strong positive cyclonic vorticity (even larger \({\varsigma }_{z}^{{abs}}/f\); see Thomas angle34 in “Methods”). The bin-average TKE dissipation rates as a function of PV and Ri show that both the low PV and low Ri are associated with the large TKE dissipation rates (Fig. 6c, d). However, it is also shown that extremely large dissipation rates of O(10−5 W kg−1) are accompanied by the negative PV and Ri~1 rather than smallest Ri, while slightly more moderate but still very large dissipation rates of O(10−6 W kg−1) can also be associated with positive PV but with relatively small Ri (Fig. 6b). These results suggest that the extremely strong turbulence occurs even with Ri ~ O(1) in the streak of the negative PV extending from the northeastern slope of the seamount, while strong turbulence can also be generated when Ri is small enough even with positive PV on the southwestern slope of the seamount. The Thomas angle34 \(\Phi\) (“Methods”) shows that the strong turbulence with negative PV2D is associated with a range of \(\Phi\) (Fig. 6a), suggesting that the energy dissipation occurs through both the lateral and vertical shear of the Kuroshio. However, the absolute vorticity in the vicinity of the seamount is much smaller ~−2f (Fig. 4) compared with the case discussed in the previous study34 ~+0.4f, implying that lateral shear of the Kuroshio is a very important source of the instability in our case. The slope Burger number35, -vx/f Ri is positive with vx/f ~−3, and Ri ~1, implying also the dominant source of the instability to be lateral shear18.

Fig. 4: Current velocity and absolute vorticity near Hirase submarine rise in the Tokara Strait during the June 2018 cruise.
figure 4

The average upper 200 m current is shown as vectors along the ship track, and color indicates absolute vorticity (f + vx − uy)f –1 computed using the optimal interpolation of measured velocity with decorrelation length of 50 km, where f is the Coriolis parameter, v and u are meridional and zonal velocity, respectively, and subscripts x and y are derivatives along the zonal and meridional directions, respectively. Contours represent the topography (m).

Full size image
Fig. 5: Observed two-dimensional potential vorticity and dissipation rates during June 2018 cruise.
figure 5

The vertical section of the two-dimensional potential vorticity PV2D (10–8 m–1 s–1) computed with the geostrophic vertical shear (Eq. (4) in “Methods”) around Hirase submarine rise is shown in (a, b), and the measured turbulent kinetic energy dissipation rates (log10 W kg−1) are shown in (c, d). The vertical sections in (a, c) are along the red line in Fig. 4, and those in (b, d) are along the blue line in Fig. 4. Contours in (a–d) represent isopycnals. The white contours in (c, d) are at PV = 0.

Full size image
Fig. 6: Relation between observed dissipation rate and potential vorticity and Richardson number.
figure 6

a Average dissipation rates as a function of potential vorticity (PV2D) and Thomas angle34 Φ. b Average dissipation rates as a function of potential vorticity (PV2D) and ADCP Richardson number. (c) Average dissipation rate as a function of potential vorticity (10–8 m–1 s–1) and d ADCP Richardson number. Error bar shows 95% confidence interval obtained by the bootstrap method. The average is not shown for the data with only one sample in (c, d).

Full size image

Although two-dimensional PV shows that the negative PV2D values are accompanied by the large TKE dissipation rates, the PV2D can also be contaminated by the internal waves. Accordingly, another set of tow-yo surveys were repeated near the same Hirase submarine rise in the Tokara Strait during November 2019. In this cruise, the Underway-conductivity-temperature-depth (Underway-CTD) was deployed to obtain three-dimensional density distribution, and flow field was measured by the shipboard ADCP prior to the turbulence measurements. These density and velocity data are mapped onto the grid with the lateral decorrelation scale of 70 km, which are then used to compute three-dimensional PV (Fig. 7). The PV shows similar patterns to the absolute vorticity during June 2018 cruise, where negative and positive values extend toward the downstream direction from the northeastern and the southwestern slopes, respectively (Fig. 7). The TKE dissipation rates measured from eastern (leg 1) and western slopes (leg 2) to the downstream regions show strong heterogeneity in their magnitudes, varying by 3 orders of magnitude within a few tens of kilometers (Fig. 8). The larger dissipation rates are found in the subsurface layer below 150 m depth on the eastern side of the rise in the leg 1 (Fig. 8a), which are accompanied by the negative PV values in the same region and depths (red line in Fig. 7c, d). The large dissipation rates in the upper 100 m in the southern section of leg 1 (Fig. 8a) also coincide with the negative PV (red line in Fig. 7a, b). The correspondence between large dissipation rates and negative PV is similarly found in leg 2. Again, similar to the June 2018 cruise, the average TKE dissipation rates as a function of PV for both legs show that the larger dissipation rates are found with the smaller PV, especially for leg 2 (Fig. 9). For leg 2, this tendency is unchanged with the PV computed using the geostrophic vertical shear, while this tendency disappears for the leg 1 (Fig. 9). Similar to the observations in June 2018, the averaged dissipation rates, however, show a slight increasing trend toward larger positive PV too (blue line of Fig. 9), reflecting the strong turbulence found even with the large positive PV on the cyclonic side of the seamount. In the region very close to the topographic features, the previous studies pointed out that vorticity tilting can result in enhancement of the vertical shear and associated turbulence36,37. By computing the magnitudes of stretching and tilting terms of vorticity, it is shown that the vorticity stretching and tilting can enhance or reduce the vertical shear to change Ri rapidly (Supplementary Fig. S12). The magnitudes of these terms are especially large at 100 m depth both on the northeastern (anticyclonic) and southwestern (cyclonic) slopes of the seamount, whereas the relatively larger magnitude is found only on the cyclonic side at 200 m depth. The deeper extent of the vertical shear strengthening or weakening on the cyclonic side of the seamount caused by the vorticity stretching and tilting is consistent with the large dissipation rates with the low Ri but large positive PV on the cyclonic side. Note, however, that the largest dissipation rates are more associated with the negative PV rather than smallest Ri (Fig. 6a, b).

Fig. 7: Observed three-dimensional potential vorticity during November 2019 cruise.
figure 7

Three-dimensional PV (Eq. (3) in “Methods”) sliced at (a) 50, (b) 100, (c) 200, and (d) 300 m depths (10–9 m–1 s–1). Solid lines indicate UVMP observation lines for (red) leg 1, starting from eastern side of the Hirase submarine rise toward south and southwestward, and (blue) leg 2, starting from western side of the rise toward south and southeastward. The broken black line indicates the ship track for the UCTD observations.

Full size image
Fig. 8: Measured turbulent kinetic energy dissipation rates during November 2019 cruise.
figure 8

Measured dissipation rates (log10 W kg−1) for (a) leg 1 along the red line in Fig. 7 and for (b) leg 2 along the blue line in Fig. 7.

Full size image
Fig. 9: Relation between measured dissipation rates and potential vorticity during November 2019 cruise.
figure 9

Average turbulent kinetic energy dissipation rates (log10 W kg−1) measured during November 2019 cruise as a function of PV (10–9 m–1 s–1). Solid lines are PV (Eq. (3) in “Methods”) computed with the vertical shear of the lateral velocity measured by the ADCP data with error bars, 95% confidence interval for (red) leg 1 and (blue) leg 2. Thin solid lines are PV computed with the geostrophic vertical shear (see “Methods”).

Full size image

Discussion

These results from the observations and associated numerical model provide evidence that the PV associated with the submesoscale flows in the Kuroshio near the seamounts profoundly affects the spatial heterogeneity of the microscale turbulent mixing and energy dissipation. Although our observations and the numerical simulations cannot resolve all the scales from larger scales to the submesoscale instability and the associated microscale turbulence at once, the correspondence between the negative PV at submesoscales and the large turbulent dissipation rates at microscales suggests that the negative PV generated on the steep slopes of the seamounts and associated inertial–symmetric instability followed by the K-H instability are the most plausible sources of the observed 100-km-wide 100–1000-fold enhancement in turbulent dissipation rates along the Kuroshio across the Tokara Strait (Fig. 10). Note that, during the tow-yo turbulence surveys in November 2017, the fortnightly tidal phase was in neap tide for the legs a–c, where the most intense turbulence near the seamounts is observed. Therefore, the observed turbulence level may not be at its highest level.

Fig. 10: Summary schematic of this study.
figure 10

The upstream Kuroshio quasi-steadily flows over shallow topography and seamounts in the Tokara Strait. The steep slope of these bathymetric features can generate negative potential vorticity on their northeastern slopes. Near-field turbulence is generated by lee waves and vorticity tilting/stretching in close proximity (~5–10 km) to the seamounts. Long stretches of persisting turbulence can occur in the negative potential vorticity streaks and its vicinity where the high-vertical wavenumber near inertial waves are generated, with an along stream scale of ~100 km in the downstream direction. As the low PV corresponds to the lowered minimum internal-wave frequency, these generated and/or amplified near-inertial waves can be trapped in the vicinity of the negative PV streaks and induce secondary turbulence. Therefore, the flow of the Kuroshio over seamounts could inherently provide the very efficient mixing hotspots with surprisingly large spatial scale.

Full size image

The surrounding water containing positive PV, next to the unstable negative PV region, allows inertia-gravity waves. Several studies4,30,31 have shown that the disturbances induced by the gravity wave breaking and turbulence in the geostrophic flow can generate inertial oscillations with scales similar to that of the disturbances. The strong turbulence near the seamount associated with the lee waves and negative PV from the bottom boundary layer of ~100 m thickness is, therefore, the likely source of observed high-vertical wavenumber near-inertial internal waves. Because these near-inertial waves inherently have very small group velocities, they do not have much ability to propagate but are mostly advected and trapped near the Kuroshio. Because the low but positive PV near the streak of the negative PV is also associated with the low Ri and the large anticyclonic vorticity (Eqs. (10) and (12) in “Methods”), the minimum frequency of the internal waves38,39,40,41 is anomalously lowered in these low PV regions (Eq. (12) in “Methods”). Therefore, generated and/or amplified high-vertical wavenumber near-inertial internal waves can be trapped in the low but positive PV waters near the negative PV streaks, inducing the secondary turbulence in addition to that caused by the near-field disturbances and the K-H instability associated with the inertial–symmetric instability. This is consistent with the large amplitude near-inertial internal waves and strong turbulence observed around the seamounts in the region of the lowered minimum internal-wave frequency27 and their downstream ~O(100 km) regions along the Kuroshio41 (Figs. 1 and 2). The secondary turbulence caused by vertical high wavenumber near-inertial waves in the low PV water could extend the region of strong turbulence further to the downstream region. Our findings based on the intensive in situ observations with the numerical simulations reveal that the elevated mixing caused by the subinertial flows over the topographic features can continue to extend much farther in downstream regions through the combination of submesoscale inertial–symmetric instability associated with the negative PV streaks and the trapping of the near-inertial waves generated and amplified in the regions of low but positive PV. Although detailed generation mechanisms of the near-inertial waves in the Kuroshio near the seamounts of the Tokara Strait are still not clear, the combined set of the multiscale mixing processes near the bottom of the ocean illustrated by this study shed light on how the subinertial flow over seamounts leads to the turbulent mixing in addition to that caused locally by lee waves alone and demonstrate how the Kuroshio over the seamounts creates large and efficient mixing hotspots (Fig. 10). The inertial–symmetric instability is fueled both by vertical and horizontal velocity shear of the subinertial flows. These mechanisms explain why the resultant turbulence is longer lasting along the Kuroshio than that estimated for the local mixing caused by lee waves. They are also consistent with the recently proposed unified turbulence spectrum model18 interpreting the source of the turbulence observed in geophysical flows to also involve lateral velocity shear, not just vertical shear of internal waves.

In contrast to the surface oligotrophic water, the subsurface Kuroshio is counterintuitively a nutrient stream20,21,22,23, transporting a large amount of nutrients, which are vital for photosynthesis and CO2 uptake by the ocean19. However, these nutrients in the dark subsurface Kuroshio are not available for phytoplankton growth unless they are injected to sunlit surface layers. The vertical turbulent eddy diffusivity estimated by the observations shows enhanced values below 100 m depth, where the Kuroshio nutrient stream forms a vertical gradient of nutrient concentrations20,21,22,23, suggesting that there is a large upward nutrient diapycnal flux to the euphotic zone (uppermost O(100 m) water column) across the Tokara Strait26. Although the symmetric instability grows along isopycnal at most and is considered to be inefficient to mix the water, a recent study42 suggests that the secondary induced systematic ageostrophic flows can extract geostrophic potential energy as much as that for the kinetic energy. Also, the secondary K-H instability can produce vertical billows, inducing diapycnal mixing. Using observed microscale thermal dissipation rates with the simultaneously measured TKE dissipation rates, the mixing efficiency factor Γ can be directly computed (see “Methods”). The obtained mixing efficiency factor shows typical range 0–0.5 even with the negative PV, although there is a tendency of low Γ with relatively low PV and Thomas angle (Supplementary Fig. S13a), suggesting that strong turbulence in the Tokara Strait can destroy stratification and mix the water and tracers vertically. However, it has still been elusive on how much nutrients can be supplied by the turbulent vertical mixing in the geostrophic currents flowing over the topographic features, including the Kuroshio43. This is because the simultaneous measurements of turbulence and nutrient concentrations are still very limited44, calling for more observational and modeling studies in the near future. These submesoscale processes and concomitant mixing are currently missing in the climate models and need to be resolved or well parameterized for better understanding and prediction of the ocean’s response to climate variability.

Methods

Instrumentation and observations

The data used in this manuscript were obtained by the three shipboard observational campaigns conducted in November 12–21, 2017, June 18–24, 2018, and November 16–25, 2019 in the upstream Kuroshio region in the Tokara Strait using the R/T/V Kagoshima maru. The shipboard ADCP (75 kHz 30° beam angle, Ocean Surveyor, Teledyne RDI) measured the horizontal velocity at 80 levels with 16 m vertical bin-size during the November 2017 cruise and 128 levels with 8 m vertical bin-size during the June 2018 and the November 2019 cruises45.

The Underway-VMP (UVMP), which consists of a Vertical Microstructure Profiler 250 (VMP250, Rockland Scientific International, Victoria, B.C., Canada) and an Underway-CTD winch (Teledyne Oceanscience, CA, USA), was used in the study area. The VMP250 carries two shear probes, two FP07 thermistors, a pressure sensor, an accelerometer, and a CTD package. The VMP250 measured temperature, conductivity, and pressure at 64 Hz, turbulent shear, microscale temperature gradient, and acceleration components of the instrument at 512 Hz. The data were used only for the downcast while the VMP250 descended roughly at a quasi-free fall speed of 0.7 m s–1 on average. The tow-yo UVMP observations were conducted with a ship speed relative to the water at 1–2 m s–1. The VMP250 reaches approximately 300 m depth after 7 min, depending on the current, and recovering it to the surface takes about 7–8 min, which enabled us to profile every 15 min with a lateral resolution of 0.9–1.8 km. Above the seamounts with shallower bottom depths, the profiling required shorter duration, and the lateral resolution became correspondingly higher45. During the November 2019 cruise, tow-yo observations using the Underway-CTD were conducted with a ship speed of 3–4 m s−1 to obtain three-dimensional density distribution down to 500 m depth in the downstream region of the Hirase submarine rise in the Tokara Strait45.

Back-rotation of the shear

Velocity and its vertical gradient (vertical shear) caused by the near-inertial internal waves rotate with time. When the observations span over a longer or equivalent time scale to the inertial time scale, the spatial structures of velocity and shear can be aliased by the rotating internal-wave-induced current and shear. To avoid this temporal aliasing, the velocity or velocity shear can be rotated backward or forward in time with respect to the reference time using

$$Z\left({t}_{0}\right)=Z\left(t\right){e}^{i\left(t-{t}_{0}\right)\bar{f}}$$
(1)

where \(Z\left(t\right)={u}_{z}\left(t\right)+i{v}_{z}\left(t\right)\) is the complex variable consisting of observed zonal \({u}_{z}\,\) and meridional shear \({v}_{z}\,\) at arbitrary time t, i is an imaginary unit, \(\bar{f}\) is the mean Coriolis frequency assuming near-inertial internal waves, and resultant \(Z\left({t}_{0}\right)\,\) is the back-rotated shear with respect to the reference time t0.

Potential vorticity

Without friction, Ertel’s PV q is conserved following a fluid parcel, Dq/Dt = 0 where q is

$$q=-\frac{1}{{\rho }_{0}}\left[\left(\frac{\partial w}{\partial y}-\frac{\partial v}{\partial z}\right)\frac{\partial \rho }{\partial x}+\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right)\frac{\partial \rho }{\partial y}+\left(f+\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\frac{\partial \rho }{\partial z}\right],$$
(2)

where \(\rho\) is the density of water and \({\rho }_{0}\) the reference density, u, v, and w are zonal, meridional, and vertical velocities, respectively, and x, y, z are the respective coordinates along the zonal, meridional, and vertical directions. To compute the PV, density measured by the Underway-CTD and horizontal velocity measured by the shipboard ADCP during the observations in November 2019 were optimally mapped on the grid with the lateral resolution of 250 m with the decorrelation scale of 70 km, neglecting vertical velocity in Eq. (2), i.e.,

$${PV}=-\frac{1}{{\rho }_{0}}\left[-\frac{\partial v}{\partial z}\frac{\partial \rho }{\partial x}+\frac{\partial u}{\partial z}\frac{\partial \rho }{\partial y}+\left(f+\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}\right)\frac{\partial \rho }{\partial z}\right],$$
(3)

The PV is obtained using Eq. (3) also in the numerical simulation. To estimate the PV q, during June 2018 cruise (Fig. 5), the lateral velocity data measured by the shipboard ADCP and the temperature and salinity obtained using the UVMP were bin-averaged with 1 km and 8 m bin-size for lateral and vertical direction, respectively. For cross-stream transect observations, the lateral velocity data were decomposed into parallel and normal components to the observation line and assumed to be the across-stream and alongstream current component, respectively (Fig. 4). Because the cross-stream velocity variation dominates that of the alongstream direction (Fig. 4), the PV is estimated assuming a two-dimensional front neglecting the alongstream gradients and vertical velocity, i.e.,

$${{{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}=-\frac{1}{{\rho }_{0}}\left[\left(f+\frac{\partial v}{\partial x}\right)\frac{\partial \rho }{\partial z}-\frac{\partial v}{\partial z}\frac{\partial \rho }{\partial x}\right],$$
(4)

assuming x and y are the cross-stream and alongstream directions, respectively. When the PV2D is computed for the observed vertical section (Fig. 5a, b), the vertical shear in Eq. (4) is replaced with the geostrophic vertical shear, i.e., \(\frac{\partial v}{\partial z}=-\frac{g}{{f\rho }_{0}}\frac{\partial \rho }{\partial x}\).

TKE dissipation rate

The TKE dissipation rate \(\epsilon\) can be obtained using

$$\epsilon =\frac{15}{4}\upsilon \left[\overline{{\left(\frac{\partial u}{\partial z}\right)}^{2}}+\overline{{\left(\frac{\partial v}{\partial z}\right)}^{2}}\right],$$
(5)

where \(\upsilon\) is kinematic viscosity and \(\overline{{\left(\frac{\partial u}{\partial z}\right)}^{2}}\) and \(\overline{{\left(\frac{\partial v}{\partial z}\right)}^{2}}\) are the turbulent shear variances for the lateral turbulent velocity components normal to each other. The turbulent shear variances are computed by integrating turbulent shear spectra with respect to the vertical wavenumber from approximately 1 cpm to half the Kolmogorov wavenumber. However, the actual wavenumber range for the integration is adjusted to avoid integrating variance from noise. For the wavenumber range, where the data are contaminated by noise, the Nasmyth empirical shear spectrum46 is integrated. One shear spectrum is computed over 8 s, which is equivalent to 5–6 m vertical bin-size, with an overlap of 4 s. When the shear spectra do not fit well with the Nasmyth empirical shear spectrum, the data for that depth bin are discarded.

Microscale thermal variance dissipation rate

Assuming isotropic turbulence, the microscale thermal variance dissipation rate \(\chi\) can be obtained using

$$\chi =6{k}_{T}\left[\overline{{\left(\frac{\partial T}{\partial z}\right)}^{2}}\right]$$
(6)

where \(\overline{{\left(\frac{\partial T}{\partial z}\right)}^{2}}\) is the microscale vertical temperature gradient variance, and \({k}_{T}\) is the molecular diffusivity for heat.

Osborn model of vertical eddy diffusivity

The turbulent vertical eddy diffusivity can be estimated using measured TKE dissipation rates and the buoyancy frequency32,

$${K}_{\rho }=\frac{{R}_{f}}{1-{R}_{f}}\frac{\epsilon }{{N}^{2}}=\Gamma \frac{\epsilon }{{N}^{2}},$$
(7)

where Rf is estimated in the laboratory as 0.17 and is called flux Richardson number, the ratio of buoyancy destruction to the shear production term in the TKE equation, also known as the mixing efficiency, \(\Gamma\) is called mixing efficiency factor, and N2 is the buoyancy frequency square defined as −\(\frac{g}{{\rho }_{o}}\frac{\partial \rho }{\partial z}\), where g is the gravitational acceleration.

Cox–Osborn model of vertical eddy thermal diffusivity

The vertical eddy thermal diffusivity can be obtained by,

$${K}_{\theta }=\frac{\chi }{2{\left({\bar{{{{{{\rm{T}}}}}}}}_{z}\right)}^{2}},$$
(8)

where \({\bar{{{{{{\rm{T}}}}}}}}_{z}\,\) is the mean temperature vertical gradient47.

Mixing efficiency factor \(\Gamma\)

Unlike the molecular diffusion, mechanical turbulence can mix momentum, density, and heat equally, i.e., \({K}_{\rho }={K}_{\theta }\). Using Eqs. (7) and (8), the mixing efficiency factor \(\Gamma\) can be obtained by

$$\Gamma =\frac{\chi {N}^{2}}{2{\left({\bar{{{{{{\rm{T}}}}}}}}_{z}\right)}^{2}\epsilon }$$
(9)

Thomas angle

Symmetric instability occurs when Ertel’s PV changes its sign from that of the ambient fluid. It is convenient to consider the quantity \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) by multiplying f with the \({{{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) because \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) becomes negative when flow is in a symmetrically unstable state regardless of whether it is in Northern or Southern Hemisphere. Using the thermal–wind relation, the \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) can be written as

$${{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}=\frac{1}{g}\left[f\left(f+\frac{\partial v}{\partial x}\right){N}^{2}-{f}^{2}{\left(\frac{\partial v}{\partial z}\right)}^{2}\right]$$
(10)

The \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) becomes negative when \({f}^{2}{\left(\frac{\partial v}{\partial z}\right)}^{2}\, > \; f\left(f+\frac{\partial v}{\partial x}\right){N}^{2}\), i.e., \(f/\left(f+\frac{\partial v}{\partial x}\right) \, > \; {N}^{2}/{\left(\frac{\partial v}{\partial z}\right)}^{2}\). The \({N}^{2}/{\left(\frac{\partial v}{\partial z}\right)}^{2}\)is the geostrophic Richardson number, Ri. When Ri is smaller than \(f/\left(f+\frac{\partial v}{\partial x}\right)\), then \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) becomes negative. Thomas angle34 \(\Phi\) is computed as

$$\Phi ={{{\tan }}}^{-1}\left(-\frac{1}{{{{{{{\rm{Ri}}}}}}}}\right)$$
(11)

When \(\Phi\) is smaller than \({\Phi }_{c}={{{{{{\rm{tan }}}}}}}^{-1}{-\varsigma }_{z}^{{abs}}/f\), the \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) is negative and the flow is symmetrically unstable34, where \({\varsigma }_{z}^{{abs}}=f+\frac{\partial v}{\partial x}\). Because relative vorticity on the anticyclonic side of the flow is negative, \(f/\left(f+\frac{\partial v}{\partial x}\right)\) and \({\Phi }_{c}\) are larger, which enable us to have negative \({{f{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}\) with larger Ri. Even with zero relative vorticity, the criterion is satisfied when Ri < 1, which is four times greater Richardson number than 0.25, the critical value for the K-H instability. Note also that when \(\Phi\) becomes smaller, the Ri is smaller. Thomas et al.‘s study34 reported that the source of the energy dissipated by the instability depends strongly on \(\Phi\). When \(-90\, < \, \Phi\, < \, -45\), symmetric instability dissipates energy mostly from geostrophic vertical shear, whereas inertial instability dominantly dissipates energy from geostrophic lateral shear when \(-45\, < \, \Phi\, < \, {\Phi }_{c}\).

Minimum internal-wave frequency

For a meridional two-dimensional front, the minimum frequency of the internal waves is exactly equal to \(\sqrt{{{gf{{{{{\rm{PV}}}}}}}}_{2{{{{{\rm{D}}}}}}}/{N}^{2}}\), the square root of Eq. (10) divided by the buoyancy frequency square, i.e.,

$${\omega }_{{\min }}=\sqrt{f\left(f+\frac{\partial v}{\partial x}\right)-{f}^{2}\frac{1}{{{{{{{\rm{Ri}}}}}}}}}$$
(12)

This illustrates that the negative PV does not allow internal waves. The minimum internal-wave frequency is lowered by anticyclonic vorticity and the small Ri38,39,40.

Numerical simulations

Model set-up

In this study, the ROMS33 was used with four-level nested grids to reproduce the observed flow in the upstream Kuroshio in the Tokara Strait. The outermost model grid covered the entire subtropical gyre in the North Pacific with a lateral resolution of 10–15 km. The second coarsest grid covered the western coast of Japan with a lateral resolution of 5 km, which included the 1.5-km-resolution third grid for off Kyushu, the Okinawa Trough, and the Tokara regions. The finest grid was for the Tokara Strait with 500-m resolution. The 500-m topography data available from the Japan Oceanographic Data Center (JODC) were used for the finest grid. Finer vertical resolution was used near the surface and the bottom boundary layers for the 88 vertical levels. The model vertical diffusion was parameterized with the K-Profile Parameterization and the lateral Laplacian viscosity in the finest grid was parameterized using the Smagorinsky scheme. Initially, for simplicity, tidal forcing was not considered. The monthly climatological surface fluxes were forced at the surface and the lateral open boundary conditions were set by the Levitus climatological data for the coarsest grid with nudging fluxes. Bottom drag was modeled with the quadratic bottom friction with drag coefficient of 0.004. The simulation with the coarsest grid was conducted for 9 years, and the nested simulation was conducted from October through December of year 9. The results after 20 days, from initialization until the end of November, are presented in the main portion of this manuscript, consistent with the observation period. For the case with the realistic tidal forcing, tidal constituents M2, S2, N2, K1, and O1 were forced from the open boundaries of the second coarsest nested grid.

Lagrangian analysis

Numerical model results showed internal-wave generation caused by the Kuroshio flowing over seamounts. The strong Kuroshio Current can Doppler-shift the frequency of generated internal waves. To identify the intrinsic frequency of the induced internal waves avoiding Doppler smearing, 1000 particles were released within upper 150 m depth from the upstream side of the Tokara Strait 12 times every 2 days in the simulation.