Introduction

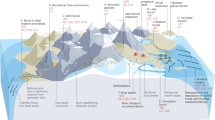
Deep-sea mining of polymetallic nodules is under consideration as a new global extractive industry due to the large resources of nickel, cobalt, copper, and manganese, which are substantial compared to land-based reserves1,2. An environmental concern, however, is the scale and impact of the sediment plumes that will be created. Two types of plumes are potentially associated with such an activity (Fig. 1). Inevitably, there will be a sediment plume generated by a nodule collector vehicle driving on the seabed. In addition, some mining proposals consider discharging a midwater sediment plume from a surface operation vessel, the plume comprising water and some sediment brought up with the nodules, nodule fines, and water used to clean the nodules aboard the vessel. Although the midwater discharge material has sometimes been referred to as tailings3,4,5,6, tailings are waste leftover after ore processing7, and to date there are no known proposals to release tailings from nodule mining operations at sea. An alternative to a midwater discharge being considered is to try and release the same material in a more localized manner close to the seabed.

Fig. 1: Schematic of a polymetallic nodule mining operation.
figure 1

From top to bottom, the three zoom-in panels illustrate the surface operation vessel, the midwater sediment plume, and the nodule collector operating on the seabed. The midwater plume comprises two stages: (i) the dynamic plume, in which the sediment-laden discharge water rapidly descends and dilutes to a neutral buoyancy depth, and (ii) the subsequent ambient plume that is advected by the ocean current and subject to background turbulence and settling.

Full size image

A midwater plume would likely be released in the disphotic or aphotic zone to mitigate impact on processes, such as photosynthetic activity and vertical migrations8. In order to assess the environmental impact of a midwater plume, it is crucial to understand that there are two different phases of the plume. The first is the dynamic plume phase that occurs in the immediate vicinity of the release (i.e., before the advecting ocean currents take over), which sets the initial plume depth and dilution. The physical processes in the dynamic plume are the rapid descent and turbulent dilution of sediment-laden water with certain initial physical conditions (e.g., volume flux, momentum flux, and buoyancy flux) in a background ocean environment characterized by the vertical stratification and vertical shear (i.e., vertical velocity profile). The relevant length and time scales are tens to hundreds of meters, and minutes to tens of minutes, respectively. Thereafter, the second phase is the ambient plume phase, for which key processes are the advection, settling, and turbulent diffusion of sediment. The appropriate length and timescales of the ambient plume are much larger than those of the dynamic plume.

The relevant model for a dynamic plume is well established9,10,11, accounting for shear and its effect on turbulent entrainment into the plume12. Recently, this model has been used to make predictions about the properties of midwater plumes for nodule mining13. The key non-dimensional parameters governing the nature of the dynamic plume are10 (i) the Reynolds number (Re(z) = 2b(z)w(z)\({\nu }^{-1}\)), which characterizes turbulence intensity in the dynamic plume, (ii) the densimetric Froude number (\({Fr}(z)=w(z){\left({g}^{{\prime} }b(z)\right)}^{-0.5}\)) characterizing the relative importance of momentum to buoyancy forces, and (iii) the buoyancy number (Δ(z) = \({N(z)}^{2}{w(z)}^{2}{g^{\prime} }^{-2}\)) characterizing the importance of the background stratification in influencing the plume vertical extent; here, w is the vertical velocity in the centerline of the plume at a given vertical coordinate \(z\), b is the radius of the plume at a given \(z\), \(\nu\) is the kinematic viscosity of water (10−6 m2 s−1 in this article), g′ is the reduced gravity of the plume (\(g^{\prime} =g({\rho }_{{{{\rm{p}}}}}-{\rho }_{{{{\rm{b}}}}})\)\({\rho }_{{{{\rm{b}}}}}^{-1}\)), \(g\) is the gravitational acceleration, \({\rho }_{{{{\rm{p}}}}}\) is the plume density, \({\rho }_{{{{\rm{b}}}}}\) is the density of the background ocean water, N is the buoyancy frequency (N = (\(-g{\rho }_{0}^{-1}\partial {\rho }_{{{{\rm{b}}}}}/\partial {{{\rm{z}}}}\) )0.5), and \({\rho }_{0}\) is a constant reference density.

To study ambient plume behavior, previous studies5,14 ran decade-long simulations for a midwater release at a depth of 500 m. Transport of fine sediment over thousands of kilometers was identified, which is not surprising. Ocean currents at 500–1500 m of depth throughout the Clarion Clipperton Fracture Zone (CCFZ) are in the range 0.01–0.1 m s−1 with spatiotemporal variability in both magnitude and direction15,16 (Supplementary Fig. 1). Under such conditions a 10 μm diameter particle would take around one year to settle 3000 m, and on that time scale, background currents can transport material large distances. From an environmental perspective, however, important metrics to determine are quantities such as suspended sediment concentration, sedimentation rate and seabed deposition. The model of Segschneider and Sundermann14, which was coarsely resolved in space (500 km) and time (1 month), predicted deposition rates of several mm per year within a few hundred kilometers of a mining site and over several decades, compared to background rates of 1 μm per year17. But the assumed sediment discharge rate was an order of magnitude larger than those estimated for a commercial-scale nodule mining operation18, and the simulation did not use any dynamic plume model to determine the ambient plume initial conditions. More recent deep-sea nodule mining sediment plume modeling efforts19,20 have been focused on the sediment plume from a collector vehicle on the seabed, which has a very different dynamic behavior compared to the midwater plume.

A key uncertainty for midwater plumes is the role of flocculation, whereby individual particles aggregate into larger flocs. In their midwater plume studies, Rzeznik et al.13 implicitly assumed that flocculation was not significant for a dynamic plume, treating the sediment as a passive tracer. In a recent study, Gillard et al.19 analyzed the flocculation of CCFZ sediment with a median particle size of 20 μm under a variety of concentrations and shear rates. Their results showed that for concentrations up to 500 mg L−1 and shear rates below 10 s−1, flocculation results in mm-scale flocs on timescales of minutes to tens of minutes. The settling velocities of these larger flocs were several mm s−1, which could potentially influence dynamic plume behavior.

Engineering field data are scarce for midwater plume releases. Surface plume releases were conducted at the Blake Plateau21 and as part of the Deep Ocean Mining Environmental Study (DOMES) effort in the CCFZ22. Compared to the midwater column, the background current is stronger near the ocean surface and the mixed layer presents a very different stratification profile, and so these studies provide relatively little insight into the evolution of a midwater plume. The most relevant study was the MESEDA experiment in the Red Sea23,24. Echosounder measurements were used to monitor a plume discharged at 400 m of depth and traces of Iridium, added as tracer, were detected 90 km away from the release site, although no specific concentrations were reported. Some complementary modeling was performed, but few quantitative results were established, and the ultimate conclusion was that further research was needed25.

The lack of engineering field data notwithstanding, insight can come from modeling and field studies of natural plumes, such as those emitted by hydrothermal vents26. Dynamic hydrothermal plumes—which are positively buoyant—can have vertical extents up to several hundred meters and dilution factors exceeding 104 (i.e., the discharge concentration is reduced by a factor of 104) on short time and length scales. The ambient plumes associated with hydrothermal vents have detectable signatures across ocean basins that are greatly influenced by background currents26,27.

To address the current knowledge gap for midwater plumes3, we performed the PLUMEX field study offshore of Southern California, in the Pacific Ocean. A mixing, storage, and pumping system was designed and used to discharge plumes into the ocean in a dynamical regime characteristic of a commercial mining operation18 (referred to as “commercial plume” in this article). The centerpiece of the field experiment was the discharge of a plume using CCFZ sediment. Real-time numerical model forecasting was run in parallel with the field experiments to predict the ocean conditions, and the corresponding ambient plume advection in the field study area. Here, we present results from the PLUMEX field study. These results validate the use of dynamic plume modeling without any significant influence of flocculation. We thus use the validated dynamic plume model to provide realistic source conditions for an ocean-scale numerical simulation of an ambient midwater plume created by a commercial nodule mining operation in the CCFZ.

Results

Discharge operations and parameters

The R/V Sally Ride operated in the Pacific Ocean 50 km off the coast of California from Feb 26th to Mar 5th 2018. A pumping system was configured to draw water from near the ocean surface onto the vessel, combine it with a highly concentrated mixture of sediment laden water or saltwater with Rhodamine dye, and then discharge the mixture at depth through a pipe (see “Dynamic plume creation system” section). The typical discharge time was 45 minutes, which was long enough to ensure: (i) well-established dynamic plume behavior, and (ii) a resulting ambient plume that was sufficiently large to track. During the discharge, the vessel was stationary and the dynamic plume in the vicinity of the vessel was monitored with a Phased Array Doppler Sonar (PADS) and a vertical profiler (epsilometer). It took about 1–3 min for parcels of fluid discharged from the pipe nozzle to descend to the base of the dynamic plume, after which they became part of the ambient plume carried by the ocean currents. At the end of the 45-min discharge period, the resulting ambient plume was tracked and monitored via tow-yo profiling using the CTD cage. The ambient plume tracking was supported by two operational tools: (i) an advection model that used the current velocity measured by the shipboard Acoustic Doppler Current Profiler (ADCP), and (ii) a forecast of the ocean currents obtained with the MIT-MSEAS model. See “Methods” section for more details.

The discharge parameters for the three plumes discussed in this manuscript (two saltwater and one sediment) are summarized in Table 1, including the volume (Q0 = π b02 w0), momentum (M0 = π b02 w02), and buoyancy fluxes (F0 = π b02w0 g′). Further details on the ocean stratification and background currents are included in Supplementary Figs. 2, 3. The peak stratification, where N2 is maximum, was ~40 m deep. We therefore set the discharge for a depth of 60 m, below both the mixed layer and the peak stratification. The background currents at the discharge depth were on the order of 0.1 m s−1 or less, which is within the range of current velocities observed in the CCFZ16,28, as demonstrated by the 6-year-long timeseries of daily average current velocity magnitude presented in Supplementary Fig. 1. Therefore, both the dynamic plume characteristics18 (encapsulated by Re, Fr, and Δ) and the environmental conditions are consistent with a commercial-scale plume released at greater depths in the CCFZ. Specifically, the dimensionless parameters for our dynamic plume were Re ~O(105), Fr ~O(10), and Δ ~O(10−2), and so our plume was in the same turbulent dynamic regime as a commercial plume, and similarly dominated by momentum and impacted by background stratification. For comparison, the plume parameters estimated for a commercial-scale mining operation18 are listed in Table 1.

Table 1 Summary of measured (m) and calculated (c) dynamic plume parameters at the discharge depth.
Full size table

Dynamic plume monitoring

The Phased Array Doppler Sonar (PADS) system29 mounted off the starboard side of the ship, adjacent to the discharge pipe, obtained cross-sectional images of the dynamic plume’s backscatter intensity (see “Dynamic plume monitoring system” section). Saltwater Plume 1 (Fig. 2a) descends from the release depth of 59.5 ± 0.3 m down to a depth of ~105 m, with a characteristic width at the base of ~20 m; there is some rebound back up to a depth of ~95 m. In comparison, the CCFZ sediment plume and Saltwater plume 2 (Fig. 2b, c) have a smaller vertical extent than Saltwater Plume 1, because the sediment and Saltwater 2 plumes have lower initial buoyancy and momentum fluxes (Table 1). The vertical extent of a dynamic plume scales as F01/4N−3/4, and since Saltwater plume 1 has an initial buoyancy flux ~7 times larger and the average buoyancy frequency was about three times lower, it is expected to have a vertical extent ~3 times that of the other two experimental plumes, in accordance with the PADS observations (Table 2). Also noteworthy is that the PADS images of the CCFZ sediment and Saltwater 2 plumes (Fig. 2b, c) show the same behavior for two plumes that have the same dynamic properties, but one created using sediment and the other saltwater. This reveals that the sediment acts as a passive tracer only influencing the plume density13. Superposed on top of each image is a prediction of our DP1 dynamic plume model (see “Dynamic plume models” section), showing good agreement with the PADS data in terms of shape and maximum depth.

Fig. 2: PADS backscatter intensity images.
figure 2

a Saltwater plume 1, 30 min after the start of a 45-min release, b CCFZ sediment plume, 22 min after the start of the release, and c saltwater plume 2, 19 min after the start of the release. The superimposed black lines are the predictions from the DP1 model (see “Dynamic plume models” section). The three intensity patches at the top of each image are acoustic reflections from the connectors of the discharge pipe, which vary in intensity because of slight changes of PADS alignment during the discharge. It took about 1–3 min for water exiting the discharge nozzle at 60 m depth to descend to the base of the dynamic plume. The DP1 model density, vertical velocity, and width results are in Supplementary Fig. 4. The ocean background backscatter intensity observed by the PADS is in Supplementary Fig. 5.

Full size image
Table 2 Plume vertical extent and dilution factors measured during PLUMEX field studies and predicted by the DP1 and DP2 dynamic plume models.
Full size table

During the 45-min dynamic plume release we performed fast vertical profiling with a custom profiler (epsilometer) that carried a turbidity sensor, fluorometer (to measure the concentration of the Rhodamine dye added as a tracer to the plume water), and conductivity, temperature and turbulence sensors (see “Dynamic plume monitoring system” section). We present one example of a profile (Fig. 3) obtained during the CCFZ sediment plume release. The location of the epsilometer was ~30 m astern of the discharge pipe, so measurements were made in the spreading part of the plume rather than the descending part of the dynamic plume. As expected, the plume was highly turbulent (O(10−6) W kg−1), with turbulent kinetic energy dissipation rates elevated three orders of magnitude above ocean background levels (O(10−9) W kg−1) (Fig. 3c).

Fig. 3: Example of an epsilometer profile measured during the discharge of the CCFZ sediment plume.
figure 3

The profile was obtained 38 min after the start of the 45-min discharge. The water being sampled at this time would have been discharged into the ocean about 6–7 min earlier (i.e., the time it takes for a fluid released from the discharge nozzle to descend to neutral buoyancy in the dynamic plume and be carried by ocean currents past the epsilometer). a Temperature and salinity data. b The density and buoyancy frequency (N2) derived from data in a; the density profile is significantly smoother than the temperature and salinity profiles as changes in the latter two result in smaller relative changes in density. c The turbulent kinetic energy dissipation rate (ε) detected by the two independent turbulence probes (s1 and s2). The inverse dilution factors (as a percentage of the initial concentration) of sediment and Rhodamine tracer are presented in d with error bounds indicated for each by the min and max signals associated with the corresponding sensor calibrations. An additional epsilometer profile and a comment on the observations can be found in Supplementary Fig. 6 and Supplementary Notes 1, respectively.

Full size image

The maximum plume depth measured by the epsilometer for the CCFZ plume was 79.1 ± 0.5 m (Fig. 3), with a spreading plume thickness between 5–9 m, which corresponds to a 30–50% of the total plume length and is consistent with other laboratory and field observations10,30,31. The Rhodamine dye and sediment concentrations had characteristic values that were 1–2% of the initial discharge concentration; this substantial reduction is due to turbulent entrainment. These dilution levels are well aligned with observations from laboratory experiments32 and field measurements26,33,34,35,36 of dynamic plumes. The epsilometer clearly detected the salinity and temperature signals of the plume; the turbulence was vigorous enough to create static instabilities in the density profile (as shown by negative values of N2 in Fig. 3b) indicating that the plume had not quite reached a level of neutral buoyancy, and hence was still prone to further rebound and mixing. This is supported by the fact that, compared to the epsilometer measurements, the DP2 dynamic plume model (which models plumes at their level of neutral buoyancy) slightly underpredicts plume depth, and overpredicts plume dilution at the measurement location. Overall, the plume depth and dilution factors recorded by the epsilometer are well aligned with model predictions and with PADS data (Table 2).

The results in Figs. 2 and 3 reveal that flocculation was not a significant factor for the dynamic plume. The model predictions and observations are in good agreement, which would not have occurred if mm-scale flocs with mm s−1 settling velocities were present13. Furthermore, the epsilometer fluorescence and turbidity signals are in good agreement; if large aggregates had formed and settled relative to the tracer dye these signals would be offset by tens of cm and there would be notable differences in the magnitudes and forms of these two signals. This lack of influence of flocculation on the dynamic plume is readily understood. Gillard et al.19 report that the amount of flocculation and size of the flocs decrease for high turbulent shear rates (>10 s−1) and low concentrations (<10 mg L−1). The mean initial energy dissipation rate of the dynamic CCFZ plume37 is >O(1) m2 s−3 and this turbulence level is sufficient to initially disaggregate the sediment upon discharge38 (similarly, the initial Kolmogorov turbulence length scale is <30 μm, which is small enough to break up and prevent the formation of flocs). As it descends, the disaggregated sediment in the dynamic plume rapidly dilutes (over the timescale of 1–2 min). This limits the role of flocculation due to the short time spent at moderate concentrations and turbulence levels that are conducive to flocculation, before reaching sufficiently low concentrations O(10 mg L−1) that are not conducive to flocculation. A proposed phenomenon involving sediment fallout and interstitial fluid rise for consideration in the vicinity of deep-sea mining midwater plumes39 was not observed. This is because the initial turbulent disaggregation of the sediment and relatively short time scales of the dynamic plume kept particle settling speeds very low which, along with the rapid and substantial dilution of the discharge water, resulted in very small volume fractions that do not support a substantial rebound of interstitial water.

Ambient plume monitoring

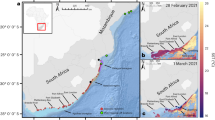
After 45 min of dynamic plume discharge, the resulting ambient plume, advected by the background ocean currents, was tracked (Fig. 4) by repeatedly cycling the ship’s CTD cage up-and-down while underway (a procedure referred to as tow-yo, see “Ambient plume monitoring system” section). Two operational tools were used to facilitate the ambient plume tracking: (i) the ADCP advection model, and (ii) the MIT-MSEAS modeling system40,41,42. The ADCP advection model integrated the ocean current velocity data measured by the shipboard ADCP at the observed plume depth to estimate the location of the plume at any time (see “Ambient plume monitoring system” section). The MIT-MSEAS modeling system40,41,42, was run daily to obtain forecasts of the expected direction of ambient plume advection (see “MIT-MSEAS numerical model” section). In total, the ambient plume was transected 13 times; the locations of the direct observations are highlighted in Fig. 4a.

Fig. 4: CCFZ sediment ambient plume tracking.
figure 4

a The dynamic plume was released over 45 min at the location marked by the blue cross producing an ambient plume. The grey line represents the ship track during the tow-yo sampling. The dots on top of the ship track are the start locations of the tow-yo downcasts with (red) and without (blue) ambient plume detections. The open circles (blue and red) correspond to ship position (and ambient plume observations) at the indicated time in minutes from the start of the plume release. The red circles indicate where water samples were taken for the results presented in Fig. 6b–d. The numbers 0–17 in green indicate the start of the R/V transects (i.e., transect 0 starts at label 0 and goes to label 1) and correspond to the numbers indicated on top of Fig. 5a, b. b The ambient plume location estimated using the ADCP advection model (hatched patches) and forecast by the MIT-MSEAS model (shaded patches) 78 (blue), 120 (grey), 250 (green), and 371 (red) minutes after the start of the plume release (see “MIT-MSEAS numerical model” section). The brown line next to the release location corresponds to the initial centerline (streakline) of the ambient plume, obtained with the ADCP advection model. The width of the ADCP advection model plume is based on the initial tow-yo observations (~120 m), plus the consideration of a lateral effective diffusivity of 0.1 m2 s−1 (since the ADCP advection model can only estimate the location of the ambient plume’s centerline).

Full size image

The initial length of the ambient plume was estimated to be ~270 m based on a consistent 0.1 m s−1 current throughout the 45 min of plume discharge. Consistent with this, from the tow-yo data, the length and width of the ambient plume were determined to be ~260 m and 100–150 m, respectively. The predictions of the ambient plume location obtained with the ADCP advection model and the forecast of the MIT-MSEAS modeling system 78, 120, 250, and 371 min after the start of the plume release, are presented in Fig. 4b, for comparison with the highlighted locations of the actual ambient plume observations. Overall, the independent MIT-MSEAS and ADCP-advection estimates were consistent, and the ambient plume was monitored for over seven hours, only ceasing operations to prepare for the next day’s experiments. During the tracking, multiple water samples were obtained to analyze the sediment and tracer concentrations and the particle size distribution in the laboratory after the experiments.

The concentrations of Rhodamine dye and sediment detected by the sensors as a function of time, scaled by the corresponding discharge initial concentrations, as a function of time are presented in Fig. 5a, b. In the first two hundred minutes, the CCFZ plume resided in the depth range 64–76 m, consistent with dynamic plume model predictions and epsilometer observations (Fig. 3). A downward vertical displacement of several meters occurred towards the end of this period due to the heaving (vertical motion) of background density contours (isopycnals). Seven transects across the plume were obtained, finding minimum dilution factors (i.e., maximum concentrations) for Rhodamine and sediment of 215–250 and 250–309 (0.3–0.5% of the plume initial concentration), respectively (Fig. 4b). These observed concentrations are 3–4 times lower than those detected by the epsilometer in the vicinity of the dynamic plume release, which can be attributed to continued turbulent mixing during the early spreading phase of the plume followed by the subsequent lateral (but, given the timescales involved, not vertical) ocean turbulent diffusivity acting over the first few hours43. The vertical thickness of the ambient plume was on the order of a few meters, and for several profiles we detected a multi-layered structure that extended over 5–10 m in the vertical (Fig. 5a, b). This multilayered structure is likely due to the combination of vertical motion of the discharge pipe, caused by heaving of the ship on the ocean surface, and heaving of the ocean isopycnals. It is also noted that multilayered structures generated via other physical mechanisms have been reported in other studies of plume discharges in stratified environments32,44.

Fig. 5: Tow-yo observations of the CCFZ sediment ambient plume.
figure 5

a Time series of inverse dilution factor (as a percentage of initial discharge concentration) for CCFZ sediment and b dye tracer. The red circles indicate samples for which data is presented in Fig. 6. The vertical dotted lines indicate the start/end of each transect and the numbering from 0 to 17 at the top corresponds to the numbered locations indicated in Fig. 4. c Evolution of the CCFZ sediment ambient plume temperature (red crosses) and salinity (blue dots) over time. d Evolution of the ratio between the ambient plume sediment and tracer dilution factors. Error bars represent the standard deviation.

Full size image

Over the time scale of two-to-four hundred minutes six more tow-yo transects across the ambient plume were obtained. The plume was noticeably deeper at 73–88 m than during the first two hundred minutes, as a result of both a continued downward motion of the isopycnals, and the plume itself crossing the isopycnals. Relative to the isopycnals, the plume descended 5 m at an average vertical velocity of ~0.2 mm s−1. This observed crossing of isopycnals is explained by the increase of the plume density as a result of a temperature decrease (~0.2 °C), and salinity increase (~0.1 PSU) of the plume water as it mixed and equilibrated with the ambient (Fig. 5c) via turbulent diffusion. This, and the fact that both the dyed plume water and the sediment turbidity signals remained aligned in the vertical, indicate that the crossing of isopycnals was not a result of sediment settling. The observed maximum concentration levels of sediment and dye were as low or lower than values detected during the first two hundred minutes (Fig. 5d), which is consistent with lateral diffusive processes acting over several hours43; although, it cannot be discounted that a different section of the plume was investigated.

Given that our tow-yo measurements could reasonably expect to detect at least a ~1 m offset between dye and sediment, the absence of any offset sets an upper bound for the settling speed of the sediment of 0.05 mm s−1 during the ambient plume phase. Furthermore, the constant 1–1 ratio between sediment and dye concentrations throughout the tow-yo tracking reveals no significant settling out of the particles (Fig. 5d). As such, no significant flocculation occurred during the ambient plume phase, which can be attributed to the very low concentration of sediment19.

The particle size distribution of the disaggregated discharge sediment plume (Fig. 6a) was determined using water samples from the discharge pipe. The results are compared to the corresponding particle size distributions of samples obtained within the plume in Fig. 6b–d, collected at the locations shown with red circles in Figs. 4 and 5a, b, and with the ocean background levels presented in Fig. 6e. The absolute values for the discharge sample concentration were roughly three orders of magnitude greater than those for the samples obtained within the ambient plume, which in turn are two orders of magnitude greater than the measured background levels. The qualitative form of the distribution for the discharge (Fig. 6a) and for the plume samples (Fig. 6b–d) is quite similar, with a median particle size of 9–12 μm. The distributions taken from the ambient plume are somewhat more skewed in favor of a peak around 12 μm with relatively fewer particles in the range 2–5 μm. This could be due to processes that occurred during the retrieval, storage and processing of samples; only in situ measurements of particle size distributions in the ocean could discern this.

Fig. 6: Laboratory analysis of particle size distribution.
figure 6

Samples were obtained in a the discharge pipe, b–d different sections of the ambient plume 78, 120 and 371 min after the start of the plume release (indicated by the red circles in Figs. 4a, b and 5a, b), and e the background environment at 58 m of depth. The left vertical axis indicates the volume fraction of the distribution (%) and the right vertical axis the mass concentration (mg L−1) for each particle size in the sample. The median particle size is indicated by a black vertical dotted line.

Full size image

Numerical modeling of a commercial midwater plume

Two principal outcomes from the PLUMEX field studies are that: (i) model predictions for a dynamic plume work well for estimating the initial concentration and equilibrium depth of the resultant ambient plume, and (ii) flocculation does not play a significant role due to initial high turbulent shear rates rapidly followed by low sediment concentrations. Building on this understanding, we use the validated DP1 dynamic plume model to provide realistic source conditions for a regional-scale numerical simulation of an ambient plume from a commercial nodule mining operation in the CCFZ. We used the TELEMAC model (see “TELEMAC numerical model” section), which is an established model that has previously been used for case-studies of deep-sea mining sediment plumes45,46, to hindcast ocean conditions and the associated transport and mixing. The goal of the TELEMAC model is not to predict the exact ocean conditions at a given date, but to provide physically reasonable ocean dynamics as the basis for a plausible model of a midwater ambient plume. The parameters for the commercial scale plume are presented in column 4 of Table 1. The sediment particles are assumed to have a settling speed of 0.1 mm s−1, which is aligned with the PLUMEX field studies observations.

Midwater column ocean currents in the CCFZ are characterized by intermittent transitions between prevailing current directions. This is evident in the 6-year long current velocity dataset from the CCFZ included in Supplementary Fig. 1, consistent with previous studies close to the seabed in the CCFZ15, and adequately captured by the TELEMAC model (Supplementary Figs. 7–9). Due to the nature of the currents in the CCFZ, we find that an ambient plume generally exists in one of two states. For a prevailing current direction over several days, the ambient plume becomes elongated and aligned with the current direction over the course of just a few days (Fig. 7a). The area enclosed by a dilution factor contour does not continue to grow because advective transport within the plume becomes balanced by turbulent diffusion at its boundaries. When there is no prevailing current for a while or there is a transition from one prevailing direction to another, the plume assumes a more compact and distorted shape (Fig. 7b).

Fig. 7: TELEMAC numerical simulation of continuous commercial scale sediment plume release over 90 days.
figure 7

Top view of the 10,000 (orange), 40,000 (yellow), 100,000 (dark blue) and 400,000 (light blue) dilution factor contours of the plume for a a prevalent current (day 36 of the simulation) and b a current transition (day 88 of the simulation). These contours show the maximum horizontal extent of each 3D contour level and are not a cross section at a specific depth. c  Horizontal projected area of the plume dilution factor contours. d Maximum vertical extent of the plume across the entire domain as a function of time. The current velocity and direction at the location and depth of the discharge can be found in Supplementary Fig. 7.

Full size image

Estimates for the area and vertical extent of the plume throughout the 90-day simulation are presented in Fig. 7c, d, respectively. For these model runs, a dilution factor of 400,000 corresponds to a sediment concentration of 20 μg L−1, which is around the reported background level in the CCFZ47,48,49. Accordingly, dilution factors of 100,000 and 40,000 correspond to plume concentrations of 80 μg L−1 and 200 μg L−1, respectively. The average horizontal area and vertical extent of the 400,000 dilution factor contour are 480 km2 and 350 m, respectively. For the 100,000 and 40,000 dilution factor contours these values are substantially smaller, being 81 km2 and 208 m, and 25 km2 and 155 m, respectively. These results reveal that the choice of an environmentally acceptable threshold value has a substantial influence on the extent of impact of an ambient plume.

Another conclusion that can be drawn is that the scale of the plume is significantly influenced by the amount of sediment discharged. The current simulation assumed a discharge of 0.56 m3 s−1 at a concentration of 8.3 g L−1, but if the concentration of the discharge were doubled (or halved) for the same flow rate, the 100,000 dilution factor contour would roughly correspond to a sediment concentration twice (or half) 80 μg L−1, respectively. Thus, engineering of the collector and riser system to limit the amount of sediment brought up with the nodules will play a primary role in setting the scale of impact of a midwater plume discharge.

Discussion

The results of the PLUMEX study reveal that a midwater plume comprises two phases. First is the dynamic plume, which has a predictable form and dilution in the vicinity of the discharge, accounting for factors such as the vertical density and velocity profile at the discharge location. A key finding is that flocculation of sediment does not play a notable role due to initially high turbulent shear rates at the top of the dynamic plume, and low concentrations at the base of the dynamic plume due to rapid turbulent entrainment. Expected dilution factors in the immediate vicinity of a dynamic plume will be on the order of 1000. Since the dilution factor varies as F03/4Q0−1N−5/4, then the key factors influencing dilution are the discharged sediment mass flux (which is the main parameter controlling F03/4Q0−1) and the discharge depth (which controls N).

The resulting ambient plume does not grow indefinitely but rather establishes its form on the timescale of a few days in the presence of time varying background currents. The extent of the boundaries of the ambient plume is set by a balance between new sediment coming from the discharge and the dilution of sediment by turbulent ocean processes. The ambient plume is not significantly affected by flocculation due to low sediment concentrations, and has a vertical and horizontal extent that is notably influenced by (i) the amount of discharged sediment, (ii) the definition of environmentally acceptable threshold levels, and (iii) background turbulent diffusivity. In the case of a prevailing current, sediment transport is dominated by advection in the direction of the current, and by turbulent diffusion in the direction normal to it. The length of an ambient plume remains unaffected to first order by changes in diffusivity, but the width (and thus the area and volume) above a certain threshold level will be impacted. For example, an increase (decrease) by a factor of ten in horizontal diffusivity will increase (decrease) the width of the plume by a factor of three, but will reduce (increase) concentrations within that plume by a factor of three because it scales with the square root of the diffusivity (see Supplementary Notes 2). We note that if the current is not steady for sufficient time to establish this behavior (a few days), the plume may become more localized, which is the scenario in Fig. 7b. All this serves to highlight that obtaining good data on horizontal and vertical turbulent processes and diffusivities in the CCFZ will be key to further improving model predictions of the scale of impact of a midwater plume. For our simulations we used a value of 0.3 m2 s−1 for horizontal diffusivity20,46 and 0.03 m2 s−1 for effective vertical diffusivity16,50, which are applied as a modeling approximation of subgrid scale physical mixing processes.

Our 90-day model produced no prediction of ambient plume sediment deposition on the seabed because of the small settling velocities of the particles and the irrelevance of flocculation. It takes about 400 days for a 10 μm particle with a 0.1 mm s−1 settling velocity to settle 3500 m to the seabed; over that period the sediment can travel 1400 km assuming an average current velocity of 4 cm s−1 (Supplementary Fig. 1), being continually diluted en-route. In the vertical, however, settling is expected to dominate over turbulent diffusion for such time scales. The polydisperse nature of the plume will then play a relevant role as larger particles will settle faster than smaller ones, resulting in an effective vertical diffusion of the plume. We also note that the use of the DP1 model to set the source conditions for the ambient plume does not take into consideration the additional mixing, that occurs in the transition between the dynamic and ambient plume phases due to the elevated turbulence levels observed close to the discharge (Fig. 3c), which contribute to the additional dilution we observed further from the discharge during the sediment plume tracking (i.e., dilution factors increasing from around 100 to around 1000).

We extrapolate our current understanding to estimate the scale of a nodule mining operation running at full capacity for 20 years. An operation with an annual production of 3 million tons of dry nodules operating 260 days per year has been estimated to discharge about 5.4 kg s−1 of sediment and 2.7 kg s−1 of nodules fines in the form of a midwater plume from the mining vessel18. Based on the estimated loads of sediments and fines, one mining operation would discharge a total of ~1.2 × 108 kg of sediment (Ms) and ~6.1 × 107 kg of fines (Mf) into the ocean per year. The particle size of the discharged nodule fines depends on the separation process applied prior to the discharge; a three stage separation system is expected to result in the discharge of nodule fines within the same size class of the discharged seafloor sediments51, with nodule fines consisting of manganese oxides and iron oxyhydroxide particles that are thermodynamically stable in oxygenated seawater52. There is currently no evidence that dissolved metals would be released along with the sediments and fines.

Recognizing that it takes about 1 year for 10 μm sediment to settle to the bottom from the midwater column, over which time sediment can readily be transported up to 1000 km in very different directions by variable ocean currents throughout a 20-year commercial mining operation, the area over which the sediment and fines settle is a few million square kilometers (i.e., comparable to the scale of the CCFZ). This results in a sedimentation rate on the order of 0.01 μm per year at the seabed compared to background sedimentation rates of 1 μm per year17. Details of the calculation and additional scenarios can be found on Supplementary Notes 4 and Supplementary Table 1. In regards to sediment concentrations in the water column, the results in Fig. 7 show the expected area above different threshold levels at any given time for a commercial operation discharge with the parameters indicated in Table 1, ranging from 25 to 500 km2. Using the analytical model (Supplementary Fig. 10) at a given instant in time the corresponding volume of water ranges from 6.8 to 680 km3 for sediment concentrations from 200 to 20 μg L−1, respectively (for the parameters listed in Supplementary Notes 2). Potentially a more relevant metric is the total water volume that over a year of operations exceeds a concentration of 200 and 20 μg L−1 at some point in time, which is 335 and 3350 km3, respectively; for comparison the volume of water in the CCFZ is around 18 million km3. We reiterate that as well as being significantly influenced by threshold levels, these areas and volumes are notably impacted by the value of background turbulent diffusivities in the CCFZ, which future environmental baseline cruises can help better constrain (see “TELEMAC numerical model” section and Supplementary Notes 2).

Finally, from an environmental impact perspective, it is now important to build on this work and clearly determine the key metrics that are responsible for creating environmental impact, beyond the simple concepts of sedimentation rate or sediment concentration commonly discussed and presented here. More sophisticated metrics are likely needed, such as the total volume of ocean water above threshold level for a certain time, which is relevant to biology that moves with the ocean, or the percentage of time the concentration exceeds threshold levels at a fixed location near a mining operation, which would seem appropriate for biology that remains close to one location. And while progress is being made on the understanding of the midwater (e.g.,53,54) and benthic ecosystems in the CCFZ (e.g.,55,56), there still exist significant knowledge gaps to inform the setting of environmentally acceptable threshold levels3.

Methods

Dynamic plume creation system

Installed on the main deck of R/V Sally Ride, the plume creation system comprised a cylindrical mixing tank (9 m3), a storage tank (34 m3), two centrifugal pumps (Power Prime DV200c and DV150c with a maximum flow rate of 0.3 m3 s−1 and 0.18 m3 s−1, respectively), three submersible mixing pumps (Tsurumi LB1500), a suction and a discharge hose (Fig. 8). The plume creation started in the mixing tank, equipped with two submersible pumps, where the salt or the highly concentrated mixture of CCFZ sediment was mixed with additional water pumped from the ocean surface. Because of ship and experimental operational constraints it was not possible to pump water from greater depth, which would have slightly increased the initial density of the plume. Once the content of the mixing tank was homogeneously mixed, it was transferred to the storage tank, also equipped with submersible mixing pumps. The process was repeated until the required amount of salt or sediment was added. Then 4.7 L of Rhodamine WT (21% concentrate) dye was added in the mixing tank to serve as a passive tracer, with an initial concentration of 5.3 ± 0.3 ppm at the discharge.

Fig. 8: Plume creation system.
figure 8

a The R/V Sally Ride during PLUMEX field studies. b Schematic of the aft main deck where the plume creation equipment was installed. Red squares correspond to the location of the salt bags used to increase the initial density of the salt water plumes. Brown squares indicate the location of the totes with the mixture of salt water and CCFZ sediment. The epsilometer was deployed from the epsilometer boom (in green). c A top view of the main deck with some key items labelled.

Full size image

The main centrifugal pump was used to pump a controlled flow rate of water from the ocean surface through the discharge hose, whose nozzle was located ~60 m deep. The auxiliary centrifugal pump, at the same time, injected a controlled flow rate (0.01 m3 s−1 on average for the three plumes) of the highly concentrated mixture of sediment (or salt water) from the storage tank immediately before the inlet of the main pump. The main pump and the highly turbulent flow were responsible for mixing both streams. The control of the flow rates of water from the ocean surface and from the storage tank allowed adjustment of the initial characteristics of the discharge plume. The flow rates were monitored throughout the plume discharge, and water samples were obtained from the discharge line and analyzed afterwards in the lab to determine sediment and tracer concentrations, and water salinity.

Over two tons of sediment were obtained from the Belgian exploration area in the CCFZ using a box corer and stored for 12 months in four closed containers. A week before the discharge, artificial sea water was added to enable mixing and disaggregation of the sediment using an industrial paddle mixer (QEP 21660 HeavyDuty Power-Mixer) for 30 min at 700 rpm. This process was repeated seven times before the plume discharge. Three hours before the discharge, the blend of sediment and artificial sea water was mixed again with the paddle mixer and transferred from the containers to the mixing tank (T2 in Fig. 8b, c) using two submersible pumps. The mixing tank was partially filled with ~4 m3 of ocean surface water and contained two 5HP submersible pumps to enhance mixing and avoid sediment particle settling. The purpose of the plume creation procedure was not to fully disaggregate the sediment, but to mimic the type of pumping and flow conditions that the sediment is expected to experience during a nodule-mining operation. However, according to observations in laboratory experiments with cohesive sediment38 it is likely that the disaggregation was complete or almost complete given that the turbulence levels during PLUMEX were significantly higher than the achievable levels in a laboratory setup. For the salt plumes, a certain amount of salt (5.4 t for Saltwater plume 1, and 1.4 t for Saltwater plume 2) was dissolved in the mixing tank to prepare a high-salinity water stock.

Dynamic plume monitoring system

For each experiment a dynamic plume was discharged for a period of 45 min, during which a number of sensors measured key parameters of the plume. The vessel remained stationary during the discharge using a dynamic positioning system, and the monitoring effort was a challenge to coordinate with as many as five different elements operating from the side of the vessel at one time. The sensors enabled a comprehensive interrogation of the dynamic plume in the vicinity of the vessel, combining acoustic imaging of the plume and vertical profiling in the vicinity of the plume, and were as follows:

Thermistor

An SBE 56 thermistor mounted at the nozzle of the discharge hose determined the initial temperature of the dynamic plume during the discharge. The initial mean temperature was 14.80 ± 0.03 °C for Saltwater plume 1, 14.8 ± 0.3 °C for the CCFZ sediment plume, and 14.59 ± 0.06 °C for Saltwater plume 2 (Supplementary Fig. 12). Temperature data was recorded every second and used to determine the density of the discharge water.

Shipboard ADCP

A shipboard Teledyne RDI Ocean Surveyor (38 and 150 kHz) and a shipboard Teledyne RDI Mariner Workhorse (300 kHz) measured the current velocity and heading in the water column with 5-minute ensemble-averaging. The data was acquired using VMDAS and processed using WinADCP. The real time ADCP data was used to determine the vessel’s orientation during the dynamic plume discharge, so that the epsilometer was profiling the water column downstream of the discharge. The ADCP data was only further used by the ADCP advection model (see “Ambient plume monitoring system” section).

Phased array doppler sonar

A custom Phased Array Doppler Sonar (PADS)29 was deployed from the starboard side of the vessel, 4 m forward from the discharge hose at a depth of 8 m, with tethers on each end to hold it parallel to the hull, and a third tether off-center to adjust the vertical angle athwartship ~5° either side. The PADS backscatter intensity was used to obtain real-time images of the dynamic plume during the discharge (Fig. 2). The data and communication cables were run into a controller to set the timing, sample-rate and transmit sequence, and then to a computer to store the raw data and conduct the beam-forming. The beam-formed data was then mapped onto a regular cartesian grid with ~2 m spacing between points in both directions. The PADS operates near 200 kHz, with a wavelength of 8 mm. The main sources of backscatter are the variations in sound speed induced by temperature differences between the dynamic plume and the background water, and the dynamic plume turbulence. Salinity and sediment have a less significant effect on the sound speed, which is why both the saltwater plumes and the CCFZ sediment plume present similar acoustic backscatter (Fig. 2). Although it is common practice to use the acoustic backscatter and/or attenuation to estimate sediment concentration, the established procedures to do so cannot be directly applied to the PADS data because of the very different properties and turbulence levels of the dynamic plume compared to the background ocean water. Furthermore, the characteristic CCFZ sediment particle size of O(10) μm was too small to generate a relevant backscatter given the wavelength of the PADS acoustic signal.

Epsilometer

A vertical microstructure profiler, known as the epsilometer, was deployed from the stern of the vessel at a horizontal distance of 30 m from the discharge hose (Fig. 8b). It therefore sampled fluid spreading from the base of the dynamic plume. The epsilometer was configured to conduct vertical profiles very close to the discharge and obtain in-situ measurements of the sediment and tracer concentrations, and the turbulence, temperature and salinity signals. The profiler was fabricated by the Multi-scale Ocean Dynamics (MOD) group at the Scripps institution of oceanography (SIO) following techniques developed at the Applied Physics Laboratory (University of Washington). The system was deployed with a 3D-printed dropping body for profiling from the SIO fast-CTD winch. This winch assures free-falling profiles (decoupled from the ship’s motion and line tension) by continuously easing the tension on the tether. The profiler free-falls at ~0.6 m s−1 while telemetering data back to the ship via a communication tether with a Kevlar strength member. The epsilometer was equipped with an SBE49CTD sensor to monitor the ocean stratification, the plume salinity and temperature signals, and determine its depth. Additionally, an ECO Triplet, airfoil, and thermistor were mounted on the epsilometer. As the ocean current advected the plume, the orientation of the vessel was set based on the current direction measured by the shipboard ADCP, so that both the discharge hose and the epsilometer were aligned with the current heading.

Scattering fluorescence and turbidity sensor

The ECO Triplet (Sea-Bird Scientific) scattering fluorescence sensors mounted on the epsilometer and the CTD rosette had three independent optic sensors with the capability of working at three different wavelengths: 670 nm for turbidity, 570 nm for Rhodamine dye concentration, and 650 nm for chlorophyll. The sensors were calibrated for each plume discharge using a water sample of the actual plume, obtained from the discharge line. Each sample was diluted and measured with the sensors several times until reaching dilution factors up to 50,000, which was close to the lower detection threshold of the sensor (Supplementary Fig. 13).

Turbulence sensor

The turbulence sensor mounted on the epsilometer is a custom turbulence profiler developed by the MOD group at SIO measuring the turbulent dissipation rate of kinetic energy (ε). The sensor samples shear and temperature at 320 Hz using custom shear probes and FPO7 thermistors beads. Associated with these high frequency measurements, the SBE49CTD was used to vertically locate the profiler. To compute the ε profiles, the time series from two independent shear probes mounted on the profiler are split in one and a half second scans (~1 m) to compute shear spectra. ε is the product of the integration of these spectra over the sensitive range of the instrument, which is between ~10−10 W kg−1 and ~10−5 W kg−1. The lower and upper limits of this range are defined by the sensor electronics noise (low epsilons) and the fall rate (upper epsilons). The ε measurements are corrected for the vehicle’s vibration using the coherent part of the acceleration and shear signal.

Dynamic plume discharge samples

Samples were extracted from the discharge hose every 5 min during the discharge of the plumes and four of them were analyzed in the lab afterwards. The analysis comprised salinity (conductivity), rhodamine dye concentration, total suspended solids (TSS) concentration, and particle size distribution (PSD). The salinity, rhodamine dye concentration and TSS (together with the plume discharge temperature measured by the SBE56 thermistor) were measured to determine and control the plume initial density. Upon return to shore, the PSD was determined with an Accusizer780/780AD, which is based on the single particle optical sensing technique. The TSS was determined by filtering the water samples through a 0.45 μm regenerated cellulose filter and then weighting.

Ambient plume monitoring system

After the end of the 45-min dynamic plume discharge, the PADS and the epsilometer were recovered onboard and, within a 5 min turnaround time, the CTD rosette was deployed from the vessel underway to track the ambient plume as it was advected by the ocean current. In initial test experiments this process took sufficiently long (over 3 h) that we were unable to locate the ambient plume. The procedure was improved over the course of several experiments, so that the time between finishing the discharge of the dynamic plume and commencing tracking of the ambient plume was reduced to 5 min.

CTD tow-yo

The CTD rosette was equipped with an SBE911plus CTD sensor, an ECO Triplet scattering fluorescence sensor, and twenty Niskin bottles (10 L).

Plume tracking procedure

The CCFZ plume was tracked and monitored during seven hours, conducting a total of 13 transects across and along the plume at a velocity of 0.25 m s−1. In that period, the CTD rosette was constantly profiling for a total of 121 downcasts at depths between 50 to 120 m to characterize the evolution of the plume in terms of concentration, depth, thickness, location and dimensions. The ship track was determined based on a combination of the estimated locations of the plume using the ADCP model and the forecasts using the MIT-MSEAS modeling system (Fig. 4 and see “MIT-MSEAS numerical model” section).

ADCP advection model

The ADCP advection model was developed to estimate the location of the ambient plume and guide the tracking phase of the field studies. The shipboard Teledyne RDI Ocean Surveyor 150 kHz ADCP measured the ocean current velocity with a time resolution of 5 min and a vertical spatial resolution of 8 m. The current velocity data at the ambient plume depth was integrated over time to estimate the length and location of the ambient plume after the discharge. The width of the model predictions shown in Fig. 2b correspond to the observed ambient plume width and the consideration of plume diffusion; the ADCP advection model only predicts the location of the ambient plume centerline.

Dynamic plume models

Two dynamic plume models were used in this study. The DP1 model predicted the shape and maximum depth of the dynamic plume. The DP2 model predicted the neutral buoyancy height (trap depth) of the dynamic plume, accounting for any rebound from the maximum depth of the dynamic plume.

DP1 model

The dynamic plume model 1 (DP1 model)13, based on the classic semi-analytical turbulent plume model developed by Morton et al.9, was applied to estimate the near field dynamic plume behavior. The model captures the descent of the plume from the discharge nozzle to its maximum depth at which it has zero vertical momentum. The results from the model are presented in Fig. 2 and Table 2.

The classic plume model was modified to include the effect of a background cross flow12 in order to assess the relevant influence of the ocean current on the dynamic plume characteristics. The model predicts the dynamic plume vertical velocity, maximum depth, width, and dilution factors in the vicinity of the discharge. Three of the five governing differential equations of the model are derived from the mass, momentum, and buoyancy conservation principles. The two additional equations are obtained from the analysis of the plume kinematics. The system of equations is closed and solved by applying the entrainment assumption9. The dynamic plume is assumed to be a single-phase fluid, which this work has shown to be reasonable for plumes in the dynamic regime and with the sediment characteristics of interest for polymetallic nodule mining activities32. The model receives as inputs the ocean background stratification, the ocean current profile, and plume initial characteristics and also accounts for compressibility of seawater and heat transfer through the discharge pipe13.

DP2 model

The DP2 model is based on semi-analytical expressions for the neutral buoyancy level (or trap depth, hd) and volumetric dilution (D) for a plume generated from a continuous buoyancy source (single-phase or multiphase) in a stratified environment57. The semi-analytical expressions were fitted through laboratory experiments in which trap depths were determined from measurements of a source towed through a density stratified laboratory tank. For small sediment settling velocities (as in the case of the CCFZ sediment) the trap depth and dilution factor are \({h}_{{{{\rm{d}}}}}\,=\,2.8{(F{N}^{-3})}^{1/4}{e}^{-0.596{U}_{a}{({FN})}^{-1/4}}\), and \(D=2g({\rho }_{0}/{\rho }_{{{{\rm{a}}}}}-1)/({N}^{2}/{h}_{t})-1\) where Ua is the current velocity.

MIT-MSEAS numerical model

The multi-resolution data-assimilative MIT-MSEAS modeling system provided forecasts for the PLUMEX field experiment. The daily forecasts of the oceanographic fields and the estimated ambient plume advection guided experimental planning. Before each experiment, the MIT-MSEAS modelling system was used to determine which location was the best one for a successful experiment; we sought to avoid locations with unreasonably high background ocean velocities or complex vertical transports. The modeling system40,41 was set up over an area 687 × 720 km, with 2-way nesting domains of resolutions of 1.5 and 0.5 km, and 100 optimized terrain following vertical levels. The model bathymetry was obtained from the 15 arcseconds SRMT15 data set58. The tidal forcing fields were computed from the high resolution TPXO8-Atlas from OSU59 and reprocessed for the higher resolution bathymetry60 and nonlinear bottom drag. The forecasts were initialized from the 1/12°HYCOM (Hybrid Coordinate Ocean Model) daily analysis fields, but with updates based on varied in-situ and remote data of opportunity, and assimilating the PLUMEX CTD data.

The MIT-MSEAS forecasts of the ocean fields were used as the input to the plume advection computation. The plumes were assumed to be passively advected by the background ocean currents61, and governed by the advective-transport equation. The partial differential equation is solved using a novel composition-based advection methodology62. A collocated Cartesian grid was used with 5th order spatial and 3rd order temporal accurate finite volume numerical schemes. The velocity output of the implicit 2-way nested ocean model was interpolated four times in each horizontal direction for higher resolution, resulting in a horizontal grid spacing of 125 m and vertical grid spacing of 2 m. A numerical time step of 5 min was used. The results (Fig. 4) are a vertical projection of the three-dimensional plume onto a horizontal plane. Additional information on the plume predictions is available42 and details are also presented in Supplementary Notes 3.

TELEMAC numerical model

The TELEMAC (v7p2) numerical model63 was used to simulate a nodule mining region in the CCFZ and model the transport of a commercial-scale ambient plume via advection and diffusion (Fig. 7). TELEMAC is a finite element hydrodynamic model that solves the three-dimensional shallow water equations in order to resolve the flow field. The model was driven by atmospheric data from NAVGEM64, both tidal boundary conditions from OSU/TPXO59, as well as large scale ocean current data from HYCOM65. Two new implementations in the TELEMAC code were included for this application. First, a functionality allowing HYCOM data to be nudged to the local model near the boundaries. Second, the KPP turbulence model66 as implemented in GOTM67 and the Smagorinsky model were coupled to TELEMAC68 to model the vertical and horizontal turbulence, respectively. On top of the turbulence model, typical ocean background diffusivities and viscosities were applied (horizontal and vertical viscosities were 50 m2 s−1 and 10−4 m2 s−1, respectively, and effective horizontal and vertical diffusivities were 0.3 m2 s−1 and 0.03 m2 s−1, respectively). The values of diffusivity are selected to parameterize the subgrid scale turbulent mixing and are based on values commonly found in the literature16,20,46,50. On the other hand, the values of viscosity are defined to ensure the stability of the explicit numeric scheme applied in the TELEMAC model. Comparison of the model results with in-situ current velocity field measurements from the CCFZ and with a diffusion analytical model are included in Supplementary Figs. 8, 9 and Supplementary Notes 2, respectively.

The model domain consists of a rectangular area of size 6.78° × 6.64° (756 × 763 km) containing the Clarion-Clipperton Zone in the Northeastern Pacific. The boundaries of the model are 127° 55.2′W, 121° 7.2′W, 11° 16.8′N, and 17° 55.2′N (Supplementary Fig. 11). The unstructured mesh consisted of 196,278 triangular elements, with the element size varying between 200 m in the zone of interest around the release of the plume up to 10,000 m near the boundaries of the model. The model comprised 73 vertical layers, with z-layers (fixed vertical coordinates in the top 1000 m of the model and sigma coordinates below this). Refinement of the vertical mesh was applied near the bottom, as well as near the free surface and around the plume release location, where the mesh size is 100 m (1000 m below the free surface). The mesh-based Reynolds number was between 2 and 3 for the simulations.

For the plume, the near field DP1 model set the initial conditions for the ambient plume. The DP1 model used the flow field and background density stratification field from the TELEMAC model for every time step. For the far field motion of the plume, the model applies a standard advection-diffusion model for a passive tracer, taking into account the vertical and horizontal eddy viscosity from the turbulence model and the settling of the sediment particles, using a constant settling velocity of 0.1 mm s−1, which is characteristic of a 10 μm sediment particle.