Introduction

Photoacclimation is a dynamic physiological response to light availability, manifested as variations of the intracellular concentrations of light-harvesting pigments, which are most commonly observed as chlorophyll. Under low light conditions, phytoplankton increase their chlorophyll to carbon biomass ratio in a cell (cellular chl:phyC) in order to harvest more photons1,2,3. The cellular chl:phyC ratio is also constrained by nutrient availability and temperature1,2,3,4. Data5 compiled from incubation experiments reveal that cellular chl:phyC ratios vary by a factor of 606. In field data, cellular chl:phyC varies by a factor of 107,8. Geider3 proposed an empirical formula using differential equations for the dynamics of cellular chl:phyC, based on the results of incubation experiments. Other empirically based formulae for cellular chl:phyC have been developed to estimate net oceanic primary production from satellite observations6,9.

Photoacclimation, via changes in cellular chl:phyC, substantially impacts bulk chlorophyll concentrations and the resultant global distribution of oceanic chlorophyll. Vertical chlorophyll profiles generally exhibit maxima below the ocean surface, which are termed subsurface chlorophyll maxima (SCM) or deep chlorophyll maxima. SCM are observed nearly ubiquitously, in subtropical10, equatorial11,12,13, subpolar14, polar15,16,17,18, and upwelling regions19. Observations reveal substantial regional differences in typical SCM depth, which varies from 100–160 m in the subtropics10, to around 40 m in subpolar regions14. SCM depth is closely associated with the depth of the nutricline20, at which nutrient concentrations sharply increase downward. The mechanisms underlying SCM formation have long been discussed and debated20. In subtropical regions, photoacclimation is recognized as an important mechanism underlying SCM formation21,22,23,24, where it is attributed mostly to increases in cellular chl:phyC with depth. For equatorial SCM, some studies have highlighted the importance of photoacclimation25, while others regard SCM as peaks of biomass26. In the subpolar, polar, and upwelling regions, the role of photoacclimation in SCM formation remains unclear.

The purpose of the study is to evaluate to what degree photoacclimation, based on strategic resource optimization, determines global distributions of chlorophyll and hence SCM. We implemented the 0D Flexible Phytoplankton Functional Type (FlexPFT) model of Smith et al.27 within a global biogeochemical ocean circulation model. The FlexPFT model combines theories for phytoplankton physiology as proposed by Pahlow28 and others29,30. This theory accounts for intracellular resource allocation among structural material, nutrient uptake, and light harvesting associated with the chloroplast (Supplementary Fig. 1a). Phytoplankton are assumed to optimize their resource allocation to nutrient uptake versus light-harvesting biomolecules, depending on light, nutrient, and temperature conditions, in order to maximize their growth rate. Under low light and nutrient-replete conditions, phytoplankton increase their resource allocation for light harvesting (chloroplast) while decreasing that for nutrient uptake (Supplementary Fig. 1b). This resource allocation theory has recently provided the first theoretical derivation31 of the widely applied empirical Droop cell quota model32. Pahlow’s model28 has also explained the results of incubation experiments33.

Results and discussion

Role of photoacclimation in SCM formation

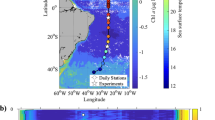
The simulation reproduces the regional differences in SCM depth among subpolar, subtropical, and equatorial regions as observed in the North Pacific and Atlantic, with a slightly shallower SCM in the Atlantic subtropical regions (Fig. 1a–d). Simulated SCM is frequently located around the nutricline, where vertical nutrient gradients are steepest (Fig. 1e, f). Since chlorophyll concentration is given by the product of phytoplankton carbon biomass concentration (phyC) (Fig. 1g, h) and cellular chl:phyC (Fig. 1i, j), SCM depth varies with latitude as a consequence of regional differences in the vertical profiles of phyC and cellular chl:phyC. phyC is maximal at the surface in most oceanic regions, (Fig. 1g, h), consistent with observations34. Maximal values of cellular chl:phyC (Fig. 1i, j), on the other hand, tend to occur at greater depths (60–130 m). This result highlights the need to account for photoacclimation when modeling and interpreting observations of chlorophyll, which despite being the most commonly observed metric of phytoplankton, is not a good proxy for their biomass4,6.

Fig. 1: Meridional sections of biogeochemical variables associated with the formation of subsurface chlorophyll maxima in the North Pacific and Atlantic Oceans.
figure 1

Distributions from the North Pacific (160° E, R/V Hakuho-Maru KH12-314, 6 July 2012 to 14 Aug 2012) and Atlantic (Atlantic Meridional Transect AMT-14, 26 April 2004 to 02 June 2004) of a, b observed chlorophyll concentration (μg chl L−1). Simulated distributions during July and May in 2004 (the final simulation year), respectively, of c, d chlorophyll concentration (μg chl L−1), e, f nitrate (NO3) concentration (μmol N L−1), g, h phytoplankton carbon biomass concentration (phyC, μmol C L−1), i, j cellular chlorophyll to carbon ratio (chl:phyC in a cell, g chl molC−1), k, l chloroplast chlorophyll to carbon ratio (chl:phyC in the chloroplast, g chl molC−1), m, n fractional resource allocation to chloroplast.

Full size image

By comparing the vertical profiles of chlorophyll concentration, cellular chl:phyC, and phyC in the subtropical, equatorial, subpolar, Antarctic, and upwelling regions (Fig. 2), respectively, we show that photoacclimation mainly determines the SCM depth. In our model results, SCM do not correspond to the maxima of phyC, which is consistent with previous laboratory results4. In subtropical regions, SCM appear at 118 m depth, at which phyC is one-third of its surface value, while cellular chl:phyC is 50 times its value at the surface (Fig. 2f). Since the cellular chl:phyC varies more over depth than does phyC, the SCM depth resides near the depth of the maximum cellular chl:phyC (Fig. 2a), i.e., deep SCM are formed. In subpolar regions, where the SCM are shallow (28 m depth), cellular chl:phyC at the surface is about 1/5 of its maximum at 82 m depth, while phyC at the surface is about 16 times its value at 82 m (Fig. 2h). Therefore, the SCM depth occurs near the depth of the maximum phyC, relatively close to the surface (Fig. 2c). Hence in these regions, the SCM depth is primarily determined by the extent to which cellular chl:phyC at the surface is less than its maximum value, which occurs in the subsurface. This SCM formation mechanism is common to the equatorial (Fig. 2b, g), Antarctic (Fig. 2d, i), and upwelling regions (Fig. 2e, j).

Fig. 2: Simulated vertical distributions of chlorophyll concentration, phytoplankton carbon biomass concentration and cellular chlorophyll to carbon ratios.
figure 2

a–e Simulated representative vertical distributions of chlorophyll concentration (μg chl L−1) and f–j phytoplankton carbon biomass concentration (phyC, μmol C L−1, broken blue line) and cellular chlorophyll to carbon ratio (cellular chl:phyC, g chl molC−1, solid red line) in a, f the subtropical center in May, b, g equator in May, c, h subpolar region in July, d, i Antarctic Ocean in January, and e, j upwelling region in July in 2004 (the final simulation year).

Full size image

In the resource allocation theory, cellular chl:phyC is the product of the chlorophyll to carbon biomass ratio within the chloroplast (chloroplast chl:phyC) (Fig. 1k, l), and the resource allocation ratio for (i.e., the ‘size’ of) the chloroplast (Fig. 1m, n). For example, if chloroplast chl:phyC is 0.3 g chl mol C−1 and the resource allocation ratio for the chloroplast is 0.5 (non-dimensional), cellular chl:phyC is 0.15 g chl mol C−1. Chloroplast chl:phyC depends on only light intensity27. As light intensity decreases with depth, chloroplast chl:phyC increases from the surface to its maximal depth, which is about 90 m in equatorial regions and 50 m in subpolar regions. Below the maximal depth, chloroplast chl:phyC decreases with depth. The balance between benefits and respiration costs of maintaining chlorophyll30 determines the depth of maximal chloroplast chl:phyC. The depth of maximal chloroplast chl:phyC is, in turn, a major determinant of the depth of maximal cellular chl:phyC.

Values of the intracellular resource allocation ratio to the chloroplast near 0 (or 1) mean that resources are mainly allocated to nutrient uptake (or light harvesting), with minimal allocation to the competing use. At depths below about 130 m, where light intensity is consistently low, this resource allocation is heavily skewed toward the chloroplast in all oceanic regions. By contrast, above about 130 m in low nutrient regions such as the subtropics, this resource allocation is heavily skewed toward nutrient uptake, and therefore few resources are allocated to the chloroplast. On the contrary, near the surface in high nutrient, e.g., subpolar, regions, phytoplankton resource allocation is more evenly balanced between chloroplast and nutrient uptake. Regional differences in the fractional resource allocation to the chloroplast caused by different nutrient conditions mainly determine regional patterns of cellular chl:phyC. This explains why cellular chl:phyC tends to be very low near the surface in the subtropics, and more generally, why SCM tend to be deeper in low nutrient regions than in high nutrient regions.

Previous observational studies have highlighted the important role of nutricline depth as a determinant of SCM depth. Resource allocation theory provides a more detailed mechanistic basis for the dependence of SCM depth on nutricline depth as well as light. Because nutrient concentrations increase steeply with depth near the nutricline, fractional resource allocation to the chloroplast also increases steeply downward, resulting in sharp increases in cellular chl:phyC. As a result, maximal bulk chlorophyll concentration, i.e., SCM formation, tends to occur around the nutricline. Significant relations among the strong vertical gradients of cellular chl:phyC, nutricline, and SCM obtained in our model are consistent with a previous study for the California Current System35.

Global SCM distribution

The simulated global patterns in SCM depth (Fig. 3) are consistent with observed results, as described below. In our simulation, SCM are ubiquitous across the global ocean as in a SCM estimation from observed surface chlorophyll distributions36. Global features, such as a remarkable change in SCM depth across the subtropical-subpolar boundary and SCM shallowing in upwelling regions, agree with patterns of the satellite-estimated global SCM distribution36. The simulation also successfully describes observed shallowing of SCM depths toward the coasts20,21. In summer in the Arctic and Antarctic Ocean, the simulated SCM depth of 50–65 m is in line with observations15,16,17,18. In February and August, SCM occur at similar depths in most of oceanic regions. The successful simulation of the global patterns in SCM depth was achieved by explicitly incorporating phytoplankton’s resource allocation strategy into the model.

Fig. 3: Simulated global distributions of subsurface chlorophyll maxima depth.
figure 3

Subsurface chlorophyll maxima (SCM) depth (m) in a February and b August in the final simulation year. Blank regions in the ocean show that chlorophyll concentration is maximal at the ocean surface. Black lines indicate the cruise tracks of R/V Hakuho-Maru KH12-3 and AMT-14 displayed in Fig. 1. White stars indicate the locations of representative profiles displayed in Fig. 2.

Full size image

Limitations of the model

Our model employs only one generic phytoplankton species, and therefore does not explicitly resolve community composition. In case studies in which the chlorophyll-specific initial slope of growth versus irradiance, aI, is changed (Supplementary Fig. 2), increasing aI causes deeper SCM and increase in chlorophyll concentration around the SCM, which improves reproducibility of chlorophyll around SCM, but at the expense of making surface chlorophyll concentration deviate far from the observations. In the standard case, our model is tuned in order to simulate both surface and deep chlorophyll concentration to a reasonable degree with the single generic phytoplankton species. However, different photoacclimation responses have been observed for different phytoplankton lineages37. In the future, by introducing surface and deep species having different traits for irradiance, our model can be expected to reproduce more realistic SCM depth and chlorophyll concentration around the SCM. Another limitation of our model is that it represents chlorophyll concentration only at scales larger than about 10 m due to its vertical resolution. For finer-scale vertical variation of chlorophyll concentration, aggregation related to swimming behavior or buoyancy control20 may play some roles. A mesoscale eddy has been observed to alter SCM depth substantially, from 80 to 120 m38, which is beyond the scope of this study due to the coarse resolution of our physical model.

Relevance to future climate change

Climate change is expected to alter the oceanic environment, especially temperature, stratification, and nutrient supply rates. Its impact on phytoplankton39, which are the sustaining basis of marine food chains, will be crucial for humankind. Our research has proceeded on the premise that improving models’ ability to reproduce the observed chlorophyll distribution will yield more reliable future projections. By establishing a mechanistic link between the individual-level photoacclimation response of phytoplankton and chlorophyll distributions at the global scale, our results provide a more sound basis for interpreting chlorophyll observations and predicting how oceanic phytoplankton in particular, and hence marine ecosystems more broadly, will respond to future climate change.

Methods

Physical model

The physical part of the model is a global Oceanic General Circulation Model, Meteorological Research Institute Community Ocean Model version 3 (MRI.COM3)40. The model has horizontal resolutions of 1° in longitude and 0.5° in latitude south of 64° N, and tripolar coordinates are applied north of 64° N. The model is discretized in 51 vertical layers. In the upper 160 m, tracers are calculated at depths of 2.0, 6.5, 12.25, 19.25, 27.5, 37.75, 50.5, 65.5, 82.25, 100.0, 118.2, 137.5, and 157.75 m, and therefore vertical variation in chlorophyll concentration below the grid-scale is not represented in our model. The model was forced with realistic wind stress, surface heat and freshwater fluxes40.

Marine ecosystem model

We developed a marine ecosystem model composed of phytoplankton, zooplankton, nitrate, ammonia, particulate organic nitrogen, dissolved organic nitrogen, dissolved iron (Fed), and particulate iron. Our model is a 3D version of the FlexPFT model27 and is called the FlexPFT-3D model. The main changes of the FlexPFT-3D from original FlexPFT model are the introduction of iron limitation and substitution of the carbon-based phytoplankton biomass in the original with nitrogen-based biomass herein. The iron cycle is based on the nitrogen-, silicon- and iron-regulated Marine Ecosystem Model41 including the process of scavenging and iron input from dust and sediment. Dissolved iron starts from the distribution calculated by the Biological Elemental Cycling model in Misumi et al.42. Nitrate starts from the distribution of World Ocean Database 199843. After the connection of the physical model, a 20 years of historical simulation (1985–2004) is performed. In addition to the standard case with the chlorophyll-specific initial slope of growth versus irradiance, aI, of 0.35 m2 E−1 mol C (g chl)−1, the case studies with aI of 0.5 and 1.0 m2 E−1 mol C (g chl)−1 were implemented. The case studies are calculated from 2003 to 2004, starting from the distributions of biological variables at the end of 2002 in the standard case.

Phytoplankton growth

The procedures of numerical integration of phytoplankton concentration are described here. Readers can construct a numerical model using the following equations. The derivations of the following equations from theories are presented by Smith et al.27 (hereafter Smith2016). Values of biological parameters are described in Supplementary Table 1.

In accordance with Pahlow’s resource allocation theory28, the FlexPFT model assumes that resources are allocated among structural material, nutrient uptake and, light harvesting (Supplementary Fig. 1a). The fraction of structural material is assumed to be Qs/Q, where Q is the nitrogen cell quota, which is the intracellular nitrogen to carbon ratio (mol N mol C−1), and Qs is the structural cell quota (mol N mol C−1) given as a fixed parameter. The fraction of nutrient uptake is defined as fV (non-dimensional), so that the residual fraction available for light-harvesting is equal to \((1-\frac{{Q}_{{\rm{s}}}}{Q}-{f}_{{\rm{v}}})\). Optimal uptake kinetics further sub-divides the resources allocated to nutrient uptake between surface uptake sites (affinity) and enzymes for assimilation (maximum uptake rate), the fraction of which is given by fA and (1 − fA), respectively. Under nutrient-deficient conditions, the number of surface uptake sites (and hence affinity) increases, while enzyme concentration (hence, maximum uptake rate) decreases. The FlexPFT model assumes instantaneous resource allocation, which means that resource allocation tracks temporal environmental change with no lag time. It has elsewhere been demonstrated that an instantaneous acclimation model provides an accurate approximation of a fully dynamic acclimation model44.

We assume that acclimation responds to daily-averaged environmental conditions, which are used to calculate the optimal values of fV, fA, and Q as \({f}_{V}^{o}\), \({f}_{A}^{o}\), and \({Q}^{o}\). The optimal values are estimated at the beginning of a day and are retained for the following 24 h. The daily-averaged environmental variables of the seawater temperature, T (°C), intensity of photosynthetically active radiation, I, nitrogen concentration, [N], which is the sum of nitrate and ammonia concentrations, and dissolved iron concentration, [Fed] are defined as \(\bar{T}\), \(\bar{I}\), \([\bar{{\rm{N}}}]\), and \([{\overline{{\rm{Fe}}}}_{{\rm{d}}}]\), respectively. Based on the assumption that diurnal variation of temperature and nutrient are very small, T, [N] and [Fed] at the beginning of a day are used as \(\bar{T}\), \([\bar{{\rm{N}}}]\), and \([{\overline{{\rm{Fe}}}}_{{\rm{d}}}]\), respectively. For \(\bar{I}\), we use the average in sunshine duration in a day, which is slightly modified from the daily average in Smith2016.

Phytoplankton growth rate per unit carbon biomass (day−1), μ, is given by

$$\mu ={\hat{\mu }}^{I}\left(1-\frac{{Q}_{{\rm{s}}}}{{Q}^{o}}-{f}_{V}^{o}\right)-{\zeta }^{N}{f}_{V}^{o}{\hat{V}}^{N},$$
(1)

where \({\hat{\mu }}^{I}\) is the potential carbon fixation rate per unit carbon biomass (day−1), \({\zeta }^{N}\) is the energetic respiratory cost of assimilating inorganic nitrogen (0.6 mol C mol N−1), and \({\hat{V}}^{N}\) is the potential nitrogen uptake rate per unit carbon biomass (mol N mol C−1 day−1). Equation (1) represents the balance of net carbon fixation and respiration costs of nitrogen uptake, which are proportional to the fraction of resource allocation. \({\hat{V}}^{N}([\bar{{\rm{N}}}],\,\bar{T})\) is

$${\hat{V}}^{N}([\bar{{\rm{N}}}],\bar{T})=\frac{{\hat{V}}_{0}[\bar{{\rm{N}}}]}{(\frac{{\hat{V}}_{0}}{{\hat{A}}_{0}})+2\sqrt{\frac{{\hat{V}}_{0}[\bar{{\rm{N}}}]}{{\hat{A}}_{0}}}+[\bar{{\rm{N}}}]},$$
(2)

where \({\hat{A}}_{0}\) and \({\hat{V}}_{0}\) are the maximum value of affinity and maximum nitrogen uptake rate.

From here, we will explain how the optimized values such as \({f}_{V}^{o}\), \({f}_{A}^{o}\), and \({Q}^{o}\) are calculated. The optimal fraction of resource allocation to affinity, \({f}_{A}^{o}\), is given by

$${f}_{A}^{o}={[1+\sqrt{\frac{{\hat{A}}_{0}[\bar{{\rm{N}}}]}{F(\bar{T}){\hat{V}}_{0}}}]}^{-1},$$
(3)

which is derived by substituting Eqs. (18) and (19) in Smith2016 into Eq. (17). \(F(\bar{T})\) is temperature dependence, defined as

$$F(\bar{T})=\exp \{-\frac{{E}_{a}}{R}[\frac{1}{\bar{T}+298}-\frac{1}{{T}_{{\rm{ref}}}+298}]\,\},$$
(4)

where Ea is the parameter of the activation energy of 4.8 × 104 J mol−1, R is the gas constant of 8.3145 J (mol K)−1, and Tref is the reference temperature of 20 °C.

Optimization for light-harvesting is described below. The potential carbon fixation rate per unit carbon biomass (day−1), \({\hat{\mu }}^{I}\,\)(day−1), in Eq. (1) is

$${\hat{\mu }}^{I}(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}])={\hat{\mu }}_{0}\frac{[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]}{[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]+{k}_{{\rm{Fe}}}}S(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}])F(\bar{T}),$$
(5)

where \({\hat{\mu }}_{0}\) and kFe are the maximum carbon fixation rate and half saturation constant for iron, respectively. S specifies the dependence of light. Defining \({\hat{\mu }}_{0}^{{\rm{limFe}}}={\hat{\mu }}_{0}\frac{[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]}{[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]+{k}_{{\rm{Fe}}}}\),

$${\hat{\mu }}^{I}(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}])={\hat{\mu }}_{0}^{{\rm{limFe}}}S(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]\,)F(\bar{T}).\,$$
(6)

Iron limitation is imposed by substituting \({\hat{\mu }}_{0}\) to \({\hat{\mu }}_{0}^{{\rm{limFe}}}\) in all equations in Smith2016. S is defined as

$$S(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]\,)=1-\exp \{\frac{-{a}_{I}{\hat{\Theta }}^{o}\bar{I}}{{\hat{\mu }}_{0}^{{\rm{limFe}}}F(\bar{T})}\},$$
(7)

where \({a}_{I}\) is the chlorophyll-specific initial slope of growth versus irradiance. \({\hat{\Theta }}^{o}\), optimal chloroplast chl:phyC (g chl (mol C)−1), is

$${\hat{\Theta }}^{o} = \; \frac{1}{{\zeta }^{{\rm{chl}}}}+\frac{{\hat{\mu }}_{0}^{{\rm{limFe}}}}{{a}_{I}\bar{I}}\{1-{W}_{0}[(1+\frac{{R}_{M}^{{\rm{chl}}}}{{L}_{{\rm{d}}}{\hat{\mu }}_{0}^{{\rm{limFe}}}})\exp (1+\frac{{a}_{I}\bar{I}}{{\zeta }^{{\rm{chl}}}{\hat{\mu }}_{0}^{{\rm{limFe}}}})\,]\,\}\,(\bar{I} > {I}_{0})\\ {\hat{\Theta }}^{o} = \; 0\,(\bar{I}\le {I}_{0}),$$
(8)

where constant parameters \({{\rm{\zeta }}}^{{\rm{chl}}}\) and \({R}_{M}^{{\rm{chl}}}\) are the respiratory cost of photosynthesis (mol C (g chl)−1) and the loss rate of chlorophyll (day−1), respectively. Ld is the fractional day length in 24 h. W0 is the zero-branch of Lambert’s W function. I0 is the threshold irradiance below which the respiratory costs overweight the benefits of producing chlorophyll:

$${I}_{0}=\frac{{\zeta }^{{\rm{chl}}}{R}_{M}^{{\rm{chl}}}}{{L}_{{\rm{d}}}{a}_{I}}.\,$$
(9)

The optimal fraction of resource allocation to nutrient uptake, \({f}_{V}^{o}\), is

$${f}_{V}^{o}=\frac{{\hat{\mu }}^{I}(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}]){Q}_{{\rm{s}}}}{{\hat{V}}^{N}([\bar{{\rm{N}}}],\bar{T})}[-1+\sqrt{{[{Q}_{{\rm{s}}}(\frac{{\hat{\mu }}^{I}(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}])}{{\hat{V}}^{N}([\bar{{\rm{N}}}],\bar{T})}+{\zeta }^{N})]}^{-1}+1}\,]$$
(10)

The optimal nitrogen cell quota, \({Q}^{o}\) is

$${Q}^{o}={Q}_{{\rm{s}}}[1+\sqrt{1+{[{Q}_{{\rm{s}}}(\frac{{\hat{\mu }}^{I}(\bar{I},\bar{T},[{\overline{{\rm{Fe}}}}_{{\rm{d}}}])}{{\hat{V}}^{N}([\bar{{\rm{N}}}],\bar{T})}+{\zeta }^{N})]}^{-1}}\,]$$
(11)

Optimal cellular chl:phyC (g chl (mol C)−1), \({\Theta }^{o}\), is

$${\Theta }^{o}=(1-\frac{{Q}_{{\rm{s}}}}{{Q}^{o}}-{f}_{V}^{o}){\hat{\Theta }}^{o}$$
(12)

which is the multiplication of the fraction of resource allocation to light-harvesting and optimal chloroplast chl:phyC. The cellular chl:phyC and chloroplast chl:phyC in Figs. 1 and 2 are optimal cellular chl:phyC, \({\Theta }^{o}\), and optimal chloroplast chl:phyC, \({\hat{\Theta }}^{o}\), respectively. The relation in Eq. (12) is displayed in Fig. 1i-n. If we artificially turn off the optimization of resource allocation by applying the constant \({Q}^{o}\) and \({f}_{V}^{o}\) to the all grid points, optimal cellular chl:phyC (Fig. 1i,j) only depends on optimal chloroplast chl:phyC (Fig. 1k, l), and therefore significant variation of SCM depth across the equatorial, subtropical, and subpolar regions is not reproduced.

In the above equations, Eqs. (3), (8), (10), (11), and (12), optimized values related to acclimation processes are obtained and then used in calculating the phytoplankton growth rate. Phytoplankton growth rate per unit carbon biomass (day−1), \(\mu\), in Eq. (1) is calculated at each time step:

$$\mu (I,T,[{\rm{N}}],[{{\rm{Fe}}}_{{\rm{d}}}])=\frac{{\hat{\mu }}^{I}(I,T,[{{\rm{Fe}}}_{{\rm{d}}}]){f}_{V}^{o}(1-{f}_{A}^{o}){\hat{V}}_{0}{f}_{A}^{o}{\hat{A}}_{0}[{\rm{N}}]}{{\hat{\mu }}^{I}(I,T,[{{\rm{Fe}}}_{{\rm{d}}}]){Q}_{0}(1-{f}_{A}^{o}){\hat{V}}_{0}+({\hat{\mu }}^{I}(I,T,[{{\rm{Fe}}}_{{\rm{d}}}]){Q}_{0}+{f}_{V}^{o}(1-{f}_{A}^{o}){\hat{V}}_{0}){f}_{A}^{o}{\hat{A}}_{0}[{\rm{N}}]},$$
(13)

where \({\hat{\mu }}^{I}(I,\,T,\,[{{\rm{Fe}}}_{{\rm{d}}}])\) is obtained by substituting I, T, and [Fed] for \(\bar{I}\), \(\bar{{\rm{T}}}\), and \([{\overline{{\rm{Fe}}}}_{{\rm{d}}}]\) in Eq. (5), respectively. Note that the model calculates circadian variation in solar irradiance, I, and therefore the phytoplankton growth rate, μ, reaches its maximum at noon local time and is zero during night. On the other hand, phytoplankton optimization is assumed to respond to daily-averaged conditions. The FlexPFT model introduces phytoplankton respiration proportional to chlorophyll content, which is another important originality of Pahlow’s resource allocation theory30,33.

The carbon biomass-specific respiratory costs of maintaining chlorophyll, Rchl, is

$${R}^{{\rm{chl}}}(I,T,[{\rm{N}}],[{{\rm{Fe}}}_{{\rm{d}}}])=({\hat{\mu }}^{I}(I,T,[{{\rm{Fe}}}_{{\rm{d}}}])+{R}_{M}^{{\rm{chl}}}){{\rm{\zeta }}}^{{\rm{chl}}}{\Theta }^{o}.\,$$
(14)

The growth rate per unit nitrogen biomass, \({\mu }_{{\rm{N}}}\), is equal to that per unit carbon biomass, μ. Instantaneous acclimation assumes that the quota of nitrogen to carbon biomass obtained by phytoplankton growth is equal to the nitrogen quota in a cell: \(\frac{{\mu }_{{\rm{N}}}[{{\rm{p}}}^{{\rm{N}}}]}{\mu [{{\rm{p}}}^{{\rm{C}}}]}={Q}^{o}\), where [pC] and [pN] are phytoplankton carbon and nitrogen concentration in a cell, respectively. Since \(\frac{[{{\rm{p}}}^{{\rm{N}}}]}{[{{\rm{p}}}^{C}]}={Q}^{o}\), \({\mu }_{{\rm{N}}}=\mu\). When temporal \({Q}^{o}\) change occurs, to satisfy the mass conservation, carbon or nitrogen biomass is adjusted with the other fixed. The FlexPFT fixes carbon biomass, while the FlexPFT-3D fixes nitrogen biomass to the temporal \({Q}^{o}\) change.

The rate of change in the phytoplankton nitrogen concentration, [pN], except for the advection and diffusion terms is given by the following equation:

$$\frac{\partial [{{\rm{p}}}^{{\rm{N}}}]}{\partial t}=\mu [{{\rm{p}}}^{{\rm{N}}}]-({R}^{{\rm{chl}}}+{R}^{{\rm{cnst}}})[{{\rm{p}}}^{{\rm{N}}}]-{M}_{{\rm{p}}}{[{{\rm{p}}}^{{\rm{N}}}]}^{2}-({\rm{extracellular}}\,{\rm{excretion}})-({\rm{grazing}}),$$
(15)

where Rcnst and Mp are the coefficient of respiration not related to chlorophyll concentration and mortality rate coefficient, respectively. The extracellular excretion is

$$({\rm{extracellular}}\,{\rm{excretion}})={\gamma }_{{\rm{ex}}}[(\mu -{R}^{{\rm{chl}}})[{{\rm{p}}}^{{\rm{N}}}]],$$
(16)

where \({\gamma }_{{\rm{ex}}}\) is the coefficient of extracellular excretion. The grazing term is represented by

$$({\rm{grazing}})={G}_{20\deg }F(T)[{{\rm{z}}}^{{\rm{N}}}]\frac{{[{{\rm{p}}}^{{\rm{N}}}]}^{{a}_{{\rm{H}}}}}{{({k}_{{\rm{H}}})}^{{a}_{{\rm{H}}}}+{[{{\rm{p}}}^{{\rm{N}}}]}^{{a}_{{\rm{H}}}}},$$
(17)

where G20deg is the maximum grazing rate at 20 °C, and [zN] is zooplankton concentration. Temperature dependency, F(T), is obtained by substituting T for \(\bar{T}\) in Eq. (4). \({a}_{{\rm{H}}}\) is the parameter controlling Holling-type grazing, which takes a value from 1 to 2. kH is the grazing coefficient in Holling-type grazing.

Once [pN] is calculated, phytoplankton carbon concentration (mol C L−1), and chlorophyll concentration (g chl L−1) are uniquely determined in an environmental condition, without prognostic calculation. Therefore, an instantaneous acclimation model can represent stoichiometric flexibility with lower computational costs compared with a dynamic acclimation model44.

Model validation

The spatial pattern of simulated annually mean chlorophyll at the ocean surface agrees with that of satellite observation45 (Supplementary Fig. 3). The model reproduced the contrast of the surface chlorophyll concentration between subtropical and subpolar regions, although simulated surface chlorophyll concentration in subtropical regions is lower than that of the observation partly due to the lack of nitrogen fixers. Nitrogen fixation is estimated to support about 30–50% of carbon export in subtropical regions46,47. Simulated surface chlorophyll distribution in the Pacific equatorial region is close to the observed.

Our model properly simulates the meridional distribution of nitrate compared with that of observations48 (Supplementary Fig. 4). The simulated horizontal distribution of primary production is consistent with that estimated by satellite data9,49 (Supplementary Fig. 5), although simulated primary production is underestimated in subtropical regions, associated with the underestimation of surface chlorophyll in these regions (Supplementary Fig. 3).