Abstract
Proxy-based reconstructions of the past suggest that the Pacific ocean has often shown El Niño-like warming after low-latitude volcanic eruptions, while climate model simulations have suggested diverse responses. Here we present simulations from a coupled ocean–atmosphere model that illuminate the roles of ocean preconditioning, eruption magnitude and timing, and air–sea feedbacks in the El Niño/Southern Oscillation (ENSO) response to these eruptions. A deterministic component of the response, which dominates for boreal summer eruptions, leads to cooler tropical Pacific sea surface temperatures in the eruption year and El Niño-like warming the following year. A stochastic component is also important, especially for boreal winter eruptions. The simulated ENSO response depends nonlinearly on the eruption magnitude and the tropical Pacific conditions before the eruption. We conclude that adequate sampling is critical to accurately assess the ENSO responses in both models and observations.
Similar content being viewed by others
Introduction
As Earth’s main source of seasonal-to-interannual climate anomalies1,2, the El Niño/Southern Oscillation (ENSO) influences environmental hazards all over the globe3,4,5,6,7. ENSO is a coupled atmosphere-ocean phenomenon describing the anomalous change of trade winds and sea surface temperature (SST) in the equatorial Pacific. ENSO alternates between positive (El Niño) and negative (La Niña) phases causing, respectively, anomalous warming and cooling of the equatorial Central and Eastern Pacific8. The SST anomaly averaged over the Niño3.4 region (170–120W, 5S–5N) is commonly used as an ENSO index, as it is highly correlated with many of the atmospheric and oceanic changes observed during ENSO events.
El Niños have varying strengths and involve a diverse spectrum of SST patterns and impacts9,10. For example, SST anomalies for weak and moderate El Niños tend to peak in the Central Pacific (CP), while SST anomalies for stronger El Niños usually extend into the Eastern Pacific (EP)8,11,12,13. CP and EP El Niños involve different physical processes and affect global climate differently14,15. They are, therefore, needed to be studied separately.
ENSO is sensitive to external forcing on different time scales. Solar forcing is responsible for millennial ENSO variability due to orbitally induced changes in insolation16, and it can also explain the decadal variability related to the sunspot activity cycle17. Global warming can significantly alter ENSO18,19,20,21,22,23,24,25,26,27,28,29, but this remains uncertain due to the difficulty in simulating ENSO. Strong volcanic eruptions can suddenly disrupt ENSO on a short time scale (2–5 years) and may serve as a natural experiment in helping to illuminate the mechanisms of ENSO’s sensitivities to external forcings30,31,32,33,34.
Volcanic plumes formed by explosive low-latitude eruptions can reach the lower stratosphere, where they can spread globally—affecting the planet’s energy balance, heating the lower stratosphere, and cooling the Earth’s surface and the troposphere. The redistribution of radiative heating in the atmosphere causes complex dynamical responses of the ocean and atmosphere, which can lead to, for example, winter warming in Northern Europe and Asia35,36,37, or anomalous cooling in the Middle East38. It has also been observed that the majority of recent eruptions of this kind coincided with or were followed by El Niño-like conditions in the tropical Pacific39,40. Over the past decade, the response of ENSO to volcanic forcing has received significant attention41,42,43,44,45,46,47,48,49,50,51,52,53,54,55, although consensus on the response mechanisms has not yet been reached.
A number of hypotheses have been proposed to describe the mechanism of the ENSO response to volcanic eruptions. For low-latitude eruptions, some studies favor the land-ocean temperature gradient (LOTG)44,52,54,55 or ocean-dynamical thermostat (ODT) mechanisms41,42,56,57. Both mechanisms may trigger westerly wind anomalies, which in turn lead to the formation of an El Niño-like response after strong volcanic eruptions. The LOTG is based on the different thermal capacity of land and ocean; the volcanically induced temperature gradient between the Maritime continent and the WP ocean usually weakens the trade winds. However, in our previous study49, we found it to be relatively short-lived. We concluded that the SST gradient further controls the westerly wind anomalies initiated by the LOTG over the CP resulting from the ODT41,56,57. The ODT is based on the ocean’s ability to moderate the SST response caused by the radiative forcing more effectively in the equatorial EP upwelling region, leading to temperature differences between the Western Pacific and EP. Since the ODT is sensitive to the strength of equatorial ocean upwelling, its intensity is closely related to the ENSO preconditioning49 and, therefore, may also be the reason for different strength of the El Niño-like response in the Pacific after volcanic eruptions.
A study using the Community Earth System Model (CESM) suggested another mechanism attributing an El Niño-like response in the following (second) year after the low-latitude eruption to meridional energy advection, excited by the wind stress curl induced by equatorial cooling of the ocean surface48. A study using the Institute Pierre Simone Laplace (IPSL) climate model attributed an El Niño-like response to a volcanically induced rapid cooling of the African continent, which weakened the West-African monsoon and induced westerly wind anomalies over the Western Pacific (WP)50. A study using the Norwegian Earth System Model considered the ENSO response to the tropical volcanic eruptions with asymmetrically distributed aerosol plume. It reports that the main response mechanisms are the extratropical circulation changes, including the shift of the Pacific jet and the cyclonic surface pressure anomaly near the Pacific mid-latitudes, and to a lesser extent, the shift of the Intertropical Convergence Zone58. For high-latitude eruptions, it has been proposed that a strong volcanic eruption in the Northern Hemisphere could shift the Intertropical Convergence Zone (ITCZ) southward and thus trigger an El Niño-like response47.
However, the inconsistencies between the ENSO responses to strong volcanic eruptions and their mechanisms reported by the above studies may arise from the incomplete sampling for time composites and ensembles. When analyzing the ENSO response to volcanic forcing, the sampling criteria should necessarily account for:
-
ENSO preconditioning (or an ENSO onset) that is associated with a set of atmospheric and oceanic conditions preceding the eruption44,47,49. These ICs are referred to here as Neutral, El Niño, or La Niña onsets, if in the absence of external forcing, they lead to either neutral, positive, or negative ENSO years, respectively. The tropical Pacific response highly depends on the ocean preconditioning regardless of the eruption type (high-latitude or low-latitude). For example, Neutral or El Niño onsets are more likely to be affected by low-latitude eruptions44,49 than a La Niña onset. Moreover, CP El Niño onsets respond more strongly than EP El Niño onsets49.
-
Volcanic eruption timing relative to the seasonal cycle or ENSO48,49 that may hide strong stochasticity of the ENSO response. Generally, ENSO is sensitive to even tiny perturbations that occur during the boreal winter. However, if the perturbation happens during the boreal summer, the ENSO response is more robust49,59, which is consistent with the well-known boreal spring predictability barrier for ENSO60. Therefore, considering that volcanic eruptions may take place any time during the year61, it is important to analyze the impacts of differently timed volcanic eruptions separately.
-
Volcanic eruption magnitude that is responsible for the strength of the ENSO response. The stronger the volcanic eruption is, the more significant the ENSO response it should cause. For example, the Tambora eruption in 1815, which was three times stronger than the Pinatubo eruption in 1991, would cool the EP surface more in the first year, and then trigger a warmer El Niño in the second year than would a Pinatubo-size eruption42,44,48,49,62,63.
-
Volcanic eruption location that is responsible for the distribution and lifetime of the aerosol plume. The volcanic aerosols are usually globally distributed for most low-latitude eruptions, although sometimes they may be trapped by one hemisphere58, and hemispherically-distributed for high-latitude eruptions64,65,66. Both types of eruptions can cause a significant ENSO response67. However, the ENSO response to high-latitude eruptions is less pronounced than the response to low-latitude eruptions due to the relatively shorter aerosol lifetime and different response mechanisms involved46,47,51,68,69.
The present study focuses on the effects of low-latitude eruptions on ENSO. We examine the ENSO response sensitivity to the volcanic eruptions taking into account volcanic magnitude and season as well as the ENSO state (preconditioning) before the eruption. We also test different mechanisms of the ENSO response to low-latitude eruptions and therefore address the following questions:
-
Why is the ENSO response sensitive to the equatorial Pacific preconditioning and the season of the eruption?
-
How does the ENSO response scale with the magnitude of volcanic forcing?
-
What is the main driving mechanism behind volcanic impacts on ENSO?
We attempt to answer these questions and resolve apparent inconsistencies in the model studies and observations using a suite of 6200 climate simulations from the CM2.1 climate model developed at the Geophysical Fluid Dynamics Laboratory (GFDL)70. The simulated ENSO response is found to consist of both a deterministic impact of volcanic aerosol forcing and a stochastic dispersion arising from weather noise and ENSO chaos. The deterministic impact—characterized by cooling of the tropical Pacific in the first year after the eruption, followed by El Niño-like warming in the second year—is clearest for June eruptions, while for February eruptions it is obscured by effects of stochastic westerly wind events in the west Pacific during boreal spring. The ENSO response also depends nonlinearly on the eruption magnitude and on tropical Pacific conditions before the eruption, with the deterministic response strongest before a moderate El Niño and weakest before La Niña. Experiments with prescribed land temperatures are performed to attribute the responses to volcanically induced land-ocean temperature gradients and the equatorial Pacific ocean-dynamical thermostat, and the latter is found to dominate the responses in CM2.1, contrasting with results from other models. The results highlight the importance of adequate sampling of ENSO responses to volcanic eruptions, illuminate the physical mechanisms of those responses, and clarify their sensitivities to ocean preconditioning and model biases.
Results
First, to classify possible ENSO responses to different eruptions, we designed and performed extensive numerical experiments with the CM2.1 model, combining different ENSO onsets and 1991 Pinatubo-size and 1815 Tambora-size volcanic eruptions, which could occur in February, April, or June.
The total response to a perturbation is defined here as a difference between the perturbed (with a volcano) and control (without a volcano) experiments. For each ENSO preconditioning, the control ensembles are generated using different initial conditions (ICs). The perturbed experiments are designed as grand-ensembles of simulations to deal with strong ENSO variability and high sensitivity to small perturbations. The grand-ensembles are performed as the ensembles of ensembles, i.e., by perturbing each member of the control IC ensemble with the ensemble of slightly different, or perturbed, forcings (see Methods).
Components of the ENSO response
The previous studies44,47,50,58, considered only the total climate response to volcanic forcing with respect to the climatology or control experiments. However, the total ENSO response to a volcanic eruption can be decomposed into two components: stochastic and deterministic49. To compare our results with the previous studies, one should sum the stochastic and deterministic components.
The stochastic (or chaotic) component arises from the ENSO response to a tiny perturbation, referred to here as the Butterfly perturbation, which causes dispersion of the control ensemble trajectories due to the intrinsic chaotic behavior of the climate system. It depends on the perturbation’s seasonal timing and can be calculated for a given ENSO preconditioning using Butterfly grand-ensemble simulations. The choice of ICs and details of the Butterfly grand-ensemble setup are described in Methods.
The deterministic component is associated specifically with large volcanic forcing and should scale (not necessarily linear) with the magnitude of this forcing. It is expected to emerge most strongly from the stochastic dispersion for volcanic eruptions that occur after boreal spring, the season of strongest wind noise and coupled instability71 in the equatorial Pacific. For a given ENSO preconditioning, the deterministic component is found by comparing the “volcano plus butterfly” grand-ensemble against the “butterfly” grand-ensemble. For details of the volcanic grand-ensemble setup, please refer to Methods.
ENSO response to Butterfly perturbations
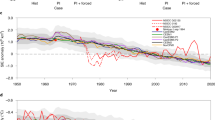
Previously, only the response of the strong El Niño onset to small perturbations was analyzed49. In this section, we test the responses of six different ENSO onsets to Butterfly perturbations applied in three different seasons. Figure 1 illustrates the Niño3.4 calculated for each member of the control ensembles (solid green curves) and Butterfly grand-ensembles (solid gray curves). A few months after perturbation, the Butterfly grand-ensemble spread is generally much larger than that of the control ensemble, especially for the February and April perturbations. This indicates that the control ENSO trajectories, which were selected according to their boreal winter Niño3.4 (see Methods), achieved those Niño3.4 values in part due to their particular (random) realizations of stochastic atmospheric noise. This stochastic ENSO response is especially strong in boreal winter and spring; hence the ENSO trajectories after June perturbations (third column in Fig. 1) tend to see less rapid dispersion. The control ENSO trajectories only identify the 1-January initial conditions that were conducive to the development of particular ENSO phases by boreal winter (October/November/December, OND); while the Butterfly grand-ensemble most adequately describes the plume of possible ENSO trajectories emanating from those ICs.
Control and perturbed Niño3.4 (K) and their responses to February (a–f), April (g–l), or June (m–r) Butterfly and volcanic perturbations. Eruption times are marked by brown triangles. Each row represents an individual control ENSO onset group: La Niña (a, g, m), Neutral (b, h, n), weak El Niño (c, i, o), moderate El Niño (d, j, p), strong El Niño (e, k, q), and extreme El Niño (f, l, r) (see Experimental setup for ENSO event definitions). Spaghetti curves represent individual Niño3.4 trajectories from the control ensemble (green) and Butterfly grand-ensemble (gray). The median of each Butterfly grand-ensemble (ButterflyMED) is shown as a thick gray curve with dots. Dashed green curve represents the stochastic response calculated as the ButterflyMED minus the control ensemble median (ControlMED, Supplementary Fig. 1); this is the correction that would be needed to remove the post-initialization stochastic selection bias present in the control ensemble. The deterministic response to the Pinatubo-size (blue) and Tambora-size (red) volcanic forcings is calculated as the corresponding volcanic grand-ensemble median (PinatuboMED or TamboraMED, Supplementary Fig. 1) minus ButterflyMED. Orange-shaded two-tailed bootstrap confidence intervals calculated from the Butterfly grand-ensemble medians help to detect the statistical significance of the deterministic signal of the eruption median relative to the Butterfly median at 0.05 significance level. Yellow-shaded vertical bands indicate the seasons OND 1991 and SON 1992 used to summarize ENSO responses in Fig. 2.
The difference between the medians of the Butterfly grand-ensemble and control ensemble distributions (green dashed curve) summarizes the role that stochastic processes played in producing the control ensemble. The smaller the absolute value of this difference, the less important the stochastic noise was relative to ocean preconditioning for event development. Figure 1d–f shows that moderate-to-extreme El Niño onsets are more influenced by stochastic atmospheric processes than La Niña, neutral, or weak El Niño onsets, especially when perturbed in boreal winter or spring.
Figure 2 compares the median Niño3.4 of the control ensemble (green dots) and Butterfly grand-ensemble (box-and-whiskers) in the first (OND 1991) and second (SON 1992) year after perturbation. The spread of the Butterfly grand-ensemble in the first year is larger for perturbations made before June. During February and April perturbations, the ENSO trajectories have more time to disperse and are also subject to the strong noise and instability. The selected control moderate-to-extreme El Niños are at the high end of their respective Butterfly grand-ensemble distributions, again indicating the key role that stochastic forcing played in the events selected from the control run. Retrospectively perturbing the trajectories is unlikely to reproduce the particular lucky sequence of strong stochastic forcing that aided the development of many of the control El Niños; thus, these perturbations usually result in weaker El Niños. This would also hold for a volcanic perturbation—hence the need for a Butterfly grand-ensemble. The Butterfly grand-ensemble serves as a reference against which to compare any cooling seen in the volcanic runs and illuminate a deterministic response.
Niño3.4 (K) averaged over the first-year boreal winter (OND 1991) after the a February, b April, or c June perturbations. Green dots show the 10-member medians of the unperturbed control ensembles, for various types of ENSO events identified in the control run (abscissa; see Experimental setup for event definitions). Box-and-whiskers show the distribution (median, quartiles, extrema) of the 100-member Butterfly grand-ensemble; blue dots show the median of the 100-member Pinatubo grand-ensemble; red dots show the median of the 100-member Tambora grand-ensemble. Horizontal shaded bands indicate the Niño3.4 ranges for the various ENSO onsets defined in Experimental setup: La Niña (blue), Neutral (light gray), weak El Niño (yellow), moderate El Niño (orange), strong El Niño (red), and extreme El Niño (dark red); (d–f) as in (a–c), but for Niño3.4 averaged over SON 1992. Full time-series of the control and perturbed ENSO states is shown in Supplementary Fig. 1.
ENSO response to volcanic forcing
For February eruptions, the deterministic responses to volcanic forcing (blue and red lines in Fig. 1) are relatively weak during the first year, and comparable in magnitude to the effects of noise in the control run (dashed green line). The eruption responses are the weakest for La Niña, Neutral, and weak El Niño onsets, although all event types see an appreciable volcanically induced decrease of the Niño3.4 after March 1993. The response to a February volcanic eruption is generally difficult to detect, in the face of the large ensemble dispersion driven by chaotic instabilities during the first boreal spring after the eruption.
It has been previously discussed that explosive February and April eruptions are able to impact weak El Niño onsets significantly, leading to a La Niña-like cooling in the eruption year, followed by El Niño-like warming the following year48,62,63. In our simulations, the substantial negative Niño3.4 responses (defined as a sum of stochastic and deterministic responses) to the February eruptions are likewise detected for moderate, strong, and extreme El Niño onsets at the end of the eruption year. However, this cooling contains both deterministic (forced by volcanic radiative cooling) and stochastic components, and the latter is significant.
Compared to the February eruptions, the April volcanic eruptions induce stronger deterministic responses, with robust cooling in the first year (Fig. 2b). The El Niño cases also exhibit a clear warming response in the second year, particularly for the Tambora-size eruption (Fig. 1i–l). This result harmonizes with the recent study based on the proxy data72, which reports a moderate-to-strong El Niño in the period 1815–1817. The El Niño started in 1815 as a moderate event and then strengthened in 1816–1817, becoming one of the strongest El Niños of the millennium. Our simulations support this proxy finding. If the Tambora eruption in April 1815 coincided with the development of a weak or moderate El Niño (Fig. 1i, j), the El Niño is likely to be slightly suppressed by volcanic forcing in the first year and is more likely to be intensified and extended in the second year. The El Chichón eruption in 1982 is another example of an April eruption that coincided with an El Niño. Although this eruption was smaller than the Pinatubo-size eruption simulated here, its plume was mostly distributed in the Northern Hemisphere and had there almost the same climate impact as Pinatubo. Ref. 73 noted that the strong EP El Niño 1982–1983 had started before the eruption of El Chichón, and thus was not its consequence. Our simulations (Fig. 1k, l) demonstrate that if at the time of the April eruption there is a development of a strong El Niño event, the deterministic impact of an El Chichón-size or Pinatubo-size eruption (blue curve) is unlikely to be seen49. This result is confirmed by SST observations that report a normal duration of the 1982–1983 El Niño event.
The ENSO responses to June volcanic eruptions (Figs. 1m–r and 2c, f) are comparable in magnitude to those for the April eruptions, but the signal is less clouded by stochastic dispersion since the perturbation occurs after boreal spring. Figure 2f shows that the deterministic El Niño-like response during the second year after the June eruptions is the strongest for weak and moderate El Niño onsets. The setup, which involves weak CP El Niño (Fig. 1c), is in line with the Pinatubo 1991 eruption49. It shows an El Niño development in the first year (gray curve) and a weaker El Niño-like response to the Pinatubo eruption in the second year (red curve). In this case, the first-year El Niño is not affected by the volcanic eruption; however, the second-year response is definitely a deterministic response to the volcano. The Neutral onset response is weaker than the response of the weak El Niño onset because clouds in the WP reduce volcanic radiative cooling for the Neutral ENSO onset and shift to the CP for the weak El Niño onset. The La Niña onset shows no response even to Tambora-size eruptions.
Ref. 44 previously found that the response of the equatorial Pacific to volcanic eruptions scales linearly with respect to the magnitude of the volcanic eruption. We find that the deterministic responses to April and June eruptions increase with the magnitude of the volcanic aerosol forcing; however, tripling the eruption magnitude (from Pinatubo to Tambora-size) does not triple the Pacific response, and the increase strongly depends on the ocean preconditioning. When the deterministic volcanic impact is overwhelmed by the stochastic component (as for February or April eruptions), the total responses to Pinatubo-size and Tambora-size eruptions may be largely indistinguishable.
Besides the conventional SST Niño3.4, we analyzed the deterministic response of the relative SST (RSST) (Supplementary Fig. 2)50. The relative SST is widely used in studies of the convection and winds, coupling, and remote teleconnections, etc.74,75,76. The RSST Niño3.4 index is calculated as the difference between the conventional SST Niño3.4 and the surface temperature anomaly of the tropical belt (20∘ S-20∘ N). In contrast with the conventional Niño3.4, we detected an “RSST El Niño-like response” in every case regardless of the ENSO preconditioning or timing and strength of the volcanic eruption. The RSST diagnostics is highly relevant to the “dynamical response” of the atmosphere and is complementary to the conventional Niño3.4 SST index. When looking at the response to volcanic eruptions using the RSST, one should always expect higher index values compared to the regular SST due to removed averaged tropical cooling (Supplementary Fig. 2, dashed lines). However, the combined usage of both RSST and SST Niño3.4 indexes can shed light on the local SST response (relevant also to coral paleo records) versus remote response (teleconnections via the atmospheric bridge, relevant also to tree ring paleo records). For example, a coral proxy found in the equatorial CP (responding to local SST) might not detect a volcanic response at all77, while remotely located coral or tree ring proxies (responding to RSST and shifts in tropical convection) might detect an El Niño-like response.
Response mechanisms
In this section, we test three mechanisms of the volcanic impact on ENSO with respect to their sensitivity to ENSO phase and the magnitude of radiative forcing in CM2.1: LOTG44,49, ODT41,42,49,56,57, and cooling of African continent50.
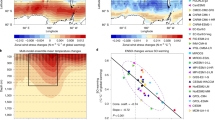
Figure 3a, d, g, j compares the spatio-temporal patterns of the ensemble median deterministic responses to June Tambora-size eruptions for four different ENSO onsets (Supplementary Fig. 3). To simplify the explanation of the mechanisms involved in the ENSO response shown in the Hovmöller diagram, we illustrate the mechanisms causing cooling of the EP in the first half a year after the eruption (Fig. 4a) and warming in the next year (Fig. 4b).
Hovmöller (longitude vs. time) diagrams of land and sea surface temperature responses (K, shaded) and zonal wind deterministic response (m/s, black contours every 0.5 m/s) to a June 1991 Tambora-size eruption, averaged 5∘S-5∘N during June 1991–June 1993. The response is calculated as the Tambora grand-ensemble median minus the Butterfly grand-ensemble median, for experiments without continental temperature override (left column) and with temperature override over Africa (middle column) and the Maritime&Australia continents (right column). Rows indicate responses of La Niña (a–c), Neutral (d–f), weak El Niño (g–i), and extreme El Niño (j–l) onsets (see Experimental setup for event definitions). Medians are calculated from 100-member grand-ensembles for the experiments without override, and 50-member grand-ensembles for the experiments with override (Table 4). Dashed lines bound the Indian ocean (red), Pacific ocean (black), and Niño3.4 region (green).
Schematic of the mechanisms involved in the equatorial Pacific response to explosive low-latitude volcanic eruptions a 0--6 months and b 6--18 months after the eruption, for different ENSO preconditioning: La Niña, Neutral, weak Central Pacific (CP) El Niño, and extreme Eastern Pacific (EP) El Niño. See Experimental setup for ENSO event definitions. The deterministic responses of the land and sea surface temperature and trade winds (Fig. 3a, d, g, j) are shown. The control sea surface height (SSH) is shown as dashed black line, the SSH after the volcanic perturbation is shown as solid black line. The control SSH differs between a and b due to transition to the relaxation phase.
Two processes trigger the initial cooling. Firstly, the land temperature responds to volcanically induced reduction of the solar flux faster than the ocean temperature. The trade winds transport colder air from the American continent towards the ocean, thus cooling the ocean surface (Fig. 4a). Secondly, the upwelling, intensified by strengthened off-shore winds, brings more cold water to the surface through vertical-advective cooling in the EP. During the La Niña conditions (Supplementary Fig. 3), the trade winds are the strongest, and the background vertical temperature gradient is the sharpest due to the shallowest background thermocline; thus, the strongest EP cooling is detected. The weakest EP cooling is associated with the strong El Niño onset because of the weakest trade winds and no vertical-advective cooling response due to the deepest background thermocline.
In the WP, the LOTG between the M&A continent and the ocean initiates a trade wind decrease responsible for the later El Niño-like response. However, the strong LOTG is short-lived and functions only until the ocean itself responds to radiative cooling.
Half a year after the eruption, the ODT is responsible for non-uniform cooling of the equatorial Pacific. The ODT is sensitive to the background equatorial ocean upwelling, thermocline depth, and thus to the ENSO preconditioning. Figure 3d, g and Fig. 4c demonstrate that in the case of the neutral and weak (CP) El Niño onsets, the WP cools more strongly than the EP because the relatively shallow thermocline and intense EP upwelling attenuate the response of the EP SST to volcanic radiative forcing. This reduces the westward SST gradient in the WP/CP, leading to strong and long-lasting westerly wind anomalies and strong thermocline feedback characterized by the sea surface height (SSH) response (Supplementary Fig. 4e, i) that cause an El Niño-like response in a year after the volcanic eruption. The analysis of the ocean upper layer heat budget, previously summarized in Fig. 7 of ref. 49, reveals an interplay of three advective terms (zonal, meridional, and vertical), which explain the El Niño-like warming in the case of Neutral and weak CP El Niño preconditionings. In contrast, both La Niña and extreme EP El Niño onsets do not develop a strong zonal SST gradient as the response to volcanic forcing. In the case of extreme (EP) El Niño, uniformly deep background thermocline (no upwelling) allows broader cooling of the equatorial Pacific, which extends to the EP. It results in a weaker SST gradient and, therefore, weaker zonal wind response, weaker zonal feedbacks, and a weaker El Niño-like response to volcanic forcing. The weak warming of the strong EP El Niño onset is found to be mostly caused by the thermocline effect, while the zonal and meridional advection contribution to this warming is smaller49. In the case of La Niña onset, an extended upwelling area in the equatorial Pacific and the weakest thermocline feedback lead to no response to volcanic forcing.
To identify the importance of the rapid land cooling effect caused by reduced solar heating during the initial stages of a volcanic eruption, we perform additional experiments using the land surface temperature override over Africa and Maritime&Australia (M&A) continent (Fig. 5), i.e., preventing the land temperature in these regions from responding to volcanic forcing. This approach rectifies the effect of rapid land cooling on ENSO seen in the IPSL model experiments50. A detailed description of the temperature override experiments is represented in Methods. Figure 3 shows that the tropical Pacific SST and zonal wind deterministic responses in the experiments with Africa (middle column) or M&A (right column) land temperature override are all very similar to the original “no override” experiment. Thus at least in the CM2.1, the continental cooling appears to play a less important role than the ODT.
In this study, we did not consider the possible effect of volcanically induced cooling of the Asian continent, even though the summer Asian monsoon and ENSO are closely related78. The developing El Niño can depress the Asian monsoon in the summer, and then the weakened Asian monsoon relaxes the trade winds in the equatorial Pacific and may enhance the upcoming El Niño or prolong it. Potentially, cooling after strong volcanic eruptions may weaken the summer monsoon and generate an even stronger/more extended warm episode. However, the peak of Asian continent cooling after the summer eruption is reached in boreal winter during the dry monsoon season; however, the WP wind response is the strongest in September–November of the first year after a strong summer eruption. Therefore, in the CM2.1, the equatorial Pacific trade winds may depend less on the changes in Asian or West-African monsoons and more on the equatorial Pacific SST changes.
Discussion
This study explores the sensitivity of ENSO response to explosive tropical volcanic eruptions. We performed grand-ensemble (ensembles of ensembles) simulations in the GFDL CM2.1 model to explore how the ENSO response depends on the ocean preconditioning and the season and magnitude of the eruption. These experiments consist of 6200 perturbed simulations and over 19,000 model years. To our knowledge, this is the most extensive set of simulations yet applied to this topic.
This unique experimental framework allows us to separate the stochastic and deterministic components of ENSO response. The partial contribution of these components strongly depends on the timing of the eruption. For February eruptions, the stochastic component prevails, meaning that boreal spring instabilities strongly influence the ENSO. Therefore, the impact of February volcanic eruptions on ENSO is relatively difficult to detect even for Tambora-size eruptions. For April or June volcanic eruptions, however, the stochastic component diminishes; the deterministic volcanically induced cooling of the Pacific ocean is seen in the first year after the eruption and is followed by El Niño-like warming in the second year for neutral and weak-to-moderate El Niño preconditionings. La Niña preconditioning is relatively insensitive to strong volcanic eruptions regardless of the season.
The deterministic responses to April and June eruptions increase with the magnitude of the volcanic aerosol forcing, although at a different rate depending on the ocean preconditioning.
We analyzed the different response mechanisms by overriding land surface temperatures over Africa and the Maritime& Australia continents. We showed that, at least in CM2.1, the ocean-dynamical thermostat plays a key role, while the continental cooling and associated atmospheric circulation changes together with the land-ocean temperature gradient mechanism play a relatively smaller role in the ENSO response beyond the first half a year after the eruption. These findings contrast with previous results from the IPSL model50 and should also be investigated in other models. Another potentially influential mechanism may be related to the Asian continent cooling, the largest landmass in the Pacific ocean proximity. This mechanism has not been analyzed in this study, although its role should be tested in further studies.
This study highlights the importance of using the appropriate tools for modeling, accurate experimental setup, and analysis methods of the ENSO response to volcanic eruptions. Each model has its own tropical climate and ENSO behavior, which does not always reproduce the observed characteristics well79,80. Our results indicate that the ocean state before the eruption, particularly the intensity and zonal extent of the ocean-dynamical thermostat, are important controls on the ENSO response to volcanic cooling. Thus, model biases could also affect the ENSO response and may help to explain why studies of volcanic impacts on ENSO have produced seemingly conflicting results.
Empirical analyses of observations77 and model ensemble outputs42,62 usually disregard the timing of an eruption and the ENSO preconditioning when sampling postvolcanic years. However, since the eruption timing is essential for the ENSO response48,49, such pooled sampling might misrepresent the impact of eruptions on ENSO. We also showed that the choice of the analyzed index (SST vs. RSST) matters and may explain ENSO states’ inconsistencies after strong volcanic eruptions reported by the local (e.g., ref. 77) and remote proxy studies (e.g., ref. 39). We believe that more selective sampling and intercomparison of results from multiple models instead of multi-model ensemble studies could help clarify the sensitivity of ENSO to volcanic forcing.
Methods
Model description
CM2.1 coupled climate model captures the main aspects of tropical Pacific climate and ENSO81 (Table 1). CM2.1 has been extensively used to explore historical, paleo, and future ENSO variability and predictability59,82,83,84,85 and was involved in the Coupled Model Intercomparison Project phase 3 (CMIP3) and the IPCC Fourth Assessment Report (IPCC AR4). CM2.1 was also used to study volcanic impacts on the Middle East and North Africa (MENA) region86, the Arctic Oscillation37, and the Atlantic Meridional Overturning Circulation87.
CM2.1 combines four submodels70: atmosphere, ocean, land, and sea ice. The atmospheric component of the GFDL CM2.1 is run at 2∘ latitude by 2.5∘ longitude horizontal resolution with 24 vertical levels reaching 40-km altitude and a finite-volume dynamical core. The atmospheric physics module has a 0.5 h time step. The atmospheric radiation module includes shortwave and longwave components, which are calculated every three hours. The radiative transfer calculations in the CM2.1 model are performed using spatially and temporarily varying aerosol optical properties. The atmospheric composition, incoming solar radiation, and land cover are kept at the 1990 level. The oceanic component uses a tripolar horizontal grid at 1∘ latitude by 1∘ longitude telescoping to 1/3 ∘ near the equator with 50 vertical levels refined to 10 m spacing over the top 220 m, and 2 h time step. The land component shares the atmosphere’s horizontal grid. The sea ice component is based on GFDL Sea Ice Simulator, which is a dynamical model with three vertical layers, one snow and two ice, and five ice thickness categories.
The coupler is used to organize the communication between the submodels. It computes and passes the fluxes from one submodel to another in such a way that each submodel receives an appropriately gridded input. The coupling of the ocean and atmosphere occurs every 2 h, which is equal to the time step of the ocean model. All fluxes are conserved to within machine precision.
Experimental setup
To isolate the effect of volcanic or other perturbations on each ENSO onset, we run control (no sulfate aerosols) and perturbed (with sulfate aerosols) simulations. We start the pairs of simulations from the same initial conditions (ICs), and each experiment is run for 3 years. For consistency, we relabel the initial time as January 1, 1991.
Initial conditions and control ensembles
To generate a pool of ICs, we perform a historical 500-year run without volcanic aerosols. We then use ranges of Niño3.4 averaged over October/November/December (OND) to define six groups of simulated ENSO events: La Niña (below -2K), Neutral (−0.2 to 0.2K), weak El Niño (1–1.5K), moderate El Niño (1.5–2.2K), strong El Niño (2.2–3K), and extreme El Niño (above 3K) (Table 2, Fig. 6). The ranges slightly differ from the conventional ones due to model biases—CM2.1 tends to slightly overestimate El Niño amplitudes. For each of these six groups, ten events with corresponding ENSO amplitude are randomly selected. For each selected event, the model trajectory is traced back in time to January 1 of the event year, and the model state at that time is identified as the IC for that event. The subsequent 3 years of evolution of the 10 control runs in each group is denoted as the control ensemble.
Boreal winter control ENSO states at each of the selected control ENSO groups: La Niña, Neutral, weak El Niño, moderate El Niño, strong El Niño, and extreme El Niño are shown as December 1991 monthly mean sea and land surface temperature (K, shading) and wind at 10 m (m/s, arrows) ensemble mean anomalies calculated with respect to the climatology, and total precipitation (mm day−1, contours).
The ICs should not be confused with the ENSO phase “onset”, which defines the model state of ENSO before the perturbation.
Perturbed forcing
To impose the Butterfly perturbations and Pinatubo-size and Tambora-size volcanic eruptions in CM2.1, we prescribe the volcanic aerosol optical properties using the SATO1.8 dataset88,89 containing the aerosol extinction (ϵ0), single scattering albedo, and asymmetry parameter of the aerosol cloud after Pinatubo in June 1991. Supplementary Fig. 5 shows the spatio-temporal evolution of the SATO1.8 extinction aerosol optical depth.
Rather than perturbing the initial conditions, we instead used slightly perturbed forcings to generate the initial ensemble spread (the two methods would produce effectively the same result). The Butterfly and volcanic cases have the same spatio-temporal pattern of the aerosol cloud as they use the SATO1.8 dataset multiplied by a scalar αp, where p = [1,...10] is the ordinal index (Table 3), and shifted by four months earlier for February perturbations and by two months for April perturbations. For small (“butterfly”) perturbations, αp, starts from 0.001 and increases with the step 0.001, thus making it equivalent to the perturbation caused by the aerosol optical depth thousand times smaller than that of Pinatubo eruption. For Pinatubo-size eruptions, the aerosol extinctions is scaled by 1 + αp, and for Tambora-size eruptions, this coefficient is equal to 3 + αp.
Butterfly grand-ensembles
To obtain a stochastic response of each ENSO onset to boreal winter, spring, and summer perturbations, the model is run for three years starting from each of the control onset initial conditions, but with perturbed forcing applied in each season separately. Thus, we alternately add a “butterfly” atmospheric perturbation to generate an alternative ENSO trajectory that diverges chaotically from the original control trajectory. This process is repeated with 10 butterfly perturbations, giving a 10-member perturbed forcing ensemble for each initial condition. This resembles what is commonly done in “perfect-model” predictability studies59. These 10 butterfly trajectories for each of the 10 onset initial conditions yield a “grand-ensemble” of 100 ENSO trajectories for each of the six ENSO groups in each perturbation season.
Volcanic grand-ensembles
To assess the impact of volcanic forcing, we repeat the 100-member grand-ensembles as above, but add to the Butterfly perturbation a volcanic aerosol perturbation comparable to that from 1991 Pinatubo or 1815 Tambora40,87 eruptions. This is done for each ENSO onset and eruption timing and magnitude (Table 3). The control ensembles, Butterfly grand-ensembles, and volcanic grand-ensembles are all identical before the aerosol perturbations are applied. The difference between the Butterfly and volcanic grand-ensemble distributions, which is calculated here as the difference of grand-ensemble medians, then isolates the effects of the volcanic forcing49, i.e., the deterministic response. To test the seasonal dependence of the response, three different sets of experiments are performed with volcanic forcing consistent with eruptions in February, April, or June. As we prescribe aerosol optical properties for each of the perturbations, the original Pinatubo dataset89 is modified according to the perturbation and the start date of the perturbation is shifted for February and April eruptions. In every case, the aerosol optical depth reaches the peak in eight months after the perturbation. The Butterfly, Pinatubo, and Tambora seasonal experiments (Table 3) thus amount to a total of 3 × 3 × 10 × 10 × 6 × 3 years or 16,200 years of simulation.
Override grand-ensembles
To test the rapid land cooling hypothesis, we perform additional experiments, in which the eruption-induced land cooling is suppressed in particular regions (Fig. 5)—namely Africa as suggested by50 and the Maritime&Australia (M&A) continents, which is well positioned geographically to affect the WP winds through LOTG44,49. We override the land surface temperature in these regions using archived hourly data from the original 500-year control simulation in which there was no volcanic cooling.
To account for any changes in climate or ENSO arising from the override procedure itself, we first conduct two new 100-year 1990 control simulations (without volcanic forcing) in which the land surface temperature in the selected regions is overridden by the hourly data from the original control run (Table 4). Comparison of the ENSO phase frequencies of the control simulations with and without override is provided in Table 1. For each of the 4 ENSO event types (La Niña (below −2K), Neutral (−0.2 to 0.2K), weak El Niño (1–1.5K), and extreme El Niño (above 3K)), we then choose five new ICs from the new 100-year controls, and perform new 50-member ensemble Butterfly and Tambora experiments with the land temperature overridden (see Table 4). The land-override control, land-override Butterfly, and land-override Eruption runs only differ in their volcanic aerosol forcing. The land-override ensembles amount to a total of 2 × 2 × 5 × 10 × 4 × 3 years or 2400 years of simulation.
Stochastic and deterministic responses
To evaluate the volcanic impact on ENSO, we mainly analyze the responses of two variables: SST and zonal wind at 10 m (u). For a given variable ψ in the absence of volcanic forcing, the cumulative influence of the initial conditions plus noise and chaotic instability is measured by the distribution of the Butterfly grand-ensemble. The median of the Butterfly grand-ensemble is
where ϵ0 is the Pinatubo aerosol extinction, and an overbar denotes a median (not a mean) over all initial conditions k = [1, 2, …, 10] and perturbed forcings p.
The median of a volcanic grand-ensemble is
where V is the volcanic forcing magnitude (V = 1 for Pinatubo, V = 3 for Tambora). The deterministic response ψV,d to strong volcanic perturbation is defined here as the median of the eruption grand-ensemble minus the median of the Butterfly grand-ensemble:
The contribution of noise to the ENSO events drawn from the control is measured by distinguishing the control ensemble from the Butterfly grand-ensemble, which we again summarize using a difference of ensemble medians. The median of the control ensemble is
and a measure of the cumulative influence of stochasticity on the selected control events, i.e., the stochastic response, is
Data availability
All simulation data used in this study are archived in the KAUST Supercomputing Laboratory. The postprocessed data files and figures are available on request from the corresponding author.
Code availability
The CM2.1 climate model is developed by the Geophysical Fluid Dynamics Laboratory (GFDL) and is publicly available at https://www.gfdl.noaa.gov/modeling-systems-group-public-releases/. The modified version of the CM2.1, which was used in the study and allows to perform land surface temperature override, can be downloaded from KAUST repository https://doi.org/10.25781/KAUST-6MBB9. The archive includes all necessary files needed to reproduce the results—the model source code, input data, SATO1.8 volcanic dataset, and “perturbed forcing” and “grand-ensemble” sample scripts. The post-processing and visualization Python code is available on request from the corresponding author.
References
Trenberth, K. E. The definition of El Niño. Bull. Am. Meteorol. Soc. 78, 2771–2777 (1997).
McPhaden, M. J., Zebiak, S. E. & Glantz, M. H. ENSO as an integrating concept in earth science. Science 314, 1740–1745 (2006).
Grove, R. H. Global impact of the 1789-93 El Niño. Nature 393, 318 (1998).
Grove, R. H. The great El Niño of 1789–93 and its global consequences: reconstructing an extreme climate event in world environmental history. Medieval Hist. J 10, 75–98 (2006).
Chen, Y. et al. A pan-tropical cascade of fire driven by El Niño/Southern Oscillation. Nat. Clim. Change 7, 906 (2017).
Aceituno, P. et al. The 1877–1878 El Niño episode: associated impacts in South America. Clim Change 92, 389–416 (2009).
Diaz, H. F. & McCabe, G. J. A possible connection between the 1878 yellow fever epidemic in the southern United States and the 1877–78 El Niño episode. Bull. Am. Meteorol. Soc. 80, 21–28 (1999).
Rasmusson, E. M. & Carpenter, T. H. Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Niño. Month. Weather Rev. 110, 354–384 (1982).
Karnauskas, K. B. Can we distinguish canonical El Niño from Modoki? Geophys. Res. Lett. 40, 5246–5251 (2013).
Capotondi, A. et al. Understanding ENSO diversity. Bull. Ame. Meteorol. Soc. 96, 921–938 (2015).
Zheng, F., Fang, X.-H., Yu, J.-Y. & Zhu, J. Asymmetry of the Bjerknes positive feedback between the two types of El Niño. Geophys. Res. Lett. 41, 7651–7657 (2014).
Fang, X.-H., Zheng, F. & Zhu, J. The cloud-radiative effect when simulating strength asymmetry in two types of e l n iño events using cmip5 models. J. Geophys. Res. 120, 4357–4369 (2015).
Ashok, K., Behera, S. K., Rao, S. A., Weng, H. & Yamagata, T. El Niño Modoki and its possible teleconnection. J. Geophys. Res. 112, C11 (2007).
Kling, H. Climate variability risks for electricity supply. Nat. Energy 2, 916 (2017).
Glantz, M. H. Currents of Change: Impacts of El Niño and La Niña on Climate and Society (Cambridge University Press, 2001).
Moy, C. M., Seltzer, G. O., Rodbell, D. T. & Anderson, D. M. Variability of el niño/southern oscillation activity at millennial timescales during the holocene epoch. Nature 420, 162–165 (2002).
Landscheidt, T. Solar forcing of El Niño and La Niña. In: The solar cycle and terrestrial climate (eds. Vázquez, M., Schmieder, B.) vol. 463, pp. 135–140 (European Space Agency, Special Publication, 2000).
Van Oldenborgh, G. J., Philip, S. & Collins, M. El Niño in a changing climate: a multi-model study. Ocean Sci. 1, 81–95 (2005).
Yeh, S.-W. et al. El Niño in a changing climate. Nature 461, 511–514 (2009).
Ashok, K. & Yamagata, T. Climate change: the El Niño with a difference. Nature 461, 481 (2009).
Collins, M. et al. The impact of global warming on the tropical Pacific Ocean and El Niño. Nat. Geosci. 3, 391–397 (2010).
Vecchi, G. A. & Wittenberg, A. T. El Niño and our future climate: where do we stand? Wiley Interdiscip. Rev. 1, 260–270 (2010).
Cai, W. et al. Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Change 4, 111–116 (2014).
Cai, W. et al. Increased frequency of extreme La Niña events under greenhouse warming. Nat. Clim. Change 5, 132 (2015).
Cai, W. et al. ENSO and greenhouse warming. Nat. Clim. Change 5, 849 (2015).
DiNezio, P. N. et al. Climate response of the equatorial Pacific to global warming. J. Clim. 22, 4873–4892 (2009).
Fedorov, A. V. & Philander, S. G. Is El Niño changing? Science 288, 1997–2002 (2000).
Latif, M. & Keenlyside, N. S. El Niño/Southern Oscillation response to global warming. Proc. Natl Acad. Sci. USA 106, 20578–20583 (2009).
Cai, W. et al. Increased variability of eastern Pacific El Niño under greenhouse warming. Nature 564, 201 (2018).
Robock, A. Volcanic eruptions and climate. Rev. Geophys. 38, 191–219 (2000).
Stenchikov, G. In: Climate Change: observed impacts on planet Earth, 1st edn. (ed. Letcher, T. M.) ch. 4, pp. 77–102 (Elsevier, 2009).
Timmreck, C. Modeling the climatic effects of large explosive volcanic eruptions. Wiley Interdiscip. Rev. 3, 545–564 (2012).
Meehl, G. A., Teng, H., Maher, N. & England, M. H. Effects of the mount pinatubo eruption on decadal climate prediction skill of pacific sea surface temperatures. Geophys. Res. Lett. 42, 10–840 (2015).
Timmreck, C., Pohlmann, H., Illing, S. & Kadow, C. The impact of stratospheric volcanic aerosol on decadal-scale climate predictions. Geophys. Res. Lett. 43, 834–842 (2016).
Robock, A. & Mao, J. Winter warming from large volcanic eruptions. Geophys. Res. Lett. 19, 2405–2408 (1992).
Zambri, B., LeGrande, A. N., Robock, A. & Slawinska, J. Northern hemisphere winter warming and summer monsoon reduction after volcanic eruptions over the last millennium. J. Geophys. Res. 122, 7971–7989 (2017).
Stenchikov, G. et al. Arctic Oscillation response to volcanic eruptions in the IPCC AR4 climate models. J. Geophys. Res. 111, D7 (2006).
Osipov, S. & Stenchikov, G. Regional effects of the mount pinatubo eruption on the middle east and the red sea. J. Geophys. Res. 122, 8894–8912 (2017).
Adams, J. B., Mann, M. E. & Ammann, C. M. Proxy evidence for an El Niño-like response to volcanic forcing. Nature 426, 274–278 (2003).
Raible, C. C. et al. Tambora 1815 as a test case for high impact volcanic eruptions: Earth system effects. Wiley Interdiscip. Rev. 7, 569–589 (2016).
Mann, M. E., Cane, M. A., Zebiak, S. E. & Clement, A. Volcanic and solar forcing of the tropical Pacific over the past 1000 years. J. Clim. 18, 447–456 (2005).
Emile-Geay, J., Seager, R., Cane, M. A., Cook, E. R. & Haug, G. H. Volcanoes and ENSO over the past millennium. J. Clim. 21, 3134–3148 (2008).
McGregor, S., Timmermann, A. & Timm, O. A unified proxy for ENSO and PDO variability since 1650. Clim. Past 6, 1–17 (2010).
Ohba, M., Shiogama, H., Yokohata, T. & Watanabe, M. Impact of strong tropical volcanic eruptions on ENSO simulated in a coupled GCM. J. Clim. 26, 5169–5182 (2013).
Maher, N., McGregor, S., England, M. H. & Gupta, A. S. Effects of volcanism on tropical variability. Geophys. Res. Lett. 42, 6024–6033 (2015).
Pausata, F. S., Chafik, L., Caballero, R. & Battisti, D. S. Impacts of high-latitude volcanic eruptions on ENSO and AMOC. Proc. Natl Acad. Sci. USA 112, 13784–13788 (2015).
Pausata, F. S., Karamperidou, C., Caballero, R. & Battisti, D. S. ENSO response to high-latitude volcanic eruptions in the Northern Hemisphere: the role of the initial conditions. Geophys. Res. Lett. 43, 8694–8702 (2016).
Stevenson, S., Fasullo, J. T., Otto-Bliesner, B. L., Tomas, R. A. & Gao, C. Role of eruption season in reconciling model and proxy responses to tropical volcanism. Proc. Natl Acad. Sci. USA 114, 1822–1826 (2017).
Predybaylo, E., Stenchikov, G. L., Wittenberg, A. T. & Zeng, F. Impacts of a Pinatubo-size volcanic eruption on ENSO. J. Geophys. Res. 122, 925–947 (2017).
Khodri, M. et al. Tropical explosive volcanic eruptions can trigger El Niño by cooling tropical Africa. Nat. Commun. 8, 778 (2017).
Sun, W. et al. How Northern high-latitude volcanic eruptions in different seasons affect ENSO. J. Clim. 32, 3245–3262 (2019).
Wang, T. et al. Modulation of ENSO evolution by strong tropical volcanic eruptions. Clim. Dyn. 51, 2433–2453 (2018).
Liu, F. et al. How do tropical, Northern hemispheric, and Southern hemispheric volcanic eruptions affect ENSO under different initial ocean conditions? Geophys. Res. Lett. 45, 13–041 (2018).
Miao, J., Wang, T., Wang, H. & Sun, J. Interannual weakening of the tropical pacific walker circulation due to strong tropical volcanism. Adv. Atmos. Sci. 35, 645–658 (2018).
Eddebbar, Y. A. et al. El Niño–like physical and biogeochemical ocean response to tropical eruptions. J. Clim. 32, 2627–2649 (2019).
Clement, A. C., Seager, R., Cane, M. A. & Zebiak, S. E. An ocean dynamical thermostat. J. Clim. 9, 2190–2196 (1996).
Seager, R., Zebiak, S. E. & Cane, M. A. A model of the tropical Pacific sea surface temperature climatology. J. Geophys. Res. 93, 1265–1280 (1988).
Pausata, F. S., Zanchettin, D., Karamperidou, C., Caballero, R. & Battisti, D. S. ITCZ shift and extratropical teleconnections drive ENSO response to volcanic eruptions. Sci. Adv. 6, eaaz5006 (2020).
Wittenberg, A. T., Rosati, A., Delworth, T. L., Vecchi, G. A. & Zeng, F. ENSO modulation: is it decadally predictable? J. Clim. 27, 2667–2681 (2014).
McPhaden, M. J. Tropical Pacific Ocean heat content variations and ENSO persistence barriers. Geophys. Res. Lett. 30, 9 (2003).
Mason, B. G., Pyle, D. M., Dade, W. B. & Jupp, T. Seasonality of volcanic eruptions. J. Geophys. Res. 109, B4 (2004).
McGregor, S. & Timmermann, A. The effect of explosive tropical volcanism on ENSO. J. Clim. 24, 2178–2191 (2011).
Li, J. et al. El Niño modulations over the past seven centuries. Nat. Clim. Change 3, 822–826 (2013).
Oman, L., Robock, A., Stenchikov, G., Schmidt, G. A. & Ruedy, R. Climatic response to high-latitude volcanic eruptions. J. Geophys. Res. 110, D13 (2005).
Kravitz, B. & Robock, A. Climate effects of high-latitude volcanic eruptions: role of the time of year. J. Geophys. Res. 116, D1 (2011).
Schneider, D. P., Ammann, C. M., Otto-Bliesner, B. L. & Kaufman, D. S. Climate response to large, high-latitude and low-latitude volcanic eruptions in the community climate system model. J. Geophys. Res. 114, D15 (2009).
Liu, F. et al. Divergent El Niño responses to volcanic eruptions at different latitudes over the past millennium. Clim. Dyn. 50, 3799–3812 (2018).
Colose, C. M., LeGrande, A. N. & Vuille, M. Hemispherically asymmetric volcanic forcing of tropical hydroclimate during the last millennium. Earth Syst. Dyn. 7, 681–696 (2016).
Stevenson, S., Otto-Bliesner, B., Fasullo, J. & Brady, E. “El Niño-like” hydroclimate responses to last millennium volcanic eruptions. J. Clim. 29, 2907–2921 (2016).
Delworth, T. L. et al. GFDL’s CM2 global coupled climate models. Part I: formulation and simulation characteristics. J. Clim. 19, 643–674 (2006).
Samelson, R. M. & Tziperman, E. Instability of the chaotic ENSO: the growth-phase predictability barrier. J. Atmos. Sci. 58, 3613–3625 (2001).
Duan, J., Wu, P. & Ma, Z. Reconciling the discrepancy of post-volcanic cooling estimated from tree-ring reconstructions and model simulations over the Tibetan Plateau. Atmosphere 10, 738 (2019).
Robock, A., Taylor, K. E., Stenchikov, G. L. & Liu, Y. GCM evaluation of a mechanism for El Niño triggering by the El Chichón ash cloud. Geophys. Res. Lett. 22, 2369–2372 (1995).
Vecchi, G. A. et al. Tropical cyclone sensitivities to co 2 doubling: roles of atmospheric resolution, synoptic variability and background climate changes. Clim. Dyn. 53, 5999–6033 (2019).
Vecchi, G. A. & Soden, B. J. Effect of remote sea surface temperature change on tropical cyclone potential intensity. Nature 450, 1066–1070 (2007).
Wang, S. & Sobel, A. H. Response of convection to relative sea surface temperature: cloud-resolving simulations in two and three dimensions. J. Geophys. Res. 116, D11 (2011).
Dee, S. G. et al. No consistent ENSO response to volcanic forcing over the last millennium. Science 367, 1477–1481 (2020).
Chung, C. & Nigam, S. Asian summer monsoon-ENSO feedback on the Cane–Zebiak model ENSO. J. Clim. 12, 2787–2807 (1999).
Gabriel, C. & Robock, A. Stratospheric geoengineering impacts on El Niño/Southern Oscillation. Atmos. Chem. Phys. 15, 11949–11966 (2015).
Chen, C., Cane, M. A., Wittenberg, A. T. & Chen, D. ENSO in the CMIP5 simulations: life cycles, diversity, and responses to climate change. J. Clim. 30, 775–801 (2017).
Wittenberg, A. T., Rosati, A., Lau, N.-C. & Ploshay, J. J. GFDL’s CM2 global coupled climate models. Part III: tropical Pacific climate and ENSO. J. Clim. 19, 698–722 (2006).
Wittenberg, A. T. Are historical records sufficient to constrain ENSO simulations? Geophys. Res. Lett. 36, L12702 (2009).
McGregor, S., Timmermann, A., England, M. H., Elison Timm, O. & Wittenberg, A. T. Inferred changes in El Niño-Southern Oscillation variance over the past six centuries. Clim. Past 9, 2269–2284 (2013).
Karamperidou, C., Cane, M. A., Lall, U. & Wittenberg, A. T. Intrinsic modulation of ENSO predictability viewed through a local Lyapunov lens. Clim. Dyn. 42, 253–270 (2014).
Atwood, A. R., Battisti, D. S., Wittenberg, A. T., Roberts, W. & Vimont, D. J. Characterizing unforced multi-decadal variability of ENSO: a case study with the GFDL CM2.1 coupled GCM. Clim. Dyn. 49, 2845–2862 (2017).
Dogar, M. M., Stenchikov, G., Osipov, S., Wyman, B. & Zhao, M. Sensitivity of the regional climate in the Middle East and North Africa to volcanic perturbations. J. Geophys. Res. 122, 7922–7948 (2017).
Stenchikov, G. et al. Volcanic signals in oceans. J. Geophys. Res. 114, D16 (2009).
Sato, M., Hansen, J. E., McCormick, M. P. & Pollack, J. B. Stratospheric aerosol optical depths, 1850–1990. J. Geophys. Res. 98, 22987–22994 (1993).
Stenchikov, G. L. et al. Radiative forcing from the 1991 Mount Pinatubo volcanic eruption. J. Geophys. Res. 103, 13837–13857 (1998).
Acknowledgements
The research reported in this publication was supported by the King Abdullah University of Science and Technology (KAUST). In particular, for computer time, we acknowledge the resources of the KAUST Supercomputing Laboratory.
Author information
Authors and Affiliations
Contributions
G.S., E.P., and A.W. designed and planned the experiments. S.O. modified the model. E.P. carried out the experiments and analyzed the data. E.P., G.S., and A.W. wrote the manuscript. G.S. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Predybaylo, E., Stenchikov, G., Wittenberg, A.T. et al. El Niño/Southern Oscillation response to low-latitude volcanic eruptions depends on ocean pre-conditions and eruption timing. Commun Earth Environ 1, 12 (2020). https://doi.org/10.1038/s43247-020-0013-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-0013-y
This article is cited by
-
Volcanic contribution to the 1990s North Pacific climate shift in winter
Scientific Reports (2023)
-
Forced changes in the Pacific Walker circulation over the past millennium
Nature (2023)
-
A Review of El Niño Southern Oscillation Linkage to Strong Volcanic Eruptions and Post-Volcanic Winter Warming
Earth Systems and Environment (2023)
-
A re-appraisal of the ENSO response to volcanism with paleoclimate data assimilation
Nature Communications (2022)
-
Projections of faster onset and slower decay of El Niño in the 21st century
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.