Abstract
The life cycle water scarcity footprint is a tool to evaluate anthropogenic contributions to regional water scarcity along global supply chains. Here, we complement it by a classification of the risk from human water use, a comprehensive conceptualisation of water use and a spatially-explicit impact assessment to a midpoint approach that assesses the risk of on-site and remote freshwater scarcity. For a 2 MWh Lithium-ion battery storage, the quantitative Water Scarcity Footprint, comprising physically used water, accounts for 33,155 regionally weighted m3 with highest contributions from Chilean lithium mining. The qualitative Water Scarcity Footprint, the virtual volume required to dilute pollutant emissions to safe concentrations, is approximately determined to 52 million m3 of regionally weighted demineralised water with highest contributions from copper and aluminium mining operations. As mining operations seem to have the highest impact, we recommend to consider the spatially-explicit water scarcity footprint for assessment of global material supply.
Similar content being viewed by others
Introduction
Preliminary work on the water footprint. The original concept of the water footprint (WF)1,2 defines three components of the WF: 1) Blue water is the sum of evaporation from ground- and surface waters, of water transfer to different basins and of product incorporated water. 2) Green water is the sum of evapotranspiration from soils and plants as well as of water incorporated in plant products. 3) Grey water is the virtual volume needed to adequately dilute pollutions that are discharged into water bodies below generally valid thresholds. Having established that water scarcity exists at regional and local level3, this has been developed further by a variety of “water scarcity footprint” (WSF) approaches4,5,6,7,8 to include the assessment of water use with respect to regional water supply conditions. The DIN ISO EN 14046:2016-079 standard also proposes the WSFs as current state of art. Moreover, the integration of the WF into Life Cycle Assessment (LCA) has been a central focus of many scientific studies10: With the help of extensive inventory databases WSFs have been integrated into Life Cycle Assessment to quantify and assess the WSF of processes and products with respect to different water related risks5,6,8,11,12,13,14,15,16,17. Currently, there is consensus about the DIN EN ISO compliant approach AWARE8 (Available WAter REmaining) within the LCA community8,18, a midpoint Life Cycle Impact Assessment (LCIA) method to evaluate water stress on basin level by comparing human water consumption and environmental water requirements to hydrological water availability.
Requirements for a modified water scarcity footprint concept
Despite these general guidelines, there are still many conceptual inconsistencies, particularly noticeable when comparing different systems. In order to determine spatially explicit WSFs of product supply chains, this research wants to overcome the issues that (1) classifications of the risk associated with human water consumption differ, (2) there is a lack of a comprehensive conceptualisation of water use in LCA within a consistent hydrological framework and (3) that there is a lack of applied regionalisation.
Regarding the first issue, the risk classification spans the frame for goal and scope of a life cycle wide WSF. Different W(S)F studies refer to different burdens or damages or define “water scarcity” differently. Table 1 gives an overview of classifications of the potential burden (midpoint) and the potential (damage), referred to as “risk” in general in the following, of some selected studies. While it becomes evident from Table 1, that there is not one common risk related to human water consumption, there is a general perception of “water scarcity” and thus supply risk. As a first step, this study classifies a risk of human water consumption at midpoint level for LCA applications and then goes one step further by defining impacts as exceedance of the Safe-Operating-Space (SOS), which is derived from the Sustainable Development Goals19.
Second, blue, green and grey water have been established as commonly used sub-indicators for the W(S)F. However, it has often been discussed whether green water does contribute to environmental water flows and water scarcity at all or if it is more a matter of land use change assessment11. From a systems perspective, blue and green water are inseparably linked. In LCA, the distinction between blue and green water is not consistent because the term blue water refers to the source of the water, while green water refers to the fact that it has been used by plants. The indicator “grey water” (as per definition2), representing a virtual volume that is initially not a real environmental flow, has often been critically reviewed as well20,21. Nevertheless, it offers the opportunity to quantify the impact on water quality on a volumetric basis22. As reduced water quality can lower water availability for users with higher demands for quality, it can contribute to the risk of “water scarcity”. This study balances natural and process water flows within the classified risk and comprehensively conceptualises water use in LCA against the background of a consistent hydrological framework. After that, sub-indicators of the WSF are derived from this.
Third, while the locations of a production facility or a final consumer are often known within life cycle wide WSF assessments, the upstream supply chains are not or only partly spatially explicit. However, identifying the place of water use is crucial for an impact assessment with respect to regional water supply conditions. Some conceptual, data and software modifications are necessary to implement a spatially explicit impact assessment of the supply chain.
Global lithium demand and mining
The energy transition in Western industrialised nations should help to lower their fossil fuel footprint23 and minimise harmful environmental effects caused by greenhouse gases. However, promoted new technologies could contribute to environmental issues, such as regional “water scarcity”, in other regions of the world. As lithium-ion (Li-ion) based energy storages are a promising technology24, global lithium demand is expected to double or even triple by 202525. In total 67% of the world’s economically mineable lithium resources are supposed to be located in Argentina, Bolivia and Chile26. There, lithium is predominantly made up of unconsolidated brines in extensive, arid salt flats (called salars)27. Applied mining techniques are based on the concept of evaporation: Lithium-rich groundwater is pumped to the surface and injected into evaporation ponds28 to concentrate the brine to a Li-content of 6.7%29 by the process “lithium brine inspissation”. Actually, mining of brines is not extraction of rock, but water. This specific setting already points to regional water scarcity. In terms of hard rock mining water quality is affected by flotation, leaching and filtration of lithium minerals30,31.
Hence, a spatially explicit supply chain for global lithium mining (Supplementary Table 1) is linked to the production of a Li-ion battery storage, which serves as case study with great relevance and topicality to illustrate the presented concept. This study 1) classifies the risk that the WSF addresses, 2) balances natural and human controlled water flows comprehensively in a consistent hydrological framework to also derive WSF (sub-)indicators, 3) adapts the sustainability assessment with the existing LCA midpoint indicator AWARE8 and 4) demonstrates the methodological framework on a Li-ion battery storage.
Results
The methodological framework (presented in the “Methods” section below) is demonstrated calculating a spatially explicit water scarcity footprint of a Li-ion battery storage32 with the open source LCA software openLCA 1.9.0 (https://openlca.org) and the ecoinvent 3.5 database29. Water use is evaluated cradle-to-gate for the construction phase of the battery. Processes for global Lithium mining, manufacturing of battery cells and building of the storage were created (Supplementary Figures 1, 2 and Supplementary Tables 2–5) and are spatially explicit, for all other processes along the supply chain default data are used. The evaluation thus takes into account the entire supply chain, as modelled with ecoinvent 3.5, not only the regionalised lithium input. All processes that contribute more than 1% to the total quantitative and qualitative WSF are shown in the evaluation of the results. The functional unit of the Li-ion battery was chosen to ensure comparability to other electrical energy storage technologies and is the amount of usable electricity, which can be provided based on a unified energy feed-in of 2 MWh per day32. The resulting storage consists of 34,800 kg Li-ion battery cells, requiring 1523 kg of lithium carbonate.
Results can for example be downscaled by a factor 700,000 to a 50 g battery cell, which would be the typical weight of a standard smartphone battery pack. The share of the contributions from regionalised Li-mining and the distribution of remote impacts along the global supply chain stay the same.
Quantitative water scarcity footprint of the modelled Li-ion battery storage
The quantitative Water Scarcity Footprint, WSFquan of the modelled Li-ion battery storage is 33.155 regionally weighted m3 along the entire supply chain from cradle to gate per functional unit (Supplementary Table 6 and 7). Evapotranspiration losses represent the largest part of the physical water consumption with 29.352 m3. Product-incorporated water accounts for 3803 m3, which equals 11% of the total WSFquan. Water transfers have not been detected along the supply chain of the case study.
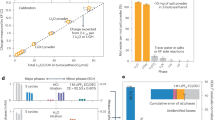
Figure 1a shows processes and flows that contribute more than 1% to the total WSFquan, respectively. They account for 62% of the total WSFquan altogether. The remaining 38% consist of a large number of processes, each of which contributes very little. Figure 1 illustrates hotspots of water use along the supply chain—in an unweighted (Fig. 1c) as well as a globally weighted manner (Fig. 1a).
a Shows the distribution of process water uses greater than 1% along the supply chain of the Li-ion battery-storage in m3 from left to right. Processes are represented by boxes, abbreviations see below. Inputs with no provider are direct inputs. Water flows are weighted with the CFAWARE of the respective region if known. Flows weighted with a CFAWARE < 5 are classified as uncritical (green), with 5–10 as semi-critical (yellow) and with > 10 as critical (red, see also chapter 2.3). There is only one small flow in green from “Li – Guemes, AR” to “cathode prod”. The bar charts in (b) illustrate the effect of weighting for the three greatest flows in numbers: The left number represents the unweighted evaporative water loss, respectively, whereas the right number is the unweighted evaporation multiplied by the CFAWARE, which is 89 for Atacama, Chile, 88 for Zabuye, China, and 25 for Rest-of-Asia (RAS). c Shows all flows from (a) unweighted for visual comparison to demonstrate the effect of weighting. prod, production; liq, liquid; elec prod, electricity production; roll, rolling. Regions: CL, Chile; CN, China; AR, Argentina; RNA, Rest-of-North-America; RAS, Rest-of-Asia; RoW, Rest-of-World.
Looking at unweighted, physical water use, four flows are particularly relevant in terms of quantity (position in the supply chain indicated in Fig. 1a): A combined process that extracts gold, silver, zinc, lead and copper, the production of liquid oxygen and nitrogen as well as direct water inputs of the lithium manganese cathode production and the graphite anode production that are not further differentiated.
Weighted flows are classified uncritical (green), semicritical (yellow) and critical (red) depending on their AWARE characterisation factor CFAWARE (uncritical with CFAWARE < 5, semicritical with CFAWARE between 5 and 10, critical CFAWARE > 10). Figure 1a reveals hotspots of water use especially in resource extraction at the beginning of the supply chain: Lithium extraction from lithium brine in the Salar de Atacama in Chile and the Lake Zabuye in China accounts for 31% of the total regionally weighted WSFquan. This is due to high CFAWARE for these regions. Copper production in “Northern America” (Cu – RNA, as referred to by ecoinvent 3.5) and “Asia” (Cu – RAS, as referred to by ecoinvent 3.5) as well as coal production in China also reveal great regionally weighted volumes.
The weighting accounts for 91% of the final result in the Li-ion battery storage case study, meaning that without weighting the WSFquan would be 3007 m3 instead of 33.155 m3 (Fig. 1b). However, in a few limited cases the regional weighting can decrease the physical water use as well, if the CFAWARE is below 1. Since CFAWARE are given in relation to the world average, this applies to regions of the world where the available water remaining is greater than the world average (chapter 2.3). For example in case of lithium carbonate production in Guemes, Argentina, the CFAWARE is 0.29, and the physical water use diminishes from 90 m3 to 26 m3 by multiplication with 0.29.
Figure 2 illustrates the spatially explicit analysis of WSFquan. Circles are representing the size of water use on a water stress map according to CFAWARE, classified according to the regional water scarcity. The spatial resolution is very different depending on data availability: Lithium mining processes are indicated by point coordinates, while most other processes refer to a country. Some processes can only be resolved down to geographical regions. Figure 2 shows no higher levels of aggregation, such as Rest-of-World or global. The lowest level of disaggregation of the CFAWARE is basin level.
Quantitative Water Scarcity Footprint (WSFquan) per functional unit of processes that contribute most along the supply chain of the Li-ion battery storage on a CFAWARE background map. Processes that contribute more than 1% to WSFquan are shown with their spatial reference: Blue dots are point coordinates, blue lines are countries or geographical regions according to ecoinvent 3.5. “Asia” is marked with a black line for better differentiation from “CN”. The circles represent the weighted physical volume of water (WSFquan) used at the respective location along the Li-ion battery storage supply chain. The colour of the circles corresponds to the colour of the CF with which the corresponding water volume is assessed: For point coordinates basin CFAWARE are used as shown in the map, for countries or geographical regions weighted average CFAWARE are used that are calculated by the presented LCA software implementation of AWARE (Supplementary Chapter 4.3). CL, Chile; CN, China; Cu-mining, copper mining; Li-mining, Lithium mining. The map was created by the authors using the data from Boulay et al.8.
Qualitative water scarcity footprint of the modelled Li-ion battery storage
The qualitative Water Scarcity Footprint WSFqual requires 19 to 85 (median 52) million globally weighted m3 of demineralised water for process aluminium emissions to water per functional unit (Supplementary Table 8). It outnumbers WSFquan by far, which is less than 1% of WSFqual. The span of 19–85 million m3 results from using a high and a low value for the geogenic background concentration for processes without specific location (Table 2).
The processes listed in Table 2 account for approximately 92% of the total WSFqual. The listed processes are ecoinvent 3.5 standard processes and are used repeatedly along the supply chain, if no further regionalisation is provided. Hence, the results are aggregated, meaning that the respective process can be part of the supply chain more than once. Most deliver to global copper production needed for the production of the battery anode or are associated to global aluminium production, which is needed in cathode production and construction in general. The lithium brine mining processes that were considered in this study do not produce emissions to water based on the reviewed literature and are not regarded relevant in virtual dilution, consequently.
Uncertainty analysis
Uncertainties are determined by Monte-Carlo-Simulation, “a stochastic method to estimate the uncertainty of the model output”33, using the simulation tool of the software openLCA and the ecoinvent 3.5 database. It contains uncertainties for most data, while for inventory data created for this study for the global lithium supply (Supplementary Chapter 1) no uncertainties can be determined and a log-normal distribution with a standard deviation of 1 is assumed. This is in line with the recommendations of the LCA guidelines34. For the product system Li-ion battery storage, including the entire supply chain with approximately 110,000 linked processes, the uncertainties are huge (relative standard deviation (RSD) of 60% for WSFquan and of 450% for WSFqual).
Lee et al.33 carried out an uncertainty analysis with AWARE for a case study in Korea and also revealed high RSD values (177 and 185%). They found that Monte-Carlo-Simulation can have problems to display the distribution function of the CFAWARE correctly. This is supported by Hung & Ma35 who generally note, that the selection of the LCIA method is an important source of uncertainty.
Discussion
Conceptual innovations
The presented LCA-WSF can comprehensively assess the risk of natural freshwater scarcity for humans and nature caused by water use associated to a distinct global supply chain in a spatially explicit way. A precondition is to regionalise and conceptualise the LCA water inventory by using the water flows we identified in the risk analysis. This was carried out for the lithium supply chain. From the identified water flows WF (sub-)indicators were derived. These are weighted in a spatially explicit LCA, for which the AWARE software implementation was adapted.
Hence, hotspots of water use can be identified along the supply chain for unweighted, purely physical water volumes as well as regionally weighted volumes. Other spatially explicit studies on water footprints and other footprints also attach great importance to this difference36. However, the regionalisation of the upstream supply chain has not been the focus of most analyses of the WF of energy systems for different reasons37,38,39,40. Different kinds of water use in the course of human-induced processes can be illuminated with the help of the deduced sub-indicators (evapotranspiration losses, product incorporated water, water transfers, virtual dilution volumes), while uniting them under a common risk, which is the reduction of available water remaining if it results in an exceedance of the SOS. Previous water footprint studies have placed less emphasis on this. Inseparable forms of freshwater (former blue and green water) are no longer distinguished, which in the past often led to confusion and ambiguity in WF studies.
Data shortages
Challenges still arise from data shortages. Within the scope of this study, only the inventory data for Li-mining have been enhanced and regionalised. Any other relevant mining processes within the analysis, for example copper mining, rely on data that have not been further regionalised so far. The contribution of Li-mining may be overestimated compared to other mining resources. For better-resolved results, more detailed regionalisation of more processes along global supply chains is required; an effort the LCA community is continuously working on. This analysis gives a first hint which processes contribute the most and should be focused on, e.g., “treatment of sulfidic tailings”, weighted with a CFAWARE of one here, would reveal even higher LCA-WSFs in regions with high CFAWARE. Figure 1 shows that the production of liquid oxygen and nitrogen is responsible for a relative high share (5.8%), of the total WSFquan. The authors presume a mistake in the ecoinvent 3.5 database in this special case (Supplementary Tables 9–14).
Moreover, the underlying hydrological modelling data do not contain all kinds of human water consumption, e. g. mining activities are not considered (Table 3). First calculations indicate that CFAWARE may be underestimated by up to 100% in some basins due to that.
Virtual dilution volumes outnumber physical volumes by far. This is because aluminium emissions along global supply chains are high and the suggested target concentration of 0.2 mg/l41 is low. In addition, the variable geogenic background concentration has a decisive influence on the final result that spans from 15, calculated with high geogenic background concentration to 80 million unweighted m3, calculated with low geogenic background concentration, so it must be determined with sufficient accuracy. The data basis for geogenic background concentrations on a global level should be further improved.
To measure, assess and reduce product water footprints more research is needed in particular in the field of water use in the mining sector. Water pollution from diffuse sources, such as leakage from stockpile overburdens, may be a serious threat to water resources and a subject to future research.
Findings and recommendations
Zhang et al. 201742 analysed the water footprint of inter-provincial electricity transmission in China and found that 12.7% of the national total thermoelectric water consumption are transferred as virtual water across provinces. This indicates that water use plays an important role in the electricity sector in general. The presented study goes a step further and for investigates the remote impacts of an electric storage technology, a Li-ion battery storage, along its regionalised upstream supply chain. The hotspots of water use along the global supply chain of the modelled Li-ion battery storage are mainly associated with mining activities. Lithium brine mining in Chile and in China are responsible for the greatest evapotranspiration losses along the supply chain of the Li-ion battery, while the probability of natural freshwater scarcity for humans and nature is very high in these countries. Satisfying the global lithium demand by extracting lithium there or in regions with similar conditions will probably cause problem shifting: Climate footprints may be reduced by using electric vehicles in European countries, but in turn, the probability of natural freshwater scarcity will increase in lithium supplying countries. More attention should be paid to this fact before politicians and companies in Western nations increasingly focus on electric mobility. We regard the avoidance of problem shifting as a crucial task on the way to a sustainable and long-term global energy transition. The reduction of water quality by other mining processes like copper or aluminium extraction is another critical issue within this nexus as the associated volumes can be huge: The virtual dilution required along the supply chain of the Li-ion battery storage is in the order of magnitude of 23% of the German total annual drinking water demand. However, impacts from water pollution on regional freshwater scarcity have not been part of LCA WF so far, as the water quality has not been assessed in an integrated manner as virtual dilution volume before. To evaluate product water footprints and identify critical hotspots, it is crucial to consider virtual dilution of pollution in order to capture scarcity of (clean) water sufficiently.
Methods
Classification of the risk associated with human water consumption
For an appropriate risk definition the interaction between drivers, pressures and state (as defined in the Drivers-Pressures-State-Impact-Response (DPSIR) framework43) is systematically described for human freshwater consumption: Fig. 3 shows how the anthroposphere as driver puts pressure on the state via inputs and outputs, such as water intake or return of wastewater. The state on basin level is the natural freshwater availability, prescribed by the natural hydrological flow system. The impact from the input and output related pressures on the hydrosphere is the change of natural freshwater availability, in terms of quantity and quality. Within the DPSIR concept, any change of natural freshwater availability can be considered as impact. The concept provided here goes further and compares this change of the state to what is regarded the SOS, as outlined by the Sustainable Development Goals. Here, we consider as impact the risk of an exceedance of the SOS. The SOS is defined in accordance with Alcamo et al.3, where “water scarcity” in a river basin has been defined as a withdrawal-to-availability ratio greater than 0.43 (details in chapter 2.3). The DPSIR framework includes that detrimental impacts are considered by politics and society. To implement the objectives of the Sustainable Development Goals, human activities would have to be directed and production and consumption processes to be adapted in order to meet the SOS. In addition, other pressures, such as climate change, also influence natural freshwater availability, and, similar to other water users, contribute to the change of natural freshwater availability (Fig. 3). These external factors are not considered explicitly in the LCA-WSF, while the corresponding data enter the hydrological modelling. The risk of human freshwater consumption can now be classified as the potential change of natural freshwater availability that exceeds the SOS, and thus describes the risk of freshwater scarcity for humans and nature. It is expressed in volumes of available freshwater remaining8. This goes beyond conventional life cycle impact assessment methods, where the SOS is usually not considered. Within LCA framework the classified risk can be located at midpoint level. The presented midpoint LCA-WSF assesses the on-site and remote probability of natural freshwater scarcity for humans and nature caused by water use along human supply chains in a spatially explicit way. “Natural freshwater” refers to basin-specific water in its naturally occurring water quality.
Interaction of drivers (anthroposphere), pressures (input and output), state (hydrosphere), impacts (change of state) and response (Sustainable Development Goals, SDGs) for human water consumption according to the Drivers-Pressures-State-Impacts-Response (DPSIR) approach43. SOS Safe Operating Space.
Distinction of relevant water flows and deduction of WSF (sub-)indicators
The deduction of LCA-WSF (sub-) indicators is based in Fig. 3, but carried out on grid cell level to relate the indicators, prepared for use in LCA, spatially to the hydrological modelling data. The entire surface of the earth can be subdivided into single grid cells with a 5 × 5 arcminute spatial resolution (about 9 × 9 km at the equator), which is the basis of geospatial data structures. One such grid cell is currently the smallest scale to combine local process inventories along supply chains and hydrological modelling data needed to identify the SOS (further explanations in chapter 4.3). As the scale of assessment can vary depending on the scope of the LCA-WSF (global, country, basin, regional, local), the basic concept (Fig. 3) as well as the grid cell balance (Fig. 4) can be applied to any of these scales (more information Supplementary Figure 3, 4). The balance is carried out on grid cell to match the resolution of the global hydrological model WaterGAP. Due to uncertainties of the model, water scarcity is not determined on grid cell, but basin level.
Balance of natural water flows and deduction of the “Availability-Minus-Demand” (AMDi) as introduced by Boulay et al. 20178. The hydrological water availability is compared to all processes on the grid cell that use water. inaw, hydrological inflow from upstream cell; paw, precipitation; eaw, evapotranspiration; outaw, hydrological outflow to downstream cell; inp, intake of water; outp, outflow of water; ininc, intake of water via product inflow (incorporated water) from upstream supply chain; ep, evapotranspiration; transp, water transfer to different catchment area; outinc, outflow of water via product flow (incorporated water).
Figure 4 shows the physical water balance for natural water flows on grid cell level with AMDi, representing the Availability-Minus-Demand. This term is consistent with the work of Boulay et al.8. The index “i” represents the respective catchment area. AMDi is determined by the inflow from upstream cells inaw, precipitation paw, outflow from water using processes to AMDi outp, the water intake by water using processes inp, evapotranspiration eaw and the outflow to downstream cells outaw. AMDi is determined for each grid cell by balancing the sum of the aforementioned flows, respectively, i.e., there is no distinction between different sources of water, water uses or water users.
Balancing AMDi,t=x+1 with the general equation mt=x+1 = mt=x + dm dt−1, where m represents a stock, t = x a certain point in time and t = x + 1 a later point in time, results in Eq. (1).
The time period between x and x+1 depends on the particular case study and can be varied. In hydrological considerations, a year or a month is common. The reference is the functional unit of the product systems under consideration, e.g., 1 kg lithium. An indirect time reference can be established by taking into account the time needed to produce this functional unit. To isolate the contribution of a single process within the totality of water-using processes, an allocation of inp, ininc, ep, transp, out, and outinc is performed based on the percentage of water use of the respective process out of the total water use of all processes. Equation (2) provides an important basic condition for this: The balance of inflows and outflows of water using processes is zero, respectively, meaning that processes do not have an own water stock. Water that is actually taken from AMDi and stored by water using processes is treated as still being available and belonging to AMDi. Changes, either caused by the implementation of a new process or the change of an existing process, are reflected by an increase or decrease of inp or outp and influence the result of the balance according to Eq. (1)). Since it is necessary to consider all water-using processes in order to identify the potential contribution to water stress, water flows are not related to a previous, potentially natural or reference state, but are counted as such (Supplementary Chapter 4.2).
The water balance shows, which water flows are relevant to identify the contribution of the sum of all water-using processes in a reference area to water stress. The same water flows are used to describe the water use of a single process (e. g. a case study for which a WSF should be calculated). If they are weighted according to the regional water stress, water footprint indicators are obtained. They are grouped into two LCA-WSF midpoint indicators: (1) The quantitative Water Scarcity Footprint WSFquan comprises all physical volumes of water use. According to the physical water balance (Fig. 4 and Eq. (2)), used water is the portion of water taken from AMDi that is not returned. It includes evapotranspiration losses (ep), water transfers (transp) and product incorporated water (outinc) per functional unit. Thus, the abstraction or intake of water on the input side of a water-using process per functional unit is indirectly considered as water use by accounting of the resulting output flows. Evapotranspiration loss ep refers to consumptive, evaporative water use and is already well-known from former W(S)F studies7,8. Evapotranspiration from plant systems is included in this indicator, which represents the former “green” water2. The indicator transp accounts for water that is removed from the hydrological water cycle by water transfers, e.g., through water pipelines. Product incorporated water outinc represents water that is bound to the output product flow. For example, concentrated Li-brine, the output product of the first refinement step in lithium production, has a water content of approximately 90% weight. (2) The qualitative Water Scarcity Footprint WSFqual comprises all virtual dilution volumes (VDV) per functional unit. Different methodological approaches for the assessment of water quality exist20,21,44, and the concept of virtual dilution is best suited here to assess the contribution of water pollution to a potential change of natural freshwater availability that exceeds the SOS: Each emission to water represents an additional burden (“material emission to water” Fig. 3) and, in practical terms, reduces the availability of water with adequate quality. To ensure that the water quality of AMDi is not reduced any additional emission would have to be diluted. Table 4 summarises the sub-indicators and establishes their relationship to the Sustainable Development Goals.
The “grey water footprint” is a commonly used approach to determine the VDV2,45,46,47,48,49,50, usually calculated according to Hoekstra et al. 2011 2. The grey water footprint is calculated by the VDV required to dilute the additional of a specific substance loads introduced by a human activity in a specific catchment area i. The calculation takes into account a target concentration for s, defined as ctarg,s [mg l−1], as well as the geogenic preload with s of the regionally available water measured as cgeo,s [mg l−1]. The dilution volume is calculated by dividing the loads [mg] by the difference of ctarg,s [mg l−1] and cgeo,s [mg l−1].
However, the equation is undefined for ctarg,s = cgeo,s and leads to negative results for ctarg,s < cgeo,s (Supplementary Figures 5, 6). The authors present here a different approach with the following basic rationale: 1) For loads of substances which occur also naturally in water, the human activity should not alter cgeo,s. 2) For loads of natural and anthropogenic substances, for which cgeo,s equals zero, specific target values should not be exceeded. 3) Consequently, the minimum volume of water to dilute load,s to cgeo,s would assume the use of demineralised water. This is a general difference to the approach of Hoekstra et al. 2011, where regionally pre-loaded water is used for dilution (Supplementary Chapter 4.2). The VDV with demineralised water VDVs,i,dem is calculated by dividing load,s in a catchment area i by the cgeo,s (Eq. (3), FU = functional unit).
For better applicability in LCA, units are changed to kg and m3 and loads measured per functional unit. Within an LCA analysis, loads are represented by elementary flows. According to Eq. (3) an input is diluted with demineralised water, as it can be provided in practice by desalinating water from AMDi in desalinisation plants, to the geogenic background concentration to adapt the emission to the regional water characteristics. This corresponds to the idea of regionalisation of the WSF, according to which the change of the regional initial conditions is evaluated.
Equation (3) is not defined, if cgeo,s equals zero, which is unlikely for natural substances in reality, but is the rule for anthropogenic substances such as pesticides or medical compounds and their residues. In such cases ctarg,s should not be exceeded. Therefore, if cgeo,s = 0 or cgeo > ctarg, VDVs,i, dem should then calculated based on ctarg,s (Eq. (4), Supplementary Chapter 4.2).
For the Li-ion battery storage the VDV is calculated accordingly. If the geogenic background concentration cgeo,s in the specific catchment area is not known due to missing data or uncertainties, median substance specific groundwater concentrations from Europe, Middle East, Russia, India, China, Australia, North America, and South America are used to calculate approximate results (Supplementary Table 15). The target concentration ctarg,s is the substance-specific limit value recommended by the first international water quality standard, the drinking water standard of the World Health Organisation41. The VDV is calculated along the supply chain of the case study only for aluminium, that is emitted to water via process recharge (VDVAl,i,dem). Aluminium is considered here as a stand-in for water pollution, as the authors have noticed that in processes along global supply chains it often makes the largest contribution to water pollution. This approach ensures that all other substances with smaller contributions to the dilution volume are also diluted.
WSFquan and WSFqual of a process include all water uses that contribute to the risk classified in chapter 2.1 within the definition of the LCA-WSF.
Regionalisation through combination of regionalised inventory and Life Cycle Impact Assessment
To perform a regionalised LCIA the inventory of the case study is regionalised by implementing the world lithium production on mine site level to the ecoinvent 3.5 database (Supplementary Chapter 1). For the LCIA itself, different methods exist for the W(S)F. AWARE8 is currently a widely accepted approach. CFAWARE are calculated by comparing the basin specific available water remaining to the consumption-weighted world average value. The available water remaining is calculated by subtracting human water consumption and environmental water requirements from the hydrological water availability of a catchment area i, referred to as Availability-Minus-Demand AMDi. The data basis of the calculations are Pastor et al.51 and the hydrological modelling framework WaterGAP252, where the hydrological water availability is modelled as well as the human water consumption on grid cell level, including consumption models for agriculture, manufacturing, industry, households and electricity generation. Values are expressed in (m2 ∙ month) m−3, which is the “surface-time equivalent required to generate one cubic metre of unused water” in the respective basin8. CFAWARE can reach from 0.1 (lowest water stress level) to 100 m3world eq. m−3basin (scale is cut-off at 100, which is set as highest water stress level). Quantitative results from the inventory analysis are multiplied with the CFAWARE, thus transforming them into globally weighted, theoretical volumes with respect to regional conditions.
The SOS is defined here in accordance with Alcamo et al.3 who defined severe water scarcity as a withdrawal-to-availability ratio greater than 0.43. However, for the AWARE approach the SOS has not yet been defined. By transferring the definition by Alcamo et al.3 to the AWARE method, the limit between water stress and no water stress is estimated to a CFAWARE of 5 as a counterpart to a withdrawal-to-availability ratio of 0.4 (Supplementary Table 16). CFAWARE between 5 and 10 represents moderate and CFAWARE > 10 severe water stress. Hence, the CFAWARE of a respective basin defines its water stress level and indicates whether the combined water consumption of water using processes leads to an exceedance of the SOS by reducing the hydrological storage (Fig. 4). We have translated this classification into an AWARE map (underlying Fig. 2), where basin CFAWARE < 5 are coloured in green, CFAWARE 5–10 in yellow and CFAWARE > 10 in red. Because of the wide range, CFAWARE 10–100 is divided into three ranges (10–30, 30–60, and 60–100) with darkening shades of red. Table 5 compares the DPSIR nomenclature with the equivalents at catchment and grid cell level and those used throughout this study. Table 3 provides an overview of the different specifications of WaterGAP2, the AWARE method and the presented approach.
Next to adapting the process inventories, the AWARE software implementation was modified for the purpose of this study (Supplementary Figure 7–14 and Supplementary Table 17). The most important difference to the original publication is that water volumes are not weighted if their location is unknown. This reflects the conviction of the authors that if no spatially explicit information is available, no regionalised impact assessment can be carried out. Using a world average characterisation factor for water is mathematically possible, but contradicts the idea behind regionalisation. Aggregation of catchment level CFAWARE, necessary if processes along the supply chain refer to a country or higher aggregated geographical region, e.g., “Europe”, is performed based on the consumption-weighted approach already used by Boulay et al8.
Data availability
Life Cycle Inventory (LCI) data of lithium production and the Li-ion battery storage as well as LCIA methods and data that support the findings of this study have been stored at Mendeley Data53. Other LCI data that support the findings of this study are available from ecoinvent (www.ecoinvent.org), but restrictions apply to the availability of these data, which were used under license for the current study, and so are not publicly available. The original AWARE method is for example available from https://www.openlca.org/ and the underlying data from the publication of Boulay et al.8 are available from http://www.wulca-waterlca.org/.
References
Hoekstra, A. Y. & Hung, P. Q. Virtual water trade: a quantification of virtual water flows between nations in relation to international crop trade. Value Water Res. Rep. Ser. 11, 1–120 (2002).
Hoekstra, A. Y., Chapagain, A. K., Aldaya, M. M. & Mekonnen, M. M. The Water Footprint Assessment Manual. (2011).
Alcamo, J. et al. Global estimates of water withdrawals and availability under current and future “business-as-usual” conditions. Hydrol. Sci. J. 48, 339–348 (2003).
Alcamo, J., Flörke, M. & Märker, M. Future long-term changes in global water resources driven by socio-economic and climatic changes. Hydrol. Sci. J. 52, 247–275 (2007).
Pfister, S., Koehler, A. & Hellweg, S. Assessing the environmental impacts of freshwater consumption in LCA. Environ. Sci. Technol. 43, 4098–4104 (2009).
Boulay, A., Bulle, C., Deschênes, L. & Margni, M. LCA Characterisation of Freshwater Use on Human Health and Through Compensation. Towar. Life Cycle Sustain. Manag. (2011). https://doi.org/10.1007/978-94-007-1899-9_19
Berger, M., Van Der Ent, R., Eisner, S., Bach, V. & Finkbeiner, M. Water accounting and vulnerability evaluation (WAVE): Considering atmospheric evaporation recycling and the risk of freshwater depletion in water footprinting. Environ. Sci. Technol. 48, 4521–4528 (2014).
Boulay, A. M. et al. The WULCA consensus characterization model for water scarcity footprints: assessing impacts of water consumption based on available water remaining (AWARE). Int. J. Life Cycle Assess. 23, 368–378 (2018).
Deutsches Institut für Normung e. V. DIN EN ISO 14046:2016-07: Umweltmanagement – Wasser-Fußabdruck – Grundsätze, Anforderungen und Leitlinien (ISO 14046:2014). (2016). https://doi.org/10.31030/2416232
Kounina, A. et al. Review of methods addressing freshwater use in life cycle inventory and impact assessment. Int. J. Life Cycle Assess. 18, 707–721 (2013).
Ridoutt, B. G. & Pfister, S. A revised approach to water footprinting to make transparent the impacts of consumption and production on global freshwater scarcity. Glob. Environ. Chang. 20, 113–120 (2010).
Boulay, A. M., Bulle, C., Bayart, J. B., Deschênes, L. & Margni, M. Regional characterization of freshwater use in LCA: Modeling direct impacts on human health. Environ. Sci. Technol. 45, 8948–8957 (2011).
Bösch, M. E., Hellweg, S., Huijbregts, M. A. J. & Frischknecht, R. Applying Cumulative Exergy Demand (CExD) indicators to the ecoinvent database. Int. J. Life Cycle Assess. 12, 181–190 (2007).
Hanafiah, M. M., Xenopoulos, M. A., Pfister, S., Leuven, R. S. E. W. & Huijbregts, M. A. J. Characterization factors for water consumption and greenhouse gas emissions based on freshwater fish species extinction. Environ. Sci. Technol. 45, 5272–5278 (2011).
Milà I Canals, L. et al. Assessing freshwater use impacts in LCA: Part I - Inventory modelling and characterisation factors for the main impact pathways. Int. J. Life Cycle Assess. 14, 28–42 (2009).
Motoshita, M., Itsubo, N. & Inaba, A. Development of impact factors on damage to health by infectious diseases caused by domestic water scarcity. Int. J. Life Cycle Assess. 16, 65–73 (2011).
Zelm, R. Van et al. Implementing groundwater extraction in life cycle impact assessment: characterization factors based on plant species richness for the Netherlands. Environ. Sci. Technol. 45, 629–635, https://doi.org/10.1021/es102383v (2011).
Deutsches Insitut für Normung e. V. DIN EN ISO 14040:2006: Umweltmanagement – Ökobilanz – Grundsätze und Rahmenbedingungen. (2016).
European Commission. EU SDG Indicator Set 2018 Result of the Review in Preparation of the 2018 Edition of the Eu Sdg Monitoring Report. (2018).
Ridoutt, B. G. & Pfister, S. A new water footprint calculation method integrating consumptive and degradative water use into a single stand-alone weighted indicator. Int. J. Life Cycle Assess. 18, 204–207 (2013).
Boulay, A. M., Bouchard, C., Bulle, C., Deschênes, L. & Margni, M. Categorizing water for LCA inventory. Int. J. Life Cycle Assess. 16, 639–651 (2011).
Van Vliet, M. T. H., Florke, M. & Wada, Y. Quality matters for water scarcity. Nat. Geosci. 10, 800–802 (2017).
Wang, H. et al. Scarcity-weighted fossil fuel footprint of China at the provincial level. Appl. Energy 258, 114081 (2020).
Vikström, H., Davidsson, S. & Höök, M. Lithium availability and future production outlooks. Appl. Energy 110, 252–266 (2013).
Rohstoffagentur in der BGR, D. DERA Rohstoffinformation Nr. 33: Rohstoffrisikobewertung Lithium. (2017).
Rongguo, C., Juan, G., Liwen, Y., Huy, D. & Liedtke, M. Supply and Demand of Lithium and Gallium. (2016).
Lines, G. C. Hydrology and surface morphology of the Bonneville salt flats and pilot valley playa, Utah. (Dept. of the Interior, Geological Survey, 1979). https://doi.org/10.3133/wsp2057
Braga, P., França, S. & Junior, C. How big is the lithium market in Brazil? Impc 2014, 1–10 (2014).
Wernet, G. et al. The ecoinvent database version 3 (part I): overview and methodology. Int. J. Life Cycle Assess. 21, 1218–1230 (2016).
Margarido, F., Vieceli, N., Durão, F., Guimarães, C. & Nogueira, C. A. Minero-metallurgical processes for lithium recovery from pegmatitic ores. Comun. Geológicas. 101, 795–798 (2014).
Meshram, P., Pandey, B. D. & Mankhand, T. R. Extraction of lithium from primary and secondary sources by pre-treatment, leaching and separation: a comprehensive review. Hydrometallurgy 150, 192–208 (2014).
Mostert, C., Ostrander, B., Bringezu, S. & Kneiske, T. M. Comparing Electrical Energy Storage Technologies Regarding Their Material and Carbon Footprint. Energies 11, 3386 (2018). https://doi.org/10.3390/en11123386
Lee, J. S., Lee, M. H., Chun, Y. Y. & Lee, K. M. Uncertainty analysis of the water scarcity footprint based on the AWARE model considering temporal variations. Water (Switzerland) 10, 1–13 (2018).
(IPCC), I. P. on C. C. Guidelines for National Greenhouse Gas Inventories Chapter 3 of Volume 1. (2006).
Hung, M. L. & Ma, H. W. Quantifying system uncertainty of life cycle assessment based on Monte Carlo simulation. Int. J. Life Cycle Assess. 14, 19–27 (2009).
Font Vivanco, D., Sprecher, B. & Hertwich, E. Scarcity-weighted global land and metal footprints. Ecol. Indic. 83, 323–327 (2017).
Galan del Castillo, E. & Velazquez, E. From water to energy: The virtual water content and water footprint of biofuel consumption in Spain. Energy Policy 38, 1345–1352 (2010).
Okadera, T., Chontanawat, J. & Gheewala, S. H. Water footprint for energy production and supply in Thailand. Energy 77, 49–56 (2014).
Okadera, T., Geng, Y., Fujita, T., Dong, H. & Liu, Z. Evaluating the water footprint of the energy supply of Liaoning Province, China: A regional input – output analysis approach. Energy Policy 78, 148–157 (2015).
Jursova, S., Burchart-Korol, D. & Pustejovska, P. Carbon footprint and water footprint of electric vehicles and batteries charging in view of various sources of power supply in the Czech Republic. Environ. - MDPI 6, 1–11 (2019).
WHO. A global overview of national regulations and standards for drinking-water quality. (2018).
Zhang, C. et al. Virtual scarce water embodied in inter-provincial electricity transmission in China. Appl. Energy 187, 438–448 (2017).
Smeets, E. & Weterings, R. Environmental indicators: Typology and overview. European Environment Agency (1999).
Bayart, J. B., Worbe, S., Grimaud, J. & Aoustin, E. The Water Impact Index: A simplified single-indicator approach for water footprinting. Int. J. Life Cycle Assess. 19, 1336–1344 (2014).
Chapagain, A. K., Hoekstra, A. Y., Savenije, H. H. G. & Gautam, R. The water footprint of cotton consumption: An assessment of the impact of worldwide consumption of cotton products on the water resources in the cotton producing countries’. Ecol. Econ. 60, 186–203 (2006).
Mekonnen, M. M. & Hoekstra, A. Y. The green, blue and grey water footprint of crops and derived crop products. Hydrol. Earth Syst. Sci 15, 1577–1600 (2011).
Mekonnen, M. M. & Hoekstra, A. Y. The green, blue and grey water footprint of farm animals and animal products. Value Water Res. Rep. 48, 1–50 (2010).
Gerbens-Leenes, P. W., Hoekstra, A. Y. & van der Meer, T. The water footprint of energy from biomass: a quantitative assessment and consequences of an increasing share of bio-energy in energy supply. Ecol. Econ. 68, 1052–1060 (2009).
Mekonnen, M. M. & Hoekstra, A. Y. The blue water footprint of electricity from hydropower. Hydrol. Earth Syst. Sci. 16, 179–187 (2012).
Franke, N. & Mathews, R. Grey Water Footprint Indicator of Water Pollution in the Production of Organic vs. Conventional Cotton in India. (2011).
Pastor, A. V., Ludwig, F., Biemans, H., Hoff, H. & Kabat, P. Accounting for environmental flow requirements in global water assessments. Hydrol. Earth Syst. Sci. 18, 5041–5059 (2014).
Flörke, M. et al. Domestic and industrial water uses of the past 60 years as a mirror of socio-economic development: a global simulation study. Glob. Environ. Chang. 23, 144–156 (2013).
Schomberg, A. Data to calculate a spatially-explicit water scarcity footprint in LCA. Mendeley Data, V1 (2020). https://doi.org/10.17632/34vzndtmfj.1
Acknowledgements
This research work was performed as part of the project “Wasserressourcen als bedeutsamer Faktor der Energiewende auf lokaler und globaler Ebene”, WANDEL (02WGR1430A), carried out with the support of the Federal Ministry of Education and Research (BMBF) within its research initiative “Global Resource Water (GRoW)”.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
A.C.S. and S.B. are responsible for the conceptual elaboration with support from M.F., who also supervised the project WANDEL. A.C.S. developed the LCA models, operationalised the methodology, calculated and evaluated the results and created the figures, wrote the main paper and Supplementary Information. S.B. extensively revised the manuscript and M.F. revised the manuscript with a focus on hydrological aspects. All authors discussed the results and implications and commented on the manuscript at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schomberg, A.C., Bringezu, S. & Flörke, M. Extended life cycle assessment reveals the spatially-explicit water scarcity footprint of a lithium-ion battery storage. Commun Earth Environ 2, 11 (2021). https://doi.org/10.1038/s43247-020-00080-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-00080-9
This article is cited by
-
Water quality footprint of agricultural emissions of nitrogen, phosphorus and glyphosate associated with German bioeconomy
Communications Earth & Environment (2023)
-
Spatially explicit life cycle assessments reveal hotspots of environmental impacts from renewable electricity generation
Communications Earth & Environment (2022)
-
Tracing the origin of lithium in Li-ion batteries using lithium isotopes
Nature Communications (2022)
-
Towards sustainable extraction of technology materials through integrated approaches
Nature Reviews Earth & Environment (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.