Abstract
Climate models and/or their output are usually bias-corrected for climate impact studies. The underlying assumption of these corrections is that climate biases are essentially stationary between historical and future climate states. Under very strong climate change, the validity of this assumption is uncertain, so the practical benefit of bias corrections remains an open question. Here, this issue is addressed in the context of bias correcting the climate models themselves. Employing the ARPEGE, LMDZ and CanAM4 atmospheric models, we undertook experiments in which one centre’s atmospheric model takes another centre’s coupled model as observations during the historical period, to define the bias correction, and as the reference under future projections of strong climate change, to evaluate its impact. This allows testing of the stationarity assumption directly from the historical through future periods for three different models. These experiments provide evidence for the validity of the new bias-corrected model approach. In particular, temperature, wind and pressure biases are reduced by 40–60% and, with few exceptions, more than 50% of the improvement obtained over the historical period is on average preserved after 100 years of strong climate change. Below 3 °C global average surface temperature increase, these corrections globally retain 80% of their benefit.
Similar content being viewed by others
Introduction
For most practical purposes of climate change impact assessment, regional-scale climate change information is required1. This information begins with large-scale climate change information produced from coupled atmosphere-ocean global climate models (CGCMs). Critical features at these scales include the placement and intensity of major atmospheric centers of action, such as jet streams, and patterns of variability particularly on interannual and monthly time scales. Finer regional scale and boundary-layer climate are then derived from CGCM output by statistical and dynamical downscaling2, thereby adding value to the climate change information produced by CGCMs. It is well known that CGCMs can contain substantial biases in large-scale features, which are often of the order of the projected centennial climate change signal itself3. This fact is sometimes referred to as the garbage in-garbage out problem of regional climate modeling4, which denotes the fact that model output is necessarily worthless incorrect if the input is wrong. This problem can be partially compensated for by appropriate selection of the driving coupled climate model4,5,6, and post hoc bias adjustment of the large-scale or downscaled regional climate change information6,7,8. However, large-scale climate information biases remain and in particular circulation biases continue to undermine the potential value added by the downscaling exercise4,9.
As an additional tool to support the reduction of CGCM biases of large-scale climate change information, an empirical bias-correction (EBC) approach for simulations with atmosphere-only general circulation models (AGCMs) has been proposed and applied10. This approach uses bias-corrected sea-surface temperatures and sea ice coupled with in situ, or run-time, corrections of large-scale climate model biases, following previous work11,12, where this method had been applied in the context of seasonal predictions. The EBC involves the derivation of an annual cycle of cyclostationary forcings over the historical period for the atmosphere-only (AGCM) counterpart of a CGCM (see “Methods” section). The EBC is then applied to the AGCM for atmosphere-only future climate projections employing bias-corrected sea-surface temperatures and sea ice from the CGCM with the goal of reducing general circulation biases in future projections. As with all bias correction methods, the utility of the EBC approach rests on the assumption that climate biases are essentially stationary between historical and future climate states. It is not at all obvious that the stationarity assumption should hold given the large external forcing perturbations associated with many scenarios of future climate change.
In this study, the utility of the EBC approach is investigated by employing model data as a proxy for observations to allow an explicit testing of the stationarity assumption. We employ coupled atmosphere-ocean climate models (CGCMs) and their associated AGCMs from three independent climate modeling centers, and pair each center’s AGCM with another center’s CGCM (see “Methods” section). For each pair, an EBC is derived for the AGCM using the historical simulations of the CGCM as the observational reference. The EBC approach is then used in the AGCM for future projections. The historical and future climate (in particular the atmospheric circulation) simulated by the corrected and the uncorrected AGCMs is then compared to that of the reference CGCM. In such a perfect model (or pseudo-reality) experiment13,14,15,16, one can explicitly test the stationarity assumption and so the utility of the EBC procedure across several models and several reference versions of pseudo observations. It is arguable that employing CGCM model output as a proxy for observations provides an even more stringent test of the EBC methodology as all CGCMs were developed independently, and each have unique historical climatologies and future projections. The fundamental question addressed here is whether, and to what extent, the improvement obtained by construction for the present-day reference climate is preserved in the future (here, over 100 years under a very strong emission scenario). While the EBC method was initially developed and tested for a seasonal prediction context11,12, more recent work10 heuristically applied it for Antarctic climate projections. This paper provides the first proof of the validity of this method in the context of projections of strong climate change.
In the following, the EBC approach is assessed for its ability to improve climatological (20-year) mean values and statistics of interannual and synoptic time scale variability. The results show that using this bias correction method consistently improves the simulated climate on this large range of time scales, and more importantly, that a large part of the improvement obtained for the present reference period is preserved under strong climate change.
Results
Climatological means
Figure 1 displays time series of the global mean square error of 20-year running-mean averages of monthly climatological means of fundamental atmospheric variables at representative levels in the free troposphere (air temperature T, zonal wind speed u, meridional wind speed v, geopotential height zg) and surface air pressure ps. For each corrected AGCM, the error is calculated with respect to the monthly climatology of the target CGCM at each level, vertically averaged if applicable, and normalized by dividing by the corresponding error of the uncorrected version of the AGCM. The figure shows clearly that except for surface pressure in ARPEGE after 2080, the corrected AGCMs continue to outperform the uncorrected versions systematically, and that for almost all variables and models, there is no substantial degradation of the error scores after the 1981–2000 calibration period. For most variables and models, the mean square error of the corrected AGCMs are fairly stable in time, with typical values of about 40–60% of the MSE of their uncorrected versions (see also Supplementary Fig. 1).
Global average mean square error (MSE) of the corrected AGCM runs relative to the uncorrected reference runs for 20-year running means of fundamental atmospheric circulation variables (air temperature T, zonal wind speed u, meridional wind speed v, geopotential height zg, and surface air pressure ps (over areas with surface height below 1000 m)). MSE of T, u, v, and zg are averaged over four representative pressure levels (850, 700, 500, and 300 hPa (200 hPa for LMDZ)). a LMDZ; b CanAM4; c ARPEGE.
The degradation of the surface pressure and geopotential height scores for ARPEGE in the latter half of the twenty-first century is due to a positive bias of the target IPSL-coupled model over the Southern Ocean during the reference period and a negative sea-level pressure trend in that model over the twenty-first century (see Supplementary Fig. 2). While the corrected version of the ARPEGE AGCM better represents the present sea-level pressure over the Southern Ocean of the ISPL-coupled model, both the corrected and uncorrected versions of the AGCM do not reproduce the strong twenty-first century trend simulated by the target model that compensates for its present-day bias, leading to a strong error of the corrected AGCM by the end of the twenty-first century. This is consistent with the fact that the IPSL and CNRM coupled models represent opposite extremes of the Coupled Model Intercomparison Project phase 5 (CMIP5) spectrum regarding the trends of Southern Hemisphere jet and Southern Annular Mode17. The ARPGE/IPSL-CM combination is thus a test of the most unfavorable possible situation. For the other AGCMs and other variables of the ARPEGE model, 80% of the MSE reduction obtained for the 1981–2000 reference period is preserved at least until about 2070, when the global mean surface air temperature change with respect to the reference period attains about 3 °C. A striking example is the 500 hPa geopotential height in the CanAM4 model, displayed in Fig. 2, which emulates very well both the present and future global geopotential height distribution of the CNRM-CM coupled model. Supplementary Figs. 3–6, which display similar maps for all models and additional variables, confirm that a general and consistent improvement is obtained for the present and, importantly, largely conserved in the projections. We note that while the amplitude of the biases is quite systematically reduced in the corrected runs, the spatial patterns of the biases are often similar between the uncorrected and the corrected versions, and between the reference and projection period.
Annual mean 500 hPa geopotential height difference (in m) between CanAM and CNRM-CM. a Uncorrected, 1981–2000; b corrected, 1981–2000; c uncorrected, 2081–2100; d corrected, 2081–2100. The global mean error is subtracted to highlight the spatial structures over global mean errors. RMSE of the CanAM4 simulation with respect to the CNRM reference (in m), before and after subtraction of the global mean error, is given in parentheses in the panel titles.
While free atmosphere temperature and wind fields were nudged and corrected in our simulations, atmospheric mass (that is, surface pressure and geopotential height fields) was not. Good and stable performance for these variables (at least up to about 3 °C global mean surface air temperature change), linked to the extratropical wind fields by the near-geostrophic relation, is therefore an indicator of consistent and robust improvement of the simulated atmospheric circulation. These improvements, both for the reference and the projection periods, are also visible in the location and intensity of atmospheric centers of action such as the Southern Westerlies (Supplementary Fig. 7) and the Aleutian low (Supplementary Fig. 8).
Interannual variability
For the climatological means of wind and temperature, and, indirectly, geopotential heights and sea-level pressure, the improvement during the 1981–2000 reference period is obtained by construction, while the preservation of the benefit of the bias correction beyond that period is an indicator of the validity of the method. Conversely, emergent climate system properties such as patterns of interannual circulation variability are not necessarily improved by construction even during the reference period. However, as can be seen in Fig. 3, the corrected AGCMs do better represent the spatial patterns of the interannual extratropical circulation variability of the target coupled models than the uncorrected AGCMs. Across the three models, the squared spatial correlation coefficient r2 between the first 500 hPa geopotential empirical orthogonal functions (EOFs) of the AGCMs and the target coupled models is higher for the corrected than the uncorrected models during 83% of the simulation period, and no systematic degradation can be seen in the latter part of the period. This includes a number of situations, where improvement is particularly challenging because the spatial patterns of the first EOF in the AGCM and in its reference coupled model are very similar (that is, the spatial r2 is close to 1 already in the uncorrected version). For the 500-hPa zonal wind speed, the corresponding successful proportion is 78%. This indicates that the corrected AGCMs quite systematically simulate interannual circulation variability patterns that are in better agreement with those of the target pseudo-reality coupled model, and this improvement is preserved under strong climate change. This ability of the EBC to improve second-order climate statistics is consistent with a previous study12 that demonstrated improved interannual variability for ten fields in the context of EBC seasonal predictions.
Squared spatial correlation coefficient (r2) of the first EOF of monthly mean extratropical (polewards of 30°N and S) 500 hPa geopotential (20-year periods), bias-corrected minus uncorrected simulation. a Northern hemisphere winter (DJF); b Northern hemisphere summer (JJA); c Southern hemisphere winter (DJF); d Southern hemisphere summer (JJA).
Synoptic variability
A similarly fundamental emerging circulation characteristic is the sea-level pressure variability on the synoptic time scale between 2 and 6 days18, dominated by extratropical storm tracks. As shown in Fig. 4, the corrected AGCMs quite consistently (during 87% of the simulation period across the three models) exhibit a reduced global average mean square error of the temporal standard deviation of band-pass (2–6 days) filtered daily sea-level pressure, and again, a beneficial effect of correcting the mean circulation characteristics remains visible until at least about 2070. In two out of the three corrected AGCMs, only a negligible long-term increase of the relative MSE is observed over the twenty-first century. This improvement in the global-mean synoptic variability is consistent with an improved intensity and location of the variability maxima, as can be seen for example for the Aleutian Low in winter in Supplementary Fig. 8.
Global average mean square error (MSE) of the corrected AGCM runs relative to the uncorrected reference runs for 20-year running averages of the temporal standard deviation of band-pass (2–6 days) filtered daily sea-level pressure (full lines). Values are calculated every 5 years. Dashed lines indicate the linear regression over the full period. The black constant line at y = 1, indicating the limit above which the benefit of the bias correction vanishes, is provided for visual guidance.
Discussion
Taken together, our results show that the run-time empirical bias correction (EBC) method tested here improves simulated atmospheric circulation characteristics on a broad range of temporal scales. In addition to the climatological mean values, which are improved by construction over the historical period, emergent circulation properties such as patterns and intensities of interannual and synoptic-scale circulation variability are also improved. Most importantly, our pseudoreality test clearly shows that the improvements on climatological, interannual, and synoptic time scales are to a very large part preserved under strong climate change of the order of an about 3 °C global surface air temperature change. In some cases, the relative biases of the corrected models even decrease over time, suggesting that the bias correction, as implemented here, does not over-constrain the models. This method for run-time bias corrections of large-scale atmospheric circulation models thus remains valid under strongly nonstationary conditions. Validity of this bias-correction method is further supported recent work19, which based on the analysis of CMIP5 results, has shown striking stationarity of large-scale climate model bias patterns under strong climate change.
The EBC approach is by construction expected to have little impact on the magnitude of the climate change response of the uncorrected CGCM as its sea-surface temperatures (SSTs) and sea ice are utilized as boundary conditions for the AGCM future projections (see “Methods” section). Benefit comes rather from circulation improvements about the CGCM’s changing climate signal, which should then improve its subsequent downscaling. The ability of the EBC to alter the control circulation upon which climate-change external forcings are applied, while leaving all other properties of the model unchanged, means that it additionally provides an interesting tool to disentangle the influences of model formulation vs. basic state on the circulation response itself. As such the EBC methodology will also provide a direct means to probe such questions and will compliment existing approaches (e.g., emergent constraints).
The bias correction does not seem to fix the location of features of the atmospheric circulation in space, as can be seen in Supplementary Fig. 7, which shows that the southward shift of the Southern Westerlies over the twenty-first century is similar in the free and in the bias-corrected versions for all AGCMs, confirming previous results10. This means that the simulated regional-scale climate change is not damped by the bias correction.
Our results immediately open broad perspectives for improved climate change projections on a large range of spatial scales beyond the > ∼100 km scale already covered by typical AGCMs. Applying the EBC method, AGCMs can be used to re-analyze climate change information from large-scale coupled climate model projections. As demonstrated by this study, the atmospheric run-time bias correction technique can be combined with the more usual bias correction of the prescribed oceanic boundary conditions for AGCM climate change experiments, which consists of imposing the ocean surface condition change (SST and sea-ice change) from a coupled climate model on observed ocean surface conditions20,21,22. This results in present-day AGCM control runs with substantially reduced biases, and in consistently corrected climate change runs10. Such sets of consistent control runs and projections come at modest numerical cost, because only AGCM simulations without long ocean spinups are required. Output of EBC simulations with bias-corrected large-scale tropospheric circulation characteristics can then be used to drive higher-resolution limited area atmosphere models, or to directly drive regional or global ocean models, and land surface or ice sheet models leading to an overall reduction in the uncertainty of their climate products.
Although the main objective of the EBC is to provide a method for improving the simulated global large-scale circulation, it is worth noting that the corrected simulations also show improved statistics for precipitation, which is a physical quantity that one might suspect could suffer from possible inconsistencies and perturbations introduced by the ad hoc correction terms. For two out of the three AGCMs, the global MSE of precipitation in the corrected AGCM versions is consistently below 85% of the MSE of the uncorrected reference version for the entire 1980–2100 timespan, and for the third AGCM, while there is no strong improvement obtained for the present-day reference period, the precipitation MSE of the corrected version sharply drops after 2020, attaining values below 0.85 after 2050 (see Supplementary Fig. 9). The EBC thus improves even emergent physical properties such as precipitation, reducing errors that are connected indirectly to the reduction of atmospheric circulation biases (type 1 errors23). However, errors in simulated precipitation rates due to insufficiencies of the physical parameterizations (type 3 errors23) will not be corrected by the EBC method used here.
There are several areas where the results of the EBC might be improved over those presented here. By retuning free physical parameters of the AGCMs during the nudging stage, the magnitudes of their nudging tendencies and bias correction terms might be reduced. A possible extension of this bias correction approach is its application in a coupled context, with nudging applied in the atmosphere and/or ocean. Furthermore, conditional bias adjustments, frequently suggested and applied in posthoc correction methods9,24,25 could also be implemented in our method, possibly based on run-time classification of synoptic situations. This could reduce the remaining mean biases. Finally, mean biases will likely depend on the nudging timescale used in Eq. 1 to derive the EBC and more optimal choices might lead to improvements over the results presented here.
In summary, our work provides strong evidence for the validity of the EBC approach as a consistent, robust, versatile, simple to implement, and numerically affordable methodology to address the garbage in–garbage out problem of regional climate change projections4. We conclude that empirical bias corrections have the potential to substantially reduce uncertainty in the output of coupled climate change experiments, particularly in coordinated exercises like CMIP26, and to improve the quality of atmospheric driving data for downstream downscaling activities such as the Coordinated Regional Downscaling Experiment (CORDEX)1 and climate change impact analyses.
Methods
The run-time bias-correction method for atmospheric models is based on a two-step approach11. The following description of the method is similar to descriptions given in previous work by the authors10,12.
The first step consists of nudging27 the atmospheric model to a time-varying reference state. At each model time step, the local value of a selected prognostic variable X is adjusted by applying a Newtonian relaxation towards a reference state XR:
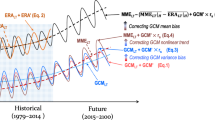
Here, the first part of the equation (\({\partial X}/{\partial t}\) = F(X)) represent the prognostic evolution of the unconstrained AGCM and τ is the nudging time constant, chosen to be 3 days in this study. While the time-varying reference state XR is usually taken from 6-hourly output of atmospheric (re-)analyses, here it is prescribed to be 6-hourly three-dimensional time-varying output of a coupled model. The nudged variables are air temperature and zonal and meridional wind above the atmospheric boundary layer. The detailed implementation of the smooth transition from no nudging at the surface to full nudging above the boundary layer varies among the participating models and is not critical, since the focus of this work is on free-atmosphere circulation characteristics, but typically the models are fully nudged above about 1500 m for grid points with surface altitude close to sea level. Specifically, the LMDZ5 AGCM28 was nudged towards the first ensemble member of the CanESM229 historical run of the CMIP5 coordinated experiment30 over the 1981–2000 reference period; the CanAM4 AGCM31 was nudged towards the CNRM-CM5.132 CMIP5 historical run (first ensemble member); and the ARPEGE-Climat v5.2 AGCM32 was nudged towards the first ensemble member of the IPSL-CM533 CMIP5 historical run (see Fig. 5). These AGCM nudging reference runs are performed over the 20 year period 1981–2000 and employ the SST and sea-ice concentration of the respective target/reference coupled models as lower boundary conditions. This nudged simulation, by construction, has almost vanishing circulation biases.
Arrows indicate which AGCM emulates which CMIP5 coupled model (CM); for example, LMDZ emulates CanESM2. The AGCMs are corrected towards their respective target coupled model for the 1981–2000 period, using the SST and sea-ice concentration from the target CM. They are then run into the future under the RCP8.5 scenario, using SST and sea-ice anomalies from their own coupled model (for example, IPSL-CM in the case of LMDZ). The uncorrected control runs use the same oceanic boundary conditions.
For the second step, the nudging tendencies in Eq. 1 from the reference runs are time averaged to produce a climatological seasonal cycle of the applied correction term resulting in:
The operator \(\overline {\left( Y \right)} ^{{\mathrm{AC}}}\) designates the annual cycle of Y12. The climatological, but seasonally and spatially varying correction terms G correspond to the mean nudging tendencies required to maintain atmospheric conditions close to those of the reference coupled model. The bias correction then consists of adding these cyclo-stationary temporally and spatially varying terms to the prognostic equations of the AGCM:
This yields an empirically bias-corrected solution for X.
The empirically bias-corrected run for the reference period used the same oceanic boundary conditions as the nudged run. The RCP8.5 run until 2100 then used the same atmospheric correction terms, and, during the CMIP5 projection period (2006–2100), month-by-month sea-surface condition (SST and sea ice) anomalies from the AGCM’s own coupled model CMIP5 projection run (e.g., IPSL-CM5 for LMDZ5) superimposed on the 1981–2000 average sea-surface conditions from the target coupled model (e.g., CanESM2 for LMDZ5) using an anomaly method20. Standard CMIP5 atmospheric boundary conditions (greenhouse gas concentrations etc.) are used in the AGCM runs. The corrected AGCM reference and projections runs are then evaluated against the climate simulated by the target coupled model.
It is important to recognize that the EBC methodology imposes the same perturbative sea-surface forcing change between the future and historical periods in the AGCM future projections as that of its own coupled model CMIP5 projection run (i.e., sea-surface bias corrections cancel out in the difference). Consequently, the global surface atmospheric temperature change in these EBC experiments is strongly constrained to be that of its own coupled model. The climate sensitivities of the three target coupled CMIP5 models are broadly comparable34: 4.1 °C for IPSL-CM5; 3.3 °C for CNRM-CM5.1; 3.7 °C for CanESM2 and so, we have not attempted to compensate for such differences in our analyses.
Data availability
The CMIP5 output used to nudge the LMDZ, ARPEGE, and CanAM models (global 6-hourly atmospheric temperature and winds, and global monthly SST and sea-ice fields for 1981–2000 from the first run of the historical ensembles of the IPSL, CanESM, and CNRM-CM CMIP5 models) is available from the ESGF (see https://www.earthsystemcog.org/projects/cog/). AGCM output that supports the findings of this study are available from the corresponding author upon reasonable request. The scripts and prepared data used to produce Figs. 1–4 of this work are available on https://doi.org/10.5281/zenodo.4018860.
Code availability
CanAM is freely available on https://gitlab.com/cccma/canam. LMDZ is freely available on https://lmdz.lmd.jussieu.fr/. Documentation of the Météo France ARPEGE model is available on https://www.umr-cnrm.fr/IMG/pdf/arp62ca.july2017.pdf.
References
Gutowski, J. W. et al. WCRP COordinated Regional Downscaling EXperiment (CORDEX): a diagnostic MIP for CMIP6. Geosci. Model Dev. 9, 4087–4095 (2016).
Giorgi, F. & Gutowski, W. J. Regional dynamical downscaling and the CORDEX initiative. Annu. Rev. Environ. Resour. 40, 467–490 (2015).
Flato, G. et al. Evaluation of Climate Models. in Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change 741–866. https://doi.org/10.1017/CBO9781107415324 (2013).
Hall, A. Projecting regional change. Science 346, 1460–1462 (2014).
Agosta, C., Fettweis, X. & Datta, R. Evaluation of the CMIP5 models in the aim of regional modelling of the Antarctic surface mass balance. Cryosphere 9, 2311–2321 (2015).
Maraun, D. Bias correcting climate change simulations—a critical review. Curr. Clim. Change Rep. 2, 211–220 (2016).
Paeth, H. et al. An effective drift correction for dynamical downscaling of decadal global climate predictions. Clim. Dyn. 52, 1343–1357 (2019).
Sansom, P. G., Ferro, C. A. T., Stephenson, D. B., Goddard, L. & Mason, S. J. Best practices for postprocessing ensemble climate forecasts. Part I: Selecting appropriate recalibration methods. J. Clim. 29, 7247–7264 (2016).
Maraun, D. et al. Towards process-informed bias correction of climate change simulations. Nat. Clim. Change 7, 664–773 (2017).
Krinner, G., Beaumet, J., Favier, V., Déqué, M. & Brutel-Vuilmet, C. Empirical run-time bias correction for Antarctic regional climate projections with a stretched-grid AGCM. J. Adv. Model. Earth Syst. 11, 64–82 (2019).
Guldberg, A., Kaas, E., Déqué, M., Yang, S. & Vester Thorsen, S. Reduction of systematic errors by empirical model correction: impact on seasonal prediction skill. Tellus A 57, 575–588 (2005).
Kharin, V. V. & Scinocca, J. F. The impact of model fidelity on seasonal predictive skill. Geophys. Res. Lett. 39, 1–6 (2012).
Maraun, D. Nonstationarities of regional climate model biases in European seasonal mean temperature and precipitation sums. Geophys. Res. Lett. 39, L06706 (2012).
Charles, S. P., Bates, B. C., Whetton, P. H. & Hughes, J. P. Validation of downscaling models for changed climate conditions: case study of southwestern Australia. Clim. Res. 12, 1–14 (1999).
Vrac, M., Stein, M. L., Hayhoe, K. & Liang, X. Z. A general method for validating statistical downscaling methods under future climate change. Geophys. Res. Lett. 34, L18701 (2007).
de Elía, R. et al. Forecasting skill limits of nested, limited-area models: a perfect-model approach. Mon. Weather Rev. 130, 2006–2023 (2002).
Chavaillaz, Y., Codron, F. & Kageyama, M. Southern westerlies in LGM and future (RCP4.5) climates. Clim. Past 9, 517–524 (2013).
Gulev, S. K., Jung, T. & Ruprecht, E. Climatology and interannual variability in the intensity of synoptic-scale processes in the North Atlantic from the NCEP-NCAR reanalysis data. J. Clim. 15, 809–828 (2002).
Krinner, G. & Flanner, M. G. Striking stationarity of large-scale climate model bias patterns under strong climate change. Proc. Natl Acad. Sci. 115, 9462–9466 (2018).
Beaumet, J., Krinner, G., Déqué, M., Haarsma, R. & Li, L. Assessing bias-corrections of oceanic surface conditions for atmospheric models. Geosci. Model Dev. 12, 321–342 (2019).
Hernández-Díaz, L., Laprise, R., Nikiéma, O. & Winger, K. 3-Step dynamical downscaling with empirical correction of sea-surface conditions: application to a CORDEX Africa simulation. Clim. Dyn. 48, 2215–2233 (2017).
Krinner, G., Largeron, C., Ménégoz, M., Agosta, C. & Brutel-Vuilmet, C. Oceanic forcing of Antarctic climate change: a study using a stretched-grid atmospheric general circulation model. J. Clim. 27, 5786–5800 (2014).
Eden, J. M., Widmann, M., Grawe, D. & Rast, S. Skill, correction, and downscaling of GCM-simulated precipitation. J. Clim. 25, 3970–3984 (2012).
Goddard, L. et al. A verification framework for interannual-to-decadal predictions experiments. Clim. Dyn. 40, 245–272 (2013).
Boberg, F. & Christensen, J. H. Overestimation of Mediterranean summer temperature projections due to model deficiencies. Nat. Clim. Change 2, 433–436 (2012).
Eyring, V. et al. Overview of the coupled model intercomparison project phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 9, 1937–1958 (2016).
Jeuken, A. B. M., Siegmund, P. C., Heijboer, L. C., Feichter, J. & Bengtsson, L. On the potential of assimilating meteorological analyses in a global climate model for the purpose of model validation. J. Geophys. Res. Atmos. 101, 16939–16950 (1996).
Hourdin, F. et al. Impact of the LMDZ atmospheric grid configuration on the climate and sensitivity of the IPSL-CM5A coupled model. Clim. Dyn. 40, 2167–2192 (2013).
Arora, V. K. et al. Carbon emission limits required to satisfy future representative concentration pathways of greenhouse gases. Geophys. Res. Lett. 38, L05805 (2011).
Taylor, K. E., Stouffer, R. J. & Meehl, G. A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012).
Von Salzen, K. et al. The Canadian fourth generation atmospheric global climate model (CanAM4). Part I: representation of physical processes. Atmos. Ocean 51, 104–125 (2013).
Voldoire, A. et al. The CNRM-CM5.1 global climate model: Description and basic evaluation. Clim. Dyn. 40, 2091–2121 (2013).
Dufresne, J. L. et al. Climate change projections using the IPSL-CM5 earth system model: from CMIP3 to CMIP5. Clim. Dyn. 40, 2123–2165 (2013).
Andrews, T., Gregory, J. M., Webb, M. J. & Taylor, K. E. Forcing, feedbacks and climate sensitivity in CMIP5 coupled atmosphere-ocean climate models. Geophys. Res. Lett. 39, L09712 (2012).
Acknowledgements
This publication was supported by PROTECT. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 869304. This is PROTECT contribution number 1. We thank Michel Déqué for numerous discussions and carrying out the ARPEGE simulations. G.K. thanks CanSISE, CCCma and University of Victoria for financial and logistic support during a research stay in Victoria, BC, Canada. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modeling, which is responsible for CMIP, and we thank the CCCma, IPSL and CNRM climate modeling groups for producing and making available their model output. For CMIP5 the U.S. Department of Energy’s Program for Climate Model Diagnosis and Intercomparison provides coordinating support and led development of software infrastructure in partnership with the Global Organization for Earth System Science Portals.
Author information
Authors and Affiliations
Contributions
G.K., V.K., and J.S. designed the study. G.K., V.K., R.R., J.S., and F.C. contributed to the analysis and discussion of the model output and to the drafting and revision of the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editors: Heike Langenberg.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Krinner, G., Kharin, V., Roehrig, R. et al. Historically-based run-time bias corrections substantially improve model projections of 100 years of future climate change. Commun Earth Environ 1, 29 (2020). https://doi.org/10.1038/s43247-020-00035-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-00035-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.