Abstract
Earthquake occurrence is ultimately controlled by tectonic stress load. Nevertheless, the 2019, Mw = 4.9, Le Teil earthquake in southern France occurred in an area where strain rates are relatively low. Human operations can produce increases in stress load and degradation of strength on nearby active faults, which raises the potential for failure. Here we present estimates of the rupture geometry and source directivity of the Le Teil earthquake based on differential synthetic aperture radar interferometry and seismic data. We find that almost two centuries of mass removal at a nearby cement quarry likely provided the required stress change to hasten the occurrence of the Le Teil earthquake by more than 18,000 years. We suggest that further mass removal in the area might lead to even stronger earthquakes, by activating deeper sectors of the same fault plane.
Similar content being viewed by others
Introduction
Regional and local stress conditions driven by tectonic forces and, in particular, the value of the differential stress on the fault drives the occurrence of earthquakes. Nevertheless, large scale industrial activity might result in stress variation large enough to induce earthquakes or—added to the tectonic stress—to overcome the fault strength, advancing the time to the next expected rupture. Physical processes commonly considered capable of inducing or triggering seismic events by anthropogenic activities include underground volumetric changes, fluid pressure diffusion with/without fluid flow in rock fractures/pores, and thermal stress variations due to temperature gradients (e.g., ref. 1,2,3,4,5,6,7). Besides, a very limited number of cases also report about causal relationship between earthquakes and mass removing from Earth’s surface, related to quarry activity2,8,9,10.
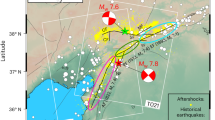
On November 11, 2019, an MW = 4.9 earthquake rocked southeastern France, close to the small town of Le Teil and about 10 km from Montelimar. Four people were injured and hundreds of buildings damaged, some of which collapsed. The earthquake happened in the proximity of the NE–SW, southeast-dipping, St. Thomé-La Rouvière fault (LRf) system11, which marks the southeastern border of the Massif Central over almost 150 km12, in an area where intense rock extraction has been proceeding since the eighteenth century. The fault system is associated with the Variscan orogeny (more than 280 Ma) and during the Oligocene age (about 30 Ma) was characterized by extensional tectonics13. The region is characterized by a very low seismic activity rate, with maximum magnitude ranging between 3 and 4, as deduced from the seismic catalog of the French national seismic network RéNaSS (https://renass.unistra.fr/recherche: last accessed April 2020). Important historical earthquakes occurred in 1773 and 1873, about 30 km S-SE of Le Teil, with maximum intensity level IMAX VIII14. The current phase of tectonic deformation in the area, starting ~20 Ma, is characterized by NW-SE compression, coherent with the 140° direction indicated by the World Stress Map (http://www.world-stress-map.org; last accessed July 2020), and associated with a relatively low strain rate ~0.5 × 10−9 year−1 (ref. 15,16,17). Nevertheless, no evidence of cumulate compressional deformation has been detected along the ruptures associated with the 2019 earthquake and, remarkably, the geologic evidences suggest that the La Rouvière fault could have been inactive since million years18.
Based on the above piece of evidence, we analyzed the source characteristics of the Le Teil earthquake and investigated the possible link with the nearby industrial activities. Our results indicate that the extraction activity could have triggered the Le Teil earthquake. In this case, we estimate a clock advance larger than 18,000 years.
Results
Geodetic data inversion
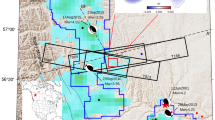
Hypocentral locations for the 2019 event provided by different institutions are quite scattered. The ones better constrained, being obtained from regional—rather than teleseismic—first arrivals travel times, are located a few kilometers southwest of Le Teil, at a depth shallower than 5 km (Fig. 1a; Table 1). The epicentral area is characterized by an intricate structural setting, with several faults trending approximately NE–SW, interconnected with minor NW–SE structures11,12. Coseismic ground ruptures18 (Fig. 1b) have only been detected along the northern end of LRf, close to Le Teil, where it trends about N50°. The fault mechanisms issued by French and international institutions (Fig. 1b; Table 1) indicate compressive source kinematics associated with a NE–SW trending plane, compatible with both the azimuth of the major faults in the area and the local stress field. The observed surface effects are located 1–2 km E–SE from the instrumental epicenters and are proximal to a large quarry complex where large volumes of limestone have been continuously removed for almost two centuries. This circumstance, along with the very low rate of seismicity in the region, raised public concern about the possible anthropogenic origin of the earthquake (e.g., https://www.nationalgeographic.com/science/2019/11/weird-earthquake-crack-france-geologists-buzzing/), in particular regarding extraction activities in the Le Teil quarry, located only 1 km east of the surface ruptures (Fig. 1a, b).
a Map showing distinct locations of the 2019 earthquake (Table 1), quarry blasts and earthquakes from the RéNaSS catalog (https://renass.unistra.fr/recherche; last accessed April 2020), and the main geological lineaments12. b Perspective view with indication of the La Rouviere (LRf) and La Chade (LCf) faults, and coseismic ground ruptures18. The mechanism from SismoAzur (Table 1) is also reported. Both images are as of August 25, 2018.
We used space-borne differential synthetic aperture radar interferometry (DInSAR) measurements to derive the static ground displacements caused by the Le Teil earthquake. The deformed surface (Fig. 2) is elongated in the NE–SW direction, similar to the orientation of the LRf, with an extent of about 12 km2. Clear ground uplift results on the SE side of LRf, with a maximum over 10 cm, while a general subsidence results across the fault, with a slightly smaller maximum with respect to the uplift. Notably, a clear asymmetry is evident in the northern sector of the deformed zone, in correspondence of a minor fault located at the base of La Chade Hill’s NW flank12, calling for a more complex geometry of the ruptured area. Thus, to model the source geometry, we computed the analytical solutions for shear dislocation in an elastic and homogeneous half-space19, reproducing the coseismic surface deformation associated with the Le Teil earthquake. Our preferred solution (see “Methods” section and Supplementary Table 1) is characterized by almost pure reverse faulting on two distinct surfaces, F1 and F2, with an area smaller than 3.5 × 1.9 km2 and 1.8 × 1.9 km2, respectively (Fig. 2). F1 strikes 43.2°, with dip 52.1°, and coincides with the central sector of the LRf, while F2, oriented at 25.4° and dipping 68.1°, is located slightly northeast of F1 and exactly corresponds with the La Chade Hill fault (LCf). Both model dislocations are located within 1 km from the surface and the distributed slip model features two main slip patches, one on each of the two planes. The maximum slip values are 0.29 m and 0.21 m, respectively for F1 and F2, both located at depth of about 0.7 km.
a Data, modeling results, and residuals for line-of-sight surface displacement for ascending (ASC) and descending (DESC) orbits DinSAR interferograms. The fault trace of the two retrieved rupture planes is indicated by magenta lines, while the black contour depicts the Le Teil quarry. b The dislocation resulting from the inversion of the ground deformation data is displayed in both perspective and plane view. Each pixel is 100 × 100 m2.
Source directivity analysis
It is worth noting that the instrumental hypocentral locations do not appear to be compatible with the causative faults resulting from the geodetic modeling. Thus, in order to get a deeper understanding of the earthquake source, we also investigated the source directivity by analysing the spectrum apparent corner frequency of the seismograms recorded at 16 stations within 300 km from the source, at different azimuths. A bilateral rupture results, with the dominant direction at 241 ± 8° and a secondary one at about 60°, associated with considerably lower seismic moment release (see “Methods” section). Moreover, the ratio between the rupture velocity vr and the S-wave velocity is 0.5 ± 0.1, which indicates a rather slow rupture propagation velocity. These results put clear constraints on the location of the nucleation point, implying that the rupture likely nucleated either on the northern end of F1 or on the southern end of F2, i.e., in between the two main slip patches and about 1 km east of the instrumental epicentral locations (Fig. 1), and propagated on the two planes in opposite directions, at very shallow depth (within approximately 1 km). This latter feature is usually associated with seismicity induced/triggered by anthropogenic activity1,2,20
Estimation of the mass removal
The documentation of the possible link between the earthquake and the mass removal from the close Le Teil quarry requires a volume estimate of the mass removed from the Earth’s surface since the beginning of the extraction activity in 1833. To this aim, we reconstructed the topographic changes of the Le Teil quarry area by developing digital surface models (DSM) at various dates (Fig. 3a; see “Methods” section). To increase coherency and avoid large outliers, we split the whole period into a few intervals. We used archive stereo aerial image pairs from the Institute National de l’Information Géographique et Forestiére (IGN), for 1946, 1979, 2007, and 2011, the most recent available. In order to recreate the pre-extraction topography of the site, we used the Carte de l’État-Major that dates back to 1846–1857, the earliest available topographic map of a suitable scale (1:40,000). We determined the volume extracted up to 2011, during the distinct time periods, from the comparison of the point clouds extracted from the topographic data (Fig. 3b). The rate of volume removal has been increasing dramatically through time—also thanks to the technological progress—from about 100,000 m3/year, operated up to the middle twentieth century, to more than 1,000,000 m3/year, i.e., more than one order of magnitude, with a substantial acceleration in the last decades (see “Methods” section).
a Digital Surface Model (DSM) of the considered area at successive times. b Computation of the rock volumes retrieved by numerically comparing the available DSM. c Coulomb stress change, computed for μ′ = 0.4, caused by the mass removed from the Le Teil quarry on the fault planes associated with the 2019 earthquake. The black contours in the rightmost panel outline the area with coseismic slip larger than 0.28 m for F1 and larger than 0.20 m for F2. d Normal and shear stress components of the Coulomb stress change for the whole analyzed period. The small black square indicates the point where the shear stress illustrated in Fig. 4 is computed.
Stress change caused by the quarry activity
We attempt to quantify the stress change induced on the faults associated with the 2019 earthquake by the mass subtracted from the Le Teil quarry. For each analyzed time interval we estimated the equivalent vertical force distribution corresponding to the total extracted rock, with a grid spacing of 2 m, and used the Boussinesq’s solution of three-dimensional elastostatics to compute the stress change in terms of Coulomb failure function variation, ΔCFF = Δτ + μ′Δσn, on both model faults (Fig. 3c).
The cumulative ΔCFF is characterized by relatively large areas of high stress increase on both of the considered faults. In particular, a large patch of stress increase resulted on the northern half of the LRf, with maximum corresponding to 0.19 MPa, while the Coulomb stress increased on most of the LCf, reaching a maximum change of 0.18 MPa. These values are less than one order of magnitude smaller than the stress drop Δσ = 1.3 MPa estimated for the 2019 earthquake (see “Methods” section). Remarkably, (1) the portions of the causative faults where the slip distribution resulting from the inversion of the geodetic data displays a locked segment at the surface (southern end of the LCf and northern end of the LRf) are associated with areas of negative or almost zero Coulomb stress change, and (2) the overall stress increase area is located right in between the two fault planes, in the middle of the major slip patches (Fig. 2). When considered with the result of the directivity analysis, this evidence further supports the location of the rupture nucleation in the central part of the surface deformed area, on any of the two planes, i.e., where the surface mass removal caused the maximum stress change (Fig. 3c, and about 1 km east of the epicentral location resulting from first arrival travel times (Table 1).
Discussion
Overall, our results pose specific questions on the possible effects of the anthropic activity on the earthquake occurrence. In particular, (1) did the mass removal induce or trigger the earthquake and, (2) in the latter case, what is the clock advance with respect to the time the event would have occurred under the tectonic stress load alone? The tectonic horizontal strain (shortening) rate in the area is ~0.5 × 10−9 year−1 (ref. 15,16,17), oriented N140°. By considering only the LRf, releasing most of the seismic moment during the Le Teil earthquake, this suggests that an earthquake on this fault could have occurred anyway sometime in the future but the quarry activity triggered it, hastening its occurrence. There is no information on past seismic events on this fault and no speculation can be done on the possible recurrence time of sizeable earthquakes associated with it. However, by assuming an average rigidity of G = 32 GPa for the crust, the horizontal stressing rate \(\dot \sigma = G{\it{\dot \epsilon }}\) associated with the mentioned shear strain rate \({\it{\dot \epsilon }}\) would be ~15 Pa/year. By considering the single plane solution, the projections of this stress rate on the fault correspond respectively to ~13 Pa/year and ~6 Pa/year for the normal σn and shear τ stress components. The estimated cumulative maximum Coulomb stress change on the fault due to the total mass subtraction is 0.19 MPa by 2011, corresponding to maximum normal Δσn = 0.21 MPa and shear stress Δτ = 0.11 MPa. By accounting for the uncertainty in the estimated volumes (see “Methods” section), these stress values can be considered reliable within ±10%. Noteworthy, considering that about 10% of the total stress change derives from the mass removal in 1833–1946, the larger uncertainty associated with the reconstruction of the initial reference topography (see Methods and Supplementary Information), would only affect the final stress calculation by <5%.
The shear stress value resulting from the quarry activity is one order of magnitude larger than what is typically considered sufficient to trigger an earthquake (0.01 MPa), pointing to an anthropogenic effect on the origin of the seismic event21. In fact, these results allow stating that the rock extraction from the quarry likely have triggered the 2019 Le Teil earthquake by dramatically accelerating the loading of the fault and hastening its unlocking. Incidentally, we note that even considering the upper extreme for the stress drop (Δτ = 2.0 MPa, see “Methods” section), this would not change our conclusion and the hypothesis of a significant anthropogenic effect on the origin for the earthquake still holds.
The time advance can be estimated by dividing the cumulative stress change associated with the quarry activity by the tectonic stress rate22. About 18,000 years is the time required for the tectonic forces to load on the fault a stress amount similar to the change produced by ~180 years of rock extraction from the quarry (Fig. 4). However, in this computation we did not include the mass removal relative to the period 2011–2019—because this information is not available to us—thus the above conclusions represent a conservative estimate. Assuming for 2011–2019 the same average extraction rate calculated for the period 2007–2011 (and the same location), the total normal and shear stress change would be Δσn = 0.26 MPa and Δτ = 0.15 MPa, respectively, corresponding to a time advance of ~ 25,000 years, making the triggering hypothesis even more realistic. Considering the remarkable increase in the number and the magnitude of the quarry blasts in the area in the last few years (Supplementary Fig. 1), the recent extraction rate could have been even higher than what assumed and the estimated stress load would be larger.
The increment of the shear stress on the faults of the 2019 earthquake caused by the tectonic forces (blue line; exaggerated vertical scale), starting from the previous (unknown) earthquake, and by the Le Teil quarry activity (0.19 MPa; gray line). The anthropogenic shear stress is computed at the point marked by the small black square in Fig. 3. The total shear stress on the fault is represented by the red line. The horizontal gray line on top marks the fault strength.
In addition to the static stress change, the above results cannot exclude that the dynamic shaking from the quarry blasts possibly could have had a role in contributing to trigger the event, either in terms of short-term dynamic stress (due to transient stress perturbation) or by material fatigue due the repeated shaking.
Finally, the unusual aspect ratio and the very shallow distribution of the coseismic slip, very similar to other cases of triggered earthquakes23, could be interpreted as an indication that the stress change associated with the quarry extraction was enough to overcome the fault strength at shallow depth, but not sufficient to exceed the fault resistance deeper than that. In this hypothesis and especially if on deeper portions of the fault there is near-critical preexisting tectonic stress, additional future mass removal might trigger deeper slip, possibly causing a stronger earthquake than the one that occurred on November 11, 2019.
Methods
DInSAR data analysis
In order to investigate the ground displacements associated with the considered seismic event, we exploited the Differential Synthetic Aperture Radar (SAR) Interferometry (DInSAR) technique, which allows the analysis of surface displacements along the radar line-of-sight (LOS). The SAR data considered were acquired by the Sentinel-1 (S1) constellation of the Copernicus European Program. Benefiting from the short revisit time and the small spatial baseline separation of the S1 constellation, we generated several coseismic differential interferograms (Supplementary Table 2) with a spatial sampling of about 15 m following an averaging operation (multilook) in the azimuth direction to reduce the speckle noise. Among the generated interferograms we selected those less affected by undesired phase artifacts (atmospheric phase delays, decorrelation noise, etc.) for the seismic source modeling discussed in the following section, thus preserving good spatial coverage and interferometric coherence. In particular, the employed S1 data pairs were acquired on November 6–12, 2019 (Supplementary Fig. 2A), and on October 31 and November 12, 2019 (Supplementary Fig. 2B) along the ascending (ASC) and the descending (DESC) orbits, respectively. On both interferograms, several fringes located near the epicentral area are clearly visible; note that each fringe corresponds to a LOS displacement of about 2.8 cm (i.e., half of the employed S1 C-band wavelength λ = 5.546 cm). Subsequently, starting from the selected interferograms, we generated their corresponding LOS displacement maps (Fig. 1a) through a phase unwrapping operation24.
By superimposing the fault traces on the selected pair of interferograms (Supplementary Fig. 2C, D and Fig. 1d) it is evident that the deformed area, extending for about 12 km2, is elongated in the NE–SW direction, very similar to the orientation of the LRf. Moreover, a clear asymmetry is clearly visible in the northern sector of the deformed zone, in correspondence of a minor fault located at the base of La Chade Hill’s NW flank (Supplementary Fig. 2E, F), suggesting a complex geometry of the ruptured area. This is also evident in the map of the vertical component of the retrieved deformation pattern (Supplementary Fig. 3A) that we computed from the unwrapped interferograms, together with the East-West deformation map (Supplementary Fig. 3B). Note that the maximum uplift is about 11 cm while the amplitude of the subsidence is appreciably smaller, with a maximum displacement of about 4 cm. For the horizontal displacements, the area affected by westward motion is rather extended, with a maximum value of about 8 cm, while eastward motions are more concentrated on the SW side of the LRf and shows a maximum displacement of about 7 cm.
Surface deformation data modeling
In order to retrieve the fault parameters, we jointly inverted the DInSAR displacements retrieved from ASC and DESC orbits by applying a consolidated two-step approach that consists of a nonlinear optimization to constrain the fault geometry, assuming a uniform slip, followed by a linear inversion to retrieve the slip distribution on the fault plane25. We modeled the LOS displacements retrieved from the DInSAR interferograms with a finite rectangular dislocation in an elastic and homogeneous half-space19, also applying a compensation for the local topography26 and assessing possible offsets and linear ramps affecting the DInSAR measurements. Moreover, data were preliminarily resampled over a regular grid (70 m spacing in all the considered area) to reduce the computation load. Starting from a nonlinear inversion algorithm based on the Levenberg–Marquardt least-squares approach, we searched for the source parameters of one or two rectangular dislocations with uniform slip and, thanks to multiple random restarts implemented within the approach, it was possible to catch the global minimum during the optimization process.
The second step of our modeling is represented by the linear inversion process with the computation of the nonuniform slip distribution, in order to have a more accurate estimate of the slip distribution along the fault plane. In particular, the linear inversion was performed by using as starting model, in terms of dimensions and orientation, the fault obtained from the previous nonlinear inversion discretized into 0.1 × 0.1 km2 patches and inverting the following system:
where dDInSAR represents the DInSAR displacements vector, G is the Green’s matrix with the point-source functions, m is the vector of slip values for each patch (initially assumed as the value resulting from the nonlinear inversion), and ∇2 is a smoothing Laplacian operator weighted by an empirical coefficient k to guarantee a reliable slip varying across the fault. The choice of the parameter k depends on the compromise between the data fit and the smoothness of the slip distribution. We tested several values and selected k = 0.007, since appreciably higher residuals resulted for k ≥ 0.01 and similar residuals but inconsistent slip values (larger than 70 cm), with too rapidly varying slip distribution, resulted for k ≤ 0.004. Further constraints were introduced by imposing nonnegative slip (reverse slip only) values obtained via nonlinear inversion.
The surface deformation derived from the interferometric measurements acquired along ASC and DESC orbits reveals a spoon-like geometry, characterized by a NE–SW striking main distinctive displacement pattern (Supplementary Fig. 2). Thus, we first investigated solutions associated with homogeneous dislocation on a single planar source for which all source parameters were set free during the nonlinear inversion. Then, keeping the plane obtained in the geometry inversion fixed, we searched for the best slip distribution. The preferred solution (Supplementary Table 1) consists of a 4.1 × 1.0 km2 reverse fault, oriented N50° and dipping 62.3° southeast, with rake 116.5° and dislocation characterized by two separate major patches, located respectively north and south of the quarry, with a maximum slip in excess of 0.3 m (Supplementary Fig. 4). Although the single fault solution accounts for most of the observed DInSAR data, it is associated with large residuals, comparable to the maximum surface deformation (Supplementary Fig. 4). Also, it is worth noting that this solution does not align with any, and actually crosscuts all the faults mapped in the area. Thus, considering these observations, we tested a composite solution, with two fault planes. Similar to what was done for the single fault, we first searched for the best geometry for the two planes, by means of nonlinear inversion with uniform dislocation, and then solved for the slip distribution on the two fault surfaces with fixed geometry by linear inversion. Based on the features of the DInSAR data described above and on the local geology11,12, we tested several positions for the two faults in the uniform slip, nonlinear inversion, always keeping free strike, dip, rake (uniform for each plane), and dislocation. Eventually, we obtained solutions (Supplementary Table 1) noticeably reducing the residuals and, most importantly, compatible with the faults observed at the surface (Fig. 2b and Supplementary Figs. 2 and 3). The two planes coincide respectively with the central sector of LRf and to a structural lineament at the base of the La Chade Hill, both supposed to be SE dipping11, where the quarry is located. The preferred solution is characterized by a slip distribution shallower than 1 km depth. In particular, for the plane F1 the solution displays a 3 km-long, two-lobed patch with maximum slip of 0.29 m located on the northern half of the fault, while a maximum slip of 0.21 m results for F2, located approximately at the center of the fault.
Finally, as for the uncertainties associated with the slip solution we report the standard deviation (Supplementary Fig. 5) as obtained from the model covariance matrix, following an approach25 that accounts also for the noise covariance.
Source directivity analysis and stress drop estimate
We studied source directivity by using a simplified version of the directivity function Cd (ref. 27) for a bilateral linear rupture model:
where ϑ is the angle between the ray leaving the source and the direction of rupture propagation φ (ref. 28), and α is the Mach-number, that is, the ratio between the rupture velocity vr and the S-wave velocity. The percent unilateral rupture e parameter is defined as (2L′ − L)/L, where L is the total rupture length and L′ is the length of the dominant rupture29. A value of e = 1 corresponds to a unilateral rupture, whereas e = 0 corresponds to a bilateral rupture.
The effect of the directivity on the source spectrum is to increase the corner frequency at those stations located in the same direction as the rupture propagation and to decrease the corner frequency in the opposite direction (e.g., ref. 30). This effect can be modeled assuming that the apparent corner frequency is given by fca = fc Cd with fc indicating the actual corner frequency and fca the corner frequencies at various azimuths estimated from the source spectrum.
We retrieved waveforms corrected by the instrumental response at 22 stations from the Réseau Sismologique et Géodesique Français (http://seismology.resif.fr/#WelcomePlace; last accessed April 2020) (Supplementary Fig. 6A). We filtered all the waveforms in the frequency band 0.01–20 Hz. First, we discarded the stations with a low signal-to-noise ratio, which resulted to be poor at all the stations located at an elevation higher than 900 m, reducing the number of stations to 16. Then, we windowed the waveforms by cutting from 2 s before the manual S-wave picking to 6 s after. We applied a 5 per cent cosine taper function and zero padding before computing the Fourier amplitude spectra. The spectra were then smoothed by applying an average moving window with a four-point half width. Finally, we computed the S-wave displacement spectra from the modulus of the three components velocity or acceleration spectra by dividing the spectra by 2π or 4π2, respectively.
We assumed an ω−2 theoretical source spectrum model31, which is given by:
where Ω0 is the long-period spectral amplitude, f the frequency, fc the corner frequency. As for the anelastic attenuation we assumed the model \(A\left( {f,T} \right) = e^{ - \pi fT/Q\left( f \right)}\), where Q(f) = Q0f n and T is the travel time of the S phase. Using Eq. (2), together with the attenuation model, we fit the observed spectra through a grid search approach, to infer Ω0, fc, Q0 and n. As for Ω0, we normalized the spectrum and explored the range (0.7, 1.3), while the range of exploration for fc was (0.1, 2.0). Finally, we explored Q0 in the range (0,300) and n in the range (0, 2.0). The parameter Ω0 is then used to compute the seismic moment32 through the formulation:
where R is the hypocentral distance, ρ is the density, assumed here 2690 kg m−3; and c is S-wave velocity assumed to be 3.5 km s−1. \(R_{\theta \varphi }\) is the average S-wave radiation pattern assumed to be 0.7 and F is the free-surface coefficient (fixed to 2). As for the uncertainty on each inferred parameter we used an approach33 providing confidence intervals based on jack-knife variance analysis. The computed fc as function of the station azimuth are finally fit by using the Cd function and the nonlinear Levenberg–Marquardt least-squares algorithm.
The observed displacement spectra together with the best-fit models are shown in the upper panels of Supplementary Fig. 6B. The average seismic moment value is 3.4 × 1016 (2.4 × 1016, 4.9 × 1016) N m corresponding to MW = 4.9. As for the anelastic attenuation, we found that a Q frequency independent model (i.e., n = 0) provides the best fit, with Q0 = 190 (193, 198). The estimated corner frequencies are shown in the lower panel of Supplementary Fig. 6B as a function of the station azimuth. The result clearly indicates at least one range of azimuths where the fc value increases with respect to the other directions. The fit with the Cd function, which is shown in the same panel, provides an e-value of 0.3 ± 0.1 indicating a bilateral rupture and a Mach-number of 0.5 ± 0.1 suggesting a rather low rupture propagation. The dominant rupture direction is at 241 ± 8° while the secondary direction is at about 60°. Using the average value of the estimated corner frequencies corresponding to 0.6 (0.5, 0.7) Hz and the seismic moment, we computed the static stress Δσ = 0.44 M0/r3, with the source radius given by r = 0.37vS/fc (ref. 28), being vS the S-wave velocity. We obtained r = 2158 (2044, 2846) m and Δσ = 1.3 (0.9, 2.0) MPa.
Calculation of the rock volume extracted from the quarry
We used multi-temporal DSM to estimate the removed volume of rock in the Le Teil quarry. Topographic map resolution, quality, and accuracy varies a lot with time, so a more robust method of change detection using high-resolution topography from stereo aerial imagery is preferred. However, the Le Teil quarry was established in 1833 and this technique is only available for the modern era. Thus, distinct methods must be used for the different time periods.
For the recent period, we used scanned stereo aerial images of the study area, available from the Institute National de l’Information Géographique et Forestiére (IGN). We used archive stereo aerial image pairs for 1946, 1979, 2007, and 2011 (Supplementary Table 3). We extracted DSM from stereo imagery using MicMac software34, following the procedure illustrated in Supplementary Fig. 7. For each group of stereo images, tie-points between images and camera frame/lens parameters were calculated. Using ground control points, we performed bundle adjustment and refinement of the camera calibration. Ground control points were picked from the latest IGN orthophoto map (coordinates in UTM zone 31 north, WGS84) and elevation values were extracted from ALOS Global Digital Surface Model. Then, DSM and orthophotos were produced. A point cloud was extracted from the Malt DSM and colored with RGB values from the orthophoto map (Supplementary Fig. 7). A detailed photogrammetric point cloud of 2007 covering a much larger area is available from the OpenTopography facility (https://doi.org/10.5069/G9BC3WQ4; last accessed April 2020).
Incidentally, we remark that there is a strip of images dated 1932 available from IGN, but processing produced many artifacts due to scanned film’s poor preservation and noise. Coregistration with 1946 data was also poor, with large residuals; thus, we decided not to use the 1932 dataset. We did not use the most recent set of digital aerial images provided by IGN (dated 2013), as the poor radiometric quality of the files leads to a low quality matching over the quarry area, thus rendering the dataset unusable for terrain change detection.
In order to estimate the initial reference topography of the site as best as possible, we searched for the earliest available topographic map on a suitable scale. We used the Carte de l’État-Major-feuile Privas S.O. (Supplementary Fig. 8), a map compiled between 1846 and 1857 at a scale 1:40,000. We georeferenced a high-resolution scan obtained from IGN (https://www.geoportail.gouv.fr/donnees/carte-de-letat-major-1820-1866; last accessed April 2020). A concise description of the main map-series features and how to spatially process each map sheet is also available35. As the map does not provide detailed and accurate contour lines, we extracted a dense set of elevation contours from the 1946 DSM. These contours were clipped at the maximum extent of quarry boundaries traced from the 1946 orthophoto (Supplementary Figs. 8 and 9). Using the 1846–1857 map as a reference for general relief representation and taking into consideration the geomorphologic features (Rhône river escarpment, drainage, and ridgelines) of the area around the quarry, contours were traced manually in order to fill the blank area and reconstruct the 1833 relief. By assuming for the reconstructed topographic height an uncertainty of 10 m over the whole quarry area as of 1946 (~300,000 m2), the uncertainty in the volume removed in the period 1833–1946 (larger than 11,000,000 m3) deriving from the procedure of reconstruction of the initial topography would be <30%.
Starting from the evolution of the topography, we estimated the volume of the mass progressively removed from the quarry. Instead of comparing the first and last DSM available, in order to increase coherency and avoid very large outliers we split the analysis into intervals: 1833–1946, 1946–1979, 1979–2007, and 2007–2011. Original DSM raster files were clipped and resampled into a common pixel size (3 m) and then converted into point clouds. Point clouds were co-registered using the ICP matching tool from CloudCompare software (http://www.danielgm.net/cc; last accessed April 2020) and then each pair was processed with the Multiscale Model to Model Cloud Comparison (M3C2). This technique computes the local distance between two-point clouds along the normal surface direction which tracks 3D variations in surface orientation36. M3C2 distance raster files were cropped using the quarry boundary traced manually from orthophoto maps for each period, and removed volume (Supplementary Table 4. The uncertainty in the determination of the removed volume for each period is also reported) was calculated using raster statistics.
Boussinesq’s solution of 3-D elastostatic loading
We adopted the analytic solution in Cartesian coordinates (x1, x2, x3) of the three-dimensional elastostatics for the response of a semi-infinite solid (x3 ≥ 0) to an arbitrary normal load P0 on its boundary37. We considered the displacements and the stress components given the shear modulus μ and the Poisson ratio ν. If P0 is applied at (x01, x02, x3) then the displacement components in a generic point (x1, x2, x3) are given by:
where \(R = \sqrt {\left( {x_1 - x_{01}} \right)^2\, +\, \left( {x_2 - x_{02}} \right)^2\, +\, x_3^2}\). The components of the displacement can be used to compute the strain tensor ε and the stress tensor σ in the same point (x1, x2, x3). Under the hypothesis of infinitesimal deformation and for isotropic medium, εij = 1/2(dUi/dxj + dUj/dxi) and σij = λδijεkk + 2μεij, where λ is the second Lame’s parameter and δij the Kronecker delta. In particular, for the application presented in this study we used the six components of the stress tensor, which have the following expressions:
In order to quantify the effect of the removal of the rock mass from the quarry on the prescribed fault, we assumed that extraction operation is equivalent to the application of a set of vertical forces P0 = h·dA·ρ·g (being h the height of the eroded rock column computed from the DEM, ρ the rock density, g the acceleration of gravity and dA the elementary area of the DEM), at the surface of the investigated volume. Given the linearity of the model, the net effect on the fault in terms of σij is obtained by summing the contributions of the single forces. By decomposing σij in its normal component Δσn (assumed positive if the fault is unclamped) and shear component Δτ (assumed positive in the direction of the slip) along the fault and assuming a given value of the fault effective friction coefficient μ′ we computed the Coulomb stress change ΔCFF = Δτ + μ′Δσn. Specifically, we investigated three values of μ’ = 0.4, 0.5, 0.6 (Supplementary Fig. 10), generally assumed as plausible effective friction coefficient for natural faults38,39 and minor differences resulted in the maximum values, while no change in the general ΔCFF pattern. Conservatively, in order to estimate the effect of the quarry activity on the faults associated with the Le Teil earthquake, we used the results for μ = 0.4 (Fig. 3c), associated with the lower maximum value.
Data availability
The photogrammetric point cloud used in this study is available in the OpenTopography repository, https://doi.org/10.5069/G9BC3WQ4, while all the other datasets generated during and/or analyzed during the current study are available in the Zenodo repository, https://doi.org/10.5281/zenodo.3973027.
Code availability
All the custom codes used in this study are available from the V.D.N. (email: denovellis.v@irea.cnr.it) on request.
Change history
18 February 2021
A Correction to this paper has been published: https://doi.org/10.1038/s43247-021-00109-7
References
Grigoli, F. et al. The November 2017 MW 5.5 Pohang earthquake: a possible case of induced seismicity in South Korea. Science 360, 1003–1006 (2018).
Foulger, G. R., Wilson, M. P., Gluyas, J. G., Julian, B. R. & Davies, R. J. Global review of human‐induced earthquakes. Earth‐Sci. Rev. 178, 438–514 (2018).
Dahm, T. et al. Recommendation for the discrimination of human-related and natural seismicity. J. Seismol. 17, 197–202 (2013).
Deichmann, N. & Giardini, D. Earthquakes induced by the stimulation of an enhanced geothermal system below Basel (Switzerland). Seismol. Res. Lett. 80, 784–798 (2009).
Ellsworth, W. L. Injection‐induced earthquakes. Science 341, 1225942 (2013).
Amos, C. B. et al. Uplift and seismicity driven by groundwater depletion in central California. Nature 509, 483–486 (2014).
Lei, X. et al. Fault reactivation and earthquakes with magnitudes of up to MW 4.7 induced by shale‐gas hydraulic fracturing in Sichuan Basin, China. Sci. Rep. 7, 7971 (2017).
González, P. J., Tiampo, K. F., Palano, M., Cannavò, F. & Fernandez, J. The 2011 Lorca earthquake slip distribution controlled by groundwater crustal unloading. Nat. Geosci. 5, 821–825 (2012).
Klose, C. D. Mechanical and statistical evidence of the causality of human-made mass shifts on the Earth’s upper crust and the occurrence of earthquakes. J. Seismol. 17, 109–135 (2013).
Qian, Y. et al. An extremely shallow MW4.1 thrust earthquake in the eastern Sichuan Basin (China) likely triggered by unloading during infrastructure construction. Geophys. Res. Lett. 46, 13775–13784 (2019).
Elmi, S. et al. Notice explicative de la carte géologique de France (1/50000), Feuille Aubenas (865) (Edition du BRGM, Orléans, 1996).
Saint Martin, M. Carte géologique harmonisée du département de l’Ardèche notice technique (BRGM7RP-57097-FR, Bureau de Recherches Géologiques et Minières, 2009).
Hannouz, E. et al. Geomorphology of the cumulative deformation since Oligocene age on the Mw 4.9 Le Teil earthquake fault (South of France, 11/11/19), EGU General Assembly 2020, Online, 4–8 May 2020, EGU2020-20740, https://doi.org/10.5194/egusphere-egu2020-20740 (2020)
Thouvenot, T. et al. The ML 5.3 Épagny (French Alps) earthquake of 1996 July 15: a long-awaited event on the Vuache Fault. Geophys. J. Int. 35, 876–892 (1998).
Tesauro, M., Hollenstein, C., Egli, R., Geiger, A. & Kahle, H.-G. Analysis of central western Europe deformation using GPS and seismic data. J. Geodyn. 42, 194–209 (2006).
Nguyen, H. N., Vernant, P., Mazzotti, S., Khazaradze, G. & Asensio, E. 3D GPS velocity field and its implications on the present-day post-orogenic deformation of the Western Alps and Pyrenees. Solid Earth 7, 1349–1363 (2016).
Masson, C., Mazzotti, S., Vernant, P. & Doerflinger, E. Extracting small deformation beyond individual station precision from dense Global Navigation Satellite System (GNSS) networks in France and western Europe. Solid Earth 10, 1905–1920 (2019).
Ritz, J.-F., et al. The Mw4.9 Le Teil surface-rupturing earthquake in southern France: new insight on seismic hazard assessment in stable continental regions, EGU General Assembly 2020, Online, 4–8 May 2020, EGU2020-8409, https://doi.org/10.5194/egusphere-egu2020-8409 (2020).
Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 82, 1018–1040 (1992).
Davis, S. D. & Frohlich, C. Did (or will) fluid injection cause earthquakes? Criteria for a rational assessment. Seismol. Res. Lett. 64, 207–224 (1993).
S. Hirschberger, S. Wiemer, P. Burgherr, Eds., Energy from the Earth. Deep geothermal as resource for the future (TA-Swiss, vdf Hochschulverlag AG, Zürich, 2015).
Pino, N. A., Convertito, V. & Madariaga, R. Clock advance and magnitude limitation through fault interaction: the case of the 2016 central Italy earthquake sequence. Sci. Rep. 9, 5005 (2019).
Wang, S. et al. Changes in groundwater level possibly encourage shallow earthquakes in central Australia: The 2016 Petermann Ranges earthquake. Geophys. Res. Lett. 46, 3189–3198 (2019).
Costantini, M. A novel phase unwrapping method based on network programming. IEEE Trans. Geosci. Remote Sens. 36, 813–821 (1998).
Atzori, S., Manunta, M. & Fornaro, G., . & Athanassios Ganas, S. Salvi. Postseismic displacement of the 1999 Athens earthquake retrieved by the differential interferometry by synthetic aperture radar time series. J. Geophys. Res. 133, B09309 (2008).
Williams, C. A. & Wadge, G. An accurate and efficient method for including the effects of topography in three-dimensional elastic models of ground deformation with applications to radar interferometry. J. Geophys. Res. 105, 8103–8120 (2000).
Ben-Menahem, A. Radiation of seismic surface waves from finite moving sources. Bull. Seism. Soc. Am. 51, 401–453 (1961).
Joyner, W. B. Directivity for non-uniform ruptures. Bull. Seismol. Soc. Am. 81, 1391–1395 (1991).
Boatwright, J. The persistence of directivity in small earthquakes. Bull. Seismol. Soc. Am. 97, 1850–1861 (2007).
Convertito, V., Pino, N. A. & Di, F. Luccio, Investigating source directivity of moderate earthquakes by multiple approach: the 2013 Matese (southern Italy) MW = 5 event. Geophys. J. Int. 207, 1513–1528 (2016).
Brune, J. N. Tectonic stress and the spectra of seismic shear waves from earthquakes. J. Geophys. Res. 75, 4997–5009 (1970).
Aki, K. & Richards, P. G. Quantitative seismology. (University Science, Sausalito, CA, 2002).
Prieto, G. A., Thomson, D. J., Vernon, F. L., Shearer, P. M. & Parker, R. L. Confidence intervals for earthquake source parameters. Geophys. J. Int. 168, 1227–1234 (2007).
Rupnik, E., Daakir, M. & Deseilligny, M. Pierrot. MicMac—a free, open-source solution for photogrammetry. Open Geospatial Data Softw. Stand 2, 14 (2017).
Favre, C., et al. Digitalisation des cartes anciennes. Manuel pour la vectorisation de l’usage des sols et le géoréférencement des minutes 1:40 000 de la carte d’états-major, Version 12.8, INRA (http://docs.gip-ecofor.org/public/forets_ancienne/Manuel_digitalisation_EM_Favre_et_al_2016_v12.8.pdf; 2016).
Lague, D., Brodu, N. & Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: application to the Rangitikei canyon (N-Z). ISPRS J. Photogram. Remote Sens. 82, 10–26 (2013).
Hetnarski, R. B. & Ignaczak, J. The mathematical theory of elasticity. (CRC Press Taylor & Francis Group, Boca Raton, FL, 2011).
King, G. C., Stein, R. S. & Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 84, 935–953 (1994).
Toda, S., Stein, R. S., Reasenberg, P. A., Dieterich, J. H. & Yoshida, A. Stress transferred by the 1995 Mw= 6.9 Kobe, Japan, shock: effect on aftershocks and future earthquake probabilities. J. Geophys. Res. 103, 24543–24565 (1998).
Acknowledgements
The authors thank E. Valerio for her contribution to geodetic data analysis and modeling and S. Atzori for fruitful discussions on the geodetic inversion procedure. This work was partially funded by the PRIN project MATISSE (Bando 2017, Prot. 20177EPPN2), the EPOS-SP project (GA 871121), the I-AMICA (PONa3_00363) project, and the 2019-2021 IREA-CNR and Italian Civil Protection Department (DPC) agreement. As for this latter and the IREA-CNR authors, this paper represents the authors’ ideas and does not necessarily corresponds to the official opinion and policies of DPC.
Author information
Authors and Affiliations
Contributions
V.C., V.D.N., and N.A.P. conceived the study, interpreted the results, and wrote the paper, with contribution from S.V.; R.L., F.C., and M.F.M.T. analyzed the DInSAR data; V.D.N. inverted the geodetic data; S.V. performed the analyses relative to the estimate of the volume removed from the quarry; V.C. and N.A.P. performed Coulomb stress and rupture directivity analyses. All the authors contributed to review the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor Joe Aslin
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Novellis, V., Convertito, V., Valkaniotis, S. et al. Coincident locations of rupture nucleation during the 2019 Le Teil earthquake, France and maximum stress change from local cement quarrying. Commun Earth Environ 1, 20 (2020). https://doi.org/10.1038/s43247-020-00021-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-020-00021-6
This article is cited by
-
The 2 December 2020 MW 4.6, Kallithea (Viotia), central Greece earthquake: a very shallow damaging rupture detected by InSAR and its role in strain accommodation by neotectonic normal faults
Acta Geophysica (2023)
-
Regional physics-based simulation of ground motion within the Rhȏne Valley, France, during the MW 4.9 2019 Le Teil earthquake
Bulletin of Earthquake Engineering (2023)
-
Post-publication careers: ground ruptured, community united
Communications Earth & Environment (2022)
-
Exceptional ground motion during the shallow Mw 4.9 2019 Le Teil earthquake, France
Communications Earth & Environment (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.