Introduction

Room temperature ionic liquids (RTILs) are organic salts with low melting points, usually consisting of large asymmetric organic cations, such as imidazolium and pyridinium, quaternary ammonium, or phosphonium, paired with inorganic or organic anions exhibiting a varying degree of complexity1. In recent years, they have attracted much attention due to their unique and tunable properties, which render them promising alternatives for a broad range of applications in lithium-ion batteries, supercapacitors, solar cells, and gas absorption2,3,4. Like other liquids, spatial restriction and low dimensionality significantly affect the RTILs properties; they alter phase transition properties5, wetting, enforce layering at interfaces1,6,7,8, and enhance ionic mobility9,10,11,12,13. However, the mechanism underlying the molecular arrangement and motion of RTILs under confinement is still obscure. Interestingly, molecular dynamics (MD) simulations have shown that RTILs in carbon and silica nanochannels diffuse discretely in coaxial shells8, however, there is no firm experimental evidence on this.

One of the most common methods to study fluid diffusion in restricted geometries is the pulsed-field gradient (PFG) NMR14,15. An alternative method is to use the strong stray field gradient (SFG) of a superconductive magnet instead of the PFG16,17,18. For unrestricted 3D diffusion, by applying a Hahn echo π/2-τ-π pulse sequence the nuclear spin echo decays according to formula16,17

$$h\left(\tau ,G\right)=h\left(0\right)\exp \left(-\frac{2\tau }{{{\rm T}}_{2}}\right)\exp \left(-\frac{2}{3}{\gamma }^{2}{G}^{2}D{\tau }^{3}\right),$$
(1)

where γ is the nuclear gyromagnetic ratio, G is the SFG, T2 is the spin-spin relaxation time, and D is the self-diffusion coefficient. The mean square displacement along the magnetic field gradient is given by the relation \(\left\langle {z}^{2}\right\rangle =2D\tau\). However, in the case of diffusion in 1D narrow channels, such as CNTs19, biological porins20, or cylindrical silica nanopores21, \(\left\langle {z}^{2}\right\rangle =2a{\tau }^{\kappa }\), with \(0\le \kappa \le 1\), and the NMR signal attenuation in the SFG is given by relation22,23,24

$$h\left(\tau ,G,\kappa \right)=h\left(0\right)\sqrt{\frac{{{{{{\rm{\pi }}}}}}}{8a\alpha (\tau ,G,\kappa )}}{erf}\left[\sqrt{2a\alpha (\tau ,G,\kappa )}\right],$$
(2)

where \(\alpha \left(\tau ,G,\kappa \right)={\frac{\left({2}^{\kappa }-2\right)}{(\kappa +1)(\kappa +2)}\gamma }^{2}{G}^{2}{\tau }^{\kappa +2}\), a is the mobility factor, i.e. the 1D analog of the self-diffusion coefficient D, and \({erf}\left[x\right]\) is the error function. In the extreme case of ultra-narrow pore-channels comparable to the size of the diffusing molecules, the so-called single file diffusion (SFD) takes place19,25,26,27,28,29,30, with \(\kappa =0.5\).

The presence of SFD has been detected with both PFG and SFG methods, by varying the magnetic field gradient amplitude and recording the spin-echo decay (SED) signal. In this way, SFD of water in single-wall carbon nanotubes (CNTs)25, CF4 in AlPO4-5 zeolites26, as well as of Xenon in dipeptides31 was detected. In addition, the anomalous diffusion of 3He in solid hydrogen at 1.4 K was excellently studied24. However, in the case of complex diffusion processes in multiphasic systems, such as transcellular ion diffusion, or ionic motion in ionogels, divergence from normal diffusion can be masked by the multiple diffusion processes.

In the present study we have focused on the 1-butyl-3-methyl imidazolium tricyanomethanide [BMIM]+[TCM]− RTIL, confined into MCM-41 and SBA-15 mesoporous silica systems. By employing 1H NMR diffusion experiments in different effective \({T}_{2}^{{\prime} }\) relaxation windows, in the strong SFG of G = 34.7 Tm−1, we succeeded to resolve the diffusion dynamics of adsorbed and mobile RTIL cations. Aided by atomistic MD simulations, the analysis of the NMR results in the case of MCM-41 indicates the appearance of non-Fickian stratified diffusion, with the central RTIL component obeying a diffusion law very close to SFD.

Results and discussion

1H NMR \({{{{{{\rm{T}}}}}}}_{2}^{{\prime} }\) analysis: resolving adsorbed and free-tumbling RTIL molecules in MCM-41 and SBA-15

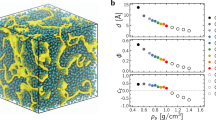
According to the nitrogen porosimetry in Fig. 1a, the mean pore-sizes of MCM-41 and SBA-15 are ∼4.09 nm and ∼7.31 nm, respectively, while the size of the [BMIM]+ cation is ∼0.81 nm. Upon entering the pores, a layer of [BMIM]+[TCM]− molecules adsorbed on the silica walls is formed, as demonstrated in the (MD) simulation snapshot of RTIL in partially filled MCM-41 (left upper panel of Fig. 1a) and evidenced in the nitrogen porosimetry measurements presented in Section 1 of the Supplementary Methods and in Supplementary Fig. 1. This corroborates with small angle neutron scattering experiments32 (SANS) on [BMIM]+[PF6]−, which show that inside MCM-41 the ionic liquid forms a hollow tubular shell, in contact with the silica wall. By increasing the RTIL concentration, a radially modulated RTIL density profile is observed (middle upper panel of Fig. 1a), exhibiting distinct diffusion properties as discussed below. This agrees with previous MD simulations, which show that depending on the size of the aliphatic non-polar chain of the cation, RTILs close to interfaces segregate into alternating polar and non-polar regions6,7. Furthermore, the self-diffusion coefficient D of RTIL confined in silica and carbon porous systems was predicted to decrease radially from the center to the silica (carbon) walls8.

Fig. 1: Adsorbed and mobile [BMIM]+ cations resolved with 1H NMR \({{T}}_{2}^{{\prime} }\) distribution analysis.
figure 1

a Snapshots of MD simulations of [BMIM]+[TCM]− inside MCM-41 at low and high RTIL concentration (blue: nitrogen, grey: carbon, white: hydrogen, yellow: silicon, red: oxygen). The yellow lines are the relevant radial RTIL density profiles. By increasing the RTIL concentration, the density appears to be radially modulated. The lower panel shows the liquid nitrogen porosimetry curves of MCM-41 (blue) and SBA-15 (red). b CPMG SEDs at RT of [BMIM]+[TCM]− confined into MCM-41 (blue line) and SBA-15 (red line). The inset shows the effective spin-spin relaxation time \({T}_{2}^{{\prime} }\) distribution by inverting the CPMG SEDs. c The Hahn SEDs of [BMIM]+[TCM]− in bulk form (white circles), as well as inside MCM-41 (blue circles) and SBA-15 (red circles). Solid lines are fits to Eq. (1). The inset shows the relevant Hahn SEDs at 400 K. d CPMG SEDs at 400 K of [BMIM]+[TCM]− confined into MCM-41 (blue line) and SBA-15 (red line). The inset shows the \({T}_{2}^{{\prime} }\) distribution by inverting the CPMGs.

Full size image

To enlighten experimentally the dynamics of this intriguing dynamic molecular ordering (DMO), 1H NMR Carr-Purcell-Meiboom-Gill (CPMG) SED measurements were performed at various temperatures, using fully dehydrated MCM-41 and SBA-15 samples, saturated with RTIL according to the procedure described in the Methods section. Experiments were carried out at Larmor frequency of 100 MHz in a SFG of G = 34.7 T ∙ m−1. In a CPMG experiment, described in detail in Section 2 of the Supplementary Methods, the SED curve is acquired with the π/2-τ-π-(2τ-π)n pulse sequence, decaying exponentially with an effective \({T}_{2}^{{\prime} }\), which includes diffusion, as illustrated in Supplementary equation (3) and Supplementary Fig. 3b–d. Since \({T}_{2}^{{\prime} }\) of adsorbed molecules in a porous system are sufficiently shorter than \({T}_{2}^{{\prime} }\) of free-tumbling bulk-like molecules33, NMR signals from adsorbed and free tumbling RTIL ions may in principle be resolved by inverting the experimental CPMG SED curves. For this, a Tikhonov regularization algorithm34,35 was implemented, as explained in the Supplementary Methods (section 2(iii)) and shown in Supplementary Fig. 2.

Figure 1b, d show CPMG SEDs versus time of [BMIM]+[TCM]− intruded into MCM-41 (blue lines) and SBA-15 (red lines) at RT and 400 K, whereas insets show the relevant \({T}_{2}^{{\prime} }\) distributions. In both samples at RT two \({T}_{2}^{{\prime} }\) components are resolved, assigned to the adsorbed (low-\({T}_{2}^{{\prime} }\)) and free tumbling (high-\({T}_{2}^{{\prime} }\)) RTIL cations, while at 400 K both samples acquire the same single peaked \({T}_{2}^{{\prime} }\)  distribution. This is due to the enhanced mobility of the adsorbed [BMIM]+ cations at elevated temperatures, as discussed below. Contrary to the CPMGs, the Hahn SEDs are markedly different in the two samples, as shown in Fig. 1c. In bulk RTIL (empty circles), the SED follows unrestricted diffusion, described by Eq. (1). On the other hand, in both MCM-41 and SBA-15, Hahn SEDs diverge from the exponential τ3 decay, due to the strong intermixing of various diffusing processes. Especially, in the case of MCM-41 a tail is observed at long times, which is a characteristic feature of anomalous diffusion23,24,25.

1H NMR \({{{{{{\rm{T}}}}}}}_{2}^{{\prime} }\)-resolved diffusion experiments: detection of subdiffusion close to SFD at RT

To acquaint with these intriguing results, we have performed a series of CPMG experiments by varying at each step the time interval τ between the π/2 and first π pulse, as explained in Section 3 of the Supplementary Methods and illustrated in Supplementary Fig. 4. In this way, the diffusion footage is encoded in successive CPMGs. Subsequently, by inverting the CPMGs and recording the integral of each \({T}_{2}^{{\prime} }\) component vs. τ, the diffusion dynamics of each RTIL signal component is imprinted on the Hahn SEDs across the \({T}_{2}^{{\prime} }\) distribution. This is excellently seen in Fig. 2a, c, which show the contour plots of the Hahn SED across the \({T}_{2}^{{\prime} }\) distribution for the MCM-41 and SBA-15 at room temperature, respectively. The green lines are the projections of the integrated signal intensity onto the \({T}_{2}^{{\prime} }\) axis. In both systems, two signal components are observed corresponding to the adsorbed and mobile RTIL cations. A third small peak at \({T}_{2}^{{\prime} }\) < 100 μs belongs apparently to silica–OH groups.

Fig. 2: 1H NMR \({T}_{2}^{{\prime} }\)-resolved Hahn SEDs of [BMIM]+[TCM]− confined in MCM-41 and SBA-15 at RT.
figure 2

a Hahn SEDs across the 1H NMR \({T}_{2}^{{\prime} }\) distribution of the RTIL confined in MCM-41. The dark cyan line is the projection of the signal intensity on the \({T}_{2}^{{\prime} }\) -axis. b The Hahn SED vs. τ of signals 1 and 2 in Fig. 2a. Signal 1 recalls SFD (orange color line), whereas signal 2 corresponds to adsorbed [BMIM]+ cations (blue line - exponential decay). c Hahn SEDs across the 1H NMR \({T}_{2}^{{\prime} }\) distribution of the RTIL confined in SBA-15. The dark cyan line is the projection of the signal intensity on the \({T}_{2}^{{\prime} }\) -axis. As previously, the two signals correspond to adsorbed and mobile [BMIM]+ cations. d The Hahn SED vs. τ of signals 1 and 2 in Fig. 2c. The diffusion of signal 1 is closer to unrestricted diffusion (red line).

Full size image

Figure 2b, d show the relevant Hahn SEDs. Component 2 is observed to decay exponentially (blue line), as expected for immobilized (adsorbed) ions with an effective T2 ∼ 0.7 ms. On the contrary, “mobile” [BMIM]+ cations inside SBA-15 follow a nearly τ3 exponential decay (red line), while in the case of MCM-41 the SED is much closer to Eq. (2) with κ = 0.5 (orange color line). The nearly SFD in the latter case indicates that RTIL molecules in the bulk pore space diffuse coherently along the pore-axis, experiencing difficulty to surpass each other.

To further validate these results, experiments were performed on two ionogels, with MCM-41, and SBA-15 soaked into [BMIM]+[TCM]− at concentrations of 10% and 3% per weight, respectively. Figure 3a, c show the relevant contour plots of the Hahn SEDs vs. the \({T}_{2}^{{\prime} }\) distribution. In the case of MCM-41, three signal components are resolved corresponding to bulk [BMIM]+ (signal 1), [BMIM]+ inside the pores (signal 2), and [BMIM]+ adsorbed on the silica walls (signal 3); the latter two components acquire precisely the same \({T}_{2}^{{\prime} }\) values as those in Fig. 2a. Notably, the Hahn SED of signal 1 follows the exponential τ3 decay described by Eq. (1) (black line on the right panel), while signal 2 decays according to the SFD mechanism (orange color line) and signal 3 decays exponentially (blue line), as expected for adsorbed [BMIM]+ cations. To the best of our knowledge, this is the first time that the NMR signals of a multiphasic ionogel are resolved according to the diffusion characteristics of each component.

Fig. 3: 1H NMR \({{T}}_{2}^{{\prime} }\)-resolved Hahn SEDs of oversaturated [BMIM]+[TCM]−/MCM-41 and SBA-15 ionogels at RT.
figure 3

a Hahn SEDs across the 1H NMR \({T}_{2}^{{\prime} }\) distribution of the MCM-41 ionogel. The dark cyan line is the projection of the signal intensity on the \({T}_{2}^{{\prime} }\)-axis. Three signals are observed corresponding to external bulk (signal 1), confined mobile (signal 2), and adsorbed (signal 3) [BMIM]+ cations. b The Hahn SED vs. τ of signals 1, 2, and 3 in Fig. 3a. As in Fig. 3, signal 1 follows unrestricted diffusion (black line), signal 2 exhibits SFD (orange color line), while signal 3 is decaying exponentially (blue line), as expected for immobilized cations. c 1H NMR Hahn SED across the \({T}_{2}^{{\prime} }\) distribution of the SBA-15 ionogel. The dark cyan line is the projection of the signal intensity on the \({T}_{2}^{{\prime} }\) -axis. Signals 1 and 2 belong to the external bulk [BMIM]+ cations, whereas only a very weak signal of [BMIM]+ entrapped into SBA-15 is observed, due to the high dilution. d The Hahn SED of signals 1 and 2 follow unrestricted diffusion (black lines).

Full size image

In the case of oversaturated SBA-15, the bulk out-of-pores NMR signal component dominates, as it corresponds to the main ionogel component. Notably the \({T}_{2}^{{\prime} }\) distribution is slightly broadened, becoming asymmetric in the lower \({T}_{2}^{{\prime} }\)-values, whereas the relevant self-diffusion coefficients D acquired by fitting the data to Eq. (1) are in the range 5.6 – 6.0 × 10−11 m2 s−1. The asymmetry might stem from a fast exchange between bulk external [BMIM]+ cations and cations adsorbed on shallow nanopores on the external surfaces of SBA-15, as also implied by the nitrogen porosimetry in Fig. 1a. Most spectacularly, by magnifying the \({T}_{2}^{{\prime} }\) region between 6-30 ms, the weak \({T}_{2}^{{\prime} }\) signal of [BMIM]+ inside the SBA-15 is unveiled. However, the relevant Hahn SED (signal 3 in Fig. 3d) is very weak and difficult to fit.

Figure 4 shows 1H NMR Hahn SED and 2D diffusion-relaxation (D − \({T}_{2}^{{\prime} }\)) experiments at 400 K of the MCM-41 sample analyzed in Fig. 1, 2. At this temperature the RTIL is no more adsorbed on the pore walls, as already shown in Fig. 1d. However, the Hahn SED follows neither an exponential τ3 decay (i.e. according to Eq. (1)), nor a SFD according to Eq. (2), as clearly seen in Fig. 4a. Notably, an excellent fit is acquired by inverting the Hahn SED data according to Eq. (1) with a 1D Tikhonov regularization inversion algorithm17,18,34,35, corresponding to a doubly peaked distribution of the D values with peaks at ∼3 × 10−11 m2 s−1 and 2 × 10−10 m2 s−1, respectively. It is worth noting that the ratio (\({D}_{{{\mbox{bulk}}}}/{D}_{{{\mbox{adsorbed}}}}\) ~ 10) of the above two \(D\) values is comparable to the one reported by Nayeri et al. in C6C1ImTFSI confined in silica gels36.

Fig. 4: 2D 1H NMR diffusion-relaxation (D − \({{T}}_{2}^{{\prime} }\)) spectrum at 400 K.
figure 4

a The 1H NMR Hahn SED of [BMIM]+[TCM]− confined in MCM-41 at 400 K. The green line is the fit, and the inset the relevant self-diffusion coefficient D distribution, acquired by using a Tikhonof regularization inversion algorithm34,35. The blue and orange color lines are the single exponential τ3 decay according to Eq. (1) and SFD, according to Eq. (2) with κ = 0.5, respectively. b The 1H NMR D − \({T}_{2}^{{\prime} }\) spectrum at 400 K. At elevated temperatures adsorbed [BMIM]+[TCM]− molecules at the MCM-41 pore walls become more mobile; a distribution of D values is observed, with the slower D-component belonging to molecules very close to the pore walls. The red dotted line declares the D value of the bulk RTIL at 400 K. The inset is snapshot of a molecular dynamics simulation at 400 K. The yellow line is the radial RTIL density distribution.

Full size image

To validate this result, a 2D 1H NMR D − \({T}_{2}^{{\prime} }\) experiment was performed at 400 K. In a D − \({T}_{2}^{{\prime} }\) experiment a sequence of CPMG SEDs is acquired as described in Section 4 of the Supplementary Methods with the pulse sequence depicted in Supplementary Fig. 4, and subsequently inverted with a 2D inversion algorithm17,18,34,35, where a distribution of diffusion processes is considered following the τ3 exponential decay described in Eq. (1). The relevant D − \({T}_{2}^{{\prime} }\) contour plot at 400 K is shown in Fig. 4b. A doubly peaked D-distribution is observed in agreement with the Hahn SED experiment; the slightly higher \(D\) values in the case of the D − \({T}_{2}^{{\prime} }\) experiment are due to the small sample heating by the long pulse-trains in the CPMG experiments. Furthermore, the low-D signal component acquires a slightly lower \({T}_{2}^{{\prime} }\) value in comparison to the strong high-D signal; nevertheless, the two signals indicated with arrows in Fig. 4b cannot be resolved in the \({T}_{2}^{{\prime} }\) projection. The inset in Fig. 4b illustrates an MD snapshot of the high concentration RTIL in MCM-41 at 400 K showing a bimodal RTIL radial density profile with distinct diffusion properties, as discussed below, that cannot be resolved with NMR. The weak NMR signal with the slow diffusion, is most probably coming from RTIL molecules very close to the silica walls, with the low D-values caused by hydrogen bond interactions between the RTIL and the silica silanol groups.

DFT and MD-simulations: cooperative motion and stratified diffusion of RTIL molecules in MCM-41

To comprehend the theoretical background of the above experimental results, free cluster static and molecular dynamic density functional theory (DFT) calculations (presented in detail in Section 5 of the Supplementary Methods, Supplementary Tables 2–4, and Supplementary Figs. 5 & 6) were performed with the ORCA software package37,38. Geometry optimization showed that the adsorption of the RTIL is governed by hydrogen bonding with the silanol groups of the silica surface. The interaction energy between adsorbed RTIL molecules with the silica was calculated to be ~−24.8 Kcal∙mol−1, whereas the interaction energy between “free” and “adsorbed” RTIL molecules was found ~−9.4 Kcal mol−1, and ~−14.2 Kcal∙mol−1 between “free” RTIL molecules. This implies that free RTIL molecules inside the silica channels are weakly interacting with the adsorbed RTILs. The non-polar butyl “tail” of [BMIM]+ appears to be repulsed from the polar surface of MCM-41 leaning away from the silica (Supplementary Fig. 5); however, in the presence of a high concentration of RTIL, the orientation of the adsorbed RTIL ions depends on the charge balance in their local environment, as clearly demonstrated in Fig. 5a–d, and Supplementary Movie 1.

Fig. 5: Dynamic molecular ordering of IL inside MCM-41.
figure 5

a–d Snapshots of ab initio molecular dynamics (AIMD) simulation at 300 K of RTIL molecules confined between two silica “slabs” 3.8 nm apart of each other (blue: nitrogen, dark grey: carbon, white: hydrogen, yellow: silicon, red: oxygen). The structure was constraint in the z-axis (vertical to the Figure plane). Most of the RTIL molecules are interacting strongly with the silica surface, whereas the rest are tumbling in the intermediate space, interacting weakly with each other and the adsorbed RTIL molecules. Interaction energies are given in the main article and Supplementary Table 3. Notably, “free” RTIL ions form a dynamically ordered state of alternating negatively and positively charged ions (see also Supplementary Movie 1). e Snapshot of a molecular dynamics simulation of RTIL confined in MCM-41 at 300 K. The yellow line is the RTIL radial density distribution. f The MD calculated mean square molecular displacement (MSD) of the RTIL molecules in bulk RTIL and confined in MCM-41 (inner and outer radial shells). At initial times MSD in all cases varies as \(\left\langle {z}^{2}\right\rangle \sim {\tau }^{0.5}\).

Full size image

To visualize the way that the RTIL molecular arrangement evolves with time, ab initio molecular dynamics (AIMD) simulations were performed with the ORCA software package, by simulating the pore channel of MCM-41 with two silica “slabs” set at ⁓4 nm apart of each other and placing a number of RTIL molecules in the space between them. As illustrated in Fig. 5a–d and Supplementary Movie 1, a fluctuating layer of adsorbed RTIL molecules is formed, interacting with the “free” RTIL molecules in the bulk space. At the same time, Coulomb interactions enforce the “free” RTIL molecules to arrange into a flexible “chain” of alternating [BMIM]+ and [TCM]− ions, diffusing cooperatively in the space between the slabs. It is highly probable that the presence of cooperative displacements in the limited pore-space of MCM-41 is the origin of the observed sub-diffusion with NMR. To validate this intriguing effect in the real system, MD simulations were performed on an MCM-41 silica pore model with a pore diameter of 4.0 nm, filled with RTIL. Two configurations with 3000 and 4550 RTIL molecules, respectively, were studied at 300 K and 400 K. At low concentration, the RTIL molecules are adsorbed on the silica surface, forming a hollowed tubular shell (Fig. 1a), whereas at high concentration, the MD density profile across the radius at both temperatures shows an oscillatory behavior (Fig. 5e and 6d), segregating the system into strata of alternating high and low density, in agreement with previous results on ionic liquids close to terminating surfaces6,7. To examine the possibility of stratified diffusion in the pores, the time dependence of the axial mean square displacement MSD was examined in shells at different radial distances from the pore-center. The MSD vs. time in two representative shells (0-0.4 nm and 1.3-2.0 nm) are displayed in Fig. 5f. For reasons of comparison, the radial MSD vs. time of the bulk RTIL is also presented in the same Figure. Lines are fits performed with the formula \(\left\langle {z}^{2}\right\rangle \propto {\tau }^{\kappa }\), for \({\tau < \tau }_{1}\), and \(\left\langle {z}^{2}\right\rangle \propto \tau\), for \({\tau > \tau }_{1}\) (\(\left\langle {z}^{2}\right\rangle\) is replaced by \(\left\langle {r}^{2}\right\rangle\) in the bulk system), using an automated fit method as described in ref. 39. The best fit parameters are listed in Supplementary Table 5. According to these parameters, for \(\tau < {\tau }_{1}\), the RTIL molecules in all three cases exhibit a sub-diffusive behavior (\({{{{{\rm{MSD}}}}}} \sim {\tau }^{0.5}\)), whereas for \({\tau > \tau }_{1}\) diffusion turns to normal (Fickian) diffusion (\({{\mbox{MSD}}} \sim \tau\)).

Fig. 6: 1H NMR \({{T}}_{2}^{{\prime} }\) vs. T measurements combined with MD simulations.
figure 6

a The mean \({T}_{2}^{{\prime} }\) vs. T for bulk and confined [BMIM]+[TCM]− in MCM-41 and SBA-15. The inset shows the derivatives of the heat flow in the relevant Differential Scanning Calorimetry (DSC) experiments. b \({T}_{2}^{{\prime} }\) distributions of [BMIM]+[TCM]− in MCM-41 at various temperatures. c, d Snapshots of a molecular dynamics simulation of RTIL at low and high concentration confined in MCM-41 at 400 K. Yellow lines are the radial RTIL density. A bimodal RTIL density distribution is observed at high concentration. e The MSD in both shells varies at initial times as \(\left\langle {z}^{2}\right\rangle \sim {\tau }^{0.5}\), due to the cage effect. A similar phenomenon is observed in the low RTIL concentration case.

Full size image

Despite the relative difference between experimental and theoretical D values, the MD simulation results justify the assignment of the NMR results in MCM-41 to stratified axial diffusion. First, the calculated bulk RTIL D = 2.5 · 10−11 m2 s−1 at 300 K, is nearly 4 times higher than D = 0.65 · 10−11 m2 s−1 at the center of the MCM-41 pores (high concentration), as shown in Supplementary Table 5. A similar ratio is obtained by the NMR measurements with the bulk RTIL D ≈ 6 · 10−11 m2 s−1, according to Supplementary Table 1 (only estimate of D in MCM-41 is possible, due to the long-time tail in the relevant SED). Close to the silica walls MD gives D = 0.25 · 10−11 m2 s−1, which becomes even smaller at the interface with the walls; On the other hand, the NMR shows almost no diffusion at the pore-walls.

It should be noticed that at early times, the MSD in all cases varies with time as \(\sim {\tau }^{0.5}\). This behavior is due to the cage entrapment, defined by the time that the RTIL molecules need to run out of their first coordination sphere, as also reported in previous MD studies6,40. The cage effect is a general phenomenon observed in various glass forming liquids41,42 with correlated molecular displacements43. At times \({\tau > \tau }_{1}\) the MD simulations show transition to normal diffusion, a result that contradicts with the NMR results and needs further clarification. According to the MD depiction, the possibility of radial diffusion is ruled out; RTIL molecules are diffusing axially, in distinct tubular shells, in agreement with previous reports8. Hence, in the narrow space of each shell, RTIL molecules are expected to be extremely difficult to surpass each other, enforcing the system to non-Fickian diffusion. This phenomenon is not observed in the timescale of the MD simulations (up to few ns), whereas the relevant 1H NMR diffusion measurements (in the μs-to-ms time scale) provide unequivocal evidence of sub-diffusive molecular motion, close to the SFD. It is not clear whether this is due to transition from Fickian to non-Fickian sub-diffusion at long times, as previously reported in colloidal particles constrained in one-dimensional channels44,45, or due to inadequacy of the MD setup, e.g., force-fields need to be reconsidered to capture the long-time sub-diffusion of RTILs under strong confinement.

The effect of temperature on the dynamics of RTIL under confinement

By increasing temperature, adsorbed [BMIM]+ cations gradually become more mobile, and for T > 360 K a single phase is observed according to the \({T}_{2}^{{\prime} }\) distributions in Fig. 6b. This agrees with the MD simulation at 400 K in Fig. 6c–e. The RTIL density in Fig. 6d is doubly peaked and slightly shifted inwards, in comparison to the density at 300 K in Fig. 5e, whereas the MSD vs. time curve of the outer adsorbed RTIL shell approaches that of the inner fast diffusing shell, indicating enhanced mobility in both shells, making the two components indistinguishable in the NMR diffusion experiments. A similar [BMIM]+ mobility enhancement of adsorbed RTIL was observed to take place abruptly at ⁓320 K in [BMIM]+[TFSI]−, with 1H NMR fast field cycling T1 vs. frequency measurements46.

The intriguing DMO of RTIL in MCM-41 might also explain the delayed freezing during cooling in comparison to SBA-15. The \({T}_{2}^{{\prime} }\) dynamics can be mainly distinguished in two regions: the high-temperature region I and the low-temperature region II, separated by the glass transition temperature \({T}_{{{{{{\rm{g}}}}}}}\)47, as shown in Fig. 6a. Freezing is expressed as decreasing of \({T}_{2}^{{\prime} }\) on approaching Tg, because \(1/{T}_{2}^{{\prime} }\sim J(0)\), where J(0) is the spectral density of ultraslow molecular fluctuations48. It appears that confinement into both kinds of silica pores accelerates glassification, in comparison to the bulk RTIL. However, in the case of MCM-41 glassification is evolving slower than in SBA-15, whereas at low temperatures molecular motions of RTIL in MCM-41 (such as librations and CH3 rotations), appear to be stronger than in the other two systems, as implied by the higher \({T}_{2}^{{\prime} }\) values for T < Tg.

Comparison with other systems exhibiting sub-diffusion

It is interesting to note some striking similarities of this system with water inside hydrophobic carbon nanotubes (CNTs)49. In narrow CNTs (d < 1.0 nm) water is found to diffuse as a single file by a very large number of studies, both theoretical27,28,29 and experimental17,18. In the next CNT diameter range, 1.0 nm <d < 1.2 nm, water molecules have more available space to bypass each other, hence SFD gets replaced by classical (i.e., Fickian) diffusion and the water-chain structure is replaced by a water-tube made of stacked water-rings15,17,19,29,30. Nonetheless, the situation for wider CNTs becomes even more interesting and has striking similarities with the case of RTIL in MCM-41, as in the diameter-range of 1.2 nm <d < 4.0 nm, MD simulations20 and NMR studies report the co-existence of a fast diffusing central water-chain17,18, eventually diffusing in a single-file mode25, which is surrounded by one or more water-tubes diffusing classically.

Finally, we would like to comment on the fact that sublinear diffusion with exponent \(\kappa \sim 0.5\) has been reported in glass forming polymer systems50,51, accounting for the structural relaxation of the system on approaching Tg from above, where correlation functions and subsequently the NMR SEDs are described with a stretched exponential or Kohlrausch–Williams–Watts function \(h\left(t\right)={h}_{0}\exp [-{\left(t/{t}_{w}\right)}^{\kappa }]\)52. This scenario is in principle possible in the glass forming [BMIM]+[TCM]−, however, the observation of normal (linear) diffusion in the bulk system makes this option as highly improbable, and the most plausible scenario to explain the NMR diffusion data in the restricted MCM-41 space is the consideration of diffusion in coaxial shells following a nearly SFD law. In this context, NMR studies on 1-alkyl-3-methylimidazolium tricyanomethanide systems ([CnMIM]+][TCM]−), with different alkyl-chain lengths (n = 2, 4, 6, 8), i.e., different geometric restrictions in the limited MCM-41 space, which is the next step to this study, are expected to add important information on the nature of the sub-diffusion process. A second point that needs to be further considered is the observation with MD simulations of normal diffusion after the cage-effect time period. The indisputable observation of sub-diffusion with NMR shows that this issue needs to be further clarified from the theoretical point of view.

Conclusion

In conclusion, by combining 1H NMR diffusion experiments in different \({T}_{2}^{{\prime} }\) relaxation windows with ab initio and classical MD simulations, we have shown that the RTIL [BMIM]+[TCM]− when confined in the MCM-41 silica nanopores, exhibits an intriguing DMO effect. At room temperature, a layer of RTIL molecules is adsorbed on the pore-walls, responding to the local electric charge fluctuations from “free” tumbling [BMIM]+[TCM]− pair of ions in the bulk pore volume. Remarkably, the density of the RTIL molecules, appears to be radially modulated in coaxial shells diffusing discretely, which according to NMR, at long times follows a nearly SFD law. In the case of SBA-15 this phenomenon is limited only close to the silica walls; the rest of the RTIL behaves like the bulk RTIL. The experimental evidence for this extraordinary DMO effect provides key information regarding the use of RTIL-based composites in energy storage applications. Furthermore, the applied NMR methodology is highly promising for enlightening complex multiphasic diffusion in a variety of fluidic processes ranging from living matter to nanofluidic technologies.

Methods

Materials

The ionic liquid (IL) 1-butyl-3-methylimidazolium tricyanomethanide [BMIM]+[TCM]− (mass fraction purity >98%, with 720 ppm H2O content) was purchased by IoLiTec GmbH. Mesoporous materials MCM-41 (pore size 4.09 nm) and SBA-15 (pore size of 7.31 nm) were acquired by Sigma Aldrich Corp. and ACS Material LLC, respectively.

Samples for the NMR experiments were prepared inside Γ-shaped NMR quartz tubes having inner/outer diameters of 3.0 mm/5.0 mm respectively, and lengths of 25 mm. Three types of samples were prepared: bulk [BMIM]+[TCM]− and two ionogels [BMIM]+[TCM]−/MCM-41, [BMIM]+[TCM]−/SBA-15 fabricated by intruding the IL into MCM-41 and SBA-15, respectively. Two samples were prepared for each category, for data reproducibility purposes.

The sample preparation involved a specially constructed gas manifold system connected to a turbomolecular pump. The quartz tube, filled with about 20 mg of MCM-41 or SBA-15, was attached to the manifold, and each sample was outgassed at a high vacuum (10−7 mbar) and 180 °C for 24 hours. Subsequently, after bringing the sample to ambient temperature, a toggle valve connecting the manifold to the turbomolecular pump was closed, and a second valve was opened to suction a methanol/IL solution and soak the sample under vacuum. The concentration of the IL in the solution was determined to have the IL phase confined into the pores of the sample and avoid excess IL in the quartz tube after methanol evaporation. To calculate the IL concentration that suffices to fill the pores, the total pore volume, the mass of the sample, and the free volume of the quartz tube were considered. Methanol was slowly evaporated at 50 °C at ambient pressure and then the samples further outgassed at 90 °C under high vacuum for 24 hours before been flame sealed. The bulk IL sample was placed into a quartz tube with a syringe, then outgassed at 90 °C under a high vacuum for 24 hours, and flame sealed. As described in Section 1 of the Supplementary Methods, porosimetry results before and after IL impregnation (shown in Supplementary Fig. 1) confirmed the complete blockage of the MCM and SBA pores by the IL.

NMR experiments

1H NMR experiments were performed in the stray field of a 4.7 T Bruker superconducting magnet providing a 34.7 T ∙ m−1 constant magnetic field gradient at 1H NMR Larmor frequency 101.168 MHz.

A broadband coherent pulse NMR spectrometer was used, operating in the frequency range 5 MHz – 1 GHz. The π/2 pulse length was set to 2 μs; with this setup, a slice of the sample with a thickness of ∼0.7 mm along the z-axis was possible to excite. The 1H NMR effective spin-spin relaxation (\({T}_{2}^{{\prime} }\)) and self-diffusion coefficient D measurements were accomplished by combining the Hahn echo and the Carr-Purcell-Meiboom-Gill (CPMG) pulse sequences, as described in the Supplementary Methods section 2.

For the \({T}_{2}^{{\prime} }\) vs. temperature measurements, in the temperature range 100 K to 400 K, an Oxford 1200CF continuous-flow cryostat was employed, with an accuracy of\(\,\pm 0.1\,{{{{{\rm{K}}}}}}\). The samples were initially cooled down to 100 K, and the NMR measurements were obtained on heating to rule out any thermal hysteresis effects.

Computational methods

To qualitatively examine the Silica – RTIL system and validate the experimental results, a series of free cluster DFT simulations were conducted. Geometry optimizations and frequency analysis were performed using the ORCA suite of programs and the PBEh-3c parametrized functional37,38,53. For the simulation of the silica surface, a cluster of silanol tetrahedra was cropped from the cif file in ref. 54. Molecular structures processing was conducted with Chemcraft software55.

The desorption of the RTIL from the silica surface was examined with the help of Ab Initio Molecular Dynamics (AIMD) simulations, using the ORCA suite of programs. Subsequently, AIMD simulations were performed by simulating the pore channel of MCM-41 with two silica “slabs” set at 3.8 nm apart of each other and placing a number of RTIL molecules in the space between them. The PBEh-3c parametrized functional was implemented, along with the Beredsen thermostat, and the time step was fixed at 0.5fs53. Geometry constraints were applied on silicon atoms to simulate the solid surface of the silica better.

Molecular dynamics (MD) simulations were used to investigate the concentration-dependent complex dynamic molecular ordering of the RTIL in the MCM-41 silica nanopores. Two systems with 3000 and 4550 molecules of [BMIM]+[TCM]− were studied at two temperatures, i.e. 300 K and 400 K.

The MCM-41 was prepared using the method presented by Gallo et al.56. The constructed pore diameter was 4.0 nm. The silica pore model was filled with RTIL by placing the molecules randomly, using the Packmol program57. All-atom MD simulations were performed using the GROMACS 202058. For MCM-41, we used the same force-field parameters reported by Gallo et al.56. The force field parameters for the [BMIM]+ cation were taken from Cadena et al.59, whereas force field parameters for [TCM]− anion were taken from the OPLS force field60. The equations of motion were integrated with a time-step of 2 fs. Constant temperature and pressure (NVT) ensemble conditions were targeted in our simulations. A Berendsen thermostat was used to set the desired temperature. The pressure was kept constant at 1 bar using the Perrinello-Rahman barostat61. Periodic boundary conditions were applied along the z-axis. The Particle Mesh Ewald summation method62 with a grid spacing of 0.16 nm and interpolation of order 4 was used for electrostatic interactions calculations. LINCS algorithm63 was utilized to constrain the covalent bond including hydrogen bonds. Data is recorded every 1 ps for further analysis. We employed the first steep descent minimization run for 10000 steps to remove the bad contact that may come due to the random placement of RTIL. Following minimization, the systems were equilibrated with positional restraint under NVT ensemble at the desired temperature for 10 ns. Then under constant temperature and pressure, simulations were performed under 10 ns at 1 bar using the Berendsen thermostat. Finally, the production run was performed for 100 ns without any positional restraint.