Introduction

The widely available and used conventional superconductors consist of spin-singlet Cooper pairs, which are devoid of a net spin. Unconventional superconductors, in contrast, host qualitatively distinct phenomena and Cooper pair properties1. Their limited experimental availability, however, has driven the scientific community to try and engineer heterostructures comprising conventional superconductors into effectively unconventional ones2,3,4,5,6, e.g., in achieving Majorana bound states7. In particular, the highly desired spinful spin-triplet Cooper pairs can be generated from a conventional superconductor if the latter interacts with two or more noncollinear magnetic moments2,3,4,5,6. With this design principle, a wide range of magnet-superconductor hybrids with multiple magnetic layers to generate and detect spinful Cooper pairs have been investigated8,9,10,11. The challenge of detecting a spin or its flow directly has resulted in the need for increasingly complex magnet-superconductor hybrids rendering their direct detection a highly demanding, debated, and pursued goal12,13,14,15.

The ambition is to go beyond detection, and towards exploiting the fascinating physics of these unconventional Cooper pairs for phenomena that are otherwise out of reach16. Noncollinear ground states of magnets17,18 and spin-orbit coupling19,20 have been exploited in generating equilibrium spinful Cooper pairs. These have allowed control over static properties, such as magnetic anisotropy19,20 or superconducting critical temperature21, of various superconductor-magnet hybrids. Nevertheless, on-demand steering and movement of spinful Cooper pairs is highly desired and has remained an outstanding challenge. For example, a directed flow of the spinful Cooper pairs could be used for delivering nondissipative spin transfer torques and magnetic switching22,23,24,25,26,27. Such goals face a similar challenge that even when a complex heterostructure generates spinful Cooper pairs, it becomes difficult to steer them. An injected charge current predominantly converts into a conventional spinless supercurrent22. Due to such reasons, several advantages of magnet-superconductor heterostructures realized in various concepts and devices are still dominated by the quasiparticle properties6,28,29,30,31,32,33,34. The exploiting of spinful Cooper pairs for exciting physics and devices has been impeded by the complex hybrids needed to generate them and the difficulty of steering them.

In this work, we uncover a ubiquitous existence and control of spinful Cooper pairs in the simplest magnet-superconductor hybrid—a bilayer—that has escaped attention thus far. We find that a magnon, the quasiparticle of spin waves in a magnet, with nonzero wavevector induces a cloud of spinful Cooper pairs in the adjacent superconductor [Fig. 1a]. This accompanying cloud screens the magnon spin giving rise to a composite heavy quasiparticle with an enhanced effective mass, which is termed ‘magnon-cooparon’ due to its similarity to the polaron quasiparticle as discussed below. This induction of spinful Cooper pairs in a conventional superconductor is caused by the noncollinear magnetization profile of a spin wave with a finite wavevector [Fig. 1b], an effect not seen when considering ferromagnetic resonance of the uniform magnon mode. Furthermore, we demonstrate theoretically that magnon-cooparons enable a magnonic directional coupler35,36 composed of two separate ferromagnetic wires with coupling lengths shorter than previously feasible, thereby allowing smaller devices. Thus, it enables a valuable application in magnon-based logic and circuits37,38. The magnon-cooparon is reminiscent of the fermionic polaron quasiparticle created by screening of an electron by a phonon cloud39, although the magnon-cooparon is a bosonic excitation. Considering the gradual discovery of polaron and its variants in a wide range of phenomena39,40, we expect magnon-cooparon to find a similarly important role in a broad range of magnet-superconductor hybrids. This concept can also significantly expand the range of reported effects related to the mutual influence of superconductivity and magnons10,11,12,13,14,31,32,33,41,42,43,44,45,46,47,48,49.

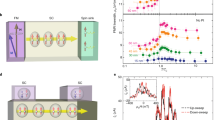
Fig. 1: Schematic depiction of the system under investigation and the magnon-cooparon quasiparticle.
figure 1

a A localized spin flip or magnon wave packet induces a surrounding cloud of spinful triplet Cooper pairs in an adjacent conventional spin-singlet superconductor. The spatially varying magnetization or spin profile (depicted via a dashed line) associated with the excitation induces spinful condensate, that screens the magnon spin, in the otherwise spinless superconductor. The resulting quasiparticle, termed magnon-cooparon, bears a smaller spin and larger effective mass. Note that we depict magnetic moments (which point opposite to spins on account of the negative gyromagnetic ratio) in the FI, while depicting electronic spins in S. b A spin wave with wavenumber k propagates in an in-plane direction. The associated noncollinear magnetization profile (red arrows) induces an analogous spatially varying exchange field (black arrows) in the adjacent superconductor, resulting in spinful triplet condensate.

Full size image

Results

Emergence and effective mass of magnon-cooparons

We consider a bilayer as depicted in Fig. 1b, in which a ferromagnetic insulator FI (e.g., yttrium iron garnet) is interfaced with a conventional spin-singlet s-wave superconductor S (e.g., Nb). The two layers with thicknesses dFI and dS (≪ξS, the superconducting coherence length) are considered thin such that physical properties vary only in the in-plane direction. In its ground state, the FI is assumed to be magnetized along the z direction. For S/FI structures, the effects induced exchange field in the superconductor is well-documented experimentally by measurements of the spin-split DOS6. At the same time, for S/FM heterostructures, where FM means a ferromagnetic metal, the well-pronounced homogeneous spin-split DOS was not reported. The physical reason for this can be related to the leakage of Cooper pairs into the ferromagnet and, consequently, a much stronger suppression of superconductivity at S/FM interfaces. Therefore, we expect that the renormalization of the magnon spin and stiffness by the cloud of triplet pairs, generated in the superconductor should be smaller in S/FM structures. On the other hand, in S/FM heterostructures, there is a proximity effect, that is, penetration of Cooper pairs into the ferromagnet. In principle, in this case, the cloud of triplet pairs, screening the magnon, could be generated directly in the ferromagnetic metal. We expect that the qualitative physics of the renormalization should be similar.

We wish to examine wavevector-resolved excitations of the hybrid, and thus obtain the complete information needed for examining arbitrary wavepackets generated by a given experimental method. To this end, we assume the existence of a spin wave with wavevector kez in the FI [Fig. 1b] such that the magnetization unit vector m(r, t) = m0 + δm(r, t) consists of the equilibrium part m0 = ez and the excitation part \(\delta {{{{{{{\bf{m}}}}}}}}({{{{{{{\bf{r}}}}}}}},t)=\delta m[\cos (kz+\omega t){{{{{{{{\bf{e}}}}}}}}}_{x}+\sin (kz+\omega t){{{{{{{{\bf{e}}}}}}}}}_{y}]\exp (-\kappa t)\). While we consider an excitation with a wavevector along ez, our analysis is general and valid for any in-plane wavevector. The magnetization dynamics is described within the Landau–Lifshitz–Gilbert framework as

$$\dot{{{{{{{{\bf{m}}}}}}}}}=-\gamma \left({{{{{{{\bf{m}}}}}}}}\times {{{{{{{{\bf{H}}}}}}}}}_{{{{{{{{\rm{eff}}}}}}}}}\right)+\alpha \left({{{{{{{\bf{m}}}}}}}}\times \dot{{{{{{{{\bf{m}}}}}}}}}\right)+\tilde{J}\left({{{{{{{\bf{m}}}}}}}}\times {{{{{{{\bf{s}}}}}}}}\right),$$
(1)

where −γ with γ > 0 is the FI gyromagnetic ratio, α is the Gilbert damping parameter, Heff is the effective magnetic field in the FI, and \(\tilde{J}\equiv J/{d}_{{{{{{{{\rm{FI}}}}}}}}}\) with J parameterizing interfacial exchange interaction between FI and S. The last term on the right-hand side of Eq. (1) accounts for the spin torque exerted on the magnetization by the spin density s it induces in S50. Expressing s = s0m0 + δs∥δm + δs⊥(δm × m0) and substituting the expressions for s and m in Eq. (1) above, we obtain

$$\omega ={D}_{{{{{{{{\rm{m}}}}}}}}}{k}^{2}+\gamma K+\tilde{J}\left(\delta {s}_{\parallel }-{s}_{0}\right),$$
(2)
$$\kappa =\alpha \omega -\tilde{J}\delta {s}_{\perp },$$
(3)

where Dm is the FI spin wave stiffness and K parameterizes a uniaxial anisotropy. Thus, the spin density s induced in the S may renormalize both the excitation frequency and its lifetime.

We now evaluate the induced spin density s treating S using the quasiclassical Green’s functions framework4,6,51. Working in the dirty limit, we need to solve the Usadel equation for the 8 × 8 matrix Green’s function \(\check{g}\) in spin, particle-hole, and Keldysh spaces:

$${{{{{{{\rm{i}}}}}}}}D{{{{{{{\boldsymbol{\nabla }}}}}}}}\left(\check{g}\otimes {{{{{{{\boldsymbol{\nabla }}}}}}}}\check{g}\right)={\left[\epsilon \hat{{\mathbb{I}}}{\hat{\tau }}_{z}\hat{{\mathbb{I}}}-{{{{{{{\bf{h}}}}}}}}\cdot \hat {{{{{\boldsymbol{\sigma }}}}}}{\hat{\tau }}_{z}\hat{{\mathbb{I}}}+{{{{{{{\rm{i}}}}}}}}\Delta \hat{{\mathbb{I}}}{\hat{\tau }}_{y}\hat{{\mathbb{I}}},\check{g}\right]}_{\otimes },$$
(4)

where \(\hat{{\mathbb{I}}}\) is the 2 × 2 identity matrix, outer-product between the 2 × 2 matrices (decorated by overhead \(\hat{}\)) in obtaining an 8 × 8 matrix (identified via an overhead \(\check{}\)) is implied, and we set ℏ = 1 throughout this letter. Further, working in the mixed (ϵ, t) representation, we employ the notation [A, B]⊗ ≡ A ⊗ B − B ⊗ A with \(A\otimes B\equiv \exp [({{{{{{{\rm{i}}}}}}}}/2)({\partial }_{{\epsilon }_{1}}{\partial }_{{t}_{2}}-{\partial }_{{\epsilon }_{2}}{\partial }_{{t}_{1}})]A({\epsilon }_{1},{t}_{1})B({\epsilon }_{2},{t}_{2}){| }_{{\epsilon }_{1} = {\epsilon }_{2} = \epsilon ,{t}_{1} = {t}_{2} = t}\). \({\hat{\tau }}_{x,y,z}\) and \({\hat{\sigma }}_{x,y,z}\) are Pauli matrices in particle-hole and spin spaces, respectively. A real Δ accounts for the intrinsic conventional spin-singlet order parameter of the superconductor. The term \({{{{{{{\bf{h}}}}}}}}\cdot \hat{\sigma }\) accounts for the exchange field induced by the adjacent FI layer4,6,52,53,54,55,56,57. The exchange field bears units of energy and corresponds to the spin-splitting it causes. For the magnetization profile associated with the excitation under consideration, we obtain

$${{{{{{{\bf{h}}}}}}}}={h}_{0}{{{{{{{{\bf{e}}}}}}}}}_{z}+\delta h\left[\cos (kz+\omega t){{{{{{{{\bf{e}}}}}}}}}_{x}+\sin (kz+\omega t){{{{{{{{\bf{e}}}}}}}}}_{y}\right],$$
(5)

where h0 and δh respectively capture the static and dynamic components of the induced exchange field h = JMsm/2γdS, with Ms the FI saturation magnetization. The contribution of the superconductor dynamics to the excitation under consideration can be evaluated by solving Eqs. (4) and (5) up to the first order in δh. The desired spin density in the superconductor is evaluated as6

$${{{{{{{\bf{s}}}}}}}}=-\frac{{N}_{{{{{{{{\rm{F}}}}}}}}}}{16}\int\,d\epsilon {{{{{{{{\rm{Tr}}}}}}}}}_{4}\left[\left(\hat{\sigma }{\hat{\tau }}_{z}\right){\breve{g}}^{{{{{{{{\rm{K}}}}}}}}}\right],$$
(6)

where \({{{{{{{{\rm{Tr}}}}}}}}}_{4}\) denotes trace over a 4 × 4 matrix (decorated by an \({{{{{\mathrm{overhead}}}}}}^{\breve{}}\)), \({\breve{g}}^{{{{{{{{\rm{K}}}}}}}}}\) is the 4 × 4 Keldysh component of the full 8 × 8 Green’s function \(\check{g}\), and NF is the normal state density of states at the Fermi level in S.

Following the method outlined above and detailed in Supplementary Note 1, we obtain analytic expressions for s [Eq. (6)], and thus, the excitation frequency [Eq. (2)] and lifetime [Eq. (3)]. These unwieldy expressions simplify considerably in the adiabatic limit of ω ≪ T, that we discuss first. Further, quasiparticles are found to not play an important role in this limit, leaving the focus on the superfluid condensate. We find δs⊥ → 0 in this limit such that the excitation decay rate [Eq. (3)] is not influenced by S. δs∥ − s0 is found to scale as ~k2 in this limit, such that the excitation frequency becomes \(\omega ={\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}{k}^{2}+\gamma K\) with \({\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}\equiv {D}_{{{{{{{{\rm{m}}}}}}}}}+\delta {D}_{{{{{{{{\rm{m}}}}}}}}}\) and

$$\delta {D}_{{{{{{{{\rm{m}}}}}}}}}=-\frac{\pi {N}_{{{{{{{{\rm{F}}}}}}}}}\gamma {d}_{{{{{{{{\rm{S}}}}}}}}}D{\Delta }^{2}}{16{T}_{{{{{{{{\rm{c}}}}}}}}}{d}_{{{{{{{{\rm{FI}}}}}}}}}{M}_{{{{{{{{\rm{s}}}}}}}}}}\left[\frac{1}{x}\tanh x-\frac{1}{{\cosh }^{2}x}\right],$$
(7)

where x = h0/2Tc, and Tc is the superconducting critical temperature taking into account the static exchange field h0. In obtaining Eq. (7), we further worked in the limit ∣T − Tc∣ ≪ Tc. The same stiffness renormalization [Eq. (7)] is obtained from purely energy considerations within the Ginzburg–Landau framework58. The effective mass meff of the composite quasiparticle is obtained as \({m}_{{{{{{{{\rm{eff}}}}}}}}}=1/2{\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}=1/(2{D}_{{{{{{{{\rm{m}}}}}}}}}+2\delta {D}_{{{{{{{{\rm{m}}}}}}}}})\). Since δDm < 0 [Eq. (7)], the effective mass of the composite quasiparticle is enhanced as compared to that of a magnon. Numerically evaluated δDm, without making the adiabatic approximation, plotted in Fig. 2 versus temperature, further shows the direct role of the superconducting condensate and suggests temperature as a handle to control the quasiparticle effective mass. The material parameters assumed in Fig. 2 are detailed further below, together with the discussion on experimental detection.

Fig. 2: Magnon-cooparon effective mass variation.
figure 2

Relative change in the spin stiffness δDm/Dm as a function of temperature T for different values of the static exchange field h0 induced in S. A reduction of the spin stiffness signifies an increased effective mass of the composite excitation. Tc is the critical temperature of the superconductor. Δ0 is the superconducting gap when T = h0 = 0. The dashed line plots the analytic result [Eq. (7)] obtained in the limit T → Tc.

Full size image

Thus, this composite quasiparticle shares some similarities with the polaron39. The latter, predicted almost a century ago59,60 and having found numerous applications throughout condensed matter physics39,40, is formed when an electron is screened by the phonon cloud leading to a heavy fermionic excitation. The quasiparticle under consideration is a bosonic magnon spin being screened by a superconducting condensate. Due to this similarity (and yet many distinctions) with the polaron, we term this spin flip surrounded by a spinful Cooper pairs cloud [Fig. 1a] magnon-cooparon. Physically, a finite wavenumber k is needed to create spinful Cooper pairs, in an otherwise spinless conventional superconductor, via a noncollinear exchange field [Fig. 1b]. This explains the ~k2 dependence of the frequency renormalization, as well as the previous studies investigating uniform (k = 0) magnon modes not encountering the magnon-cooparon.

Finally, going beyond the adiabatic approximation ω ≪ T, we find a nonzero renormalization of the k = 0 mode frequency and the decay rate ~k2, as detailed in Supplementary Note 2. Similar effects are expected based on spin pumping into a normal metal or quasiparticles in a superconductor31,61,62. Specifically, when quasiparticle spin relaxation is disregarded, the increase in decay rate requires a spin sink, which may be provided by the noncollinear magnetic moment in a second magnet63. In our case, a spatially distinct part of the same magnet provides the noncollinear spin absorption channel, thereby short-circuiting the spin wave. Hence, in this case, too, the unique dynamic noncollinearity of the finite-k spin wave results in novel effects.

Spin of magnon-cooparons

The cloud of spinful Cooper pairs screening the magnon spin that increases its effective mass further implies that (i) the total spin of magnon-cooparon is reduced from 1 and (ii) a magnon spin current jmez in FI is accompanied by a superfluid spin current jSez in S. We now address these effects and ascertain the net spin of the magnon-cooparon.

Since the dc spin current jm accompanying a spin wave or magnon scales as δm2, we anticipate jS to scale as δh2, confirming this via a rigorous calculation detailed in Supplementary Note 3. As a result, we now need to solve Eq. (4) for the matrix Green’s function up to the second order in δh. Since this is a more demanding calculation than that carried out above, we restrict ourselves to the adiabatic approximation ω ≪ T and the limit ∣T − Tc∣ ≪ Tc in the rest of our analysis. The spin current flowing along the direction of magnon propagation (ez here) in S is then obtained as6

$${{{{{{{{\bf{j}}}}}}}}}_{{{{{{{{\rm{S}}}}}}}}}{{{{{{{{\bf{e}}}}}}}}}_{z}=\frac{{N}_{{{{{{{{\rm{F}}}}}}}}}D}{16}\int\,d\epsilon \,{{{{{{{{\rm{Tr}}}}}}}}}_{4}\left[\left(\hat{\sigma }\hat{{\mathbb{I}}}\right){\left(\check{g}{\partial }_{z}\check{g}\right)}^{{{{{{{{\rm{K}}}}}}}}}\right]{{{{{{{{\bf{e}}}}}}}}}_{z},$$
(8)

where the direction of jS pertains to the spin space. On explicit evaluation shown in Supplementary Note 3, jS is found to bear only a z component, as can be expected from its screening of the magnon spin, which itself bears only a z component. The total spin current may thus be expressed as

$${{{{{{{{\bf{j}}}}}}}}}_{{{{{{{{\rm{m}}}}}}}}}+{{{{{{{{\bf{j}}}}}}}}}_{{{{{{{{\rm{S}}}}}}}}}=S{v}_{k}{n}_{k}{{{{{{{{\bf{e}}}}}}}}}_{z}\equiv \left(1+\frac{{j}_{{{{{{{{\rm{Sz}}}}}}}}}}{{j}_{{{{{{{{\rm{m}}}}}}}}}}\right){v}_{k}{n}_{k}\,{{{{{{{{\bf{e}}}}}}}}}_{z},$$
(9)

where \({v}_{k}=2{\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}k\) is the magnon-cooparon group velocity, nk is the number of excitations, and S becomes its net spin evaluated via

$$\frac{{j}_{{{{{{{{\rm{Sz}}}}}}}}}}{{j}_{{{{{{{{\rm{m}}}}}}}}}}=-\frac{8{N}_{{{{{{{{\rm{F}}}}}}}}}D\gamma }{{\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}{M}_{{{{{{{{\rm{s}}}}}}}}}}\mathop{\sum}\limits_{{\omega }_{n} > 0}\frac{\pi {T}_{{{{{{{{\rm{c}}}}}}}}}{\Delta }^{2}{h}_{0}^{2}{\omega }_{n}^{2}}{{\left({\omega }_{n}^{2}+{h}_{0}^{2}\right)}^{2}{\left(2{\omega }_{n}+D{k}^{2}\right)}^{2}},$$
(10)

where ωn are the fermionic Matsubara frequencies. Since jSz/jm < 0, the net spin of the magnon-cooparon is reduced from 1 as per our expectation from the screening. Equation (10) shows that the dynamical induction of spinful Cooper pairs always causes screening, and, thus, a reduction in the excitation net spin. Further, similar to the relative change in the spin stiffness (Fig. 2), the spin reduction ∣jSz/jm∣ ≲ 1 for typical material parameters, as estimated further below.

Superfluid-mediated magnonic directional coupler

Since the Cooper pairs cloud comprising a magnon-cooparon extends over a length ~ξS, it enables the transfer of energy from a spin wave in one FI wire to another, nonlocally (Fig. 3). Thus, two FI wires deposited on a conventional superconductor within ~ξS from each other act as a magnonic directional coupler35,36, proposed to be a key building block in wave-based logic and computing64,65. The magnon-cooparon-based design that we demonstrate here offers stronger coupling strengths, smaller footprint, additional control (e.g., via temperature), and universality (e.g., for antiferromagnets55,66) as compared to the dipole-interaction-based designs considered previously35,36.

Fig. 3: Schematic depiction of a magnonic directional coupler based on magnon-cooparons.
figure 3

A spin wave propagating through one FI wire is controllably transferred to the second FI wire.

Full size image

Considering the setup depicted in Fig. 3, we now assume the existence of spin waves with the wavevector kez in both FIs, assumed identical for simplicity. As a result, there exists the same static exchange field h0 in S below both the FI wires. However, distinct dynamic exchange fields δhl,r, similar to Eq. (5), exist in S below each of the FI wires. These are proportional to the respective spin wave amplitudes δml,r in the two FIs. Solving the Usadel equation (4) under this exchange field profile as detailed in the SM, we obtain the spin density in S: s(x) = sl(x) + sr(x) with

$${{{{{{{{\bf{s}}}}}}}}}_{{{{{{{{\rm{l,r}}}}}}}}}(x)={s}_{0}(x)+{s}_{{{{{{{{\rm{loc}}}}}}}}}(x)\frac{\delta {{{{{{{{\bf{h}}}}}}}}}_{{{{{{{{\rm{l,r}}}}}}}}}}{{h}_{0}}+{s}_{{{{{{{{\rm{nl}}}}}}}}}(x)\frac{\delta {{{{{{{{\bf{h}}}}}}}}}_{{{{{{{{\rm{r,l}}}}}}}}}}{{h}_{0}}.$$
(11)

Here, the contributions s0 and sloc are due to the static and dynamic exchange fields induced by the FI directly above the S region. Thus, these are identical to our analysis of the magnon-cooparon in a FI/S bilayer. The nonlocal contribution snl(x) characterizes the spin density generated in S below the left FI by the right one, and vice versa. Relegating its detailed expression to the SM, we note that for d ≲ ξS, snl is comparable to the spin density sloc accompanying a magnon-cooparon.

The induced nonlocal spin density leads to a fieldlike spin torque with the contribution \(\tilde{J}{\bar{s}}_{{{{{{{{\rm{nl}}}}}}}}}{{{{{{{{\bf{m}}}}}}}}}_{{{{{{{{\rm{l,r}}}}}}}}}\times {{{{{{{{\bf{m}}}}}}}}}_{{{{{{{{\rm{r,l}}}}}}}}}\) to the magnetization dynamics \({\dot{{{{{{{{\bf{m}}}}}}}}}}_{{{{{{{{\rm{l,r}}}}}}}}}\) in the two FIs46, where \({\bar{s}}_{{{{{{{{\rm{nl}}}}}}}}}\) is snl(x) averaged over the width t of the FI wire (Fig. 3), ad detailed further in Supplementary Note 4. The resulting eigenmodes are magnon-cooparons distributed over the two FIs and the S layer with dispersion: \({\omega }_{\pm }=\gamma K+{\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}{k}^{2}\mp \tilde{J}{\bar{s}}_{{{{{{{{\rm{nl}}}}}}}}}\). Hence, a pure spin wave injected with frequency ω into the left FI transfers its energy via the spinful superfluid to the right FI after traveling the so-called65 coupling length L:

$$L=\frac{2\pi }{{k}_{+}-{k}_{-}}=\frac{\pi {\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}({k}_{+}+{k}_{-})}{\tilde{J}{\bar{s}}_{{{{{{{{\rm{nl}}}}}}}}}},$$
(12)

where k± are the wavenumbers corresponding to the frequency ω of the injected spin wave. A smaller L allows the transfer of energy and the concomitant implementation of logic operations in smaller devices and, thus is desirable.

Numerical estimates and experimental detection

We now employ material parameters pertinent to yttrium iron garnet67 as FI and Nb as S in finding the effects discussed above to be large. We consider Dm = 5 ⋅ 10−29erg ⋅ cm2, Ms = 140 G, γ = 1.76 ⋅ 107 G−1 s−1, γK = 10−17 erg, D = 3 cm2 s−1, NF = 1.3 ⋅ 1035erg−1 cm−3, Δ0 = 18 K, and \({\xi }_{{{{{{{{\rm{S}}}}}}}}}=\sqrt{D/{\Delta }_{0}} \sim 10\) nm. Further, we consider dFI = dS. Figure 2 plotted with these values, shows a large enhancement of the effective mass with decreasing temperature. This can be measured using, for example, the Brillouin Light Scattering technique68 employed regularly in measuring magnon group velocities69. Furthermore, the enhanced effective mass, and thus an altered spin conductivity, will manifest itself in the typical nonlocal magnonic spin transport experiment70,71. As the magnon spin conductivity scales as \(\sim 1/\sqrt{{D}_{{{{{{{{\rm{m}}}}}}}}}}\)72, its fractional modification due to the magnon-cooparon formation is given by −δDm/2Dm and is expected to be large (Fig. 2). Besides the in situ control via, for example, temperature, the FI thickness can be used to engineer \({\tilde{D}}_{m}\) ex situ. A negative value of \({\tilde{D}}_{{{{{{{{\rm{m}}}}}}}}}\) signifies that our assumed uniformly ordered magnetization is no longer the ground state73.

With the material parameters above, h0 = 0.61Δ0, and T = 0.9Tc, the net spin of the magnon-cooparon [Eq. (9)] is evaluated as 0.4, reduced from spin 1 of the bare magnon. Further, assuming t = 10ξS, d = ξS and (k+ + k−)/2 = 107 m−1, the coupling length L [Eq. (12)] of the magnon-cooparon based directional coupler is evaluated as ~100 nm. This is an order of magnitude smaller than the coupling length afforded by dipolar-interaction-based designs35,36. The experimental realization of the magnon-cooparon-based directional coupler can follow the procedure similar to its dipole-interaction-based counterpart36,64 with the FI layers deposited on a superconductor instead of a substrate. Magnons with nonzero k are often generated by applying ac voltage to a narrow conductor deposited on the FI36,64. The resulting spatially varying Oersted magnetic field bears a broadband k spectrum and excites the finite-k magnon that matches the frequency of the exciting voltage. Several other techniques can also generate finite-k magnons by exploiting the same lack of k-conservation in hybrid systems74.

Conclusions

We have demonstrated theoretically the ubiquitous existence of a quasiparticle, termed magnon-cooparon, comprising a spin flip in a magnetic insulator screened by a spinful Cooper pairs cloud in an adjacent conventional superconductor. The nonlocal nature of the magnon-cooparon is then exploited to propose a high performance magnonic directional coupler. While we have focused on a uniformly ordered ferromagnetic insulator, our analysis is general and anticipates an important role for magnon-cooparons in a wide range of hybrids comprising different magnetic insulators with various ground states.

Methods

Our theoretical method is a combination of the Landau–Lifshitz–Gilbert (LLG) equation to describe the dynamics of the magnetization in the ferromagnetic part of the system and the nonequilibrium quasiclassical theory in terms of Usadel equations for Green’s functions to describe the conductivity electrons in the superconducting part. Green’s function is used to calculate the electron spin polarization in the superconductor. The coupling between the LLG equation and the Usadel equation results from the S/FI interface exchange hamiltonian. It provides the spin torque term in the LLG equation, determined by the electron spin polarization in the superconductor. Simultaneously the exchange hamiltonian gives rise to the exchange field term in the Usadel equation, which is generated by the FI magnetization.

The coupled system of the LLG and Usadel equations is solved analytically to obtain expressions for the magnon dispersion via the electron spin polarization and for the quasiclassical Green’s function via the magnetization profile. The self-consistency between these quantities is achieved numerically. The superconducting order parameter is also calculated self-consistently via Green’s function in the framework of this procedure. The closed analytical results for the renormalization of a magnon stiffness and its spin were obtained in the limiting case of high temperatures Δ ≪ Tc and adiabatic approximation ω ≪ T.