Navigating the minefield of battery literature

Abstract

The field of battery research is highly active with an ever-increasing number of publications. This makes it extremely challenging for researchers to stay on top of the latest developments. In addition, and particularly challenging for those new to the battery field, a number of fundamental errors or inaccuracies frequently occur in published papers, creating additional barriers to understanding an already complicated field. Such errors and inaccuracies are potentially problematic given how battery research is focused toward those materials with promising performance metrics, which subsequently influences where research efforts are placed. This discussion seeks to clarify a few such recurring errors and inaccuracies, including electrolyte ideality, ion conduction and transference, Sand’s time and lithium-dendrite, cycle number and reversibility, and capacity and energy calculations. This discussion is intended to encourage researchers to follow rigorous reporting standards when publishing their battery research, which will help to ensure that findings can be reproduced by others.

Introduction

The importance of developing new battery materials and chemistries, and its significance to our civilization in general, does not need to be emphasized here, as it can be found in the opening statements of nearly all battery research papers. Such importance is directly reflected in the number of published articles on the battery subject, which is ever-increasing and makes it essentially impossible for any individual to completely follow the literature. To make it more challenging for researchers new to the field, a substantial number of these publications fail to meet the high standard of rigorous practice, thus creating an additional barrier to understanding. In this context, the published literature itself may constitute a key hurdle to progress in battery research, and a barrier to entry for new researchers.

What I intend to do in this short discussion is to help researchers new to the field, who may be grappling with the inundation of literature published each week, many of which claim a “breakthrough”, and these early career scientists who may be struggling to comprehend a complicated jargon system that is already established, accepted, and taken for granted by the battery research community, or those puzzled by the many seemingly conflicting results from various, or even sometimes the same, sources.

An interesting article published recently described, in a humorous and satirical manner, the confusion and frustration that the public often faces when breakthroughs are reported in the literature¹. While the article precisely pinpointed multiple traps that one should be aware of while reading battery literature, it is necessary to emphasize that the overwhelming majority of researchers are honest, who would not intentionally mislead or confuse their readers. The difficulties encountered by novice readers, and sometimes by myself as well, mainly arise from the complexities of the topic, in particular from the fact that a battery is a system, where at least three variables co-exist: cathode, anode and electrolyte. The possible number of combinations of these significantly increases if one counts other inert but nonetheless essential components (substrates, separators, conductive additives and even packaging materials). Furthermore, many journals apply a stringent word limit on research articles, thus forcing authors to showcase their main achievements in the main text, while less glamorous but potentially critical information is relegated to Supplement Information sections.

Thus, any data suggesting the improvement of a single battery component must be framed into the appropriate context before a rigorous comparison can be made with other studies. The battery community has noticed the situation and started taking certain remedial actions, such as the standard protocols published by the principal investigators of a major US government battery program². Meanwhile, in an effort to minimize the misunderstanding in reporting battery material progress and standardize data comparability, two journals recently initiated a stringent checklist for standardizing the reporting of battery performance^3,4. However, given the complexities of battery chemistry and materials, the problems are unlikely to be solved quickly.

Specific to the area of electrolytes, interfaces, and interphases, which has been my primary focus over the past decades, a few frequently-encountered misconceptions or inaccuracies are highlighted and discussed here. While many of these points are wellknown to veteran researchers, they are potential traps to people who are new to the field. The reason for these errors and inaccuracies recurring in the literature likely arises from the inertia of many authors, who are used to copying from prior literature without really understanding the origin and the concomitant constraints of those original concepts. Although in most cases such misconceptions constitute little or no direct harm to the scientific contents of those papers involved, they do create barriers for new researchers. Clarifying these points will ensure that the battery literature is more accurately reported, understood, and, ultimately, more reproducible.

Departure from ideality

Ion transport is the most important and hence most thoroughly interrogated property of electrolytes, which is precisely defined by four independent sets of quantities: ion conductivity (σ) or molar conductivity (Λ), ion mobility (μ_±) or ion self-diffusion/salt diffusion coefficients (D_± or D), ion transport/transference number (t_± or T_±), and the mean activity coefficients (γ_±).

In the literature on electrolytes we often see the following relations, or their variations, displayed by authors when describing their electrolyte materials:

$$\sigma =\sum {z}_{i}F{c}_{i}{\mu }_{i}$$

(1)

$$\Lambda =\frac{{z}_{i}{e}_{0}F}{{k}_{B}T}({D}_{+}+{D}_{-})=\frac{{z}_{i}{F}^{2}}{RT}({D}_{+}+{D}_{-})$$

(2)

$${t}_{+}=\frac{{D}_{+}}{{D}_{+}+{D}_{-}}$$

(3)

in which σ represents ion conductivity, z_i the valence of the ions, F the Faraday constant, c_i the ionic concentration, μ_i the ionic mobility, Λ the molar ion conductivity; e₀ the elemental charge, k_B the Boltzmann Constant, T the temperature, D₊ and D₋ the cationic and anionic diffusion coefficients, R the gas constant, and t₊ the cationic transference number, respectively.

One hidden assumption lies underneath all these relations: electrolyte ideality, which requires that: (1) the salt is completely dissociated into free ions; (2) all free ions participate in the diffusion and migration; (3) each free ion, wrapped in a classical Bernal-Fowler solvation sheath, does not feel the existence of any other ions, and hence moves independently. This requirement originated from the classical electrolyte science built on the meticulous experiments of Kohlrausch, Arrhenius, and others in the early days, as well as the theoretical models developed by Debye and Hückel, Nernst and Einstein, etc⁵. In fact, the summation signs (Σ or +) in these equations imply a simple additive nature of these quantities, which is only valid when the ions are completely independent.

To meet the requirements for ideality, the salt concentration in the electrolyte needs to be infinitely low, while the dielectric constant of the solvent needs to be sufficiently high, so that the independence of each individual ion is ensured. The upper threshold salt concentration for ideality is 0.01 N (or 0.01 M, for monovalent electrolytes) in aqueous electrolytes, meaning that any concentration above this threshold disqualifies an electrolyte from being ideal. In non-aqueous electrolytes, this concentration threshold would be much lower. In fact, it has been proven experimentally that lithium-ion battery electrolytes already behave like a non-ideal, concentrated electrolyte even when the salt concentration is only 0.1 M⁶.

Therefore, none of the electrolytes used in practical electrochemical devices (supercapacitors, batteries, fuel cells, etc.) meets these ideality requirements, simply because low salt concentrations do not provide sufficient ionic current to support a meaningful rate for cell reactions (Fig. 1). In other words, the application of any of these three equations on practical electrolytes violates their validity. Nonetheless, they are applied/cited extensively in electrolyte papers.

Fig. 1: The ideality requirement of electrolyte is not met at practical salt concentrations.

The electrolyte ideality can only be approximately approached at extremely diluted solutions (<0.01 M); at concentrations above 0.01 M, the cations and anions are so strongly interacting with each other that ion-pairs form; at moderate concentrations (0.01–0.5 M) solvent-separated ions (SSIP) and close ion-pairs (CIP) coexist; at super-concentrations (>5 M), the aggregates (AGG) and nano-heterogeneity arise and constitute the extended solution structures.

The influence arising from the gap between the ideality requirement and the non-ideal practical electrolytes is universal, but not always apparent. One example is the popular approach of determining an ion’s transference number using pulse-field gradient nuclear magnetic resonance (pfg-NMR) techniques. The self-diffusion coefficients measured for the cation (such as ⁷Li in Li⁺) and anion (such as ¹⁹F in PF₆⁻) allow one to apply Eq. 3 to calculate cationic transference number without considering that in practical electrolytes, especially at high or super-concentrations, complicated ionic speciation occurs. Taking the electrolyte for lithium-ion batteries as an example, the dissolution of the salt, lithium hexafluorophosphate (LiPF₆), does not simply produce free Li⁺ and PF₆⁻. Instead, various spectroscopic techniques reveal that complicated ionic species are formed:

$${{{{\rm{L}}}}}{i}^{+}P{F}_{6}^{-}(solid)\to L{i}^{+}+P{F}_{6}^{-}+{[L{i}^{+}P{F}_{6}^{-}]}^{0}+{[2L{i}^{+}P{F}_{6}^{-}]}^{+}\\ +{[{{{{\rm{L}}}}}{i}^{+}2P{F}_{6}^{-}]}^{-}+\ldots +{[n{{{{\rm{L}}}}}{i}^{+}mP{F}_{6}^{-}]}^{n-m}$$

(4)

The presence of these ion-pairs, complexes, and clusters significantly complicates how ionic species travel across the electrolyte under an applied electric field. Under these conditions, the neutral species, such as the close ion-pair ${[{{{{\rm{L}}}}}{i}^{+}P{F}_{6}^{-}]}^{0}$, do not make any contribution to the Li⁺-migration, while the complexes such as ${[{{{{\rm{L}}}}}{i}^{+}2P{F}_{6}^{-}]}^{-}$ contribute negatively, i.e., carrying Li⁺ in the wrong direction. In light of this behavior, the use of pfg-NMR data in Eq. 3 would inevitably over-estimate the Li⁺-transference number, because it reports the self-diffusion coefficient of Li⁺ by counting in all ⁷Li nuclei in the electrolyte, regardless of whether they are in a neutral or negatively-charged species. In fact, most Li⁺-transference number generated from pfg-NMR are scattered around the value of 0.5, which strongly implies that the cation and anion are closely associated in their movement, as they would be in ion-pairs or clusters.

In practical electrolytes with the ionic speciation described in Eq. 4, the Li⁺-transference number should be expressed as:

$${T}_{{{{{\rm{Li}}}}}}={t}_{{{{{\rm{L}}}}}{i}^{+}}+2{t}_{{[2{{{{\rm{L}}}}}{i}^{+}{X}^{-}]}^{+}}-{t}_{{[{{{{\rm{L}}}}}{i}^{+}2{X}^{-}]}^{-}}+\ldots +(n-m){t}_{{[n{{{{\rm{L}}}}}{i}^{+}mP{{{{{\rm{F}}}}}}_{6}^{-}]}^{n-m}}$$

(5)

where t_i represents the transport number for each individual species.

Note here that we have two distinct concepts: transport number and transference number. The latter is of interest because it quantifies, per Coulomb of charge passed through the electrolyte, how many moles of Li⁺, no matter in what species it exists, are carried with the current. Only in ideal electrolytes are the transport numbers and transference numbers identical.

Now, as described by Eq. 5, unless one has precise and quantitative knowledge about the ionic speciation, it is impossible to determine the transference number. Most ion transference numbers reported in battery literature were obtained from Eq. 3, hence they do not reflect the actual capability of an electrolyte in supporting the cell reaction. In a broader context, the design of new electrolytes should not follow any guidelines implied by Eqs. 1–3 too strictly, because they already deviate from reality.

Is there a reliable technique to measure transference?

Among the four transport quantities (σ, μ_±, D_± and T_±), the measurement of ion transference number proves to be the most challenging, because of the departure from ideality and the complicated ion speciation in practical electrolytes. Thus far, there have been no reliable and easy technique to ensure an accurate determination of T_±. The literature is full of conflicting data and there is an ongoing controversy regarding validity and accuracy of different models or the critical role of reference frame—a topic which will not be elaborated here. A word of caution is to be aware of the exact conditions under which the ion transference numbers are measured.

By definition, the most direct and accurate way of quantifying ion transference number is Hittorf Approach, which is based on a direct chemical analysis of different sections of electrolyte after passing a known quantity of charge across the electrolyte⁷. However, this method is rather laborious and technically difficult for those electrolytes sensitive to ambient interference (moisture, oxygen, etc.). Li⁺-conducting electrolytes unfortunately belong to this class. To the best of my knowledge, the only real Hittorf measurement on Li⁺-conducting electrolytes was carried out by Bruce and colleagues, who used a polymeric electrolyte consisting of lithium perchlorate dissolved in polyethylene oxide, and conducted the experiment at high temperature (120 °C) because of the low ion conductivity and low ionic transference number of the electrolyte⁸. The transference numbers were determined by accurately weighing the polymeric electrolyte sliced by razor blade at various sections of the cell. The reported ${T}_{{{{{\rm{L}}}}}{i}^{+}}$ is 0.06 ± 0.05, which differs by an order of magnitude from the Li⁺-transference numbers obtained from other methods, including pfg-NMR. A pseudo-Hittorf approach was applied by Valøen et al. on a lithium-ion battery electrolyte (LiPF₆ in carbonate mixtures), who did not directly analyze the electrolyte composition under applied constant current, but instead estimated it by measuring the change in potential of the concentration cell. Much higher Li⁺-transference numbers (0.36–0.41) were reported, with higher uncertainty⁶.

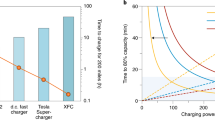
Besides pfg-NMR, the most popular method that deserves our attention is the Bruce-Vincent Approach⁹. This electrochemical method is a combination of AC impedance and DC polarization. The Bruce-Vincent Approach has been used extensively in electrolyte research papers and is responsible for nearly half of the Li⁺-transference numbers reported. In this approach, one constructs an electrochemical cell consisting of a pair of symmetric electrodes, such as lithium-metal (Li⁰), so that at least one of the ions (Li⁺ in this case) is not blocked by either electrode. Then a DC polarization at constant voltage is applied on the cell, and the decay of the cell current is monitored until it reaches a plateau, the so-called “steady state” (Fig. 2). At the initial state the current i₀ should be contributed by the migration of both cation and anion, while at steady state, the only contribution to the current i_SS should come from the cation migration, because the anion is blocked by the electrodes. Thus, one could intuitively argue that the cation transference number could be calculated by:

$${T}_{{{{{\rm{L}}}}}{i}^{+}}=\frac{{i}_{SS}}{{i}_{0}}$$

(6)

Fig. 2: Bruce-Vincent Method of measuring ion transference number from steady state in DC polarization curve.

The equation only holds true under very stringent constraints: ideal electrolyte, absence of convection, and small DC voltage.

The question is, under what conditions does Eq. 6 hold true? Bruce and Vincent rigorously analyzed the concentration gradients and the potential distribution across the cell when steady state is established, and concluded that Eq. 6 only holds true under these conditions: (1) the electrolyte is ideal (so that there is no complicated speciation); (2) the electrolyte is immobilized, i.e., solid or semi-solid (so that there is no convection to disrupt the establishment of a linear concentration gradient); (3) the DC voltage must be small (<10 mV, so that the potential distribution across the cell could be linearized). In the case of Li⁰ symmetric cells, one must also consider the presence of interphases and the evolution of interphasial resistance with time, hence Eq. 6 is modified as:

$${T}_{+}=\frac{{i}_{SS}}{{i}_{0}}\frac{\Delta V-{i}_{0}{R}_{CT}^{0}}{\Delta V-{i}_{SS}{R}_{CT}^{SS}}$$

(7)

where ΔV is the applied DC voltage, while ${R}_{CT}^{0}$ and ${R}_{CT}^{SS}$ are the interphasial resistances measured at the initial and the steady state, respectively¹⁰. The initial current i₀ can be more accurately calculated from AC impedance instead of being derived from DC polarization curve.

Bruce and Vincent initially only applied Eq. 7 on various polymeric electrolytes based on polyethylene oxide (PEO), which at least satisfy the convection-free requirement, although they are hardly ideal. However, like Eq. 3 based on pfg-NMR technique, this method was soon extensively applied on almost all electrolyte systems under investigation, including various liquid electrolytes, despite the stringent constraints set by the analysis of Bruce and Vincent. Some Li⁺-transference numbers measured by Bruce-Vincent Approach in non-aqueous ether electrolytes even approach incredible values of 0.7–0.8, which incur high suspicion. In this sense, ion transference numbers determined with this approach must be treated with caution, as all practical electrolytes almost inevitably violate the convection-free and ideality requirements.

What transference number really means

Setting aside the discussion of electrolyte ideality, applicability of Eqs. 3 or 7, as well as the interphase evolution, let us assume that our electrolyte is perfectly ideal. One simple but important question comes to mind, which is often lost in literature when reporting ion transference numbers: what does an ion transference number really mean with respect to the performance of an electrochemical device?

By definition, the transference number denotes how effectively the non-blocked ion is transferred by a unit Coulomb of current, serving as an important quantity to evaluate an electrolyte. But how it translates into cell performance is not always straightforward. For example, the Li⁺-transference number for the state-of-the-art electrolyte used in lithium-ion batteries, 1.2 M LiPF₆ dissolved in mixture of ethylene carbonate (EC) and dimethyl carbonate (DMC), is reported to be between 0.3–0.4 if measured by Bruce-Vincent or pfg-NMR techniques. To keep things simple, we will take ${T}_{{{{{\rm{L}}}}}{i}^{+}}$ = 0.30. Accordingly the transference number for PF₆⁻ is 0.70 (In fact, 1.2 M LiPF₆ in EC/DMC does not meet the ideality requirement and is only being used here as an example). Does this mean that, when a lithium-ion battery works, 30% of the current is carried by the movement of Li⁺, while 70% of the current is delivered by the movement of PF₆⁻? The answer is “no”, and the actual situation is rather complicated, even when the electrolyte is ideal, i.e., in absence of ion speciation.

Most batteries, including lithium-ion battery or lithium-metal battery, are anion-blocking devices, which means that the electrodes are reversible toward cation (Li⁺) but forbid anion to cross the electrode/electrolyte interfaces. By comparison, let us imagine an ideal electrolyte sandwiched between a pair of anion-blocking electrodes which is suddenly subject to an external field. At the very instant when the field is switched on, i.e., t = 0, both cation and anion start to move, but in opposite directions. At this instant, the overall current i₀ is indeed contributed by 30% cationic migration and 70% anionic migration. With time elapsing, however, the anion is increasingly accumulated at one of the electrode (anode) and depleted at the other (the cathode), because neither electrode allows its passage. Such accumulation and depletion build up a concentration gradient, which in turn drives a diffusion in the opposite direction of the anionic migration. The competition between the anionic migration and diffusion is responsible for the decaying curve of the current as seen in Fig. 2 when 0 < t < t_SS, until eventually the steady state is reached, where the diffusional current completely counter-balanced the migration current of anion. Thus, at steady state, the anionic transference number ${T}_{{{{{\rm{P}}}}}{F}_{6}^{-}}$ is zero, and the cationic transference number ${T}_{{{{{\rm{L}}}}}{i}^{+}}$ is 1.0 because it is now the only ion that migrates.

In other words, the reported number ${T}_{{{{{\rm{L}}}}}{i}^{+}}$ = 0.30 and ${T}_{{{{{\rm{P}}}}}{F}_{6}^{-}}$ = 0.70 only applies at the very instant when the ions in the electrolyte start the migration driven by external field, and an anion concentration gradient is absent. Now one might wonder though, if the measured ion transference number only dictates the current distribution at the initial instant when the electrolyte is subject to electric field, why is it still important in defining the capability of an electrolyte? It is because it determines the magnitude of i_SS, which sets an upper limit of current that an electrolyte can deliver under the anion-blocking condition. Referring to the above example of the electrolyte in lithium-ion battery, if its overall ion conductivity (σ_Total) as measured by AC impedance spectra is 10 mS/cm, the Li⁺-conductivity (σ_Li) available from it is only:

$${\sigma }_{{{{{\rm{Li}}}}}}={T}_{{{{{\rm{L}}}}}{i}^{+}}\times {\sigma }_{{{{{\rm{Total}}}}}}=3\,{{{{{\rm{mS/cm}}}}}}$$

(8)

which can provide a maximum current density of:

$${i}_{{{{{\rm{max}}}}}}=E\times {\sigma }_{{{{{\rm{Li}}}}}}=4.0\frac{V}{0.01\,{{{{\rm{cm}}}}}}\times 3\times {10}^{-3}\frac{S}{{{{{\rm{cm}}}}}}=1.2\,A/{{{{\rm{c}}}}}{m}^{2}$$

(9)

where E is the electric field applied on the electrolyte by the cathode and anode of the lithium-ion battery, and it is estimated to be 4.0 V across a cell with inter-electrode distance of 0.01 cm (or 100 μm). In reality, the actual current density would be much lower due to the interphasial resistances and tortuosity in separators. Nevertheless, a high ${T}_{{{{{\rm{L}}}}}{i}^{+}}$ would be critical to supporting cell reactions at high charge or discharge rates.

Sand’s time and Li dendrite

The pursuit for batteries with higher energy density recently revived research on lithium-metal batteries as a successor to lithium-ion batteries. After abandoning the system for several decades due to major safety issues, one of the issues researchers face today is still the dangerous Li⁰-morphologies formed when Li⁰ crystallizes under electrochemical conditions, resulting in Li⁰-dendrites and dead Li⁰. In discussing the mechanism for the formation of these Li⁰-morphologies, a recurring factor mentioned in the literature is the so-called Sand’s Time, given by:

$${\tau }_{{{{{\rm{Sand}}}}}}=\pi {D}_{{{{{\rm{ambp}}}}}}{\left[\frac{nF{c}_{0}}{2{i}_{{{{{\rm{CT}}}}}}(1-{T}_{+})}\right]}^{2}$$

(10)

where F is Faraday constant, c₀ the salt concentration in bulk electrolyte, i_CT the charge-transfer current at the surface, and D_ambp the ambipolar diffusion coefficient defined by the self-diffusion coefficient of individual cation (D₊) and anion (D₋):

$${D}_{{{{{\rm{ambp}}}}}}=\frac{2{D}_{+}{D}_{-}}{{D}_{+}+{D}_{-}}$$

(11)

τ_Sand predicts when the Li⁺-concentration at the electrode surface becomes zero, which was solved from Fick’s Second Law under boundary conditions of constant flux. Its correlation with dendrite formation was originally made by Sand in 1899 when studying the copper dendrite growth in aqueous electrolytes, with the argument that, when the metallic cation concentration becomes zero at electrode surface, the local current density would be maximized, which favors the fast nucleation of the nascent metal species and subsequent dendrite formation¹¹. The consideration of any interphase is notably absent there.

Brissot et al. transplanted the concept to Li⁰-dendrites to polymer electrolytes based on PEO, and proposed that Sand’s Time marks the onset of Li⁰-dendrite occurrence in the Li⁰-symmetric cell they constructed¹². Because PEO, like all ether-based electrolytes, remains relatively stable with Li⁰, the interphase therein are not as apparent as in other ester-based electrolytes, therefore the approach undertaken by Brissot et al. could be justified on certain approximation. However, after Brissot et al., especially in the recent decade, the application of Sand’s Time has been extrapolated to all electrolytes under investigation, including liquid non-aqueous electrolytes that, with certainty, no longer satisfy the original constraint under which Sand’s Time was derived.

Specific capacity and energy density

Two of the most important and closely-watched battery or material performance metrics are the specific capacity and energy density number, which are in the unit of mAh per gram (mAh g⁻¹) or watt-hour per kilo-gram (Wh Kg⁻¹), respectively. The former (specific capacity) measures how much charge one gram of the electrode material can accommodate, and the latter (gravimetric energy density) describes how much energy a battery can deliver when normalized against the weight of the battery.

The trap here lies in “per gram of what?” and “per kilo gram of what?”, as the number shifts considerably depending on the normalization. To make things worse, currently there is no standard regarding what weight should be used, and each approach has its own justification (Fig. 3). Let us look at capacity first. Taking Li⁰ anode as the first example, its specific capacity is calculated from the half reaction:

$${{{{{\rm{L}}}}}}{{{{{\rm{i}}}}}}^{+}+e\to {{{{\rm{L}}}}}{i}^{0}$$

(12)

whose corresponding capacity per gram of Li⁰ should be given as:

$${C}_{{{{{\rm{Li}}}}}} = \frac{F}{{M}_{{{{{\rm{Li}}}}}}}=\frac{96485(A\cdot s\cdot mo{l}^{-1})}{6.95(g\cdot mo{l}^{-1})}=13,882\,A\cdot s\,{g}^{-1}\\ = \,3856.31\,mAh\,{g}^{-1}$$

(13)

Fig. 3: The comparison among specific capacity of a single electrode, the whole cell, and the corresponding energy density.

A typical lithium-ion battery based on graphitic anode and lithium iron phosphate (LiFePO₄) is used as example here to demonstrate the possible variations in capacity and energy density values based on different masses. The actual energy density of commercial LiFePO₄ cells is 130–200 Wh Kg⁻¹ depending on cell engineering. This number includes everything in the cell, including inert components (electrolyte, separator, packaging etc.).

Note that the weight of substrate used here is Li⁰ itself, or the weight of the whole electrode. Now consider the anode materials used in lithium-ion batteries, i.e., the graphite which serves as intercalation host to accommodate Li⁺:

$$6{{{{{\rm{C}}}}}}+{{{{\rm{L}}}}}{i}^{+}+e\to {[{C}_{6}Li]}^{0}$$

(14)

whose corresponding capacity per gram of graphite often reported in literature was calculated as:

$${C}_{G} = \frac{F}{6\times {M}_{G}}=\frac{96485(A\cdot s\cdot mo{l}^{-1})}{72(g\cdot mo{l}^{-1})}=1340.69\,A\cdot s\,{g}^{-1} \\ = \,372\,mAh\,{g}^{-1}$$

(15)

This calculation only accounts for the weight of the host graphite (C₆), without counting the Li. The justification for this calculation approach is that one wants to focus on the capability of graphite material as container for Li⁺. Nevertheless, we see that the specific capacity numbers for Li⁰ (3856 mAh g⁻¹) and graphite (372 mAh g⁻¹) are not directly comparable, because they were calculated on different basis.

This type of inconsistent comparison could lead to ridiculous results if one is not careful. A classic example is silicon (Si), which can accommodates 4.4 Li⁺ per Si atom:

$${{{{{\rm{Si}}}}}}+4.4\,{{{{\rm{L}}}}}{i}^{+}+4.4e\to {[L{i}_{4.4}Si]}^{0}$$

(16)

whose corresponding capacity per gram of Si according to the way we dealt with graphite should be:

$${C}_{{{{{\rm{Si}}}}}} = \frac{F}{{M}_{{{{{\rm{Si}}}}}}}=\frac{4.4\times 96485(A\cdot s\cdot mo{l}^{-1})}{28.01(g\cdot mo{l}^{-1})}=15,156\,A\cdot s\,{g}^{-1}\\ = \,4210\,mAh\,{g}^{-1}$$

(17)

A simple comparison between Eq. 17 and Eq. 13 could lead one to claim that a Si anode can deliver higher specific capacity than Li⁰, which is clearly incorrect.

To make a proper comparison between Si and Li⁰, one has to ensure their capacities are calculated on the same basis. Thus, if one only counts the weight of the container, like what we did for Si and graphite, then the specific capacity for Li⁰ would be infinite ($\infty$), because there is no container involved; On the other hand, if the total weight of the whole electrode is used as the substrate weight, then the specific capacity for Si would be corrected as:

$${C}_{{{{{\rm{Si}}}}}} =\frac{F}{{M}_{{{{{\rm{L}}}}}{i}_{4.4}Si}}=\frac{4.4\times 96485(A\cdot s\cdot mo{l}^{-1})}{(28.01+4.4\times 6.95)(g\cdot mo{l}^{-1})}\\ = 7245.84\,A\cdot s\,{g}^{-1}=2012\,mAh\,{g}^{-1}$$

(18)

This makes more sense when compared with the specific capacity of Li⁰ (3856 mAh g⁻¹). Likewise, the specific capacity for graphite should be recalculated as well:

$${C}_{G} =\frac{F}{6\times {M}_{G}+{M}_{{{{{\rm{Li}}}}}}}=\frac{96485(A\cdot s\cdot mo{l}^{-1})}{78.95(g\cdot mo{l}^{-1})}=1222.10\,A\cdot s\,{g}^{-1} \\ =339.47\,mAh\,{g}^{-1}$$

(19)

The capacity numbers mentioned above are all based on a single electrode, no matter using just the container weight or the whole electrode weight. Although there is no battery consists of a single electrode, there is rather strong justification (and convenience) for knowing a single electrode capacity, because when developing new materials and evaluating its capability, one wants to focus on only the intrinsic properties of this material while minimizing the interference from the other electrode as much as possible. Besides, the counter-electrodes of the new material in future batteries remains uncertain, therefore it is more convenient to keep the numbers based on single electrode handy for freedom of selecting and coupling with potential counter electrode materials.

However, when it comes to calculate the capacity of a whole battery, one has to remember now that a battery consists of two electrodes, and these two electrodes must work together to deliver reversible capacity. The whole cell capacity then is given by:

$${C}_{{{{{\rm{Cell}}}}}}=\frac{{C}_{{{{{\rm{Anode}}}}}}\times {C}_{{{{{\rm{Cathode}}}}}}}{{C}_{{{{{\rm{Anode}}}}}}+{C}_{{{{{\rm{Cathode}}}}}}}$$

(20)

when the weight of other components (electrolyte, separator, packaging etc.) are ignored for simplicity. One can immediately tell that the specific capacity numbers calculated based on single electrode would be further reduced in real cells. The additional information that Eq. 20 tells us is that the specific capacities for single electrodes are coupled together. The improvement in the specific capacity of any single electrode would be inevitably reduced by the other electrode. In other words, the capacity of the whole cell is ultimately limited by the electrode with the lower specific capacity.

The energy output of a cell is decided by the product of cell capacity and cell voltage:

$${E}_{{{{{\rm{Cell}}}}}}={\int }_{0}^{{q}_{{{{{\rm{max}}}}}}}V(q)dq$$

(21)

where V(q) indicates that the cell voltage is not a constant but a function of capacity q, while the whole cell energy is given by the area enclosed by the cell voltage from 0 to the maximum capacity produced by the cell chemistry q_max. Via Eq. 21, the above discrepancies in different specific capacities would translate into the energy density as well.

When reading battery papers reporting new materials capacity or energy and comparing them with existing systems, one needs to be extremely careful about the basis used to calculate these numbers, as many authors may not indicate these subtleties explicitly. This can be especially important for research papers that are promoted by popular media or news releases, as a general readership may not understand these issues.

Cycle number and cycle life

One critical parameter used to evaluate a rechargeable battery is its reversibility, which is often quantified by cycle life and Coulombic efficiency. A state-of-the-art lithium ion battery can support thousands of deep cycles before its capacity decays to 80% of the original value, while the Coulombic efficiency per cycle is as high as 99.99%. In the modern battery literature, a rechargeable cell built with the new electrode or electrolyte materials is not considered impressive if its cycle number is less than 1000. In this “arms race”, cycle numbers as high as 100,000 and even approaching millions have been reported.

But the number of cycles is by no means equivalent to real cycle life. A common approach often used by researchers is to cycle the cell at a very fast rate, so that a very high number of cycles can be accumulated in a relatively short time. While one may argue that high rate cycling is also a merit because it validates the good power density of the cell, which is of course correct, we must also realize that the high rate cycling may cover up the parasitic reactions and self-discharge that a battery suffers, and leave us a false impression of excellent reversibility. As Dahn and colleagues pointed out repeatedly, what really tests the reversibility of a battery is the Coulombic efficiency during each cycle, which need to be determined with high precision¹³.

In this context, low rate cycling may prove to be a harsh test for reversibility of the battery chemistry, as it exposes the cell components (electrodes, electrolytes, etc.) to electrochemical extremities (i.e., 100% charged state) at much longer timeframe. Those cells with intrinsic self-discharge issues, such as sulfur-based chemistry, would especially need such harsh low rate tests to verify the reversibility.

Outlook

This short discussion highlights a few inaccuracies that the author has frequently observed in the literature, at presentations and in grant proposals. By discussing them here it is hoped that new researchers will avoid the same errors. It should be noted that my own early publications may have contained some of the errors mentioned here; science progresses by learning from our own errors, as well as by learning from others. As such, this article does not intend to demean any research effort, but to raise awareness of common problems, so that the battery literature becomes more reliable and reproducible. Finally, it is only by understanding the fundamentals of how battery performance is measured that readers can assess for themselves how reliable a particular claim is.