Introduction

The never-ending journey of material scientists exploring materials from the vast expanse of chemical space has now found a powerful computational guide called deep learning. In material research driven by deep learning, an artificial neural network (ANN) is trained by structure-property datasets to develop the predictive capability of properties based on the observed structure. Such ANNs have been used to discover new materials with targeted properties1,2 in the field of chemical compounds3,4,5, solid-state inorganic materials6,7,8, and materials with periodic structures9,10. For the ANN to function, the material structure must be precisely defined, and an expansive set of structure-property data, usually provided by public databases, must be available for training.

However, the structures of tangible materials most prevalent in our daily life, such as plastic composites, metal alloys, and rubbers are too complex to be defined, i.e., they are not periodic and may have multiple levels of structural hierarchy. As such, structure-property databases do not exist, which makes it impractical to apply deep learning to these classes of materials. However, recent advances in deep-learning technologies might provide a rational route to overcome this limitation. The generative adversarial network (GAN), developed by Ian Goodfellow in 201411, is a new class of ANN that can computationally generate fake images of abstract objects, such as human faces, cats, and dogs. This technology has the potential to carry out deep-learning research on a very wide range of materials, and, in recent years, substantial efforts have been placed along this direction12,13,14,15,16,17. For example, Kim et al.16 have created zeolites with a user-desired methane heat of adsorption. Mao et al.17 have proposed an experience-free approach to design configurations of architected materials with GANs that reach the Hashin-Shtrikman upper bounds of isotropic elasticity and strain energy storage. Banko et al.13 have extracted the synthesis-composition vs microstructure of thin films. Although these studies represent important advances, to move forward and possibly surpass existing technologies requires the ability to implement virtual experiments on tangible materials, where the processing of materials into a tangible form, characterization of the structure, and measurement of properties are all reproduced on computers.

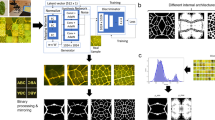
Here we propose a deep-learning-based computational framework that can implement virtual experiments on tangible materials with hierarchical, nondefinable, and nonperiodic structures (Fig. 1a). Central to our work reported here is the use of multiple GANs that create fake images of the structures of the form at different scales with various compositions. These images were merged into a tiled image that includes information of the hierarchical structure, from which an ANN predicted multiple properties (Fig. 1a).

Fig. 1: Concept of the deep-learning-based computational framework for virtual experiments.
figure 1

a Schematic of the process flow of real experiments versus computational procedure of virtual experiments. b Digital photograph of carbon nanotube (CNT) film featured in this article as an example of tangible materials. c SEM images of a CNT film at different magnifications showing the hierarchical structure.

Full size image

Results and discussion

Tangible and hierarchical structures

Although our computational framework can be applied to various tangible material systems, in this work we featured carbon nanotube (CNT) films (Fig. 1b). The CNT films were fabricated through vacuum filtration of CNTs dispersed in solution, and the surface structure was characterized by scanning electron microscopy (SEM) at multiple magnifications. In addition, the electrical conductivity and specific surface area of the films were measured (Fig. 1a). Films of CNTs represent excellent examples of hierarchical structures because CNTs spontaneously entangle by strong Van der Waals interaction and form complex networks from the nanometer to the millimeter length scales due to their one-dimensional structure and exceptionally high aspect ratios. The structural hierarchy of the CNT films is shown by a series of SEM images taken at increasing magnifications (Fig. 1c), i.e., at the lowest magnification, a superhighway network of large CNT bundles; at higher magnification, mid-sized bundles with visible internal structure; and at the highest magnification, a random network of fine CNT bundles. We would like to note that the structural hierarchy, such as the porosity of the fine network structure and tortuosity of the dendritic-like structure governs the electrical conductivity. Although referenced identically by the name, CNTs, their structures vary widely in such ways as length, diameter, crystallinity, and wall number18,19,20. This diversity makes CNTs an excellent test-bed material for this work because of the unique opportunity to fabricate an assortment of CNT films with different structures and properties. Here, we chose seven commercial CNTs (eDips, SG, Tuball, JEIO, Knano, Nanocyl, Cnano) that encompass a wide range of structures with wall numbers varying from 1 to 8.9, diameters varying from 1.8 to 15 nm, crystallinities (estimated by the Raman G-band/D-band ratio) varying from 0.5 to 59, and lengths varying from <1 μm to more than 100 μm (Supplementary Table 1).

Structural representation by conditional GANs

Our approach to predict properties of tangible materials by virtual experiments is based on training multiple GANs from real SEM images to make possible the creation of fake images of CNT films at various scales and compositions. Generation of fake images by a GAN includes the effects of dispersion, filtration, and SEM observation executed on the computer. Each GAN is made from two ANNs, i.e., a generator and a discriminator (Supplementary Figs. 1 and 2), that are simultaneously trained by an adversarial learning process. The generator generates fake SEM images of CNT films, and the discriminator differentiates fake from real11,21. When introducing the architecture of conditional GAN, generation of fake structures of arbitrary compositions can be controlled by an input of one-hot vector of composition into generator.

The training protocol of the GAN was decided by the balance among conflicting criteria of generator and discriminator (see also Supplementary Fig. 3). Images on the order of 10,000 s are required for each training point, cropped real SEM images were used to increase image number. In addition, the pixel resolution of images must be minimized to reduce memory usage and enable learning convergence within a reasonable time. Furthermore, the pixel resolution must be sufficiently high to capture the characteristic structural features of the CNT film for the accurate prediction of properties. Taking these factors into account, for 17 CNT films (seven types of CNTs and ten mixtures of CNTs, see also Supplementary Table 2) we took ~300 SEM images (960 × 1280 pixels) at a fixed magnification and divided them into 128 × 128 pixels, rotated 90 degrees for four times, and thus obtained 17 sets of ~12,000 training data. For each conditional GAN model, we implemented 50,000 iteration steps of the adversarial learning process and snapshots (Supplementary Fig. 4a) at different iteration levels show how the fake image of the generator evolved from random noise to structures that resemble the training data. This process was repeated to train four GANs at the four different SEM magnifications (×2k, ×20k, ×50k, and ×100k). The potential of the multi-scale GANs framework was shown by a side-by-side comparison of the (Fig. 2a) fake and real images of the 28 CNT films (seven types of CNTs at four different scales). Although the real CNT film images showed a wide variation in structure exhibiting the hierarchy as well as the difference in the CNT structures, exceptional similarity can be seen in all 28 pairs of fake and real images. This demonstrated the versatility of conditional GANs to process the wide range of structures of these tangible materials (see also Supplementary Figs. 5 and 6).

Fig. 2: Potential of generative adversarial network (GAN) to create fake CNT film SEM images and accuracy of ANN prediction of properties.
figure 2

a Comparison of real (experimental) and fake (created by conditional GAN) SEM images of CNT films made of seven types of CNT at four different scales. b Binarization procedure of the image analysis showing the two descriptors. c Frequency histograms of the width of CNT and void size compared between real and fake images. d Median values of the CNT width and void size calculated from real versus fake CNT film images (seven types of CNT, eDips (red), SG (orange), Tuball (magenta), JEIO (green), Knano (purple), Nanocyl (light blue), Cnano (blue), at 3 magnifications). e Four fake images of a CNT film at different magnifications tiled together to serve as the input of the ANN to predict properties. f Measured versus predicted values of electrical conductivity and specific surface area (blue: validation set, red: test set). g Prediction reliabilities of electrical conductivity (upper) and specific surface area (lower) predicted from tiled images versus single magnification.

Full size image

Image analysis was implemented to quantitively assess the similarity between the fake and real CNT film images. Two descriptors (Fig. 2b), i.e., the width of CNT bundle structure and void diameter were chosen to characterize the structure of the CNT films. Specifically, ~200 real and fake images of CNT films for each of the 21 cases (seven types and three scales)18 were binarized (Fig. 2b) where white/black pixels represent CNTs/voids, respectively. The frequency histograms of the width of CNTs and void diameter were calculated from the binary images, and two examples (Cnano at ×50k, JEIO at ×20k) are shown in Fig. 2c. While the frequency histograms differed significantly between Cnano at 50k and JEIO at ×20k, the agreement between the fake and real images was excellent for both cases, which illustrates the ability of a conditional GAN to reproduce highly diverse structures among CNT films. Furthermore, correlation plots (Fig. 2d) between the fake and real mean values for the width of CNTs and void diameter, calculated from the histograms, provided correlation coefficients of 0.78 and 0.84, respectively, demonstrating the potential of conditional GAN to accurately create fake images of various CNT films.

The properties of the CNT film were predicted by a structure-property ANN (Supplementary Fig. 7), however, our approach differs substantially from previous efforts, because training and prediction processes were entirely accomplished on fake images created by conditional GANs, and fake images representing different scales were tiled and merged into one to provide information about the hierarchical structure (Fig. 2e). By this approach, computational prediction of properties of tangible materials possessing structural hierarchy was made possible. Our structure-property ANN was trained to predict the electrical conductivity and specific surface area of CNT films (see also Supplementary Fig. 8). Specifically, the training was carried out on the 17 CNT films (seven types and ten mixtures of CNTs), and for each training point, 256 images (128 × 128 pixels) were created from each of the four GANs representing different magnifications, divided into four 64 × 64 pixels, rotated 90 degrees four times, providing 4000 images, and combination of tiling further increased the dataset to 12,000, of which 90% was used for training and 10% for validation. Once trained, the values of 256 predictions were averaged to provide the properties of a specific film.

Predicted versus experimental values of the electrical conductivity and specific surface area (Fig. 2f), for the validation and test sets, spanned a wide range, with prediction reliabilities (R2) of 0.99/0.85 for electrical conductivity and 0.99/0.42 for specific surface area, respectively. These results demonstrated the potential of our deep-learning based-computational framework to implement virtual experiments. Overall, this level of accuracy was sufficient to predict the properties of the CNT films to study relationships among structures and properties, as demonstrated later. It should be mentioned here that previous researches have elucidated that the electrical conductivity/specific surface of CNTs are strongly correlated to their length, crystallinity, and wall number19,20, however, the resolution of SEM is unable to resolve all of these CNT features even at the highest resolution, and thus not directly included here all. The influence of these undetected important structures of individual CNTs on properties must have been reflected indirectly through the difference in the network structure and hierarchy of the CNT films. The significance of using the tiling technique (Fig. 2f) for accurate property prediction is demonstrated by the comparison of the prediction reliabilities of the electrical conductivity from tiled multiple-magnification images against that of a single magnification for the 17 CNT films (Fig. 2g). Whereas the reliabilities show a large variation among the films and magnifications, the prediction reliabilities based on tiled images were consistently high.

Virtual experiments of CNT films

The potential of predicting properties of tangible materials by virtual experiments cannot be overstated. To highlight this aspect, we predicted the electrical conductivities and specific surface areas of 1716 CNT films composed of diverse compositions (Supplementary Data 1) and plotted the results into an Ashby map of surface area and electrical conductivity (Fig. 3a). We note that the 1716 virtual experiments were executed independently. However, plots in the Ashby map shows smooth transitions in color, which means continuous changes in composition with property, thus indicating that our naive deep-learning framework could capture the property trends on the material composition. We also stress that constructing this map experimentally would require years, however, in our case, once trained, these virtual experiments were completed within an hour. This speed underscores the great advantage of deep learning.

Fig. 3: Predicted properties of 1716 CNT films.
figure 3

a Ashby map of predicted electrical conductivity against predicted specific surface area. The colors of each point represent the content of the CNT mixtures as determined by the hue average of the contributing CNT types. (eDips (red), SG (orange), Tuball (magenta), JEIO (green), Knano (purple), Nanocyl (light blue), Cnano (blue)). b, c Wall number phase diagrams of CNT films (single-wall (red), double-wall (green), triple-wall (magenta), and multi-wall (blue) carbon nanotubes). d, e Economic performance of CNT films of electrical conductivity (d) and specific surface area (e). Yellow stars show the economic Pareto optimal solutions showing the most economical CNT film at the specific property. A difference of one in economic performance is equivalent to a ten-fold difference in costs. f, g Contents of CNT mixtures at Pareto optimal solutions at specific electrical conductivity (f) and specific surface area (g).

Full size image

The results of the 1716 virtual experiments can serve as a database for research on tangible materials, analogous to databases of molecules and solids used in cheminformatics. For this, we present several examples. First, the predicted properties of CNT films formed a triangular domain that covers a very wide region within the Ashby map. This originates from the wide structural variation of the CNTs. Moreover, an inverse relationship between the specific surface area and the electrical conductivity was observed, which means no single CNT film possesses both the highest levels of surface area and electrical conductivity.

Second, the plots in the Ashby map were recolored (Fig. 3b) to show the weighted average wall number of the CNT films, from which a wall-number phase diagram (Fig. 3c) was constructed. The phase diagram showed that both properties rapidly decrease with increase in wall number, implying wall number as a crucial structural parameter of CNT films. Films exhibiting the highest conductivities and specific surface areas were both composed from single-walled carbon nanotubes (SWNTs), but from different types, one with higher crystallinity and smaller diameter giving higher conductivity, and the other with lower crystallinity and larger diameter. The former/latter SWNTs formed a tightly/loosely packed bundle resulting in low/high specific surface areas. This is the origin of the inverse relationship between electrical conductivity and specific surface area. Moreover, considerable overlap among the wall-number domains was observed, e.g., the upper boundary of the double-walled carbon nanotube (DWNT) is nearly equivalent to that of the SWNTs. This means that the influence of a small addition of multi-walled carbon nanotubes (MWNTs) in a SWNT film is negligible and the properties are dominantly determined by the SWNT network.

Third, the database is not only useful for science but is also invaluable to develop practical applications. Frequently, the mission of developing real applications is to pursue the most cost-effective mixture of materials while satisfying the target properties. Currently, highly functional SWNTs are hundreds of times more expensive than MWNTs, and to examine economical solutions, we defined (Supplementary Methods) and calculated the economic performance of the CNT films (larger value = more cost-effective) and plotted them against the electrical conductivity (Fig. 3d) and specific surface area (Fig. 3e), respectively. Both figures clearly show that an increase in properties results in a drop in economic performance. The CNT films at the upper boundary (highlighted by yellow stars) represent the economic Pareto optimal solutions, i.e., the most economical CNT film at that specific property. The compositions of the Pareto optimal solutions vary with electrical conductivity level (Fig. 3f). For example, it changes from large diameter MWNT mixtures (Cnano-Nanocyl (−10 S cm−1), Cnano-Knano (−30 S cm−1)), to medium diameter, fewer walled mixtures (Tuball-Knano (−120 S cm−1)), to smaller diameter, longer length mixtures (Tuball-JEIO (−240 S cm−1)), to small diameter, highly crystalline mixtures (eDips-Tuball (−330 S cm−1), eDips (−360 S cm−1)). In contrast, the compositions of Pareto optimal solutions follow a different course for specific surface area (Fig. 3g) as it begins from large-diameter, MWNT mixtures (Cnano-Nanocyl (−240 m2 g−1), JEIO-Knano (−300 m2 g−1)), to large diameter, few-wall CNTs (JEIO-Nanocyl (−580 m2 g−1), JEIO (−660 m2 g−1)), to longer, SWNT-rich mixtures (SG-JEIO (−970 m2 g−1), SG (−1020 m2 g−1)). The compositions of optimal solutions differ for electrical conductivity and specific surface area. These predicted trends are valuable in developing real applications and would be difficult to obtain experimentally.

Inverse design of supercapacitors

The database can be used to seek the compositions of CNT films that possess an intended property, and this ability would open opportunities for the inverse design of applications. For example, CNTs films are known to be well-suited for supercapacitors electrodes due to their high surface area and electrical conductivity22,23. From the Ashby map we selected several CNT films with varying and targeted properties (Supplementary Fig. 9) and constructed two-electrode electric double-layer capacitor (EDLC) cells using a H2SO4 electrolyte. The galvanic discharge curves and impedance spectroscopies (Supplementary Fig. 10) were measured from which the energy densities and relaxation time constants (a measure of the speed of operation) were calculated and plotted against the specific surface area (Fig. 4a) and electrical conductivity (Fig. 4b). The specific surface area/electrical conductivity showed a strong and monotonical correlation with energy/density/relaxation time constant. These results mean one can determine the mixture of CNTs for EDLC cell electrodes that meets a target energy density and relaxation time constant, and by combing the economic Pareto optimal solutions, even can address to the most economical electrode.

Fig. 4: Relationship between performance of capacitor and properties of CNT films.
figure 4

a Energy density versus specific surface area, b relaxation time constant versus electrical conductivity.

Full size image

Conclusion

In summary, we proposed a general deep-learning-based computational framework that predicts properties by using conditional GAN to create fake structural images (SEM) of materials (CNT films) with hierarchical, non-definable, and non-periodic structures. Our approach is not only limited to CNT films but is readily extendable to other tangible material provided structural information is experimentally available and the properties have enough correlation with the structure, and thus we believe our approach represents an important step forward in expanding the scope of materials artificial intelligence can be applied.

Methods

CNT film fabrication

Seven commercial CNTs were used in this study. Four MWNTs (FloTube 9000, NC7000, K-nanos 100p, JC142) and three SWNTs (SG-CNT HT, Meijo eDIPS EC2.0, Tuball) were purchased or received from JiangSu CNano Technology Co. Ltd., Nanocyl SA., Kumho Petrochemical Co. Ltd., JEIO Co. Ltd., Zeon Corporation, Meijo Nano Carbon Co., Ltd. and OCSiAl. Details of CNTs are described in our previous work (ref. 18) and Supplementary Table 1. Each CNT was dispersed in methyl isobutyl ketone by a bead milling process. Mixtures of CNTs were prepared by mixing multiple CNT dispersions with arbitrary vol%. Then each mixture of CNT dispersion was filtered by a PTFE membrane filter and dried at 300 °C in vacuum.

SEM characterization

SEM measurements were carried out using a field-emission SEM (Hitachi, SU8220) under an acceleration voltage of 5 kV and an emission current of 10 μA.

Electrical conductivity measurement

Electrical conductivities of CNT films were measured by a four-point probe method using a resistivity meter Loresta-GP MCP-T610 (Mitsubishi Chemical Analytech).

Surface area measurement

To estimate Brunauer-Emmett-Teller (BET) specific surface areas of CNT films, N2 adsorption isotherms at 77 K were measured by a surface area and pore size distribution analyzer BELSORP-mini and -max (MicrotracBEL) after preheating at 300 °C for 3 h.

Fabrication and characterization of CNT supercapacitors

After vacuum drying of the CNT films (100 µm thick), supercapacitor electrodes were prepared by assembling a current collector (Pt mesh)/CNT film/separator (porous cellulose filter) structure. 1 M sulfuric acid was used as electrolyte solution. Electrochemical characteristics were measured by a VMP3 galvanostat/potentiostat/frequency response analyzer (Princeton Applied Research). The galvanostatic discharge curves and impedance spectrum of Fig. 4 are shown in Supplementary Fig. 10.

Generation of virtual fake CNT images by GAN

The structure of the conditional GAN models was based on the BigGAN framework21. In this study we used open-source code of BigGAN from ref. 24. The basic structures of generator and discriminator of conditional GAN used in this study are shown in Supplementary Figs. 1 and 2. For generator (Supplementary Fig. 1), inputs of latent values as well as one-hot vector of class were used to generate fake images at a demanded class. The input of one-hot vector of the class was introduced to class-conditional batch normalization layers in ResBlock(including skip connection of upsampling). For discriminator (Supplementary Fig. 2), inputs of the image are assessed in the model and the output was the logit of the truth of the structures by comparing the one-hot vector of the class of the input image. Training protocol of the generator and discriminator of the current conditional GAN is shown in Supplementary Fig. 3. Generated fake images from generator and inputs of latent and class were assessed by discriminator to obtain fake logits. Real image was also evaluated by the discriminator to obtain the output of the real logit. From these logits of real and fake images are used to calculate the loss of generator and discriminator. In the architecture of BigGAN, orthogonal regularization of weights of models was introduced to the total loss of optimization. The procedure for training conditional GAN models from real SEM images are as follows. SEM images of CNT films were cropped into small images with 128 × 128 pixels. Each image was rotated 90 degrees four times to increase the variation of the data. A generative model of fake CNT films was constructed based on the conditional GAN. Four conditional GAN models of CNT films with different magnifications (×2k, ×20k, ×50k, ×100k) were trained with 50,000 epochs until both generators of fake images and discriminator of generated images were well converged (Supplementary Fig. 4). For each iteration, 1200 images for each kind of CNT (seven types and ten mixtures of CNTs) were randomly sampled and used for training. Generation of fake images at an arbitrary composition is described in Supplementary Fig. 5. Product of one-hot vectors of classes and composition vectors were calculated to for representing intermediate structures of different classes (here, in other words, representing mixtures of multiple CNTs). Vector of intermediate composition is introduced to the class-conditional batch norm layers in each ResBlock. In addition to the one-hot vector, latent values after the parameterizing by truncation normal were also introduced to the generator in BigGAN model. Two hundred and fifty six fake images for each with desired kind and contents of CNT mixture were generated by changing the values of latent (see also Supplementary Fig. 6 for generated images of CNT mixtures at the arbitrary combination). Example codes and trained weights of conditional GAN models (four models for different magnifications) are available in ref. 25 (see also Supplementary Note 1). To validate the morphology of real and fake CNT images, void size and width of CNT were compared. To calculate void size and width of CNT, both real and fake images were subjected to binarization to separate domains of CNT and voids.

Prediction of properties of CNT films using tiling of images and deep learning

To include multi-scale information on hierarchical structure, we proposed a method for virtual experimentation based on tiling images of four different magnifications. First, generated fake images were cropped into 64 × 64 and compressed size into 32 × 32. Second, the compressed fake images of four magnifications were randomly selected and rotated (0, 90, 180, 270 degrees). Finally, four fake images were joined into a single image by arranging an image at ×2k into upper left, ×20k into upper right, ×50k into lower left, and ×100k into lower right.

To predict the properties including electrical conductivity and specific surface area, convolution neural network (CNN) was introduced. The architecture of CNN used in this study is described in Supplementary Fig. 7. The structure of CNN is standard, consisting of convolution layers and fully connected layers with several max-pooling or dropout layers. The architecture of CNN can also be referred to ref. 26. To investigate the effect of tiling on the prediction accuracies of properties, five CNN models including a model for tiled images and four models for individual magnification (×2k, ×20k, ×50k, ×100k) were constructed. The images for 17 CNT films (Supplementary Table 2) were gathered and randomly shaffled, then divided into training and validation sets with the ratio of 90–10%. Test set of additional 12 CNT films (Supplementary Table 3) was used to evaluate the prediction reliabilities of CNN models. All CNN models were trained with 100 epochs to sufficiently converge the models (see also Supplementary Fig. 8). Prediction reliabilities of CNN models were calculated from the coefficients of determination between measured and predicted properties of CNT films.

Virtual experimentation of CNT films

In total, 1716 conditions of CNT compositions, including binary and ternary CNT mixtures, were analyzed by conditional GAN and CNN models. Despite the lack of implementing ternary CNT mixtures in training/testing of models leading to relatively less accuracy compared to pure CNTs and binary mixtures, the tendency of the relationship between the structures and the properties can be sufficiently analyzed from the current virtual experimentation. Two hundred and fifty-six images of each condition were generated by conditional GAN models. After creating tiled images, electrical conductivity and specific surface area were calculated. In total, 1716 pairs of electrical conductivity and specific surface area were plotted in an Ashby map with the horizontal axis of electrical conductivity and the vertical axis of specific surface area (Fig. 3). To classify the 1716 points of virtual experimentations, the wall number and economic performance of each condition were calculated. All data plotted in the Ashby map is attached in Supplementary Data 1.

Classification of the Ashby map by wall number was conducted by drawing four lines of the convex hull of averaged wall number. Four classes, single (<2), double (<3), triple (<4), and multi-walled, were visualized in the Ashby map.