Introduction

Two-dimensional electrons gases (2DEGs) formed at the interface of heterojunctions are at the core of field effect devices, and also have led to the observation of new phenomena such as quantum Hall effect, exploiting the increased mobility of charge carriers1,2,3,4,5,6,7,8. With technological advances in modern electronics, it is possible to grow single crystals made of Si or other mainstream semiconductors to purities of 99.999999% that are free of dislocations. Such high-quality crystals have a very low density of defects which scatter and impede the flow of charge carriers, but their mobilities are limited by scattering of ionized dopants, which are necessary to provide mobile carriers in the materials. 2DEG has been introduced to circumvent this issue by spatially separating the ionized dopants from the free carriers. Modulation doping, polarization doping, field effect doping or combination of these have been used to realize 2DEG in several semiconductors9.

In perovskite system, 2DEG behavior in LaAlO3/SrTiO3 (LAO/STO) interface has been studied extensively for more than a decade10,11,12,13,14,15,16. The polar catastrophe model, also known as the charge transfer model, has been widely cited to explain the origin of 2DEG in LAO/STO interface. This model assumes that a polar LAO has a built-in electric field when deposited on a non-polar STO terminated with TiO2 layer. Emergence of the built-in electric field can also be interpreted as a result from the discontinuity of the formal polarization, according to the modern theory of polarization. As the LAO thickness increases beyond the critical thickness, the potential difference between the two surfaces of LAO resulting from the built-in electric field leads to electronic reconstruction, forming 2DEG at the interface. While the polar catastrophe model can account for the observation of the critical thickness for conduction, there are some experimental findings that are hard to explain using the polar catastrophe model: the 2DEG density much lower than 3 × 1014 cm−2 which is expected from the model and no observation yet of the isolated conducting p-type interfaces on an AlO2-terminated LaAlO3 surface in spite of some related experimental and theoretical studies17,18. Other mechanisms such as oxygen vacancies, cation interdiffusion, or strain-induced distortion have also been proposed to explain experimental observations12,13,16.

Recently, another perovskite polar/non-polar interface, LaInO3/BaSnO3 (LIO/BSO), has been reported to have 2DEG19,20,21,22,23. It was proposed that the 2DEG formation may be related with the polar nature of LIO, since the interfaces of non-polar BaHfO3 or SrZrO3 with La-doped BSO (BLSO) showed no conductance enhancement20, while the effect of oxygen vacancies and cation diffusion on the conductance of the interface have been tested and ruled out. Subsequently, it has been suggested22 that polarization in LIO near the interface with BSO induces 2DEG, based on the experimental data that showed the n2D increases for the first 16 Å (~4 unit cells) of LIO, starts to decrease for thicker LIO, and then approaches to a constant value for thicker LIO beyond 100 Å (~25 unit cells). Such “interface polarization” model can explain, by using a large conduction band offset at the interface, the lack of the critical thickness of LIO for 2DEG formation. In these LIO/BSO interfaces the oxygen stability and the high mobility in BSO24 at room temperature would provide a big advantage in sorting out the complex phenomena in such polar perovskite interfaces as well as an effective channel layer for high-power field effect transistors.

To identify the origin of 2DEG formation in the LIO/BLSO interface and understand the controlling parameters of field effect transistors for transparent oxide electronics based on such 2DEG, a study of an interface between BSO and another polar perovskite oxide can be very helpful. We have chosen LaGaO3 (LGO), which is a polar perovskite oxide like the LIO and share the same orthorhombic structure of the GdFeO3 type25,26,27. While the pseudocubic lattice constant of LIO, apc\(={\left(\sqrt{{a}^{2}+{b}^{2}}/2\cdot c/2\right)}^{1/2}\) = 4.117 Å, almost matches with the lattice constant of the cubic BSO (4.116 Å), apc of LGO is 3.890 Å, significantly lower than that of LIO. LGO is expected to have a larger band gap and a larger conduction band offset with BSO than those of LIO28,29,30, suggesting that the n2D of LGO/BSO would be as large as that of LIO/BSO, if not larger, as long as the polarization remains same20.

We have studied electrical and structural properties of LaIn1−xGaxO3 (LIGO)/BSO interface as functions of the Ga ratio, x, and the thickness of the LIGO to study the mechanism behind 2DEG formation at the interface. When 10 nm of LIGO was deposited, conductance (σs) and carrier density (n2D) of the interface decreased as Ga ratio increased. Scanning transmission microscopy (STEM) revealed that a few layers near the interface are coherently strained when Ga ratio is small but LIGO layers became relaxed for large Ga ratio by creating dislocations several nanometers away from the interface first and then moving closer to the interface as Ga ratio further increases. Based on experimental results and Poisson–Schrödinger (P–S) simulations of n2D, we discuss the relationship between the microstructure and the 2DEG formation at the interface.

Results and discussion

Although the 0.3% BLSO is not conducting, the slight doping is necessary to compensate for the large density deep acceptor states (5–6 × 1019 cm−3) in BSO on STO substrates22. Lastly, the LIGO layer was deposited on the channel layer by using a stencil mask so as not to screen the entire contact area. We grew the LIGO layer by sequential deposition from an LIO and an LGO target and we made sure that each cycle is less than a unit cell for uniformity in alloying. The Ga alloying ratio was calculated from the shot ratio and the deposition rate for each target. Such Ga alloying ratio agreed well with the chemical analysis by EDS (electron diffraction spectroscopy), as shown in Supplementary Figs. S1–S4 in the Supplementary Material. Chemical maps in 10 nm scale in Supplementary Fig. S5 and STEM images in 100 nm scale in Supplementary Fig. S6 show well-defined interface between BLSO and LIGO. Keithley 4200 SCS was used to measure electrical properties of channels. Hall measurements were conducted when the channel conductances were high enough for measurement.

Electrical measurement

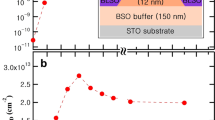
Figure 1a shows the measured electrical conductance of the channel depending on the Ga alloying ratio and the thickness of the LIGO layers. In the case of 81% Ga alloying ratio, the direct Hall measurement was not possible due to its low conductance. LGO/BLSO interface did not show noticeable conductance enhancement, excluding La diffusion as a possible origin of 2DEG formation, consistent with our previous report20. This indicates that growing epitaxial polar materials on top of BLSO is not sufficient to induce 2DEG formation, which poses a question about what other additional properties than its intrinsic polar structure may be involved with the 2DEG formation. When LIGO thickness is over 10 nm, increasing the Ga ratio leads to the decrease of the interface conductance, σs. As far as σs variation on the thickness of the LIGO layer is concerned, the overall behavior (increasing first, then decreasing in reverse, and eventually approaching to a constant conductance as LIGO becomes thicker) are similar as long as there is conductance enhancement.

Fig. 1: Electrical transport properties of the LIGO/0.3% BLSO interfaces.
figure 1

a Conductance (σs), b sheet carrier density (n2D), and c Hall mobility (μ) as a function of the LIGO thickness for various Ga alloying contents. The inset is a cross-sectional schematic diagram of the BLSO/LIGO interfaces.

Full size image

Considering the “interface polarization” in LIO can be correlated to the structural change caused by the orthorhombic/cubic epitaxial strain in the case of LIO/BLSO interface, as reported previously22, σs variation as a function of Ga alloying can also be viewed as variation in the epitaxial strain between the orthorhombic LIGO and the cubic BLSO layers. The epitaxial strain between LIO and BLSO is different from the usual biaxial strain that exist in the coherent epitaxial growth between two lattice-mismatched materials in other 2DEGs such as (AlGa)As/GaAs2,5,6, (AlGa)N/GaN3,9, and (MgZn)O/ZnO4,7,8. Such biaxial strain can exist in tens of nm in the growth direction (in the case of a few % lattice mismatch) and causes spontaneous and piezoelectric polarization discontinuity in the case of (AlGa)N/GaN and (MgZn)O/ZnO whose wurtzite crystal structure does not have inversion symmetry. In the case of LIO/BLSO, there exist orthorhombic domains (a = 5.7229 Å, b = 5.9404 Å, and c = 8.2158 Å) of LIO on BLSO31,32, and in each domain one direction is tensilely strained and the other direction is compressively strained while alternating the strain direction from one domain to the next. This alternating uniaxial-like strain is a very unique situation for perovskites since the average pseudocubic lattice constant (apc) of LIO almost matches that of BLSO. Such orthorhombic/cubic epitaxial strain seems to exist in only a few unit cells22,31,32 in the growth direction unlike the lattice-mismatched epitaxial growth where the biaxial strain can exist in tens of nm. However, as we alloy LIO with Ga and reduce its lattice constants, we start to increase the lattice-mismatched tensile strain in both in-plane directions. Judging from σs variation with its maximum occurring at 4–6 unit cells of LIGO, LIGO also seems to have interface polarization induced by combination of its intrinsic polar structure and the accompanying orthorhombic/cubic epitaxial strain. Since the lattice mismatch between the LGO and the BSO is significantly large (5.5%), the LGO is expected to be easily relaxed on BSO by creating dislocations, resulting in very small epitaxial strain (Fig. 2). Therefore we expect the LIGO will become more relaxed as the Ga ratio increases. Such increasing degree of relaxation with increasing lattice mismatch has also been reported in the (AlGa)N/GaN system9. The 2D carrier density (n2D) and the Hall mobility (μ) at the interfaces obtained by Hall measurement are shown in Fig. 1b, c. For a higher Ga alloying ratio the peak shape for the maximum n2D becomes broader and its position increases from 4 unit cell to 6 unit cell thickness. We observed that μ increases as n2D increases, consistent with the reported behavior of μ in BSO films where μ is limited by threading dislocation scattering33,34.

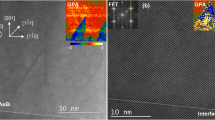
Fig. 2: Cross-sectional high-angle annular dark field scanning transmission electron microscope (HAADF-STEM) images of BLSO/LIGO interface in various Ga alloying ratios.
figure 2

Coherent epitaxial growth is confirmed when the Ga alloying ratio is 0, 20, and 42%, but dislocations are observed when the alloying ratio is 61, 81, and 100%. The white circles represent dislocations where extra (110)pc layers start to appear. It is easier to observe the dislocations in the [110]pc direction. The growth direction is [001]pc and the lateral direction is [100]pc.

Full size image

Microstructural measurement

To investigate local structures near the interface, STEM was performed on LIGO/BLSO interfaces. Figure 2 shows that all layers are epitaxially grown. However, there exist areas in the images that disrupt the periodic lattice structure by creating an extra (100)pc plane when Ga ratio is higher than 42%, which comes from the local collapse of the periodic structure resulting from the lattice mismatch, as in the case of dislocations. STEM image in Supplementary Figs. S7 and S8 in the Supplementary Material also exhibit such deviation from the pseudomorphic structure at high Ga alloying ratios. To quantitatively analyze STEM images, 2D Gaussian fitting was performed on STEM images using an open-source software Atomap, as shown in Supplementary Fig. S9 (ref. 35). While image simulations are necessary for more accurate analysis of the atomic positions, 2D Gaussian fitting can be useful as a first approximation. STEM images used for the analysis are shown in the Supplementary Material. We compared the average lattice constants of LIGO at a 2–3 nm away from the interface with those of BLSO at 2–3 nm away from the interface by averaging over 11–18 unit cells laterally and 2–3 unit cells in the growth direction. Figure 3 shows the obtained lattice constants of LIGO depending on the Ga ratio. Relative lattice constants, defined as (aLIGO − aBLSO)/aBLSO, of LIGO were deduced, where aLIGO, and aBLSO are lattice constants of LIGO and BLSO, respectively. We found that in-plane lattice constant of LIGO near the interface was almost pinned with that of BLSO up to 61% Ga ratio and then began to relax from 81% Ga ratio. However, the out-of-plane lattice constants decreased as the Ga ratio increased, consistent with our expectations.

Fig. 3: Relative in-plane lattice constants and out-of-plane lattice constants obtained from STEM as a function of the Ga alloying ratio.
figure 3

Once the aLIGO and aBLSO are obtained from the average lattice constants of LIGO and BLSO at 2–3 nm away from the interface, the relative lattice constants, (aLIGO ‒ aBLSO)/aBLSO, are calculated. The lattice constants were obtained by averaging over 11–18 unit cells laterally and 2–3 unit cells in the growth direction. The error bars represent the standard deviations.

Full size image

In order to further understand how the LIGO films relax as they grow thicker and the lattice mismatch with BSO becomes larger, we measured the reciprocal space mapping (RSM) of 50-nm-thick LIGO grown epitaxially on BSO. Figures 4 and 5 show that 41% LIGO already started to relax from the BSO in-plane lattice by creating dislocations, while the interfacial in-plane lattice constants by STEM in Fig. 3 suggest that even 42 and 61% LIGO are pinned with BSO lattice. Therefore, following scenarios can be made. LIO grows epitaxially in a coherent manner on BSO. Although LIO forms domains to relieve the orthorhombic/cubic strain after a few unit cells, there are no new dislocations formed in LIO as it becomes thicker (the threading dislocations in the BSO seem to continue in LIO by coherent epitaxy as shown in Supplementary Fig. S6). As Ga is alloyed up to 21%, no significant change is seen except for the small tensile strain in LIGO. When the Ga ratio is further increased, new dislocations form inside LIGO, first away from the interface, to relieve the increasing tensile strain. As the Ga ratio reaches 61 and 80%, the dislocations move closer to the interface. In the case of LGO, new dislocations start to form right from the interface, destroying the coherent epitaxial growth.

Fig. 4: Reciprocal space maps in various Ga alloying ratios.
figure 4

Maps are of pseudocubic (103) reflections for 50-nm-thick LIGO and 10-nm-thick BSO films on (001) STO substrates.

Full size image
Fig. 5: In-plane lattice constant (ax) and out-of-plane lattice constant (az) obtained from the RSMs.
figure 5

Values for LIO are from ref. 17 and shown as the triangular marks. apc are the pseudocubic lattice constants from the bulk LIO and LGO. The small error bars represent the standard deviation in the Gaussian fitting of the peaks.

Full size image

P–S simulations

We performed P–S simulation of LIGO/BLSO interface with 0.3% La doping to find the appropriate interface polarization settings for each LIGO. The program developed by G. Snider36,37 was used and the material parameters same as those in our previous paper22 were used. P–S simulation calculates one-dimensional Poisson equation and Schrödinger equation self-consistently by an iterative way. First, using a trial potential in the Schrödinger equation, one gets eigenfunctions and energy eigenvalues. Then one puts these eigenfunctions and eigenvalues into the Poisson equation and gets a modified potential as a solution. One puts this potential back into the Schrödinger equation again and continues this process until a solution satisfies both equations. This can be broadly used in calculation for band bending and charge distribution in semiconductor heterostructures.

Figure 6a shows polarizations in LIGO needed in P–S simulation to reproduce experimental n2D results and Fig. 6b compares the simulation results with the experimental data. The polarization and n2D for LIO/BLSO interface are taken from the previous paper22. One can notice that a small decrease in the polarization value generates a relatively larger decrease in n2D. This is due to the fact that the large conduction band drop at the interface, about 3.1 eV in the LIO/BLSO case, is necessary from the intrinsic conduction band offset (~1.6 eV) plus the interface polarization (~1.5 eV) to generate the 0.6 eV deep quantum well at the interface22. For example, 20% decrease of the polarization by Ga alloying will decrease the depth of the quantum well by nearly 50%, thereby the n2D by approximately that much. Furthermore, compared with the polarization in LIO existing up to 4 unit cells near the interface, LIGO has the polarization persisting up to 5~6 unit cells. This results from the change in LIGO thickness for the maximum n2D. In case of LIGO/BLSO interface, n2D value peaks at 5–6 unit cell thickness, whereas LIO/BLSO interface exhibits a peak at 4 unit cell LIO thickness. In our simulations for x = 20, 42, and 61%, we used the same deep donor density of 2 × 1020 cm−3 in LIGO, as in the case of LIO (x = 0)22,23. This generated good overall fittings in all the cases although in LIGO cases the initial decay of the n2D is slightly slower than the simulation and there remains slight gradual decrease over a long length (100 nm) scale. Although speculative at present, such decay of n2D over a long length scale may have something to do with the epitaxial strain relaxation, as can be predicted by the differences in the local interfacial properties by STEM (Figs. 2 and 3) and in average properties by RSM (Figs. 4 and 5) of 50-nm-thick LIGO. Since increasing Ga ratio in LIGO not only changes polarizations in LIGO but may also change many parameters that can affect n2D such as the conduction band offset and/or the defect densities, further studies are needed to clearly identify the relationship between the strain and the polarization.

Fig. 6: Self-consistent Poisson–Schrödinger simulation for 0.3% BLSO/LIGO interface.
figure 6

NDD = 2 × 1020 cm−3 was used in all LIGO layers within 5 nm near the interface. a Interface polarization values used for simulation. b Comparison of n2D by experiments (dots) with those by simulation (lines).

Full size image

Figure 7a displays the total interface polarization summed over the interfacial thickness from Fig. 6a as a function of Ga alloying ratio. For the 81% Ga alloying ratio, we estimated the n2D and the mobility values assuming the typical inter-dependence between them24. In the case of LGO, while assuming the overall shape of the interface polarization as a function of its thickness in Fig. 6a, we estimated the maximum total interface polarization for zero n2D value, which is 113 μC cm−2 unit cell. The way the total interface resistance drops as a function of the Ga alloying ratio looks consistent with the decrease of the coherent epitaxial strain as well as the conductance of 2DEG plotted in Fig. 7b. As the lattice mismatch increase and the associated dislocations are created and move closer to the interface, the total interface polarization decreases fast, leading to disappearance of 2DEG.

Fig. 7: Comparison of total interfacial polarization with sheet conductance.
figure 7

a The total interfacial polarization summed from Fig. 6a. The values for 81% LIGO were calculated from the estimated n2D = 1–3 × 1012 cm−2 by assuming that n2D and μ follow the decreasing trend shown in Fig. 1 as the alloying ratio increases. In the case of LGO, we found the minimum polarization value, about 113 μC cm−2 unit cell, which can produce non-zero n2D by assuming a similar thickness dependence of the interface polarization. b Sheet conductance of 2DEG with 10-nm-thick LIGO as a function of Ga alloying ratio.

Full size image

When an orthorhombic perovskite grows coherently on a cubic perovskite, two types of epitaxial strains can exist: one is the shorter range (a few unit cells) orthorhombic/cubic strain and the other is longer range (a few tens of unit cells) lattice-mismatched biaxial strain. Since the orthorhombic crystal structure possesses inversion symmetry, the lattice-mismatched biaxial strain does not cause piezoelectric polarization, as opposed to the cases of (AlGa)N/GaN and (MgZn)O/ZnO. In the case of LIGO/BLSO, only the interfacial polarization seems possible due to the inversion symmetry breaking near the interface. This can explain the very small drop in the total interface polarization in Fig. 7a at 20 and 40% Ga alloying ratio as long as the coherent epitaxial growth is maintained. However, when the lattice mismatch becomes larger, the resulting dislocations start to form near the interface, which starts to affect the coherent epitaxial growth, simultaneously the orthorhombic/cubic strain near the interface, and consequently the interface polarization associated with it.

Conclusions

We have investigated LIGO/BLSO interface to identify the origin of the conductance enhancement. The conductance of the interface reached its maximum value around 20 Å (4–6 unit cells) of LIGO layers, decreased in reverse, and approached to a constant value as LIGO layers became thicker. As the Ga ratio increased, the interface conductance decreased and LGO/BLSO did not show any noticeable conductance enhancement. STEM and RSM studies of the interfaces suggest that the dislocations in LIGO created by the lattice mismatch with BSO disrupt the coherent epitaxy near the interface and suppress the 2DEG formation. Further studies of the relation between the strain in LIGO and the interface polarization can provide deeper understanding of 2DEG formation at oxide interfaces as well as insight into tuning the 2DEG properties.

Methods

We used the same geometric pattern as the one employed in our previous paper about LIO/BLSO interface20,21,22,23. A schematic for the vertical structure of the interfaces are shown in the inset of Fig. 1. Samples were grown on TiO2-terminated STO (001) substrates at 750 °C in 100 mTorr of oxygen pressure. Pulsed laser deposition using KrF excimer laser was used with energy fluence in the range of 1.2–1.5 J/cm2. All targets were provided by Toshima Manufacturing, Co. in Japan. We first deposited 150 nm undoped BSO buffer layer to reduce the effect of threading dislocations. Second, 12 nm of 0.3% BLSO (Ba0.997La0.003SnO3) square channel layer was grown and 4% BLSO (Ba0.96La0.04SnO3) contact layers were deposited on the four corners of the channel by using two Si-based stencil masks.

For Ga alloying ratio measurement chemical analysis by EDS was employed.

For structural investigation, STEM and RSM were performed using JEM-ARM200F and X’pert Pro, respectively.

We performed P–S simulation by using the program developed by G. Snider36,37.