Abstract
3D printing using conventional stereolithography is challenging because the polymerized layers adhere to the solid constraining interface. The mechanical separation forces lead to poor process reliability and limit the geometrical design space of the printed parts. Here, these challenges are overcome by utilizing a static inert immiscible liquid below the resin as the constraining interface. We elucidate the mechanisms that enable the static liquid to mitigate stiction in both discrete layer-by-layer and continuous layerless growth modes. The inert liquid functions as a dewetting interface during the discrete growth and as a carrier of oxygen to inhibit polymerization during the continuous growth. This method enables a wide range of process conditions, such as exposure and resin properties, which facilitates micrometer scale resolutions and dimensional accuracies above 95%. We demonstrate multi-scale microstructures with feature sizes ranging from 16 μm to thousands of micrometers and functional devices with aspect ratios greater than 50:1 without using sacrificial supports. This process can enable additive 3D microfabrication of functional devices for a variety of applications.
Similar content being viewed by others
Introduction
Recent advances in additive manufacturing have shown great potential to enable rapid fabrication of functional devices for diverse applications such as microelectronics1, sensors2, structural and optical metamaterials3,4, micro-optics5,6, and biomedical devices7,8. One promising approach for additive three-dimensional (3D) printing of microdevices is stereolithography (SLA) because of its high resolution and scalability to large areas9,10,11. However, microfabrication using conventional SLA systems is challenging because stiction forces12 cause adhesion of the polymerized layer to the solid constraining interface. Separation of the 3D object from the solid interface requires mechanical intervention such as pulling and sliding. The resulting separation forces, which are proportional to the polymerized area, can damage the printed parts and lead to poor reliability13,14,15,16. The large mechanical separation forces impose limitations on the geometries that can be printed and introduces a need for supporting scaffolds.
Recent advances in 3D printing have employed layerless growth techniques to mitigate stiction forces and improve vertical print speeds. Tumbleston et al.17,18 used an oxygen-permeable membrane to inhibit polymerization at the solid interface. The inhibition caused by oxygen prevents adhesion of the polymer to the solid interface by creating a dead zone, a thin layer of unreacted resin, adjacent to the solid interface. Walker et al.19.leveraged the shear stress caused by a moving immiscible liquid below the resin to prevent adhesion of the polymer by the immiscible liquid. De Beer et al.20 used dual-wavelength irradiation to concurrently photopolymerize while also inhibiting the reaction at the solid interface. All of these methods, which employ continuous growth, produce 3D objects by continuously elevating the substrate as a flux of fresh resin flows into the polymerization zone.
Although high vertical print speeds have been demonstrated with continuous growth, the requirement of a stable dead zone and adequate resin replenishment places constraints on process conditions such as exposure energy, resin viscosity, and concentration of additives in the resin (resin properties), such as photoinitiator and absorbing dye17,19,20,21. These constraints result in a trade-off between vertical print speeds, vertical resolution (cured depth), lateral resolution (cured width), and mechanical properties (green strength) of the printed parts. Within the context of this work and photolithography, the resolution is defined as the smallest feature size that can be printed for a range of process conditions and variations—also known as the process window22. The narrow process window of continuous growth limits the maximum cross-sectional area of the printed parts21, fabrication of microdevices that require high spatial resolution—e.g., fabrication of microfluidic flow channels using high-resolution resins23—and modulation of the mechanical properties of the printed parts by varying the exposure and resin properties10,24. In such cases, discrete layer-by-layer growth may be utilized to attain a wider process window, but at the cost of stiction forces.
We report on photopolymerization at a static liquid constrained interface for SLA. This process mitigates mechanical separation forces in both discrete layer-by-layer and continuous layerless growth modes and enables reliable fabrication of 3D objects without a need for supporting scaffolds. The mechanisms that facilitate a static liquid to mitigate stiction in both growth modes are elucidated. It is shown that discrete growth is advantageous for microfabrication since high spatial resolution and dimensional accuracies can be achieved because of reduced constraints over the process conditions such as exposure and resin properties—while continuous growth can be utilized when high vertical print speeds, smooth surface finish, and isotropic mechanical properties are desired. Furthermore, we demonstrate that this projection SLA process can enable the fabrication of microstructures and functional devices with multi-scale geometries.
Results and discussion
Photopolymerization at a static inert immiscible liquid interface
Our SLA process utilizes photopolymerization at the interface of two immiscible liquids. In this method, polymerization of the liquid resin occurs near the interface of an inert liquid that is immiscible with the resin (Fig. 1a). The inert liquid, which is stationary below the resin, functions as a constraining interface, similar to a solid window, e.g., glass, polydimethylsiloxane (PDMS), or fluorinated ethylene propylene film, in a conventional SLA system. Upon exposure to patterned ultraviolet (UV) light, only the resin undergoes cross-linking chemical reaction to form a solid polymer, whereas the inert liquid remains unchanged (see Supplementary Note 1). Contrary to reactions at liquid–liquid interfaces that are used for material synthesis25, our approach can be used to additively manufacture 3D objects with arbitrary geometries.
a Schematic of an SLA system that contains an inert immiscible liquid below the photopolymerizable resin as the constraining interface. Spatially selective polymerization occurs through the projection of patterned UV light. b Vial containing two immiscible phases: top phase is a resin, and the bottom phase is an inert liquid that is transparent to UV light and has a higher density than the resin. The blue glow from the resin is caused by a fluorescent dye in the resin. c Scheme of the continuous layerless growth process. Fresh resin flows into the polymerization zone comprising of a dead zone and a cure zone as the substrate is continuously elevated. The dead zone is a finite region of unreacted resin because of oxygen inhibition from the inert liquid. The onset of polymerization occurs within the cure zone. d Series of time-lapse schematics (cross-sectional view) and corresponding experimental observations (viewed through the transparent glass window) showing the dewetting of the inert liquid from the polymerized layer during the discrete layer-by-layer growth process (also shown in Supplementary Movie 1).
Selection of an inert liquid for the SLA process requires that the inert liquid is chemically inert, transparent to the wavelength of light used for photopolymerization, has a higher density than the resin, is highly immiscible with the resin, and has low surface energy. In this work, perfluorocarbon-based fluorinated oils, such as 3 M Fluorinert were investigated as the inert liquid, while the feasibility of using perfluoropolyether-based fluorinated oils, such as Solvay Fomblin, was also confirmed. These fluorinated oils were found to be ideal candidates when using 1,6-hexanediol diacrylate (HDDA)-based resin (Fig. 1b) and have also been shown to be compatible with a wide range of SLA resins19. The properties of the fluorinated oils investigated in this work allow the inert liquid to serve dual functions—a polymerization inhibiting interface for continuous growth and as a dewetting interface for discrete growth (Fig. 1c, d).
Continuous growth using oxygen inhibition from the inert liquid
The schematic in Fig. 1c shows how continuous growth using a static liquid interface can be achieved. As the substrate (not shown) is continuously elevated, fresh unreacted resin replenishes into the polymerization zone. The polymerization zone is defined as a finite region composed of a dead zone and a cure zone. This region is characterized by a gradient of increasing degree of solidification, where the degree of solidification is null at the inert liquid interface and it increases toward the fully solidified polymer interface. Within the dead zone, no polymerization of the resin occurs because of oxygen inhibition17,26. The presence of the dead zone prevents wetting of the solidified polymer by the inert liquid because this region is occupied by a finite layer of unreacted resin. Within the cure zone, the onset of gelation (solidification) occurs because the oxygen concentration falls below a critical value. The spatial and temporal degree of polymerization within the cure zone has been modeled by Walker et al.19.
Continuous growth can be enabled when the inert liquid functions as a carrier of inhibiting reactants such as oxygen to create a dead zone. When using fluorinated oils, we found evidence of a dead zone adjacent to the inert liquid interface. Using a differential resin technique (see Methods), we characterized the dead zone thickness as a function of exposure intensity for Fluorinert (Fig. 2a). Since perfluorocarbons, such as Fluorinert, are known to have high oxygen solubility27,28, the mechanism causing the inhibition of polymerization is attributed to the diffusion of oxygen from the bulk of the Fluorinert to the polymerization interface. To support this theory, we reduced the dissolved oxygen concentration in the Fluorinert by nitrogen purging (see Methods). Under this condition, we observed not only a smaller dead zone thickness but also an increase in the lateral cured width of the polymer when compared with the non-purged Fluorinert under ambient conditions (see Fig. 2a). The reduction in polymerization vertically and laterally, caused by the dissolved oxygen in Fluorinert, behaves similarly to the model by Dendukuri et al.26 for a PDMS interface. The relationship between the dead zone thickness and process parameters, such as exposure intensity and concentration of photoinitiator, when using a static inert liquid is given by Supplementary Equation 1 (see Supplementary Note 2).
a Comparison of Fluorinert (inert liquid) with and without de-oxygenation and its effect on the dead zone thickness and lateral cured width as a function of exposure intensity. b Effect of exposure intensity and time on the dead zone thickness and lateral cured width for a differential resin thickness of 150 μm. Decreasing exposure time is commensurate with a faster growth rate in the continuous growth mode. The targeted lateral dimension in both a and b was 1000 μm. The vertical error bars in a and b represent the standard deviation of repeatability. c Smooth-surfaced ellipsoidal microstructures fabricated at a rate of 3 μm s−1 in the continuous growth mode using a static liquid interface.
The dead zone thickness is dynamic and is dependent on the process conditions such as growth rate, exposure intensity, and resin properties. We used the differential resin technique to characterize the dependence of the dead zone thickness and lateral cured width on exposure intensity and time (Fig. 2b). In this differential characterization, decreasing the exposure time while keeping the exposure intensity constant is commensurate with a faster growth rate (substrate elevation rate) during the continuous growth mode. We observed that as the exposure intensity and time decrease, the dead zone thickness increases and the lateral cured width decreases. Using this framework, we determined the process conditions required to achieve sufficient lateral polymerization, and we demonstrated ellipsoidal microstructures with smooth surfaces grown at a rate of 3 μm s−1 as shown in Fig. 2c.
Realization of high spatial resolution and large cross-sectional area is challenging during continuous growth. A viable continuous growth process requires adequate replenishment of the resin into the polymerization zone21. This constrains both the polymerization zone to a minimum thickness and the underlying process conditions. We empirically determined that a dead zone thickness >50–75 μm must be maintained for a stable growth process. If the dead zone collapses below a critical thickness, wetting of the polymer by the inert liquid occurs, resulting in defects as shown in Supplementary Fig. 4 (also see Supplementary Note 3). The thickness of the dead zone and the cure zone can be increased by increasing the growth rate or by decreasing the exposure intensity and the concentration of additives in the resin17,19. However, these process conditions result in a trade-off with the spatial resolution and green strength of the fabricated parts as evident from Fig. 2b and Supplementary Fig. 5 (also see Supplementary Note 4). In order to attain high spatial resolution, reduced constraints over the process window, and larger cross-sectional area, discrete growth can be utilized when using a static liquid interface. This is because discrete growth does not rely on maintaining a dead zone—once the dead zone collapses, the process simply requires a dewetting step to replenish the polymerization zone with fresh resin before exposure of the subsequent layer as shown in the schematic of Fig. 1d.
Discrete growth enables a wider process window
The schematic in Fig. 1d illustrates the discrete layer-by-layer growth process using a static liquid interface. During the exposure of UV light, the dead zone collapses and interfacial forces cause wetting of the polymerized layer by the inert liquid. As the 3D object is separated from the inert liquid interface, the polymer layer is dewetted, resulting in a gradual shrinking of the inert liquid’s capillary bridge (also shown in Supplementary Movie 1). Because of the deformable nature of the inert liquid during dewetting, an interfacial phenomenon, the 3D object experiences virtually zero mechanical separation forces (see Supplementary Note 5). Therefore, a liquid constrained interface offers a significant advantage for fabrication of devices with large cross-sectional area (tens of millimeters in size) as evident from Supplementary Movie 1, large overhangs, and high aspect ratio microstructures, which are prone to failure because of stiction forces when using a solid constrained interface (see Supplementary Fig. 7).
The vertical distance required to fully dewet the polymer can be estimated by the capillary length, \(\kappa ^{ - 1} = \sqrt {\gamma /\left( {\rho g} \right)}\), where γ and ρ are the surface tension and density of the inert liquid respectively, and g is the gravitational acceleration29. In practice, however, the exact distance required to fully dewet the polymer depends on the surface tension between the interacting phases, viscosity, contact area, and pull-off velocity30. For example, the dewetting distance can be reduced by decreasing the viscosity of the inert liquid or by decreasing the pull-off velocity. In our work, when using Fluorinert as the inert liquid, the capillary length can be estimated to κ−1 ≈ 0.9 mm. However, we observed dewetting distances ranging from 0.4 mm to 1.1 mm for pull-off velocities of 20–400 μm s−1 and a polymerized area of 60 mm2. Furthermore, the low surface energy of fluorinated oils allowed the dewetting to occur without the formation of a residual volume of the inert liquid adhered to the polymerized layer.
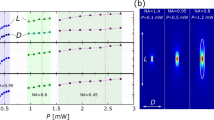
Using discrete growth, higher lateral resolution can be realized with a wider process window. To demonstrate this, we characterized the lateral resolution as a function of resin properties, exposure intensity, and exposure dose (see Methods). The polymerization curves in Fig. 3a, b show the dependence of the isolated lateral polymerized feature sizes on the process conditions and the designed lateral target dimensions. In Fig. 3a, we compare two resins with differing concentrations of photoinitiator and absorbing dye. Increasing only the photoinitiator results in a faster polymerization rate10,26, whereas increasing both the photoinitiator and dye results in a higher vertical resolution (reduced cured depth)10,17. We observe that when using a resin with a higher photoinitiator and dye concentration, convergence towards the target dimensions can be achieved. The lack of convergence for the resin with a lower photoinitiator and dye concentration (same resin used in Fig. 2b), even at large exposure doses, is attributed to the oxygen inhibiting nature of the inert liquid—quenching of photoinitiated radicals by the oxygen in the inert liquid results in a decrease of lateral polymer chain propagation. In Fig. 3b, we observe that by increasing the exposure intensity, faster lateral growth and convergence towards the target dimensions can be realized. The faster lateral growth occurs because of an increase in photoinitiated radical production caused by the higher exposure intensity. Furthermore, we observe that the lateral growth curves in Fig. 3a, b have two distinct regions, where the first region is characterized by rapid growth, and the second region is characterized by a slow steady growth towards the target dimension. This behavior is inherent in the polymerization kinetics, as modeled by Dendukuri et al.26, where the growth of the polymer occurs from the center outwards after the dissolved oxygen in the resin drops below a critical concentration.
a The effect of modifying resin properties by varying the concentration of photoinitiator, [PI], and absorbing dye, [Ab], on the convergence of polymerized feature size to the target dimension. b The effect of increasing the exposure intensity on speed of polymerization and convergence to the target dimension. c Accuracy and variation, given as percent deviation from target dimension, of polymerized features as a function of exposure dose while keeping exposure intensity and resin properties constant. The vertical error bars in a–c represent the standard deviation of duplicated features over the entire projection area.
For a given process window, there is an optimal exposure dose that can be determined to achieve high fidelity and minimize variations in the polymerized feature sizes. Figure 3c shows the accuracy, as percent deviation from the target lateral dimension, of polymerized features for a range of exposure doses. When using near-optimal exposure dose, we demonstrate accuracies above 95% for target dimensions ranging from 40 μm to 1000 μm within the same print process. Furthermore, we observe that features with smaller target dimensions require higher exposure doses and are more sensitive to variations compared to features with larger target dimensions—a behavior not unique to our process31,32. We reason that the smaller feature sizes are more susceptible to competition between radical propagation and radical quenching by oxygen from the ambient. In addition, the heat generated by the exothermic photopolymerization reaction also contributes to the polymerization rate33. Therefore, when target dimensions decrease, the localized heat generated also decreases, resulting in slower curing of the isolated features. Furthermore, as target dimensions reach the same order of magnitude as the pixel size on the digital micromirror device (DMD) array (~8 μm in our work), the localized intensity decreases11, which effectively decreases the polymerization rate.
Using the static liquid interface, we demonstrate a variety of 3D microdevices fabricated using discrete growth and without sacrificial supports (shown in Fig. 4). The 15:1 aspect ratio, 1 mm tall helical coils, pillars, and funnels in Fig. 4a demonstrate that delicate overhanging geometries with feature sizes below 75 μm can be fabricated. The dense array of channels (1 mm deep, 75 μm diameter holes, and 16 μm minimum solid wall width) shown in Fig. 4b illustrates the 63:1 aspect ratio and high-pitch resolution achieved through dye loading in the resin and by leveraging the oxygen inhibiting nature of fluorinated oils. Up to 5 mm deep array of channels with diameters ranging from 50 μm to 500 μm have been fabricated (not shown). The 25:1 aspect ratio, 1.5 mm long, and 60 μm wide suspended cantilever beams shown in Fig. 4c illustrate the capability to fabricate building blocks of micromechanical devices. Furthermore, we demonstrate the capability of our process to rapidly fabricate an electrothermal actuator34,35, a functional microelectromechanical system (MEMS) device realized after metallization of the 3D-printed part (Fig. 4d). Because of thermal expansion caused by Joule heating, in-plane displacement of the 3D-printed actuator as a function of electrical current through the device can be observed in Supplementary Fig. 6 and Supplementary Movie 2. Manufacturing of the devices shown in this work would be challenging in a conventional solid constrained SLA system without the use of sacrificial supports, which are needed to prevent failure from mechanical separation forces. Although the wide range of devices shown here can be fabricated using the two-photon approach32, the parallel patterning using projection SLA allows scalability of our process for larger area devices with higher throughput.
a Array of helical coils, pillars, and funnels that are 1 mm tall. Such high aspect ratio features do not break during the fabrication process because the dewetting step from the inert liquid does not lead to mechanical separation forces. Furthermore, the 13 μm per layer thickness shows the ability to achieve high vertical resolution by dye loading in the resin. b Densely packed array of channels (holes) that are 75 μm in diameter and 1 mm deep. The minimum solid wall width between each channel is ~16 μm. c A microdevice with a suspended ring tethered to an array of suspended cantilever beams, which are 1.5 mm long and 60 μm wide. d An electrothermal actuator (MEMS device) that displaces in-plane when heated with electrical current. The actuation of this device is demonstrated in Supplementary Fig. 6 and Supplementary Movie 2.
Conclusion
The static liquid constrained SLA process mitigates mechanical separation forces, thus enabling reliable manufacturing of 3D objects with unconstrainted geometric freedom—i.e., cross-sectional area, overhangs, and aspect ratio. The flexibility over the growth mode (continuous or discrete), within the same process, facilitates a wider process window. Specifically, discrete growth allows greater freedom over the process parameters such as exposure and resin properties, therefore, fabrication of devices can be tuned to the desired spatial resolution, fidelity, and green strength. By using resins functionalized with ceramics36,37,38,39, glass40, and electrically conductive fillers41 and integration of new materials, our process can enable multi-scale additive manufacturing to become a potential commercially viable complement to micromachining and soft lithography. This process can extend the development of novel devices for numerous applications including biomedical devices, MEMS sensors and actuators, microrobots, radio frequency components, electronics packaging to energy harvesting, and storage.
Methods
Materials
Photopolymerizable resin was composed of monomer, photoinitiator, and passively absorbing dye. Monomer HDDA was purchased from Sartomer. Photoinitiator, 4,4′-bis(dimethylamino)benzophenone, was purchased from Sigma-Aldrich. Absorbing dye, 2,5-bis(5-tert-butyl-benzoxazol-2-yl)thiophene, was obtained from Mayzo. The inert liquid Fluorinert FC-43, was obtained from 3 M, and Solvay Fomblin, was purchased from Sigma-Aldrich.
Resin formulation
Formulating the resins for the SLA process required varying the concentrations of photoinitiator and absorbing dye in the monomer solution. The concentration of photoinitiator up to 0.5% wt. and dye up to 0.2% wt were varied in the monomer. These additives affect the polymerization rate and depth of UV light penetration into the resin. We used the frontal photopolymerization method42,43 to characterize the resins. The characterized cured depth response to the exposure energy dose followed the “working curve” equation given by, \({\mathrm{C}}_{\mathrm{d}} = {\mathrm{D}}_{\mathrm{p}}\,{\mathrm{ln}}\left( {\frac{{E{\mathrm{o}}}}{{E{\mathrm{c}}}}} \right)\), where Eo is the incident exposure energy dose, Ec is the critical energy dose required for the onset of polymerization, and Dp is the characteristic penetration depth describing the rate of light intensity decrease10. Using this approach, we designed various resins to meet the desired process specifications such as vertical resolution (cured depth), lateral resolution (cured width), and polymerization speed.
UV projection system and focusing
Patterning of the projected UV light was achieved by using a Texas Instruments digital light processing projector. The UV illumination source was a 385 nm light-emitting diode. We define the effective projected pixel size as the product of the pixel size on the DMD array (~8 μm) and the magnification of the projection optics. This effective pixel size determines the minimum patternable resolution of the polymerized feature sizes. The projection optics used in our system had a magnification of ×1.0, except where noted, therefore, the designed feature size and projected feature size always had a 1:1 relationship.
The projected image was confirmed to be in focus at the interface between the inert liquid and the resin using two methods. The first method consisted of projecting a Siemens star pattern and visually confirming the focus. The fluorescent dye in the resin assisted in imaging the projected image at the inert liquid and resin interface. The second method consisted of fine-tuning the focus by experimentally quantifying the lateral resolution for a fixed exposure condition.
Characterization of dead zone thickness
The dead zone thickness was characterized by using a differential technique as shown in the schematic of Supplementary Fig. 1a. An array of squares (1 mm × 1 mm) were exposed in a predefined resin gap of 150 μm with varying UV intensity and a fixed amount of exposure time. After polymerization, the uncured resin was rinsed away with a solvent. The thickness of the cured array of squares was measured using an optical profilometer, where the reference plane was the base polymer onto which the cured squares were polymerized (Supplementary Fig. 1b). The dead zone thickness was determined from the difference between the predefined resin gap and the measured thickness of the cured squares.
De-oxygenation of the inert liquid
The presence of the dead zone in the resin adjacent to the interface of the inert liquid (fluorinated oil) is attributed to the diffusion of the oxygen from the bulk of the inert liquid to the resin interface. The oxygen concentration gradient near the interface is driven by the differences in reported oxygen solubilities of ~35–44 mM in perfluorochemicals28 and ~1.17 mM in HDDA monomer44. Therefore, an equal volume of air saturated inert liquid contains 30–38× higher concentration of oxygen than HDDA-based resin.
We characterized the dead zone under two different conditions of Fluorinert (inert liquid): ambient state (oxygen rich) and oxygen-depleted state. The Fluorinert in the ambient state (without any treatment) is assumed to be oxygen-rich because of its high oxygen solubility27,28. In order to deplete oxygen, Fluorinert was purged with nitrogen prior to the dead zone characterization. The resin used for any of these characterizations was not purged with nitrogen. Each data point in Fig. 2a, b was repeated three times, where the error bars represent the standard deviation. The total experimental duration under each state of Fluorinert was 4 hours. The minimal variability in the dead zone thickness for the oxygen-depleted Fluorinert indicates that the rate of re-diffusion of oxygen back into the Fluorinert from the resin that was exposed to the ambient air was minimal during the experimental timeframe.
The volume of inert liquid and resin used during the characterization of dead zone was 15 mL and 25 mL, respectively. It was assumed that the concentration of oxygen in the inert liquid was much larger than the concentration of oxygen in the resin. Therefore, the formation of the dead zone during the relatively short UV exposure periods was limited by diffusion of oxygen from the bulk of the inert liquid to the localized region of UV exposure.
Characterization of lateral resolution
The lateral resolution in the graphs shown in Fig. 3 was characterized by polymerization of isolated lines with varying widths (Supplementary Fig. 2). The array of polymerized features are considered to be “isolated” because the spacing between each feature was maximized to reduce “cross-talk”11. The polymerized lines are composed of 10 layers, where each layer was 25 μm thick, thus resulting in a total height of 250 μm. The fabricated samples were rinsed with ethyl acetate and dried using compressed nitrogen prior to measurement under the microscope. The isolated features were repeated over the entire projection area to determine the variability caused by non-uniform intensity distribution over the projection area. The error bars shown in the graphs of Fig. 3 are the standard deviation over the entire projection area.
Electrothermal actuator
The actuator shown in Fig. 4 of the main text, Supplementary Fig. 6 and Supplementary Movie 2 utilizes a V-shaped bent beam design34,35. After 3D printing the polymer structure, the surface of the polymer device was metalized with aluminum using thermal evaporation. Wires were bonded onto the contact pads (static anchors) of the device using silver conductive epoxy.
Data availability
All data that support the findings of this study are available in the main text or the supplementary information. Additional data related to this paper may be requested from the corresponding authors upon reasonable request.
References
Wu, S.-Y., Yang, C., Hsu, W. & Lin, L. 3D-printed microelectronics for integrated circuitry and passive wireless sensors. Microsyst. Nanoeng. 1, 15013 (2015).
Xu, Y. et al. The boom in 3D-printed sensor technology. Sensors 17, 1166 (2017).
Zheng, X. et al. Ultralight, ultrastiff mechanical metamaterials. Science 344, 1373–1377 (2014).
Sadeqi, A., Rezaei Nejad, H., Owyeung, R. E. & Sonkusale, S. Three dimensional printing of metamaterial embedded geometrical optics (MEGO). Microsyst. Nanoeng. 5, 16 (2019).
Thiele, S., Arzenbacher, K., Gissibl, T., Giessen, H. & Herkommer, A. M. 3D-printed eagle eye: compound microlens system for foveated imaging. Sci. Adv. 3, e1602655 (2017).
Chen, X. et al. High-speed 3D printing of millimeter-size customized aspheric imaging lenses with sub 7 nm surface roughness. Adv. Mater. 30, 1705683 (2018).
Grigoryan, B. et al. Multivascular networks and functional intravascular topologies within biocompatible hydrogels. Science 364, 458–464 (2019).
Beckwith, A. L., Borenstein, J. T. & Velásquez-García, L. F. Monolithic, 3D-Printed Microfluidic Platform for Recapitulation of Dynamic Tumor Microenvironments. J. Microelectromech. Systems 27, 1009–1022 (2018).
Vaezi, M., Seitz, H. & Yang, S. A review on 3D micro-additive manufacturing technologies. Int. J. Adv. Manuf. Technol. 67, 1721–1754 (2013).
Jacobs, P. F. & Reid, D. T. Rapid prototyping & manufacturing: fundamentals of stereolithography (Society of Manufacturing Engineers in cooperation with the Computer and Automated Systems Association of SME, 1992).
Sun, C., Fang, N., Wu, D. M. & Zhang, X. Projection micro-stereolithography using digital micro-mirror dynamic mask. Sens. Actuators A 121, 113–120 (2005).
Bhushan, B. Adhesion and stiction: mechanisms, measurement techniques, and methods for reduction. J. Vac. Sci. Technol.21, 2262 (2003).
Huang, Y.-M. & Jiang, C.-P. On-line force monitoring of platform ascending rapid prototyping system. J. Mater. Process. Technol. 159, 257–264 (2005).
Pan, Y., Zhou, C. & Chen, Y. A fast mask projection stereolithography process for fabricating digital models in minutes. J. Manuf. Sci. Eng. 134, 051011 (2012).
Pan, Y., He, H., Xu, J. & Feinerman, A. Study of separation force in constrained surface projection stereolithography. Rapid Prototyping J. 23, 353–361 (2017).
Liravi, F., Das, S. & Zhou, C. Separation force analysis and prediction based on cohesive element model for constrained-surface Stereolithography processes. Comput. Aided Des. 69, 134–142 (2015).
Tumbleston, J. R. et al. Continuous liquid interface production of 3D objects. Science 347, 1349–1352 (2015).
Janusziewicz, R., Tumbleston, J. R., Quintanilla, A. L., Mecham, S. J. & DeSimone, J. M. Layerless fabrication with continuous liquid interface production. Proc. Natl. Acad. Sci. 113, 11703–11708 (2016).
Walker, D. A., Hedrick, J. L. & Mirkin, C. A. Rapid, large-volume, thermally controlled 3D printing using a mobile liquid interface. Science 366, 360–364 (2019).
de Beer, M. P. et al. Rapid, continuous additive manufacturing by volumetric polymerization inhibition patterning. Sci. Adv. 5, eaau8723 (2019).
Li, X., Mao, H., Pan, Y. & Chen, Y. Mask video projection-based stereolithography with continuous resin flow. J. Manuf. Sci. Eng. 141, 081007 (2019).
Mack, C. Fundamental Principles of Optical Lithography. https://doi.org/10.1002/9780470723876. (John Wiley & Sons, Ltd, 2007).
Gong, H., Bickham, B. P., Woolley, A. T. & Nordin, G. P. Custom 3D printer and resin for 18 μm × 20 μm microfluidic flow channels. Lab Chip 17, 2899–2909 (2017).
Zhao, Z. et al. Origami by frontal photopolymerization. Sci. Adv. 3, e1602326 (2017).
Piradashvili, K., Alexandrino, E. M., Wurm, F. R. & Landfester, K. Reactions and polymerizations at the liquid–liquid interface. Chemical Reviews 116, 2141–2169 (2016).
Dendukuri, D. et al. Modeling of oxygen-inhibited free radical photopolymerization in a PDMS microfluidic device. Macromolecules 41, 8547–8556 (2008).
Wesseler, E. P., Iltis, R. & Clark, L. C. The solubility of oxygen in highly fluorinated liquids. J. Fluorine Chem. 9, 137–146 (1977).
Lowe, K. C., Davey, M. R. & Power, J. B. Perfluorochemicals: their applications and benefits to cell culture. Trends Biotechnol. 16, 272–277 (1998).
Gennes, P.-G. de, Brochard-Wyart, F. & Quéré, D. Capillarity and wetting phenomena: drops, bubbles, pearls, waves (Springer, 2010).
Vagharchakian, L., Restagno, F. & Léger, L. Capillary bridge formation and breakage: a test to characterize antiadhesive surfaces. J. Phys. Chem. B 113, 3769–3775 (2009).
Xiang, N., Yi, H., Chen, K., Wang, S. & Ni, Z. Investigation of the maskless lithography technique for the rapid and cost-effective prototyping of microfluidic devices in laboratories. J. Micromech. Microeng. 23, 025016 (2013).
Saha, S. K. et al. Scalable submicrometer additive manufacturing. Science 366, 105–109 (2019).
Odian, G. Principles of Polymerization (John Wiley & Sons, Inc., 2004).
Que, L., Park, J.-S. & Gianchandani, Y. B. Bent-beam electro-thermal actuators for high force applications. In Technical Digest. IEEE International MEMS 99 Conference. Twelfth IEEE International Conference on Micro Electro Mechanical Systems (Cat. No.99CH36291) 31–36, https://doi.org/10.1109/MEMSYS.1999.746747 (1999).
Sinclair, M. J. A high force low area MEMS thermal actuator. ITHERM 2000. In The Seventh Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (Cat. No.00CH37069) 1, 127–132 (2000).
Zhang, X., Jiang, X. N. & Sun, C. Micro-stereolithography of polymeric and ceramic microstructures. Sens. Actuat. A Phys. 77, 149–156 (1999).
Halloran, J. W. et al. Photopolymerization of powder suspensions for shaping ceramics. J. Eur. Ceram. Soc. 31, 2613–2619 (2011).
Liew, L.-A. et al. Fabrication of SiCN MEMS by photopolymerization of pre-ceramic polymer. Sens. Actuator A: Phys. 95, 120–134 (2002).
Eckel, Z. C. et al. Additive manufacturing of polymer-derived ceramics. Science 351, 58–62 (2016).
Kotz, F. et al. Three-dimensional printing of transparent fused silica glass. Nature 544, 337–339 (2017).
Scordo, G. et al. A novel highly electrically conductive composite resin for stereolithography. Mater. Today Commun. 19, 12–17 (2019).
Vitale, A., Hennessy, M. G., Matar, O. K. & Cabral, J. T. A unified approach for patterning via frontal photopolymerization. Advanced Materials 27, 6118–6124 (2015).
Bennett, J. & Measuring, U. V. curing parameters of commercial photopolymers used in additive manufacturing. Addit. Manuf. 18, 203–212 (2017).
Gou, L., Coretsopoulos, C. N. & Scranton, A. B. Measurement of the dissolved oxygen concentration in acrylate monomers with a novel photochemical method. J. Polym. Scie.Part A: Poly. Chem. 42, 1285–1292 (2004).
Acknowledgements
We acknowledge the use of the facilities of Research Service Centers at University of Florida and thank their staff David Hays, Bill Lewis, and Al Ogden for their insights and technical discussions. We thank the following individuals (listed in alphabetical order) who have assisted on various aspects of the project: Michael Braddock, Alexandra Garraud, Seth Goldberg, Benjamin Hair, Pracheetee Joag, Jonathan Liu, Abhinav Pandey, Dennys Pelegrin, Raphael Puzio, Brandon Rosenthal, and Liang Zhou. This work was supported by Nanoptics Inc., Florida High Tech Corridor Council, National Institutes of Health (NIH) Small Business Innovation Research (SBIR) under contract 1R43HG005288-01, and National Science Foundation I/UCRC on Multi-functional Integrated System Technology (MIST) Center IIP-1439644 and IIP-1939009.
Author information
Authors and Affiliations
Contributions
A.A.B. and T.N. conceived the idea. A.A.B. designed, conducted the research, and wrote the manuscript. T.N., R.T.F. and Y.N. provided technical guidance in various aspects of the project. T.N. directed the work. All authors contributed to ideas investigated in this work and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
A.A.B. and T.N. are inventors on a patent application, PCT/US2019/013154, related to this work filed by the University of Florida. The other authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bhanvadia, A.A., Farley, R.T., Noh, Y. et al. High-resolution stereolithography using a static liquid constrained interface. Commun Mater 2, 41 (2021). https://doi.org/10.1038/s43246-021-00145-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00145-y
This article is cited by
-
3D printing of hollow geometries using blocking liquid substitution stereolithography
Scientific Reports (2023)