Abstract
Nanomaterials undergoing cyclic swelling-deswelling benefit from inner void spaces that help accommodate significant volumetric changes. Such flexibility, however, typically comes at a price of reduced mechanical stability, which leads to component deterioration and, eventually, failure. Here, we identify an optimised building block for silicon-based lithium-ion battery (LIB) anodes, fabricate it with a ligand- and effluent-free cluster beam deposition method, and investigate its robustness by atomistic computer simulations. A columnar amorphous-silicon film was grown on a tantalum-nanoparticle scaffold due to its shadowing effect. PeakForce quantitative nanomechanical mapping revealed a critical change in mechanical behaviour when columns touched forming a vaulted structure. The resulting maximisation of measured elastic modulus (~120 GPa) is ascribed to arch action, a well-known civil engineering concept. The vaulted nanostructure displays a sealed surface resistant to deformation that results in reduced electrode-electrolyte interface and increased Coulombic efficiency. More importantly, its vertical repetition in a double-layered aqueduct-like structure improves both the capacity retention and Coulombic efficiency of the LIB.
Similar content being viewed by others
Introduction
Si-based anodes are a promising alternative to graphite for high-energy LIBs because of their up-to-tenfold increase in theoretical capacity1,2,3. However, the huge volume change during lithiation hinders the formation of stable solid electrolyte interfaces (SEIs)4 and causes electrode fracture5. Low mechanical stability of both SEIs and the entire electrodes is an impediment to the commercialisation of LIBs with silicon anodes, but composite anodes containing silicon additives are already being marketed (https://www.3m.com/3M/en_US/company-us/all-3m-products/~/3M-Battery-Anode/, http://sinodesystems.com/en/). The matrices used (usually of carbon or of polymeric nature) play a dual role: they connect electrically and physically the silicon components (typically nanoparticles of sizes below their break-up limit), and provide a steady electrode–electrolyte interface, enabling the formation of a stable SEI6. An alternative strategy is the use of stiff shells; however, the shells need to be thick in order to avert fracture and debonding from the core, hindering lithium diffusion7. Thus, increasing the amount of silicon in anodes or designing a pure Si anode while maintaining satisfactory mechanical stability remains a challenge for high-energy LIB technology.
There exists an intrinsic connection between mechanical issues and electrochemical performance of silicon anodes (and all battery electrodes in general), lying on the compressive stress built up during lithiation, which is subsequently released during delithiation8. When this compressive stress exceeds the yield strength9,10, the electrode deforms to accommodate the volume change11,12. For this reason, mechanical property studies by in situ-modulated optical solid-state spectrometry and nanoindentation have increased over the last few years, showing the variation in elastic modulus (defined as displacement divided by stress, E = σ/ε) with respect to the structure13, the state of charge14,15, or the binder16. However, although these studies provide important information on the mechanical behaviour of silicon anodes, they mostly lack spatial resolution. Quantitative information on the effect of nanostructure on the elastic properties can be obtained by atomic force microscopy (AFM) in PeakForce quantitative nanomechanical mapping (PF-QNM) mode. However, despite its sensitivity on nanostructure17, the technique has scarcely been used for the study of battery electrodes18,19, where it can provide valuable insight on surface deformability and, thus, SEI stability.
This work introduces a specific columnar thin-film nanoarchitecture synthesised using nanoparticles, denoted as vaulted structure. The name alludes to the civil engineering definition of a multi-arch structure sustained on columns, characterised by its high elastic modulus. Silicon anodes with vaulted structures simultaneously show good electrochemical performance combined with high mechanical stability and low lithium consumption during formation of SEI, addressing the two main challenges for silicon anode commercialisation. This structural unit of optimal electrochemical performance is identified by a distinct transition in mechanical behaviour exactly when individual silicon columns merge to form closed arches (but not beyond that point, with further growth of amorphous-silicon film on top); most importantly, its mechanical stability can be improved further if reiterated vertically, due to clamping effect. The introduction of vaulted structure and arch action brings many new possibilities in the design of new materials for batteries, but also for other applications in which the surface is under strong and variable stress action.
Results and discussion
Overview of design strategy and vaulted structure concept
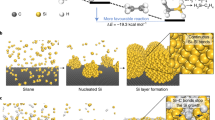
Samples were grown directly on substrates by sequential and independently controlled cluster beam deposition (CBD) of Ta nanoparticles and RF sputtering of silicon thin films (Supplementary Fig. 1). This set-up enables the fabrication of binder-free, high-purity films (grown in high-vacuum conditions) with good control over the thin-film thickness and nanoparticle size and shape20,21,22. First, crystalline Ta nanoparticles were deposited (Fig. 1a, step 1), forming a porous nanoparticulated film that acted as a nano scaffold (denoted TaNS) for the fabrication of the silicon anode. Silicon films of various thicknesses were subsequently sputtered onto TaNs at an acute angle in order to exploit the shadowing effect by TaNs; this led to silicon initially growing in a columnar structure (Fig. 1a, step 2)23. Column diameters increased with thickness until the column tops contacted one another, closing the surface via the formation of a vaulted (arched) structure (Fig. 1b). Further silicon deposition formed a continuous amorphous film via Volmer–Weber (island) growth, labelled as the sedimentary structure (Fig. 1c). Subsequent thermal annealing (Fig. 1a, step 3) enhanced defect mobility and eventual annihilation at the surfaces of each structure. In the case of columnar structures, this process increased their rigidity. Conversely, in sedimentary structures, voids remained trapped inside the silicon layers, as their migration barrier towards some free surface was significantly higher, resulting in sponge-like porous films.
a–c Schematic breakdown of growth process into three steps: deposition of TaNS, columnar growth of silicon amorphous film exploiting the shadowing effect of the TaNS and thermal annealing at 150 °C enhancing the mobility and consequent annihilation of voids at open surfaces (indicated by the red arrows). Grey spheres represent Ta nanoparticles and silicon is designated in blue. The mechanical response under the force of the nanoindenter is indicated for the three structures under study: d columnar, e vaulted, and f sedimentary. The nanoindenter for PF-QNM measurements is shown in green, exerting a compressive force on silicon samples (red arrow). White arrows indicate film stresses, irrespective of indentation; the film response under the nanoindenter is shown in yellow. Red dashed lines indicate sample deformations and small red arrows represent the force distribution in the columns.
Variations in silicon film structures affect profoundly their mechanical properties. In PF-QNM measurements performed here, a nanoindenter exerts a vertical force (Fig. 1d–f, red arrow) on the top of each structure. In the columnar structure, compressive stresses lead to each column maintaining its shape and individuality (Fig. 1d, white arrows). The columns readily deform until they touch one another and a clamping effect hinders further deformation. This leads to an increase in E with film thickness, due to increased proximity of the columns. The extreme case occurs in the vaulted structure (Fig. 1e), where the tops of the columns are already in touch with each other; as a result, clamping occurs immediately under the force of the nanoindenter without the need for initial deformation, and high E value is measured. This effect resembles arch action as described in civil engineering, where an arch transmits stress to the ground and responds by pushing outwards. In the sedimentary structure (Fig. 1f), E is related to surface domes; under force from the nanoindenter, silicon atoms at hilltops easily diffuse to valleys. E is also affected by the underlying pores that soften the silicon layer. As a result, low E values are registered.
Due to its high void space content and sealed surface, the vaulted structure can be used as a nanostructure unit capable of dissipating lithiation (or other) stress while avoiding the cracking observed in electrodes based on the sedimentary structure. When the vaulted structure is vertically reiterated (i.e., a vaulted nanostructure is deposited on top of another repeatedly, with each layer forming a single-vaulted nanostructure unit), a thin-film electrode is created, which increases the amount of silicon-active material, while maintaining optimised mechanical and surface stability during battery cycling. Further, the concept of nanovault architecture as a repeating nanostructure unit can be applied broadly for the design of novel materials requiring high stress tolerance.
Correlation between morphology and mechanical properties
Henceforth, samples are named according to the scheme hX, where h is the film thickness (in nm) and X designates the structure type: C (columnar), V (vaulted) and S (sedimentary), as determined by combined PF-QNM and electron microscopy characterisation.
The nanoporous TaNS consists of crystalline Ta nanoparticles (3 nm in diameter and narrow-size distribution)24,25, which maintain their individuality due to CBD enabling soft landing26. Transmission electron microscopy (TEM) lamella images (Fig. 2a, b) show TaNS thickness of ~10 nm and confirm the amorphous nature of the overlaid silicon layer. Silicon thin-film thickness increases linearly with time at a rate of 1.69 nm min−1 (via X-ray reflection (XRR), Supplementary Figs. 2 and 3). Although the Ta content is less than 0.5 at%, as estimated by X-ray photoelectron spectroscopy (Supplementary Fig. 4), it induces granular morphology (Fig. 2c, d) and ensues high roughness to the silicon films (in the range of 3.3–3.8 nm vs. 0.8 nm when silicon is grown directly on the substrate, Supplementary Fig. 2).
TEM lamella images of samples: a 54V and b 216S show the nanoparticulate nature of TaNS and the amorphous nature of Si. The observed Pt layer was deposited during lamella fabrication. SEM top-view images of samples: c 54V and d 216S, and the corresponding cross-section images: e 54V (inset is magnified) and f 216S. 54V corresponds to the vaulted structure, where column tops contact one another, while in 216S structure columns already merge into a continuous film with Volmer–Weber growth, as the domed morphology suggests (sedimentary structure). The substrate used for the preparation of samples for this structural characterisation is Si(111).
Sample 54V presents columns of increasing diameter, resembling inverse truncated cones that touch at the top, forming a vaulted structure as shown by cross-sectional scanning electron microscopy (SEM, Fig. 2e). This columnar structure (which begins to form at the start of the silicon growth phase, Supplementary Fig. 5 for 25C) results from the shadowing effect of TaNS, due to the disruption TaNS brings to the incident beam of silicon atoms27. The columnar structure is also observed at the bottom of 216S (Fig. 2f); however, as more silicon is deposited on the vaulted layer, the silicon stratum becomes continuous without long-range structural ordering, due to the amorphous nature of sputtered Si28. Subsequently, domes are formed on top of the continuous film, reducing the local surface energy. These domes withstand compressive stresses initially until a limit is reached, whereupon the stresses become tensile. This causes the diffusion of silicon adatoms from hilltops to valleys29. As domes coalesce, the thickness of the continuous film increases, which is typical for Volmer–Weber (island) thin-film growth30.
Topography and elastic modulus mapping of samples 25C, 54V and 155S show cusps and valleys at the nanoscale, measured by PF-QNM using an AFM operated in PF tapping mode (Fig. 3a). Silicon samples were prepared on Si(111) for these measurements, although E measurements are valid for any substrate when TaNS is deposited between the substrate and sputtered silicon (Supplementary Fig. 6). All sedimentary samples show very strong correlation (~1) between topographic and E features (Supplementary Fig. 7); thus, E cusps and valleys are related to surface morphology31,32,33. Reduced correlation is found for the vaulted structure (0.8) that decreases notably for the columnar structure (with dispersed values in the range of 0–0.6). This suggests that other factors besides surface morphology are responsible for E cusps and valleys, probably associated with the presence of honeycomb-like density-deficit regions in-between columnar structures (void networks), and the existence of incomplete arches in 54V.
The substrate used for preparation of samples is Si(111), but similar results are obtained for Cu foil substrates (Supplementary Fig. 6). a Topography and elastic moduli of samples 25C, 54V, and 155S. The same scale is used in E mappings of the three samples for easier comparison; note that E of 54V is saturated in a high fraction of the mapping. b Histograms of E for several indicated samples. E increases from the columnar to the vaulted structure (upper histogram) and decreases for the sedimentary structure (lower histogram). c E values with the highest weights in the histogram plotted against film thickness, h, of all samples. The change of E vs. h corresponds to the transition from columnar to Volmer–Weber silicon growth, which is the region where column tops touch and form a vaulted structure.
E-value distribution in mappings is shown in histograms (Fig. 3b), and, for each sample, the thickness is associated with an E-value peak (Fig. 3c). Samples with columnar structure show polynomial increase with film thickness, being similar for 15C and 25C (~40 GPa), that is probably related to TaNS. E increases with film thickness until the columns touch each other forming multiple arches, and E reaches a maximum with extremely high values reaching up to 250 GPa. Sedimentary structures have similar E values to columnar structures (~40 GPa), independent of film thickness. Control experiments where step 3 of the fabrication process was omitted confirmed the importance of thermal annealing for the strengthening of the columnar structures (but not the sedimentary structure) through the mobilisation and ensuing eradication of voids (Supplementary Fig. 8). The strong correlation with topographic mappings implies that E measurements are restricted to the domed structure of the silicon surface. This is different than in columnar and vaulted samples, in which the granular surface represents the column tops.
Explanation of structural and mechanical characteristics by atomistic simulations
A group of molecular dynamics (MD) simulations were performed that mimic the deposition process of the TaNS–Si film composite onto a rotating substrate holder. In the presence of the nano scaffold, the vicinity of the nanoparticles was shadowed from the deposited silicon atoms, as shown in Fig. 4a, left panel (also Supplementary Figs. 9, 10, and Supplementary Movie 1 and 2); hence, the columnar structure first formed on top of the nanoparticles. With prolonged deposition time, the columns merged, initially forming the vaulted and finally the sedimentary structure, in excellent agreement with the experiment. In contrast, in control simulations without nanoparticles (Fig. 4b), a sedimentary structure formed from the beginning of the deposition (Supplementary Movie 3). Thus, it is clearly demonstrated that the shadowing effect of the nano scaffold is essential for the formation of the vaulted structure.
a Silicon deposited on a NP (duplicated along the (100) direction, due to periodic boundary conditions) at 500 K follows columnar growth and forms a vaulted structure. The simulation box, sliced for clear observation, is viewed along the (110) direction. The right panel only depicts the sliced surface mesh inside the deposited layer (i.e., without the atoms), indicating the presence of voids. b Same but without the NP. A sedimentary structure forms from the start of the deposition, also leading to extensive voids throughout. c Eight instances with NPs selected from the growth simulations, sliced and viewed along the (100) direction. d Evolution of the force–depth curve; a compress–hold–decompress loop was performed with a flat-diamond carbon tip at 500 K. e Initial linear elastic deformation within displacements of 2 nm, with linear regression fitting (solid lines). f Stiffness of the corresponding structures as a function of thickness, clearly demonstrating the rigidity of the vaulted structure.
Surface construction analysis accentuates the location and size of voids inside the deposited structures, as indicated by the grey surface meshes in Fig. 4a, b, right panels. Within the same simulation, large voids form only inside the sedimentary region, and the estimated porosity increases from 0.09 to 0.3. This can be explained by the finite-size effect of the columnar structure. Small vacancy clusters near open surfaces can be filled up quickly by a few displacements of surface atoms or by newly deposited atoms. In contrast, larger voids forming under the surface of the sedimentary structure need a collective movement of silicon atoms, which is significantly slower. Moreover, the activation enthalpy (migration barrier) for the self-diffusion in amorphous silicon is about 2.7 eV34,35,36; therefore, once large voids are formed in the sedimentary region, they remain stable under the annealing condition, which has a profound effect on the elastic properties (Supplementary Fig. 11).
Mechanical characteristics derived from PF-QNM measurements were explained by simulated compress–hold–decompress loops. As shown in Fig. 4c, we selected eight instances with nanoscaffolds from the first group of simulations. The evolution of the feedback forces can be tracked with time and the displacement of the plates on top of the silicon layers; the full process is included in Supplementary Movie 4. The feedback forces clearly distinguish the different displacement stages, as indicated by the dashed lines in Fig. 4d. From the force vs. displacement curves, we extracted the stiffness of the structures during the loading phase, indicated by the solid lines in Fig. 4e. Clearly, the stiffness reached a maximum when the columnar structure evolved into the vaulted structure, as shown in Fig. 4f. This can be explained by the fact that in the initial elastic deformation zone (displacement from 1 to 2 nm), the vaulted structures (i.e., 20.8–26.3-nm cases) reach the maximum contact area–minimum porosity combined with a relatively small thickness. The stiffness extracted from the decompression phase (where the contact area is approximately the same for all structures) follows spring-like behaviour with a porosity of 0.3 (Supplementary Fig. 12).
Vaulted structure as a building block in electrodes for LIBs
The commonly reported fracture of silicon anodes is associated with the extensive volumetric expansion (300–400%) accumulating mechanical stress in the electrode. This effect limits the thickness and size of silicon thin films and nanoparticles, respectively, utilised as anodes in LIBs. Sputtered silicon thin films on rough substrates may increase the stability of the electrode during cycling, but film thickness remains limited37,38.
The vaulted nanostructure is a promising structure unit for assembling silicon anodes for LIBs due to the combination of its internal columnar structure and sealed surface in contact with the electrolyte. Charge cycles of samples 15C, 54V and 155S at 0.5 C in semibatteries with Li foil as reference and counter electrodes (Fig. 5a) represent each sample type (Supplementary Fig. 13) and indicate the decisive role of the nanostructure. 54V shows the highest capacities during the first 60 cycles, followed by 15C. Both samples show an initial increase in the capacity associated with the activation phenomenon (Supplementary Fig. 14)39,40. Despite the 250% expansion of 54V (Supplementary Fig. 15), the capacity retention is similar to that of the columnar structure, but with higher Coulombic efficiency. In contrast, 155S shows fast capacity fade, especially during the first fifteen cycles, attributed to the loss of active material due to detachment from the substrate, as attested by SEM (Supplementary Fig. 14). This effect can also explain the high Coulombic efficiency of 96–100% for 155S (Fig. 5b), compared with 85–96% registered for sample 54V, and 60–85% for 15C. For samples 54V and 15C, the Coulombic efficiency reflects an irreversible consumption of lithium in side reactions during charge (usually the formation of SEI), and low values during cycling indicate the exposure of fresh electrode to the electrolyte due to fracturing. Thus, the vaulted structure of 54V forms a seal between the electrode and the electrolyte, reducing lithium consumption in side reactions. Attending the capacity vs. cycle number, it is observed that the capacity plot of the vaulted structure crosses the plot obtained for the columnar structure. A first interpretation could be that the “impenetrable” surface of the vaulted structure is “unsealed” during cycling, thus resembling the columnar structure. Nevertheless, electrochemical impedance spectroscopy (EIS, Supplementary Fig. 16) at different numbers of cycling clearly shows different behaviour. The resistance associated with electrode/electrolyte interface phenomena (charge transfer resistance, Rct)41,42 is approximately three times higher for 15C than for 54V after 3, 10, 50 and 75 cycles, indicating that the SEI layers formed at the columnar and vaulted structures are different, and remain so during cycling. Therefore, the capacity fade of the vaulted structure does not seem to be related with the surface, but with the bottom of the electrode; this can explain the tendency of the vaulted structure to resemble the columnar, rather than the sedimentary, structure more closely. Indeed, the sealed surface of 54 V protects the surface while allowing the same fast charge/discharge as in the columnar structure (charge–discharge and Coulombic efficiency plots at 5 C are shown in Supplementary Fig. 17). This is in agreement with a recent chemomechanical model demonstrating that anode materials of high E values can sustain higher lithiation stresses before buckling43.
Panels a, b refer to representative columnar vs. vaulted vs. sedimentary structures, and c, d refer to single- vs. double vaulted structure containing equal amounts of Si. Anodes are assembled in semibatteries using Li foil for reference and counter electrodes, and 1.0 M LiPF6 in a 50:50 (w/w) mixture of EC:DEC (ethylene carbonate:diethyl carbonate) as the electrolyte. a, c Charge capacity (Si electrode delithiation), and b, d Coulombic efficiency of semibatteries cycled at 0.5 C between 0.01 and 1 V.
In the literature, it is discussed how the nanostructure of silicon can improve its mechanical stability, e.g., by proposing columnar structures and a particle size below which silicon nanoparticulate anodes can be lithiated/delithiated without breaking6,44,45,46, or a thickness limit below which silicon thin-film anodes can be stable, which may be increased by patterning the substrate. In either case, however, the nanostructure increases the electrode/electrolyte interface, increasing the Rct and an unstable SEI that is regenerated. This problem can be addressed using shells47,48,49,50,51 to seal nanostructured silicon while maintaining the integrity of the electrode and allowing the formation of a stable SEI; however, this leads to a reduction in LIB energy density, provides a further step in the synthesis of the material and maybe detachment between the shell and the core. Another strategy to enhance the mechanical stability of Si-based anodes is either by increasing the anode’s elastic modulus with new binders for silicon composites16 or by physically constraining volume expansion52.
Since the vaulted structure is generated by the TaNS, it can be assembled independently of the substrate. Therefore, it is possible to maximise its thickness limit for a single-layer thin film, and then reproduce this nanostructure vertically, thus increasing the total amount of silicon in the anode. This is demonstrated when a second TaNS is deposited on top of an existing silicon vaulted structure, followed by further silicon deposition. The second TaNS layer prevents columns from merging towards a sedimentary structure, generating a second vaulted structure instead (Supplementary Fig. 18), denoted D54V in reference to the double 54V layer. The D54V sample also demonstrates a heterogeneous E profile, with values in the same range observed for the single layer (Supplementary Fig. 19).
To rule out film thickness effects, the electrochemical performance of sample D54V was compared with a sedimentary sample, 110S (i.e., with a single TaNS layer) that contains the same amount of silicon (Fig. 5c, d). The initial capacity of D54V is 3230 mAh g−1, and after ~5% increase for the activation phenomenon in the first cycle, it shows capacity retention of 88% after 100 cycles (2832 mAh g−1). In contrast, a strong activation phenomenon is observed for the 110S sample, reaching a maximum capacity of 2700 mAh g−1 after 20 cycles and decreasing 45% after 100 cycles (1477 mAh g−1). D54V also shows improved electrochemical performance compared to single-layer 54V, with similar capacity during the first 50 cycles but higher capacity retention and Coulombic efficiency, with values ranging between 90 and 98% (Supplementary Fig. 20). The construction of the bilayer strongly enhances the mechanical stability of the electrode, which retains this structure after charge–discharge cycling (Supplementary Fig. 21). The interlayer of Ta nanoparticles is probably increasing the electrical conductivity of the electrode, facilitating the preferential lithiation at the intermixed Ta–Si interface providing stability to lithiation/delithiation reactions, as reported for multilayered silicon electrodes53.
The electrochemical response of the studied electrodes is strongly coupled with their mechanical and structural properties. The single-layer vaulted structure provides fast paths for Li-ion diffusion along the anode54, and space for silicon to expand in, thus mitigating the stress caused by the lithiation process and preventing film cracking that impairs sedimentary structures. It can also seal the electrode significantly reducing side reactions and the formation of SEI that columnar structures suffer from. After 20 cycles, there is a capacity fade and the Coulombic efficiency maximum is 95%. This may be attributed to free space for expansion in the perpendicular direction that can cause mechanical failure in the long term, despite the clamping effect in the lateral directions of the film. However, repeating the vaulted structure imposes a new clamping effect in the perpendicular direction, improving both capacity retention and Coulombic efficiency, thus improving overall mechanical stability.
Conclusions
A nanoarchitecture facilitated by NPs is introduced for silicon-based LIB anodes. Its fabrication involves depositing a-silicon on top of a NP scaffold, leading to a columnar structure due to shadowing by the scaffold. During columnar growth, a pronounced peak in the elastic modulus exactly when columns (of increasing diameter) contact each other marks the sealing of the anode surface and indicates the creation of a vault-like structure (further silicon deposition leads to a featureless layer of sedimentary nature, and the elastic modulus value decreases to one- third of that of the vaulted structure). This mechanical behaviour was reproduced theoretically and suggests the effect of arch action at the nanoscale.
The vaulted nanoarchitecture presents possibilities for new designs in silicon anodes for LIBs, showing enhanced performance in terms of capacity retention, charge–discharge rate and Coulombic efficiency. More importantly, the fabrication strategy allows the vertical repetition of this nanostructural unit, demonstrated with the construction of a double-layer aqueduct-like structure that retains the structural and mechanical features of the single layer, but improves capacity retention and Coulombic efficiency while doubling the amount of silicon in the anode. In summary, the vaulted structure is a platform that can be piled up increasing the total amount of silicon, thus forming the basis of silicon anodes with sealed surfaces for stable SEIs and inner cavities that partly accommodate volume changes and mitigate stresses. Beyond silicon anodes for LIBs, it is also eligible for other materials and applications where surface mechanics play a critical role.
Methods
Sample preparation
All samples were prepared using a gas-phase deposition system (Mantis Deposition Ltd) at high vacuum (2.0 × 10−8 mbar), supported by a rotatory holder (2 rpm for all depositions) to yield homogeneous film deposition. For Ta nanoparticle deposition, Ar gas flow of 60 standard cubic centimetres per minute, DC magnetron power of 45 W and aggregation zone length of 100 mm were selected. The silicon thin film was deposited with a 110-W RF-sputtering source, using an Ar pressure of 2.1 × 10−3 mbar. The magnetron sputtering targets, silicon (n-type, purity > 99.999%, resistivity < 0.001 W m) and tantalum (>99.95% purity), was purchased from Kurt J. Lesker. All depositions were performed at ambient temperature (~298 K, as measured by the substrate holder thermocouple), and with no external bias applied to the substrate. Finally, all anodes were annealed at 150 °C for 60 min at Ar pressure of 8 × 10−3 mbar.
FIB-SEM and TEM lamellae characterisation
Cross-sections and sample surfaces were imaged by means of focused ion beam (FIB) milling combined with SEM using an FEI Helios G3 UC FIB-SEM. The same FIB-SEM system, equipped with a Pt deposition needle and an OMNIPROBETM extraction needle, was used to prepare TEM lamellae. They were prepared using the conventional “H-bar” technique by cutting two trenches from the sample where a strip of Pt thin film was deposited in situ to protect the surface area of interest while milling. The thin slab milled from the sample was then thinned to about 40 nm so that the TEM beam could pass through. Using the extraction needle, lamellae were then transported to the tops of TEM half-grids where they welded with the Pt deposition needle. TEM lamellae were imaged using FEI Titan Environmental TEM equipped with a spherical aberration image corrector at an operating voltage of 300 kV.
PF-QNM measurements
Surface morphology and elastic moduli of silicon samples were measured using an AFM (Multimode 8, Bruker) operating in PeakForce tapping mode. Sample imaging and PF-QNM™ measurements were performed with an ultra-high-force cantilever (DNISP-HS) with a diamond tip from Bruker (~71.5-kHz resonant frequency, 432 N/m spring constant and ~40 nm of nominal tip radius). The standard relative method was used for E measurements with fused silica (nominal E: ~72 GPa) as a reference sample. By this method, the cantilever deflection sensitivity calibration was first performed on a hard-sapphire sample by fitting the linear portion of the force–distance curve in ramp mode. The spring constant value during measurements was taken as 432 N/m from the calibration sheet provided by the manufacturer. The reference sample (fused silica) was then loaded for PF-QNM measurement followed by peak force set point adjustment in order to get the desired deformation (1–2 nm). Subsequently, the tip radius parameter was changed so that the measured elastic modulus of the reference sample met its exact value (72 GPa). After calibration with the reference sample for the tip radius, PF-QNM measurement was performed on Ta–Si samples and the peak force set point was adjusted so that its deformation matched with the reference sample. AFM images (512 × 512 pixels) were captured at scan rate of 0.5 Hz and analysed with Nanoscope Analysis (Ver. 9) software. While no reduction process was applied to the modulus-mapping images or data, it was a quantitative property measurement by the standard relative method. Tip cleaning was performed with indentations on a gold surface followed by separate tip calibration for each sample.
For PF-QNM, a z-piezo sensor tapped on the surface of the sample and measured the force–distance curve at every imaging pixel. From the force–distance curve, E was determined by fitting the DMT model to the section of the force–distance curve where the sample and the tip were in contact, using the following equation55:
where Ftip, R, d, Fadh and k are the applied force, tip radius, deformation, adhesion force and the cantilever spring constant, respectively.
The reduced modulus (Er) is related to Young’s modulus (E) of the sample as55
where Ei and vi are Young’s modulus and Poisson’s ratio of the AFM tip and v is the Poisson’s ratio of the sample. The contribution of the second term in Eq. 2 is negligible, since Ei ≫ E.
Electrochemical characterisation
For electrochemical characterisation, samples were prepared on Cu foil (0.25-mm thick, Puratronic 99.9985%, AlfaAesar). The electrochemical characterisation was carried out using a two-electrode Swagelok cell with metallic lithium foil as a reference and counter electrode. Ethylene carbonate (EC > 99%), diethyl carbonate (DEC > 99%) and lithium hexafluorophosphate (LiPF6 > 99.99%) for the electrolyte were purchased from Sigma-Aldrich, as well as the lithium foil (thickness 0.38 mm, 99.9%) and Celgard (25-mm thickness) from MTI Corporation were used as a separator. The electrolyte solution was 1.0 M LiPF6 in 50:50 (w/w) mixture of EC:DEC. All batteries were assembled inside an Ar glovebox (UNICO) with O2 and humidity below 0.25 ppm. Charge–discharge measurements were performed using two 8-channel battery analysers (0.005–1 mA and 0.02–10 mA up to 5 V, MTI Corp.) in the voltage window of 0.01–1 V. For the calculation of charge–discharge rate, 1 C was defined as 3579 mAh g−1. After three cycles at 0.5 C, the semi battery was opened inside the Ar glovebox and the anode rinsed three times with dimethyl carbonate (DMC > 99%) and dried under high vacuum (1.0 × 10−6 mbar) for at least 12 h. The samples were taken outside and scratched with a diamond pen before introduction into the FIB-SEM.
Computational methods
We performed two groups of MD simulations (i) to elucidate the formation mechanism of the vaulted structure, and (ii) to explain the variation in mechanical properties of the structures at different growth stages.
In the first group, we simulated the deposition of the silicon layer with and without the nanoparticle scaffold. Initially, an amorphous-silicon substrate was prepared by a fast heating (3000 K for 100 ps)–quenching (500 K for 100 ps) process in the isothermal–isobaric ensemble at 0 bar. The size of the thermalised simulation cells was 109 × 109 × 55 Å initially. Next, we opened the top surface and fixed an atomic layer within 6 Å at the bottom, and performed additional relaxation for 50 ps in the canonical ensemble. For the structure with the nanoparticle scaffold, the nanoparticle was deposited on the amorphous-silicon substrate naturally. We placed a diamond-lattice silicon nanoparticle 5 nm in diameter at 15 Å above the surface at the (0, 0) position laterally. The silicon nanoparticle was thermalised at 500 K for 50 ps and was next given an additional velocity of 20 m/s so it would land on the substrate, where it was allowed to relax for another 50 ps. Film growth was simulated by adding a new silicon atom from the top of the cell every 200 MD steps; 215,563 silicon atoms were added in total (at an average deposition rate of 1.1 nm/ns). In order to mimic the rotating substrate of the experimental setup, the initial velocities of the deposited atoms were set to rotate at a rate of 1 round/ns, performed in 20-ps steps. The angle of incidence was 30° from the surface and the total velocity was 1000 m/s. No scaling of velocity was applied to the non-deposited atoms. The temperature of the deposited atoms (except those fixed at the bottom) was controlled by applying a Langevin thermostat56 to the group of deposited atoms located 1 nm below the open surface. This group was updated every 2.8 ns, so the atoms deposited during that period were scaled after the update. The simulation was carried out for about 40 ns with a time step of 1 fs. We also performed benchmarking simulations with different nanoparticle and cell sizes and temperatures, or with two nanoparticles explicitly following the same procedures as described above.
The second group of simulations involved mechanical measurements with a simulated AFM tip; deposited structures of different thicknesses (after 5, 10, …, 40 ns of deposition time) were picked out and relaxed at 500 K for 200 ps. Later, we placed a flat-diamond carbon plate 5 Å in thickness at 5 Å above the surface. Each AFM measurement was simulated until the loading depth reached about 3.5 nm (0.01 nm/ps for 400 ps), followed by a holding step at a fixed position of the tip for 600 ps. Finally, the tip was retracted at a speed of 0.002 nm/ps for 400 ps. The evolution of the feedback force was recorded.
All simulations were conducted using the classical MD code LAMMPS57, and the visualisation of the results was done with OVITO58. We used an environment-dependent interatomic potential (EDIP) parametrised for silicon59. The EDIP significantly outperforms other existing potentials for silicon, including the popular Stillinger–Weber and Tersoff potentials60,61, when tested for bulk phases, defects and phase transitions. EDIP has been used to study the liquid-amorphous transition, self-diffusion, crystal plasticity, brittle fracture, solid-phase epitaxial growth and amorphous structures. The C–Si interactions in the purely repulsive Ziegler–Biersack–Littmark potential were used to obtain non-adhesive feedback–force curve62.
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
Change history
10 February 2021
The original version of this Article was updated shortly after publication, because the Description of Additional Supplementary Files and Supplementary Information were inadvertently swapped. The error has now been correct in the HTML version of the Article.
References
Sun, Y., Liu, N. & Cui, Y. Promises and challenges of nanomaterials for lithium-based rechargeable batteries. Nat. Energy 1, 16071 (2016).
Quintero Cortes, F. J., Boebinger, M. G., Xu, M., Ulvestad, A. & McDowell, M. T. Operando synchrotron measurement of strain evolution in individual alloying anode particles within lithium batteries. ACS Energy Lett. 3, 349 (2018).
Li, H. et al. Circumventing huge volume strain in alloy anodes of lithium batteries. Nat. Commun. 11, 1584 (2020).
Li, Y. et al. Growth of conformal graphene cages on micrometre-sized silicon particles as stable battery anodes. Nat. Energy 1, 15029 (2016).
Su, X. et al. Silicon‐based nanomaterials for lithium‐ion batteries: a review. Adv. Energy Mater. 4, 1300882 (2014).
Jin, Y., Zhu, B., Lu, Z., Liu, N. & Zhu, J. Challenges and recent progress in the development of Si anodes for lithium‐ion battery. Adv. Energy Mater. 7, 1700715 (2017).
Zhao, K., Pharr, M., Hartle, L., Vlassak, J. J. & Suo, Z. Fracture and debonding in lithium-ion batteries with electrodes of hollow core–shell nanostructures. J. Power Sources 218, 6 (2012).
Tavassol, H., Jones, E. M. C., Sottos, N. R. & Gewirth, A. A. Electrochemical stiffness in lithium-ion batteries. Nat. Mater. 15, 1182 (2016).
Sethuraman, V. A., Chon, M. J., Shimshak, M., Srinivasan, V. & Guduru, P. R. In situ measurements of stress evolution in silicon thin films during electrochemical lithiation and delithiation. J. Power Sources 195, 5062 (2010).
Lee, S. W. et al. Kinetics and fracture resistance of lithiated silicon nanostructure pairs controlled by their mechanical interaction. Nat. Commun. 6, 7533 (2015).
Zhao, K. et al. Lithium-assisted plastic deformation of silicon electrodes in lithium-ion batteries: a first-principles theoretical study. Nano Lett. 11, 2962 (2011).
Bucci, G., Nadimpalli, S. P. V., Sethuraman, V. A., Bower, A. F. & Guduru, P. R. Measurement and modeling of the mechanical and electrochemical response of amorphous Si thin film electrodes during cyclic lithiation. J. Mech. Phys. Solids 62, 276 (2014).
Yin, S. et al. Silicon lithium-ion battery anode with enhanced performance: multiple effects of silver nanoparticles. J. Mater. Sci. Technol. 34, 1902 (2018).
Wang, Y. et al. Mechanical property evolution of silicon composite electrodes studied by environmental nanoindentation. Adv. Energy Mater. 8, 1702578 (2018).
Li, D. et al. In situ measurement of mechanical property and stress evolution in a composite silicon electrode. J. Power Sources 366, 80 (2017).
Hernandez, C. R. et al. A facile and very effective method to enhance the mechanical strength and the cyclability of Si‐based electrodes for Li‐ion batteries. Adv. Energy Mater. 8, 1701787 (2018).
Zhai, C., Hanaor, D., Proust, G., Brassat, L. & Gan, Y. Interfacial electro-mechanical behaviour at rough surfaces. Extreme Mechanics Lett. 9, 422 (2016).
Lang, S.-Y. et al. Insight into the interfacial process and mechanism in lithium–sulfur batteries: an in situ AFM study. Angew. Chem. 55, 15835 (2016).
Yuan, Y. et al. Rational tuning of a Li4SiO4-based hybrid interface with unique stepwise prelithiation for dendrite-proof and high-rate lithium anodes. ACS Appl. Mater. Interf. 12, 39362 (2020).
Grammatikopoulos, P., Steinhauer, S., Vernieres, J., Singh, V. & Sowwan, M. Nanoparticle design by gas-phase synthesis. Adv. Phys. X 1, 81 (2016).
Zhao, J. et al. Formation mechanism of Fe nanocubes by magnetron sputtering inert gas condensation. ACS Nano 10, 4684 (2016).
Grammatikopoulos, P. Atomistic modeling of the nucleation and growth of pure and hybrid nanoparticles by cluster beam deposition. Curr. Opin. Chem. Eng. 23, 164 (2019).
A. Lakhtakia, R. Messier. Sculptured Thin Films: Nanoengineered Morphology and Optics. (SPIE Press, Bellingham, 2005).
Singh, V. et al. Assembly of tantalum porous films with graded oxidation profile from size-selected nanoparticles. J. Nanopart. Res. 16, 2373 (2014).
Haro, M. et al. Nanoscale heterogeneity of multilayered Si anodes with embedded nanoparticle scaffolds for Li-ion batteries. Adv. Sci. 4, 1700180 (2017).
Paillard, V. et al. Diamondlike carbon films obtained by low energy cluster beam deposition: evidence of a memory effect of the properties of free carbon clusters. Phys. Rev. Lett. 71, 4170 (1993).
Ye, D.-X., Karabacak, T., Picu, R. C., Wang, G.-C. & Lu, T.-M. Uniform Si nanostructures grown by oblique angle deposition with substrate swing rotation. Nanotechnology 16, 1717 (2005).
Mayr, S. G. & Samwer, K. Model for intrinsic stress formation in amorphous thin films. Phys. Rev. Lett. 87, 036105 (2001).
Floro, J. A., Kotula, P. G., Seel, S. C. & Srolovitz, D. J. Origins of growth stresses in amorphous semiconductor thin films. Phys. Rev. Lett. 91, 096101 (2003).
Sheldon, B. W. et al. Competition between tensile and compressive stress mechanisms during Volmer-Weber growth of aluminum nitride films. J. Appl. Phys. 98, 043509 (2005).
Buzio, R., Boragno, C., Biscarini, F., Buatier de Mongeot, F. & Valbusa, U. The contact mechanics of fractal surfaces. Nat. Mater. 2, 233 (2003).
Pastewka, L. et al. Finite-size scaling in the interfacial stiffness of rough elastic contacts. Phys. Rev. E 87, 062809 (2013).
Zhai, C., Gan, Y., Hanaor, D., Proust, G. & Retraint, D. The role of surface structure in normal contact stiffness. Exp. Mech. 56, 359 (2016).
Kirschbaum, J. et al. Self-diffusion in amorphous silicon by local bond rearrangements. Phys. Rev. Lett. 120, 225902 (2018).
Kallel, H., Mousseau, Schiettekatte, F. Phys. Rev. Lett. 105, 045503 (2010).
Song, Y., Malek, R. & Mousseau, N. Optimal activation and diffusion paths of perfect events in amorphous silicon. Phys. Rev. B 62, 15680 (2000).
Sethuraman, V. A., Kowolik, K. & Srinivasan, V. Increased cycling efficiency and rate capability of copper-coated silicon anodes in lithium-ion batteries. J. Power Sources 196, 393 (2011).
Takamura, T., Ohara, S., Uehara, M., Suzuki, J. & Sekine, K. A vacuum deposited Si film having a Li extraction capacity over 2000 mAh/g with a long cycle life. J. Power Sources 129, 96 (2004).
He, K. et al. Transitions from near-surface to interior redox upon lithiation in conversion electrode materials. Nano Lett. 15, 1437 (2015).
Liu, C., Zhang, C., Fu, H., Nan, X. & Cao, G. Exploiting high‐performance anode through tuning the character of chemical bonds for Li‐ion batteries and capacitors. Adv. Energy Mater. 7, 1601127 (2017).
Vicente, N., Haro, M. & Garcia-Belmonte, G. New approaches to the lithiation kinetics in reaction-limited battery electrodes through electrochemical impedance spectroscopy. Chem. Commun. 54, 1025 (2018).
Park, K.-J. et al. A high-capacity Li[Ni0.8Co0.06Mn0.14]O2 positive electrode with a dual concentration gradient for next-generation lithium-ion batteries. J. Mater. Chem. A 3, 22183 (2015).
Boebinger, M. G. et al. Spontaneous and reversible hollowing of alloy anode nanocrystals for stable battery cycling. Nat. Nanotechnol. 15, 475 (2020).
Chi, S.-S. et al. Solid polymer electrolyte soft interface layer with 3D lithium anode for all-solid-state lithium batteries. Energy Storage Mater. 17, 309 (2019).
Lee, S. W., McDowell, M. T., Berla, L. A., Nix, W. D. & Cui, Y. Fracture of crystalline silicon nanopillars during electrochemical lithium insertion. Proc. Natl Acad. Sci. USA 109, 4080–1704085 (2012).
Goldman, J. L., Long, B. R., Gewirth, A. A. & Nuzzo, R. G. Strain anisotropies and self-limiting capacities in single-crystalline 3D silicon microstructures: models for high energy density lithium-ion battery anodes. Adv. Funct. Mater. 21, 2412–2422 (2011).
Wang, J. et al. Shell-protective secondary silicon nanostructures as pressure-resistant high-volumetric-capacity anodes for lithium-ion batteries. Nano Lett. 18, 7060–7065 (2018).
Xu, Q. et al. Watermelon‐inspired Si/C microspheres with hierarchical buffer structures for densely compacted lithium‐ion battery anodes. Adv. Energy Mater. 7, 160148 (2017).
Ko, M. et al. Scalable synthesis of silicon-nanolayer-embedded graphite for high-energy lithium-ion batteries. Nat. Energy 1, 16113 (2016).
Agyeman, D. A., Song, K., Lee, G.-H., Park, M. & Kang, Y.-M. Carbon-coated Si nanoparticles anchored between reduced graphene oxides as an extremely reversible anode material for high energy-density Li-ion battery. Adv. Energy Mater. 6, 1600904 (2016).
Haro, M. et al. Germanium coating boosts lithium uptake in Si nanotube battery anodes. Phys. Chem. Chem. Phys. 16, 17930 (2014).
Li, X. et al. Mesoporous silicon sponge as an anti-pulverization structure for high-performance lithium-ion battery anodes. Nat. Commun. 5, 4105 (2014).
Fister, T. T. et al. Lithium intercalation behavior in multilayer silicon electrodes. Adv. Energy Mater. 4, 1301494 (2014).
Wang, J. W. et al. Two-phase electrochemical lithiation in amorphous silicon. Nano Lett. 13, 709 (2013).
Morales-Rivas, L. et al. Nanomechanical characterization of nanostructured bainitic steel: peak force microscopy and nanoindentation with AFM. Sci. Rep. 5, 17164 (2015).
Schneider, T. & Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 17, 1302 (1978).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO—the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2009).
Justo, J. F., Bazant, M. Z., Kaxiras, E., Bulatov, V. V. & Yip, S. Interatomic potential for silicon defects and disordered phases. Phys. Rev. B 58, 2539 (1998).
Stillinger, F. H. & Weber, T. A. Computer simulation of local order in condensed phases of silicon. Phys. Rev. B 31, 5262 (1985).
Tersoff, J. New empirical approach for the structure and energy of covalent systems. Phys. Rev. B 37, 6991 (1988).
Zeigler, J. F., Biersack, J. P., Littmark, U. The Stopping and Range of Ions in Solids (1st ed.) (Pergamon Press, New York, 1985).
Acknowledgements
This work was supported by funding from the Okinawa Institute of Science and Technology Graduate University (OIST). The Finnish IT Center for Science (CSC) and the Center for Computational Science and Engineering at SUSTech provided computational resources. MH acknowledges financial support from the MICINN (Spain) through the Ramon y Cajal Fellowship (Grant no. RYC-2018-025222-I) and PID2019-108247RA-I00. The authors acknowledge Nan Jian for TEM measurements, Steven D Aird for editing advice during paper preparation, Pavel Puchenkov for the 3D schematic of the experimental setup and Noriko Ishizu from OIST Mech. Eng. & Microfabrication Support Section for XPS measurements and analysis support.
Author information
Authors and Affiliations
Contributions
M.H. and P.G. conceived the idea and identified the anode’s critical behaviour. M.H. performed the electrochemistry experiments, provided the main literature review, and was responsible for the experimental side of the project. P.Ku. conducted and analysed the PF-QNM measurements. J.Z. ran MD simulations and explained the structure formation and its correlation to the mechanical properties. P.K. identified the vaulted structure through SEM lamellae imaging. A.J.P. performed the depositions. Z.Z. provided additional SEM measurements. T.B. performed AFM studies and identified the critical threshold in mechanical strength. V.S. provided the deposition methodology and guided T.B. E.J.J.-P. performed the XRR measurements and analysis. E.T. performed statistical analysis of PF-QNM results. K.N. and F.D. guided the MD simulations. M.S. provided the original idea for a layered composite anode. P.G. supervised T.B. and P.K., and coordinated the simulation-experiment synergy. M.H. and P.G. are the main authors of the paper; P.Ku., J.Z. and A.J.P. also contributed. All authors contributed to editing the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: John Plummer
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haro, M., Kumar, P., Zhao, J. et al. Nano-vault architecture mitigates stress in silicon-based anodes for lithium-ion batteries. Commun Mater 2, 16 (2021). https://doi.org/10.1038/s43246-021-00119-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-021-00119-0