Abstract
Superconducting proximity devices using low-dimensional semiconducting elements enable a ballistic regime in the proximity transport. The use of topological insulators in such devices is considered promising owing to the peculiar transport properties these materials offer, as well the hope of inducing topological superconductivity and Majorana phenomena via proximity effects. Here we demonstrate the fabrication and superconducting properties of proximity Josephson devices integrating nanocrystals single of Bi2Te2.3Se0.7 with a thickness of a few unit cells. Single junctions display typical characteristics of planar Josephson devices; junctions integrating two nanocrystals behave as nanodimensional superconducting quantum interference devices. A peculiar temperature and magnetic field evolution of the Josephson current along with the observed excess current effect point towards the ballistic proximity regime of topological channels. This suggests the proposed devices are promising for testing topological superconducting phenomena in two-dimensions.
Similar content being viewed by others
Introduction
The surface electronic modes of three-dimensional (3D) topological insulators are protected by a spin–momentum locking. The resulting unique electronic properties are revealed in hybrid systems, where topological insulators are brought into contact with conventional superconductors1,2,3,4,5. It is expected that the superconducting correlations induced into topological insulators by proximity may have, in addition to the trivial s-wave order, a chiral px + py component6. This combination may lead to a topological superconducting order with a degenerate ground state characterized by exotic edge modes—Majorana fermions1,2,7,8,9,10,11. The latter are believed to become a basis for topological quantum computation, with the quantum bits encoded by Majorana bound states in a nonlocal way2,3,12,13,14,15,16,17. Moreover, the implementation of ballistic topological insulator-based hybrids could advance the realization of new kinds of qubits18,19,20. Topological insulator-based hybrids are also promising for studying new spin transport phenomena21,22,23, for realizing a new generation of gate-tunable Josephson devices24. In this context, the 3D topological insulators coupled to conventional s-wave superconductors are currently studied extremely actively24,25,26,27,28,29,30,31,32,33,34,35,36.
Usually, the topological insulator parts of these superconducting hybrids are realized by exfoliation of a flake from a bulk topological insulator crystal24,32,33,34,35,36. The main disadvantage of the exfoliation method is the uncontrolled shape, thickness, lateral size, and orientation of the resulted flakes. Moreover, numerous atomic defects and surface quintuple steps already existing in the pristine crystal or created during the exfoliation process6,24,37 modify the electron transport properties of the devices38.
The physical vapor deposition (PVD) technique does not suffer from the disadvantages of the exfoliation method and, at the same time, it is much simpler and cheaper than the fully controlled growth by molecular-beam epitaxy6. The PVD method enables a reproducible synthesis of single crystals of various layered quasi-two-dimensional materials including topological insulators (i.e., Bi2Se3, Bi2Te3)39,40,41,42,43,44. The resulted single crystals have a well-defined crystallographic orientation; their composition, thickness, size, and the surface density on the desired substrate can be controlled.
The thickness control is particularly important for 3D TIs in which the trivial (bulky) electronic channels usually dominate the transport properties and mask the response of the topological (surface) modes. By reducing the thickness, one lowers the contribution of trivial bulk channels into the total conduction, thus forcing the topological modes to carry the electric current. Recently, Bi2Se2Te and Bi2Te2Se were predicted to be topological insulators45; the latter system having one of the highest bulk resistivity46,47,48,49,50, due to a low carrier density in the trivial channel51. For nonstoichiometric alloy Bi2Te3−xSex, key factors that determine the nontrivial topological properties, such as the crystal structure, spin-orbit coupling strength and bulk bandgap are close to those of Bi2Se3 and Bi2Te3. Bi2Te3−xSex is expected to remain topological for all atomic ratios 0 ≤ x ≤1, similar to the case of (BixSb1−x)2Te3 topological insulator52,53. This gives a chance for the realization of ultrathin Bi2Te3−xSex crystal-based devices in which the topological channels dominate the electron transport54.
In the present work, we report on the growth of ultrathin single nanocrystals of the three-dimensional topological insulator Bi2Te2.3Se0.749,54 and their successful integration into proximity Josephson junctions. We demonstrate that due to a very small thickness of the crystals, the quantum-coherent magneto-transport properties of the implemented devices are dominated by the topological surface channels. The experiments are compared with numerical simulations performed in the frameworks of the diffusive and ballistic models55, witnessing for a strong Josephson coupling and the predominantly ballistic coherent electron transport.
Results
Elaboration of single Bi2Te2.3Se0.7 nanocrystals containing Josephson junctions
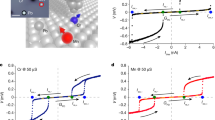
Synthesis of topological insulator nanocrystals was carried out by the PVD technique39. Figure 1a–d demonstrates the sample preparation technique, growth result, and electronic transport property evolution. The design of the setup is sketched in Fig. 1a. The source material, polycrystalline Bi2Te2Se melt47, was placed on a tantalum-covered copper heater. The substrate, a 5 × 10-mm2 Si (100) wafer, was put on a separate support at a distance ~10 cm, all inside a quartz tube. Before growth, the quartz tube was evacuated and then filled with a 99.9995% pure Ar gas. During deposition, Ar was circulated at a pressure of 100 Torr. The temperatures of the source and substrate were kept at 550 ± 10 ∘C and 350 ± 10 ∘C respectively. After ~10 min of deposition, the heaters were switched off and the system was left to cool down.
a Schematic view on the physical vapor deposition (PVD) growth cell. The Bi2Te3−xSex nanocrystals grow on Si substrate by Ar-flow-assisted atomic transport from the evaporated target (Bi2Te2Se alloy). Inset: schematics of the Josephson junctions studied in this work. The junctions are made of a single nanocrystal contacted by overlaying Nb electrodes. b Atomic structure of Bi2Te3−xSex with presented crystallographic axes and quintuple layer (QL) marker, SEM image of the substrate covered by Bi2Te2.3Se0.7 nanocrystals, respectively. Inset: a top view on a selected crystal with superposed crystallographic axes and atomic structure. White scale bars correspond to 1 μm and 100 nm, respectively. c Temperature dependence of the two-terminal device resistance R(T) and various steps of the transition of devices to the superconducting (SC) state. Characteristic temperatures of the superconducting transition of Nb leads, overlapped Nb/Bi2Te2.3Se0.7 contacts, and open parts of Bi2Te2.3Se0.7 are shown by an arrow and two vertical dashed lines. The three steps of the transition are colored in gray. Schematic view on three steps of the transition, the superconducting parts are colored in blue/gray, normal parts—in red. TI—topological insulator, Δmini—superconducting mini gap, Tc, \({T}_{{\rm{c}}}^{{\rm{Nb}}}\), \({T}_{{\rm{c}}}^{{\rm{mini}}}\)—critical temperatures at different stage. d Current–voltage I(V) characteristics of the devices SJ1, SJ2, SJ3, and SQ1, SQ2 at T = 700 mK in zero magnetic field manifest Josephson junction behavior, SEM scanning electron microscopy.
Owing to a strong mismatch between the unit-cell parameters of SiO2/Si and Bi2Te3−xSex, a Vollmer–Weber growth occurs56, at which separated 3D particles grow directly on the substrate. The scanning electron microscopy (SEM) revealed a collection of flat-top single nanocrystals randomly spread over the surface of the substrate, Fig. 1b. They are very thin, d = 15–30 nm, that corresponds to stacks of 12–25 quintuple layers57, and have the lateral size of 100–1500 nm. The inset in Fig. 1b demonstrates that the crystals are well faceted, making straightforward the identification of their crystallographic orientation.
The structure and composition of the nanocrystals were analyzed using X-ray diffraction spectroscopy (XRD), energy-dispersive X-ray spectroscopy (EDX), and electron-backscatter diffraction spectroscopy (EBSD). The measurements showed that the nanocrystals are structurally identical to Bi2Se3 and Bi2Te3; their composition is close to Bi2Te2.3Se0.7. Further details are presented in the “Methods” section: “Energy-dispersive X-ray spectroscopy”, “Electron backscatter diffraction”, “X-ray diffraction”, correspondingly and in Supplementary Figs. 1–3.
Nanocrystal-based proximity Josephson junctions were realized by magnetron sputtering of Nb onto e-beam patterned surface of the substrate covered with Bi2Te2.3Se0.7 nanocrystals. The contacts superconductor—topological insulator are realized in the regions where Nb overlaps Bi2Te2.3Se0.7. Just before Nb deposition, these regions were Ar-plasma etched to enhance the contact transparency. The geometry of the devices is schematized in the inset of Fig. 1a. Several independent junctions were realized on the same substrate within a single growth/lithography/sputtering sequence (see the “Methods” section: “E-beam lithography and Nb deposition” for further details).
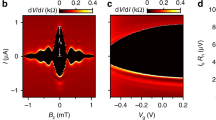
Figure 2a–o depicts all devices and results of I(V,H) transport measurements. Figure 2a–c presents SEM images of three Josephson junctions (SJ1, SJ2, and SJ3), each containing one single nanocrystal (colored in magenta) connected between two 500-nm-wide Nb electrodes (colored in blue) separated by a gap L ≈ 135 nm. The three junctions differ by the size of the nanocrystals they contain. In SJ1, the nanocrystal is smaller than the width of Nb leads; in SJ2, it is almost equal; in SJ3, the nanocrystal is significantly larger. Other Josephson junctions (SQ1 and SQ2 in Fig. 2d–e), contain two nanocrystals connected in parallel.
a–e SEM images of Nb-Bi2Te2.3Se0.7-Nb Josephson junctions. The junctions have a width Ww−l of 135, 412, 524, 298 and 490 nm (from a to e respectively) and ~135 nm distance between Nb leads. f–j 2D color plots of differential resistance (dV/dI) versus current bias and applied magnetic field of (f) SJ1, (g) SJ2, (h) SJ3, (i) SQ1, and (j) SQ2, measured at T = 700 mK for the samples depicted in (a–e) respectively. The superconducting region is visible in dark blue, with a resistance R = 0 Ω, while the nonsuperconducting regions appear as light-blue areas, and exhibit R > 0 Ω. k–o Critical current as a function of an external magnetic field for all samples. The Fraunhofer pattern is clearly visible, and a fit using Eq. (1) is shown as the red line, valid for a short junction. The size of the circles corresponds to the measurement error. k Junction SJ1 based on the smallest nanoplate behaves in a different way. Its critical current does not oscillate with the magnetic field, but monotonically decays. l Junction SJ2 based on the nanocrystal. Its critical current exhibits several Fraunhover-like oscillations with periodicity δH ≈ 12.9 mT. m Junction SJ3 based on the widest nanocrystal. δH ≈ 8.2 mT. n Junction SQ1 based on two nanocrystals. Its critical current exhibits several Fraunhover-like oscillations with periodicity δH ≈ 10.5 mT. o Junction SQ2 based on two nanocrystals with δH ≈ 13.5 mT. SEM scanning electron microscopy.
Experimental results
We now present magneto-transport properties of the five junctions. Figure 1c shows the temperature dependence of the Josephson junctions resistance R(T) in zero magnetic field. As the temperature is lowered, the junctions undergo several transitions, before they reach the superconducting state (the corresponding temperature windows are marked by vertical gray bands). Color schemes presented in Fig. 1c help in identifying these essential steps (see also the “Methods” section: “Measurement details” and Supplementary Figs. 4 and 5). At 8.5–9 K a tiny jump (~20–30 Ω) in resistance witnesses for the expected superconducting transition of Nb leads (the critical temperature \({T}_{{\rm{c}}}^{{\rm{Nb}}}\) is marked by black vertical arrow). The superconducting transition of Bi2Te2.3Se0.7 regions overlapped with Nb takes place at 2.5–5.5 K. This transition is progressive, due to a poor Nb/topological insulator interface, and a competition between the superconducting correlations induced from Nb and normal quasiparticles injected from the uncovered parts of Bi2Te2.3Se0.7 crystal. As a result, the decay of R(T) depends on the details of the Nb/Bi2Te2.3Se0.7 interface barrier and on the geometry of each Josephson junction. At Tc ≈ 2.5 K Nb-covered parts of the crystals become superconducting; in all devices, the residual resistance falls below 90 Ω. At yet lower temperatures, the resistance of the devices decays again, reflecting the progression of the superconducting correlations by proximity from the Nb-overlapped parts of Bi2Te2.3Se0.7 nanocrystals toward the uncovered parts. Below ~1 K the resistance of all junctions becomes immeasurably small.
The current–voltage V(I) characteristics measured below 1 K confirmed that all devices behave as Josephson junctions. The plots in Fig. 1d demonstrate that at low current bias, the devices remain in the zero-resistance state. The state lasts till some critical current value Ic = 0.2–1.3 μA at which each Josephson junction abruptly jumps into a resistive state. Above Ic, V(I) curves asymptotically approach the Ohm’s law; the corresponding normal-state resistance is \({R}_{{\rm{n}}}^{\exp }\) = 19–80 Ω (Table 1). Upon up–down current cycling, no hysteretic behavior is observed.
All devices demonstrate a sharp rise of the critical current with decreasing temperature (presented in Fig. 3 and discussed later); no sign of Ic(T) saturation, characteristic to diffusive Josephson junctions, was observed down to 700 mK. In general, the shape of the curves is typical of superconductor/normal metal/superconductor (SC/NM/SC) Josephson junctions having highly transparent SC/NM interfaces58.
When an external field H is applied, the critical current of the junctions exhibits pronounced Ic(H) oscillations. The oscillatory behavior, presented in Fig. 2a–e, strongly depends on the detailed shape/size of Bi2Te2.3Se0.7 nanocrystals and on how they are connected to Nb leads. In Fig. 2f–j we present 2D plots of the color-coded differential resistance dV/dI of each junction as a function of the bias current and the external magnetic field; Ic(H) variations are plotted in Fig. 2k–o, respectively. These curves clearly remind Fraunhofer-like Ic(H) interference patterns.
Discussion
The analysis of the observed magnetic field response requires considering the Meissner diamagnetism of Nb electrodes, leading to the field enhancement in the junction area by a geometry-dependent “focusing” factor α ~1.3–1.9, as compared with an externally applied field H (See the “Methods” section: “Magnetic flux focusing” and Supplementary Fig. 6). Figure 2f–o presents the field dependence of the critical current Ic(H) for the studied junctions. The narrowest junction SJ1 shows a smooth monotonic Ic(H) decay, Fig. 2f, k. It can be accounted for by considering additional field-generated supercurrents inside Bi2Te2.3Se0.7 nanocrystal that interfere destructively with the Josephson current flowing through the junction. The main effect of these additional currents on Ic(H) is produced in the area ~L × Weff of the nanocrystal, Weff being an effective width of the region where most of Josephson current flows. From the SEM image of SJ1 in Fig. 2a, one would expect Weff to be smaller than the physical width of the crystal, Weff < Wcrys ≈ 440 nm (Table 1), due to narrow S/N contacts (~140 nm).
The red solid line in Fig. 2k is the best fit obtained within the ballistic approximation59. The fit is obtained taking a very reasonable Weff = 268 nm. The model fits well the experimental data, yet taken alone, this fact does not rule out the possibility of a diffusive transport. Indeed, a theory developed by Bergeret and Cuevas60 withing the diffusive Usadel formalism also correctly reproduces the bell-shaped Ic(H) dependence; the best fit is presented as a black solid line in Fig. 2k. These fitting parameters are reasonable Weff = 400 nm and the diffusion coefficient D = 0.02 m2s−1, leading to the mean-free path l = D/vF ≈ 35 nm, that is still within the diffusive regime l < L. Thus, at this stage, both ballistic and diffusive scenarios for the superconducting transport remain possible (details are available in the “Methods” section: “Magnetic field dependence of the critical current”).
Unlike SJ1, the junctions SJ2 and SJ3 have rather large proximity regions, Fig. 2b, c. These junctions show an oscillatory Ic(H) behavior typical of wide Josephson junctions (Fig. 2g, l, h, m): the zero-order oscillation is wider in H than the following ones. The best fit is obtained using the Fraunhofer expression, \({I}_{{\rm{c}}}(H)={I}_{{\rm{c}}}(0)| \frac{\mathrm{sin}(\Phi (H)/{\Phi }_{0})}{\Phi (H)/{\Phi }_{0}}|\) with Φ(H) = αHLWeff and Φ0 = h/2e. The deviations are most probably due to a complex geometry of these junctions, flux focusing61, and a spatially inhomogeneous magnetic field.
Ic(H) characteristics of samples SQ1 and SQ2 involving two nanocrystals connected in parallel (Fig. 2d, e) are similar to those of direct current superconducting quantum interference devices (SQUID) (Fig. 2i, n, j, o, and Table 1). The oscillation period δH is constant in H; it can be associated with the magnetic flux crossing some effective loop area Aeff of the SQUID, such that αδHAeff = Φ062. In SQ1, the period is δH ≈ 10.5 mT. For our poorly screened loops, we can reasonably assume \({A}_{{\rm{eff}}} \sim ({W}_{{\rm{L}}}^{{\rm{w}}-{\rm{l}}}/2+{W}_{{\rm{R}}}^{{\rm{w}}-{\rm{l}}}/2+\delta W)\times (L+2{\lambda }^{{\rm{Nb}}})\), where \({W}_{{\rm{L}}}^{{\rm{w}}-{\rm{l}}}\) and \({W}_{{\rm{R}}}^{{\rm{w}}-{\rm{l}}}\) are the widths of the two proximity branches, δW is the space between them, and λNb = 0.080 μm is the effective London penetration length in niobium. For SQ1, by using \({W}_{{\rm{L}}}^{{\rm{w}}-{\rm{l}}}=0.13\ \upmu\)m, \({W}_{{\rm{R}}}^{{\rm{w}}-{\rm{l}}}=0.17\ \upmu\)m, δW = 0.20 μm and L = 0.14 μm, one gets Aeff = 0.10 μm2. This results in Φ0/Aeff = 20 mT, that is, ~2 times larger than δH = 10.5 mT. The calculation done for SQ2 leads to the same result. This result is a direct proof of the field focusing inside the junctions; it also provides an independent estimate for α ≈ 2.
Though, unlike in SQUIDs, in SQ1 and SQ2, the amplitude of Ic(H) oscillations rapidly decreases with the increasing field, similarly to what is observed in single junctions SJ1–3. One can suggest that the depairing and dephasing phenomena that affect small single Josephson junction-like our SJ1 should also influence the response of SQUID-like devices in which the the junction areas are comparable with the size of the SQUID hole. As a first measure, one can combine the usual expression for SQUIDs with a bell-shaped envelope function Ic(H) (like in Fig. 2k), which would represent the depairing effects in the two crystals forming the SQUID branches, to obtain
The fits using Eq. (1) are presented as red solid lines in Fig. 2n, o for SQ1 and SQ2, respectively. Despite the simplicity of the formula, the fits show a very good agreement with the experimental data.
The magnetic field response of our Josephson junctions being compatible with both diffusive and ballistic regimes, a deeper analysis of V(I, T) characteristics is required to decide which one is realized. In general, in the nonoverlapped Bi2Te2.3Se0.7, the normal-state resistance Rn is due to two parallel conductive channels, 2D-topological ones at surfaces, and a trivial 3D channel in the bulk. Depending on the crystal quality and the position of the Fermi level, the resistivity of the trivial 3D channel is ~10−(2÷3) Ω cm48, leading, in our 15–30 nm thick crystals, to a relatively high sheet resistance Rbulk ~ 10(3÷4) Ω. Topological channels have 10–100 times lower sheet resistance, 100–200 Ω48. Taking into account the two topological channels we have in parallel, this value corresponds well to the observed Rn(T ≃ 2 K). Therefore, in agreement with48, topological (upper and lower) surface channels carry in our nanocrystals most of electric current and shunt the trivial ones.
In the equivalent ballistic picture, such a normal resistance Rn = h/2e2N ≈ 12.9/N kΩ is due to N-parallel 2e2/h conductive modes. The experimentally recorded values, 80, 44, and 19 Ω for the junctions SJ1, SJ2, and SJ3, respectively, require N ~ 160, 250, and 680. The trivial 3D band can contribute with N3D ≈ (2Wcrys/λF−3D) × (2d/λF−3D), where Wcrys and d are width and thickness of the crystal, λF−3D ≈ 30 nm is the Fermi length of the trivial 3D channel49,51,54. Estimating Wcrys and d from SEM images results in N3D ~ 55, 41 and 198 for SJ1, SJ2, and SJ3, respectively. That is 3–6 times smaller than the required N. It means that in our ultrathin nanocrystals the 3D channels cannot dominate the electron transport. Indeed, the ballistic resistance of these N3D modes would be ~234, 314, and 65 Ω, that is several times lower than the Rbulk48. This means that the trivial 3D channel is in a strongly diffusive regime. Topological surface channels can contribute with N2D ≈ 2Wcrys/λF ballistic modes, where λF is the Fermi length of the topological channel, λF = 2π/kF ≈ 6 nm51,54. This gives N2D ~ 147, 171, and 512 topological ballistic modes in SJ1, SJ2, and SJ3, respectively. As compared with N3D, these numbers are much close to N required from the experiments. Moreover, the expected total resistance of these topological ballistic modes is ~87, 75, and 25 Ω, close to the recorded \({R}_{{\rm{n}}}^{\exp }\) (Table 1). The above estimation also works for SQ1 and SQ2, leading to reasonable values 47 and 41 Ω, respectively. This means that in our devices, the normal-state electron transport through nonoverlapped regions of topological insulator crystals is insured by ballistic topological modes that shunt the diffusive contribution of trivial 3D channels.
The temperature dependence of the critical current Ic(T) in zero field for three single junctions SJ1, SJ2, and SJ3 is presented in Fig. 3. The first observation is a clear relation between the geometry of devices and their Ic(T) characteristics. The highest Ic and Tc are realized in SJ3 involving the largest nanocrystal and the strongest Nb/topological insulator overlaps; the lowest values are observed in the smallest SJ1. Another remarkable effect is an almost linear rise of the critical current when lowering temperature. This is hardly compatible with the diffusive regime, usually leading to a saturation of Ic(T) at low temperatures. Black dashed lines in Fig. 3 are fits assuming a diffusive regime55. Clearly, the fits fail in reproducing a steep rise of the critical current below ~1 K. Black solid lines in Fig. 3 represent Ic(T) fits considering a fully ballistic transport55. The fits reproduce correctly the observed fast rise of Ic(T). From these fits, we get reasonable Δmini = 0.31, 0.40, and 0.46 meV for SJ1, SJ2, and SJ3, respectively, that is Δmini/kBTc = 2.2 ± 0.2. It has to be mentioned that both fits are quite imprecise in the case of SJ2, due to a significant asymmetry of SC/NM contacts in this junction Remarkably, the estimated number N of ballistic channels carrying the supercurrent is very low: 8, 9, and 27 for junctions SJ1, SJ2, and SJ3 respectively. The fitting parameters are summarized in the “Methods” section: “Temperature dependence of the critical current” and in Supplementary Fig. 7).
Blue, green, and red open circles represent the experimental data points corresponding, respectively, to SJ1, SJ2, and SJ3 devices. The size of the circles corresponds to the measurement error. Black dashed lines: fits considering a diffusive transport (the KO-1 model). The curves fail in reproducing a steep rise of Ic(T) at low temperatures. Black solid lines: fits within the ballistic regime (the KO-2 model).
At low temperatures, V(I) curves manifest the so-called excess current phenomenon63,64, Fig. 4. At T < Tc and high currents I > Ic flowing through the device, the V(I) characteristics are linear, as expected (see red dashed lines in Fig. 4), yet they cross the horizontal axis at finite current values ± Iexc. The excess current Iexc enables evaluating the number of truly ballistic topological channels carrying the Josephson current, using the expression IexcRn = (8/3)Δmini/e63,65,66, where Rn is the net resistance of ballistic channels coupled to proximized regions under Nb electrodes. Taking Iexc = 0.52 μA found in SJ1, and the estimated Δmini, one gets Rn ~ 1.6 kΩ, which corresponds to approximately N = 8 ballistic channels. This is remarkably close to N estimated for this junction from the ballistic fits of Ic(T). (Other V(I) for SJ2, SJ3, SQ1, and SQ2 structures are presented in Supplementary Fig. 8).
Blue line: V(I) characteristics of SJ1 measured at 700 mK. Red dashed lines: extrapolated linear parts of the experimental V(I) curve at high currents determine the excess current Iexc = 0.52 μA. Black line in the inset: linear fit of V(I) at low currents; its slope defines \({R}_{{\rm{n}}}^{\exp }\) = 80 Ω for SJ1.
The number N of open ballistic channels that carry most of the supercurrent is therefore by a factor of ~19 lower than the total number N2D of surface channels available in the crystals. We can assume that each of N2D-available channels connects to the Nb electrodes in its specific manner, via diffusive overlapped regions. Only a few channels are “well connected” to these proximized regions; others are poorly linked or linked through diffusive regions with a smaller minigap; they do not contribute significantly to the excess current. Within such a picture, both Ic and Iexc are limited by N and the corresponding high Rn = h/e2N ~ 1,6 kΩ. In the normal state, however, all channels contribute to the current flow; Rn = h/e2N2D ~ 90 Ω, in agreement with the measured \({R}_{{\rm{n}}}^{\exp }\). Notice that even if the explanation of our results requires only surface channels to be considered, a possible contribution from the bulk states to the transport cannot be completely ruled out.
Finally, to further advance in the understanding of magneto-transport properties, we measured their I(V, H) characteristics of the devices at very high currents I ≫ Ic ~ 1 μA. The results of these measurements are presented in Fig. 5 for SJ1. One can clearly see that at zero field, I(V, H = 0) curve displayed in Fig. 5a is nonlinear and exhibits several bends at high currents. These nonlinearities are better revealed in the differential resistance dV/dI(I) (right red and blue curves) that manifest several jumps. At very high currents, some hysteretic (upon up/down current sweeps) jumps are observed, pointing either toward nonequilibrium phenomena or stochastic processes of the current redistribution between channels at the moments when new channels are connected (current increase) or existing ones turn off (current decrease). At a moderate current ≈ ±6 μA, a nonhysteretic jump is observed (marked by red and blue circles and arrows). The corresponding bias is V0 ≈ ±0.56 mV, close to 2Δmini/e = 0.6 mV, as expected for Andreev reflections. The evolution of V0 with temperature and field is presented, respectively, in Fig. 5b, c. The V0(T) trend is exactly what one would expect for the temperature dependence of Δmini(T). Moreover, the evolution of V0(H) in low magnetic fields makes appearing a dome of a width related to the size of the junction. The data displayed in Fig. 5b, c unambiguously relate the observed V0 feature to induced superconductivity, and specifically to the Andreev reflection processes inside the junction. Note that other peaks/jumps behave quasi-chaotically in the field; nevertheless, this “chaos” is reproducible upon the field sweeps. Interestingly, the reversal of the field direction makes the “chaos” be mirrored to reverse currents. In general, the phenomena depicted in Fig. 5 and in Supplementary Fig. 9 are rich and complex. Uncovering their origin(s) is the subject of a separate work.
a I(V) curves (blue and red lines) acquired at 700 mK for the two opposite directions of the current sweep. The corresponding differential resistance dV/dI(V) curves (at the right) shows step-like jumps separated by sharp peaks. Unlike other peaks, the one at ~±6 μA shows no hysteresis (the event is also marked by red and blue circles and arrows on I(V)). b Temperature evolution of the differential resistance dV/dI(V) spectra. Red and blue lines follow the temperature evolution of the peaks. c Evolution of the differential resistance in the magnetic field (for the two opposite directions of the field sweep). Hysteretic peaks evolve “chaotically” yet deterministically; the nonhysteretic peak shows a completely different dome-like smooth evolution.
To summarize, in this work, we have realized and studied superconductor-normal metal-superconductor Josephson devices in which individual single nanocrystals of three-dimensional topological insulator Bi2Te2.3Se0.7 were implemented as normal parts. We measured magneto-transport characteristics of three such devices comprising one single crystal and two devices implicating two crystals in parallel and working as SQUIDs. We demonstrated clear quantum interference characteristics of the devices in the magnetic field. The experimental results were compared with the existing theories developed for both diffusive and ballistic transport in the proximity of Josephson devices. The analysis showed that in the studied samples, the superconducting transport properties are dominated by topological channels, with a significant contribution of ballistic modes. Our findings open a route for the fundamental studies of coherent superconducting hybrids involving high-quality topological nanomaterials, and for the search for future types of superconducting quantum devices67.
Methods
Energy-dispersive X-ray spectroscopy (SEM EDX)
To determine the composition of the synthesized nanocrystals, the SEM EDX was used. Table 2 provides the results of EDX analysis of the source Bi2Te2Se material (S) and as-grown nanocrystals (SS). The source material was used as a reference; its composition was independently found to correspond to the stoichiometric Bi2Te2Se.
High-energy (10-keV) electrons penetrate into the sample up to ~0.5 μm, that is much larger than the crystal’s thickness. Hence raw EDX spectra demonstrate the presence of a significant amount of Si (substrate material). The content data presented in Table 2 are corrected to exclude the influence of Si. Twenty different nanocrystals were examined and showed the same content close to Bi2Te2.3Se0.7. Silicon, bismuth, tellurium, and selenium EDX maps are presented in Supplementary Fig. 1. They demonstrate that Bi and Te are fairly uniformly distributed inside crystals, with no precipitates possible.
In addition, we also attempted to study already-elaborated devices. The results for SJ2, SJ3, SQ1, and SQ2 are presented in Table 2. Though their composition was difficult to evaluate precisely because of a tiny surface of n-overlapped regions and the proximity of Nb electrodes.
Electron backscatter diffraction (EBSD)
To correlate the surface morphology with the local crystalline orientation, EBSD analysis was performed in the nonoverlapped area of a single nanocrystal (the corresponding SEM image is shown in Supplementary Fig. 2a). EBSD data confirm that the crystal structure matches that of the trigonal Bi2Te3−xSex in the PDF2 database as follows: space group R-3m h (166), a = b = 0.430 nm, c = 2.97 nm, and α = β = 90∘, γ = 120∘. The crystallographic orientation mapping using the inverse pole figure (IPF) color code along X, Y, and Z directions is shown in Supplementary Fig. 2b–e and f–i for Bi2Te3−xSex nanoplate and Si substrate, respectively. A homogeneous color of Bi2Te3−xSex nanocrystal in X, Y, and Z orientations witnesses for a perfect crystallinity of the sample.
For the investigated Bi2Te3−xSex nanoplate, the IPF along X, Y and Z directions shown in Supplementary Fig. 2j indicates that the out-of-plane orientation is <0001>, and the in-plane orientations are <1120> and <1010>. The IPF along X, Y, and Z directions for Si substrate is shown in Supplementary Fig. 2k. A comparative analysis of the IPF data for nanoplate and substrate (Supplementary Fig. 2b–e and f–i; j and k, respectively) reveals the alignment between Bi2Te3−xSex nanoparticle and Si substrate to be (0001)Bi2Te3−xSex∥ (001) Si and [1120] Bi2Te3−xSex∥ [101] Si. More details about the method could be found in ref. 68.
X-ray diffraction (XRD)
According to PDF-2 (ICDD) database, the unit-cell volume of phases Bi2(Se2Te) and Bi2Te3 is changed from 450.5 Å3 to 508.4 Å3 respectively. The unit-cell volume gradually decreases as the Se atomic fraction increases, according to Vegard’s law69, and can be approximated as \(V={V}_{{\rm{A}}}^{0}(1-Y)+{V}_{{\rm{B}}}^{0}(Y)\), where V is unit-cell volume of (\({V}_{{\rm{A}}}^{0}\) − Bi2Te3), B (\({V}_{{\rm{B}}}^{0}\) − Bi2Se3) and Y accounts for the relative concentration of the Te and Se. From this relation, the dependence of the unit-cell volume on the substitution ratio is obtained it is plotted in Supplementary Fig. 3. The expected unit-cell volume of solid solution is 486.1 Å3, which corresponds to the composition of the sample Bi2Te2.3Se0.7.
E-beam lithography and Nb deposition
After PVD growth, the substrate was covered with 250-nm PMMA e-beam resist and the windows were made by means of electron lithography for subsequent Nb film deposition. Base pressure into the magnetron chamber 5 × 10−9 mbar. Prior to Nb deposition, the unprotected parts of samples were etched in Ar plasma (RF power 60 W, acceleration voltage 483 V, pressure 2 × 10−2 mbar and duration 10 s) to remove organic and contaminating residuals from the surface. The chamber was then pumped down to base pressure (1.3 × 10−8 mbar), and filled with pure argon (99.9995%) up to a pressure of 2 × 10−2 mbar. The Ar plasma was switched on, and a 118-nm thick Nb layer was deposited by RF magnetron sputtering, with the deposition rate 0.19 nm s−1 (Ar pressure 4 × 10−3 mbar, RF power PRF = 200 W and VDC = 202 V). After deposition, the standard lift-off procedure was done.
Measurement details
Measurements are performed in a quasi-four-probes configuration, using a nanovoltmeter Keithley 2182A and precision current source Keithley 6220. All of the data presented in this paper have been measured in an Oxford Heliox VL system. For field measurements, a superconducting solenoid providing the magnetic field up to 1 T was used. The samples were mounted on a holder such that the magnetic field was perpendicular to the nanoplate surface. Stages of low-pass RC-filter placed at the cryogenic part of the sample holder (at 700 mK) to avoid the noise >1.6 Hz. (R = 1 kΩ, C = 100 mF). All 24 lines are twisted pairs of beryllium–bronze.
The room-temperature resistance is in the range of 0.8–1.5 kΩ for all junctions including the resistance of niobium wires. The resistance of niobium wires was estimated from an independent experiment and amounted to 100 Ω at room temperature and five times lower at 10-K temperatures, of the order of ~20–30 Ω. Supplementary Fig. 10 shows a typical resistance vs temperature (R(T)) in a wide range of temperatures. By lowering temperature, the R(T) follows a metallic-like behavior, down to the temperature of 10 K. At about 8 K (critical temperature of Nb) an drop of R takes place. Below this temperature, a quite broadened transition, characteristic of a progressive transition to the superconducting state, was observed. Below 1.1 K, the resistance is zero.
Magnetic flux focusing
In order to explain the features of measured Ic(H) curves, we have to take into account the existence of flux focusing on the junction due to the fact that superconducting leads repel the external magnetic field. It can change evaluation of a real magnetic field in Josephson junction by some factor α from the external field H. To estimate the magnitude of magnetic flux-focusing effect, i.e., the value of α, we used COMSOL program. We simulated our junction as several rectangular electrodes (see Supplementary Fig. 6 for certain simulation geometry) and solve Maxwell equations with the external field equal to H = 1 in infinity and without other sources of the magnetic field. The electrodes have been approximated as ideal diamagnetics (μ = 10−9), i.e., full Meissner effect. In the center of junction factor, α can reach values from 1.3 to 1.9 depending on geometry. That can cause to real magnetic field value αH (see Table 3).
Magnetic field dependence of the critical current
The same approaches are applied to fit the critical current versus external magnetic field dependencies. In the ballistic regime, the critical current versus external magnetic field dependency was found using Barzykin and Zagoskin model59. Within this approach, the expression for the Josephson current is given by
where L and W are, respectively, the length and the width of the junction, vF—Fermi velocity, λF —Fermi wavelength, Φ—the magnetic flux crossing the area L × W, Φ0 = h/2e—the magnetic flux quantum, \({\theta }_{{y}_{1}-{y}_{2}}=\arctan (({y}_{2}-{y}_{1})/L)\) is the phase difference between the points y1 and y2 situated at the edges of the S/N contacts, \({\xi }_{T}=\frac{\hslash {v}_{{\rm{F}}}}{2\pi {k}_{{\rm{B}}}T}\). In the fitting procedure, we define L and W from junction geometry, vF = 5.8 × 105 m s−1 is taken from70,71,72, and λF is calculated from the number of channels N that we take from the Ic(T) fits. The Fermi wavelength is estimated as \({\lambda }_{{\rm{F}}}=\sqrt{\frac{4S}{N}}\), where S is the cross section of the junction. The critical current is found as \({I}_{{\rm{c}}}=\mathop{\max }\nolimits_{0\le \chi <2\pi }{I}_{{\rm{s}}}(\chi )\).
In the diffusive case, the quasiclassical theory developed by Bergeret and Cuevas60 gives for the critical current
where T is the temperature, Rn is the normal-state resistance, ϵT = ℏD/L2 is the Thouless energy, where D is the diffusion coefficient, ωn = πkBT(2n + 1) are the Matsubara energies, and r = GN/GB is the channel transparency—the ratio between the normal-state conductance of the junction, GN, and the conductance of the barriers, GB, which we assume to be identical, Δmini— effective gap proximity induced into Bi2Te2Se as noted above. In this formalism, the magnetic field enters through the term ΓH = De2(αH)2W2/(6ℏ) which represents the magnetic depairing energy. In order to free from absolute critical current value, we normalize critical current the same way that it was done in the ballistic case. Thus, we can omit parameters Rn and r. We also introduce dimensionless parameter \(l=\frac{2\pi {k}_{{\rm{B}}}TL}{\hslash D}\) and rewrite the member of sum as
where Φ0 is the magnetic flux quantum. Now, there are two fitting parameters: effective width W where current circulates and dimensionless parameter l. The resulting fit for SJ1 is obtained with parameters W = 395 nm and 136 nm for ballistic and diffusive cases, respectively. Parameters are shown in Table 4.
Now, we would like to turn to SQUID field dependencies of a critical current. As it was suggested in the main text, these dependencies can be described by
where \({I}_{{\rm{c}}}^{{\rm{SJ}}}(H)\) is a bell-shaped envelope function calculated using Zagoskin’s model that was described above with certain parameters for average single Josephson junction of a SQUID (see Table 5). Fitting parameters are presented in Table 5, where WSJ and LSJ are width and length of Josephson junction playing role of an envelope and Seffective is a square of SQUID itself. All values in Table 5 are presented without the focusing factor.
Temperature dependence of the critical current
In the diffusive regime, the supercurrent is determined by the Kulik–Omelyanchuk-1 (KO-1) theory73
where χ—global phase difference between the two superconducting electrodes, ωn = πkBT(2n + 1) is the Matsubara frequency, Rn is the resistance in the normal state, \({\Omega }_{n}=\sqrt{{\omega }_{n}^{2}+{\Delta }_{{\rm{mini}}}^{2}{\cos }^{2}(\chi /2)}\), Δmini is the gap induced into the crystal and was considered having the BCS-like temperature evolution. Here and after Δmini for SJ1 extracted from I(V) curve, for SJ2 and SJ3, it is calculated assuming that the ratio \(\frac{{\Delta }_{{\rm{mini}}}}{{k}_{{\rm{B}}}{T}_{{\rm{c}}}}\) is the same for all crystals due to the same material and synthesis conditions. Tc is defined from experiment, so the only fitting parameter is Rn. Once Is(χ) dependence is established, the critical current can be found as Ic = \(\mathop{\max }\nolimits_{0\le \chi <2\pi }{I}_{{\rm{s}}}(\chi )\). The resulting curves are pictured in the main text and their parameters are shown in Table 6.
In the ballistic regime, critical current versus temperature can be described by the Galaktionov–Zaikin theory74. In this model, the supercurrent supported by N-surface modes can be written as
where μ = kx/kF is the integration variable, kF is the Fermi wave vector, kx is a wave vector of the ballistic mode along the junction, χ is a phase difference, N is the amount of conducting channels, \({t}_{1},{t}_{2}=\frac{{D}_{1,2}}{2-{D}_{1,2}},{D}_{i}\) are being the transparencies of the two SC/NM interfaces (here we assume that Di = 1), and
where L is a junction length. The coherence length at T = Tc is defined as \({\xi }_{0}=\frac{\hslash {v}_{{\rm{F}}}}{\pi {k}_{{\rm{B}}}{T}_{{\rm{c}}}}\). Switching to dimensionless units, we introduce the parameter \(l=L/{\xi }_{0}=\frac{\hslash {v}_{{\rm{F}}}}{2\pi {k}_{{\rm{B}}}{T}_{{\rm{c}}}L}\). The junction length L for our samples is determined from experimental data (Table 1) and vF = 5.8 × 105 m s−1 from literature data for this material70,71,72. Estimates for our samples provide hte value of ξ0 ~ 1 μm. Thus the junctions are in the short-junction regime l ≪ 1 described by the Kulik–Omelyanchuk-2 (KO-2) model75 and the only fitting parameter is the number of ballistic current channel N.
The resulting curves are presented in the main text and the fitting parameters are shown in Table 7. Remarkably, the number N = 8 for SJ1 matches the value deduced from the excess current phenomenon.
Data availability
Confirming that all relevant data are available from the authors.
References
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
Beenakker, C. W. J. Search for Majorana fermions in superconductors. Annu. Rev. Condens. Matter. Phys. 4, 113–136 (2013).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Qi, X. L., Hughes, T. L., Raghu, S. & Zhang, S. C. Time-reversal-invariant topological superconductors and superfluids in two and three dimensions. Phys. Rev. Lett. 102, 187001 (2009).
Charpentier, S. et al. Induced unconventional superconductivity on the surface states of Bi2Te3 topological insulator. Nat. Commun. 8, 2019 (2017).
Majorana, E. Nuovo Cimento 14, 171–184 (1937).
Kitaev, A. Y. Unpaired Majorana fermions in quantum wires. Phys. Uspekhi 44, 131–136 (2001).
Lutchyn, R. M., Sau, J. D. & Das Sarma, S. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & vonOppen, F. Helical liquids and Majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Sato, M. & Ando, Y. Topological superconductors: a review. Rep. Prog. Phys. 80, 076501 (2017).
Kastl, Ch., Karnetzky, Ch., Karl, H. & Holleitner, A. W. Ultrafast helicity control of surface currents in topological insulators with near-unity fidelity. Nature Commun. 6, 6617 (2015).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B. 75, 121306 (2007).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101 (2009).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Cha, J. J., Koski, K. J. & Cui, Y. Topological insulator nanostructures. Phys. Status Solidi RRL 1, 11 (2012).
Weber, S. J. Gatemons get serious. Nat. Nanotech. 13, 875–881 (2018).
Larsen, T. W. et al. Semiconductor-nanowire-based superconducting qubit. Phys. Rev. Lett. 115, 127001 (2015).
Casparis, L. et al. Superconducting gatemon qubit based on a proximitized two-dimensional electron gas. Nat. Nanotech. 13, 915–919 (2018).
Kou, L., Ma, Y., Sun, Z., Heine, T. & Chen, C. Two-dimensional topological insulators: progress and prospects. J. Phys. Chem. Lett. 8, 1905–1919 (2017).
Bobkova, I. V. & Bobkov, A. M. Electrically controllable spin filtering based on superconducting helical states. Phys. Rev. B 96, 224505 (2017).
Seifert, P. et al. Spin Hall photoconductance in a three-dimensional topological insulator at room temperature. Nat. Commun 9, 331 (2018).
Cho, S. et al. Symmetry protected Josephson supercurrents in three-dimensional topological insulators. Nat. Commun. 4, 1689 (2013).
Oostinga, J. B. et al. Josephson supercurrent through the topological surface states of strained Bulk HgTe. Phys. Rev. X 3, 021007 (2013).
Galletti, L. et al. Influence of topological edge states on the properties of Al/Bi2Se3/Al hybrid Josephson devices. Phys. Rev. B 89, 134512 (2014).
Seunghun, L. et al. Observation of the superconducting proximity effect in the surface state of SmB6 thin films. Phys. Rev. X 6, 031031 (2016).
Finck, A. D. K., Kurter, C., Hor, Y. S. & Van Harlingen, D. J. Phase coherence and Andreev reflection in topological insulator devices. Phys. Rev. X 4, 041022 (2014).
LeCalvezK. Signatures of a 4-π periodic Andreev bound state in topological Josephson junctions. PhD thesis, Universite of Grenoble Alpes. (2017).
Kurter, C., Finck, A. D., Hor, Y. S. & Van Harlingen, D. J. Evidence for an anomalous current - phase relation in topological insulator Josephson junctions. Nat. Commun. 6, 7130 (2015).
He, Q. L. et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator-superconductor structure. Science 357, 294–299 (2017).
Qu, F. et al. Strong superconducting proximity effect in Pb-Bi2Te3 hybrid structures. Sci. Rep. 2, 339 (2012).
Sacepe, B. et al. Gate-tuned normal and superconducting transport at the surface of a topological insulator. Nat. Commun. 2, 575 (2011).
Veldhorst, M., Molenaar, C. G., Wang, X. L., Hilgenkamp, H. & Brinkman, A. Experimental realization of superconducting quantum interference devices with topological insulator junctions. Appl. Phys. Lett. 100, 072602 (2012).
Xu, S.-Y. et al. Electrically switchable Berry curvature dipole in the monolayer topological insulator WTe2. Nat. Phys. 14, 900–906 (2018).
Li, C. et al. 4π -periodic Andreev bound states in a Dirac semimetal. Nat. Mat. 17, 875–880 (2018).
Stolyarov, V. S. et al. Double Fe-impurity charge state in the topological insulator Bi2Se3. Appl. Phys. Lett. 111, 251601 (2017).
Chen, M. et al. Selective trapping of hexagonally warped topological surface states in a triangular quantum corral. Sci. Adv. 5, eaaw3988 (2019).
Kong, D. et al. Few-layer nanoplates of Bi2Se3 and Bi2Te3 with highly tunable chemical potential. Nano Lett. 10, 2245–2250 (2010).
Yan, Y. et al. Synthesis and quantum transport properties of Bi2Se3 topological insulator nanostructures. Sci. Rep. 3, 1264 (2013).
Cui, F. et al. Tellurium-assisted epitaxial growth of large-area, highly crystalline ReS2 atomic layers on Mica substrate. Adv. Mater. 28, 5019–5024 (2016).
Crowley, J. M., Tahir-Kheli, J. & Goddard III, W. A. Accurate ab initio quantum mechanics simulations of Bi2Se3 and Bi2Te3 topological insulator surfaces. J. Phys. Chem. Lett. 6, 3792–3796 (2015).
Lee, H. Y. et al. Epitaxial growth of Bi2Te3 topological insulator thin films by temperature-gradient induced physical vapor deposition (PVD). J. Alloys Compd. 686, 989–997 (2016).
Wu, Z. et al. Bi2Te3 nanoplates’ selective growth morphology on different interfaces for enhancing thermoelectric properties. Cryst. Growth Des. 19, 3639–3646 (2019).
Wang, L. L. & Johnson, D. D. Ternary tetradymite compounds as topological insulators. Phys. Rev. B 83, 241309 (2011).
Shekhar, C. et al. Evidence of surface transport and weak antilocalization in a single crystal of the Bi2Te2Se topological insulator. Phys. Rev. B. 90, 165140 (2014).
Kapustin, A. A., Stolyarov, V. S., Bozhko, S. I., Borisenko, D. N. & Kolesnikov, N. N. Surface origin of quasi-2D Shubnikov - de Haas oscillations in Bi2Te2Se. JETP 121, 279–288 (2015).
Durand, C. et al. Differentiation of surface and bulk conductivities in topological insulators via four-probe spectroscopy. Nano Lett. 16, 2213–2220 (2016).
Miyamoto, K. et al. Topological surface states with persistent high spin polarization across the Dirac point in Bi2Te2Se and Bi2Se2Te. Phys. Rev. Lett. 109, 166802 (2012).
Jia, S. et al. Defects and high bulk resistivities in the Bi-rich tetradymite topological insulator Bi2+xTe2−xSe. Phys. Rev. B. 86, 165119 (2012).
Nurmamat, M. et al. Unoccupied topological surface state in Bi2Te2Se. Phys. Rev. B. 88, 081301 (2013).
Kong, D. et al. Ambipolar field effect in the ternary topological insulator (BixSb1−x)2Te3 by composition tuning. Nat. Nanotechnol. 6, 705–709 (2011).
Zhang, J. et al. Band structure engineering in (Bi1−xSbx)2Te3 ternary topological insulators. Nat. Commun. 2, 574 (2011).
Scanlon, D. O. et al. Controlling bulk conductivity in topological insulators: key role of anti-site defects. Adv. Mater. 24, 2154–2158 (2012).
Golubov, A. A., Kupriyanov, M. Y. & Il’ichev, E. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 76, 411 (2004).
Sharma, A., Senguttuvan, T. D., Ojha, V. N. & Husale, S. Novel synthesis of topological insulator based nanostructures (Bi2Te3) demonstrating high performance photodetection. Sci. Rep. 9, 3804 (2019).
Bland, J. A. & Basinski, S. J. The crystal structure of Bi2Te2Se. Canadian J. Phys. 39, 1040–1043 (1961).
Lee, G. H., Kim, S., Jhi, S. H. & Lee, H. J. Ultimately short ballistic vertical graphene Josephson junctions. Nat. Commun. 6, 6181 (2015).
Barzykin, V. & Zagoskin, A. M. Coherent transport and nonlocality in mesoscopic SNS junctions: anomalous magnetic interference patterns. Superlat. Microstruct. 25, 797–807 (1999).
Bergeret, F. S. & Cuevas, J. C. The vortex state and Josephson critical current of a diffusive SNS junction. J. Low Temp. Phys. 153, 304 (2008).
Dremov, V. V. et al. Local Josephson vortex generation and manipulation with a magnetic force microscope. Nat. Commun. 10, 4009 (2019).
Barone, A. & Patern, G. Physics and Applications of the Josephson Effect. (Wiley, New York, 1982).
Blonder, G. E., Tinkham, M. & Klapwijk, T. M. Transition from metallic to tunneling regimes in superconducting microconstrictions: excess current, charge imbalance and supercurrent conversion. Phys. Rev. B 25, 4515 (1982).
Bocquillon, E. et al. Gapless Andreev bound states in the quantum spin Hall insulator HgTe. Nat. Nanotech. 12, 137–143 (2017).
Zaitsev, A. V. Quasiclassical equations of the theory of superconductivity for contiguous metals and the properties of constricted microcontacts. Zh. Eksp. Teor. Fiz 86, 1742–1758 (1984).
Zaitsev, A. V. Properties of “dirty” S-S*-N and S-S*-N structures with potential barriers at metal boundaries. Pisama Zh. Eksp. Teor. Fiz 51, 35–39 (1990).
Assouline, A. et al. Spin-orbit induced phase-shift in Bi2Se3 Josephson junctions. Nat. Commun. 10, 126 (2019).
Sun, X., Lu, Z., Xiang, Y., Wang, Y. & Shi, J. Waals epitaxy of antimony islands, sheets, and thin films on single-crystalline graphene. ACS Nano 12, 6100–6108 (2018).
Vegard, L. Die konstitution der mischkristalle und die raumfllung der atome. Zeitschrift fr Physik 5, 17–26 (1921).
Neupane, M. et al. Topological surface states and Dirac point tuning in ternary topological insulators. Phys. Rev. B 85, 235406 (2012).
Xiong, J. et al. Quantum oscillations in a topological insulator Bi2Te2Se with large bulk resistivity (6Ωcm). Phys. E: Low-dimensional Syst. Nanostruct. 44, 917–920 (2012).
Reijnders, A. A. et al. Optical evidence of surface state suppression in Bi-based topological insulators. Phys. Rev. B 89, 075138 (2014).
Kulik, I. O. & Omel’anchuk, A. N. Contribution to the microscopic theory of the Josephson effect in superconducting bridges. Sov. Phys. JETP 21, 96–97 (1975).
Galaktionov, A. V. & Zaikin, A. D. Phys. Rev. B 65, 184507 (2002).
Kulik, I. O. & Omel’anchuk, A. N. Properties of superconducting microbridges in the pure limit. Sov. J. Low Temp. Phys. 3, 459–461 (1977).
Acknowledgements
We thank E. Chulkov and I. Soloviev for fruitful discussions and advice. We also thank L. Tagirov for the help with realization of EDX analysis of crystals. The samples were theoretically described owing to the support of RFBR project No. 19-52-50026. The sample preparation and transport measurements were carried out with the support of the RSF-ANR (20-42-09033). D.R. acknowledges COST Action CA16218—Nanoscale Coherent Hybrid Devices for Superconducting Quantum Technologies, French ANR grant SUPERSTRIPES. A.A.G. acknowledges support by the European Union H2020-WIDESPREAD-05-2017-Twinning project SPINTECH under Grant Agreement No. 810144. D.R. is grateful for the hospitality during a visiting professor semester at MIPT, supported by the Russian Ministry of Education and Science within the program “5top100”, M.Y.K. and A.I.G. acknowledges the partial support by the Program of Competitive Growth of Kazan Federal University.
Author information
Authors and Affiliations
Contributions
V.S.S. suggested the idea of the experiment, V.S.S. conceived the project and supervised the experiments, V.S.S. and D.S.Y. provided the PVD growth of the crystals, A.I.G., O.V.E., P.S.D. and I.V.S. realized the SEM EDX, EBSD, and XRD analysis of the crystals, V.S.S., O.V.S., and S.V.E. realized e-beam lithography of the sample and deposited the Nb film by magnetron sputtering for providing low-temperature experiments which were done by V.S.S., D.S.L., D.S.Y. and A.M.K., V.S.S., D.R., V.V.R., W.V.P., M.Y.K., and A.A.G. provided the explanation of the observed effects, S.N.K., R.A.H. did numerical modeling with contributions from V.S.S. and D.R., D.R. and V.S.S. wrote the paper with essential contributions from other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stolyarov, V.S., Yakovlev, D.S., Kozlov, S.N. et al. Josephson current mediated by ballistic topological states in Bi2Te2.3Se0.7 single nanocrystals. Commun Mater 1, 38 (2020). https://doi.org/10.1038/s43246-020-0037-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-0037-y