Abstract
Passive radiative cooling, drawing heat energy of objects to the cold outer space through the atmospheric transparent window, is significant for reducing the energy consumption of buildings. Daytime and nighttime radiative cooling have been extensively investigated in the past. However, radiative cooling which can continuously regulate its cooling temperature, like a valve, according to human need is rarely reported. In this study, we propose a reconfigurable photonic structure, based on the effective medium theory and semi-analytical calculations, for the adaptive radiative cooling by continuous variation of the emission spectra in the atmospheric window. This is realized by the deformation of a one-dimensional polydimethylsiloxane (PDMS) grating and nanoparticle-embedded PDMS thin film when subjected to mechanical stress/strain. The proposed structure reaches different stagnation temperatures under certain strains. A dynamic tuning in emissivity under different strains results in a continuously variable “ON”/“OFF” mode in a particular atmospheric window that corresponds to the deformation-induced fluctuation of the operating temperatures of the reconfigurable nanophotonic structure.
Similar content being viewed by others
Introduction
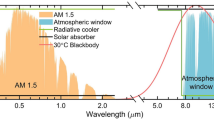
The growing demand for thermal comfort boosts the increase in the consumption of various energy sources for cooling and heating and exerts enormous stress on electricity systems over the world. It also drives up the carbon dioxide emissions and contributes to the problem of global warming. Nearly 20% of the total electricity is used by air conditioners or electric fans to regulate the temperature of buildings to be comfortable1. However, the peak wavelength (~9.7 μm) of blackbody radiation for objects on Earth (~300 K) coincides with the atmospheric highly transparent window (8–13 μm) that scarcely absorb infrared thermal radiation. Therefore, terrestrial objects can naturally radiate thermal energy to the outer space (~3 K) through the atmospheric window and hence lower their temperature, which is called passive radiative cooling2.
Effective nighttime radiative cooling has been extensively studied for organic and inorganic materials with high infrared emissivity within the atmospheric window3,4,5. However, the daytime radiative cooling is highly demanded and a challenge since the solar radiation (ASTM G-173, ~1000 Wm−2) is much higher than the potential radiative cooling (~100 Wm−2). If objects absorb only a few percents of solar irradiance, it will counteract the cooling power and heats the objects ultimately. To achieve daytime radiative cooling, a spectrally selective surface which effectively reflects solar irradiance (0.3–2.5 μm) and strongly emits heat within the infrared region (8–13 μm) simultaneously is a promising device. Consequently, several metamaterials that successfully achieve the daytime radiative cooling with an equilibrium temperature below the ambient have been experimentally investigated, such as silica-polymer hybrid metamaterial6, hierarchically porous paint-like materials7, and wood-based structural materials8. Other materials like nanophotonic structures9,10, infrared transparent aerogel11, and polymer nanofiber12 also provide various alternatives for daytime radiative cooling. These materials pave the way for applications of radiative cooling to energy-saving buildings, energy harvesting, and temperature regulation without energy consumption and achieving sustainable cooling throughout the day.
Although static radiative cooling systems can effectively save energy in summer, the cooling functionality will increase the energy consumption for heating in winter. To overcome this difficulty, a conceptive design of self-adaptive radiative cooling has been developed based on phase change material vanadium dioxide (VO2) that can adaptively turn “ON” and “OFF” radiative cooling corresponding to the ambient temperature2,13. Moreover, the phase change temperature of VO2 co-doping with tungsten (W) and strontium (Sr) can be adjusted around the room temperature by changing the amount of their inclusions14. Although these temperature-induced systems can automatically adjust the radiative cooling with ambient temperature, their performances, and applications highly based on the specific phase change temperature under the specific inclusions. Considering the rigorous manufacturing process and the fixed sole phase change temperature under specific usage scenarios, there are still some limitations on large-scale fabrications and complex practical applications. Mandal et al.15 presented porous polymer coatings with changeable optical transmittance responding to the reversible wetting as a platform for optical management from solar to thermal wavelengths. Switchable sub-ambient radiative cooling (by 3.2 °C) and above-ambient solar heating (by 21.4 °C) are achieved. Though the adaptive cooling and heating capabilities make it attracting for optical and thermal management applications, the complicated mechanical pump system and the accompanying liquid leaking impede its large-scale industrial applications.
Here, we conceptually propose a system of a reconfigurable nanophotonic structure for mechanical deformation induced radiative cooling basing on the continuously variable emission in the atmospheric window to attain diverse desired stagnation temperatures by continuous deformation adjustment according to the ambient temperature. The proposed reconfigurable nanophotonic structure consists of one layer of PDMS embedded with three species of nanoparticles: silicon carbide (SiC), silicon nitride (Si3N4), and boron nitride (BN), and a one-dimensional rectangular grating of PDMS coated with silver (Ag) thin film beneath the top PDMS layer. Different strains of the nanophotonic structure yield various stagnation temperatures. The dynamic tuning of mechanical deformation can result in a fluctuational temperature control of the nanophotonic structure around a set temperature. The elastic material based nanophotonic structure sheds light on the dynamic regulations of thermal emission.
Results
Continuous regulation of thermal emittance
The reconfigurable structure consists of a PDMS layer embedded with multi-species of nanoparticles on top of the one-dimensional PDMS grating coated by a silver thin film (Fig. 1a). The emissivity spectra in the atmospheric window of this structure are continuously tunable by the mechanical deformation of the top PDMS thin film and PDMS grating periods to stabilize at a certain temperature when subjected to a mechanical strain (Fig. 1b). We theoretically prove that the emissivity properties of the proposed system under different strains are angular-independent which is important in real applications. Theoretical analysis also shows that this system can maintain itself at a set temperature by mechanical deformation which could be potentially applied to thermal regulations for different applications, such as vehicles, buildings, and greenhouses.
a The reconfigurable photonic structure consists of a PDMS layer (thickness, h1) embedded with three species of nanoparticles: SiC, Si3N4, and BN (volume fraction, vf\({\,}_{{\mathrm{SiC}}/{\mathrm{S}}{{\mathrm{i}}}_{3}{{\mathrm{N}}}_{4}/{\mathrm{BN}}}\)). One-dimensional rectangular grating (period Λ, width w, filling ration ϕ) of PDMS (h2) coated with silver (Ag, h3) thin film is on the back side of the top PDMS layer. Case I: the structure has high solar reflectivity Rsolar that reflects most of the solar irradiance, and has high emissivity εIR in atmospheric window that can radiate heat out to the outer space when it is released. b Case II: it keeps unchanged high solar reflectivity Rsolar, while the emissivity εIR is reduced since the PDMS layer gets elongated and thinner and the period of the one-dimensional PDMS layer is increased due to the stretching, but the width of the Ag grating structure does not change. The blue dashed line shows the original state of the top PDMS layer. c Schematic showing the concept of mechanical deformation induced “ON” (black dashed line)/“OFF” (red dashed line) mode radiative cooling. The blue shading area displays the infrared atmospheric transparent window. The inset shows different stagnation temperatures under various strains of the nanophotonic structure. In the inset, the dashed black line represents the ambient temperature, and the brown/blue squares represent the stagnation temperature is higher/lower than the ambient temperature.
Figure 1c introduces the concept of the mechanical deformation induced radiative cooling. The basic principle of continuous temperature adjustment is that the thickness of the top nanoparticles embedded PDMS layer and the period of the silver-coated PDMS gratings are changed with mechanical deformation, which induces the corresponding change in emissivity of the structure with the atmospheric window (8–13 μm). This structure, like a valve, can continuously regulate its opening when subjected to different strains. The emissivity in the atmospheric window is a function of the strain. The higher the strain, the lower the emissivity. Furthermore, different strains correspond to different stagnation temperatures. A small strain yields a stagnation temperature below the ambient temperature, while a large strain represents a stagnation temperature above the ambient (the inset of the Fig. 1c).
Reconfigurable nanophotonic structure
To realize such a functionality, we employ an elastomer, PDMS, as a thermal valve to form reconfigurable metamaterials and propose a nanophotonic structure with a PDMS layer embedded with species of nanoparticles: SiC, Si3N4, and BN. one-dimensional PDMS grating layer coated with highly reflective thin film adheres to the back side of the top PDMS layer. When subjected to mechanical deformation of Δx, The PDMS structure is stretched or compressed, and the grating period Λ, and filling ratio ϕ increase or decrease. Here, it is assumed that the Ag grating strips (width w) do not undergo any deformation as it has a high Young’s modulus of 69 GPa. Therefore, the new grating period of the deformed structure is Λ ± Δx and the new filling ratio is w/(Λ ± Δx). The thickness of the top PDMS layer h1 also decreases to be h1 − Δh, as shown in Fig. 1b. The PDMS strongly absorbs infrared light when its thickness is above 1 μm as its extinction coefficient (κ) has absorption peaks from 7 μm to 13 μm16. If the thickness h1 is increased above 10 μm, it emissivity increases to 0.9 but its feature of the spectral selectivity loses, therefore we keep its thickness ~1 μm and introduce three species of dielectric nanoparticles (SiC, Si3N4, and BN) with different volume fractions (vf\({\,}_{{\mathrm{SiC}}/{\mathrm{S}}{{\mathrm{i}}}_{3}{{\mathrm{N}}}_{4}/{\mathrm{BN}}}\)) to increase the emissivity only within the atmospheric window. These three nanoparticles have separate extinction coefficient peaks from 7 μm to 13 μm (SiC: 12.8 μm17; Si3N4: 8.5 μm and 12.5 μm18; and BN: 7.09 μm and 12.45 μm18). It increases the emissivity in the atmospheric window but has no effects for the rest wavelength range. The PDMS grating strips serve as a transition layer between the top PDMS layer and the bottom Ag grating structure. Note that, when the photonic structure is deformed, the thickness of the grating PDMS layer is also reduced. Owing to Poisson’s ratio of PDMS (0.5), it is assumed that this change is negligible for the sake of simplicity. Although the strain of the structure increases to the PDMS stretching limit (ϵ = 120%), the Ag grating structure still keeps undeformed. Since Ag is highly reflective from 0.37 μm to 20 μm19, the Ag grating layer can be regarded as opaque to both the infrared and visible light considering its thickness, h3 = 400 nm and the small period, Λ = 40 nm compared to the wavelength range consider here (0.37–20 μm), that is, the Ag grating layer as a thin film to reflect all the incident light, even under 120% strain. Since the PDMS layer is transparent in the solar region as it has a negligible extinction coefficient20, the proposed structure is highly reflective in the solar region.
Theoretical analysis of spectral emissivity
In order to better fit the practical application scenarios, here, two possible scenarios of the deformation for the transition PDMS grating layer are considered. Figure 2a shows an ideal scenario – scenario I (top photonic structure). The width w of PDMS grating remains unchanged when the period elongates from Λ to Λ + Δx. In reality, the PDMS grating layer must undergo deformation to some extent. Hence, it is reasonably assumed that the bottom width wb keeps unchanged, while the top width wt elongates with the same strain to the top PDMS layer. Therefore, the PDMS grating strips become an isosceles trapezoid subjected to the mechanical stain, which represents an ideal actual deformation situation, as shown in scenario II. To illustrate the difference between scenarios I and II, the emissivity spectra of the structure under 60% strain are calculated and shown in Fig. 2b. The difference between the two scenarios cannot be negligible in the infrared region, so scenario II is adopted for the following analysis. The spectral emissivity of scenario I is higher than that of scenario II, and the reason is that the PDMS grating strip in scenario II fills more in the vacuum space than the scenario I when subjected to the same mechanical strain. It increases the infrared absorptance over the atmospheric window region. For the deformation of the PDMS grating layer, the one-dimensional strips are approximately divided into multiple layers of rectangular gratings with decreasing filling ration from top to bottom. Here, 100 layers are taken in calculations that is enough to get converged. Figure 2c shows the strain-dependent reflectivity in the wavelength range of 0.4–2.5 μm and emissivity in the wavelength range of 8–13 μm for scenario II. The solar reflectivity Rsolar increases slightly with strain and the εIR drops abruptly as the strain increases, for example, the εIR at 100% (0.23) strain is only equivalent to 32% of the εIR at the original state. This is because the thickness of the top PDMS layer decrease and the incident infrared light travels less in the top PDMS thin film. We confine the strain <120% since the PDMS film will fracture around that strain21.
a Two scenarios of the reconfigurable nanophotonic structure under stretching. Top: scenario I (constant width w) for the ideal stretching or compression due to the mechanical strain. Bottom: scenario II (constant width wt) for the real stretching situation. b The spectral emissivity of the reconfigurable metamaterials for scenario I (red curve) and scenario II (yellow curve) under 60% strain. The blue shading area shows the infrared atmospheric transparent window. c The strain ϵ dependent overall reflectively (blue solid line with squares) and emissivity (brown solid line with diamonds) for scenario II. Here, the overall solar reflectivity Rsolar is calculated from 0.4 μm to 2.5 μm, and the emissivity εIR is calculated from 8 μm to 13 μm. The inset displays the stretching scenario II.
After the optimization of variables h1, h2, h3, Λ, ϕ, and vf of SiC, Si3N4, and BN, the optimal configuration with h1 = 1100 nm, h2 = 100 nm, h3 = 400 nm, Λ = 40 nm, ϕ = 0.6, vfSiC = 3%, vf\({\,}_{{\mathrm{S}}{{\mathrm{i}}}_{3}{{\mathrm{N}}}_{4}}\) = 25%, and vfSiC = 4% can be obtained. Figure 3a shows the spectral emissivity of the reconfigurable nanophotonic structure at two limit states: original state (0% strain) and maximum stretching state (120% strain). Both the original and stretched structures show a high reflectivity in the solar irradiance region, while the original one has relatively high overall emissivity (0.79) over atmospheric window that represents the complete “ON” of radiative cooling valve. The stretched structure has an overall 0.15 emissivity from 8 μm to 13 μm and stands for the entire “OFF” feature of the valve. Besides, both the “ON” and “OFF” states have low absorptivity in the rest wavelength region (5–8 μm and 13–20 μm) for thermal radiation which avoids the absorption of heat from the ambient environment. The reflectivity spectra of the proposed structure from 300 nm to 400 nm are not available because of the lack of refractive indices of the PDMS. Considering that the Ag thin film and embedded nanoparticles (SiC, Si3N4, and BN) have absorption in these wavelengths, we provide the reflectivity spectra from 300 nm to 400 nm in Supplementary Fig. 1 based on the assumption that the refractive indices of the PDMS between 300 nm and 400 nm are identical as the values at 400 nm. The detailed analyses are available in Supplementary Note 1. It confirms that it is valid to adopt our calculation for the embedded nanoparticles with a diameter of 80 nm, since the nanoparticles with even smaller diameter affect slightly the reflectivity spectra from 300 nm to 400 nm, as analyzed in Supplementary Fig. 2 and Supplementary Note 2. The structure embedded with three species of nanoparticle inclusions has similar Rsolar while it has relative higher εIR over the atmospheric window compared with the structure of the single nanoparticle inclusions (Fig. 3b). The high Rsolar (θ) ensures an excellent reflection of sunlight from all angles of incidence (Fig. 3c, e, angle-averaged emissivity: 0.92 and 0.95), and the high εIR (θ; Fig. 3d, angle-averaged emissivity: 0.6324) of the complete “ON” state from 0° to 85° leads to a hemispherical high εIR resulting in a good radiative cooling feature. There is a quick drop of the εIR at both 0% and 120% strain modes in Fig. 3d, f when the angle of incident is above 60°. In Supplementary Fig. 3, by analyzing the angular dependent εIR of three different structures: a PDMS thin film with a Ag reflector, a PDMS thin film on top of Ag back coated PDMS gratings, and a PDMS thin film embedded with three species of nanoparticles (SiC, Si3N4, and BN) on a Ag reflector, we reasonably speculate that the quick drop of the εIR arises from the introduction of the nanoparticle inclusions, as analyzed in Supplementary Note 3. However, the low εIR (θ) of the entire “OFF” state from 0° to 85° (Fig. 3f, angle-averaged emissivity: 0.18) yields the low radiative cooling ability. Moreover, the states between the entire “ON” and “OFF” state represent different emissivity in the atmospheric window corresponding to different strains.
a Spectral emissivity of the reconfigurable nanophotonic structure at the original state (the blue solid curve) and under a maximum strain of 120% (the black solid curve) displayed with the normalized ASTM G173 solar spectrum (AM 1.5, the green shading area), the infrared atmospheric transparent window (the blue shading area) and the normalized blackbody spectrum (the red solid curve) at 300 K. b The overall solar reflectivity Rsolar and emissivity εIR of the proposed structure embedded with only a single species of SiC, Si3N4, or BN and the three mixed nanoparticles. The nanophotonic structure’s solar reflectivity Rsolar(θ) (c) and emissivity εIR (θ) (d) across various angle of incident (AOI) result in high hemispherical solar reflectivity Rsolar and emissivity εIR at original state (“ON” mode). The high solar reflectivity Rsolar(θ) (e), and the low emissivity εIR (θ) (f) across angles shows the “OFF” mode with a low hemispherical emissivity εIR under 120% strain.
Discussion
The thermal performance analysis of the reconfigurable metamaterials is evaluated by solving the energy balance equation (Fig. 4a):
a Schematic drawing of the thermal characterization setup used in the thermal performance analysis. Calculated net cooling power of the reconfigurable nanophotonic structure at different strains as a function of its own temperature at nighttime and daytime under 0.5 sun (0.5 × AM 1.5 illumination) and 0.9 sun (0.9 × AM 1.5 illumination) with (b) or without (c) polyethylene (PE) convection shield. Solid curve and dashed curve represent the nanophotonic structure are under 0% strain and 120% strain, respectively. The inset depicts the schematic of the thermal characterization setup under closed environment (b) and open to ambient (c).
It is assumed here that the backside of the photonic structure is well insulated, and only the energy transfer between the top surface of the structure, the ambient, and the outer space is considered. Here, Pr is the radiative cooling power of the structure, Pnr is the non-radiative power from the ambient, Pa is the incident thermal radiation power from the ambient, Ps stands for the incident solar power absorbed by the structure, Ta means the temperature of ambient air, and T presents the temperature of the structure. Pr can be determined as follows:
where, IBB(T, λ) = 2hc2λ−5\(\exp {(hc/\lambda {k}_{B}T-1)}^{-1}\) defines the spectral radiance of blackbody at a certain temperature. Here, h is the Planck’s constant, kB is the Boltzmann constant, and λ is the wavelength. ε(λ, θ, ϕ, Tcooler) = \(\frac{1}{\pi }\)\(\mathop{\int}\nolimits_{0}^{2\pi }{\mathrm{d}}\phi \mathop{\int}\nolimits_{0}^{\pi /2}{\varepsilon }_{\lambda }\cos \theta \sin \theta d\theta\) is the temperature-dependent emissivity of the structure22. Here, the emissivity measured at room temperature (298 K) is taken into simulation, since it is assumed that the temperature variations of the structure affect little on emissivity. θ and ϕ are the azimuthal and latitudinal angles, respectively.
The non-radiative heat transfer between the structure and ambient air is given by:
where, hnr is the non-radiative heat transfer coefficient2 ranging from 2 Wm−2K−1 to 8 Wm−2K−1. Here hnr = 8 Wm−2K−1 is set as natural air convection heat transfer to the structure. The absorbed power of the incident thermal radiation from atmosphere Pa(Ta) is given by:
The absorptivity of the atmosphere, ε(λ, θ, ϕ), is given by 1 − τ(λ, θ, ϕ). Here τ(λ, θ, ϕ) is the transmittance value of atmosphere obtained from MODTRAN423. Solar irradiation absorbed by the radiative cooler Ps(T) is given by:
Here, IAM1.5(λ) is the spectral irradiance intensity of solar irradiation at AM 1.5. ε(λ, θsun, Tcooler) is the temperature-dependent emissivity of radiative cooler. The integration is taken from 0.3 μm to 2.5 μm, which cover 97% of the solar incident power. The time-dependent temperature variations of the structure can be obtained by solving the following equation:
Since Ag has relatively high thermal conductivity (406 Wm−1K−1) and the thickness of Ag grating strips is only 400 nm, so the thermal resistance is negligible. The heat capacitance of the reconfigurable photonic structure, C, consists of the PDMS thin film and PDMS grating strip with a thickness of 1200 nm (h1 + h2).
We present the net cooling power as a function of the structure’s temperature without (Fig. 4b) and with (Fig. 4c) the influence of non-radiative heat transfer, respectively. Figures 4b, c show that the structure has a larger net cooling power in a closed environment (hnr = 0 Wm−2K−1) than the one that is open to the ambient environment (hnr = 8 Wm−2K−1) at any temperature for different strains. The net nighttime radiative cooling is higher than the daytime’s since the absorbed solar irradiance neutralizes part of the cooling power that the structure radiates out to the outer space in the daytime. The net cooling power of the original structure is higher than that of the stretched one (ϵ = 120%) whether it is open to ambient or not, and most of the stretched one’s cooling power is negative, that is, it increases the temperature of the structure. Therefore, the original and stretched states of the reconfigurable structure can be regarded as the complete “ON” and “OFF” states. The temperature of the closed environment in which the net cooling power is positive is lower than the open environment (nighttime: 260 K – 0% strain, 307 K – 0%; daytime (0.9 sun): 287 K – 0%, 313 K – 0%), this is also for the stretched state because the PE convection shield eliminates the non-radiative heating power from the ambient. Therefore, the closed environment is better for a lower desired temperature, while the open environment case is suitable for a higher expected temperature.
The stagnation temperature responses of the continuously adaptive cooling structure under various strains are presented in Fig. 5a by solving Eq. (6) using spectra under different strains. For each strain, both the structure and the ambient is assumed to be 25 °C and we set hnr = 0 Wm−2K−1 and Isolar = 1 sun. When the strain is below 20%, the net cooling power of the reconfigurable structure is positive, its temperature decreases as time evolves, and eventually reaches a stagnation temperature which below the ambient after the 50s (−10% strain → 6.1 °C temperature decrease, 0% strain → 3.9 °C temperature decrease, 10% strain → 1.24 °C temperature decrease). While the strain is above 20%, the system is approaching to the complete “OFF” state, the negative radiative cooling heats the structure up and reaches an equilibrium temperature that is above the initial temperature (20% strain → 4.69 °C temperature increase, 40% strain → 9.4 °C temperature increase, 60% strain → 14.76 °C temperature increase).
a Stagnation temperature of the reconfigurable metamaterials as a function of strains showing the structure with tunable cooling or heating abilities under different strains. Black dashed line shows the ambient temperature is assumed to be 25 °C. b Transient temperature variations of the structure when subjected to dynamic mechanical strain showing the temperature can be controlled around its set temperature. The inset represents the transient temperature variations from 300s to 600s.
Finally, the transient temperature variations of the structure is simulated as a function of time when subjected to continuously varying mechanical strains to keep at a set temperature (Fig. 5b). The system is under an environment with hnr = 0 Wm−2K−1, Isolar = 1 sun and 26 °C of the ambient temperature. The initial temperature of the structure is assumed to be 26 °C which gives humans thermal comfort. We use the spectra of the structure at the original state and 20% strain into the calculation. The set temperature of this structure in the first 300 s is 26 °C. When the structure is in the original state, the radiative cooling feature is total on, and then the structure’s temperature drops below 26 °C from 0 s to 1 s. The temperature of the structure goes up from 1 s to 2 s, since the structure is stretched by 20%. The transient temperature of the structure keeps dynamically changing between 25.7 °C and 26.05 °C after the 15 s with an average temperature of 25.8 °C. It shows that this system can control its temperature in a narrowband around the set temperature. When we change the set temperature at 300 s to be 30 °C, the structure temperature can go up to 30 °C and then stay around that point. The average temperature from 315 s to 600 s is 29.6 °C. This shows the proposed structure has a quick adjustment ability.
Above all, we have presented a conceptive reconfigurable nanophotonic design of mechanical deformation induced radiative cooling that can continuously adjust the radiative cooling when subjected to different mechanical strains. A PDMS thin film and grating strips allow the reversible stretching of the structure. Deformation of the PDMS thin film and PDMS gratings leads to a non-negligible change of the thin film thickness and filling ratio of PDMS grating strips, and hence, the spectral emissivity of the structure over the atmospheric window can be actively and continuously adjusted. Compared with other self-adaptive radiative cooling for a fixed critical temperature, our designs have various stagnation temperatures under different strains, that gives us more options for engineering applications. Moreover, strains above 20% can switch the radiative cooling to heating and the fluctuational temperature control can be achieved with a dynamic switching between 0% and 20% strain. This work verifies that the elastic materials have a great potential to be applied in the mechanical deformation induced thermal devices and energy systems at the nano length scale. As a proof of concept demonstration in this work, the elastic polymer PDMS is adopted as the host material, and other transparent soft polymers like silica gel can also serve as an alternative. Such designs can be potentially applied in a series of applications, such as green buildings, textiles, and automobiles for energy-saving and thermal comfort enhancing.
Methods
The hemispherical emissivity of the reconfigurable nanophotonic structure can be expressed as24:
where c is the speed of light in vacuum, ω is the angular frequency, and kρ is the magnitude of inplane wave vector. \({\widetilde{R}}_{{\mathrm{h}}}^{(\mu )}\) and \({\widetilde{T}}_{{\mathrm{h}}}^{(\mu )}\) are the polarization dependent effective reflection and transmission coefficients which can be calculated using the recursive relations of Fresnel coefficients of each interface25. The dielectric functions can be related to real (n) and imaginary (κ) parts of refractive index as \(\sqrt{\varepsilon }=n+i\kappa\). Dielectric functions of the materials (PDMS, SiC, Si3N4, BN, and Ag) utilized in this work are taken from literature16,20,26,27,28,29. The Bruggeman effective medium theory is employed to predict the dielectric function of the nanoparticles embedded PDMS thin film composite. Here, the diameters of these three nanopartiles are confined to be 80 nm that is much smaller than the shortest wavelength of interest (400 nm) and the thickness of the PDMS layer. Besides, the sum of the volume fractions of these nanoparticles is below 33% (the maximum volume fraction limit of Bruggeman effective medium approximation)30. Therefore, the effective dielectric function of multi-species of nanoparticles can be calculated:
where ηi is the volume fraction of different nanoparticles, εi stands for the dielectric function of different nanoparticles. ε is the dielectric function of the matrix. As the design here involves a one-dimensional grating structure of PDMS, the second order approximation of effective medium theory is used to obtain the effective dielectric properties given by31:
where εA and εB are dielectric functions of two media (PDMS and vacuum) in surface gratings. The expressions for zeroth order effective dielectric functions εTE,0 and εTM,0 are given31,32. This effective medium theory and semi-analytical approach has been experimentally demonstrated in Liu et al.’s18 recent published work and computationally verified by the Lumerical FDTD 3D Electromagnetic Simulator as shown in the Supplementary Fig. 4 and Supplementary Note 4s.
Data availability
The authors declare that the main data supporting the findings of this study are contained within the paper. All other relevant data are available from the corresponding author upon reasonable request.
Code availability
All the relevant code is available from the corresponding author upon reasonable request.
References
Agency, I. E. The Future Of Cooling: Opportunities For Energy-efficient Air Conditioning (OECD Publishing, 2018).
Ono, M., Chen, K., Li, W. & Fan, S. Self-adaptive radiative cooling based on phase change materials. Opt. Express 26, A777–A787 (2018).
Catalanotti, S. et al. The radiative cooling of selective surfaces. Solar Energy 17, 83–89 (1975).
Granqvist, C. & Hjortsberg, A. Surfaces for radiative cooling: silicon monoxide films on aluminum. Appl. Phys. Lett. 36, 139–141 (1980).
Orel, B., Gunde, M. K. & Krainer, A. Radiative cooling efficiency of white pigmented paints. Solar Energy 50, 477–482 (1993).
Zhai, Y. et al. Scalable-manufactured randomized glass-polymer hybrid metamaterial for daytime radiative cooling. Science 355, 1062–1066 (2017).
Mandal, J. et al. Hierarchically porous polymer coatings for highly efficient passive daytime radiative cooling. Science 362, 315–319 (2018).
Li, T. et al. A radiative cooling structural material. Science 364, 760–763 (2019).
Rephaeli, E., Raman, A. & Fan, S. Ultrabroadband photonic structures to achieve high-performance daytime radiative cooling. Nano Lett. 13, 1457–1461 (2013).
Raman, A. P., Anoma, M. A., Zhu, L., Rephaeli, E. & Fan, S. Passive radiative cooling below ambient air temperature under direct sunlight. Nature 515, 540–544 (2014).
Leroy, A. et al. High-performance subambient radiative cooling enabled by optically selective and thermally insulating polyethylene aerogel. Sci. Adv. 5, eaat9480 (2019).
Wang, X. et al. Scalable flexible hybrid membranes with photonic structures for daytime radiative cooling. Adv. Funct. Mater. 30, 1907562 (2020).
Wu, S.-H. et al. Thermal homeostasis using microstructured phase-change materials. Optica 4, 1390–1396 (2017).
Dietrich, M. K., Kuhl, F., Polity, A. & Klar, P. J. Optimizing thermochromic vo2 by co-doping with w and sr for smart window applications. Appl. Phys. Lett. 110, 141907 (2017).
Mandal, J. et al. Porous polymers with switchable optical transmittance for optical and thermal regulation. Joule 3, 3088–3099 (2019).
Querry, M. R. Optical Constants Of Minerals And Other Materials From The Millimeter To The Ultraviolet (Chemical Research, Development & Engineering Center, US Army Armament, 1987).
Larruquert, J. I. et al. Self-consistent optical constants of sic thin films. J. Opt. Soc. Am. A 28, 2340–2345 (2011).
Liu, X., Tian, Y., Ghanekar, A. & Zheng, Y. Spectral selectivity of multiple nanoparticles doped thin films. Opt. Express 27, A1591–A1600 (2019).
Ciesielski, A., Skowronski, L., Trzcinski, M. & Szoplik, T. Controlling the optical parameters of self-assembled silver films with wetting layers and annealing. Appl. Surf. Sci. 421, 349–356 (2017).
Zhang, X., Qiu, J., Li, X., Zhao, J. & Liu, L. Complex refractive indices measurements of polymers in visible and near-infrared bands. Appl. Opt. 59, 2337–2344 (2020).
Böhmer, J. Constructing a Platform For Testing Biomarkers Of (Infected) Red Blood Cells. PhD thesis, Faculty of Science and Engineering (2018.)
Zhang, Z. M. Nano/microscale Heat Transfer (Springer, 2007.)
Berk, A. et al. Optical Spectroscopic Techniques And Instrumentation For Atmospheric And Space Research III, 3756, 348–353 (International Society for Optics and Photonics, 1999).
Ghanekar, A., Lin, L., Su, J., Sun, H. & Zheng, Y. Role of nanoparticles in wavelength selectivity of multilayered structures in the far-field and near-field regimes. Opt. Express 23, A1129–A1139 (2015).
Chew, W. C. & Chew, W. C. Waves And Fields In Inhomogeneous Media 522 (IEEE press, New York, 1995).
Palik, E. D. Handbook of Optical Constants of Solids, Vol. 3. (Academic Press, 1998).
Luke, K., Okawachi, Y., Lamont, M. R., Gaeta, A. L. & Lipson, M. Broadband mid-infrared frequency comb generation in a si 3 n 4 microresonator. Opt. Lett. 40, 4823–4826 (2015).
Neuner III, B. et al. Midinfrared index sensing of pl-scale analytes based on surface phonon polaritons in silicon carbide. J. Phys. Chem. C 114, 7489–7491 (2010).
Yang, H. U. et al. Optical dielectric function of silver. Phys. Rev. B 91, 235137 (2015).
Choy, T. C. Effective Medium Theory: Principles And Applications, Vol. 165. (Oxford University Press, 2015).
Raguin, D. H. & Morris, G. M. Antireflection structured surfaces for the infrared spectral region. Appl. Opt. 32, 1154–1167 (1993).
Glytsis, E. & Gaylord, T. K. High-spatial-frequency binary and multilevel stairstep gratings: polarization-selective mirrors and broadband antireflection surfaces. Appl. Opt. 31, 4459–4470 (1992).
Acknowledgements
This project is supported by the National Science Foundation through grant number CBET-1941743.
Author information
Authors and Affiliations
Contributions
X.L. and Y.Z. develop the model. X.L. and Y.T. do the calculation and write the manuscript with help from all other authors. A.G., F.C., and M.A. contribute to the development of ideas and approaches. All authors provide critical feedback and help revise the final version of the manuscript. Y.Z. supervises this project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Primary handling editor: Aldo Isidori.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, X., Tian, Y., Chen, F. et al. Continuously variable emission for mechanical deformation induced radiative cooling. Commun Mater 1, 95 (2020). https://doi.org/10.1038/s43246-020-00098-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00098-8
This article is cited by
-
Bilateral passive thermal management for dynamical temperature regulation
Scientific Reports (2024)
-
Photonic structures in radiative cooling
Light: Science & Applications (2023)