Abstract
Nonlinear response in a material increases with its index of refraction as n4. Commonly, n ~ 1 so that diffraction, dispersion, and chromatic walk-off limit nonlinear scattering. Ferroelectric crystals with a periodic 3D polarization structure overcome some of these constraints through versatile Cherenkov and quasi-phase-matching mechanisms. Three-dimensional self-structuring can also lead to a giant optical refraction. Here, we perform second-harmonic-generation experiments in KTN:Li in conditions of giant broadband refraction. Enhanced response causes wavelength conversion to occur in the form of bulk Cherenkov radiation without diffraction and chromatic walk-off, even in the presence of strong wave-vector mismatch and highly focused beams. The process occurs with a wide spectral acceptance of more than 100 nm in the near infrared spectrum, an ultra-wide angular acceptance of up to ±40∘, with no polarization selectivity, and can be tuned to allow bulk supercontinuum generation. Results pave the way to highly efficient and adaptable nonlinear optical devices with the promise of single-photon-to-single-photon nonlinear optics.
Similar content being viewed by others
Introduction
Frequency conversion and parametric amplification are fundamental ingredients for a wide family of applications, including light sources, detection, optical processing, and quantum-state generation1,2,3,4. For quantum technology, a versatile and super-efficient nonlinear process is the key to photon-based quantum computing5,6,7. In most schemes, optical nonlinearity can only be effectively harnessed when the coupling mechanism is driven by a cumulative wave interaction based on constructive interference. This imposes specific constraints on the available conversion schemes, so-called phase-matching conditions that depend both on the polarization, wavelength, and direction of propagation of the interacting waves and on the specific nonlinear susceptibility of the medium1.
These constraints can be overcome in engineered ferroelectric crystals with a full three-dimensional (3D) periodic spontaneous polarization distribution through quasi-phase-matching8,9,10,11,12 and Cherenkov phase-matching13,14,15,16,17,18,19,20. 3D lattices of spontantabfigeous polarization also occur naturally in nanodisordered ferroelectrics in the form of supercrystals21, in which case the highly ordered domain mosaic also leads to giant broadband optical refraction22. This has a direct effect on nonlinear scattering. Considering material polarization P in terms of the Taylor series expansion in the propagating optical field Eopt, i.e., \(P={\epsilon }_{0}({\chi }^{(1)}{E}_{{\mathrm{{opt}}}}+{\chi }^{(2)}{E}_{{\mathrm{{opt}}}}^{2}+...)\)1,23, the first term describes linear response through the first-order susceptibility χ(1) = n2 − 1, while higher-order terms describe nonlinear effects. The validity of the expansion implies χ(m+1)/χ(m) ~ 1/Eat, where Eat is the scale of the atomic electric field of the substance. It follows that the intensity of an arbitrary allowed nonlinear scattering process scales with \({({\chi }^{(m)})}^{2}{({E}_{{\mathrm{{opt}}}})}^{2m} \sim {({\chi }^{(1)}{E}_{{\mathrm{{opt}}}})}^{2}{({E}_{{\mathrm{{opt}}}}/{E}_{{\mathrm{{at}}}})}^{2m}\), and the intensity of any higher-order scattering process scales with n4 (ref. 3). In these terms giant refraction, i.e., an index of refraction n ≫ 1 across the visible and near infrared spectrum, forms a direct route to strongly enhanced nonlinear response.
Here we investigate second-harmonic generation (SHG) in a ferroelectric supercrystal manifesting giant refraction. Enhanced response allows the process to occur through bulk nonlinear Cherenkov radiation even for highly focused non-phase-matched beams, a method to achieve constraint-free wavelength conversion.
Results and discussion
Giant refraction Cherenkov SHG
In the paradigm nonlinear optical process, SHG is generated at wavelength λ/2 (and angular frequency 2ω) by the anharmonic response of dipoles driven by the pump at wavelength λ24. The process occurs most efficiently when the converted signal interferes constructively with the pump itself, a phase-matching condition that embodies momentum conservation for the interaction. For any given material, dispersion causes phase-matching to occur naturally in the direction of the pump only for converted light (signal beam) whose wavevector k2ω forms a finite angle \({\theta }_{\mathrm{C}}^{\prime}\) relative to the pump itself kω. This leads to wavelength-dependent constraints on the process geometry while the wavevector mismatch Δk = k2ω − 2kω is accompanied by chromatic walk-off2 (see Fig. 1a, top panels). Collinear phase-matching (Δk = 0) can, in turn, be achieved using material birefringence, which introduces wavelength and polarization constraints1, and quasi-phase-matching, which requires periodic material microstructuring and is also wavelength-selective25,26. With n ≫ 1, the angle at which Cherenkov phase-matching occurs is greatly reduced (\({\theta }_{\mathrm{C}}^{\prime}\simeq 0\)) so that chromatic walk-off does not intervene (see “Giant refraction Cherenkov phase-matching” in “Methods” and in Fig. 1a (bottom panels)).
a For n ~ 1, a finite Cherenkov phase-matching \({\theta }_{\mathrm{C}}^{\prime}\) leads to a limited beam interaction region associated to a finite beam width and chromatic walk-off. For n ≫ 1, chromatic walk-off \({\theta }_{\mathrm{C}}^{\prime}\simeq 0\), so that the interaction region is expanded. b Geometry of giant refraction Cherenkov SHG for the TE and TM cases (see “Giant refraction Cherenkov SHG” section in “Methods”). c Giant refraction is observed in a nanodisordered KTN:Li crystal cooled 15 K below the TC = 313 K Curie point using a white light from a commercial projector, leading to a signature achromatic propagation orthogonal to the input facet (along z) irrespective of the launch direction \(z^{\prime}\) (and launch angle θ0) with diffraction only occuring as the beam leaves the sample (see “Giant refraction experiments” section in “Methods”). d Top view of basic evidence of giant refraction for white light propagation in KTN:Li. e, f SHG is observed using a mode-locked Ti:sa laser (see “SHG setup” section in “Methods”). g Average output SHG power versus pump input power along two different lengths of one sample (sample 1). Conversion scales with \({P}_{\omega }^{2}\) and with \({L}_{z}^{2}\) as would occur for bulk SHG conversion23. Super-broad SHG (h) wavelength and (i) angular acceptance (see “Acceptance” section in “Methods”).
The specific geometrical structure of Cherenkov SHG combined with giant refraction is illustrated in Fig. 1b. The pump propagates inside the sample along the normal to its input facet irrespective of launch angle θi (left panels) and the Cherenkov SHG copropagates with the pump inside the sample (\({\theta }_{C}^{\prime}\simeq 0\), central panels). At the output facet the pump and signal separate at a now finite angle θC, as illustrated for the two cases of transverse electric (TE) and trasverse magnetic (TM) polarizations (central and right panels, respectively). For the TE case, while the pump exits with an angle to the normal θ0 = θi, the Cherenkov SHG forms two beams angled with respect to the pump by θ0 ± θC, with the same polarization as the pump and on the incidence plane (the xz plane). In turn, for the TM case, the SHG Cherenkov radiation separates at the output in the orthogonal plane (the yz plane) (see “Giant refraction Cherenkov SHG” in “Methods”).
We perform experiments in two samples of nanodisordered oxide ferroelectric KTN:Li perovskite (see “Materials” section in “Methods”). These manifest giant refraction, with record-high broadband index of refraction (n > 26) at visible wavelengths. The effect is associated to the emergence of an underlying supercrystal21. Each lattice site of the supercrystal is the core of a periodic 3D vortex and anti-vortex structure, a mesh of spontaneous polarization that forms below the Curie point (see “Supercrystal preparation” section in “Methods”). Typical broadband giant refraction for sample 1 is reported in Fig. 1c, d (see “Giant refraction experiments” section in “Methods”). In Figs. 1e, f we illustrate the scheme used to investigate SHG using 190 fs pulses from a mode-locked Ti:Sa source (see “SHG setup” section in “Methods”). In Fig. 1g we report output SHG power versus pump input power. The observed scaling \({P}_{2\omega }\propto {({P}_{\omega })}^{2}{L}_{z}^{2}\), where Lz is the length of the sample in the z direction, is reminiscent of the undepleted pump regime of standard SHG1,23. The P2ω/Pω ratio is independent of input polarization, and output polarization is found to coincide with the input. In Fig. 1h we report SHG conversion varying the pump wavelength in the available pump spectrum (see “Acceptance” section in “Methods”). As reported in Fig. 1i, SHG conversion is observed for all accessible input angles θi (=θ0), indicating that the conversion occurs also with no input angular acceptance (see “Acceptance” section in “Methods”).
An underlying 3D nonlinear lattice
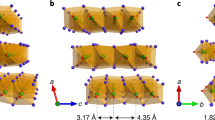
Wavelength conversion is mediated by the second-order nonlinear susceptibility response χ(2) of the KTN:Li perovskite in its noncentrosymmetric tetragonal 4 mm state. In distinction to single-domain or to quasi-phase-matching schemes, the nonlinear process is mediated by a supercrystal with its specific 3D geometry, giant refraction, and underlying ferroelectric domain structure17,27. Hence, while giant refraction causes conversion efficiency to be essentially independent of polarization, input angle, and wavelength, the details of the SHG output strongly depend on input parameters and the supercrystal structure. As illustrated in Fig. 2a, the structure of the 3D supercrystal is a volume lattice of 3D polarization vortices that emerge as the cubic symmetry is broken and polarization charge is screened21,22. The supercrystal forms from the periodic compositional disorder along the growth direction (the a-axis). Each domain has its spontaneous polarization along one of the six principal directions (the direction of the spontaneous polarization is labeled using different colors, see white arrows and colored solids in Fig. 2a). In each domain (of a given color), the corresponding nonlinear susceptibility tensor d depends on its orientation. Consider now the pump focused into a vortex site on the a, b facet of the supercrystal (Fig. 2b, c). For a TM polarization, most of the component solids lead to a net zero χ(2) effect, as light experiences a sequence of oppositely polarized tetrahedrals. The tetrahedrals that dominate χ(2) response are those with a spontaneous polarization in the a direction, if light propagates along the c direction shifted in the b direction above and below a single polarization vortex. Here conversion occurs through a sequence of solids with identically oriented polarization (see Fig. 2b). In the TE case, the situation is analogous, but the SHG signal is now produced for light propagating in the c direction in regions shifted in the a direction in proximity of the vortex (see Fig. 2c). Focusing the pump on the ab facet into a polarization vortex leads to the output intensity distribution reported in Fig. 2d–f. For a λ = 810 nm pump beam polarized at 45° with respect to the crystal a and b axes, a signature SHG Cherenkov output peaked at λ/2 = 405 nm is detected formed by two TE components in the a direction and two TM components in the b direction, the pump beam being at the center of this diamond-like distribution (Fig. 2d). For a TE pump, two TE components in the a direction are dominant (Fig. 2e), while for a TM pump, two TM components along the b-axis form (Fig. 2f). Similar results are observed in both samples 1 and 2. An illustration of the SHG experiments for a pump focused into a single polarization vortex in the ab facet and into an anti-vortex both in the bc and ac facets is reported in Fig. 2g. The situation for a pump focused onto the ac facet is reported in Fig. 2h. Here, only the b oriented ferroelectric tetrahedrals can contribute to giant refraction Cherenkov SHG, and this only for the TM polarization, a condition that is achieved focusing the pump on an anti-vortex as opposed to a vortex. The output structure preserves the TM polarization and has a greatly enhanced output angular spectrum that no longer manifests localized peaks. A similar situation occurs also for light focused onto the bc facet, as reported in Fig. 2i, where the output SHG is emitted at all available angles (see Fig. 2i inset photographs). The observed SHG follows the basic giant refraction SHG Cherenkov mechanism illustrated in Fig. 1b (see “Cherenkov SHG experiment section” in “Methods”).
a Illustration of a specific realization of a supercrystal. The spontaneous polarization, the white arrows, determines the specific χ(2) response of each composing tetrahedral (a color coding is implemented). The actual structure of a fundamental Λ × Λ × Λ cube is illustrated through a sequential build-up adding groups of tetrahedral domains. The lattice constant Λ (≃50 μm) is fixed by the built sample growth process (see “Materials” section in “Methods”). The supercrystal can have many different chiral realizations. The one illustrated here serves to explain the specific results found, relative to the crystal growth axis a. Indicated are the regions leading to strongest SHG, i.e., the core of polarization vortices in the ab facet and the core of anti-vortices in the ac and bc facets. b, c Non-zero contributions to χ(2) are illustrated for the TM (b) and TE cases (c). d–f Output spatial distribution and polarization distribution for a pump polarized at 45° (d), TE (e), and TM (f). g Schematic illustration of the experiments for a pump focused into a single polarization vortex in the ab facet and into an anti-vortex both in the bc and ac facets. h SHG for a pump focused in an anti-vortex in the ac facet. As illustrated in the inset, the only finite contribution to SHG is mediated by b polarized domains through the d15 component for TM. i SHG for a pump focused in an anti-vortex in the bc facet. Results are analogous to the ac facet, while here a full angle Cherenkov emission is clearly visible (2θC = π). Note how, in distinction to random-phase-matching, no lateral emission is observed30,37,38, and all SHG is originating, as expected, solely from the output facet (see inset photographs).
Results on Cherenkov SHG reported in Fig. 2, these including conversion for light propagating along all three principal crystal axes, provide a nonlinear corroboration of evidence of a 3D ferroelectric lattice associated to transmission microscopy21,22 and polarization transmission microscopy28. They also provide, through a direct measurement of θC, an estimate of the supercrystal 2\(\Delta n{n}_{2\omega }={(\sin {\theta }_{\mathrm{C}})}^{2}\) (see “Cherenkov SHG experiment” section in methods). In the case of Fig. 2b, 2Δnn2ω ≃ 0.08. Snell refraction experiments in this direction provide n2ω > 26, so that we expect a Δn < 0.001, corresponding to an ultra-low approximate dispersion of dn/dλ < −0.002 μm−1. The prediction fits in well with our understanding of the supercrystal phase, for which chromatic dispersion is expected to be strongly reduced. To investigate this further we directly measured supercrystal chromatic dispersion using group-velocity dispersion29 for T > TC, where no supercrystal forms, and T < TC, where the supercrystal forms. Results are reported in Fig. 3a. As expected, the onset of the supercrystal structure is accompanied by a sharp reduction in average values of dispersion, from dn/dλ ≃ −0.10 μm−1 to dn/dλ ≃ −0.06 μm−1. This, in turn, is not sufficiently small to circumvent the need for Cherenkov phase-matching (θC ≃ 0.28 in Fig. 2d–f). Strong SHG conversion does not allow a local vortex and anti-vortex dispersion measurement.
We compared supercrystal SHG in the two samples to identify possible growth and composition related effects. We found that sample 1 and 2 manifest the same geometrical behavior as regard to giant refraction and Cherenkov SHG, while their net SHG conversion efficiency is considerably different, as reported in Fig. 3b. This may be connected to the different values of Curie temperature and/or different values of Λ (70 μm for sample 1 and 50 μm for sample 2). An estimate of the effective \({\chi }_{\mathrm{{GR}}}^{(2)}\) is provided in the “\({\chi }_{\mathrm{{GR}}}^{(2)}\) evaluation” section in “Methods”.
Spectral and angular acceptance
The angle at which Cherenkov phase-matching is achieved is wavelength-dependent (θC(λ)). To characterize this we report in Fig. 4a measurements of spectral acceptance for a detector able to collect light only from a limited cone at two fixed angles θ1 (yellow dots) and θ2 (magenta dots). The result is a spectral bandwidth whose peak follows θC(λ) and whose width is in agreement with the angular acceptance (see “Angular versus wavelength acceptance” section in “Methods”). Since giant refraction allows no diffraction or pump-signal walk-off, Cherenkov phase-matching will occur for all wavelengths. In turn, not all Cherenkov SHG can actually leave the output facet of the sample, as total internal reflection occurs for wavevectors that have an internal incidence angle \(\theta_i ^{\prime} \, > \, 1/{n}_{2\omega }\) with the output facet. Hence, for a θi = 0, \(\theta_i ^{\prime} ={\theta }_{\mathrm{{C}}}^{\prime}=\arccos ({n}_{\omega }/{n}_{2\omega })\), a zero emitted SHG will result for \(\arccos ({n}_{\omega }/{n}_{2\omega }) \, > \, 1/{n}_{2\omega }\). The effect can be appreciated recalling the full angle-integrated measurement reported in Fig. 1h (blue circles). For a given pump wavelength, the same effect will occur as a function of θ0 (θi): assuming the previously evaluated \(\sqrt{2\Delta n{n}_{2\omega }}\simeq 0.28\), we expect to observe a total internal reflection for an input ∣θ0∣ > 46∘ (see “Total internal reflection” section in “Methods”). Measured values of θC(λ) are reported in Fig. 4b and are in agreement with chromatic dispersion results of Fig. 3a. In Fig. 4c we report SHG output, for a λ = 810 nm pump, for different pump launch angles, as in Fig. 1i, but distinguishing between the two Cherenkov components +θC (violet circles) and −θC (magenta circles). SHG suppression is observed for ∣θ0∣ > 25∘. Illustration of the geometry leading to SHG suppression caused by total internal reflection of the Cherenkov radiation is reported in Fig. 4d. Once again, the broad spectral and angular acceptance underline how the Cherenkov mechanism in action is not Bragg in nature nor does it relate to quasi-phase-matching.
a Spectral acceptance for a detector placed at two fixed angles (yellow and magenta circles) compared to the super-broad spectral acceptance capturing all emitted light (blue circles). b Observed Cherenkov angle versus wavelength. c Angular acceptance considering the two TE Cherenkov radiation beams separately (magenta and violet circles). d Illustration of the geometry leading to SHG suppression caused by total internal reflection of the Cherenkov radiation.
Enhanced Fresnel reflection and extreme nonlinearity
The n ≫ 1 regime leading to SHG (as discussed in Fig. 2) is accompanied by strong Fresnel reflection at the input and output facets. This does not allow a direct evaluation of enhanced wavelength conversion occuring inside the sample by detecting the converted light transmitted outside the sample. Fresnel reflection can be measured directly for the pump, that experiences a conventional R ≃ 0.2, compatible with an average index of refraction ~2.6, as expected for light focused onto the vortex and anti-vortex core22. By aligning the pump in different positions, a maximum is observed R ≃ 0.45 compatible with an average n ~ 5. In these conditions, conversion can be analyzed through the observation of beam dynamics along the propagation direction. In a standard system, this leads an evolution governed by the so-called Manley–Rowe relationships1,23. In Fig. 5a, b we report scattered SHG light from the body of the sample. Observed scattering in our experiment disappears altogether only when the sample is heated above the Curie point TC (Fig. 5c) and for T < TC leads to an almost constant SHG signal from the input facet of the sample to the output facet. Analysis of the scattered light versus propagation distance in the sample for different temperatures is reported in Fig. 5d. The transition from SHG to supercontinuum generation is achieved by doubling the input pump numerical aperture, as reported in Fig. 5e, f (see the “Supercontinuum generation” section in “Methods”). The origin of this broadband emission and its relation to specific nonlinear processes is still unclear. We recall that SHG with remarkably wide angular and spectral acceptance can be observed in multidomain ferroelectrics30,31. The enhanced tunability in these studies is associated to phase-matching supported by the underlying disordered domain structure, while in our experiments, phase-mismatch (the transverse component Δk in Fig. 1) persists. The tunability here is then a product of giant refraction that does not involve Bragg scattering. It serves to further compare our findings to highly versatile SHG in nonlinear photonic crystals32,33. Here the physical origin of efficient SHG is phase-matching mediated by vector components of the reciprocal lattice in the linear or nonlinear response. It follows that the extent of the pump beam must be larger than the lattice constant. In our case the 15 μm beam hardly occupies even a single lattice site (Λ ≃ 50 μm).
a, b Top view of pump and SHG signal scattered light (T = TC − 35 K, sample 2). c Scattered light from the body of sample 2 of SHG signal, almost constant for T < TC from the input facet of the sample to the output facet, while disappears when the sample is heated above the Curie point TC. d Analysis of the scattered light versus propagation distance in the sample for different temperatures indicates a characteristic absence of propagation dynamics for the ferroelectric case (T = TC − 35 K, magenta full circles), for the Curie temperature on heating from the ferroelectric phase (\({T}_{\mathrm{C}}^{-}\), heating from TC − 35 K to TC) and on cooling from the paraelectric phase (\({T}_{\mathrm{C}}^{+}\), cooling from TC + 10 K to TC). e Evidence of supercontinuum generation (see “Supercontinuum generation” section in “Methods”). For further details see Video in Supplementary Movie. f Spectrum and multispectral images (~10 nJ/pulse pump at input).
Conclusions
The n ≫ 1 regime forwards a wide range of hereto unobserved and highly versatile nonlinear effects that side other pioneering experiments, such as mismatch-free nonlinear propagation in zero-index materials34. In this paper we have reported our investigation of SHG in conditions of giant refraction. The converted light appears in the form of Cherenkov radiation even in the presence of phase-mismatch. This reduces constraints on launch angle, a feature that can considerably mitigate alignment requirements in nonlinear-based light sources. Furthermore, the SHG manifests increased tolerances in wavelength and polarization, a property that can be implemented to support multiple simultaneous nonlinear processes, with specific impact, for example, in the conversion of infrared images to the visible spectrum.
Methods
Giant refraction Cherenkov phase-matching
In a material with giant broadband refraction, nω, n2ω ≫ 1. At the sample input facet the plane-wave components of the pump refract according to the Snellʼs law \({\theta }_{\mathrm{r}}=\arcsin (\sin {\theta }_{\mathrm{i}}/{n}_{\omega })\simeq 0\), where θi and θr are the incidence and refraction angle. Cherenkov phase-matching occurs for SHG wavevectors at an angle relative to the pump \({\theta }_{\mathrm{C}}^{\prime}=\arccos ({n}_{\omega }/{n}_{2\omega })\simeq 0\), insomuch that Δn = (n2ω − nω)/nω ≪ 1, even for a finite n2ω − nω.
Giant refraction Cherenkov SHG
SHG polarization is \({P}_{i}^{2\omega }={d}_{ijk}{E}_{j}^{\omega }{E}_{k}^{\omega }\), where Eω is the pump field and dijk is the nonlinear optical susceptibility tensor, that has non-zero components d31, d33, and d15 for the tetragonal 4mm symmetry of KTN:Li35. Considering the TE case for a spontaneous polarization parallel to the optical polarization (along the y-axis), \({P}_{y}^{2\omega }={d}_{33}{({E}_{y}^{\omega })}^{2}\). The emitted Cherenkov radiation must then have a k2ω in a plane orthogonal to P2ω, i.e., in the incidence plane (xz) (central panels in Fig. 1b). Analogously for the TM case, in which, for a spontaneous polarization parallel to the optical polarization (along the x axis), the nonlinear polarization is dominated by the x component \({P}_{x}^{2\omega }={d}_{33}{({E}_{x}^{\omega })}^{2}\), so that Cherenkov SHG occurs in the yz plane (right panels in Fig. 1b). In the TM case, an SHG contribution arises also for a domain with a spontaneous polarization along the z-axis, i.e., \({P}_{x}^{2\omega }=2{d}_{15}{E}_{x}^{\omega }{E}_{z}^{\omega }\) and \({P}_{z}^{2\omega }={d}_{31}{({E}_{x}^{\omega })}^{2}+{d}_{33}{({E}_{z}^{\omega })}^{2}\). The emitted Cherenkov SHG will then be TM polarized and have a k2ω orthogonal to P2ω in the incidence plane xz (i.e., along the y-axis). This situation is particularly relevant for results reported in Fig. 2h, i. In this case the spontaneous polarization is oriented orthogonal to the input facet, so that while the pump is prevalently experiencing a standard index of refraction nω, the SHG is dominated by d33 and has a stronger component along the direction of spontaneous polarization. The result then is that nω/n2ω ≪ 1, so that \({\theta }_{\mathrm{C}}^{\prime}\) inside the sample remains finite, while all waves still have their Poynting vectors along the normal to the input facet (giant refraction). The angular spectrum of the focused pump can then populate, in a continuous manner, a wide angle of SHG emission around the pump average propagation direction that, on output, can even occupy the entire angular spectrum (2θC = π, Fig. 2i).
Materials
The two samples (sample 1 and sample 2) are zero-cut polished lithium-enriched solid solutions of potassium-tantalate-niobate (KTN:Li). They have the same composition K0.997Ta0.64Nb0.36O3:Li0.003, while in the flux of sample 2 traces of Mo impurities are introduced. Sample 1 measures along its three axes 4.62(a) × 3.86(b) × 1.6(c) mm while sample 2 is 6.96(a) × 3.86(b) × 1.6(c) mm. The samples form perovskites with room-temperature cubic-to-tetragonal (m3m to 4mm) ferroelectric phase-transition temperatures TC,1 = 315 K and TC,2 = 333 K. Both are grown through the top-seeded method that causes them to have a built-in spatially periodic oscillation in composition along the growth axis (the a-axis) that translates into an approximately periodic Λ = 50 μm striation grating (for sample 2) that then determines the lattice constant of the underlying supercrystal21.
Supercrystal preparation
Each sample, initially equilibrated at T = 298 K and unbiased, is heated to ≃373 K at a rate of 0.6 K/min and is DC-biased by an electric field that increases at a constant rate from 0 to 4 kV cm−1. The sample is then cooled back down to T = 298 K while the bias field remains constant at 4 kV cm−1. The DC field is applied between the two parallel faces along the a-axis (growth axis). To minimize the temperature gradient, the sample is dipped into a Teflon holder that contains temperature-resistant mineral oil. The supercrystal can now be further modified having the sample undergo successive thermal cycles, composed of a first stage in which the unbiased sample is heated to TC + 10 K at a rate of 0.35 K s−1 immediately followed by a second cooling stage to TC − 35K at a rate of 0.1 K s−1. Once the thermal protocol is completed, each sample is used for optical experiments at a given temperature T < TC.
Giant refraction experiments
The sample is cooled using a current-controlled Peltier junction to TC − 35 K and rotated by a tunable angle θ0 with respect to the optical propagation axis \(z^{\prime}\) (see scheme illustrated in Fig. 1c). Light is collected from a commercial projector (NEC-VE281X, XGA, 2800 lumens) polarized using a linear polarization filter and focused onto the input facet of the sample using a high-aperture long-working distance microscope objective (Edmund Optics, ×100, 3-mm working distance, achromatic, NA = 0.8) positioned ≃30 cm from the output lens of the projector. The top-view image in Fig. 1d is taken using an Apple iPhone7. Top-view scattered light from within the sample and from the lower metallic support indicates strong reflection from the input facet and a non-spreading propagation inside the sample normal to the input facet irrespective of wavelength, θ0, and launch polarization, and a regular diffraction of the beam exiting the sample, as expected for giant refraction.
SHG setup
SHG experiments (see scheme and photo of apparatus in Fig. 1e) are carried out in the 790–880 nm range using a Tsunami Spectra Physics Ti:Sa CW mode-locked laser (maximum output power of 0.6 W at λ = 810 ± 7 nm), with a repetition rate of 80 MHz and a pulsewidth of 190 fs. Laser beam linear polarization, TM or TE, or a superposition of the two, is set using a λ/2 waveplate. The beam is focused onto the input facet of the θ0-rotated sample using a 50-mm-focal-length lens. The pump beam is focused to an input FWHM ≃ 15 μm. The SHG pattern is detected on a white screen placed at d = 7.0 cm from the output facet of the sample using a Canon EOS 50d. SHG power P2ω is measured in Fig. 1g (and Fig. 3b) filtering and focusing converted light onto a power meter for a TM pump (and SHG).
Acceptance
Spectral acceptance is reported for θ0 = 0 in arbitrary power units P2ω normalized to the peak spectral value. Since each measurement at different wavelengths is carried out with different pump power, the output signal is rescaled appropriately, i.e., divided by the input power squared. Angular acceptance is evaluated for a 810 nm pump and for all accessible launch angles. In both spectral and angular acceptance experiments, output SHG is collected by a lens and focused onto a power meter. Note that on consequence of giant refraction, the effective propagation length in the sample is launch-angle independent and equal to the length of the sample in the propagation direction (see Fig. 1b). Wavelength dependence, due to the Fresnel reflection at output, is analyzed in Fig. 4.
Cherenkov SHG experiment
\(\cos ({\theta }_{\mathrm{C}}^{\prime})=(2{k}_{\omega }/{k}_{2\omega })={n}_{\omega }/{n}_{2\omega }\). For normal dispersion (n2ω > nω) nω = n2ω − Δn, so that since \({\theta }_{\mathrm{C}}^{\prime}\ll 1\), \({\theta }_{\mathrm{C}}^{\prime}\simeq \sqrt{2\Delta n/{n}_{2\omega }}\). Outside the sample, \(\sin ({\theta }_{\mathrm{C}})={n}_{2\omega }\sin {\theta }_{\mathrm{C}}^{\prime}\simeq {n}_{2\omega }{\theta }_{\mathrm{C}}^{\prime}\). Measuring θC leads to an estimate of \(\Delta n={(\sin ({\theta }_{\mathrm{C}}))}^{2}/(2{n}_{2\omega })\). For a pump focused on the ab facet in Fig. 2b, for both the TE and TM cases, the two SH beams emerge in the x–z (i.e., ac) and y–z (i.e., bc) planes at an angle θC ≃ 0.28 rad with respect to the pump (for all accessible values of θi). According to the Cherenkov model, this implies that \(\sqrt{2\Delta n{n}_{2\omega }}\simeq 0.28\). For light focused on the ac facet in Fig. 2h and bc facet in Fig. 2i, SHG is generated from tetrahedral domains oriented along the b-and a-axis, respectively, i.e., with a spontaneous polarization orthogonal to the input facet. Involving both d31, d33, d15, the result is a TM SHG in the bc and ac plane, respectively. The observed θC ≃ π/2 (see detailed photos in the inset of Fig. 2i), corresponding to a \(\sqrt{2\Delta n{n}_{2\omega }}\simeq 1\). A similar contribution associated to d15 in the case reported in Fig. 2b, c, where d33 contributions are dominant, and leads to the “spurious” SHG scattering in the TM case (Fig. 2f) as opposed to the TE case (Fig. 2e).
\({{\boldsymbol{\chi }}}_{\mathrm{{GR}}}^{(2)}\) evaluation
To provide an estimate of the effective nonlinear susceptibility \({\chi }_{\mathrm{{GR}}}^{(2)}\) we can make use of the simplified plane-wave model (diffraction is absent in the GR regime) described in ref. 1 (pp. 77–79). For sample 1, the time averaged powers at the output are Pω = 510 mW and P2ω = 2 μW for the 190 fs pulse train operating at 80 MHz repetition rate, while the beam waist is taken to be w0 ≃ 15 μm. For the purpose of the evaluation of peak intensity and Fresnel reflection, the regions leading to SHG for the TM case have nω ~ n2ω ~ nGR, where nGR ≫ 1. Of the input pump beam, only a portion actually interacts with the tetrahedral structures allowing SHG (the d33 solids in Fig. 2b). The fraction of active area can be evaluated measuring the Fresnel reflection at input and output facets, comparing it to what expected for regions with standard reflection (i.e., for n ≃ 2.2) and those regions that have d33 and hence an enhanced reflection associated to nGR. While longitudinal phase-matching is guaranteed by the Cherenkov-like geometry (Fig. 1a), the aperture of the pump and SHG beams remains finite (\(\Delta \theta ^{\prime} \sim \Delta {\theta }_{{\mathrm{{ext}}}}/{n}_{{\mathrm{{GR}}}}\), where Δθext ≃ 0.07). This introduces a residual longitudinal mismatch. The transverse wavevector mismatch can be evaluated considering θc ≃ 0.28 rad measured outside the sample, leading to Δk ≃ 4.4 μm−1. The result is \({\chi }_{\mathrm{{GR}}}^{(2)}\simeq 5.2\) pm V−1\({{n}^{2}}_{\mathrm{{GR}}}\). Considering even the minimum value of nGR as measured from diffraction and Snell refraction (nGR ≃ 26), we obtain an effective \({\chi }_{{\mathrm{{GR}}}}^{(2)}\simeq 3.5\times 1{0}^{3}\) pm V−1, to be compared to the measured value of standard KTN, i.e., \({\chi }_{{\mathrm{{KTN}}}}^{(2)}\simeq 168\) pm V−1 (n ≃ 2.3)36.
Angular versus wavelength acceptance
To test this we maximized SHG efficiency, i.e., Cherenkov phase-matching is established for the specific pump wavelength λ, and the SHG signal detector is placed so as to capture a single output diffraction-limited mode. As reported in Fig. 4a, changing the pump wavelength without altering the crystal and detector geometry leads to a relative spectral acceptance Δλ/λ ≃ 0.047 that is in agreement with the input pump numerical aperture 2λ/πw0 ≃ 0.05.
Total internal reflection
Total internal reflection of the SHG signal occurs at the output facet when approximately \({\theta }_{\mathrm{C}}^{\prime}+{\theta }_{\mathrm{r}}\, > \, 1/n\), where \({\theta }_{\mathrm{r}}=\sin ({\theta }_{0})/n\). Assuming that \({\theta }_{\mathrm{C}}^{\prime}=\sqrt{2\Delta n/{n}_{2\omega }}\), we have that total internal reflection occurs for \(| \sin ({\theta }_{0})| \, > \, 1-\sqrt{2\Delta n{n}_{2\omega }}\). Taking the value of \(\sqrt{2\Delta n{n}_{2\omega }}\simeq 0.28\) gives ∣θ0∣ > 46∘.
Supercontinuum generation
Experiments are carried out replacing the 50-mm lens with a 25 mm one. The pump is now focused in proximity of the input facet of sample 2 (Fig. 5e) and a characteristic white plume is detected.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Boyd, R. W. Nonlinear Optics 3rd edn (Academic, 2008).
Shen, Y. R. The Principles of Nonlinear Optics (Wiley-Interscience, New York, 1984).
Loudon, R. The Quantum Theory of Light 3rd edn (Oxford Science Publications, 2010).
Brown, E. et al. Dynamic imaging of collagen and its modulation in tumors in vivo using second-harmonic generation. Nat. Med. 9, 796–800 (2003).
Tiecke, T. G. et al. Nanophotonic quantum phase switch with a single atom. Nature 508, 241 (2014).
Reiserer, A., Kalb, N., Rempe, G. & Ritter, S. A quantum gate between a flying optical photon and a single trapped atom. Nature 508, 237 (2014).
Chang, D. E., Vuletic, V. & Lukin, M. D. Quantum nonlinear optics—photon by photon. Nat. Photonics 8, 685–694 (2014).
Wei, D. et al. Experimental demonstration of a three-dimensional lithium niobate nonlinear photonic crystal. Nat. Photonics 12, 596–600 (2018).
Xu, T. et al. Three-dimensional nonlinear photonic crystal in ferroelectric barium calcium titanate. Nat. Photonics 12, 591–595 (2018).
Zhang, X. et al. Switching effects of spontaneously formed superlattices in relaxor ferroelectrics. Opt. Mater. Express 9, 4081–4089 (2019).
Stoica, V. A. et al. Optical creation of a supercrystal with three-dimensional nanoscale periodicity. Nat. Mater. 18, 377–383 (2019).
Liu, S. et al. Nonlinear wavefront shaping with optically induced three-dimensional nonlinear photonic crystals. Nat. Commun. 10, 3208 (2019).
Jelley, J. V. Cerenkov Radiation (Pergmon Press, 1958).
Mathieu, E. Conditions for quasi Cerenkov radiation, generated by optical second harmonic polarisation in a nonlinear cristal. J. Appl. Math. Phys. 20, 433–439 (1969).
Tien, P. K., Ulrich, R. & Martin, J. Optical second harmonic generation in form of coherent Cerenkov radiation from a thin-film waveguide. Appl. Phys. Lett. 17, 447 (1970).
Zhang, Y., Gao, Z. D., Qi, Z., Zhu, S. N. & Ming, N. B. Nonlinear Cerenkov radiation in nonlinear photonic crystal waveguides. Phys. Rev. Lett. 100, 163904 (2008).
Sheng, Y. et al. Three-dimensional ferroelectric domain visualization by Cerenkov-type second harmonic generation. Opt. Express 18, 16539 (2010).
Sheng, Y. et al. Theoretical study of Cerenkov-type second-harmonic generation in periodically poled ferroelectric crystals. J. Opt. Soc. Am. B 29, 312–318 (2012).
Roppo, V. et al. Unified approach to Cerenkov second harmonic generation. Opt. Express 21, 25715–25726 (2013).
Ni, R. et al. Nonlinear Cherenkov difference-frequency generation exploiting birefringence of KTP. Appl. Phys. Lett. 108, 031104 (2016).
Pierangeli, D. et al. Super-crystals in composite ferroelectrics. Nat. Commun. 7, 10674 (2016).
Di Mei, F. et al. Giant broadband refraction in the visible in a ferroelectric perovskite. Nat. Photonics 12, 734–738 (2018).
Armstrong, J. A., Bloembergen, N., Ducuing, J. & Pershan, P. S. Interactions between light waves in a nonlinear dielectric. Phys. Rev. 127, 1918 (1962).
Kleinman, D. A. Theory of second harmonic generation of light. Phys. Rev. 128, 1761 (1962).
Fejer, M. M., Magel, G. A., Jundt, D. H. & Byer, R. L. Quasi-phase-matched second harmonic generation: tuning and tolerances. J. Quant. Electron. 28, 2631–2654 (1992).
Saltiel, S. M. et al. Multiorder nonlinear diffraction in frequency doubling processes. Opt. Lett. 34, 848–850 (2009).
Wang, J. et al. Direct evidence of correlation between the second harmonic generation anisotropy patterns and the polarization orientation of perovskite ferroelectric. Sci. Rep. 7, 9051 (2017).
Ferraro, M. et al. Observation of polarization-maintaining light propagation in depoled compositionally disordered ferroelectrics. Opt. Lett. 42, 3856–3859 (2017).
Bor, Z. & Rácz, B. Dispersion of optical materials used for picosecond spectroscopy. Appl. Opt. 24, 3440–3441 (1985).
Molina, P., Ramírez, Md. L. O. & Bausá, L. E. Strontium barium niobate as a multifunctional two-dimensional nonlinear photonic glass. Adv. Funct. Mater. 18, 709–715 (2008).
Molina, P. et al. Nonlinear prism based on the natural ferroelectric domain structure in calcium barium niobate. Appl. Phys. Lett. 94, 071111 (2009).
Mateos, L. et al. Simultaneous generation of second to fifth harmonic conical beams in a two dimensional nonlinear photonic crystal. Opt. Express 20, 29940–29948 (2012).
Li, H. X. et al. Multicolor Cerenkov conical beams generation by cascaded-χ(2) processes in radially poled nonlinear photonic crystals. Appl. Phys. Lett. 100, 101101 (2012).
Suchowski, H. et al. Phase mismatch-free nonlinear propagation in optical zero-index. Mater. Sci. 342, 1223–1226 (2013).
Yariv, A. & Yeh, P. Optical Waves in Crystals: Propagation and Control of Laser Radiation (Wiley, 2002).
Zhang, H. Y., He, X. H., Shih, Y. H., Harshavardhan, K. S. & Knauss, L. A. Optical and nonlinear optical study of KTa0.52Nb0.48O3 epitaxial film. Opt. Lett. 22, 1745–1747 (1997).
Roppo, V. et al. The role of ferroelectric domain structure in second harmonic generation in random quadratic media. Opt. Express 18, 4012–4022 (2010).
Ayoub, M., Imbrock, J. & Denz, C. Second harmonic generation in multi-domain χ2 media: from disorder to order. Opt. Express 19, 11340–11354 (2011).
Acknowledgements
This research was supported in part by the Israel Science Foundation (Grant No. 1960/16). F.D.M, and E.D.R. were supported through the ATTRACT project funded by the EC under Grant Agreement 777222, the Sapienza Ricerca di Ateneo 2019 project, and the PRIN 2017 PELM project (grant number 20177PSCKT) .
Author information
Authors and Affiliations
Contributions
A.J.A. developed and synthesized the materials. L.F., L.T., F.D.M., M.F., J.P., and D.P. carried out SHG measurements. L.F. and L.T. carried out chromatic dispersion measurements. G.P. carried out the SC poling procedure. E.D.R., F.D.M., L.F., and P.D.P. elaborated the physical framework and interpretation. L.F., L.T., F.D.M., M.F., J.P., D.P., G.P., F.X., P.D.P., A.J.A., and E.D.R. participated in discussions. E.D.R., L.F., and F.D.M. wrote the article with the help of all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Falsi, L., Tartara, L., Di Mei, F. et al. Constraint-free wavelength conversion supported by giant optical refraction in a 3D perovskite supercrystal. Commun Mater 1, 76 (2020). https://doi.org/10.1038/s43246-020-00077-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00077-z