Abstract
Many technological applications are based on functional materials that exhibit reversible first-order ferroelastic transitions, including elastocaloric refrigeration, energy harvesting, and sensing and actuation. During these phase changes inhomogeneous microstructures are formed which fit together different crystalline phases, and evolve abruptly through strain bursts related to domain nucleation and the propagation of phase fronts, accompanied by acoustic emission. Mechanical performance is strongly affected by such microstructure formation and evolution, yet visualisation of these processes remains challenging. Here we report a detailed study of the bursty dynamics during a reversible stress-induced martensitic transformation in a CuZnAl shape-memory alloy. We combine full-field strain-burst detection, performed by means of an optical grid method, with the acoustic tracking of martensitic strain avalanches using two transducers, which allows for the location of the acoustic-emission events to be determined and the measurement of their energies. The matching of these two techniques reveals interface formation, advancement, jamming and arrest at pinning points within the transforming crystal.
Similar content being viewed by others
Introduction
Martensitic transformations are first-order diffusionless phase transitions observed in a variety of crystalline materials, including metals, ceramics and proteins1,2,3. They occur via cooperative atomic motions producing rapid changes of lattice structure, and typically form inhomogeneous microstructures involving different coexisting crystalline phases and variants. Many technological applications, such as environmentally-friendly elastocaloric refrigeration,4,5,6 waste-energy harvesting7,8, smart sensing and actuating1,3, are based on functional ferroelastic2 materials, like shape-memory alloys, exhibiting highly reversible martensites7,9,10,11. The intermittent progress of the structural transformations is inherent to the first-order character of these solid-state phase transitions2. The microstructure responds to changes in environmental conditions through strain avalanching12,13, with associated bursts of acoustic emission (AE)13,14,15,16,17,18,19,20, related to the nucleation of phase domains and to phase-front advancements 12,13,14. The functional properties and stability of the material are strongly affected6,7,10,11 by these events marking microstructural evolution and reorganization, and their visualisation and thorough understanding is currently a big challenge12,13,17,21,22,23,24.
To shed light on the details of these phenomena, we have studied the strain-avalanching in the stress-induced martensitic transformation in a CuZnAl shape-memory alloy12,14. For this purpose we combined two different techniques: on the one hand, AE detection using two transducers21, which has unbeatable time resolution16 and allows for avalanche localisation and energy measurement; and, on the other hand, strain measurement via the grid method, allowing for full-field strain imaging25,26,27,28,29. These approaches, used separately so far, have much contributed to our understanding of structural transformations in crystalline solids. They are used concurrently here for the first time.
Results
Elongation test
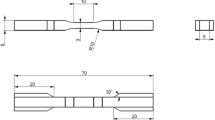
We have used a Cu68.13Zn15.74Al16.13 (at.%) single-crystal grown by the Bridgman method. The specimen is a thin elongated parallelepiped with cylindrical heads for gripping. The vertical y-axis is oriented along the sample length, and close to the [001] crystallographic direction in the bcc austenitic lattice (see refs. 14,21 and Fig. 1a, b for dimensions and details). The elongated shape of this specimen is particularly suitable for our study, which concentrates on lengthwise phase-front propagation treated in a one-dimensional (1D) setting along the y direction (see below). In the absence of applied external force, this alloy exhibits a reversible symmetry-breaking martensitic transformation at Ms = 234 K from a cubic L21 high-temperature parent phase (austenite) to a lower-temperature monoclinic 18R product phase (martensite). The transition can also be induced at room temperature by applying a uniaxial loading. Prior to the present test, an appropriate heat treatment was performed so that the alloy was in an ordered state, free from internal stresses, and with a minimum vacancy concentration. The specimen was then submitted to a series of more than 20 loading-unloading cycles to reach a stationary transition path between the parent and product phases.
a Sketch of the CuZnAl single-crystal specimen (3.85 × 35 × 1.12 mm), with photograph of the grid transferred onto it. b Detail showing the rectangular strip (outlined in white) used to extract the 1D strain profiles along the vertical y-axis, by means of x-averaging of the 2D strain maps produced by the grid method. The white-dashed lines mark the specimen sides. The dark-shaded domain on the grid was used for 2D strain mapping to avoid side effects. c Schematic view of the loading device, showing the position of the piezoelectric transducers used for the 1D localisation, along the y-axis, of the acoustic events.
Figure 1a, b also show the bidimensional grid (with pitch 0.2 mm) transferred onto the specimen25 to follow the strain evolution through the GM (see Methods). The parallel 1D study of AE along the y direction (see Methods) involved the recording of acoustic activity by means of two transducers suitably placed on the grips of the loading apparatus, as in Fig. 1c. The latter is an in-house designed gravity-based device12 producing a strictly monotonic uniaxial load, which can be applied at a very low rate. During the elongation test, with time t running in seconds, we monitored the stress-induced martensitic transformation under the following conditions: (a) preloading of 81.92 MPa; (b) constant loading rate 109.7 Pa/s, up to 88.97 MPa, with a total duration of about 64,200 s (i.e. ~8 h; room temperature: 25.7 ± 0.5 °C). After the application of the preload the force was increased very slowly so as to approach the transformation plateau in almost adiabatic conditions, and to obtain the phase transition with a minimum of precursors or spurious disturbances, and a minimal dependence on the loading history. The observed plateau (duration ~27 min) indeed resulted to be nearly horizontal, shown in black on the macroscopic stress-strain curve of Fig. 2a, with the elastic load-up portions shown in red. To ensure specimen integrity, the loading was stopped shortly after the elastic response resumed at the end of the plateau, although the residual austenite might have further transformed at higher loads. The monitoring of AE during the test, done concurrently to strain detection, recorded ~110,000 [~60,000] AE hits at the upper [lower] transducer, with the corresponding amplitudes and energies (see Methods).
a The elastic part of the stress-strain curve is indicated in red and the transformation plateau in black. Snapshots of the map for the strain component εyy are shown at various loading stages, marked by blue dots on the plateau. b Maps of all the in-plane strain components εxx, εxy, εyy, and of the local rotation angle ω, corresponding to the average-strain value \({\overline{\overline{\varepsilon }}}_{yy}=0.052\). See also Supplementary Movie 1.
Strain field evolution
By suitably processing25,26,27,28 the captured images of the deforming grid, we obtained a sequence of (x, y)-maps during the entire elongation test, giving the spatial distribution on the sample’s face of the linear in-plane strain components εxx, εxy, εyy, and of the local rotation angle ω around the z-axis. Figure 2 displays a number of such maps describing the strain evolution along the transformation plateau.
Because of the 1D character of our analysis of AE activity along the y-axis on this elongated specimen, we focus hereafter on the behaviour of the εyy strain component, whose signal-to-noise ratio is also the highest compared to εxx and εxy. The strain data animation in Supplementary Movie 1 shows the temporal evolution of the εyy-map on the sample (green austenite; red martensite). This evidences the progress of the structural phase change during the test (total duration on the plateau: about 27 min, clocked by the time counter in s, with the blue dot indicating current conditions on the stress-strain curve). We see from Fig. 2a and Supplementary Movie 1 that the austenite-to-martensite transformation mainly proceeded here through the creation and propagation of two triangular fronts (in yellow-orange on the strain maps) lying between pure austenite (in red) and pure martensite (in green). Martensite nucleated at a point with higher stress fluctuations within the bulk or on the surface of the sample. The triangular shape of the observed fronts is explained by the formation of martensitic twinned micro-layers, whose average strains are kinematically compatible with austenite and pure martensite across suitable non-parallel transversal planes in the sample, see for instance the X-microstructures analyzed in Ref. 30. Supplementary Movie 1 also shows the temporal evolution of the associated strain-rate \({\dot{\varepsilon }}_{yy}\) maps on the sample (see Methods), which clearly highlight the bursty propagation of the triangle-shaped fronts. Strain-rate values are here limited to 2.5 × 10−3 s−1 for better visualisation of the transformation intermittency investigated in detail below. While the advancing phase front carried most of the strain avalanching during the elongation, small transformation-strain bursts occurred nonetheless throughout the specimen, with small precursor events taking place also before entering the transformation plateau31, producing the slight non-linearity in the red elastic part of the stress-strain curve in Fig. 2a.
Analysis of global strain- and AE-intermittency
We first assess the global stress-strain behaviour of the specimen during the elongation test. We consider the average of the εyy strain [σyy stress] over the entire sample, denoted by \({\overline{\overline{\varepsilon }}}_{yy}\) [\({\overline{\overline{\sigma }}}_{yy}\)]. These quantities undergo a quite continuous evolution at the time scale of the plateau duration, as shown by the black curves in Figs. 2a and 3a. The corresponding strain rate \({\dot{\overline{\overline{\varepsilon }}}}_{yy}\) was then computed by taking the differences in consecutive strain maps separated by a time interval of 3.8 s. The resulting values of \({\dot{\overline{\overline{\varepsilon }}}}_{yy}\) exhibit the spiky time evolution shown in red in Fig. 3a. This clearly highlights the jerky progress of the martensitic transformation despite the very small and constant loading rate and the apparent continuity of \({\overline{\overline{\varepsilon }}}_{yy}\). The time evolution of the number of AE hits, recorded within the same 3.8-s bins, is also plotted in blue in Fig. 3a. The high correlation of this intermittent AE signal with the strain-rate spiking can be noticed, giving a scatter plot tightly clustered near the graph bisector in Fig. 3b. The off-diagonal crosses near the bottom of Fig. 3b correspond to the decoupling of the AE and the strain-rate signals at the end of the transformation plateau (shaded area of Fig. 3a). This is due to the lower phase front moving progressively out of the grid zone near the end of the loading test, so that AE recording continued while strain events could no longer be detected (see the lower orange triangle exiting through the bottom end of the strain maps in the last snapshots of Fig. 2a, and the end of Supplementary Movie 1).
a Time evolution of the average-strain rate \({\dot{\overline{\overline{\varepsilon }}}}_{yy}\) (red) and of the time-density of AE hits (blue) along the transformation plateau, where \({\overline{\overline{\varepsilon }}}_{yy}\) is the value of εyy averaged over the sample. The corresponding time evolution of \({\overline{\overline{\varepsilon }}}_{yy}\) is also shown (black). The time step is 3.8 s for both signals. The shaded area indicates the phase-front exiting the grid at the end of the test, with continuing AE recording but no strain detection. b Correlation between strain-rate and AE signal (dots), normalised by peak values near t = 63,200 s. Crosses correspond to data from the shaded zone of panel a where AE and strain-rate signals are decoupled. (The figure contains 352 dots and 68 crosses.) Pearson [Spearman] correlation value for dots ~0.90 [~0.85].
Analysis of local strain- and AE-events
The intermittent evolution of the global quantities in Fig. 3 results from the local intermittency in the underlying structural transformation within the specimen. We studied this first through the localisation of the acoustic emission in the sample. From the total ~70,000 AE hits recorded during the test, it was possible to determine the y-location of ~38,000 AE events (see Methods). Their (t, y)-chart with energies is given in Fig. 4a, with Fig. 4b displaying the corresponding AE number density. We studied at the same time the associated local space-time strain intermittency by first considering the differences between consecutive 2D εyy-strain maps, with the same 3.8-s time step as in Fig. 3a (see also Supplementary Movie 1). Through x-averaging, these maps give the y-profiles of the 1D strain rate \({\dot{\overline{\varepsilon }}}_{yy}\) vs. time t, where \({\overline{\varepsilon }}_{yy}\) is the x-average of εyy across the central strip in Fig. 1b. This produced the ~420 colour-coded 1D strain-rate y-profiles along the plateau which are represented on the same (t, y)-plane in Fig. 4c. We observe in Fig. 4a, b the nucleation of martensite marked by high-energy AE hits and high strain-rate activity near t = 62,500 s, with the ensuing separation of the two phase fronts moving towards the ends of the sample as the transformation progresses. Due to the x-averaging on the thin strip in Fig. 1b, the propagation of the triangular fronts of Fig. 1a is described here by the advancement with t of two small nearby high strain-rate intervals, forming two parallel high-activity bands in the (t, y)-plane. This is especially evident for the lower phase front in the white-dashed inset of Fig. 4c. We notice that small transformation events, detected by both strain and acoustic emission, are present also away from the phase fronts, especially in the martensitic region of the sample.
a AE event locations and energies. b Number density of localised AE events derived from the map in panel a, in bins of dimensions 0.7 mm × 3.8 s. c Profiles in y of the x-averaged strain-rate \({\dot{\overline{\varepsilon }}}_{yy}\) for each time t. Inset: detail of the austenite/martensite front propagation. d Epicenters of 1D strain-bursts, with associated size and magnitude (size represented by circle radius).
In the present 1D framework, the distinct transformation-strain avalanches on the sample are then tracked by considering, on each y-profile of \({\dot{\overline{\varepsilon }}}_{yy}\) in 4c, the set of y-coordinates whereon the value of the strain rate \({\dot{\overline{\varepsilon }}}_{yy}\) exceeds the noise threshold 3 × 10−4 s−1 (see Methods). At any given t, a 1D strain event is thus defined by each separate y-interval on which \({\dot{\overline{\varepsilon }}}_{yy}\) reaches above the threshold. This assures that localised strain-rate surges emerging from the noise floor while monitoring the phase-change reliably reflect the occurrence of a transformation burst. In this way ~1100 strain avalanches were identified on the plateau, see Fig. 4d. Besides its interval size, each 1D strain event is also characterised by its epicenter, i.e. the value of y on which \({\dot{\overline{\varepsilon }}}_{yy}\) is maximal, as well as its magnitude, defined by the sum of the squared values of \({\dot{\overline{\varepsilon }}}_{yy}\) over the interval. The results shown in the four panels of Fig. 4 clearly highlight various different aspects of the strong spatial and temporal heterogeneity in the phase-transformation activity under the slow, steady forcing. This is also underscored by the heavy-tailed distributions in Fig. 5, pointing to the emergence of scale-free behaviour in the material during the transition process, as reported earlier separately for strain12,13 and AE14,15,16 avalanching. In Fig. 5 the dashed blue line indicates a power-law distribution with exponent ~1.8, which is in the range of the AE exponents previously found in these SMAs14,15,16.
The 3.8-s time step considered above for the strain maps is orders of magnitude larger than the typical time scales of AE avalanche durations16. Each strain event evidenced in Fig. 4d thus originates from the merging of a large and variable number of microscale transition bursts. Such wide separation of scales is partially obviated by considering the density of localised AE events in suitable time bins, as done in Fig. 4b. To the latter we can thus superpose the strain-burst data of Fig. 4d. The result can be seen in Fig. 6a, where we notice the remarkably good agreement between the results of the two measurement techniques utilised to track the transformation intermittency in space and time. The inset to Fig. 6a shows the good correlation between the AE and strain data even at the present scale of local transition events, and not solely at the scale of the overall sample as in Fig. 3b. Some specific features of this concordance are seen in the close-up Fig. 6b. Here the different experimental techniques concurrently detect successive changes in the phase transformation intensity levels as they occur in the sample. We notice a low activity interval at t = 63,050-63,100 s, followed by strong activity from about t = 63,100 s to an almost complete pause near t = 63,200 s, possibly due to a strong pinning site. There ensues a rapid sequence of large transformation bursts at t = 63,210-63,230 s. Such details greatly enhance and very usefully complement the spatially opaque description of the global sample behaviour obtained via the averaged quantities in Fig. 3a.
a Superimposition of the strain avalanches in Fig. 4d onto the AE density map in Fig. 4b. Inset: correlation of strain-event magnitudes with pooled AE-event energies (normalised), when AE locations and strain avalanches are paired along the y-direction for each value of t. Pearson [Spearman] correlation is ~0.42 [~0.79]. b Temporal zoom highlighting details of the bursty phase transformation progress in the sample during the elongation test.
Discussion
We have performed a detailed investigation of the stress-induced reversible martensitic transformation in a CuZnAl shape-memory alloy, considering a simplest case wherein the phase change largely occurs through the development and advancement of two diverging austenite-martensite triangle-shaped strain fronts. We have studied the intermittent progress of these complex interfaces by combining the full-field strain-burst detection via the optical grid method, concurrently with acoustic detection allowing for the 1D localisation of AE avalanches and the measurement of their energies. The matching of these two microseismological techniques revealed the great correlation of the independently collected data for strain and acoustic events in space and time, a property which could so far only be hitherto true, due to the expected common transformational origin of these phenomena. Our results highlight with unprecedented detail interface formation, advancement, jamming, and arrest at pinning points, within the crystal undergoing the phase transformation.
The experimental approach explored here for solid-state phase transitions can be readily adapted to more general and diverse shapes of the transforming sample, and under more complex loading conditions, as might be suggested by particular applications of reversible martensitic materials. Furthermore, it can be applied to the study of analogous bursty phenomena in the plasticity32 and fracture33 of crystalline solids, as well as metallic glasses34 and porous media35, where the investigation and modeling of materials’ behavior can greatly benefit from the detailed visualization and analysis made possible by the presently described techniques.
Methods
Strain and strain-rate mapping
The strain maps were obtained via the grid method25,26,27,28,29. A bidimensional grid with pitch 0.2 mm was first printed with a 50,800 dpi photoplotter on a polymeric sheet and then transfered onto the sample surface by using a white E504 Epotecny adhesive.25 The grid was slightly rotated with respect to pixel lines to avoid aliasing and the associated parasitic fringes28. Grid images during the test were captured by a Sensicam QE camera featuring a 12-bit/1040 × 1376 pixel sensor and a 105 mm Tokina lens, with 10-ms shutter time and about 17 Hz acquisition frequency. Magnification was adjusted so that one grid pitch was encoded with about seven pixels, leading to a pixel size of 0.0274 mm on the sample. A direct-current LED system was used for lighting to avoid flickering. The grid images were processed by using the Localised Spectrum Analysis27, with a Gaussian window characterized by a 7-pixel standard deviation. The movement of the physical points between reference and current grids was compensated27, leading to the disappearance of the small local grid defects when subtracting the current and reference distributions of the phases’ modulation of the regular grid pattern caused by deformation. With the present data, the spatial resolution for strain measurements is conservatively estimated26,29 to be ~42 pixels, i.e. ~1.15 mm on the sample. The strain increments were first computed between two consecutive strain maps set apart by 64 grid images (i.e. ~3.8 s), and then divided by the corresponding 3.8 s time separation, to obtain strain rates in s−1. This choice of time step gives a convenient trade-off between the measurement and temporal resolutions for strain-rates, and for AE data processing, and produces ~420 strain-increment maps on the transformation plateau, conventionally defined from t = 62,400 s to t = 64,000 s, with duration 1600 s. The noise threshold to reliably detect strain-rate bursts was experimentally estimated by analysing the fluctuations directly in the 1D strain-rate distributions. For this purpose, a stack of 15 consecutive y-profiles was considered, obtained during about 1 min at the beginning of the test after preloading, with the specimen being still while taking the images. Due to the noise reduction because of x-averaging across N = 50 pixels (Fig. 1b), this gave a noise standard deviation of 6.70 × 10−5 s−1. The final threshold for the 1D strain-rate profiles was conservatively taken to be 4.5 times this quantity, giving a value of ~3 × 10−4 s−1. This allowed to identify 1058 1D strain bursts on the plateau.
AE detection and location
AE from the sample was detected by means of two micro-80 piezoelectric transducers from Europhysical Acoustics, working with a relatively flat response in the range 0.2–1 MHz. They were acoustically coupled to the upper and lower grips on the opposite face with respect to the camera. Electric signals were preamplified (60 dB) and input into a two-channel PCI2 acquisition system from Europhysical Acoustics, working at 40 MHz with an A/D conversion of 18 bits. Individual AE hits were defined in both channels in the following way: a hit starts at time tini when the absolute value of the preamplified signal ∣V(t)∣ from any channel crosses a noise threshold (21 dB, equivalent to 11.22 mV), and ends at tfinal when ∣V(t)∣ remains below the threshold until tfinal + 100μs. The amplitude of the hit is defined from the maximum value ∣Vmax∣ of the preamplified signal in the first 100μs, converted to dB according to A(dB) = 20log(Vmax∕1μV) −60. Then an A = 60 dB signal corresponds to a 1V peak in the preamplified signal and 1mV peak in the signal from the transducer. The energy of the hit is given by \(E=\frac{1}{10k\Omega }{\int }_{{t}_{ini}}^{{t}_{final}}{\left(V(t)\right)}^{2}dt\). N1 = 108,471 and N2 = 60,357 hits were recorded in channels 1 (upper grip) and 2 (lower grip), respectively, the asymmetry being due to the differences in the acoustic coupling of the two transducers. The hit list so acquired was analyzed for the 1D-location of the AE events, defined from any pair of consecutive hits detected in opposite channels within less than tmax = 0.038 ms, with event location given by \(y=0.5L\left(1-\frac{\Delta t}{{t}_{max}}\right)\), for L = 35 mm the length of the central part of the sample, and Δt the delay between the two hits. In this way 37,540 acoustic events were located along the y-axis of the specimen in Fig 1a, of which 26,266 belong to the 25-mm interval in the averaging zone of Fig. 1b. The source energy of a located event is estimated by \(E=\sqrt{{E}_{1}{E}_{2}}\), where E1 and E2 are the energies measured in channel 1 and 2, respectively. This formula approximately corrects for the effects of attenuation in the sample, assuming a constant exponential damping factor. Similarly, given its logarithmic character, the source amplitude is defined as A = (A1 + A2)/2.
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Otsuka, K. & Wayman, C. M. Shape Memory Materials. (Cambridge Univ. Press, Cambridge, UK, 1998).
Salje, E. K. H. Ferroelastic materials. Annu. Rev. Mat. Res. 42, 265–283 (2012).
Jani, J. M., Leary, M., Subic, A. & Gibson, M. A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 56, 1078–1113 (2014).
Bonnot, E., Romero, R., Mañosa, Ll, Vives, E. & Planes, A. Elastocaloric effect associated with the martensitic transition in shape-memory alloys. Phys. Rev. Lett. 100, 125901 (2008).
Tusek, J. et al. The elastocaloric effect: a way to cool efficiently. Adv. Energy Mater. 5, 1500361 (2015).
Frenzel, J., Eggeler, G., Quandt, E., Seelecke, S. & Kohl, M. High-performance elastocaloric materials for the engineering of bulk- and micro-cooling devices. MRS Bulletin 43, 280–284 (2018).
Gu, H., Bumke, L., Chluba, C., Quandt, E. & James, R. D. Phase engineering and supercompatibility of shape memory alloys. Materials Today 21, 265–277 (2018).
Bucsek, A., WilliamNunn, W., Jalan, B. & James, R. D. Direct conversion of heat to electricity using first-order phase transformations in ferroelectrics. Phys. Rev. Applied 12, 034043 (2019).
Bhattacharya, K., Conti, S., Zanzotto, G. & Zimmer, J. Crystal symmetry and the reversibility of martensitic transformations. Nature 428, 55–59 (2004).
Song, Y., Chen, X., Dabade, V., Shield, T. W. & James, R. D. Enhanced reversibility and unusual microstructure of a phase-transforming material. Nature 502, 85 (2013).
James, R. D. Materials from mathematics. Bull. Amer. Math. Soc. 56, 1–28 (2018).
Balandraud, X., Barrera, N., Biscari, P., Grédiac, M. & Zanzotto, G. Strain intermittency in shape-memory alloys. Phys. Rev. B 91, 174111 (2015).
Niemann, R. et al. Localizing sources of acoustic emission during the martensitic transformation. Phys. Rev. B 89, 214118 (2014).
Bonnot, E., Vives, E., Mañosa, Ll, Planes, A. & Romero, R. Acoustic emission and energy dissipation during front propagation in a stress-driven martensitic transition. Phys. Rev. B 78, 094104 (2008).
Vives, E., Soto-Parra, D., Mañosa, L., Romero, R. & Planes, A. Driving-induced crossover in the avalanche criticality of martensitic transitions. Phys. Rev. B 80, 180101R (2009).
Planes, A., MañosaLl. & Vives, E. Acoustic emission in martensitic transformations. J. Alloys Compounds 577, S699–S704 (2013).
Bolgár, M. K. et al. Thermal and acoustic noises generated by austenite/martensite transformation in NiFeGaCo single crystals. J. Alloys Comp. 658, 29–35 (2016).
Vinogradov, A. et al. On the limits of acoustic emission detectability for twinning. Materials lett. 658, 417–419 (2016).
Vinogradov, A., Vasilev, E., Linderov, M. & Merson, D. Evolution of mechanical twinning during cyclic deformation of Mg-Zn-Ca Alloys. Metals 6, 304 (2016).
Beke, D. L. et al. Acoustic emissions during structural changes in shape memory alloys. Metals 9, 58 (2019).
Vives, E., Soto-Parra, D., Mañosa, L., Romero, R. & Planes, A. Imaging the dynamics of martensitic transitions using acoustic emission. Phys. Rev. B 84, 060101 (2011).
Ossmer., H., Chluba, C., Gueltig, M., Quandt, E. & Kohl, M. Local evolution of the elastocaloric effect in TiNi-based films. Shap. Mem. Superelasticity 1, 142–152 (2015).
Tóth, L. Z., Daróczi, L., Szabó, S. & Beke, D. L. Simultaneous investigation of thermal, acoustic, and magnetic emission during martensitic transformation in single-crystalline Ni2MnGa. Phys. Rev. B 93, 144108 (2016).
Romero, F. J. et al. Scale-invariant avalanche dynamics in the temperature-driven martensitic transition of a Cu-Al-Be single crystal. Phys. Rev. B 99, 224101 (2019).
Piro, J. L. & Grédiac, M. Producing and transferring low-spatial-frequency grids for measuring displacement fields with moiré and grid methods. Exp. Techn. 28, 23–26 (2004).
Grédiac, M. & Sur, F. Effect of sensor noise on the resolution and spatial resolution of the displacement and strain maps obtained with the grid method. Strain 50, 1–27 (2014).
Grédiac, M., Sur, F. & Blaysat, B. The grid method for in-plane displacement and strain measurement: a review and analysis. Strain 52, 205–243 (2016).
Sur, F., Blaysat, B. & Grédiac, M. Determining displacement and strain maps immune from aliasing effect with the grid method. Optics Lasers Eng. 86, 317–328 (2016).
Grédiac, M., Blaysat, B. & Sur, F. A critical comparison of some metrological parameters characterizing local digital image correlation and grid method. Experim. Mech. 57, 871–903 (2017).
Seiner, H. & Landa, M. Non-classical austenite-martensite interfaces observed in single crystals of Cu-Al-Ni. Phase Transitions 82, 793–807 (2009).
Brinson, L. C., Schmidt, I. & Lammering, R. Stress-induced transformation behavior of a polycrystalline NiTi shape memory alloy: micro and macromechanical investigations via in situ optical microscopy. J. Mech. Phys. Solids. 52, 1549–1571 (2004).
Papanikolaou, S., Cui, Y. & Ghoniem, N. Avalanches and plastic flow in crystal plasticity: an overview. Mod. Sim. Mat. Sci. Eng. 26, 013001 (2017).
Athanasiou, C.-E., Hongler, M.-O. & Bellouard, Y. Unraveling brittle-fracture statistics from intermittent patterns formed during femtosecond laser exposure. Phys. Rev. Applied 8, 054013 (2017).
Antonaglia, J. et al. Bulk Metallic Glasses deform via slip avalanches. Phys. Rev. Lett. 112, 155501 (2014).
Baró, J. et al. Statistical similarity between the compression of a porous material and earthquakes. Phys. Rev. Lett. 110, 088702 (2013).
Acknowledgements
We thank Université Clermont Auvergne for the hospitality and help with computing and storage resources. E.V. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MAT2016-75823-R). G.Z. acknowledges PRIN grant 2017KL4EF3. We thank Drs. A. Planes and Ll. Mañosa for fruitful discussions.
Author information
Authors and Affiliations
Contributions
All the authors, B.B., X.B., M.G., E.V., N.B. and G.Z., contributed equally to the experiments, data analysis, discussion and preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Blaysat, B., Balandraud, X., Grédiac, M. et al. Concurrent tracking of strain and noise bursts at ferroelastic phase fronts. Commun Mater 1, 3 (2020). https://doi.org/10.1038/s43246-020-0007-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-0007-4
This article is cited by
-
Avalanche criticality during ferroelectric/ferroelastic switching
Nature Communications (2021)
-
Applying Full-Field Measurement Techniques for the Thermomechanical Characterization of Shape Memory Alloys: A Review and Classification
Shape Memory and Superelasticity (2021)