Abstract
Antiferroelectrics have potential applications in energy conversion and storage, but are scarce, particularly among oxides that otherwise display rich ferroic behaviours. A question then arises whether potential antiferroelectrics are being overlooked, simply because their corresponding ferroelectric phase has not been discovered yet. Here we report a first-principles study suggesting that this is the case for a family of ABO3 pyroxene-like materials, characterised by chains of corner-sharing BO4 tetrahedra, a well-known member being KVO3. The irregular tetrahedra have an electric dipole associated to them. In the most stable polymorph, the dipoles display an antipolar pattern with zero net moment. However, upon application of an electric field, half of the tetrahedra rotate, flipping the corresponding dipoles and reaching a ferroelectric state. We discuss the unique possibilities for tuning and optimisation of antiferroelectricity that these materials offer. We suggest that the structural features enabling this antiferroelectric behaviour can also be found in other all-important mineral families.
Similar content being viewed by others
Introduction
There is currently considerable interest in finding new antiferroelectric materials, owing to their technological importance and relative scarcity1,2,3. Applications of antiferroelectrics rely on their unique response to an applied electric bias, featuring a double hysteresis loop that is the result of a field-induced phase transition to a polar state. This double-loop makes them particularly efficient for energy applications4,5, as, for example, in pulsed-power capacitors6,7. The field-induced transformation usually results in a large mechanical response, suitable for transducers and actuators8,9. Finally, antiferroelectrics display an inverse electro-caloric effect10,11,12.
To identify new antiferroelectrics, one could proceed as follows: chosen a materials family and a pertinent high-symmetry structure (e.g. the ideal cubic phase of perovskite oxides ABO3), one could use first-principles simulations to find compositions that present similarly strong polar and antipolar phonon instabilities of this parent phase. Any such compound is likely to present metastable polar and antipolar polymorphs of similar energy. Then, if the antipolar state were more stable, and given that an electric field will always favour the polar one, we would have a good candidate to display antiferroelectric behaviour.
This is exactly the exercise that led to the discoveries here reported. We ran a high-throughput first-principles study of the phonon dispersion of >50 nonmagnetic compounds in the cubic perovskite phase, and found that alkali vanadates KVO3, RbVO3 and CsVO3 show dominant and related polar and antipolar soft modes (see Supplementary Note 1 and Supplementary Fig. 1). Then, when trying to identify the polar and antipolar polymorphs associated to these instabilities, we found that they result in very large distortions of the cubic phase, to the point that the perovskite lattice is nearly destroyed. The resulting energy minima include many low-energy antipolar polymorphs, as well as their polar counterparts. Indeed, according to our calculations, they constitute a very promising family of antiferroelectric compounds.
Results
In order to identify stable structures, we run first-principles molecular dynamics simulations of several alkali vanadates (see “Methods” and Supplementary Video 1, where we show a representative molecular dynamics calculation for KVO3 at T = 500 K starting from the perovskite phase). These simulations reveal the existence of numerous low-energy metastable polymorphs with some common features: a strong tetragonal distortion, with c/a ratios larger than 1.3; a sublattice of A cations that retain a perovskite-like configuration; and a 4-fold coordination of the vanadium atoms yielding corner-sharing VO4 tetrahedra.
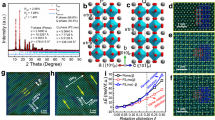
The connection between the perovskite phase and the ground state of these vanadates is sketched in Fig. 1, which shows the result of a nudged elastic band (NEB) calculation (see “Methods” for details). Starting from the perovskite structure (Fig. 1a), the system undergoes a transition to a phase with a strong tetragonal distortion, in which a first V–O bond is broken in each AVO3 unit (Fig. 1b and Supplementary Video 2). The obtained structures are reminiscent of supertetragonal phases known for perovskites like BiFeO3 and PbVO3, which show a large c/a ratio, and consequently a layered structure formed by BO5 pyramids13,14. In a subsequent step, the VO5 square pyramids rotate along the V–O bond of the apical oxygen (Fig. 1c), while the V cations move towards one of the oxygen atoms at the base of the pyramid (Fig. 1d), ending in the rupture of a second V–O bond. Each of the resulting VO4 groups is corner linked to two adjacent tetrahedra, forming chains.
Continuous path connecting the cubic perovskite phase (a) and the perovskite-derivative antipolar phase (d). The A, B and O atoms are shown in black, green and blue, respectively. Initially one B–O link per perovskite unit cell is broken due to a transition to a supertetragonal state (b), while a rotation of the resulting pyramids results in the rupture of a second B–O bond per cell (transition from c to d).
We obtain several polymorphs featuring the mentioned vertex-sharing oxygen tetrahedra, inspired by metastable phases observed in our molecular dynamics simulations. The tetrahedra can form one-dimensional (1D) zigzag (ZZ) structures along the [110] pseudo-cubic direction (Fig. 2a). The chains can alternatively follow a 1D battlement-like (BM) pattern along the [010] axis (Fig. 2b), or even form closed loops yielding zero-dimensional ring (RG) structures (Fig. 2c). In the ZZ structure, the apical oxygens point in opposite directions for adjacent chains, closely resembling what is found in inosilicate pyroxenes15,16,17, while the RG structures have close analogues in the cyclosilicate family18,19,20. The ZZ structure is the most stable one, the lowest-energy BM and RG structures lying 117 and 125 meV per formula unit (f.u.) above for KVO3. The ZZ ground state we find for KVO3 (as well as for RbVO3 and CsVO3) is orthorhombic with space group Pbcm and coincides with the experimentally observed structure16,21,22,23,24,25,26.
a, b depict two polymorphs with 1D O tetrahedra chains, with a ZZ (ground state) and a BM structure, respectively. An example of a polymorph with closed (0-dimensional) O tetrahedra structures is shown in c (RG-A). The inter-chain coupling of the dipoles is indicated by the letters A (antiferroelectric) and F (ferroelectric) in the structure names. The microscopical origin of the local dipoles (red arrows) is shown in d, where the indicated V–O bond distances are given in Å for KVO3. The ZZ-A, ZZ-i and ZZ-F states are shown schematically in e, f and g, respectively. Red (green) arrows indicate dipoles with positive (negative) out-of-plane component.
Importantly, the V–O bonds forming the backbone of the tetrahedra chains are longer than the remaining two hovering V–O bonds16,27—see bond lengths for the ZZ polymorph of KVO3 in Fig. 2d. This difference of bond lengths induces a local electric dipole, which lies along the direction defined by the V cation and the centre of the tetrahedron edge formed by the lingering oxygens, as shown in Fig. 2d.
We now focus on the ZZ phase of KVO3 since it is the ground state of the best-established compound among those studied. For a given chain, the ZZ structure gives rise to an antipolar pattern of the in-plane component of the dipoles, while the out-of-plane component remains constant. Since the apical oxygens point in opposite directions for contiguous chains, the out-of-plane component changes sign from chain to chain, yielding a striped antipolar pattern (Fig. 2e). An obvious question arises: is KVO3 antiferroelectric? A positive answer can only be given if a related ferroelectric phase accessible via an electric field is found.
We crucially realised that a rotation of a tetrahedron about the backbone edge is tantamount to switching the out-of-plane component of its electric dipole. We thus constructed a ZZ structure with ferroelectric inter-chain ordering (ZZ-F) that turned out to be stable and 135 meV per f.u. higher in energy than the antipolar ground state (ZZ-A). The polar order of the ZZ-F polymorph is shown schematically in Fig. 2g. We calculate its spontaneous polarisation28 to be 0.093 C m−2 (0.054 C m−2) for the out-of-plane (in-plane) component, around five times smaller than that of strong ferroelectric perovskites like BaTiO3 (0.43 C m−2)29. Since the V–O distances in the ZZ-A phase differ by <0.5 % from those of the ZZ-F phase, we estimate the out-of-plane sublattice polarisation in the ZZ-A phase to be ~0.046 C m−2, that is, half of the ZZ-F polarisation value. Using the tools described in “Methods”, we find that the optimised ZZ-F state has Pm symmetry. An intermediate ferrielectric state (ZZ-i), with half of the tetrahedra in one of the chains flipped (Fig. 2f), was also found to be metastable for KVO3.
What remains in order to confirm the antiferroelectric character of KVO3 is to find a connecting path for the field-induced transition. To this end, we carry out NEB calculations between the ZZ-A and the ZZ-F polymorphs. The results are shown in Fig. 3a (thick black line). A continuous energy path is found with an energy barrier of 147 meV per f.u. The switching of the dipole chain occurs in a step-wise fashion, with half of the tetrahedra rotating at a first stage—and ending up in the ZZ-i phase—and the remaining ones rotating at a second stage (see Supplementary Video 3). Note that we extend the NEB path up to a ferroelectric state in which the polarisation lies fully out of plane; we obtained such a state, with space group Pma2, by rotating half of the VO4 tetrahedra in the ZZ-A phase and performing a symmetry-constrained structural optimisation. The NEB calculation reveals that this state is a saddle point of the energy for KVO3 and therefore not stable. The two components of the spontaneous polarisation that acquire nonzero values along the switching path are shown in blue solid lines in Fig. 3a. The out-of-plane polarisation increases abruptly in the first stage, and slower in the second one. Along the path a nonzero in-plane polarisation develops, perpendicular to the tetrahedron chains, showing an oscillating behaviour due to the rigid dipoles crossing the plane of the chains in each of the two switching steps.
a Minimum energy path for switching between the ZZ-A and the ZZ-F states in KVO3 as obtained with the NEB method (solid thickest black line). Blue lines correspond to the spontaneous polarisation components out of plane (circles) and in plane, perpendicular to the chains (triangles). The vertical axis for the polarisation is shared with b and at the right of the latter. The black curves show the energy density profiles under different perpendicular electric fields, being the value of the fields indicated on each line in MV cm−1. b Estimated double hysteresis loop at T = 300 K. The only quantitative data in this diagram are the coercive fields and the value of the polarisation jumps. The small slope in the hysteresis diagram is only indicative of an expected linear response, but we have not computed the dielectric response explicitly and hence the slope is only qualitatively correct.
Finally, we estimate the behaviour of KVO3 under application of an out-of-plane electric field. The response to the applied field can be approximated by constructing an electric enthalpy with the form
where U0, P and v are, respectively, the energy, polarisation and volume at zero field at each step of the path, as obtained from first principles; \({\mathcal{E}}\) is the applied electric field. The ZZ-A state is chosen as the zero of energy for convenience. By introducing this approximated enthalpy, we avoid running costly first-principles calculations explicitly considering an applied field. In Fig. 3a the energy profile of KVO3 along the switching path is shown for different values of the field.
The hysteresis loop of the polarisation under an out-of-plane electric field can be numerically reconstructed from the enthalpies and polarisations in Fig. 3a. More specifically, we consider the case of T = 300 K, assuming a thermal energy of 26 meV per f.u., and obtain the results in Fig. 3b (See Supplementary Note 2 and Supplementary Fig. 2 for details on the calculation of these loops.) The antiferroelectric → ferroelectric switching, and the ferroelectric → antiferroelectric back-switching, occur when the applied field lowers the corresponding energy barrier below the thermal activation energy. At 300 K, this occurs for 40 MV cm−1 (switching) and 20 MV cm−1 (back-switching), and we observe a sizeable hysteresis. The efficiency of the material as an antiferroelectric capacitor would be ~50%.
The computed switching fields are very large compared to those that can be applied experimentally in similar oxides before inducing leakage (i.e., ~1 MV cm−1). To understand the implications of this result, let us first note that first-principles estimates like ours are known to exaggerate ferroelectric coercive fields by factors of up to two orders of magnitude30,31, probably because they miss effects (e.g. easier nucleation of the field-induced phase at defects) that play an important role at controlling the transformation kinetics. However, in the case of an antiferroelectric ↔ ferroelectric transformation, the coercive bias must be as large as to equalise the energies of the polar and antipolar states. Our simulations do suggest that a very strong field (of ~28 MV cm−1) is needed to achieve this in KVO3; hence, notwithstanding possible inaccuracies in our estimate, it seems unlikely KVO3 can be experimentally switched. Having said this, as we discuss below, we have reasons to believe that there are promising ways to optimise the switching characteristics of KVO3 and related compounds, for example, by means of appropriate chemical substitutions, considerably reducing the fields required to achieve antiferroelectric behaviour.
Of note are the works of Chavan and colleagues32,33 reporting a polar phase of KVO3, for which we lack structural characterisation. The existence of such a polar state, though, supports the possibility that the usual phase of KVO3—here studied—may display antiferroelectric behaviour.
Discussion
Let us start by commenting on three possibilities for antiferroelectric optimisation and tuning that these materials offer. First, our simulations indicate that the behaviour of RbVO3 and CsVO3 is very similar to that of KVO3. The ZZ-A phase is also the ground state for these compounds, and the ZZ-F phase is a metastable polymorph with an out-of-plane spontaneous polarisation of 0.078 and 0.052 C m−2, respectively. The decrease in the polarisation, as compared to the result for KVO3, can be ascribed to the larger unit cell volume. The ZZ-F state of RbVO3 shows a non-negligible in-plane component (0.037 C m−2), while for CsVO3 the polarisation is fully out of plane. The calculated energy barrier between the ZZ-A and ZZ-F states decreases with increasing size of the A cation (being of 128 and 112 meV per f.u. for RbVO3 and CsVO3, respectively). Further, the energy difference between the ZZ-F and the ZZ-A states follows the same trend, being of 117 and 97 meV per f.u. for RbVO3 and CsVO3, respectively (see Supplementary Note 3 and Supplementary Fig. 3).
Second, regarding the possibility of having different B cations, further calculations indicate that ZZ-A is a metastable structure for all the alkali tantalates and niobates, in particular for the well-studied ferroelectric KNbO3. Therefore, a morphotropic phase boundary between the ferroelectric perovskite phase and the ZZ-A phase must exist for the solid mixture KV1 − xNbxO3. Our preliminary studies indicate that such a morphotropic phase boundary occurs between x = 0.375 and 0.5. At such compositions, the energies of the antiferroelectric (ZZ-A) and ferroelectric (KNbO3-like) states become very close (cross). Hence, these solid solutions naturally provide us with antiferroelectric and ferroelectric states that are very close in energy—thus solving the main difficulty mentioned above to obtain antiferroelectric ↔ ferroelectric switching at moderate fields—and seem ideal candidates to yield antiferroelectric materials with optimised properties.
Third, as already mentioned, we find polymorphs with different tetrahedral arrangements, forming BM and RG patterns. Interestingly, for the three alkali vanadates considered, the most stable dipolar order is ferroelectric in the BM case. Moreover, the (shear) strains are distinct for the ZZ, BM and RG geometries (see the different structures of the A cation sublattice in Fig. 2). Hence, different chain arrangements, and in turn the polar order, may be accessible by growing these materials on appropriate substrates that impose suitable epitaxial conditions. Further, as can be appreciated from Fig. 2e, g, the ZZ-F state is more square in-plane than the ZZ-A, which suggests that a suitable substrate may allow us to tune the corresponding energy difference.
It is also worth noting some chemical and structural aspects of the compounds studied in this work. The origin of the peculiar polymorphs found seems to be the small size of the V5+ cation (nominally, 0.54 Å for V5+ in a 6-fold coordination, and 0.355 Å in a 4-fold coordination)34 relative to the O2− ionic radius (1.35 Å)34. The size difference is such that all vanadates lie below the octahedral limit35, which is known to lead to lower B-cation coordination in perovskites35,36,37. Further, we find that the V–O bond lengths change by <1% across the switching process between the ZZ-A and ZZ-F phases. In fact, the deviations in V–O bond lengths among all the ZZ, BM and RG polymorphs of KVO3 are below 1%, and even the differences among the three studied vanadates remain below 1%. The V–O bonds, and consequently the local dipoles, thus prove to be very rigid38, suggesting that in these materials phase transitions involving dipoles will probably be of the order–disorder type39. More importantly, this bond stiffness also ensures that the dipoles will not vanish; therefore, these compounds can be viewed as model antiferroelectrics whose behaviour is analogous to that of antiferromagnets40.
Also of note is the switching in these compounds—by quasi-rigid rotations of VO4 molecular-like groups—which is rather unique as compared to similar transformations in inorganic ferroelectric and antiferroelectric materials. Indeed, the identified switching path suggests that, in these materials, such transformations will typically occur through many steps. The present calculation shows a switching in only two steps, which seems a direct consequence of the finite size of the simulation box employed; however, larger simulation cells would probably reveal a many-step process. This is strongly reminiscent of memristors, in which the electric resistance can be tuned quasi-continuously by taking advantage of a controllable multistep transformation. Therefore, our results suggest that pyroxene-like antiferroelectrics could find application in memristor devices41.
Finally, the findings here reported hint at a promising strategy to discover further antiferroelectric materials. Pyroxenes, pyroxenoids42,43 and many other ABO3 compounds—like, for example, the recently synthesised BiGaO344 or the vanadates NH4VO324,45, TlVO346, NaVO347,48, α-AgVO349 and LiVO350, with structures akin to that of KVO3—also contain chains of irregular oxygen tetrahedra. Since such tetrahedra host an electric dipole, these compounds can be viewed to present an antipolar ground state, and are candidates to display antiferroelectric behaviour. The situation is similar to that of BiVO4, an extensively investigated material (for its catalytic properties51) that is formed by irregular VO4 tetrahedra whose corresponding electric dipoles order in an antipolar pattern, and which has recently been proposed as a possible antiferroelectric52. Hence, we hope the present work will stimulate experimental and theoretical activities to explore this intriguing possibility, namely, that some of the best known and most abundant minerals on Earth may be antiferroelectrics in disguise.
Methods
First-principles calculations
In this work, we employ first-principles calculations within the density functional theory (DFT) framework as implemented in the Vienna Ab-initio Simulation Package (VASP)53,54 to obtain the crystal structure and relative energies of the different polymorphs and compounds. The plane-wave cut-off for the basis set is set to 500 eV in all cases. We choose the Perdew–Burke–Ernzerhof functional modified for solids55 as the exchange correlation. We treat the atomic cores within the projector-augmented wave approach56, considering the following states explicitly: 3p and 4s for K; 4p and 5s for Rb; 5p and 6s for Cs; 3p, 3d and 4s for V; 2s and 2p for O. For perovskite primitive cell calculations (5-atom cell) a 6 × 6 × 6 Monkhorst-Pack57 grid is employed for sampling the Brillouin zone, which yields well-converged results for the three alkali vanadates. The primitive cell of the ZZ-A ground state of KVO3, RbVO3 and CsVO3 is a \(\sqrt{2}\times 2\sqrt{2}\times 1\) supercell with respect to the ideal perovskite; for such simulation cells we employ a 4 × 3 × 6 k-point sampling. For these calculation conditions we obtained robustly insulating solutions for all the polymorphs considered (see Supplementary Note 4 and Supplementary Fig. 4). The molecular dynamics calculations are carried out within the canonical ensemble using a Langevin thermostat, as implemented in VASP. A 2 × 2 × 2 supercell is employed for this purpose (with respect to the 5-atom cell perovskite), and the k-sampling is reduced to 2 × 2 × 2 to speed up the calculations. We perform the molecular dynamics simulations at different temperatures (ranging from 10 to 1000 K) to explore the configuration space of each compound. Representative structures of the ZZ, BM and RG phases are identified in this way, which we later optimise within DFT until atomic forces become <0.01 eV Å−1 and residual stresses become <0.1 GPa.
Symmetry determination
The space groups of the studied crystal structures are determined employing the SPGLIB library through its implementation in the PHONOPY package58.
Visualisation
We used the VESTA visualisation package59 to prepare some of the figures and Supplementary Videos. In all cases, we draw V–O bonds for V–O distances below 2.5 Å.
NEB calculations
The calculations of the switching energy barrier and the connection between the perovskite structure and the ZZ-A state are obtained through the NEB method60 along with the climbing-NEB61 modification as implemented by the Henkelman group in the Virtual Transition State Theory tools package for VASP61. A total of 19 (7) images are employed in the NEB calculations of the switching energy barrier (connection to the perovskite structure). We employ the same parameters and convergence criteria as for the structure optimisation calculations. In particular, the convergence criterion for the atomic forces is kept at 0.01 eV −1.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
All the relevant data are available from the authors upon reasonable request.
Code availability
The first-principles calculations are carried out using the open source package VASP, which is a proprietary software. The space groups of the crystal structures are obtained using the open source package PHONOPY, which is released under the BSD-3-Clause License (https://github.com/atztogo/phonopy). The visualisation software VESTA is distributed free of charge for scientific users under the VESTA license (https://jp-minerals.org/vesta/en/download.html). The Virtual Transition State Theory tools package is an open source package released under the Apache License version 2 (https://theory.cm.utexas.edu/vtsttools/download.html).
References
Roleder, K., Jankowska-Sumara, I., Kugel, G. E., Maglione, M., Fontana, M. D. & Dec, J. Antiferroelectric and ferroelectric phase transitions of the displacive and order-disorder type in PbZrO3 and PbZr1−xTixO3 single crystals. Phase Transitions 71, 287–306 (2000).
Rabe, K. M. Antiferroelectricity in Oxides: A Reexamination in Functional Metal Oxides, Ch. 7, 221–244 (Wiley, 2013).
Hao, X., Zhai, J., Kong, L. B. & Xu, Z. A comprehensive review on the progress of lead zirconate-based antiferroelectric materials. Progr. Mater. Sci. 63, 1 – 57 (2014).
Liu, Z., Lu, T., Ye, J., Wang, G., Dong, X., Withers, R. & Liu, Y. Antiferroelectrics for energy storage applications: a review. Adv. Mater. Technol. 3, 1800111 (2018).
Love, G. R. Energy storage in ceramic dielectrics. J. Am. Ceram. Soc. 73, 323–328 (1990).
Zhang, L., Jiang, S., Zeng, Y., Fu, M. & Han, K. et al. Y doping and grain size co-effects on the electrical energy storage performance of (Pb0.87Ba0.1La0.02) (Zr0.65Sn0.3Ti0.05)O3 anti-ferroelectric ceramics. Ceram. Int. 40, 5455–5460 (2014).
Chauhan, A., Patel, S., Vaish, R. & Bowen, C. R. Anti-ferroelectric ceramics for high energy density capacitors. Materials 8, 8009–8031 (2015).
Berlincourt, D. Transducers using forced transitions between ferroelectric and antiferroelectric states. IEEE Trans. Sonics Ultrason. 13, 116–124 (1966).
Zhang, S.-T., Kounga, A. B., Jo, W., Jamin, C. & Seifert, K. et al. High-strain lead-free antiferroelectric electrostrictors. Adv. Mater. 21, 4716–4720 (2009).
Mischenko, A. S., Zhang, Q., Scott, J. F., Whatmore, R. W. & Mathur, N. D. Giant electrocaloric effect in thin-film PbZr0.95Ti0.05O3. Science 311, 1270–1271 (2006).
Lu, B., Li, P., Tang, Z., Yao, Y. & Gao, X. et al. Large electrocaloric effect in relaxor ferroelectric and antiferroelectric lanthanum doped lead zirconate titanate ceramics. Sci. Rep. 7, 45335 (2017).
Novak, N., Weyland, F., Patel, S., Guo, H. & Tan, X. et al. Interplay of conventional with inverse electrocaloric response in (Pb,Nb)(Zr,Sn,Ti)O3 antiferroelectric materials. Phys. Rev. B 97, 094113 (2018).
Diéguez, O., González-Vázquez, O. E., Wojdeł, J. C. & Íñiguez, J. First-principles predictions of low-energy phases of multiferroic BiFeO3. Phys. Rev. B 83, 094105 (2011).
Shpanchenko, R. V., Chernaya, V. V., Tsirlin, A. A., Chizhov, P. S. & Sklovsky, D. E. et al. Synthesis, structure, and properties of new perovskite PbVO3. Chem. Mater. 16, 3267–3273 (2004).
Burnham, C. W., Clark, J. R., Papike, J. J. & Prewitt, C. T. A proposed crystallographic nomenclature for clinopyroxene structures. Z. Kristallogr. Cryst. Mater. 125, 109–119 (1967).
Hawthorne, F. C. & Calvo, C. The crystal chemistry of the M+VO3 (M+ = Li, Na, K, NH4, Tl, Rb, and Cs) pyroxenes. J. Solid State Chem. 22, 157–170 (1977).
Putnis, A. An Introduction to Mineral Sciences (Cambridge Univ. Press, 1992).
Zoltai, T. Classification of silicates and other minerals with tetrahedral structures. Am. Miner. 45, 960–973 (1960).
Buerger, M. J. & Zoltai, T. The relative energies of rings of tetrahedra. Z. Kristallogr. Cryst. Mater. 114, 1–8 (1960).
Colin, S., Dupre, B., Venturini, G., Malaman, B. & Gleitzer, C. Crystal structure and infrared spectrum of the cyclosilicate Ca2ZrSi4O12. J. Solid State Chem. 102, 242–249 (1993).
Evans, H. T. & Block, S. Crystal structure of KVO3. Am. Mineralogist 39, 326 (1954).
Petrasova, M., Madar, J. & Hanic, F. Crystal structure of potassium metavanadate. Chem. Zvesti 12, 410–418 (1958).
Evans, H. T. & Block, S. The crystal structure of potassium metavanadate. Chem. Papers 12, 410–418 (1958).
Evans, H. T. Crystal structure refinement and vanadium bonding in the metavanadates KVO3, NH4VO3 and KVO3H2O. Z. Kristallogr. Cryst. Mater. 114, 257–277 (1960).
Adams, D. M. & Fletcher, P. A. Vibrational spectroscopy at high pressure: Part 53. alkali metavanadates and copper metagermanate. Spectrochim. Acta Part A 44, 233–240 (1988).
de Waal, D. & Heyns, A. M. Vibrational spectra of NaVO3, KVO3 and the solid solutions (Na0.88K0.12)VO3 and (Na0.5K0.5)VO3. Mater. Res. Bull. 27, 129–136 (1992).
Angsten, T., Martin, L. W. & Asta, M. Electronic and polar properties of vanadate compounds stabilized by epitaxial strain. Chem. Mater. 30, 5870–5877 (2018).
King-Smith, R. D. & Vanderbilt, D. Theory of polarization of crystalline solids. Phys. Rev. B 47, 1651–1654 (1993).
Zhong, W., Vanderbilt, D. & Rabe, K. M. Phase transitions in BaTiO3 from first principles. Phys. Rev. Lett. 73, 1861–1864 (1994).
Lisenkov, S., Rahmedov, D. & Bellaiche, L. Electric-field-induced paths in multiferroic BiFeO3 from atomistic simulations. Phys. Rev. Lett. 103, 047204 (2009).
Daumont, C., Ren, W., Infante, I. C., Lisenkov, S. & Allibe, J. et al. Strain dependence of polarization and piezoelectric response in epitaxial BiFeO3 thin films. J. Phys. 24, 162202 (2012).
Kashid, A. P., Patil, V. V. & Chavan, S. H. Pyroelectric properties of Gd-doped KVO3 and LiVO3. Bull. Mater. Sci. 12, 57–62 (1989).
Patil, N. B., Patil, R. T. & Chavan, S. H. Dielectric hysteresis of undoped and dysprosium doped ferroelectric potassium vanadate. Bull. Mater. Sci. 12, 129–132 (1989).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767 (1976).
Filip, M. R. & Giustino, F. The geometric blueprint of perovskites. Proc. Natl Acad. Sci. USA 115, 5397–5402 (2018).
Goldschmidt, V. M. Die gesetze der krystallochemie. Naturwissenschaften 14, 477–485 (1926).
Megaw, H. Crystal Structures, Vol. 10 (WB Saunders Company, 1973).
Selbin, J. The chemistry of oxovanadium (IV). Chem. Rev. 65, 153–175 (1965).
Pérez-Mato, J. M., Ivantchev, S., García, A. & Etxebarria, I. Displacive vs. order–disorder in structural phase transitions. Ferroelectrics 236, 93–103 (2000).
Kittel, C. Theory of antiferroelectric crystals. Phys. Rev. 82, 729–732 (1951).
Chanthbouala, A., Garcia, V., Cherifi, R. O., Bouzehouane, K. & Fusil, S. et al. A ferroelectric memristor. Nat. Mater. 11, 860 (2012).
Buerger, M. J. The arrangement of atoms in crystals of the wollastonite group of metasilicates. Proc. Natl Acad. Sci USA 42, 113 (1956).
Mamedov, H. S. & Belov, N. V. Crystal structure of the minerals of the wollastonite group. I. Structure of xonotlite. Zap. Vses. Mineral. Obshchest 85, 13–38 (1956).
Belik, A. A., Wuernisha, T., Kamiyama, T., Mori, K. & Maie, M. et al. High-pressure synthesis, crystal structures, and properties of perovskite-like BiAlO3 and pyroxene-like BiGaO3. Chem. Mater. 18, 133–139 (2006).
Lukesh, J. S. The unit cell and space group of ammonium metavanadate, NH4VO3. Acta Crystallogr. 3, 476–477 (1950).
Ganne, M., Piffard, Y. & Tournoux, M. Structure cristalline de TlVO3. Can. J. Chem. 52, 3539–3543 (1974).
Marumo, F., Isobe, M., Iwai, S. & Kondō, Y. α-Form of sodium metavanadate. Acta Crystallogr. Sect. B 30, 1628–1630 (1974).
Miller, R. C., Wood, E. A., Remeika, J. P. & Savage, A. Na(Nb1−xVx)O3 system and “ferrielectricity”. J. Appl. Phys. 33, 1623–1630 (1962).
Kittaka, S., Matsuno, K. & Akashi, H. Crystal structure of α-AgVO3 and phase relation of AgVO3. J. Sol. State Chem. 142, 360–367 (1999).
Shannon, R. D. & Calvo, C. Crystal structure of LiVO3. Can. J. Chem. 51, 265–273 (1973).
Yu, J. & Kudo, A. Effects of structural variation on the photocatalytic performance of hydrothermally synthesized BiVO4. Adv. Funct. Mater. 16, 2163–2169 (2006).
Tolédano, P. & Guennou, M. Theory of antiferroelectric phase transitions. Phys. Rev. B 94, 014107 (2016).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 48, 13115–13118 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Ruzsinszky, A., Csonka, G. I., Vydrov, O. A. & Scuseria, G. E. et al. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 100, 136406 (2008).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Monkhorst, H. J. & Pack, J. D. Special points for brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Momma, K. & Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 44, 1272–1276 (2011).
Mills, G., Jónsson, H. & Schenter, G. K. Reversible work transition state theory: application to dissociative adsorption of hydrogen. Surf. Sci. 324, 305–337 (1995).
Henkelman, G., Uberuaga, B. P. & Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 113, 9901–9904 (2000).
Acknowledgements
Author information
Authors and Affiliations
Contributions
H.A. performed the calculations, produced the figures, analysed the results, and wrote the manuscript. J.Í. supervised the work, analysed the results and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aramberri, H., Íñiguez, J. Antiferroelectricity in a family of pyroxene-like oxides with rich polymorphism. Commun Mater 1, 52 (2020). https://doi.org/10.1038/s43246-020-00051-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-020-00051-9
This article is cited by
-
Antiferroelectric negative capacitance from a structural phase transition in zirconia
Nature Communications (2022)