Introduction

The United Nation sustainable development goals (SDGs; UNDP, 2015)1 closely concern sustainable cities and communities (SDG 11), requiring inclusive and sustainable urbanization with benign human-land relationships2. Particularly the SDG 11.3.1 indicator that compares population growth to land consumption is addressed; thus, balanced human-land relationship plays an important role in sustainable city development. However, governments worldwide have difficulties in balancing urban land expansion and population growth rates, as land development and population growth are not always synchronized, especially during the rapid global urbanization3,4; additionally, global urban agglomeration development leads to population concentrations in metropolises but population outflows in other cities5. Both can cause imbalanced human-land supply-demand and result in overload or underload of land resources, which deviates from SDG 11. Prior work on urbanization related consequences has mainly focused on land overload issues, such as overlarge population, heat island, traffic congestion, or pollution6, but scant attention has been paid to land underload particularly in relation to ghost cities7,8,9.

Different from the traditional image of ghost towns that are abandoned because of economic or natural resource hardship10, ghost cities/neighborhoods are generally understood as vacant areas that were newly built but uninhabited11,12,13. A number of studies have identified ghost cities based on population-related measures, using nightlight satellite images14,15, mobile phone positioning16, social media vitality7, or point-of-interest data17. The conceptual approaches towards ghost cities in these studies mostly consider population density, but ignore the land’s spatial heterogeneity, and thus the specific land carrying capacities (LCC) of diverse cities for people and economy remain undifferentiated18,19,20,21,22. In fact, cities contain distinct functional zones with varying spatial structures, i.e., heterogeneous land functional structures (LFS), that support variant human socioeconomic activities and have different LCC for people and economy23,24,25. Employing a unified threshold to extract ghost cities hence abstracts the varying LCC across different cities21,26. Besides these issues, ghost city studies have encountered another conceptual bottleneck. Wade Shepard who proposed the widely recognized definition of ghost cities suggested that there could be no ghost city but only temporary ghost stages in China27. From the perspective, ghost cities would disappear with urbanization development and population influx5; thus, ghost city might lose significance and partly lose popularity7. Whether or not this will happen, we believe a more general concept rather than the extremes of ghost cities should be developed and relevant in the long term.

To account for the unknown effects raised above, we extend the ghost cities and propose a concept of underload cities. These underload cities are defined to carry fewer people and lower economic strength than their LCC which are featured by LFS. There are three reasons for proposing the concept: 1) underload cities as a synthetical geographic concept consider not only population, but also economy and LCC, which meet the requirement of SDG 11 that highlights human-land relationship2 and are different from ghost cities that solely measure population density; 2) underload cities as an imbalanced phenomenon always exist in the process of land construction and human development, which can be more common and last even longer than ghost cities27, and thus have more profound impact on sustainable city development; and 3) underload cities are the opposite to overload cities which have been widely studied and represent another imbalanced phenomenon in urbanization5,6; thus, investigating underload cities can complement existing researches of overload cities. Based on this concept, underload cities essentially represent imbalanced human-land relationships17, and it can be imperative to identify underload cities for re-integration of land resources, coordination of human-land relationship, and promotion of sustainable city development28.

However, two methodological research gaps need to be bridged for studying underload cities. On the one hand, LFS need to be characterized. LFS represent the land’s spatial heterogeneity and refer to land functions and their spatial structures. These are the basic units where people undertake different socio-economic activities, and thus are fundamental for measuring LCC26. Three issues should be considered for extracting LFS: 1) high spatial resolution is needed to enable detailed representation of LFS28,29, but current uses of low and medium-resolution land cover/use data are not sufficient for this purpose; 2) considering land functions’ diverse representations and abstract categories, traditional satellite image classification methods cannot recognize land functions accurately26; and 3) considering land structures’ spatial complexity and heterogeneity, existing image textures and landscape matrices cannot measure land structures comprehensively and robustly29. To address these challenges, this study derives very high-resolution land functional zone maps, based on which we quantify LFS and cluster different types to express LFS robustly.

On the other hand, LCC needs to be evaluated. LCC refers to the population and economy that a city can carry considering its LFS. It measures the equilibrium state of human-land relationship and thus serves as a benchmark for identifying underload cities. Existing LCC evaluation methods are limited, because they consider either local land functions30,31, or mean population and GDP as the standard17, but few consider both32,33,34. To address the limitation, this study presents an evaluation method for LCC, measuring the correlation between LFS and population/GDP in a relational system across cities for a better benchmarking. Based on this technique, we identify China’s underload cities by comparing their actual populations and GDP to the estimated LCC.

The study will resolve the two methodological challenges raised above and identify underload cities from 81 major cities in China (Fig. 1a), including all province-level municipalities, provincial capitals, and top 50 cities in GDP, covering a total area of 983,215km2. First, we map land functional zones using very high-resolution (VHR) satellite images. Second, we characterize and cluster their LFS. Third, we evaluate LCC by combining LFS and demographic/economic data. And finally, we identify underload cities, discuss their general patterns, and compare the results with ghost cities and the SDG 11.3.1 indicator, respectively.

Fig. 1: Land functional zone maps of 81 major cities across China.
figure 1

a Distributions of the considered 81 cities whose names and detailed information are provided in the Supplementary Fig. 6. b Land functional zone map exemplified for Shanghai. The legend illustrates the 12 functional classes derived. c–f, Four selected regions in Shanghai to illustrate the land functional zones in details, where the maps are set at 60% transparency and overlapped with satellite images.

Full size image

Results

Mapping VHR land functional zones

We use VHR satellite images at 2.4 m resolution fused by multiple sensors (see Data in Methods) and multilevel semantic segmentation (see Methods) to map land functional zones. According to the codes of urban land-use classification and planning published by the Ministry of Housing and Urban-rural Development of China, we divided the land of 81 cities into 12 nonoverlapping categories of land functional zones (three residential classes, commercial, industrial, institutional, transportation, as well as undeveloped, water, open space, farmlands, and forest and grass), and generate very-high-resolution land functional zone maps (see Fig. 1 and Supplementary Fig. 7). The overall mapping accuracy is 85.0%, and a Kappa index is measured at 0.82, which are evaluated based on 25,419 test samples (see Supplementary Method). Compared to existing land cover/use data, the generated land functional zone map has two advantages. First, the map has relatively high resolution so that functional zone boundaries and categories can be more accurately represented. Second, the functional categories are closely related to socioeconomic activities, i.e., living, working, etc., which can be more applicable to human-land relationship analysis and LCC evaluation.

Characterizing and clustering land functional structures

For quantitative representations of heterogeneous land functional structures (LFS), we measure LFS of each city by 64 indices (including functional, structural, and thematic ones) which can be derived from the land functional zone maps (see Methods). These indices are defined to characterize land functional services, spatial structures, and socioeconomic attributes. This is done in reference to existing studies as they find land functional and structural indices can directly influence population distribution and economic strength26,30,31. In this study, we also presume that the socio-economic attributes, e.g., living environments and industrial types29, influence or even define LCC for population and economy. Then, we cluster LFS types at city level using these indices to robustly express land functions and structures. As the result, we group 81 cities into six types (T1-T6 in Fig. 2) using the density peaks clustering algorithm (DPCA), where the type number of 6 is detected by the DPCA considering samples’ densities and distances in feature spaces (see Methods and Supplementary Fig. 3).

Fig. 2: Six types of cities clustered based on LFS.
figure 2

a Spatial distributions of the six types. b Mean population, GDP, and representative cities of the six types. c Cities’ distributions in the LFS feature space, with structural aggregation as the x-axis and structural fractal dimension as the y-axis to represent the 2D feature space, because of their highest information entropy. A larger font size is used to highlight the six representative cities in the feature space. d–i Normalized land functional proportions for the six types. The normalized proportion of a functional category in a specific type refers to its ratio to the largest proportion of the category among all types, and their standard deviations are labeled.

Full size image

These six types differ significantly in land functions and structures (see Supplementary Table 2): T1 Comprehensively-developed cities have the largest proportions for commercial, industrial, L1-residential, L2-residential, open spaces, institutional, and transportation lands. These cities are mainly distributed in developed areas, e.g., the Yangtze river delta, the Pearl river delta, and the Shandong peninsula megalopolis. T2 Administrative-centered cities feature higher proportions of institutional and residential lands. They mainly are province-level municipalities and provincial capitals. T3 Coastal cities have the smallest undeveloped lands and are mainly distributed in the eastern coastal areas. T4 Cities with development potentials have the smallest farmland proportion but the highest proportion of undeveloped lands, indicating large developmental potentials. They are all distributed in southern China. T5 Rural-agricultural cities have the largest proportions of the categories of L3-residential and farmland, indicating a relatively developed first industry and a backward urbanization level, and they are mainly distributed in northern China. T6 Ecological cities have the smallest proportions for most kinds of built-up lands, but the largest proportion of relatively natural lands, e.g., forest and grass, and provide important ecological services. Most T6 cities are located in northwest China. The clustered six types represent LFS of diverse cities robustly, as LFS indices are relatively homogeneous in each type, so that we can describe LFS’s correlation with population/GDP type by type and accurately evaluate LCC.

Evaluating LCC based on LFS

We evaluate cities’ LCC based on LFS indices, type by type, where six LFS types generated in the prior section are considered to reduce LFS indices’ heterogeneity and improve the robustness of LCC estimation results29. Specifically, we employ stacked autoencoder (see Methods) to integrate and dimensionally reduce LFS indices, and use ordinary least squares to estimate LCC by measuring the correlation between LFS indices and population/GDP (see Methods) in each type of cities (Eq. 1 and 2),

$$LCC_c^{{{{\mathrm{Pop}}}}} = LR_u^{{{{\mathrm{Pop}}}}}\left( {\overrightarrow {{{{\boldsymbol{FS}}}}} _{{{\boldsymbol{c}}}}} \right)\left( {c \in type_u} \right),$$
(1)
$$LCC_c^{{{{\mathrm{GDP}}}}} = LR_u^{{{{\mathrm{GDP}}}}}\left( {\overrightarrow {{{{\boldsymbol{FS}}}}} _{{{\boldsymbol{c}}}}} \right)\left( {c \in type_u} \right),$$
(2)

where \(LCC_c^{{{{\mathrm{Pop}}}}}\) and \(LCC_c^{{{{\mathrm{GDP}}}}}\) refer to the city c’s LCC for population and GDP respectively, and the city c belongs to u-th LFS type (typeu). \(\overrightarrow {{{{\boldsymbol{FS}}}}} _{{{\boldsymbol{c}}}}\) denotes the LFS indices of the city c which are integrated and dimensionally reduced by stacked auto-encoder, \(LR_u^{{{{\mathrm{Pop}}}}}\) and \(LR_u^{{{{\mathrm{GDP}}}}}\) are linear regression models which are trained by cities in typeu. As presented in Fig. 3b, e, the LCC results are highly heterogeneous. This proves that different cities have different LCC, and thus ghost city analysis considering a unified population threshold are limited due to aggregation effects. According to LCC, we evaluate the cities’ land carrying conditions by two indicators, i.e., shortage in land carrying (SLC) and land carrying rate (LCR) (see Supplementary Table 3).

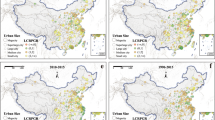
Fig. 3: Land carrying capacity (LCC), and the computations for shortage in land carrying (SLC) and land carrying rate (LCR) for 81 major cities.
figure 3

a–c the actual population of the cities, and their expected LCC for and SLC of populations. d–f the actual GDP of the cities, and their expected LCC for and SLC of GDP. g, h LCR for population and GDP of the cities. i overall LCR of the cities where dark brown represents the overload (high carrying rate), and light yellow the underload (low carrying rate).

Full size image

SLC of population and GDP are defined as differences from the actual population and GDP respectively to their expected LCC. We applied the SLC to the 81 major cities (see Supplementary Fig. 6) and their spatial distributions are shown in Fig. 3. In terms of population, we identify Zhuhai as the most underloaded in China. It features an extremely low SLC, i.e., −6.76 million people, as it has a large LCC of 8.78 million people but only 2.02 million residents. Two further eastern cities also have large LCC but carry much smaller populations: Taizhou in the Jiangsu Province (SLC of population = −4.57 million) and Jiaxing in the Zhejiang Province (−4.12 million). Even regional central cities such as Guangzhou (−3.06 million) and Xi-an (−2.63 million) are found to be underloaded for the population. The former is the capital city of the Guangdong Province, which can bear 18.36 million people considering its LCC but only carries 15.31 million residents. The latter is the capital city of the Shaanxi Province, whose LCC is 12.83 million, but it has only 10.20 million residents. The underpopulation of these cities indicates a serious waste of land resources and also imbalanced human-land relations. In terms of economy proxied by GDP, Zhuhai is found again the most underloaded city of China (SLC of GDP = −124.71 billion RMB). Some other cities are also weak in SLC with respect to economy, e.g., Jiaxing (−69.22 billion), Qinhuangdao (−42.36 billion), Tianjin (−39.53 billion), and Weifang (−36.83 billion). The negative values relate to the lower GDP than their inherent LCC, and thus the results for these cities signify inefficient land utilizations.

With LCR, we aim to measure a city’s carrying rate for population (LCRP) and GDP (LCRG), respectively. They are calculated as follows: \(LCR^{{{\mathrm{P}}}} = \frac{{Actual^{{{{\mathrm{Pop}}}}}}}{{LCC^{{{{\mathrm{Pop}}}}}}}\) and \(LCR^{{{\mathrm{G}}}} = \frac{{Actual^{{{{\mathrm{GDP}}}}}}}{{LCC^{{{{\mathrm{GDP}}}}}}}\), where ActualPop and ActualGDP refer to the actual population and GDP of the city. Then, we calculate the overall LCR as LCR = LCRP × LCRG, where LCR > 100% means relative overload and LCR < 100% denotes underload. LCRP and LCRG are calculated for 81 cities. To analyze cities’ land carrying conditions and to express the relationship between LCRP and LCRG, a LCR feature space is drawn (Fig. 4). We find a generally linear correlation of cities’ LCRP and LCRG (Fig. 4a), with a correlation coefficient of 0.68. This indicates that most cities are over- or underloaded for population and GDP simultaneously, except for 17 cites (Fig. 4b). The cities with underload population but overload GDP are located in the UO quadrant, including Taizhou (Jiangsu), Lanzhou, Changzhou, Nanjing, Wuxi, Yangzhou, and Qingdao. Conversely, the cities with overload population but underload GDP are in the OU quadrant, including Harbin, Tongling, Zhoushan, Quanzhou, Yancheng, Taizhou (Zhejiang), Jining, Foshan, Chuzhou, and Shijiazhuang. The results demonstrate that different cities have different LCR and even a city can have different carrying conditions for population and economy (LCRP vs. LCRG).

Fig. 4: Distribution of cities in LCR feature space.
figure 4

a Points represent the 81 cities in the LCR feature space, x-axis shows LCR for population (LCRP), and y-axis is LCR for GDP (LCRG). UO means underload population but overload GDP, while OU means the opposite; OO denotes overload for both, while UU is underload for both. b A close-up view of cities distributed in the UO and OU quadrants with city names, LCRP, and LCRG labeled.

Full size image

Identifying underload cities

We identify underload cities based on LCR. Cities whose \(LCR \,<\, \overline {LCR} - Std\left( {LCR} \right)\), i.e., LCR < 71.6% in this study, are defined as underload, where \(\overline {LCR}\) denotes the average LCR of 81 cities and Std(LCR) the standard deviation of LCR. Cities whose \(\overline {LCR} - Std\left( {LCR} \right) \,\le\, LCR \,<\, \overline {LCR} - \frac{1}{2}Std\left( {LCR} \right)\), i.e., 71.6% ≤ LCR < 85.8%, are considered as slightly underload; \(\overline {LCR} - \frac{1}{2}Std\left( {LCR} \right) \,\le\, LCR_c \,<\, \overline {LCR} + \frac{1}{2}Std\left( {LCR} \right)\), i.e., 85.8% ≤ LCR < 114.2%, as well-balanced; \(\overline {LCR} + \frac{1}{2}Std\left( {LCR} \right) \,\le\, LCR_c \,<\, \overline {LCR} + Std\left( {LCR} \right)\), i.e., 114.2% ≤ LCR < 128.4%, as slightly overload; \(LCR_c \ge \overline {LCR} + Std\left( {LCR} \right)\), i.e., LCR > 128.4%, as overload. This analysis intends to identify underload or overload cities in a relational system across China for a better benchmarking by comparisons. Consequently, the 81 cities are classified into five types (Fig. 5). Eight underload and 15 slightly underload cities are found, and identifying other three types is the additional contribution of the study (see Supplementary Fig. 5).

Fig. 5: Cities classified into five types in reference to land carrying rate (LCR), i.e., underload, slightly underload, well-balanced, slightly overload, and overload.
figure 5

a Cities’ LCR which are ranked in descending order. b Spatial distributions of the five types of cities.

Full size image

In our analysis, we identify 15 cities as slightly underload: Huizhou, Shaoxing, Guangzhou, Jinhua, Xuancheng, Nanjing, Lanzhou, Xi-an, Changzhou, Dalian, Huzhou, Luoyang, Zhangjiakou, Chizhou, and Guiyang. They consist of the first to fifth tiers of cities and are scattered across the country (Fig. 5b), indicating a lack of association between the slightly underload cities and their locations/city tiers. This finding is different from the common perception about cities’ loads and development levels. For example, Guangzhou has a large population and developed economy, but it is found to be slightly underloaded for population and GDP when its large LCC is taken into consideration. It is similar for Nanjing and Xi-an, both capital cities for previous dynasties, and now serving as capitals of Jiangsu and Shaanxi Provinces being population hubs with advanced economies. However, they are found to be underloaded when comparing their populations and GDP to LCC.

We further identify eight underload cities: Zhuzhou (LCR = 67.4%), Dongying (65.4%), Haikou (57.9%), Qinhuangdao (54.1%), Taizhou (Jiangsu) (52.4%), Jiaxing (47.3%), Ma-anshan (46.2%), and Zhuhai (16.91%). Among these cities, Dongying, Ma-anshan, and Jiaxing have been recognized as ghost cities in previous studies8,15,35. The main economic activities in Dongying and Ma-anshan are petroleum and steel industries. Due to the structural crisis of their industries, they have experienced slow economic development and low population growth recently8. Leichtle et al. (2019) revealed the ghost city phenomenon in Dongying with a considerable mismatch between its estimated population capacity and residential number8; Jin et al. (2017) profiled Ma-anshan with low urban vitality as a ghost city15. Additionally, an influential report “Ranking list of ghost city index in China mainland (2014)” ranked Jiaxing high as a potential ghost city35. Our findings corroborate this, as Jiaxing has a low LCRP of 53.4% and a low LCRG of 88.6%, indicating that the city is underloaded for both population and GDP. These comparisons reflect the close relationship between underload and ghost cities, and verify the rationality of the detected underload cities. The remaining five underload cities however have not been noticed in prior work, and they are identified because our approach accounts for heterogeneous LCC.

Analyzing general patterns of the underload cities

We find three general patterns of these underload cities. Firstly, the cities whose original industries are experiencing structural crisis can have slow development or even declines in population and GDP, resulting in LCC surpluses and underload cities, such as Dongying and Ma-anshan. The phenomenon is very common worldwide and occurred in many international cities, e.g., Detroit in the U.S., Hashima in Japan, and Fordlandia in Brazil15. This underload condition is often irreversible, unless new industries develop.

Secondly, the cities on the edge of urban agglomerations can be influenced by neighboring metropolises, as their population and GDP are affected by the siphon effect from surrounding cities. In this case, we find Qinghuangdao in Beijing-Tianjin-Hebei36, Zhuzhou in Changsha-Zhuzhou-Xiangtan37, Jiaxing and Taizhou (Jiangsu) in Yangtze River Delta as underload cities. Similarly, small or medium-sized cities around metropolises, e.g., New York, London, and Tokyo, can also face the same problem38.

Thirdly, the cities supported by major national policies can have fast land development with high urban expansion rates; thus, their LCC skyrocket, but their populations and economy will not rise rapidly in the short term. In this case, two Special Economic Zones of China including Zhuhai and Haikou39 are found as underload cities. This underload condition is essentially a temporary product of the construction phase, as Brasilia in 1960s and Sejong in 2010s, and can be alleviated with population influx and economic growth. Taking Zhuhai as an example, the population increase in Zhuhai has speeded up at a rate of 7% annually since 2017 and may soon catch up with that of built-up expansion40, so that the extremely underload phenomenon in Zhuhai may thus be alleviated in the future, according to the current development trend.

Comparing underload cities with ghost cities

We compare the alternative concept of underload cities with the often-used concept of ghost cities41,42, to demonstrate the significance of the broader conceptual approach. First of all, these two concepts have significant differences in definition, as ghost cities mostly consider population density, but underload cities measure population, GDP, and LCC; thus, underload cities cannot be directly related to ghost cities. If we compare both concepts in an empirical manner, we find the following: we calculate population density (PD; the ratio of population to built-up area) to identify the top ten ghost cities (see Supplementary Table 4), and examine the differences between these ten ghost cities and the findings of this study (Fig. 6). Consequently, the ten ghost cities based on low PD are: Lhasa (PD = 0.29 thousand people km−2), Dongying (0.97), Urumqi (1.00), Chizhou (1.11), Zhangjiakou (1.14), Xuancheng (1.33), Nanning (1.60), Chongqing (1.60), Qianghuangdao (1.92), and Jinhua (1.94). Six out of these ten ghost cities are detected in this study as underload or slightly underload cities, including Dongying, Qinghuangdao, Chizhou, Zhangjiakou, Xuancheng, and Jinhua.

Fig. 6: Comparison between land carrying rate (LCR) and population density (PD), highlighting the differences between underload and ghost cities.
figure 6

a, b LCR and PD of 81 cities. c–f Urumqi, Lhasa, Nanning, and Chongqing which are identified as ghost cities according to PD but nonunderload by LCR.

Full size image

Conversely, the remaining four ghost cities, i.e., Lhasa, Urumqi, Nanning, and Chongqing, are not identified as underload. These cities are located in outlying areas in western China. Due to rugged terrains and harsh natural environments, their LCC are limited. Although their low PD characterize them as ghost cities, the populations of these cities may have depleted their limited LCC, resulting in the categorization of them as non-underload. Identifying ghost or underload cities thus has implications and divergences in city planning. Let us take Nanning as an example: based on the underload city concept, Nanning has a high LCR at 133.8% (Fig. 6e), and could be considered overloaded, needing population outflow and incentives for land developments; from the ghost city viewpoint, however, a different suggestion such as more population influx and reduced land constructions could be made due to the low population density of Nanning.

In addition, among the eight underload cities identified in this study, only two are found among the ten ghost cities; while the other six have ordinary PD and are not recognized as ghost cities. These six cities have large LCC which greatly exceed their population and GDP, and thus are classified as underload. Based on the underload city concept, these six cities should increase population and limit land constructions. In contrast, from the ghost city viewpoint, the six cities can continue land constructions, which potentially exacerbates the cities’ underload conditions. The comparisons above underscore the conceptual and in consequence differences for underload and ghost cities. Employing the ghost city viewpoint could have adverse impacts on human-land relationship, for its negligence in LCC. Therefore, more conceptual approaches besides ghost cities are needed to assess land carrying conditions for sustainable city planning, and thus underload cities in synopsis allow a complementary perspective and improved analysis.

Comparing LCR to the SDG 11.3.1 indicator

SDG 11.3.1 refers to the ratio of land consumption rate to population growth rate, which measures land use efficiency5 and also concerns the human-land relationship43,44. Here, we compare LCR with SDG 11.3.1 to demonstrate the significance of this study to SDG.

Existing studies on SDG 11.3.1 measure land consumptions by impervious surface or artificial land45,46, but they mostly ignore heterogeneous land functions and structures inside impervious surface which however can greatly influence population growth47. In consequence, previous measurements of land consumption rates are limited, resulting in aggregated information on SDG 11.3.1. Differently, this study models diverse land functions and their structures (LFS) within cities to measure land consumption from socioeconomic and spatial-structural perspectives, based on which LCR can be estimated to quantify the relationship between land consumption and population with more comprehensive and detailed information. Although SDG 11.3.1 and LCR both produce aggregated evaluations at the city scale, LCR however considers intracity land-function heterogeneity and generates more meaningful results to explain the human-land relationship. Accordingly, LCR can be regarded as a complement to SDG 11.3.1 and an important indicator for evaluating sustainable city development. Furthermore, using LCR can identify two unsustainable city development modes, i.e., underload and overload cities (see Supplementary Fig. 5); thus, the concept, approaches, and findings of this study provide a different perspective for understanding the imbalanced human-land relationship and unsustainable development modes, potentially contributing to SDG.

Discussion

This study demonstrates the use of VHR satellite data and derived LFS (including land functions and structural types) to evaluate the LCC of cities, and the importance of considering LCC to identify underload cities. This study is distinct from prior works on ghost cities and the SDG 11.3.1 which mainly considers population density but does not relate to the LCC.

This study identifies eight major underload cities across China, among which five cities would not have been detected had the conventional ghost city concept been applied. We also find three general patterns of these underload cities, whose original industries are experiencing structural crisis, whose population and GDP are affected by the siphon effect from surrounding cities, and whose land development is too fast supported by major national policies. Among those, the first pattern of underload cities can be irreversible, but the third is basically a temporary construction phase and can be alleviated with population influx and economic growth.

This study also finds 15 slightly underload cities. Different from the common perceptions that big cities are over developed and congested by large populations, some big cities can be recognized as slightly underload in the study, because they could carry more people and GDP when their LFS and LCC are considered. It is suggested that these underload cities need population and GDP influx and limit further land developments, so as to best use their LCC. The findings of this study provide new insights into human-land relationships, potentially contributing to a more sustainable city development.

However, the empirical verification in this study has two limitations. Firstly, the study focuses on evaluating land loads at the scale of prefecture-level cities but ignores the heterogeneity within them. Prefecture-level cities are essentially administrative units and are usually composed of multiple county-level cities which however may have different land load conditions11. Accordingly, a local evaluation, such as underload counties/neighborhoods, should be developed to reveal heterogeneous human-land relations within cities. Secondly, this study considers a part of Chinese cities, but not include international cities in other countries, owing to the limitation of acquiring very high-resolution satellite data. In the future, international evaluations on underload cities can be conducted to find the differences in human-land relation among different nations and international cities.

In summary, we hope to work together with other scholars to resolve these limitations, and enrich the conceptual approach by studying underload cities/counties/neighborhoods and supplementing the international verification cases.

Methods

Data

For demographic and economic data, population and GDP data are retrieved from the “China city construction statistical yearbook in 2019” (https://www.mohurd.gov.cn/gongkai/fdzdgknr/sjfb/tjxx/jstjnj/index.html), where GDP represents the gross domestic product, and population refers to the resident population including both permanent (registered) and temporary residents who live there for more than six months in one year.

For land observation, satellite images covering 81 major cities are acquired by splicing and resampling images from different sensors, including SPOT-6, GF-1, and ZY-3. The image product was acquired in 2019 and basically contained three visible bands (i.e., red, green, and blue) with a very high resolution of 2.4 meters. The images have been ortho-rectified and thus provide accurate image features for mapping land functional zones. In addition, built-up area of each city is obtained from “China city construction statistical yearbook in 2019”, where built-up area refers to the developed land that carries intensive human activities.

Multilevel semantic segmentation to map land functional zone

We employ a multilevel semantic segmentation (MSS) proposed by our previous study48 to map land functional zones. MSS consists of a semantic segmentation at object level and a neighborhood optimization at block level. For the object-level semantic segmentation, it excels in classifying complex structures with strong internal heterogeneity, confusing boundaries, and multiscale representations48,49; thus, it can recognize diverse land functions. It generally has three processes, i.e., object segmentation, deep feature encoding, and semantic prediction (see Supplementary Method). For object segmentation, a multiresolution segmentation approach50 is used to segment satellite images into objects. For deep feature encoding, objects are processed by a densely connected convolutional network (DenseNet)51 and four dilated convolutions52 with different convolution kernels (1 × 1, 3 × 3, 3 × 3, 3 × 3) and dilated rates (1, 6, 12, 18). For semantic prediction, multiple deep feature maps generated by DenseNet and dilated convolutions are stacked, convoluted, and up-sampled to predict land function categories for objects. In addition, MSS considers a neighborhood optimization at block level, which uses conditional random field to model the neighboring relationship among land functional zones and eliminates the wrong classification results within roadblocks. Technical details of MSS see the reference48.

For training the model, we manually delineated and labeled 84,730 samples of land functional zones based on visual interpretations and field investigations, 70% of which are clipped into 94,306 non-overlapped patches of 512 × 512 pixels and fed into the model, where the pixels hit by manually labeled samples are set as their categories, and others are null values. The hyperparameters set in the training process are illustrated as follows. The TensorFlow system is generally used for implementation; the segmentation scale of multiresolution segmentation is set to 50; a L2-regularization is considered to avoid overfitting; an Adam optimizer with a learning rate of 2 × 10−4 is employed for training53; and cross entropy is used as loss function, i.e., \(CELoss = \frac{1}{N}\mathop {\sum }\nolimits_{i = 1}^N \mathop {\sum }\nolimits_{j = 1}^M - \widehat {y_{ij}}{{{\mathrm{log}}}}\left( {y_{ij}} \right)\), where N denotes the number of samples, M the number of land function categories, yij represents the probability that i-th sample belonging to the j-th category, and \(\widehat {y_{ij}}\) represents the real class with one-hot encoding; the semantic segmentation structure will be trained for 50,000 iterations. The hyperparameter tuning is demonstrated in our previous study48.

For evaluating mapping results, we utilize the remaining 30% samples (25,419) and measure the pixel-wise confusion matrix54. Overall accuracy, OA = NT/N, is calculated to assess mapping accuracy, where N denotes the pixel number of test samples and NT the number of accurately recognized pixels. In addition, Kappa index of mapping result is also measured \(Ka{{{\mathrm{pppa}}}} = \frac{{OA - P}}{{1 - P}}\), where \(P = \frac{{\mathop {\sum }\nolimits_{i = 1}^M A_i \times B_i}}{{N \times N}}\), M refers to the number of functional categories, Ai the pixel number of the i-th category in test samples, Bi the pixel number of the i-th category in mapping results54.

Index system for characterizing LFS

For quantitatively expressing LFS per city, we integrate indices related to land use, urban planning, and landscape pattern to propose an index system55,56,57, which includes functional, structural, and thematic indices (see Supplementary Table 1). Functional indices describe functional types and services, e.g., functional proportion, area, abundance and dominance; structural indices measure spatial structures of diverse land functions, e.g., structural fragmentation, minimum distance, aggregation; and thematic indices characterize socio-economic attributes, e.g., industrial type, living environment, public and ecological service. These indices have been verified effective to characterize land functions and structures55,56 and closely related to LCC evaluation29,30,31. All these indices can be derived from the generated land functional zone maps.

Density peaks clustering algorithm to detect robust LFS type

To reduce the influence of LFS’s heterogeneity on modeling human-land relationships, we extract robust LFS types by a state-of-the-art clustering model. We apply the density peaks clustering algorithm (DPCA)58, as DPCA excels in overcoming outliers, explicitly selecting clustering centers, and processing aspheric distributions59. DPCA recognizes samples with large local densities and large distances to other high-density samples as clustering centers, thus it mainly considers two indicators in clustering, i.e., local density and distance to high-density samples. On the one hand, local density of the i-th sample \(\rho _i = \mathop {\sum }\nolimits_{j = 1:N,j \ne i} \tau \left( {d_{ij} - d_c} \right)\), where N denotes the number of samples, dij the distance from sample i to sample j in the feature space, dc is a threshold defining the neighborhood range, and τ(x) = 1 when x < 0; on the other hand, i-th sample’s minimum distance to the samples with higher density is formulated by \(\delta _i = \mathop {{\min }}\limits_{j:\rho _j > \rho _i} (d_{ij})\) or \(\delta _i = \max (d_{ij})\) when ρi > ρj(j = 1:N,j ≠ i). Accordingly, the dij is core to DPCA, and we define dij as \(d_{ij} = {{{\mathrm{max}}}}\left( {d_{ij}^{{{\mathrm{f}}}},d_{ij}^{{{\mathrm{s}}}},d_{ij}^{{{\mathrm{t}}}}} \right)\), where \(d_{ij}^{{{\mathrm{f}}}}\) represents the distance from sample i to j in functional-index space, \(d_{ij}^{{{\mathrm{s}}}}\) that in structural-index space, \(d_{ij}^{{{\mathrm{t}}}}\) that in thematic-index space, and distances are measured by the Euclidean distance. This definition of dij ensures clusters’ homogeneity in all feature spaces.

As demonstrated above, we calculate the distances between cities in feature spaces, measure ρi and δi of each city, and select six cluster centers by ρi ≥ 7 and δi ≥ 0.5 in this study with considering the cities’ distributions in ρ-δ space (see Supplementary Fig. 3). Other cities are assigned to the clusters of their nearest neighbor with higher density.

Combining SAE and OLS to estimate LCC

Estimating LCC needs modeling the human-land relationship which is essentially to measure the correlation between LFS indices and socio-economic attributes, i.e., population and GDP in our case. However, two technical issues arise: 1) how to fuse diverse LFS indices, and 2) how to avoid the “curse of dimensionality“60 affecting correlation modeling. We use a stacked auto-encoder (SAE) to resolve these two issues. SAE has been widely used for feature fusion and dimensionality reduction61. SAE is composed of multiple auto-encoders (AEs)62, and each AE consists of three layers: input, hidden and output layers, where the input and hidden layers compose encoder, hidden, and output layers compose decoder (see Supplementary Fig. 4). For encoding, the input features \({{{\vec{\boldsymbol x}}}} \in R^N\) are dimensionally reduced into hidden features \({{{\vec{\mathbf y}}}} \in R^K\), where N refers to the dimension number of input features and K that of hidden features; for decoding, the \({{{\vec{\mathbf y}}}} \in R^K\) reconstructs \({{{\vec{\boldsymbol x}}}}^\prime \in R^N\). Accordingly, AE is formulated as:

$${{{\vec{\mathbf y}}}} = f\left( {\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{x}}}}} \cdot {{{\vec{\boldsymbol x}}}} + b_x} \right),$$
(3)
$${{{\vec{\boldsymbol x}}}}^\prime = f\left( {\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{y}}}}} \cdot {{{\vec{\boldsymbol y}}}} + b_y} \right),$$
(4)

where \(\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{x}}}}}\), \(\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{y}}}}}\), bx, and by are parameters of encoder and decoder respectively, and f(*) represents a sigmoid activation function63. Training AE is essentially to minimize the reconstruction loss between \({{{\vec{\boldsymbol x}}}}\) and \({{{\vec{\boldsymbol x}}}}^\prime\), \(RecLoss = \Vert{{{\vec{\boldsymbol x}}}} - {{{\vec{\boldsymbol x}}}}^\prime\Vert\), and the hidden features are extracted as the features after dimension reduction. Similarly, SAE is constructed by stacking multiple AEs, with each AE trained layer by layer, and only the encoder part is kept after training. The whole network is finally fine-tuned with minimizing global reconstruction loss. The hyperparameters in the training process are described as follows: three hidden layers are considered with their dimensional numbers set as 32, 16, and 8; the batch size is set as 16; every AE is trained for 150 iterations; and the whole SAE is fine-tuned for 500 iterations. As a result, the LFS indices can be nonlinearly integrated with dimensions reduced from 64 to 8, resolving the two issues demonstrated above.

We finally use original least squares (OLS) to model the human-land relationship and predict the land carrying capacity (LCC) of each city. For a city ci(1 ≤ i ≤ 81), it belongs to the u-th LFS type typeu(1 ≤ u ≤ 6), and other cities of typeu, cj ∈ typeu(1 ≤ j ≤ 81,j ≠ i), are considered to train the regression model, i.e., \(y_{c_j}^{{{{\mathrm{Pop}}}}} = \overrightarrow {{{{\boldsymbol{FS}}}}_{{{{\boldsymbol{c}}}}_{{{\boldsymbol{j}}}}}} \cdot \overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{Pop}}}}}} + b_u^{{{{\mathrm{Pop}}}}}\) and \(y_{c_j}^{{{{\mathrm{GDP}}}}} = \overrightarrow {{{{\boldsymbol{FS}}}}_{{{{\boldsymbol{c}}}}_{{{\boldsymbol{j}}}}}} \cdot \overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{GDP}}}}}} + b_u^{{{{\mathrm{GDP}}}}}\), where \(y_{c_j}^{{{{\mathrm{Pop}}}}}\) and \(y_{c_j}^{{{{\mathrm{GDP}}}}}\) denote the cj’‘ population and GDP respectively, \(\overrightarrow {{{{\boldsymbol{FS}}}}_{{{{\boldsymbol{c}}}}_{{{\boldsymbol{j}}}}}}\) the LFS indices of cj processed by SAE, and \(\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{Pop}}}}}}\), \(b_u^{{{{\mathrm{Pop}}}}}\), \(\overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{GDP}}}}}}\) and \(b_u^{{{{\mathrm{GDP}}}}}\) are parameters of the two regression models, which can be trained by cities in typeu and estimated by OLS64; thus, the LCC of ci for population and GDP can be predicted by \(LCC_{c_i}^{{{{\mathrm{Pop}}}}} = \overrightarrow {{{{\boldsymbol{FS}}}}_{{{{\boldsymbol{c}}}}_{{{\boldsymbol{i}}}}}} \cdot \overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{Pop}}}}}} + b_u^{{{{\mathrm{Pop}}}}}\) and \(LCC_{c_i}^{{{{\mathrm{GDP}}}}} = \overrightarrow {{{{\boldsymbol{FS}}}}_{{{{\boldsymbol{c}}}}_{{{\boldsymbol{i}}}}}} \cdot \overrightarrow {{{{\boldsymbol{w}}}}_{{{\boldsymbol{u}}}}^{{{{\mathbf{GDP}}}}}} + b_u^{{{{\mathrm{GDP}}}}}\).