Introduction

The coronavirus pandemic of 2019–2021 (COVID-19) is an unprecedented worldwide event. Its speed of propagation, its international reach, and the unprecedented coordinated measures for its mitigation are only possible in a world that is more connected and more urbanized than at any other time in history.

As a novel infectious disease in human populations, COVID-19 has a number of quantitative signatures to its pattern of spread. These signatures make its dynamics more difficult to contain but also easier to understand, compared to well established contagions such as influenza, for the following reasons.

First, because there is no history of previous exposure, all human populations in contact with the virus are (presumably) susceptible. Second, because COVID-19 is a respiratory disease, it is easily transmissible resulting in high reproductive numbers, R = 2.2–6.5 (refs. 1,2,3), though considerable uncertainty remains about these estimates. Third, COVID-19 appears to be characterized by reproductive numbers above the epidemic threshold (R0 > 1) everywhere around the world. This, despite slightly reduced transmission associated with higher humidity and temperature4,5,6,7. So, while heat and humidity may slow the spread of Covid-19, they alone do not bring the reproductive number below 1 (i.e., the epidemic threshold). In addition, these reproductive numbers are considerably higher than seasonal influenza8. Bringing the disease reproductive number below the epidemic threshold (R → R < 1) is the main goal of all public health interventions; once this is achieved the disease’s transmission chain reaction will shut down.

The reproductive number is the product of two factors R = β/γ, the infectious period 1/γ (a physiological property) and the contact rate β, which is a property of the population, essentially measuring the number of social contacts that can transmit the disease per unit time. Of these, only the contact rate can be changed via public health interventions.

In the absence of a vaccine, social distancing and face coverings remain the only options to slow down the spread of the disease and arrest potential mortality. Governments around the world have enacted aggressive policies, including "shelter in place" and emergency closures of all non-essential services, which carry severe economic and social consequences. However, there is still a great deal of uncertainty as to how strong social distancing recommendations must be or how long they must last9,10. In addition, regional and local variation in the severity of and compliance with restrictions are likely to impact individual cities differently.

Cities are predicated on extensive and intense face-to-face socioeconomic interactions. These interactions make cities sources of social and economic opportunity but also increase the possibility of infectious disease transmission. Many measurable properties of cities—from the size of their economies, to their crime rates, to their miles of road length—are mediated by socioeconomic interactions and are subject to well known scaling effects with population size predicted by urban scaling theory11. All of these relationships are tied to socioeconomic networks with average degree (number of social connections per capita, k) that increases approximately as a power law of city size k(N) = k0Nδ, with δ ≃ 1/6, and city size, N, as measured by population size11,12. This is thought to then cause scaling of crime rates, infectious disease spread, number of patents, etc., with city size (i.e. population). We will refer to population/city size as the number of people living in a Metropolitan Statistical Area (MSA).

For functional effects, including epidemics, occurring against the ecological backdrop of cities, the underlying concept of a city is that of daily networks of socioeconomic interactions. These are most readily defined as integrated labor markets (commuting zones), which in the US are defined by the Census since the 1960s as MSAs13. These are the "city" definitions we use in our empirical analyses. For example, the Chicago MSA represents an integrated labor market, which includes 14 counties, across three states (https://www.census.gov/programs-surveys/metro-micro/about/delineation-files.html). The MSA definitions are revised annually by the US Census to reflect highly socioeconomically linked urban places, and are the result of theory and analysis at the US Census. Though commuting ties have been used to link places, they also encompass many other activities such as shared real estate and labor markets, transportation networks, and environmental protections. For these reasons, there is an effort to (re)create analogous or improved urban functional definitions worldwide, led by the Organization for Economic Co-operation and Development (OECD)14. While adopting any other definition for the same effect would require extraordinary arguments, other ways of demarcating the boundaries of cities have been proposed. For example, morphological urban areas are defined via satellite imagery by identification of contiguous areas of development that can be distinguished from peripheral rural areas and areas of lower-density development15. However, it is as-of-yet unclear whether these alternate methods for demarcating city boundaries are superior in any way. In addition, defining city boundaries by integrated labor markets captures a variety of social interactions relevant to disease transmission beyond labor market interactions. For example, the variety of restaurants types has been shown to be greater in larger cities (integrated labor markets)16. This suggests that consumer patterns of choosing which restaurants to visit (and socialize at) is meaningfully related to city size. Consequently, we expect well principled (see below) analyses that use MSAs as the definition of a city to capture the best approximation to the vast milieu of social interactions that create urban social life and form the basis for inter-individual disease transmission.

Urban scaling theory, and the observed scaling relationships it explains, are based on a number of parameters which are general to cities and more broadly to human settlements across history17. These parameters include, but are not limited to, transportation costs, the economic benefits of social interactions, the typical distance traveled per person, the total population, the embedding of transportation networks into the physical area of settlements, and the probability of different types of social and economic interactions11. These factors combine into a cost–benefit calculus for individuals embedded in the social and built spaces of cities. In turn, this allows for the calculation of expected values for many different urban quantities as functions of city size (i.e. they all scale with city population size).

It is important to recognize that scaling relationships between urban quantities and city population size give us a way to calculate the "ecological" effects of urban networks—such as disease transmissibility—but that these quantities are not a model for the behavior at smaller scales, such as those of individuals or neighborhoods. Behaviors at those smaller scales may vary from the mean substantially because of contextual effects. This is a fundamental point that we must heed in order to avoid "ecological fallacies"18, which is why we do not make claims at that level of analysis. A few additional considerations help make these points more explicit.

First, the mathematical models that explain urban scaling explicitly identify social network densification as the primary mechanistic driver of many measurable properties of cities, including innovation, economic output, and crime. Consequently, these models explicitly link average outcomes for entire cities to the local dynamics of social interactions that may naturally transmit a disease, as averages over these local dynamics. Thus, while a particular exposure to COVID-19 is the result of an individual’s history of social contacts, the measurements of the reproductive number and case growth rates are always a population average over these histories. These measures account for the average number of transmission events that infected individuals originate on average in that population. For these reasons, epidemics are often treated as the paradigm for collective behavior on large ecological scales.

Second, urban scaling theory has been shown to apply to cities and settlements, across cultures11, and across historical time scales19,20,21. While the generality of urban scaling theory across time and culture always allows for places and neighborhoods within cities to deviate from the mean and follow more specific patterns of organization, it does suggest that the average densification of social interactions with the population size of cities is a general organizational principle of (relatively) self-contained human cities and settlements11.

Consequently, the densification of social networks in larger cities is expected to be relevant to COVID-19 disease transmission, which is known to spread primarily via social contacts10,22. Specifically, as the average contact rate is proportional to degree β ∝ k(N) (see “Methods”), we expect that initial growth rates of COVID-19 cases to be higher in larger cities (see “Methods”). For example, based on data of mobile phone social networks in Portugal12, people living in a city of 500,000 people have, on average, 11 people in their mobile phone social network, while people living in a city of 5,000,000 people have, on average, 15. This means that individuals living in larger cities have more dense social networks. Therefore, we expect the contact rate (and case growth rate) to be larger in a city of five million compared to a city of five hundred thousand. This has been previously demonstrated with early epidemic case growth of AIDS, which spreads through the sexual network subset of social networks23. However, we do not expect this to hold later in the pandemic, as social distancing and lockdowns disrupt the social networks of cities, specifically to reduce contacts, and this modifies the urban scaling laws. Later in the pandemic, when mitigation measures have been implemented, we expect neighborhood and individual variations in social network size after social distancing [during complete lockdowns this is roughly equivalent to household size, which has been demonstrated to be a significant risk factor for COVID-19 transmission24,25], face covering compliance, and availability of work-from-home26 to influence transmission rates. In addition, neighborhood and individual differences in co-morbidities are likely relevant to understanding the variance in morbidity and mortality outcomes within cities, but are not accounted for here where the focus is on transmission rates. As such, we first focused only on the beginning of the pandemic because that is the time period that was least affected by interventions to curb the spread of COVID-19, which would disrupt the social networks and socioeconomic connections that relate COVID-19 transmission rates to city size.

Results

Scaling of case growth rates

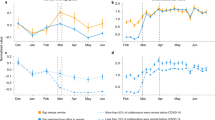
This is exactly what is found empirically. Figure 1a shows the growth rate of COVID-19 cases from March 14 to March 24, the first 11 days in which city level reported case numbers are available, vs. city size (population). While larger cities were faster to adopt preventative COVID-19 measures27, the first stay at home order in the US was effective on March 17. As a result of the incubation period for SARS-COV-2 (ref. 28), this period most likely captures case growth before large-scale behavior modification as instituted by local preventative physical/social distancing and lock-down policies. This demonstrates that, in the US, the early part of the pandemic was characterized by increasing case growth rates with city size, consistent with the expected scaling exponent of δ ~ 1/6. This scaling exponent matches other socioeconomic scaling phenomena such as patents, wealth, and information flow11,12,29,30. In contrast, Fig. 2 shows that this period of higher case growth rates in larger cities was restricted to the first few months of the pandemic. By the end of June, the scaling exponent δ is consistent with 0 (i.e. no changes in case growth rate by city size).

Fig. 1: COVID-19 cases reported by state health agencies grow faster in larger cities.
figure 1

a Estimated exponential daily growth rates of COVID-19 in US Metropolitan Areas (MSAs). These estimates were made with the assumption that cities were experiencing exponential growth of cases. The growth rate of COVID-19 cases is approximately 2.4 times faster in New York–Newark–Jersey compared to Oak Harbour, WA. b In the absence of effective controls, larger cities are expected to have more extensive epidemics than smaller cities (Eq. (1)). Higher values of R result in a greater percentage of the population eventually infected, unless this effect is curbed by controls that reduce the social contact rate. The translation of growth rates into reproductive numbers was obtained using an infectious period of 1/γ = 4.5 days. These estimated values of R are high in some cases (e.g., New York City) compared to reports in other situations and may in part be the result of the acceleration of testing in larger cities and specific places. Each estimate comes from the 11 previous (inclusive) days of data. Shaded regions represent 95% confidence intervals from OLS scaling fits.

Full size image
Fig. 2: Estimated scaling exponents (δ) for the scaling of COVID-19 case growth rates with city size in the US over the course of the pandemic.
figure 2

The early pandemic is characterized by faster growth of cases in larger cities, consistent with the predicted scaling exponent δ = 1/6. This is followed by decreasing scaling towards no scaling δ = 0, later in the pandemic as social distancing, lockdowns, and mask wearing disrupt the social/transmission networks of cities. Shaded regions indicate 95% confidence intervals.

Full size image

Since these results are based on the temporal growth rate of cases they do not depend on the total number of tests administered. Thus, our results are robust to discrepancies between positive tests and actual cases as well as absolute differences in testing capacity between cities, so long as levels of testing are consistent in each place over time. While the observed scaling of case growth rates with city size may be due to larger cities ramping up testing faster than smaller cities, we are not aware of any county or city level testing data for this early period of the US outbreak that could be used determine the influence of testing availability on these results.

Urban scaling theory only explains some (though a significant amount) of the variance in growth rates of COVID-19 cases between cities (R2 = 0.21), i.e. inter-city variation. Besides the expected uncertainty in growth rate estimations, much of this variance is likely due to unique characteristics of each city that influences the speed with which COVID-19 spreads31. For example, early pandemic hotspots in New York City were generally in dense working-class and middle-income neighborhoods, while hotspots in Chicago were generally in the city’s most vulnerable, low-income neighborhoods32 (though, see ref. 33 for evidence that early pandemic impacts were worst in New York City zip codes with the highest social vulnerability). These unique characteristics of individual cities and the neighborhoods within them could include local differences in the ramping up of testing capacity, international connectedness of each city, the type of available public transportation, the distribution of job types across income brackets, and the amount of long distance business travel that each city depends on.

While other research has implicated population density in the spread of COVID-19 (refs. 34,35), urban scaling theory and empirical evidence suggest that population density increases ~N1−α (α = 2/3) with city size36. The observed scaling exponent of COVID-19 case growth of [0.11, 0.20] ~ δ = 1/6 is thus inconsistent with a pure population density effect (i.e., 1/6 = δ < α = 2/3, see Supplementary Fig. 6). Instead we associate the scaling relationship observed here with the density of socioeconomic interactions37 which increase slower than population density with city size. These predictions of urban scaling theory have been confirmed in analyses showing that population density at the county level is not a significant predictor of cumulative COVID-19 caseload after accounting for county population24. In summary, a population density account would predict a much more intense and faster spread of COVID-19 in more dense cities than what urban scaling theory predicts based on the growth of socioeconomic interactions as cities increase in population.

A larger reproductive number for COVID-19 in larger cities has two important consequences38,39,40,41. First, the reproductive number, R, sets a finite threshold for how an epidemic outbreak propagates in a population, just like the branching rate in a chain reaction42,43. For R < 1, an introduced disease will die off because transmission will be dampened. For R > 1, disease transmission will be amplified and result in an epidemic where the disease is transmitted quickly to almost everyone (see Fig. 1B). Because we expect R ~ Nδ to increase with city size, we expect larger cities to be more susceptible to contagious diseases, but also to the spread of information (see below), which we believe is mediated by the same mechanism, i.e. socioeconomic interactions.

Second, the size of an epidemic outbreak, as measured by the percent of the population that becomes infected, is also related to the reproductive number. In complex epidemic models, this needs to be computed numerically, but for a simple Susceptible-Infected-Recovered (SIR) model42 we can integrate the dynamics and write the explicit expression (see “Methods”)

$$\frac{{S}_{\infty }}{{S}_{0}}={\mathrm e}^{-R(1-{S}_{\infty }/N)}$$
(1)

where S0 is the initial susceptible population size (before the outbreak) and S∞ is the (smaller) final population of susceptible people. A larger R ~ Nδ leads to more extensive epidemics. The percent of people infected at the end of the outbreak is 1 − S∞/N which is larger in populations with larger R, such as in larger cities. In addition, the vaccination rate, pR, or the fraction of the population that must be removed from the susceptible class when R > 1 to stop the outbreak44 is also expected to be dependent on population size. In the SIR model, this is simply pR = 1 − 1/R. As cities get larger, the fraction of individuals who must be vaccinated or, alternatively, follow social distance and face covering policies must also increase (see Supplementary Fig. 2).

Discussion

These observations have a number of implications that can inform evolving national, regional, and local responses to the outbreak of COVID-19 and help to shape response plans for future, novel infectious diseases. First, it is particularly important for larger cities to be able to act more quickly to contain surges in cases. Second, measures taken to contain outbreaks9,10 will impact cities differently based on city size. From the perspective of containing the outbreak, larger cities require faster responses, which could consist of a number of proven policies9,10, that can quickly reduce R below the epidemic threshold. These distinctions may help to bring more nuance to ongoing strategies for suppression and control of COVID-19, including gradually restoring socioeconomic activity in context appropriate and safe ways.

Because of their higher network density, insufficient social distancing or face covering compliance in larger cities may lead to bigger outbreaks and establish reservoirs for the disease, which can continue to create introductions elsewhere45,46. These dynamics may also play out within cities, though we caution in ascribing causes to neighborhood level variance in transmission rates from the present data. The results presented here suggest that communities in which people interact more densely from the perspective of disease transmission (e.g., downtowns) may similarly act as contagion reservoirs which may prolong the duration of outbreaks and potentially create secondary reinfection waves. However, the factors that lead to a higher density of social interactions in one community, for example, household size24,25 or employment in the service industry or essential worker status26, can often be the result of long term structural inequalities47,48,49,50. These factors must be accounted for when attempting to explain causal sources of differences in transmission rates within cities and in planning responses to outbreaks. In summary, our results apply to comparisons across cities, and not to neighborhoods or areas within individual cities. That is an important question, but one which these data and analyses cannot address.

Finally, as strategies for controlling Covid-19 continue to evolve, it is critical to keep in mind that almost everything that we appreciate about urban environments, including their economic prowess, their ability to innovate, and their role in their inhabitants social and mental health, is predicated on network effects mediated by socioeconomic interactions. The ability to succeed against a fast emerging epidemic like COVID-19 depends on preserving person-to-person connectivity (e.g., through technology), while stopping disease transmission. Establishing safe types of socioeconomic contact is therefore paramount so that we can succeed in controlling COVID-19 while maintaining livelihoods, socioeconomic capacity, and mental health.

The higher socioeconomic connectivity of larger cities in a fast urbanizing world makes containing emergent epidemics harder. But the density of socioeconomic connections in cities can also facilitate the faster spread of information, social coordination, and innovations necessary to stop the spread of COVID-19. This information and associated actions can easily spread more rapidly than the biological viral contagion. To fight an exponential, we need to create an even faster exponential!

Methods

Calculation of case growth rates

County level daily data from March 14 to December 14 (inclusive) were aggregated to the city level (MSAs, which are integrated labor markets) using delineation files from the US Office of Budget and Management (https://www.census.gov/programs-surveys/metro-micro/about/delineation-files.html). MSAs are groups of counties (in their entirety, i.e., not parts of counties), which make up an interconnected labor market. To our knowledge, the data covering March 14 through March 24 represent the first 10 days in which aggregated county level case statistics were available for the entire country51. Previously the few states that published county level case data did so on state health department websites and there was no central repository for COVID case data in the US. After preprocesing (see Supplementary Materials) we subtracted deaths from cases in each city and found the exponential growth rate r for each time-series of active cases (see Supplementary Material). Finally we plotted the natural logarithm of r and the natural logarithm of city population from 2018 census estimates51, and performed an ordinary least-squares linear regression to determine the slope of the scaling line.