Abstract
The formation of world-class megalopolises has been a goal of urban development agencies around the world owing to their economic advantages. On their bids of becoming a world-class megalopolis, water availability is a factor that requires consideration. China has set an ambitious goal of developing a world-class megalopolis in the water-scarce Beijing-Tianjin-Hebei (BTH) region. This study investigates the water challenge the BTH region faces and the effects of main water conservation measures in the region towards the goal. An inter-city input–output model was constructed for identifying the water gap in the region and analyzing the effectiveness of main water conservation measures under various scenarios. The results indicate a significant gap between the water required to achieve the goal of becoming a world-class megalopolis and the region’s available water resources. Although proposed water conservation measures of improving water use efficiency and reducing agricultural water use provide a modest improvement, the amount of water required for urban development still exceeds the availability. The study emphasizes the significance of agricultural water use reduction in Hebei through crop system replacement from water-intensive winter wheat to water-saving crops. The study also proposes an alternative option of adjusting the development plan through redefining the boundary of the BTH megalopolis by excluding part of cities in Hebei. The results of this study contribute to a better understanding of the effect of water scarcity on urban development and thus provide references for other water-scarce regions with ambitious urban development goals.
Similar content being viewed by others
Introduction
The past decades have witnessed significant urbanization throughout the world. According to a report by United Nations, 55% of the world’s population lives in urban areas in 2018 and this proportion is expected to increase to 68% by 20501. Acceleration of urban expansion and transformation has boosted the formation of megalopolises, which are concentrated urbanized areas with highly developed spatial form of integrated cities2. Extensive empirical studies showed the positive productivity gains from the formation of megalopolises for countries engaging in international competition and cooperation in an increasingly global economy3,4,5. The formation of megalopolises fortified urban scale economies through better access to inter-industry information flows, abundant, and diversified labor forces, specialized services, as well as general public infrastructure and facilities. World-class megalopolis represents the highest level of megalopolises. The earliest prototypical conception for world-class megalopolis can be traced back to the megalopolis of “BosWash corridor” in the northeastern United States, which included the large cities of Boston, New York, Providence, Hartford, New Haven, Philadelphia, Baltimore, and Washington6. From this study onward, the connotation has been continuously enriched by subsequent scholars7,8,9,10,11. However, a consensus on a specific definition for world-class megalopolis has yet to be reached. It is generally agreed that the common features of the world-class megalopolis should include: densely clustered cities and non-agricultural population, sufficiently large economic size, highly developed industries (particularly, tertiary industries), one or multiple internationally influential core cities and closely integrated economic connections among cities in the megalopolis. There are six internationally acknowledged world-class megalopolises, including the Atlantic Coast megalopolis, the Japan Pacific Coast megalopolis, the Great Lakes megalopolis, the Northwestern Europe megalopolis, the Yangtze River Delta megalopolis, and the British megalopolis12,13.
Not surprisingly, the formation of megalopolises has become a goal of many urban development agencies around the world. A challenge is how to ensure a rapid urban expansion sustainably. Water is indispensable in almost every production and consumption process. Water scarcity has been challenging sustainable urban development globally. In 2019, the United Nations World Water Development Report indicated that the global water use had been increasing worldwide by ~1% per year since the 1980s, driven by a combination of population growth, socio-economic development, and changing consumption patterns14. Global water demand is expected to increase by 20–30% until 2050, and much of the growth will be attributed to increase in demand of the industrial and domestic sectors15,16. Megalopolises, where agglomerations of population and production activities bring about the increasing demand for water resources, commonly encounter water crisis and this, in turn, restricts their further development17,18. Figure 119 demonstrates a high correlation between the economic growth of the world-class megalopolises and the abundance of water resources, verifying the significance of water resources to megalopolises’ economic development. A high level of economic growth requires sustained and adequate water supply, as water is the principal factor supporting the development of a region. Given the fact that the six internationally acknowledged world-class megalopolises are not water-scarce regions, the restrictive effect of water did not capture much attention in their development. As ambitious urban development goals are being put forward in a number of water-scarce regions in the world, water availability is a critical factor that requires consideration.
The Chinese government is promoting the Beijing-Tianjin-Hebei (BTH) region to become a world-class megalopolis in China in addition to the Yangtze River Delta megalopolis20. Much attention has been focused on the BTH region since the implementation of “The Plan for the Coordinated Development of Beijing, Tianjin, and Hebei” enacted by the Chinese central government in 2015. The Plan has proposed the long-term goal for the BTH region to become a world-class megalopolis. However, the BTH region is severely constrained by water availability, with an annual per capita water resources of <200 m3, approximately one-tenth and one-fortieth of the national and world averages, respectively21. In addition to water scarcity, three further shortcomings of the BTH region can be identified compared with the existing world-class megalopolises. Firstly, the economic size of the BTH region in terms of gross domestic product (GDP) is still small. In 2017, the BTH region’s GDP was 1.19 trillion USD (The exchange rate between USD and CNY is based on the averaged central parity rate of 2017, released by the People’s Bank of China), only ~30–50% of the GDP levels of the six acknowledged world-class megalopolises (Supplementary Table 1). Second, most of the world-class megalopolises are tertiary industry dominated, while the proportions of the tertiary industries in most BTH cities are lower than 50% (Supplementary Table 2). Third, cities in the BTH region are not closely connected with each other to form an integrated megalopolis. The intra-regional trade value of the BTH region takes up only 29% of the total trade value, indicating the intra-regional trade of the BTH region is not paramount in composition of their total trade (Supplementary Table 3). In order to achieve the ambitious goal of becoming a world-class megalopolis, it is requisite for the BTH region to put forth efforts to overcome these shortcomings by promoting the economic growth, adjusting industrial structure and enhancing intra-regional economic integration, while alleviating the severe water shortage.
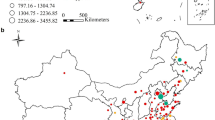
Moreover, it is worth noting that there is a significant level of heterogeneity amongst the cities in the BTH region in terms of economic development and water resources. Beijing is the most economically developed entity, with the highest GDP per capita, followed by Tianjin. Hebei is the least developed area among the three. Water conditions are relatively better in the cities in northern Hebei, with annual per capita water resources averaged over 400 m3. The cities in southern Hebei are water scarcest, with annual per capita water resources <150 m3 (Fig. 219; Supplementary Table 4). A challenging question is whether water scarcity will prevent the BTH region from becoming a world-class megalopolis. Given the significant spatial heterogeneity and nonnegligible economic connections across cities in the BTH region, it is necessary to incorporate city-level differences and inter-city connections in analyses of the region’s water challenge on its ambition to become a world-class megalopolis.
This figure shows the geographical location of the BTH region in China and the significant level of heterogeneity amongst the BTH cities in terms of economic development and water resources. The size of the yellow circles represents the level of GDP per capita and the gradation of colors represents the amount of water resources per capita in the BTH cities.
In recent years, the intensifying resource and environmental pressure has attracted an increasing attention from scholars and policymakers on the sustainable challenges encountered in urban development22,23,24,25. As one of the most fundamental and indispensable natural resources, water constraint on urban development has led to concern in public and academic circles26,27,28. Moreover, the studies that look at the water effect of developing world-class megalopolises are rare since the existing world-class megapolises are not water-scarce regions. Existing studies mainly assessed water-carrying capacity as reflected in the assessment of population carrying capacity. Water carrying capacity was typically defined as the water resources needed to sustain a healthy social and economic system, the maximum threshold of water resources to sustain human activities29,30,31,32. As the connotation of water-carrying capacity still remains divergent and elusive, a consensus on a specific definition has yet to be reached33. Moreover, previous studies investigating water constraint on urban development rarely considered the implications of intra-regional economic connections owing to lack of data. This is particularly so between different cities within the megalopolis owing to lack of information of inter-city economic connections34,35,36,37,38. Inter-city economic connections reveal how different cities depend on each other in terms of intermediate and final products and services. The pattern of inter-city economic connections is closely related to the scale and structure of water use in each city and is therefore an important factor to consider in the analyses of urban development under water constraints. Inter-city input–output model is recognized as a robust assessment tool representing inter-city economic connections as well as capturing city heterogeneities. Although the importance of city-level input–output model has been well acknowledged in the literatures, the model compilation and application are generally limited due to the unavailable data such as city-level input–output tables39. The existing studies mostly remain at the stage of proposing conceptual and methodological framework for model compilation40,41.
This study makes contribution to existing literatures in the following aspects: (i) conduct a comprehensive investigation of the restrictive effect of water resources relevant to world-class megalopolises, which were rarely studied in previous literatures. This study is of practical meanings for providing references for other water-scarce regions attempting to develop to the world-class megalopolises. (ii) Investigate the function of water in ensuring urban development from the perspective of water gap, which further enriches the connotation of water-carrying capacity. (iii) Perform an investigation on urban development under full consideration of the interaction between economic interconnections and water constraints based on an inter-city input–output optimization. We are fortunate to obtain the city-level input–output tables of Beijing, Tianjin, and 11 prefecture level cities in Hebei and then link them into the inter-city input–output model using multi-regional input–output modeling techniques42. The stability and reliability of the inter-city input–output table of the BTH region were verified through its rudimentary application in the analysis on industrial adjustment43. This approach is capable of fully reflecting the impacts of economic connections across cities on water requirements in the BTH region.
The study aims to take the BTH region as an example to investigate the effect of water scarcity on urban development by answering the following two questions: (i) how large is the water gap for the BTH region in becoming a world-class megalopolis? (ii) To what extent can the water conservation measures offset the water shortages? The Yangtze River Delta megalopolis and the Great Lakes megalopolis, which are representative of world-class megalopolises of relatively smaller economic size and larger economic size, are set as the two benchmarks for the BTH region. The results of this study contribute to a better understanding of the BTH region’s challenge of reaching economic development goals under water resources constraints, and also provide references for other water-scarce regions attempting to develop to the world-class megalopolises.
Results
Minimum water requirement for world-class megalopolis
The minimum water requirement for the BTH region to achieve the goal of becoming a world-class megalopolis is simulated by applying an inter-city input–output optimization model. The requirements for the BTH to become a world-class megalopolis are set as constraints in the optimization model. These constraints are concretized by indicators including economic size, industrial structure, and inter-city connection. The selection of these indicators was based on the aforementioned shortcomings identified by the comparison of the BTH region to the acknowledged world-class megalopolises, whereas the values of the indicators were established by referring to the benchmarking world-class megalopolises (Supplementary Table 5).
The simulation results show that to achieve the benchmarks of the Yangtze River Delta megalopolis and the Great Lakes megalopolis, the minimum annual water requirement for the BTH region would be 37.58 billion m3 and 53.26 billion m3. respectively. Given that the annual average water resources of the BTH region is 20.40 billion m344, an extra amount of 17.18 billion m3 and 32.86 billion m3 water would be needed. Even for the most achievable goal of the Yangtze River Delta megalopolis, the water gap is almost equivalent to the current amount of water resources in the BTH region. The modeling results indicate that the gap between the local water resources and the water required for becoming a world-class megalopolis is high (Fig. 319).
The bars show the minimum annual water requirement for the BTH region to achieve the benchmarking goals of the Yangtze River Delta megalopolis and the Great Lakes megalopolis. The blue line is the level of the annual average water resources in the BTH region. The red areas above the blue line represent the water gaps for the BTH region to achieve the benchmarking goals.
The BTH region’s maximum GDP without conservation measures
This section investigates the maximum GDP that the BTH region can achieve under the current conditions without the application of any additional water conservation measures, based on the simulation of the inter-city input–output optimization model. In the model, it sets maximize GDP of the BTH region as the objective function and predicted water use not exceeding the local water available as the constraint.
The results indicate that in the absence of additional water conservation measures, the maximum GDP that is achievable in the BTH region would be 1.34 trillion USD, only 12% higher than the current level of 1.19 trillion USD. The maximum GDP of the BTH region is well below that of the six acknowledged world-class megalopolises. This is significantly smaller than the existing world-class megalopolises. Even compared with the British megalopolis, which has the smallest GDP, the maximum achievable GDP for the BTH region is still ~35% lower (Fig. 419).
Effects of water conservation measures
Local governments in the BTH region have been striving to alleviate water stress by adopting water conservation measures, including improving water use efficiency, controlling agricultural water use, and adjusting industrial structures. Li et al.43 investigated the water conservation effects of industrial structure adjustments in the BTH region and found that 93.56% of the water saved from industrial structure adjustments in the BTH region could be attributed to agricultural water use reduction. Therefore, this study focuses on improving water use efficiency and restricting agricultural water use as two water conservation measures to evaluate their water conservation effects. In recent years, a series of regulations and development plans have been launched for water conservation45,46,47,48, in which specific goals for improving water use efficiency and reducing agricultural water were stipulated (Supplementary Table 6).
The simulation results indicate that by improving water use efficiency, the minimum amount of water required for the BTH region to achieve the goal of benchmark I (the Yangtze River Delta megalopolis) will fall to 30.84 billion m3, 6.74 billion m3 lower than the aforementioned minimum water requirement without any additional conservation measures. However, subsequent to conservation efforts there is still a remaining water gap of 10.44 billion m3 between the water required for development and local water resources. The results show that reducing agricultural water use is a more significant water conservation measure, leading to a water use reduction of 14.86 billion m3. However, a water gap of 2.32 billion m3 still remains. If the two measures are jointly adopted, the minimum water requirement would be decreased to 15.58 billion m3. The local water resources of the BTH region would be sufficient to meet its demand to achieve the goal of benchmark I. The results indicate the importance of adopting different water conservation approaches simultaneously when addressing water scarcity. Under the goal of benchmark II (the Great Lakes megalopolis), the water conservation effects of improving water use efficiency and reducing agricultural water use are 7.39 billion m3 and 16.4 billion m3, respectively. However, the joint effect of the two measures is 24.71 billion m3, which is incapable of offsetting the water gap for benchmark II (Fig. 519).
Upper: under the benchmarking goal of the Yangtze River Delta megalopolis. Lower: under the benchmarking goal of the Great Lakes megalopolis. The gray areas show the minimum water requirement under different situations of water conservation measure applications. The red line is the level of the annual average water resources in the BTH region. The areas above the red line represent the water gaps for the BTH region to achieve the benchmarking goals under different situations. If a gray bar is lower than the red line, it means the benchmarking goal is achievable under the corresponding application of water conservation measures. The blue areas are obtained by subtracting the latter three gray bars from the first gray bars, showing the amount of water saved from the application of the water conservation measures.
Discussion
In addition to the local water supply, the BTH region also depends on the external transfer of water from the South-to-North Water Transfer Project (SNWTP), a strategic and pioneering project aimed at balancing the uneven spatial distribution of water resources in China. The designed water transfer capacity of the SNWTP to the BTH region is 5.73 billion m3, transporting 1.24 billion m3 to Beijing, 1.02 billion m3 to Tianjin, and 3.47 billion m3 to Hebei49. In terms of the amount of water inflow, the SNWTP appears to be a highly effective means of water compensation for the BTH region. According to our simulation results, the water gaps for the BTH region to achieve the benchmarking goals of the Yangtze River Delta megalopolis and the Great Lakes megalopolis would be 17.18 billion m3 and 32.86 billion m3, respectively. Therefore, if the water transfer capacity of the SNWTP is fully exploited, it would reduce the BTH region’s water gaps by ~33% and 17%. However, a field interview conducted for this research revealed that the expense associated with using water transferred from the SNWTP was too high for local enterprises to have incentive to use it. Therefore, current utilization of SNWTP water in Hebei highly depends on financial subsidies received from the central government, and as a result most of the cities use SNWTP water for ecological purposes (groundwater recharge) rather than industrial production (Supplementary Table 7). Therefore, the use of SNWTP water in the BTH region is of high uncertainty. To meet the water requirements to ensure adequate development, the BTH region should not depend on external water transfer from the SNWTP, but control its internal water demand.
The simulation results in this study indicate that reducing agricultural water use has a vital role in water conservation. The BTH region is one of the most important wheat and maize production bases in China50,51. Particularly, Hebei’s productions of wheat account for 11% of the national total production in 201752. Given the water-intensive nature of agricultural practices, the majority of water use in Hebei is attributed to agricultural water use, which accounts for 69.4% of the province’s total water use in 201753. Therefore, controlling agricultural water use in Hebei is crucial for water conservation in the entire BTH region. Winter wheat is traditionally the most cultivated grain crop in Hebei, accounting for over 40% of the total grain production in Hebei in 201752. The stable and high yield of winter wheat depends on irrigation, since the effective precipitation in its growing period can only meet 20–30% of the wheat water requirement54. Consequently, the irrigation for winter wheat in Hebei is closely related to groundwater depletion55,56. Therefore, reduction in winter wheat is not only essential for reducing agricultural water use, but also necessary to reverse groundwater depletion and promote groundwater storage. Policies for land fallow as well as planting structure adjustments have been applied in pilot areas to encourage the extension of a single-cropping system in groundwater over-exploited areas. Instead of winter wheat, crops that consume less water, such as spring maize, summer maize, peanuts, cotton, or various cereals are encouraged to reduce the amount of water use. By applying this crop system replacement, each hectare of land can save 2700–3000 m3 of water57. Given the planting area of winter wheat in Hebei was 2.35 million hectares in 201858, this practice would at least bring about a water use reduction of 6.34 billion m3, ~50% of Hebei’s total agricultural water use. Furthermore, as a region under severe pressure from water scarcity, Hebei’s traditional position as a grain production base requires reconsideration.
A drawback of applying these measures include a negative effect on the livelihood of farmers by decreasing direct income from agricultural production. Therefore, the trade-off between the water conservation effects and the potential loss to farmers needs to be evaluated and an appropriate balance should be sought. Measures enhancing farmers’ willingness to save water, such as compensations to farmers, should also be considered.
It is worth noting that this study may have underestimated the water challenge facing the BTH region’s developmental goal of becoming a world-class megalopolis. In evaluating the water gap, annual average water resources were used as an indicator of the local water supply, an assumption that results in the overestimation of the supply of local water resources, as certain portions may not be accessible or exploitable. Moreover, the water requirement of the development goal is obtained from an optimization simulation, which provides an “ideal circumstance” result that may not be attainable in reality. Therefore, the water challenge faced by the BTH region to become a world-class megalopolis will most likely be more significant than that suggested in this study.
Historically, there have been a number of debates on the spatial boundary of the BTH megalopolis in China, from both academic community and governments. As a result, the spatial scope of the BTH region’s developing strategy has undergone a process of evolution. For example, the current Plan for the Coordinated Development of Beijing, Tianjin, and Hebei can be traced back to its source to Territorial Planning of Beijing, Tianjin, and Tangshan implemented in 1984. The 1984 Plan defined the territory of the core economic zone of the BTH region with the five cities of Beijing, Tianjin, Tangshan, Qinhuangdao, and Langfang. In 2004, Regional Planning of BTH Metropolitan Area expanded the territory of the core economic zone to 10 cities by adding five more cities to the Plan, including Shijiazhuang, Baoding, Cangzhou, Zhangjiakou, and Chengde. On the basis of 2004 Plan, the current Plan for the Coordinated Development of Beijing, Tianjin, and Hebei 2015 includes three additional cities, namely, Handan, Xingtai, and Hengshui. The current boundary of the BTH megalopolis is a compromise proposal considered by the central, provincial, and local governments from the perspective of interest balancing.
The main point of policy discussion since then has been whether the four cities in southern and central Hebei (Handan, Xingtai, Hengshui, and Cangzhou) should be included59,60. Academic discussions on the issue are conducive to formulating a more science-based plan for BTH region.
The four cities in southern and central Hebei, Handan, Xingtai, Hengshui, and Cangzhou, are geographically distant from the center of the BTH region and their economic connections with other cities of the region are weak. Moreover, the four cities are main growing areas for the water-intensive winter wheat, accounting for ~61% of winter wheat production of Hebei in 201752. In this study, the aforementioned simulations were re-applied for the BTH region excluding the four cities. The results show that the water gaps for the reduced BTH region to achieve the benchmarking goals of the Yangtze River Delta megalopolis and the Great Lakes megalopolis would be 11.15 billion m3 and 19.81 billion m3, 35 and 40% lower than the water gaps faced by the entire BTH region (Fig. 619). Therefore, adjusting the boundary of the BTH megalopolis by excluding the four cities in Hebei would be an alternative option to make the goal of becoming world-class megalopolis more achievable.
Left group: under the benchmarking goal of the Yangtze River Delta megalopolis. Right group: under the benchmarking goal of the Great Lakes megalopolis. The bars of different colors show the minimum water requirement under different situations of water conservation measure applications. The red line is the level of the annual average water resources in the four-city-excluded BTH region. The areas above the red line represent the water gaps for the four-city-excluded BTH region to achieve the benchmarking goals under different situations. If a bar is lower than the red line, it means the benchmarking goal is achievable under the corresponding application of water conservation measures.
The strategy of redefining boundary could be a feasible option for other water-scarce regions attempting to develop the world-class megalopolises hinges on the specific conditions of the megalopolis under discussion. The BTH experience can serve as a useful lesson for other megalopolises by proposing the key factors needed to be considered to make such a strategy effective. First, the exclusion of the cities should not break the geographical continuity of the megalopolis. The remaining cities should be a geographically contiguous area. Second, the excluded cities should be agricultural regions. Then, the exclusion of the cities can not only reduce water use, but also facilitate an upgraded industrial structure. Third, the excluded cities’ economic connections with other cities should be weak. Then the exclusion of the cities can be conducive to the integration of the megalopolis.
The formation of world-class megalopolises has been a goal of many urban development agencies around the world owing to their economic advantages. Often water becomes a restrictive factor when pursuing higher urban development goals. The purpose of this paper, using the BTH region as an example, is to demonstrate how the water constraint would affect the formation of the world-class megalopolis and what measures can be taken to address the challenge. The water scarcity hinders the BTH region’s development plan of becoming a world-class megalopolis in a significant way. A considerable amount of water is required to meet the water demand for achieving the goals benchmarked by the Yangtze River Delta megalopolis and the Great Lakes megalopolis. Our findings show that without additional water conservation measures taken, economic potential of the BTH region will be severely limited and the goal of making the world-class is not achievable.
Although the proposed measure of improving water use efficiency is helpful to reduce the water shortfall, it is incapable of eliminating the water constraints for the BTH region to reach its development goal of becoming the world-class megalopolis. However, if the measures of improving water use efficiency and significantly reducing agricultural water use are jointly adopted, the BTH region can reach the goal benchmarked by the Yangtze River Delta megalopolis. In order to make the goal easier to achieve, nonconventional measures such as redefining the boundary of the BTH megalopolis should be taken as an alternative plan. Our simulation results verify that redefining the boundary of the BTH megalopolis by excluding the four cities in Hebei would make the goal of making the BTH region a world-class megalopolis more achievable. To sum up, the results of this study show that the goal of becoming a world-class megalopolis is achievable for the BTH region only under certain conditions of water use or administrative planning. The required water use conditions refer to the adoption of intensive water conservation measures including improving water use efficiency and controlling agricultural water use, and the required administrative planning conditions refer to redefining the region’s boundary by excluding more heavily agricultural areas.
This study demonstrates the effect of water scarcity in preventing the BTH region from achieving a world-class megalopolis, which can also provide references for other water-scarce regions attempting to develop the world-class megalopolises. It is worth noting that the process for the BTH region reaching the developing goals is a complex issue involving multiple tradeoffs. This study can be expanded in the future through a comprehensive investigation of the impacts of these tradeoffs, which would lead to far-reaching implications for policymaking, poverty reduction, agricultural communities, behaviors, and technologies. Moreover, climate change and consumption pattern change are significant factors influencing the future water conditions of the BTH region. It is anticipated that the water scarcity in the BTH region will be further exaggerated owing to climate change and consumption pattern change. Previous literatures indicated that the risk of drought in the BTH region would increase under the impact of climate change61,62, and consumption pattern changes accompanied with urbanization, population dynamics, lifestyle changes would further increase water requirement63,64,65. As such an inclusion of these two factors will unlikely change our findings in this paper. Further research is needed to involve the two factors into a more-detailed mechanisms depicting interrelationships between water resources, economic growth and policies, which will contribute to more effective and targeted recommendations for policymaking.
This study simulates the BTH region’s achievement of world-class megalopolis status as currently defined, but an innovative vision of the world-class megalopolis is needed to be developed for water-scarce regions. With more and more water-scarce regions having higher urban development goals, water availability would become a critical factor determining whether the goals can be achieved or not. Accordingly, the criteria for world-class megalopolises may need to be redefined. A region’s ability of overcoming the restrictive effects of water scarcity might be requisite for being a world-class megalopolis in the new context. Therefore, the water-related indicators, such as adoption of advanced water-saving technologies, development of modern agriculture, regional coordination on water resource may be involved as the new criteria for world-class megalopolises in the future.
Methods
Inter-city input–output optimization model
The optimization model was developed based on the inter-city input–output table of the BTH region (2012), which was compiled based on the city input–output tables of the BTH cities, with 2012 the latest tables available. Given year 2012 is close to the period of year 2014–2015 when the BTH region’s developing goal of becoming a world-class megalopolis was designed and proposed, the data of 2012 can reflect the situation of the BTH region at that time and thus are conducive to policy evaluations. Moreover, Although the data of 2012 are not up to date, the main macroeconomic and water use related parameters in the BTH region remained relatively stable (Supplementary Table 8, Supplementary Table 9 and Supplementary Table 10), they are still capable of providing a rough profile for the economic system and water use condition of the BTH region. Detailed information for the compilation of the inter-city input–output table of the BTH region (2012) can be seen in Li et al.43. The structure and sectors of the table are shown in Supplementary Table 11 and Supplementary Table 12, respectively. In the Inter-city input–output optimization model, varied combinations of objectives and constraints were adopted in different simulations (Table 1). The objectives and constraints are detailed below.
Objectives
Objective 1: minimization of water use
The total water use of the BTH region can be obtained by adding up the amount of water used in all the sectors of all the cities in the region. The objective function is represented as:
where \(\omega _i^r\) is the direct water use coefficient of sector i in city r, representing the amount of water used to produce one monetary unit output of sector i in city r;\(x_i^r\) is the output of sector i in city r.
Objective 2: maximization of GDP
The GDP of the BTH region equals to the summation of the value-added of all the sectors of all the cities in the region. The objective function is represented as:
where \(v_i^r\) is the value-added rate of sector i in city r, representing the value-added created from one monetary unit of production of sector i in city r.
Constraints
Constraint 1: constraints of the input–output model
The basic mathematical structure of the inter-city input–output table of the BTH region (2012) consists of (14 × 16) linear equations, which represents the inter-sectorial and inter-city interdependence in terms of intermediate demand and final demand. Constraints of the input–output model can be represented as Inequality 3, which ensure the demand for each product not exceeding the production amount.
where \(a_{ij}^{rs}\) is the direct input coefficient, which indicates the amount of input required from sector i in city r to increase one monetary unit of the output of sector j in city; \(y_i^{rs}\) is the final demand of sector i supplied from city r to city s.
Constraint 2: constraints of economic size
Economic size is measured by GDP, which is a requisite for a world-class megalopolis classification. The constraint function is represented as:
where \(\underline d\) is the bottom level of the GDP, which is set based on Supplementary Table 5.
Constraint 3: constraints of industrial structure
Industrial structure constraints are set to limit the relative scales of the tertiary industries in each city. For each city, the constraint inequalities are set as:
where \(\underline \delta\) is the bottom level for the proportion of the tertiary value added, which is set based on Supplementary Table 5.
Constraint 4: constraints of inter-city economic connections
Constraints of inter-city economic connections are set to limit the internal economic connections within the BTH region, which is reflected by inter-city trade in this study. For each city, the constraint inequalities are as follows:
where \(tr^r\) is the total trade of the city r, which includes the internal trade \(tr_{local}^r\), trade with other cities inside the BTH region \(tr_{BTH}^r\), trade with other regions outside the BTH region in China \(tr_{outside\,BTH}^r\) and trade abroad \(tr_{abroad}^r\).\(tr^r\) includes the trade of intermediate goods\(\left( {\mathop {\sum}\limits_{s = 1}^{14} {\mathop {\sum}\limits_{i = 1}^{16} {\mathop {\sum}\limits_{j = 1}^{16} {a_{ij}^{rs}x_j^r} } } + \mathop {\sum}\limits_{s = 1}^{14} {\mathop {\sum}\limits_{i = 1}^{16} {\mathop {\sum}\limits_{j = 1}^{16} {a_{ji}^{sr}x_i^r} } } } \right)\) and final goods \(\left( {\mathop {\sum}\limits_{s = 1}^{14} {\mathop {\sum}\limits_{i = 1}^{16} {y_i^{rs}} } + \mathop {\sum}\limits_{s = 1}^{14} {\mathop {\sum}\limits_{i = 1}^{16} {y_i^{sr}} } } \right)\); \(\underline {ec}\) is the bottom level for the proportion of inter-city trade, which is set based on Supplementary Table 5.
Constraint 5: constraints of water use
The constraint on the amount of water used is given by:
where \(w_0\) is the annual average amount of water resources in the BTH region.
Constraint 6: constraints of water use efficiency
The function of water use efficiency is evaluated by the average amount of water used for the creation of one monetary unit of GDP. For each city, the constraint inequalities are as follows:
where \(we_0^r\) is the current level of water use efficiency of city r; \(\rho ^r\) is the increasing amplitude of the water use efficiency of city r, the values of which are determined based on Supplementary Table 6.
Constraint 7: constraints of agricultural water use
For the entire Hebei province, the constraint inequalities are represented as follows:
where \(\omega _{agr}^r\) is the direct water use coefficient of agriculture in city r; \(x_{agr}^r\) is the output of agriculture in city r; \(w_{agr}^H\) is the upper limit for agricultural water use in Hebei, the value of which is determined based on Hebei’s regulations on reducing agricultural water use66.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data related to this study are described in the figshare metadata record: https://doi.org/10.6084/m9.figshare.1313572719. The metadata record also contains 15 publicly available spreadsheets of data generated and analyzed as part of this study. The filenames are as follows: Economic growth &Water use.xlsx, The BTH economic and water resource conditions.xlsx, Water gaps.xlsx, GDP comparison.xlsx, Measure effects.xlsx, Water gaps_four-city-excluded.xlsx, Economic size.xlsx, Industrial structure.xlsx, Trade data.xlsx, Indicators for benchmarks.xlsx, Objective of water use efficiency.xlsx, SNWTP water use.xlsx, Macroeconomic parameter comparison_provincial level.xlsx, Macroeconomic parameter comparison_city level.xlsx, Water parameter comparison_city level.xlsx.
Code availability
The code used in the calculations of this study is available from the corresponding authors upon request.
References
United Nations, Department of Economic and Social Affairs, Population Division, World Urbanization Prospects: The 2018 Revision (2018).
Fang, C. & Yu, D. Urban agglomeration: An evolving concept of an emerging phenomenon. Landsc. Urban Plan. 162, 126–136 (2017).
Fujita, M. M., Krugman, P., Venables, A. J. The spatial economy-cities, regions and international trade (The MIT Press, Cambridge, 1999).
Fujita, M. M., Thisse, J. F. Economics of agglomeration-cities, industrial location and regional growth (Cambridge University Press, Cambridge, 2002).
Rosenthal, S. Stuart, S. Strange, W. C. ‘Evidence on the nature and sources of agglomeration economies’ in Handbook of Urban and Regional Economics, Henderson, J. V., Thisse, J. F. Eds. pp. 2119–2171. (Elsevier, Amsterdam, 2004).
Gottmann, J. Megalopolis, or the urbanization of the North-eastern seaboard. Econ. Geogr. 33, 189–200 (1957).
Doxiadis, C. A. The emerging great lakes megalopolis. Proc. IEEE 56, 402–424 (1968).
Morrill, R., Cromartie, J. & Hart, G. Metropolitan, urban and rural commuting areas: toward a better depiction of the United States settlement system. Urban Stud. 20, 727–748 (1999).
Kanemoto, Y. & Tokuoka, K. Proposal for the standards of metropolitan areas of Japan. J. Appl. Reg. Sci. 7, 1–15 (2002).
Lang, R. & Knox, P. K. The new metropolis: rethinking megalopolis. Reg. Stud. 43, 789–802 (2009).
Abaya Gomez, J. E. J. The size of cities: a synthesis of multi-disciplinary perspectives on the global megalopolis. Prog. Plann. 116, 1–29 (2017).
Mei, N. X. Comparison of population and industrial structure between urban agglomerations of the Pearl River Delta and world-class urban agglomerations. Mod. Econ. 10, 886–899 (2019).
Fang, C. L. et al. The Report on China’s Megalopolis Development (Science Press, Beijing, 2011).
World Water Assessment Programme. The United Nations World Water Development Report 2019 (2019).
OECD (Organization for Economic Cooperation and Development). OECD Environmental outlook to 2050: The consequences of inaction (OECD publishing, Paris, 2012).
Wada, Y. et al. Modeling global water use for the 21st century: the Water Futures and Solutions (WFaS) initiative and its approaches. Geosci. Model Dev. 9, 175–222 (2016).
Li, W. F., Hai, X., Han, L. J., Mao, J. Q. Does urbanization intensify regional water scarcity? Evidence and implications from a megaregion of China, J. Clean. Prod., 244, 118592 (2020)
McDonal, R. I. et al. Urban growth, climate change, and freshwater availability. Proc. Natl. Acad. Sci. 108, 6312–6317 (2011).
Zhang, Z., Shi, M., Chen, K., Yang, H. & Wang, S. Metadata record for the manuscript: water scarcity will constrain the formation of a world-class megalopolis in North China. figshare https://doi.org/10.6084/m9.figshare.13135727 (2020).
Political Bureau of the Central Committee of the Chinese Communist Party. The Plan for the Coordinated Development of Beijing, Tianjin and Hebei (30 April 2015).
National Bureau of Statistics of China. China Statistical Yearbook 2018 (China Statistical Press, Beijing, 2018).
Normile, D. China rethinks cities. Science 352, 916–918 (2016).
Zhang, Y. J. & Da, Y. B. The decomposition of energy-related carbon emission and its decoupling with economic growth in China. Renew. Sustain. Energy Rev. 41, 1255–1266 (2015).
Acuto, M., Parnell, S. & Seto, K. C. Building a global urban science. Nat. Sustain. 1, 2–4 (2018).
Wang, Z. B., Liang, L. W., Sun, Z. & Wang, X. M. Spatiotemporal differentiation and the factors influencing urbanization and ecological environment synergistic effects within the Beijing-Tianjin-Hebei urban agglomeration. J. Environ. Manage. 243, 227–239 (2019).
Sharma, A. K., Gray, S., Diaper, C., Liston, P. & Howe, C. Assessing integrated water management options for urban developments - Canberra case study. Urban Water J. 5, 147–159 (2008).
Brown, C. M. et al. The future of water resources systems analysis: toward a scientific framework for sustainable water management. Water Resour. Res. 51, 6110–6124 (2015).
Lerner, A. M., Eakin, H. C., Tellman, E., Bausch, J. C. & Aguilara, B. H. Governing the gaps in water governance and land-use planning in a megacity: the example of hydrological risk in Mexico city. Cities 83, 61–70 (2018).
Wang, Y. T., Cheng, H. X. & Huang, L. Water resources carrying capacity evaluation of a dense city group: a comprehensive water resources carrying capacity evaluation model of Wuhan urban agglomeration. Urban Water J. 15, 615–625 (2018).
Hunter, C. Perception of sustainable city and implications for fresh water resources management. Int. J. Environ. Pollut. 10, 84–103 (1998).
Gong, L. & Jin, C. Fuzzy comprehensive evaluation for carrying capacity of regional water resources. Water Resour. Manage. 23, 2505–2513 (2009).
Ofoezie, I. E. Human health and sustainable water resources development in Nigeria: schistosmiasis inartificial lakes. Nat. Resour. Forum 26, 150–160 (2002).
Ren, C. F., Guo, P., Li, M. & Li, R. H. An innovative method for water resources carrying capacity research - metabolic theory of regional water resources. J. Environ. Manage. 167, 139–146 (2016).
Cheng, K. et al. Adaptive allocation modeling for a complex system of regional water and land resources based on information entropy and its application. Water Resour. Manag. 29, 4977–4993 (2015).
Bolay, J. C., Cartoux, S., Cunha, A., Du, T. T. N. & Bassand, M. Sustainable development and urban growth: precarious habitat and water management in Ho Chi Minh City, Vietnam. Habitat Int. 21, 185–197 (1997).
Jensen, O. & Wu, H. Urban water security indicators: development and pilot. Environ. Sci. Policy 83, 33–45 (2018).
Li, N. et al. Optimization of industry structure based on water environmental carrying capacity under uncertainty of the Huai River Basin within Shandong Province, China. J. Clean. Prod. 112, 4594–4604 (2016).
Zhang, Z. Y., Zhang, X. L. & Shi, M. J. Urban transformation optimization model: How to evaluate industrial structure under water resource constraints? J. Clean. Prod. 195, 1497–1504 (2018).
Lenzen, M. et al. Compiling and using input-output frameworks through collaborative virtual laboratories. Sci. Total Environ. 485-486, 241–251 (2014).
Wang, Y. An industrial ecology virtual framework for policy making in China. Econ. Syst. Res. 29, 252–274 (2017).
Zheng, H. et al. Linking city-level input-output table to urban energy footprint: construction framework and application. J. Ind. Ecol. 23, 781–795 (2019).
Zhang, Z. Y., Shi, M. J. & Zhao, Z. The compilation of China interregional input-output model 2002. Econ. Syst. Res. 27, 238–256 (2015).
Li, Y. J., Zhang, Z. Y. & Shi, M. J. What should be future industrial structure of the Beijing-Tianjin-Hebei city region under water resource constraint: an inter-city input-output analysis. J. Clean. Prod. 239, 118117 (2019).
National Bureau of Statistics of China. China Statistical Yearbook 2006–2018, (China Statistical Press, Beijing, 2006–2018).
The People’s Government of Beijing Municipality. Beijing Water Development Plan for ‘the 13th Five-Year Plan’ Period, (8 August 2016).
Tianjin Municipal People’s Government. Tianjin Action Plan for Dual Control of Total Water Consumption and Intensity for ‘the 13th Five-Year Plan’ Perio, (30 March 2017).
The People’s Government of Hebei Province. Hebei Implementation Plan for Dual Control of Total Water Consumption and Intensity 2016–2020 (7 March 2017).
The People’s Government of Hebei Province. Five-year Implementation Plan for Comprehensive Treatment of Groundwater Overexploitation in Hebei Province (2018–2022), (21 June 2018).
Official website for the South-to-North Water Transfer Project, General Plan for the South-to-North Water Transfer Project Construction, http://nsbd.mwr.gov.cn/zw/gcgk/ (2002).
Qin, W., Wang, D. Z., Guo, X. S., Yang, T. M. & Oenema, O. Productivity and sustainability of rainfed wheat-soybean system in the north china plain: results from a long-term experiment and crop modelling. Sci Rep. 5, 17514 (2015).
Jeong, S. J. et al. Effects of double cropping on summer climate of the North China Plain and neighboring regions. Nat. Clim. Change 4, 615–619 (2014).
Hebei Provincial Bureau of Statistics. Hebei Economic Yearbook 2018 (China Statistics Press, Beijing, 2019)
Department of Water Resources of Hebei Province. Hebei Water Resources Bulletin 2017 (2018).
Liu, C. M., Yu, J. J. & Kendy, E. Groundwater exploitation and its impact on the environment in the North China Plain. Water Int. 26, 265–272 (2001).
Ma, L. Comprehensive management for groundwater over-exploitation in Hebei Province. China Water Resour. 7, 51–54 (2017).
Aeschbach-Hertig, W. & Gleeson, T. Regional strategies for the accelerating global problem of groundwater depletion. Nat. Geosci. 5, 853–861 (2012).
Wu, X. F. et al. Change of winter wheat planting area and its impacts on groundwater depletion in the North China Plain. J. Geogr. Sci. 29, 891–908 (2019).
National Bureau of Statistics of China. China Statistical Yearbook 2019 (China Statistical Press, Beijing, 2019).
Tan, C., Yang, K. Z. & Tan, S. Concept and compartmentalization of China’s capital circle. Geogr. Territorial Res. 16, 1–7 (2000). (In Chinese).
Li, G. P. Structure of capital circle: division and construction strategy, (China City Press, Beijing, 2004) (In Chinese).
Dai, C., Qin, X. S., Lu, W. T. & Zhang, H. K. A multimodel assessment of drought characteristics and risks over the Huang-Huai-Hai River basin, China, under climate change. Theor. Appl. Climatol. 141, 601–613 (2020).
Liu, B., Yan, Z. H., Sha, J. X. & Li, S. Drought evolution due to climate change and links to precipitation intensity in the Haihe River Basin. Water 9, 878 (2017).
Hubacek, K. & Sun, L. X. Economic and societal changes in China and their effects on water use. J. Ind. Ecol. 9, 187–200 (2005).
Liu, J. & Savenije, H. H. G. Food consumption patterns and their effect on water requirement in China. Hydrol. Earth Syst. Sci. 12, 887–898 (2008).
Hubacek, K., Guan, D., Barrett, J. & Wiedmann, T. Environmental implications of urbanization and lifestyle change in China: ecological and water footprints. J. Clean. Prod. 17, 1241–1248 (2009).
The People’s Government of Hebei Province. Hebei Implementation Plan for Dual Control of Total Water Consumption and Intensity 2016–2020 (7 March 2017).
Acknowledgements
This work is supported by National Natural Science Foundation of China (grant no. 71874183) and Key Project of the National Social Science Foundation of China (no. 15ZDC006).
Author information
Authors and Affiliations
Contributions
M.J.S. and Z.Y.Z. designed the research. Z.Y.Z. carried out the main data processing and analyses with contributions from M.J.S., K.Z.C., and H.Y. Z.Y.Z. drafted the manuscript, with significant contributions to the writings from all co-authors. All authors contributed ideas for the analyses, comments, and critiques on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, Z., Shi, M., Chen, K.Z. et al. Water scarcity will constrain the formation of a world-class megalopolis in North China. npj Urban Sustain 1, 13 (2021). https://doi.org/10.1038/s42949-020-00012-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42949-020-00012-8
This article is cited by
-
Physical and virtual water transfers in China and their implication for water planetary boundary
Environmental Science and Pollution Research (2024)
-
Urban expansion patterns and their driving forces analysis: a comparison between Chengdu-Chongqing and Middle Reaches of Yangtze River urban agglomerations
Environmental Monitoring and Assessment (2023)
-
Water resource conservation promotes synergy between economy and environment in China’s northern drylands
Frontiers of Environmental Science & Engineering (2022)