Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Data-driven discovery of intrinsic dynamics

Nature Machine Intelligence volume 4, pages 1113–1120 (2022)Cite this article

Subjects

A preprint version of the article is available at arXiv.

Abstract

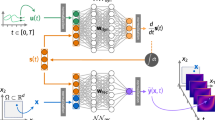
Dynamical models underpin our ability to understand and predict the behaviour of natural systems. Whether dynamical models are developed from first-principles derivations or from observational data, they are predicated on our choice of state variables. The choice of state variables is driven by convenience and intuition, and, in data-driven cases, the observed variables are often chosen to be the state variables. The dimensionality of these variables (and consequently the dynamical models) can be arbitrarily large, obscuring the underlying behaviour of the system. In truth these variables are often highly redundant and the system is driven by a much smaller set of latent intrinsic variables. In this study we combine the mathematical theory of manifolds with the representational capacity of neural networks to develop a method that learns a system’s intrinsic state variables directly from time-series data, as well as predictive models for their dynamics. What distinguishes our method is its ability to reduce data to the intrinsic dimensionality of the nonlinear manifold they live on. This ability is enabled by the concepts of charts and atlases from the theory of manifolds, whereby a manifold is represented by a collection of patches that are sewn together—a necessary representation to attain intrinsic dimensionality. We demonstrate this approach on several high-dimensional systems with low-dimensional behaviour. The resulting framework provides the ability to develop dynamical models of the lowest possible dimension, capturing the essence of a system.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: A representation of a manifold.
Fig. 2: The three basic steps of our method to learn an atlas of charts and dynamics.
Fig. 3: Quasiperiodic dynamics on the surface of a torus.
Fig. 4: A spiral wave from a lambda-omega reaction–diffusion system.
Fig. 5: Bursting data from the K−S system.

Similar content being viewed by others

Data availability

Data are available at https://doi.org/10.5281/zenodo.7219159 (ref. 63). For data that are unavailable due to size restrictions, code that exactly reproduces the data has been deposited in the same repository.

Code availability

Code is available at https://doi.org/10.5281/zenodo.7219159 (ref. 63).

References

  1. N. Watters et al. Visual interaction networks: Learning a physics simulator from video. In Advances in Neural Information Processing Systems (eds Garnett, R. et al.) Vol. 30 (Curran Associates, 2017); https://proceedings.neurips.cc/paper/2017/file/8cbd005a556ccd4211ce43f309bc0eac-Paper.pdf

  2. Gonzalez, F. J. & Balajewicz, M. Deep convolutional recurrent autoencoders for learning low-dimensional feature dynamics of fluid systems. Preprint at https://arxiv.org/abs/1808.01346 (2018).

  3. Vlachas, P. R., Byeon, W., Wan, Z. Y., Sapsis, T. P. & Koumoutsakos, P. Data-driven forecasting of high-dimensional chaotic systems with long short-term memory networks. Proc. R. Soc. A 474, 20170844 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  4. Champion, K., Lusch, B., Kutz, J. N. & Brunton, S. L. Data-driven discovery of coordinates and governing equations. Proc. Natl Acad. Sci. USA 116, 22445–22451 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  5. Carlberg, K. T. et al. Recovering missing CFD data for high-order discretizations using deep neural networks and dynamics learning. J. Comput. Phys. 395, 105–124 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  6. Linot, A. J. & Graham, M. D. Deep learning to discover and predict dynamics on an inertial manifold. Phys. Rev. E 101, 062209 (2020).

    Article  MathSciNet  Google Scholar 

  7. Maulik, R. et al. Time-series learning of latent-space dynamics for reduced-order model closure. Physica D 405, 132368 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  8. Hasegawa, K., Fukami, K., Murata, T. & Fukagata, K. Machine-learning-based reduced-order modeling for unsteady flows around bluff bodies of various shapes. Theor. Comput. Fluid Dyn. 34, 367–383 (2020).

    Article  MathSciNet  Google Scholar 

  9. Linot, A. J. & Graham, M. D. Data-driven reduced-order modeling of spatiotemporal chaos with neural ordinary differential equations. Chaos 32, 073110 (2022).

    Article  MathSciNet  Google Scholar 

  10. Maulik, R., Lusch, B. & Balaprakash, P. Reduced-order modeling of advection-dominated systems with recurrent neural networks and convolutional autoencoders. Phys. Fluids 33, 037106 (2021).

    Article  Google Scholar 

  11. Rojas, C. J. G., Dengel, A. & Ribeiro, M. D. Reduced-order model for fluid flows via neural ordinary differential equations. Preprint at https://arxiv.org/abs/2102.02248 (2021)

  12. Vlachas, P. R., Arampatzis, G., Uhler, C. & Koumoutsakos, P. Multiscale simulations of complex systems by learning their effective dynamics. Nat. Mach. Intell. 4, 359–366 (2022).

    Article  Google Scholar 

  13. Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980 (eds Rand, D. & Young, L.-S.) 366–381 (Springer, 1981).

  14. Fefferman, C., Mitter, S. & Narayanan, H. Testing the manifold hypothesis. J. Am. Mathematical Soc. 29, 983–1049 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  15. Hopf, E. A mathematical example displaying features of turbulence. Commun. Pure Appl. Math. 1, 303–322 (1948).

    Article  MathSciNet  MATH  Google Scholar 

  16. Foias, C., Sell, G. R. & Temam, R. Inertial manifolds for nonlinear evolutionary equations. J. Differ. Equ. 73, 309–353 (1988).

    MATH  Google Scholar 

  17. Temam, R. & Wang, X. M. Estimates on the lowest dimension of inertial manifolds for the Kuramoto–Sivashinsky equation in the general case. Differ. Integral Equ. 7, 1095–1108 (1994).

    MathSciNet  MATH  Google Scholar 

  18. Doering, C. R. & Gibbon, J. D. Applied Analysis of the Navier-Stokes Equations Cambridge Texts in Applied Mathematics No. 12 (Cambridge Univ. Press, 1995)

  19. Schölkopf, B., Smola, A. & Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 10, 1299–1319 (1998).

    Article  Google Scholar 

  20. Tenenbaum, J. B., De Silva, V. & Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000).

    Article  Google Scholar 

  21. Roweis, S. T. & Saul, L. K. Nonlinear dimensionality reduction by locally linear embedding. Science 290, 2323–2326 (2000).

    Article  Google Scholar 

  22. Belkin, M. & Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 15, 1373–1396 (2003).

    Article  MATH  Google Scholar 

  23. Donoho, D. L. & Grimes, C. Hessian eigenmaps: locally linear embedding techniques for high-dimensional data. Proc. Natl Acad. Sci. USA 100, 5591–5596 (2003).

    Article  MathSciNet  MATH  Google Scholar 

  24. van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).

    MATH  Google Scholar 

  25. Goodfellow, I., Bengio, Y. & Courville, A. Deep Learning (MIT Press, 2016).

  26. Ma, Y. & Fu, Y. Manifold Learning Theory and Applications Vol. 434 (CRC, 2012)

  27. Bregler, C. & Omohundro, S. Surface learning with applications to lipreading. In Advances in Neural Information Processing Systems (eds Alspector, J.) Vol. 6 (Morgan-Kaufmann, 1994); https://proceedings.neurips.cc/paper/1993/file/96b9bff013acedfb1d140579e2fbeb63-Paper.pdf

  28. Hinton G. E., Revow, M. & Dayan, P. Recognizing handwritten digits using mixtures of linear models. In Advances in Neural Information Processing Systems (eds Leen, T. et al.) Vol. 7 (MIT Press, 1995); https://proceedings.neurips.cc/paper/1994/file/5c936263f3428a40227908d5a3847c0b-Paper.pdf

  29. Kambhatla, N. & Leen, T. K. Dimension reduction by local principal component analysis. Neural Comput. 9, 1493–1516 (1997).

    Article  Google Scholar 

  30. Roweis, S., Saul, L. & Hinton, G. E. Global coordination of local linear models. In Advances in Neural Information Processing Systems (eds Ghahramani, Z.) Vol. 14 (MIT Press, 2002); https://proceedings.neurips.cc/paper/2001/file/850af92f8d9903e7a4e0559a98ecc857-Paper.pdf

  31. Brand, M. Charting a manifold. In Advances in Neural Information Processing Systems (eds. Obermayer, K.) Vol. 15, 985–992 (MIT Press, 2003); https://proceedings.neurips.cc/paper/2002/file/8929c70f8d710e412d38da624b21c3c8-Paper.pdf

  32. Amsallem, D., Zahr, M. J. & Farhat, C. Nonlinear model order reduction based on local reduced-order bases. Int. J. Numer. Meth. Eng. 92, 891–916 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  33. Pitelis, N., Russell, C. & Agapito, L. Learning a manifold as an atlas. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 1642–1649 (IEEE, 2013).

  34. Schonsheck, S, Chen, J. & Lai, R. Chart auto-encoders for manifold structured data. Preprint at https://arxiv.org/abs/1912.10094 (2019)

  35. Lee, J. M. Introduction to Smooth Manifolds (Springer, 2013)

  36. MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proc. 5th Berkeley Symposium on Mathematical Statistics and Probability Vol. 5.1, (eds Neyman, J.) 281–297 (Statistical Laboratory of the University of California, 1967).

  37. Steinhaus, H. Sur la division des corps matériels en parties. Bull. Acad. Polon. Sci 4, 801–804 (1957).

    MATH  Google Scholar 

  38. Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inform. Theory 28, 129–137 (1982).

    Article  MathSciNet  MATH  Google Scholar 

  39. Forgy, E. W. Cluster analysis of multivariate data: efficiency versus interpretability of classifications. Biometrics 21, 768–769 (1965).

    Google Scholar 

  40. Pedregosa, F. et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 12, 2825–2830 (2011).

    MathSciNet  MATH  Google Scholar 

  41. Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 2, 303–314 (1989).

    Article  MathSciNet  MATH  Google Scholar 

  42. Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 4, 251–257 (1991).

    Article  Google Scholar 

  43. Pinkus, A. Approximation theory of the MLP model in neural networks. Acta Numerica 8, 143–195 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  44. Bottou, L. & Bousquet, O. The tradeoffs of large scale learning. In Advances in Neural Information Processing Systems (edited Roweis, S.) Vol. 20 (Curran Associates, 2007); https://proceedings.neurips.cc/paper/2007/file/0d3180d672e08b4c5312dcdafdf6ef36-Paper.pdf

  45. Jing, L., Zbontar, J. & LeCun, Y. Implicit Rank-Minimizing Autoencoder. In Advances in Neural Information Processing Systems (eds Lin, H. et al.) Vol. 33 (Curran Associates, 2020); https://proceedings.neurips.cc/paper/2020/file/a9078e8653368c9c291ae2f8b74012e7-Paper.pdf

  46. Chen, B. et al. Automated discovery of fundamental variables hidden in experimental data. Nat. Comput. Sci. 2, 433–442 (2022).

    Article  Google Scholar 

  47. Kirby, M. & Armbruster, D. Reconstructing phase space from PDE simulations. Zeit. Angew. Math. Phys. 43, 999–1022 (1992).

    Article  MathSciNet  MATH  Google Scholar 

  48. Kevrekidis, I. G., Nicolaenko, B. & Scovel, J. C. Back in the saddle again: a computer assisted study of the Kuramoto–Sivashinsky equation. SIAM J. Appl.Math. 50, 760–790 (1990).

    Article  MathSciNet  MATH  Google Scholar 

  49. Whitney, H. The self-intersections of a smooth n-manifold in 2n-space. Ann Math 45, 220–246 (1944).

    Article  MathSciNet  MATH  Google Scholar 

  50. Graham, M. D. & Kevrekidis, I. G. Alternative approaches to the Karhunen-Loeve decomposition for model reduction and data analysis. Comput. Chem. Eng. 20, 495–506 (1996).

    Article  Google Scholar 

  51. Takeishi, N., Kawahara, Y. & Yairi, T. Learning Koopman invariant subspaces for dynamic mode decomposition. In Advances in Neural Information Processing Systems (eds Garnett, R. et al.) Vol. 30 (Curran Associates, 2017); https://proceedings.neurips.cc/paper/2017/file/3a835d3215755c435ef4fe9965a3f2a0-Paper.pd

  52. Lusch, B., Kutz, J. N. & Brunton, S. L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 9, 1–10 (2018).

    Article  Google Scholar 

  53. Otto, S. E. & Rowley, C. W. Linearly recurrent autoencoder networks for learning dynamics. SIAM J. Appl. Dyn. Syst. 18, 558–593 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  54. Pathak, J., Lu, Z., Hunt, B. R., Girvan, M. & Ott, E. Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data. Chaos 27, 121102 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  55. Pathak, J., Hunt, B., Girvan, M., Lu, Z. & Ott, E. Model-free prediction of large spatiotemporally chaotic systems from data: a reservoir computing approach. Phys. Rev. Lett. 120, 024102 (2018).

    Article  Google Scholar 

  56. Vlachas, P. R. et al. Backpropagation algorithms and reservoir computing in recurrent neural networks for the forecasting of complex spatiotemporal dynamics. Neural Netw. 126, 191–217 (2020).

    Article  Google Scholar 

  57. Cornea, O., Lupton, G., Oprea, J. & Tanré, D. Lusternik-Schnirelmann Category 103 (American Mathematical Society, 2003).

  58. Camastra, F. & Staiano, A. Intrinsic dimension estimation: advances and open problems. Inform. Sci. 328, 26–41 (2016).

    Article  MATH  Google Scholar 

  59. Nash, J. C1 isometric imbeddings. Ann. Math. 60, 383–396 (1954).

    Article  MathSciNet  MATH  Google Scholar 

  60. Kuiper, N. H. On C1-isometric imbeddings. I. Indag. Math. 58, 545–556 (1955).

    Article  MATH  Google Scholar 

  61. Nash, J. The imbedding problem for Riemannian manifolds. Ann. Math. 63, 20–63 (1956).

    Article  MathSciNet  MATH  Google Scholar 

  62. Borrelli, V., Jabrane, S., Lazarus, F. & Thibert, B. Flat tori in three-dimensional space and convex integration. Proc. Natl Acad. Sci. USA 109, 7218–7223 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  63. Floryan, D. & Graham, M. D. dfloryan/neural-manifold-dynamics: v1.0 (Zenodo, 2022); https://doi.org/10.5281/zenodo.7219159

Download references

Acknowledgements

We acknowledge the use of the Sabine cluster from the Research Computing Data Core at the University of Houston, and the assistance of D. A. Kaji and the Luke cluster. This work was supported by the Air Force Office of Scientific Research (grant no. FA9550-18-0174 to M.D.G.) and an Office of Naval Research grant (grant no. N00014-18-1-2865, Vannevar Bush Faculty Fellowship, to M.D.G.).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Houston, Houston, TX, USA

    Daniel Floryan

  2. Department of Chemical and Biological Engineering, University of Wisconsin–Madison, Madison, WI, USA

    Michael D. Graham

Authors
  1. Daniel Floryan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael D. Graham
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

D.F. and M.D.G. designed and performed the research, analysed the data and wrote the paper.

Corresponding authors

Correspondence to Daniel Floryan or Michael D. Graham.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Machine Intelligence thanks Stefan Schonscheck and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary discussion, tables and figures.

Supplementary Video 1

From left to right: simulation of equation (5) in the main text; model prediction using method of ref. 46, with two degrees of freedom; model prediction using method from ref. 46, with one degree of freedom; model prediction with the current approach and one degree of freedom with three charts.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Floryan, D., Graham, M.D. Data-driven discovery of intrinsic dynamics. Nat Mach Intell 4, 1113–1120 (2022). https://doi.org/10.1038/s42256-022-00575-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s42256-022-00575-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing AI and Robotics

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: AI and Robotics