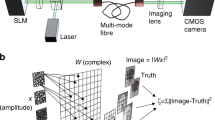
Abstract
The output of physical systems, such as the scrambled pattern formed by shining the spot of a laser pointer through fog, is often easily accessible by direct measurements. However, selection of the input of such a system to obtain a desired output is difficult, because it is an ill-posed problem; that is, there are multiple inputs yielding the same output. Information transmission through scattering media is an example of this problem. Machine learning approaches for imaging have been implemented very successfully in photonics to recover the original input phase and amplitude objects of the scattering system from the distorted intensity diffraction pattern outputs. However, controlling the output of such a system, without having examples of inputs that can produce outputs in the class of the output objects the user wants to produce, is a challenging problem. Here, we propose an online learning approach for the projection of arbitrary shapes through a multimode fibre when a sample of intensity-only measurements is taken at the output. This projection system is nonlinear, because the intensity, not the complex amplitude, is detected. We show an image projection fidelity as high as ~90%, which is on par with the gold-standard methods that characterize the system fully by phase and amplitude measurements. The generality and simplicity of the proposed approach could potentially provide a new way of target-oriented control in real-world applications when only partial measurements are available.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The directory to the dataset required to reproduce results appearing in Table 1 is provided at https://github.com/Babak70/Projector_network.
Code availability
Our neural network framework is available at https://github.com/Babak70/Projector_network and https://zenodo.org/record/3727136. Any correspondence and reasonable requests for extra materials should be directed to the corresponding author.
References
Spitz, E. & Werts, A. Transmission des images à travers une fibre optique. C. R. Hebd. Des. Seances De. L. Acad. Des. Sci. Ser. B 264, 1015 (1967).
Di Leonardo, R. & Bianchi, S. Hologram transmission through multi-mode optical fibers. Opt. Express 19, 247–254 (2011).
Čižmár, T. & Dholakia, K. Shaping the light transmission through a multimode optical fibre: complex transformation analysis and applications in biophotonics. Opt. Express 19, 18871–18884 (2011).
Čižmár, T. & Dholakia, K. Exploiting multimode waveguides for pure fibre-based imaging. Nat. Commun. 3, 1027 (2012).
Bianchi, S. & Di Leonardo, R. A multi-mode fiber probe for holographic micromanipulation and microscopy. Lab Chip 12, 635–639 (2012).
Andresen, E. R., Bouwmans, G., Monneret, S. & Rigneault, H. Toward endoscopes with no distal optics: video-rate scanning microscopy through a fiber bundle. Opt. Lett. 38, 609–611 (2013).
Gover, A., Lee, C. P. & Yariv, A. Direct transmission of pictorial information in multimode optical fibers. J. Opt. Soc. Am. 66, 306–311 (1976).
Friesem, A. A., Levy, U. & Silberberg, Y. Parallel transmission of images through single optical fibers. Proc. IEEE 71, 208–221 (1983).
Yariv, A., AuYeung, J., Fekete, D. & Pepper, D. M. Image phase compensation and real‐time holography by four‐wave mixing in optical fibers. Appl. Phys. Lett. 32, 635–637 (1978).
Yamaguchi, I. & Zhang, T. Phase-shifting digital holography. Opt. Lett. 22, 1268–1270 (1997).
Cuche, E., Bevilacqua, F. & Depeursinge, C. Digital holography for quantitative phase-contrast imaging. Opt. Lett. 24, 291–293 (1999).
Papadopoulos, I. N., Farahi, S., Moser, C. & Psaltis, D. Focusing and scanning light through a multimode optical fiber using digital phase conjugation. Opt. Express 20, 10583–10590 (2012).
Papadopoulos, I. N., Farahi, S., Moser, C. & Psaltis, D. High-resolution, lensless endoscope based on digital scanning through a multimode optical fiber. Biomed. Opt. Express 4, 260–270 (2013).
Choi, Y. et al. Scanner-free and wide-field endoscopic imaging by using a single multimode optical fiber. Phys. Rev. Lett. 109, 203901 (2012).
Caravaca-Aguirre, A. M., Niv, E., Conkey, D. B. & Piestun, R. Real-time resilient focusing through a bending multimode fiber. Opt. Express 21, 12881–12887 (2013).
Gu, R. Y., Mahalati, R. N. & Kahn, J. M. Design of flexible multi-mode fiber endoscope. Opt. Express 23, 26905–26918 (2015).
Loterie, D. et al. Digital confocal microscopy through a multimode fiber. Opt. Express 23, 23845–23858 (2015).
Popoff, S., Lerosey, G., Fink, M., Boccara, A. C. & Gigan, S. Image transmission through an opaque material. Nat. Commun. 1, 81 (2010).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
McCann, M. T., Jin, K. H. & Unser, M. Convolutional neural networks for inverse problems in imaging: a review. IEEE Signal Process Mag. 34, 85–95 (2017).
Rivenson, Y. et al. Deep learning microscopy. Optica 4, 1437–1443 (2017).
Molesky, S. et al. Inverse design in nanophotonics. Nat. Photon. 12, 659–670 (2018).
Paruzzo, F. M. et al. Chemical shifts in molecular solids by machine learning. Nat. Commun. 9, 4501 (2018).
Rahmani, B., Loterie, D., Konstantinou, G., Psaltis, D. & Moser, C. Multimode optical fiber transmission with a deep learning network. Light Sci. Appl. 7, 69 (2018).
Borhani, N., Kakkava, E., Moser, C. & Psaltis, D. Learning to see through multimode fibers. Optica 5, 960–966 (2018).
Caramazza, P., Moran, O., Murray-Smith, R. & Faccio, D. Transmission of natural scene images through a multimode fibre. Nat. Commun. 10, 2029 (2019).
Li, Y., Xue, Y. & Tian, L. Deep speckle correlation: a deep learning approach toward scalable imaging through scattering media. Optica 5, 1181–1190 (2018).
Li, S., Deng, M., Lee, J., Sinha, A. & Barbastathis, G. Imaging through glass diffusers using densely connected convolutional networks. Optica 5, 803–813 (2018).
Turpin, A., Vishniakou, I. & d Seelig, J. Light scattering control in transmission and reflection with neural networks. Opt. Express 26, 30911–30929 (2018).
Psaltis, D., Sideris, A. & Yamamura, A. A. A multilayered neural network controller. IEEE Control Syst. Mag. 8, 17–21 (1988).
Xu, Z., Yang, P., Hu, K., Xu, B. & Li, H. Deep learning control model for adaptive optics systems. Appl. Opt. 58, 1998–2009 (2019).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction (MIT Press, 2011).
Cohen, G., Afshar, S., Tapson, J. & van Schaik, A. EMNIST: an extension of MNIST to handwritten letters. Preprint at https://arxiv.org/pdf/1702.05373.pdf (2017).
Närhi, M. et al. Machine learning analysis of extreme events in optical fibre modulation instability. Nat. Commun. 9, 4923 (2018).
Xiong, W. et al. Deep learning of ultrafast pulses with a multimode fiber. Preprint at https://arxiv.org/pdf/1911.00649.pdf (2019).
Salmela, L., Lapre, C., Dudley, J. M. & Genty, G. Machine learning analysis of rogue solitons in supercontinuum generation. Sci. Rep. 10, 9596 (2020).
Teğin, U. et al. Controlling spatiotemporal nonlinearities in multimode fibers with deep neural networks. APL Photonics 5, 030804 (2020).
Davis, J. A., Cottrell, D. M., Campos, J., Yzuel, M. J. & Moreno, I. Encoding amplitude information onto phase-only filters. Appl. Opt. 38, 5004–5013 (1999).
Acknowledgements
C.M. and D.L. acknowledge financial support from Gebert Rüf Stiftung via the grant ‘Flexprint’ (GRS-057/18, Pilot Projects track).
Author information
Authors and Affiliations
Contributions
B.R. performed the experiment, analysed the data and wrote the manuscript. D.L. wrote the code for the transmission matrix measurements. E.K., N.B. and U.T. participated in the analysis and in the SLM modulation format. D.P. and C.M. proposed and supervised the project and contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 System arbitrary output control with partial measurements.
Additional examples as in Fig. 3.
Extended Data Fig. 2 Fidelity trajectory of the system’s output.
a, the fidelity trajectory of experimentally projected images versus the training iteration number is plotted for all three colors. b, while training, the instability of the system (estimated as the correlation between instances of the system’s response to a constant input signal being sent through the system over and over) is monitored over time (If the system is time-invariant, then the decorrelation plot holds a value of one continually). c, degradation in the fidelity of projected images due to the non-perfect modulation scheme as well as the variation of the system with time is shown by using the experimentally measured transmission matrix (TM) to forward the neural network’s predicted SLM images for all three colors. The fidelities in part (a) are redrawn in part (c) for comparison. As observed, the experimentally projected images (solid circles) closely follow the track of time variant TM-based relayed projections (dashed lines) and both eventually fall below the track of time-invariant TM-based relayed projections (solid lines). In the former, what is taken out from the learning algorithm is only the effect of modulation scheme, whereas in the latter, it is the lumped effect of time variation as well as the modulation scheme. The ripples in the trajectory of the graphs in (c) (dashed lines) show that the network is continuously trying to correct for the drifts.
Extended Data Fig. 3 Projection via amplitude-only control patterns.
a, examples of images projected onto a camera at the output of a MMF (wavelength 780 nm) are shown. The network is forced to generate amplitude-only control patterns. These patterns are then sent to the system and the outputs on the camera are captured. The network is trained with target images of Latin characters but it is also used to predict control patterns for target images from different categories. The visible background of the projected images accounts for the lower signal to noise ratio of the images (also lower fidelities) as compared with that of the complex value control patterns. This is attributed to missing out on controlling the phase of control signals. b, plot of the convergence speed for amplitude-only input controls.
Extended Data Fig. 4 Optical setup.
Detailed diagram of the optical setup. Control patterns are generated via the SLM, guided through the fiber and captured by the camera. L1: Aspheric lens, L2: f = 100 mm lens; L3: f = 250 mm lens; L4: f = 250 mm lens; OBJ1, OBJ2: 60x microscope objective; SLM: spatial light modulator; M1: mirror; FM: flip mirror; SMF: single mode fiber; MMF: multimode fiber, BS: beam splitter.
Extended Data Fig. 5 Neural network’s architecture.
The Actor and Model networks are comprised of two sub-networks, (Areal, Aimag) and (Mreal, Mimag) respectively, to cope with the real and imaginary parts of input-output fields. All sub-networks are fully-connected. Thereby, the input images to the Actor network is first flattened out (from size 200×200 pixels to 40000×1 vectors) and then fed to the sub-networks Areal and Aimag (input nodes 40000, output nodes 2601). In the training step, the output vectors (size 2601×1) of Areal and Aimag are passed on to Mreal and Mimag (input nodes 2601, output nodes 40000), respectively. The virtual neural network output image of the target image (size 200×200) is then produced at the output of the Model. Once trained, the output vectors of the Actor network can be directly reshaped to produce the real and imaginary parts of the SLM images (reshaping from size 2601×1 to 51×51 pixels). If these SLM images are uploaded to the SLM and sent through the fiber, they produce projected images on the camera that are similar to the target images.
Extended Data Fig. 6 Semi-supervised learning.
The Actor network is additionally trained with images used for training of the Model network. The loss function for training the Actor is comprised of two terms: the loss term in Equation. 3 and an extra mean square term with weight λ⊡ The fidelity is obtained for multiple values of λ. The original learning algorithm corresponds to the case in which λ=0⊡.
Extended Data Fig. 7 Robustness analysis.
Two scenarios of minor (a, b) and major (c, d) perturbations due to misalignment of the MMF system is studied. a- The proximal side of the fiber has been slightly blocked with a spatial filter depicted in (a). b- the fidelity plot of the projected images before and after the perturbation event (denoted by a star symbol) is shown. c- In the second scenario, the proximal side of the fiber has been slightly tilted (changed in angle). This results in a shift in the reception bandwidth of the fiber facet from spatial frequency configuration 1 to 2. d- The fidelity plot of the projected images for the perturbed system is shown.
Extended Data Fig. 8 Supervised learning architecture for amplitude-only modulation.
a- Schematic of a neural network (NN) that is made of one single network as an alternative architecture for the Actor–Model network proposed in the main text. The single NN is trained with images obtained from the camera and the corresponding input control patterns (here amplitude-only control patterns). Once trained, the target image is directly passed on to the network and is asked for its corresponding control pattern. The predicted pattern is then sent through the fiber. b- The average fidelity trajectory of the projected images of 20000 Latin alphabet characters versus the training iteration number.
Supplementary information
Supplementary Video
The video accompanying the manuscript containing animations of several projected images captured on the camera.
Rights and permissions
About this article
Cite this article
Rahmani, B., Loterie, D., Kakkava, E. et al. Actor neural networks for the robust control of partially measured nonlinear systems showcased for image propagation through diffuse media. Nat Mach Intell 2, 403–410 (2020). https://doi.org/10.1038/s42256-020-0199-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-020-0199-9
This article is cited by
-
Non-orthogonal optical multiplexing empowered by deep learning
Nature Communications (2024)
-
An actor-model framework for visual sensory encoding
Nature Communications (2024)
-
Self-supervised dynamic learning for long-term high-fidelity image transmission through unstabilized diffusive media
Nature Communications (2024)
-
Inverse design of chiral functional films by a robotic AI-guided system
Nature Communications (2023)
-
Modified variational autoencoder for inversely predicting plasmonic nanofeatures for generating structural color
Scientific Reports (2023)