A topology-based network tree for the prediction of protein–protein binding affinity changes following mutation

Abstract

The ability to predict protein–protein interactions is crucial to our understanding of a wide range of biological activities and functions in the human body, and for guiding drug discovery. Despite considerable efforts to develop suitable computational methods, predicting protein–protein interaction binding affinity changes following mutation (ΔΔG) remains a severe challenge. Algebraic topology, a champion in recent worldwide competitions for protein–ligand binding affinity predictions, is a promising approach to simplifying the complexity of biological structures. Here we introduce element- and site-specific persistent homology (a new branch of algebraic topology) to simplify the structural complexity of protein–protein complexes and embed crucial biological information into topological invariants. We also propose a new deep learning algorithm called NetTree to take advantage of convolutional neural networks and gradient-boosting trees. A topology-based network tree is constructed by integrating the topological representation and NetTree for predicting protein–protein interaction ΔΔG. Tests on major benchmark datasets indicate that the proposed topology-based network tree is an important improvement over the current state of the art in predicting ΔΔG.

Main

Protein–protein interactions (PPIs) are crucial to a wide range of biological activities and functions in the human body, including cell metabolism, signal transduction, muscle contraction and immune systems. The antibody–antigen system is one of the most essential among all PPIs and plays a unique role in the study of PPIs. Antibodies are large proteins that serve important roles in the immune system by counteracting antigens—chemicals recognized as alien by the human body. On the tip of an antibody, there is an antigen-binding fragment that contains a paratope for recognizing a unique antigen via its epitope; more specifically, a paratope consists of a set of complementarity-determining regions that have the highest conformational flexibility among sites on an antibody¹. The high selectivity of antibody–antigen recognition mechanism and the flexibility of antibodies as large proteins make antibodies a suitable platform for designing counteractants of target molecules. Antibodies have been widely used as therapeutic agents to treat human diseases. Antibody therapy has several advantages over traditional therapy, including longer serum half-life, higher avidity and selectivity, and the ability to invoke desired immune responses^2,3,4. Antibody therapy also brings hope of curing several previously incurable diseases and there are ongoing efforts in the direction of HIV vaccine development⁵ and cancer therapeutic antibodies^6,7.

Three-dimensional (3D) structural information and thermodynamic measurements are two essential components for understanding the molecular mechanism of PPIs. Many experimental methods have been developed to determine the structure of protein–protein complexes. Among them, X-ray crystallography, NMR and cryo-electron microscopy are the main workhorses⁸. The Protein Data Bank⁹, one of the largest protein structure databases, includes tens of thousands of protein–protein complex structures and is expanding at an unprecedented rate.

Site-directed mutation is a key technology for probing the thermodynamic properties of PPIs, including binding affinities of antibody–antigen interactions. Sirin et al.¹⁰ collected an AB-Bind database of mutation-induced antibody–antigen complex binding free energy changes. This database contains 1,101 mutation data entries, including 645 single-point mutations on 32 different antibody–antigen complexes. SKEMPI is a more general database for protein–protein binding affinity changes following mutation (ΔΔG)¹¹, it contains 3,047 mutation data entries for protein–protein heterodimeric complexes with experimentally determined structures.

The aforementioned databases have been widely used as benchmark tests for evaluating the predictive power of computational methods, which are indispensable for the investigation of PPIs, especially for the systematic screening of mutations^12,13. There are many reliable computational methods that can predict mutant structures on the wild-type, such as Rosetta¹⁴ and Jackal¹⁵. Computational methods for generating protein structures from sequences (for example, MODELLER¹⁶) and predicting docking poses for protein–protein complexes (for example, BioLuminate¹⁷) are also available.

The thermodynamic properties of PPIs are usually interpreted as the binding affinity or binding free energy, ΔG. Given the importance of computational methods, a variety of them have been developed that use structures to predict antibody–antigen binding affinities. DFIRE¹⁸ relies on an all-atom, distance-scaled, pairwise potential that is derived using a database of high-quality diverse protein structures, whereas STATIUM uses a pairwise statistical potential that scores how well a protein complex can accommodate different pairs of residues in the parent complex geometry. Force-fields for proteins can also be used to compute the binding free energy, representing van der Waals interactions, hydrophobic packing, electrostatics and solvation effects. These approaches include FoldX (FOLDEF)¹⁹, Discovery Studio (CHARMMPLR)²⁰ and Rosetta¹⁴. Typically, physics-based methods provide mechanistic interpretations but are not designed for handling large and diverse datasets.

Pires et al. optimized their graph-based cut-off scanning matrix (CSM) method for predicting antibody–antigen affinity changes following mutation given in the AB-Bind database²¹. This method (named mCSM-AB) was shown to outperform the aforementioned physical methods yet only achieve a Pearson’s correlation coefficient (R_P) of 0.53 with tenfold cross-validation on a set of 645 single-point mutations. The limited performance of the current methods therefore highlights a pressing need for a new generation of ΔΔG predictors that are constructed with entirely new design principles and/or innovative machine learning algorithms. Although the physics-based methods assume potential functions of certain forms and the graph-based method only considers pairwise interactions, we seek an approach that makes fewer assumptions and allows a systemic description of PPIs.

Persistent homology^22,23,24,25—a new branch of algebraic topology—is able to bridge geometry and topology, leading to a new efficient approach for the simplification of biological structural complexity^{26,27,28,29,30,31}; however, it neglects critical chemical/biological information when it is directly applied to complex biomolecular structures. Element-specific persistent homology can retain critical biological information during the topological abstraction. Paired with advanced machine learning, such as a convolutional neural network (CNN), this new topological method gives rise to some of the best predictions for protein–ligand binding affinities³², protein folding free energy changes following mutation^33,34 and drug virtual screening³⁵. This approach has won many contests in the D3R Grand Challenges, a worldwide competition series in computer-aided drug design³⁶; however, the techniques designed for protein–ligand binding analysis could not be directly applied to PPIs due to biological differences and the different characteristics of available datasets.

In the present work we introduce site-specific persistent homology that is tailored for PPI analysis. We explore the utility of site-specific persistent homology and machine learning algorithm for characterizing PPIs that are associated with site-specific mutations. We hypothesize that a topological approach that generates intrinsically low-dimensional representations of PPIs could dramatically reduce the dimensionality of antibody–antigen complexes, leading to a reliable high-throughput screening in searching for valuable mutants in protein design. To validate our hypothesis, we integrate topological descriptors with a machine learning algorithm (CNN-assisted gradient-boosting trees (GBTs)) to predict PPI ΔΔG. The resulting topology-based network tree (TopNetTree) method is found to outperform other methods on two major benchmark datasets, AB-Bind¹⁰ and SKEMPI¹¹, by a large margin. Our TopNetTree offers an accurate and reliable tool for studying PPIs.

TopNetTree model for PPI binding energy change following mutation prediction

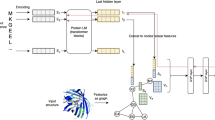
This section describes the TopNetTree model and its application to PPI ΔΔG prediction. As shown in Fig. 1, the proposed TopNetTree consists of two major modules: topology-based feature generation and a CNN-assisted GBT model (Fig. 1). For the feature generation, we mainly used element- and site-specific persistent homology to capture structural characteristics, which was enhanced by chemical–physical descriptors, whereas for the learning model we used a GBT fed with inputs from a CNN as a predictor. We demonstrate the performance of the proposed TopNetTree by three commonly used PPI benchmark datasets.

Fig. 1: An illustration of the proposed TopNetTree model.

The H₀ features are processed by a CNN whose flatten layer outputs—together with H₁,H₂ and auxiliary features—are fed into a GBT model for the final prediction.

Topological representation of PPIs

The pairwise interactions between atoms are characterized by the zeroth homology group (H₀, also known as the size function³⁷). The higher-dimensional homology groups encode higher-order patterns in PPI complexes. The first homology group (H₁), which is generated with Euclidean distance (D_e)-based filtration, characterizes loop or tunnel-like structures, as shown in Fig. 2, whereas the second homology group (H₂) describes cavity structures in PPI complexes. We obtain a comprehensive topological description of PPIs by combining various dimensions.

Fig. 2: Topological barcode change associated with a mutation.

Residue leucine in the wild-type is mutated into alanine. Barcodes are generated for carbon atoms within a cut-off of 12 Å of the mutant residue.

A topological representation should be able to extract patterns of different biological or chemical aspects (for example, hydrogen bonds between oxygen and nitrogen atoms, hydrophobicity, polarizability and so on) from a PPI system that is represented by a set of atomic coordinates (that is, a point cloud). We construct simplicial complexes using selected subsets of atomic coordinates and modified distance matrices to achieve this goal.

For the construction of an element- and site-specific persistent homology, we classify the atoms in a PPI complex into various subsets:

• (1) ${{\mathcal{A}}}_{\mathrm{m}}$: atoms of the mutation site.

• (2) ${{\mathcal{A}}}_{\mathrm{mn}}(r)$: atoms in the neighbourhood of the mutation site within a cut-off distance, r.

• (3) ${{\mathcal{A}}}_{\mathrm{Ab}}(r)$: antibody atoms within r of the binding site.

• (4) ${{\mathcal{A}}}_{\mathrm{Ag}}(r)$: antigen atoms within r of the binding site.

• (5) ${{\mathcal{A}}}_{\mathrm{ele}}({\rm{E}})$: atoms in the system that has atoms of element type, E. When characterizing interactions between atoms a_i and a_j in set ${\mathcal{A}}$ and/or set ${\mathcal{B}}$, we use a modified distance matrix to exclude the interactions between the atoms from the same set. In the following formula, 𝐷_mod is defined as the modified distance and 𝐷_e is defined as the Euclidian distance.

$${D}_{\mathrm{mod}}({a}_{i},{a}_{j})=\left\{\begin{array}{l}\infty ,\ {\rm{if}}\ {a}_{i},{a}_{j}\in {\mathcal{A}},{\rm{or}}\ {a}_{i},{a}_{j}\in {\mathcal{B}},\\ {D}_{\mathrm{e}}({a}_{i},{a}_{j}),\ {\rm{if}}\ {a}_{i}\in {\mathcal{A}}\ {\rm{and}}\ {a}_{j}\in {\mathcal{B}},\end{array}\right.$$

(1)

Specific designations for sets ${\mathcal{A}}$ and ${\mathcal{B}}$ are given in Supplementary Table 1, which summarizes various topological barcodes.

Vectorization of topological barcodes

Using persistent homology, the original 3D point-cloud data are characterized by topological barcodes that are represented as collections of intervals that capture geometric patterns, topological patterns and PPIs while dramatically simplifying complicated structural representations of a PPI-complex. The upper bound of the filtration parameter corresponds to the distance cut-off of interactions of interest, which is set to be the same for different samples in the dataset. Instead of having bounding cubes of different sizes around the binding and mutation sites, topological barcodes for different samples are in the same range of filtration values, which improves the scalability in comparison with the direct use of the original 3D data. We construct feature vectors from these sets of intervals for machine learning models.

One method of vectorization is to discretize the range of the filtration parameter into bins and record the behaviour of the barcodes in each bin³⁵. In this work we subdivide a filtration range (for example, [0, 12] Å) into bins of length 0.5 Å; namely, [0, 0.5], (0.5, 1], ⋯ , (11.5, 12] Å. For each bin, we count the numbers of persistence intervals, birth events and death events (see Fig. 3 for an illustration of filtration and persistence). This approach gives us three feature vectors for each topological barcode. Note that this characterization of birth and death might not be stable against different discretizations. As such, only H₀ barcodes obtained from the Vietoris–Rips filtration are used in our approach.

Fig. 3: Filtration and persistence.

An illustration of filtration and H₁ persistence diagram of a set of points on a plane.

One advantage of binned barcode vectorization is that it keeps the distance information that reflects the strength of hydrogen bonds, van der Waals interactions and so on. The bin representation of barcode features can be easily incorporated into a CNN, which captures and discriminates local patterns; that is, the impact of mutations.

Another method of vectorization is to summarize barcode statistics, including the sum, maximum, minimum, mean and standard derivation of bar lengths, birth values and death values. We use this method to vectorize H₁ and H₂ barcodes obtained from alpha complex filtration as these higher-dimensional barcodes are sparser than the zero-dimensional ones²³.

Machine learning models

A major challenge in the prediction of binding affinity changes following mutation for PPIs is that the data is highly complex due to 3D structures, whereas the datasets are relatively small. We designed a hybrid machine learning algorithm that combines a CNN and GBT to overcome this difficulty. The topologically simplified description of the 3D structures are further converted into concise features by the CNN module; the GBT module then builds robust predictors with effective control of overfitting.

TopGBT model

An ensemble method is a class of machine learning algorithms that builds a powerful model from weak learners. It improves the performance on the weak learners with the assumption that the individual learners are likely to make different mistakes and thus summing the weak learners will reduce the overall error. In this work we use GBTs that add a tree to the ensemble according to the current prediction error on the training data. This method (a toplogy-based GBT or TopGBT) performs well when there is a moderate number of features and is relatively robust against hyperparameter tuning and overfitting. The implementation provided by the scikit-learn package (v.0.18.1)³⁸ is used.

TopCNN model

CNNs are some of the most successful deep learning architectures, a regular CNN is a special case of a multilayer artificial neural network where only local connections are allowed between convolution layers and the weights are shared across different locations. We use a topology-based CNN (TopCNN) as an intermediate model; specifically, we feed vectorized H₀ features into CNNs to extract higher level features for the downstream model (detailed parameters and prepossessing process of our model can be found in the Supplementary Information).

TopNetTree model

CNNs can automatically extract high-level features from H₀. These CNN-extracted features are combined with features constructed from high-dimensional topological barcodes, H₁ and H₂, as the inputs of the GBTs; specifically, we build a supervised CNN model with the PPI ΔΔG as labels. After the model is trained, we feed the flatten layer neural outputs into a GBT model to rank their importance. Based on the importance, a subset of CNN features is combined with other features, such as the statistics of H₁ and H₂ barcodes, for the final GBT model as shown in Fig. 1. The GBT is used for its robustness against overfitting, good performance for moderately small data sizes and its model interpretability (further details on TopNetTree are given in the Supplementary Information).

Model performance for PPIs

We consider three datasets: the AB-Bind dataset¹⁰, the SKEMPI dataset¹¹ and the SKEMPI 2.0 dataset³⁹ to validate the proposed TopNetTree model. Two evaluation metrics (R_P and the root-mean-square error, r.m.s.e.) are used to assess the quality of prediction. Detailed information of evaluation metrics can be found in the Supplementry Information.

The prediction of AB-Bind free energy changes following mutation

The AB-Bind dataset includes 1,101 mutational data points with experimentally determined binding affinities¹⁰. We follow Pires et al.²¹ by considering only 645 single mutations across 29 antibody–antigen complexes. Among them, 87 mutations are on five complexes with homology structures. This dataset, called the AB-Bind S645 set, consists of about 20% stabilizing mutations and 80% destabilizing ones; there are 27 non-binders in the whole dataset, which are variants determined not to bind within the sensitivity of the assay. The binding affinity changes following mutation of these non-binders were set to –8 kcal mol^–1. These non-binders could be regarded as outliers in the database and have a strongly negative impact on the prediction model accuracy.

Our model achieved an R_P of 0.65 on the AB-Bind S645 dataset, which is significantly better than those of other existing methods as shown in Table 1. In comparison with non-machine learning methods such as Rosetta and bASA, our method is over 100% more accurate in terms of R_P, indicating that our topology-based machine learning methods have a better predictive power for PPI systems. Our method is about 22% more accurate than the best-existing score of R_P = 0.53 (given by mCSM-AB), indicating the power of our TopNetTree.

Table 1 Comparison of the R_P of various methods for the AB-Bind S645 set

Both GBTs and neural networks are quite sensitive to system errors as the training of a model is based on optimizing the mean-square error of the loss function. The ΔΔG of 27 non-binders (–8 kcal mol^–1) did not follow the distribution of the whole dataset. Pires et al.²¹ found that excluding non-binders from the dataset would significantly increase the performance of a prediction model. In our case, the R_P increased from 0.65 to 0.68 for the same treatment as shown in Fig. 4. We also applied a blind test on homology structures using the rest of the samples as the training set, achieving an R_P of 0.55, as shown in Fig. 4.

Fig. 4: Data and results of TopNetTree model.

a, A tenfold cross-validation on the AB-Bind S645 set that shows an R_P of 0.65 with a P-value of 5.948 × 10^–12 (r.m.s.e. = 1.57 kcal mol^–1, s.d. = 0.002 kcal mol^–1 for ten repeat experiments). b, A tenfold cross-validation on an AB-Bind dataset excluding 27 non-binders that shows an R_P of 0.68 with a P-value of 9.797 × 10^–13 (r.m.s.e. = 1.06 kcal mol^–1, s.d. = 0.0017 kcal mol^–1 for ten repeat experiments). c, A blind prediction of the AB-Bind subset associated with homology structures that shows an R_P of 0.55 with a P-value of 8.372 × 10^–12 (r.m.s.e. = 1.68 kcal mol^–1). d, Distributions of binding affinity changes following mutation of the AB-Bind dataset that are grouped concerning residue region types and alanine mutations. The maximum, minimum, mean and median values of each group are cited in the violin plot. Mean values of each group are cited in red whereas median values of each group are cited in blue. e, Prediction results for different residue region types, with an R_P of 0.60, 0.66, 0.66, 0.65 and 0.48 for the core, rim, support, interior and surface, respectively.

The performance on the SKEMPI dataset

The SKEMPI dataset¹¹ contains 3,047 binding free energy changes following mutation, which are assembled from the scientific literature for protein–protein heterodimeric complexes with experimentally determined structures; it includes single-point mutations and multipoint mutations. There are 2,317 single point mutation data entries among the whole database, which are referred to as the SKEMPI S2317 set.

Xiong et al. recently selected a subset of 1,131 non-redundant interface single-point mutations (denoted set S1131) from SKEMPI set S2317⁴⁰. The same authors applied several methods to the SKEMPI S1131 set⁴⁰, including BindProfX⁴⁰, Profile-score^41,42 FoldX¹⁹ BeAtMuSiC⁴³, SAMMBE⁴⁴ and Dcomplex⁴⁵.

Table 2 shows the Pearson correlation coefficients on tenfold cross-validations. It is found that the proposed TopNetTree is about 15% more accurate than the best-existing method.

Table 2 A comparison of the R_P values of various methods for the single-point mutation in the SKEMPI dataset of 1,131 mutations

The performance on the SKEMPI 2.0 dataset

The SKEMPI 2.0 (ref. ³⁹) database is an updated version of the SKEMPI database, containing new mutations collected after its first version, including data from three other databases: AB-Bind¹⁰, PROXiMATE⁴⁶ and dbMPIKT⁴⁷. This dataset contains 7,085 entries, including single- and multi-point mutations. By selecting only single-point mutations and excluding mutation entries without energy-change values, 4,947 data points were chosen from SKEMPI 2.0 (denoted set S4947). David et al. recently applied their updated mCSM-PPI2 method⁴⁸ to the SKEMPI2 dataset. They filtered only single-point mutations and selected 4,169 variants in 319 different complexes (denoted set S4169). Set S8338 was derived from set S4169 by setting the reverse mutation energy changes to the negative values of its original energy changes. We applied our TopNetTree model to sets S4947, S4169 and S8338. We tested set S4947 with the regular tenfold cross-validation, achieving an average R_P of 0.82 and an r.m.s.e. of 1.11 kcal mol^–1 for the tenfold cross-validation. We followed the method of tenfold stratified cross-validation used in mCSM-PPI2 paper for sets S4169 and S8338⁴⁸. For set S4169, we obtained an average R_P of 0.79 and r.m.s.e. of 1.13 kcal mol^–1, compared with the average R_P of 0.76 and r.m.s.e. of 1.19 kcal mol^–1 achieved by mCSM-PPI2. Finally, for set S8338, our method attained an average R_P of 0.85 and r.m.s.e. of 1.11 kcal mol^–1, whereas mCSM-PPI2 reported the average R_P 0.82 and r.m.s.e. of 1.18 kcal mol^–1 (ref. ⁴⁸).

We further validated our method by the blind prediction of another subset of the AB-Bind database. As SKEMPI 2.0 contains entries in the AB-Bind dataset, we chose 24 protein complexes that appear in both AB-Bind and SKEMPI 2.0 datasets as the test set for 787 mutations (denoted as the S787 set). The S4947 set, excluding the S787 set, was used as the training set. We achieved an average R_P of 0.53 and r.m.s.e. of 1.45 kcal mol^–1 on this blind test (further details are given in the Supplementary Information).

Discussion

The quality of machine learning predictions typically depends on model inputs. In our case, the inputs consist of three crucial components: protein structures, the mutation position and mutation type. In this section we discuss the influence of each component to the prediction quality.

Prediction result analysis for different protein complexes

For the AB-Bind S645 set, mutations can be separated into 24 different protein–protein complexes (we merged the complex with its homology model as one category). We did intra- and inter-protein cross-validations to further analyse the prediction quality across different protein complexes.

Inter-protein-level cross-validation

To perform inter-protein-level cross-validation for 24 different protein–protein complexes, the samples in one protein complex are taken as the test set, whereas the rest of the dataset is used as the training set (see Supplementary Table 2 for more details). For this test, our model reached an average R_P of 0.508 and a median R_P of 0.541. This performance is comparable with the result of blind test on homology models (see Fig. 4); however, the performance of the model varies among different protein families. Models trained on some protein families could extrapolate to other families; for example, the two protein families with the best results, 1KTZ and 2JEL, can reach R_P of 0.866 and 0.818, respectively, whereas the two families with the poorest results, 1FFW and 1YY9, have R_P values of –0.043 and –0.068, respectively.

Intra-protein-level leave-one-out cross-validation

Cross-validation was carried out within each protein complex. For this test, our model reached average/median ${R}_{\mathrm{P}}^{^{} }$ values of 0.170/0.215, which are significantly lower than the tenfold cross-validation result over the entire dataset. One possible reason for this behaviour is that the training set for each complex is too small with only an average of 27 samples per complex. This result also implies that our model needs a diversity of training samples to achieve stable and consistent prediction quality (see Supplementary Table 3 for more details).

Prediction result analysis for different mutation regions

The locations of the site mutations could be categorized into five different regions: interior, surface, rim, support and core (a detailed definition can be found in the Methods). In experimental data, mutations at the core or support region have a higher average energy change of around 1.8 kcal mol^–1 (1.72 kcal mol^–1 and 1.91 kcal mol^–1, respectively), whereas mutations at the rim or interior region have an average energy change of around 0.8 kcal mol^–1 (0.82 kcal mol^–1 and 0.83 kcal mol^–1, respectively), as shown in Fig. 4. On the other hand, the surface mutations have an average energy change of less than 0.2 kcal mol^–1. Similar patterns regarding mutation sites and energy changes were reported in the literature⁴⁹. A possible reason for these patterns is that different mutation regions vary in their accessibility to water; in general, surface, interior and rim regions have greater access to water than the core and support regions.

Figure 4 shows our predictions concerning different mutation regions. Average ${R}_{\mathrm{P}}^{^{} }$ values of 0.60, 0.66, 0.66, 0.65 and 0.48 were achieved for the core, rim, support, interior and surface regions, respectively. This result shows that the performance is consistent among different mutation regions except for the surface region. We believe that the relative inferior performance for surface mutations is due to its small data size and that the energy disturbance caused by surface mutations is small on average.

Prediction result analysis for different mutation types

The pattern of PPI binding affinity changes over different mutation types is important for protein design. We test how well can the model prediction resemble the distribution in experimental data. Here we investigate the behaviour of our model for 20 different amino acids types in the AB-Bind S645 set. A reverse mutation from ‘B’ to ‘A’ is considered to be the same mutation type as from ‘A’ to ‘B’, and the associated energy change admits an opposite sign (the mutations count for each mutation type can be found in Supplementary Fig. 1).

Overall, our predicted patterns are remarkably similar to those of experimental data in terms of both average binding energy changes and variance of binding energy changes, as shown in Fig. 5. It is interesting to note that all the mutations to alanine have a positive energy change—a possible reason is that mutations from a large residue to a small one could lead to a stabilizing effect to the whole system. Aside from the size of amino acids, we also categorized them into charged, polar, hydrophobic and special-case groups. In terms of binding affinity changes, we find that most mutations from polar to hydrophobic residues have a positive free energy change (for example, S to M), which means mutations from polar residues to hydrophobic residues would make the whole PPI system more stable. We also observed that a mutation from charged residues to uncharged polar residues could lead to a negative energy change; for example, lysine to serine (K to S), which means such mutations might have broken some charge–charge interaction pairs.

Fig. 5: A comparison of average experimental and prediction binding affinity changes following mutations associated with different amino acid types for the AB-Bind dataset.

The x-axis labels the residue type of the original, whereas the y-axis labels the residue type of the mutant. For a reverse mutation, its ΔΔG is taken to be the same magnitude as the original value with an opposite sign. a, Average binding affinity changes following mutation (kcal mol^–1). b, Variance of binding affinity changes following mutation (kcal mol^–1).

Although our model shares a similar pattern in the variance of energy changes with experimental data, the variance of the model predictions is generally lower than the experimental data as shown in Fig. 5. It remains a challenging task to come up with predictions with a diversity level the same as that of experimental data.

Conclusion

The importance of PPIs is evident from the intensive efforts to study them from many perspectives, including quantum mechanics, molecular mechanics, biochemistry, biophysics and molecular biology; for example, the R_P value between predicted ΔΔG values and experimental data in cross-validations of a commonly used PPI database, AB-Bind¹⁰, is only 0.53.

Topology has recently been shown to be surprisingly effective in simplifying biomolecular structural complexity^26,27,29. It has been devised to win worldwide competitions in computer-aided drug design³⁶. It is therefore of enormous importance to exploit topology for understanding PPIs. In this work, we propose TopNetTrees for ΔΔG predictions; specifically, an element- and site-specific persistent homology is introduced to characterize PPIs. Furthermore, we propose machine learning algorithms—CNN-assisted GBTs—to pair with the topological method for the prediction of PPI ΔΔG. We demonstrate that the proposed TopNetTree achieves an R_P of 0.65, which is about 22% better than the previous best result for the AB-Bind dataset. For another benchmark PPI dataset, SKEMPI, the present method significantly outperforms the state-of-the-art in the literature.

Methods

Simplicial complex and filtration

An abstract simplicial complex is a finite collection of sets of points (that is, atoms) $K={\{{\sigma }_{i}\}}_{i}$, where the elements in σ_i are called vertices and σ_i is called a k-simplex if it has k + 1 distinct vertices. If τ ⊆ σ_i then τ is called a face of σ_i. A simplicial complex, K, is valid if τ ⊆ σ_i for σ_i ∈ K indicates that τ ∈ K, and that the non-empty intersection of any two simplices σ₁, σ₂ ∈ K is a face of both σ₁ and σ₂.

In practice, it is favourable to characterize point clouds or atomic positions in various spatial scales rather than in a fixed scaled simplicial complex representation. To construct a scale-changing simplicial complex, consider a function $f:K\to {\mathbb{R}}$ that satisfies f(τ) ≤ f(σ) whenever τ ⊆ σ. Given a real value, x, f induces a subcomplex of K by constructing a sub-level set, K(x) = {σ ∈ K∣f(σ) ≤ x}. As K is finite, the range of f is also finite and the induced subcomplexes, when ordered, form a filtration of K,

$$\varnothing \subset K({x}_{1})\subset K({x}_{2})\subset \cdots \subset K({x}_{\ell })=K$$

(2)

There are many constructions of K and one that is widely used for point clouds is the Vietoris–Rips complex. Given K as the collection of all possible simplices from a set of atomic coordinates until a fixed dimension, the filtration function is defined as f_Rips(σ) = max{d(v_i, v_j)∣v_i, v_j ∈ σ} for σ ∈ K, where d is a predefined distance function between the vertices; for example, D_e. In practice, an upper bound of the filtration value is set to avoid an excessively large simplicial complex. Another efficient construction called the alpha complex²³ is often used to characterize geometry, and we denote the filtration function by ${f}_{\alpha }:{\rm{DT}}(X)\to {\mathbb{R}}$, where DT(X) is the simplicial complex that is induced by the Delaunay triangulation of the set of atomic coordinates, X (ref. ²³). The filtration function is defined as ${f}_{\alpha }(\sigma )=\max\{\frac{1}{2}{D}_{\mathrm{e}}({v}_{i},{v}_{j})| {v}_{i},{v}_{j}\in \sigma \}$ for σ ∈ DT(X). Back to molecular structures, the filtration of simplicial complexes describes the topological characteristics of interaction hypergraphs under various interaction range assumptions.

Homology and persistence

A homology group (in singular homology) of a simplicial complex topologically depicts hole-like structures of different dimensions. Given a simplicial complex, K, a k-chain is a finite formal sum of k-simplices in K; that is, $\sum _{i}{a}_{i}{\sigma }_{i}$. There are many choices for coefficients, $a_i$, and we choose ${a}_{i}\in {{\mathbb{Z}}}_{2}$ for simplicity. The kth chain group (denoted C_k(K)) comprises all of the k-chains under the addition that is induced by the addition of coefficients. A boundary operator ∂_k: C_k(K) → C_k−1(K) connects chain groups of different dimensions by mapping a chain to the alternating sum of codimension-1 faces. It suffices to define the boundary operator on simplices,

$${\partial }_{k}(\{{v}_{0},\cdots \ ,{v}_{k}\})=\sum _{i=0}^{k}{(-1)}^{i}\{{v}_{0},\cdots \ ,{\textbf{v}}_{i},\cdots \ ,{v}_{k}\},$$

(3)

where ${\textbf{v}}_{i}$ indicates the absence of vertex v_i. The kth cycle group (denoted Z_k(K)) is defined to be the kernel of ∂_k, whose members are called k-cycles. The kth boundary group is the image of ∂_k+1 and is denoted B_k(K). It follows that B_k(K) is a subgroup of Z_k(K) based on the property of boundary maps, ∂_k ∘ ∂_k+1 = 0. The kth homology group, H_k(K), is defined to be the quotient group Z_k(K)∕B_k(K). The equivalent classes in H_k(K) correspond to k-dimensional holes in K that cannot be deformed to eachother by adding or subtracting the boundary of a subcomplex.

Given a filtration as in equation (2), in addition to characterizing the homology group at each frame H_k(K(x_i)), we also want to track how topological features persist along the sequence. Viewing H_k(K(x_i)) as vector spaces together with inclusion map induced linear transformations gives a persistence module,

$${H}_{k}(K({x}_{1}))\to {H}_{k}(K({x}_{2}))\to \cdots \to {H}_{k}(K({x}_{\ell })).$$

(4)

An interval module with respect to [b, d) denoted ${{\mathbb{I}}}_{[b,d)}$ is defined as a collection of vector spaces {V_i} that are connected by linear maps, f_i: V_i → V_i+1, where ${V}_{i}={{\mathbb{Z}}}_{2}$ for i ∈ [b, d) and V_i = 0 elsewhere and f_i is identity map when possible and zero otherwise. The persistence module in equation (4) can be decomposed as a direct sum of interval modules ${\oplus }_{[b,d)\in B}{{\mathbb{I}}}_{[b,d)}$. Each ${{\mathbb{I}}}_{[b,d)}$ corresponds to a homology class that appears at filtration value b and disappears at filtration value d (the values b and d are usually called the birth and death values). The collection of these pairs, B, encodes the evolution of k-dimensional holes when varying the filtration parameter and thus records the topological configuration of the input point cloud under different interactions ranges if a distance based filtration is used. Figure 3 illustrates filtration and persistence.

Mutation regions

Mutant residue locations were classified into interface and non-interface regions. Interface residues were further classified as the rim, support or core, and non-interface residues were also further classified as surface or interior, based on the classification approach by Levy⁵⁰.

Residue classification is mainly based on the change of relative residue accessible surface area (rASA) between protein–protein complex (rASA_c) and individual protein components of complex (rASA_m), as shown in Table 3. The accessible surface area was calculated with AREAIMOL from the CCP4 suite⁵¹ and relative solvent accessibility was obtained by normalizing the absolute value with that of the same amino acid in a G–X–G peptide⁵².

Table 3 Criteria of residue regions⁵⁰, ΔrASA = rASA_m − rASA_c