Abstract
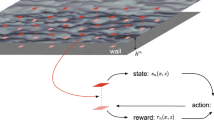
Turbulent flow models are critical for applications such as aircraft design, weather forecasting and climate prediction. Existing models are largely based on physical insight and engineering intuition. More recently, machine learning has been contributing to this endeavour with promising results. However, all efforts have focused on supervised learning, which is difficult to generalize beyond training data. Here we introduce multi-agent reinforcement learning as an automated discovery tool of turbulence models. We demonstrate the potential of this approach on large-eddy simulations of isotropic turbulence, using the recovery of statistical properties of direct numerical simulations as a reward. The closure model is a control policy enacted by cooperating agents, which detect critical spatio-temporal patterns in the flow field to estimate the unresolved subgrid-scale physics. Results obtained with multi-agent reinforcement learning algorithms based on experience replay compare favourably with established modelling approaches. Moreover, we show that the learned turbulence models generalize across grid sizes and flow conditions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
All the data analysed in this paper were produced with open-source software described in the code availability statement. Reference data and the scripts used to produce the data figures, as well as instructions to launch the reinforcement learning training and evaluate trained policies, are available on a GitHub repository (https://github.com/cselab/MARL_LES).
Code availability
Both direct numerical simulations and large-eddy simulations were performed with the flow solver CubismUP 3D (https://github.com/cselab/CubismUP_3D). The data-driven SGS models were trained with the reinforcement learning library smarties (https://github.com/cselab/smarties). The coupling between the two codes is also available through GitHub (https://github.com/cselab/MARL_LES).
Change history
07 January 2021
A Correction to this paper has been published: https://doi.org/10.1038/s42256-021-00293-3.
15 January 2021
A Correction to this paper has been published: <ExternalRef><RefSource>https://doi.org/10.1038/s42256-021-00295-1</RefSource><RefTarget Address="10.1038/s42256-021-00295-1" TargetType="DOI"/></ExternalRef>.
References
Kolmogorov, A. N. The local structure of turbulence in incompressible viscous fluid for very large reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–301 (1941).
Taylor, G. I. Statistical theory of turbulence. Parts I and II. Proc. R. Soc. Lon. A 151, 421–454 (1935).
Pope, S. B. Turbulent Flows (Cambridge Univ. Press, 2001).
Moin, P. & Mahesh, K. Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578 (1998).
Moser, R. D., Kim, J. & Mansour, N. N. Direct numerical simulation of turbulent channel flow up to Reτ= 590. Phys. Fluids 11, 943–945 (1999).
Durbin, P. A. Some recent developments in turbulence closure modeling. Annu. Rev. Fluid Mech. 50, 77–103 (2018).
Leonard, A. et al. Energy cascade in large-eddy simulations of turbulent fluid flows. Adv. Geophys. A 18, 237–248 (1974).
Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 91, 99–164 (1963).
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765 (1991).
Lilly, D. K. A proposed modification of the germano subgrid-scale closure method. Phys. Fluids A 4, 633–635 (1992).
Lee, C., Kim, J., Babcock, D. & Goodman, R. Application of neural networks to turbulence control for drag reduction. Phys. Fluids 9, 1740–1747 (1997).
Milano, M. & Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 182, 1–26 (2002).
Duraisamy, K., Iaccarino, G. & Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 51, 357–377 (2019).
Sarghini, F., De Felice, G. & Santini, S. Neural networks based subgrid scale modeling in large eddy simulations. Comput. Fluids 32, 97–108 (2003).
Gamahara, M. & Hattori, Y. Searching for turbulence models by artificial neural network. Phys. Rev. Fluids 2, 054604 (2017).
Xie, C., Wang, J., Li, H., Wan, M. & Chen, S. Artificial neural network mixed model for large eddy simulation of compressible isotropic turbulence. Phys. Fluids 31, 085112 (2019).
Vollant, A., Balarac, G. & Corre, C. Subgrid-scale scalar flux modelling based on optimal estimation theory and machine-learning procedures. J. Turbul. 18, 854–878 (2017).
Hickel, S., Franz, S., Adams, N. & Koumoutsakos, P. Optimization of an implicit subgrid-scale model for LES. In Proc. 21st International Congress of Theoretical and Applied Mechanics (Springer, 2004).
Maulik, R. & San, O. A neural network approach for the blind deconvolution of turbulent flows. J. Fluid Mech. 831, 151–181 (2017).
Sirignano, J., MacArt, J. F. & Freund, J. B. DPM: A deep learning PDE augmentation method with application to large-eddy simulation. J. Comput. Phys. 423, 109811 (2020).
Wu, J.-L., Xiao, H. & Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: a comprehensive framework. Phys. Rev. Fluids 3, 074602 (2018).
Nadiga, B. & Livescu, D. Instability of the perfect subgrid model in implicit-filtering large eddy simulation of geostrophic turbulence. Phys. Rev. E 75, 046303 (2007).
Beck, A., Flad, D. & Munz, C.-D. Deep neural networks for data-driven LES closure models. J. Comput. Phys. 398, 108910 (2019).
Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction 2nd edn (MIT Press, 2018).
Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).
Silver, D. et al. Mastering the game of go with deep neural networks and tree search. Nature 529, 484–489 (2016).
Levine, S., Finn, C., Darrell, T. & Abbeel, P. End-to-end training of deep visuomotor policies. J. Mach. Learn. Res. 17, 1334–1373 (2016).
Akkaya, I. et al. Solving Rubik’s cube with a robot hand. Preprint at https://arxiv.org/abs/1910.07113 (2019).
Garnier, P. et al. A review on deep reinforcement learning for fluid mechanics. Preprint at https://arxiv.org/abs/1908.04127 (2019).
Gazzola, M., Hejazialhosseini, B. & Koumoutsakos, P. Reinforcement learning and wavelet adapted vortex methods for simulations of self-propelled swimmers. SIAM J. Sci. Comput. 36, B622–B639 (2014).
Reddy, G., Celani, A., Sejnowski, T. J. & Vergassola, M. Learning to soar in turbulent environments. Proc. Natl Acad. Sci. USA 113, E4877–E4884 (2016).
Novati, G. et al. Synchronisation through learning for two self-propelled swimmers. Bioinspir. Biomim. 12, 036001 (2017).
Verma, S., Novati, G. & Koumoutsakos, P. Efficient collective swimming by harnessing vortices through deep reinforcement learning. Proc. Natl Acad. Sci. USA 115, 5849–5854 (2018).
Belus, V. et al. Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film. AIP Adv. 9, 125014 (2019).
Biferale, L., Bonaccorso, F., Buzzicotti, M., Clark Di Leoni, P. & Gustavsson, K. Zermelo’s problem: optimal point-to-point navigation in 2D turbulent flows using reinforcement learning. Chaos 29, 103138 (2019).
Novati, G., Mahadevan, L. & Koumoutsakos, P. Controlled gliding and perching through deep-reinforcement-learning. Phys. Rev. Fluids 4, 093902 (2019).
François-Lavet, V. et al. An Introduction to Deep Reinforcement Learning 219–354 (Foundations and Trends in Machine Learning Vol. 11, 2018).
Ling, J., Kurzawski, A. & Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 807, 155–166 (2016).
Pope, S. A more general effective-viscosity hypothesis. J. Fluid Mech. 72, 331–340 (1975).
Buşoniu, L., Babuška, R. & De Schutter, B. in Innovations in Multi-Agent Systems and Applications – 1 (eds Srinivasan, D. & Jain, L. C.) 183–221 (Springer, 2010).
Novati, G. & Koumoutsakos, P. Remember and forget for experience replay. In Proc. 36th International Conference on Machine Learning 97, 4851–4860 (2019).
Lin, L. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 8, 69–97 (1992).
Meyers, J., Geurts, B. J. & Baelmans, M. Database analysis of errors in large-eddy simulation. Phys. Fluids 15, 2740–2755 (2003).
Zhiyin, Y. Large-eddy simulation: past, present and the future. Chin. J. Aeronaut. 28, 11–24 (2015).
Degris, T., White, M. & Sutton, R. S. Off-policy actor-critic. In Proc. 29th International Conference on Machine Learning 179–186 (2012).
Munos, R., Stepleton, T., Harutyunyan, A. & Bellemare, M. Safe and efficient off-policy reinforcement learning. In Advances in Neural Information Processing Systems 29 1054–1062 (2016).
Glorot, X. & Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proc. 13th International Conference on Artificial Intelligence and Statistics 9, 249–256 (2010).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. In Proc. 3rd International Conference on Learning Representations (ICLR) (2014).
Ghosal, S., Lund, T. S., Moin, P. & Akselvoll, K. A dynamic localization model for large-eddy simulation of turbulent flows. J. Fluid Mech. 286, 229–255 (1995).
Chorin, A. J. A numerical method for solving incompressible viscous flow problems. J. Comput. Phys. 2, 12–26 (1967).
Rogallo, R. S. & Moin, P. Numerical simulation of turbulent flows. Annu. Rev. Fluid Mech. 16, 99–137 (1984).
Acknowledgements
We are very grateful to H. J. Bae (Harvard University) and A. Leonard (Caltech) for insightful feedback on the manuscript, and to J. Canton and M. Boden (ETH Zürich) for valuable discussions throughout the course of this work. We acknowledge support by the European Research Council Advanced Investigator Award 341117. Computational resources were provided by the Swiss National Supercomputing Centre (CSCS) Project s929.
Author information
Authors and Affiliations
Contributions
G.N. and P.K. designed the research. G.N. and H.L.L. wrote the simulation software. G.N., H.L.L. and P.K. carried out the research. G.N. and P.K. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Machine Intelligence thanks Elie Hachem, Jonathan Freund and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Novati, G., de Laroussilhe, H.L. & Koumoutsakos, P. Automating turbulence modelling by multi-agent reinforcement learning. Nat Mach Intell 3, 87–96 (2021). https://doi.org/10.1038/s42256-020-00272-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-020-00272-0
This article is cited by
-
Deep learning in computational mechanics: a review
Computational Mechanics (2024)
-
Spatial planning of urban communities via deep reinforcement learning
Nature Computational Science (2023)
-
The transformative potential of machine learning for experiments in fluid mechanics
Nature Reviews Physics (2023)
-
Super-resolution analysis via machine learning: a survey for fluid flows
Theoretical and Computational Fluid Dynamics (2023)
-
Scientific multi-agent reinforcement learning for wall-models of turbulent flows
Nature Communications (2022)