Abstract
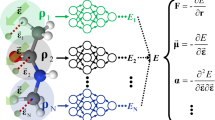
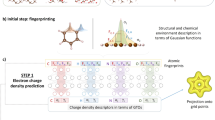
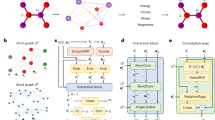
Neural network force field (NNFF) is a method for performing regression on atomic structure–force relationships, bypassing the expensive quantum mechanics calculations that prevent the execution of long ab initio quality molecular dynamics (MD) simulations. However, most NNFF methods for complex multi-element atomic systems indirectly predict atomic force vectors by exploiting just atomic structure rotation-invariant features and network-feature spatial derivatives, which are computationally expensive. Here, we show a staggered NNFF architecture that exploits both rotation-invariant and -covariant features to directly predict atomic force vectors without using spatial derivatives, and we demonstrate 2.2× NNFF–MD acceleration over a state-of-the-art C++ engine using a Python engine. This fast architecture enables us to develop NNFF for complex ternary- and quaternary-element extended systems composed of long polymer chains, amorphous oxide and surface chemical reactions. The rotation-invariant–covariant architecture described here can also directly predict complex covariant vector outputs from local environments, in other domains beyond computational material science.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The atomic structure–force dataset (for systems A, B and C) is available through a Code Ocean compute capsule (https://doi.org/10.24433/CO.2788051.v1). The Python code for training the NNFF of the DCF approach of this work is available through a Code Ocean compute capsule (https://doi.org/10.24422/CO.2788051.v1).
References
Plimpton, S. J. & Thompson, A. P. Computational aspects of many-body potentials. MRS Bull. 37, 513–521 (2012).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
Gastegger, M. & Marquetand, P. High-dimensional neural network potentials for organic reactions and an improved training algorithm. J. Chem. Theory Comput. 11, 2187–2198 (2015).
Bassman, L. et al. Active learning for accelerated design of layered materials. npj Comput. Mater. 4, 74 (2018).
Huan, T. D. et al. A universal strategy for the creation of machine learning-based atomistic force fields. npj Comput. Mater. 3, 37 (2017).
Friederich, P., Konrad, M., Strunk, T. & Wenzel, W. Machine learning of correlated dihedral potentials for atomistic molecular force fields. Sci. Rep. 8, 2559 (2018).
Li, Y. et al. Machine learning force field parameters from ab initio data. J. Chem. Theory Comput. 13, 4492–4503 (2017).
Smith, J. S., Isayev, O. & Roitberg, A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 8, 3192–3203 (2017).
Zong, H., Pilania, G., Ding, X., Ackland, G. J. & Lookman, T. Developing an interatomic potential for martensitic phase transformations in zirconium by machine learning. npj Comput. Mater. 4, 48 (2018).
Jha, D. et al. ElemNet: deep learning the chemistry of materials from only elemental composition. Sci. Rep. 8, 17593 (2018).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B Condens. Matter Mater. Phys. 89, 094104 (2014).
Glielmo, A., Sollich, P. & De Vita, A. Accurate interatomic force fields via machine learning with covariant kernels. Phys. Rev. B 95, 214302 (2017).
Chmiela, S. et al. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 3, e1603015 (2017).
Chmiela, S., Sauceda, H. E., Müller, K. R. & Tkatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 9, 3887 (2018).
Bartok, A. P., Payne, M. C., Kondor, R. & Csanyi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Zeni, C. et al. Building machine learning force fields for nanoclusters. J. Chem. Phys. 148, 241379 (2018).
Vandermause, J., Torrisi, S. B., Batzner, S., Kolpak, A. M. & Kozinsky, B. On-the-fly Bayesian active learning of interpretable force-fields for atomistic rare events. Preprint at https://arxiv.org/abs/1904.02042 (2019).
Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural network potentials. J. Chem. Phys. 134, 074106 (2011).
Li, W., Ando, Y., Minamitani, E. & Watanabe, S. Study of Li atom diffusion in amorphous Li3PO4 with neural network potential. J. Chem. Phys. 147, 214106 (2017).
Rajak, P., Kalia, R. K., Nakano, A. & Vashishta, P. Neural network analysis of dynamic fracture in a layered material. MRS Adv. 4, 1109–1117 (2019).
Handley, C. M. & Popelier, P. L. A. Potential energy surfaces fitted by artificial neural networks. J. Phys. Chem. A 114, 3371–3383 (2010).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Krizhevsky, A., Sutskever, I. & Hinton, G. E. ImageNet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 25, 1097–1105 (2012).
Niepert, M., Ahmed, M. & Kutzkov, K. Learning convolutional neural networks for graphs. In Proceedings of the 33rd International Conference on Machine Learning 48, 2014–2023 (2016).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Schütt, K. T., Sauceda, H. E., Kindermans, P. J., Tkatchenko, A. & Müller, K. R. SchNet—a deep learning architecture for molecules and materials. J. Chem. Phys. 148, 241722 (2018).
Zhang, L., Han, J. & Car, R. Deep potential molecular dynamics: a scalable model with the accuracy of quantum mechanics. Phys. Rev. Lett. 120, 143001 (2018).
Zhang, L. et al. End-to-end symmetry preserving inter-atomic potential energy model for finite and extended systems. Adv. Neural Inf. Process. Syst. 32, 4436–4446 (2018).
Kutz, J. N. Deep learning in fluid dynamics. J. Fluid Mech. 814, 1–4 (2017).
McCracken, M. F. Artificial neural networks in fluid dynamics: a novel approach to the Navier–Stokes equations. In P roceedings of the Practice and Experience on Advanced Research Computing 80 (ACM, 2018).
Yang, K.-T. Artificial neural networks (ANNs): a new paradigm for thermal science and engineering. J. Heat Transfer 130, 093001 (2008).
Li, Z., Kermode, J. R. & De Vita, A. Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces. Phys. Rev. Lett. 114, 1–5 (2015).
Kondor, R. N-body networks: a covariant hierarchical neural network architecture for learning atomic potentials. Preprint at https://arxiv.org/abs/1803.01588 (2018).
Thomas, N. et al. Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds. Preprint at https://arxiv.org/abs/1802.08219 (2018).
Molinari, N., Mailoa, J. P. & Kozinsky, B. Effect of salt concentration on ion clustering and transport in polymer solid electrolytes: a molecular dynamics study of PEO-LiTFSI. Chem. Mater. 30, 6298–6306 (2018).
Brooks, D. J., Merinov, B. V., Goddard, W. A., Kozinsky, B. & Mailoa, J. Atomistic description of ionic diffusion in PEO-LiTFSI: effect of temperature, molecular weight and ionic concentration. Macromolecules 51, 8987–8995 (2018).
Hermann, A., Chaudhuri, T. & Spagnol, P. Bipolar plates for PEM fuel cells: a review. Int. J. Hydrogen Energy 30, 1297–1302 (2005).
Banks, J. L. et al. Integrated Modeling Program, Applied Chemical Theory (IMPACT). J. Comput. Chem. 26, 1752–1780 (2005).
Pedone, A., Malavasi, G., Menziani, M. C., Cormack, A. N. & Segre, U. A new self-consistent empirical interatomic potential model for oxides, silicates and silicas-based glasses. J. Phys. Chem. B 110, 11780–11795 (2006).
van Duin, A. C. T., Dasgupta, S., Lorant, F. & Goddard, W. A. ReaxFF: a reactive force field for hydrocarbons. J. Phys. Chem. A 105, 9396–9409 (2001).
Khorshidi, A. & Peterson, A. A. Amp: a modular approach to machine learning in atomistic simulations. Comput. Phys. Commun. 207, 310–324 (2016).
Imbalzano, G. et al. Automatic selection of atomic fingerprints and reference configurations for machine-learning potentials. J. Chem. Phys. 148, 241730 (2018).
Kolb, B., Lentz, L. C. & Kolpak, A. M. Discovering charge density functionals and structure–property relationships with PROPhet: a general framework for coupling machine learning and first-principles methods. Sci. Rep. 7, 1192 (2017).
Merz, P. T. & Shirts, M. R. Testing for physical validity in molecular simulations. PLoS One 13, e0202764 (2018).
Gupta, A. & Zou, J. Feedback GAN for DNA optimizes protein functions. Nat. Mach. Intell. 1, 105–111 (2019).
Junquera, J., Paz, Ó., Sánchez-Portal, D. & Artacho, E. Numerical atomic orbitals for linear-scaling calculations. Phys. Rev. B 64, 23511 (2001).
Kresse, G. & Hafner, J. Ab initio molecular dynamcis for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmuller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Nose, S. A unified formulation of the constant temperature molecular dynamics methods. J. Phys. Chem. B 81, 511–519 (1984).
Herr, J. E., Yao, K., McIntyre, R., Toth, D. W. & Parkhill, J. Metadynamics for training neural network model chemistries: a competitive assessment. J. Chem. Phys. 148, 241710 (2018).
Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).
Cordero, B. et al. Covalent radii revisited. Dalton Trans. 2008, 2832–2838 (2008).
Press, W. H., Teukolsky, S. A., Vettering, W. T. & Flannery, B. P. Numerical Recipes: The Art of Scientific Computing 3rd edn (Cambridge Univ. Press, 2007).
Wang, L.-P. et al. Discovering chemistry with an ab initio nanoreactor. Nat. Chem. 6, 1044–1048 (2014).
Zheng, S. & Pfaendtner, J. Car–Parrinello molecular dynamics + metadynamics study of high-temperature methanol oxidation reactions using generic collective variables. J. Phys. Chem. C 118, 10764–10770 (2014).
Artrith, N. & Behler, J. High-dimensional neural network potentials for metal surfaces: a prototype study for copper. Phys. Rev. B 85, 1–13 (2012).
Gastegger, M., Behler, J. & Marquetand, P. Machine learning molecular dynamics for the simulation of infrared spectra. Chem. Sci. 8, 6924–6935 (2017).
Pinker, E. Reporting accuracy of rare event classifiers. npj Digit. Med. 1, 56 (2018).
Acknowledgements
We thank S. Falkner and C. Cunha from the Bosch Center for Artificial Intelligence (BCAI) for feedback on NNFF algorithm accuracy improvement. This research used resources of the Oak Ridge Leadership Computing Facility at Oak Ridge National Laboratory, which is supported by the Office of Science of the Department of Energy under contract DE-AC05-00OR22725. The research was partially funded by the Advanced Research Projects Agency – Energy (ARPA-E), US Department of Energy, under award no. DE-AR0000775.
Author information
Authors and Affiliations
Contributions
J.P.M. conceived and implemented the staggered rotation-invariant and -covariant feature separation algorithm. J.P.M., M.K., G.S., S.T.L., C.A. and N.M. generated the training and test datasets for systems A, B and C. J.P.M. evaluated the NNFF accuracy. S.L.B., J.P.M. and M.K. performed the computational cost analysis. S.T.L. developed the HMM for generation of the system C reaction dataset. J.P.M., S.L.B. and J.V. built the DCF Python-based MD engine. M.K. developed the DCF Fortran acceleration for Python. J.P.M. performed the DCF MD study and error analysis. B.K. mentors the research at Bosch and is the primary academic supervisor for S.L.B. and J.V. on this work. J.P.M. wrote the manuscript. All authors contributed to manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–6, Tables 1–6 and notes.
Rights and permissions
About this article
Cite this article
Mailoa, J.P., Kornbluth, M., Batzner, S. et al. A fast neural network approach for direct covariant forces prediction in complex multi-element extended systems. Nat Mach Intell 1, 471–479 (2019). https://doi.org/10.1038/s42256-019-0098-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-019-0098-0
This article is cited by
-
Machine learning heralding a new development phase in molecular dynamics simulations
Artificial Intelligence Review (2024)
-
Learning local equivariant representations for large-scale atomistic dynamics
Nature Communications (2023)
-
Uncertainty-aware molecular dynamics from Bayesian active learning for phase transformations and thermal transport in SiC
npj Computational Materials (2023)
-
E(3)-equivariant graph neural networks for data-efficient and accurate interatomic potentials
Nature Communications (2022)
-
Active learning of reactive Bayesian force fields applied to heterogeneous catalysis dynamics of H/Pt
Nature Communications (2022)