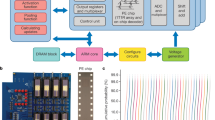
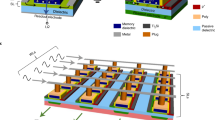
Abstract
The explosive growth of machine learning is largely due to the recent advancements in hardware and architecture. The engineering of network structures, taking advantage of the spatial or temporal translational isometry of patterns, naturally leads to bio-inspired, shared-weight structures such as convolutional neural networks, which have markedly reduced the number of free parameters. State-of-the-art microarchitectures commonly rely on weight-sharing techniques, but still suffer from the von Neumann bottleneck of transistor-based platforms. Here, we experimentally demonstrate the in situ training of a five-level convolutional neural network that self-adapts to non-idealities of the one-transistor one-memristor array to classify the MNIST dataset, achieving similar accuracy to the memristor-based multilayer perceptron with a reduction in trainable parameters of ~75% owing to the shared weights. In addition, the memristors encoded both spatial and temporal translational invariance simultaneously in a convolutional long short-term memory network—a memristor-based neural network with intrinsic 3D input processing—which was trained in situ to classify a synthetic MNIST sequence dataset using just 850 weights. These proof-of-principle demonstrations combine the architectural advantages of weight sharing and the area/energy efficiency boost of the memristors, paving the way to future edge artificial intelligence.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other finding of this study are available in a Zenondo repository at https://doi.org/10.5281/zenodo.3273475.
Code availability
The code that support the plots within this paper and other finding of this study is available in a Zenondo repository at https://doi.org/10.5281/zenodo.3277298 and https://github.com/zhongruiwang/memristorCNN. The code that supports the communication between the custom-built measurement system and the integrated chip is available from the corresponding author on reasonable request.
References
Hubel, D. H. & Wiesel, T. N. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 195, 215–243 (1968).
LeCun, Y., Bottou, L., Bengio, Y. & Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998).
Simonyan, K. & Zisserman, A. Very deep convolutional networks for large-scale image recognition. Preprint at https://arxiv.org/abs/1409.1556 (2014).
Szegedy, C. et al. Going deeper with convolutions. In Proc. IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2015).
He, K., Zhang, X., Ren, S. & Sun, J. Deep residual learning for image recognition. In Proc. IEEE Conference on Computer Vision and Pattern Recognition 770–778 (IEEE, 2016).
Shi, X. et al. Convolutional LSTM network: a machine learning approach for precipitation nowcasting. In Advances in Neural Information Processing Systems 802–810 (NIPS, 2015).
Buonomano, D. V. & Maass, W. State-dependent computations: spatiotemporal processing in cortical networks. Nat. Rev. Neurosci. 10, 113–125 (2009).
Patraucean, V., Handa, A. & Cipolla, R. Spatio-temporal video autoencoder with differentiable memory. Preprint at https://arxiv.org/abs/1511.06309 (2015).
Jouppi, N. P. et al. In-datacenter performance analysis of a tensor processing unit. In Proc. 44th Annual International Symposium on Computer Architecture (ACM/IEEE, 2017).
Chen, Y.-H., Krishna, T., Emer, J. S. & Sze, V. Eyeriss: an energy-efficient reconfigurable accelerator for deep convolutional neural networks. IEEE J. Solid St. Circ. 52, 127–138 (2017).
Chen, Y. et al. Dadiannao: a machine-learning supercomputer. In Proc. 47th Annual IEEE/ACM International Symposium on Microarchitecture 609–622 (IEEE/ACM, 2014).
Tsai, H., Ambrogio, S., Narayanan, P., Shelby, R. M. & Burr, G. W. Recent progress in analog memory-based accelerators for deep learning. J. Phys. D 51, 283001 (2018).
Ielmini, D. & Wong, H. S. P. In-memory computing with resistive switching devices. Nat. Electron 1, 333–343 (2018).
Zidan, M. A., Strachan, J. P. & Lu, W. D. The future of electronics based on memristive systems. Nat. Electron 1, 22–29 (2018).
Yu, S. Neuro-inspired computing with emerging nonvolatile memorys. Proc. IEEE 106, 260–285 (2018).
Strukov, D. B., Snider, G. S., Stewart, D. R. & Williams, R. S. The missing memristor found. Nature 453, 80–83 (2008).
Jo, S. H. et al. Nanoscale memristor device as synapse in neuromorphic systems. Nano Lett. 10, 1297–1301 (2010).
Yu, S., Wu, Y., Jeyasingh, R., Kuzum, D. & Wong, H. S. P. An electronic synapse device based on metal oxide resistive switching memory for neuromorphic computation. IEEE Trans. Elect. Dev. 58, 2729–2737 (2011).
Eryilmaz, S. B. et al. Brain-like associative learning using a nanoscale non-volatile phase change synaptic device array. Front. Neurosci. 8, 205 (2014).
Burr, G. W. et al. Experimental demonstration and tolerancing of a large-scale neural network (165 000 Synapses) using phase-change memory as the synaptic weight element. IEEE Trans. Elect. Dev. 62, 3498–3507 (2015).
Prezioso, M. et al. Training and operation of an integrated neuromorphic network based on metal-oxide memristors. Nature 521, 61–64 (2015).
Ambrogio, S. et al. Unsupervised learning by spike timing dependent plasticity in phase change memory (PCM) synapses. Front. Neurosci. 10, 56 (2016).
Hu, M. et al. Dot-product engine for neuromorphic computing: programming 1T1M crossbar to accelerate matrix-vector multiplication. In 53rd ACM/EDAC/IEEE Design Automation Conference (ACM/IEEE, 2016).
Hu, M. et al. Memristor-based analog computation and neural network classification with a dot product engine. Adv. Mater. 30, 1705914 (2018).
Li, C. et al. Analogue signal and image processing with large memristor crossbars. Nat. Electron. 1, 52–59 (2018).
Nili, H. et al. Hardware-intrinsic security primitives enabled by analogue state and nonlinear conductance variations in integrated memristors. Nat. Electron. 1, 197–202 (2018).
Le Gallo, M. et al. Mixed-precision in-memory computing. Nat. Electron. 1, 246–253 (2018).
Zidan, M. A. et al. A general memristor-based partial differential equation solver. Nat. Electron. 1, 411–420 (2018).
Jeong, Y., Lee, J., Moon, J., Shin, J. H. & Lu, W. D. K-means data clustering with memristor networks. Nano Lett. 18, 4447–4453 (2018).
Shin, J. H., Jeong, Y. J., Zidan, M. A., Wang, Q. & Lu, W. D. Hardware acceleration of simulated annealing of spin glass by RRAM crossbar array. In 2018 IEEE International Electron Devices Meeting 3.3.1–3.3.4 (IEEE, 2018).
Sun, Z. et al. Solving matrix equations in one step with cross-point resistive arrays. Proc. Natl Acad. Sci. USA 116, 4123–4128 (2019).
Sheridan, P. M. et al. Sparse coding with memristor networks. Nat. Nanotechnol. 12, 784–789 (2017).
Choi, S., Shin, J. H., Lee, J., Sheridan, P. & Lu, W. D. Experimental demonstration of feature extraction and dimensionality reduction using memristor networks. Nano Lett. 17, 3113–3118 (2017).
Yao, P. et al. Face classification using electronic synapses. Nat. Commun. 8, 15199 (2017).
Ambrogio, S. et al. Equivalent-accuracy accelerated neural-network training using analogue memory. Nature 558, 60–67 (2018).
Bayat, F. M. et al. Implementation of multilayer perceptron network with highly uniform passive memristive crossbar circuits. Nat. Commun. 9, 2331 (2018).
Boybat, I. et al. Neuromorphic computing with multi-memristive synapses. Nat. Commun. 9, 2514 (2018).
Chen, W.-H. et al. A 65nm 1Mb nonvolatile computing-in-memory ReRAM macro with sub-16ns multiply-and-accumulate for binary DNN AI edge processors. In 2018 IEEE International Solid-State Circuits Conference 494–496 (IEEE, 2018).
Xue, C.-X. et al. A 1Mb multibit ReRAM computing-in-memory macro with 14.6 ns parallel MAC computing time for CNN based AI edge processors. In 2019 IEEE International Solid-State Circuits Conference 388–390 (IEEE, 2019).
Mochida, R. et al. A 4M synapses integrated analog ReRAM based 66.5 TOPS/W neural-network processor with cell current controlled writing and flexible network architecture. In 2018 IEEE Symposium on VLSI Technology 175–176 (IEEE, 2018).
Gokmen, T., Onen, M. & Haensch, W. Training deep convolutional neural networks with resistive cross-point devices. Front Neurosci. 11, 538 (2017).
Li, C. et al. Long short-term memory networks in memristor crossbar arrays. Nat. Mach. Intell. 1, 49–57 (2019).
Sun, X. et al. XNOR-RRAM: a scalable and parallel resistive synaptic architecture for binary neural networks. In 2018 Design, Automation & Test in Europe Conference & Exhibition 1423–1428 (IEEE, 2018).
Gao, L., Chen, P.-Y. & Yu, S. Demonstration of convolution kernel operation on resistive cross-point array. IEEE Elect. Dev. Lett. 37, 870–873 (2016).
Li, C. et al. Efficient and self-adaptive in-situ learning in multilayer memristor neural networks. Nat. Commun. 9, 2385 (2018).
Yang, J. J. et al. High switching endurance in TaOx memristive devices. Appl. Phys. Lett. 97, 232102 (2010).
Tieleman, T. & Hinton, G. Lecture 6.5-rmsprop: divide the gradient by a running average of its recent magnitude. COURSERA: Neural networks for machine learning 4, 26–31 (2012).
Choi, S. et al. SiGe epitaxial memory for neuromorphic computing with reproducible high performance based on engineered dislocations. Nat. Mater. 17, 335–340 (2018).
Graves, A., Mohamed, A.-r. & Hinton, G. Speech recognition with deep recurrent neural networks. In 2013 IEEE International Conference on Acoustics, Speech and Signal Processing 6645–6649 (IEEE, 2013).
An, G. The effects of adding noise during backpropagation training on a generalization performance. Neural Comput. 8, 643–674 (1996).
Wang, Z. et al. Reinforcement learning with analogue memristor arrays. Nat. Electron. 2, 115–124 (2019).
Rumelhart, D. E., Hinton, G. E. & Williams, R. J. Learning representations by back-propagating errors. Nature 323, 533–536 (1986).
Werbos, P. J. Backpropagation through time: what it does and how to do it. Proc. IEEE 78, 1550–1560 (1990).
Acknowledgements
This work was supported in part by the US Air Force Research Laboratory (grant no. FA8750-18-2-0122) and the Defense Advanced Research Projects Agency (contract no. D17PC00304). Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of US Air Force Research Laboratory. H.W. was supported by the Beijing Advanced Innovation Center for Future Chip and National Science Foundation of China (grant no. 61674089 and 61674092). Part of the device fabrication was conducted in the clean room of the Center for Hierarchical Manufacturing, an National Science Foundation Nanoscale Science and Engineering Center located at the University of Massachusetts Amherst.
Author information
Authors and Affiliations
Contributions
J.J.Y. conceived the idea. J.J.Y., Q.X. and Z.W. designed the experiments. Z.W., C.L., P.L., Y.N. and W.S. performed the programming, measurements, data analysis and simulation. M.R., P.Y, C.L. and N.G. built the integrated chips. P.L., Y.L., M.H. and J.P.S. designed the measurement system and firmware. Q.Q., H.W., N.M., Q.W. and R.S.W. helped with experiments and data analysis. J.J.Y. and Z.W wrote the manuscript. All authors discussed the results and implications and commented on the manuscript at all stages.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
Supplementary Figs. 1–13, Tables 1–6 and Notes 1–4
Supplementary Video 1
The in situ training of the 60,000 MNIST training images with the five-level CNN. The upper left panel shows the in-batch training accuracy, which raised sharply from 1 to 200 mini-batches and stayed around 90% accuracy in the rest course. The lower left 3 columns show the corresponding weights of the 15 kernels of size 3 × 3 of the first convolutional layer. Each weight is calculated by dividing the averaged conductance differences of the 2 differential pairs by the constant Rgw (see Methods). (The weights are arranged in the same way as those in Supplementary Figure 6.) The middle 4 columns show the corresponding weights of the 4 kernels of size 2 × 2 (×15) of the second convolutional layer. The right two columns show the corresponding weights of the 64 × 10 fully connected layer.
Supplementary Video 2
The inference of 10,000 MNIST test-set images with the five-level CNN. The left panel shows the image to be classified. The middle panel shows the raw output currents of the fully connected layer neurons. The right panel shows the corresponding Bayesian probabilities based on the softmax function. Blue colour bars are with valid classifications while red ones with misclassifications.
Supplementary Video 3
The in situ training of the 5,958 MNIST-sequence training set with the ConvLSTM. The upper left panel shows the in-batch training accuracy which raised sharply from 1 to 50 minibatches and stayed around 95% accuracy in the rest course. The lower left 4 columns show the corresponding weights of the 5 input kernels of size 3 × 3 of the cell input, input gate, forget gate, and output gate of the ConvLSTM layer. Each weight is calculated by dividing the averaged conductance differences of the 2 differential pairs by the constant conductance-to-weight ratio Rgw (see Method). (The weights are arranged in the same way as those in Supplementary Figure 8). The middle 4 columns show the corresponding weights of the 5 recurrent input kernels of size 2 × 2 (×5) of the cell input, input gate, forget gate, and output gate of the ConvLSTM layer. The right column shows the corresponding weights of the 45 × 6 fully connected layer.
Supplementary Video 4
The inference of 1,010 MNIST-sequence test-set with the ConvLSTM. The left 3 panels show the MNIST-sequence to be classified. The fourth panel shows the raw output currents of the fully connected layer neurons at different time steps (time step 1: blue; time step 2: red, time step 3: orange). The corresponding Bayesian probabilities (of the last time step) based on the softmax function are with the last panel. Blue colour bars are with valid classifications while red ones with misclassifications.
Rights and permissions
About this article
Cite this article
Wang, Z., Li, C., Lin, P. et al. In situ training of feed-forward and recurrent convolutional memristor networks. Nat Mach Intell 1, 434–442 (2019). https://doi.org/10.1038/s42256-019-0089-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42256-019-0089-1
This article is cited by
-
Purely self-rectifying memristor-based passive crossbar array for artificial neural network accelerators
Nature Communications (2024)
-
Pruning and quantization algorithm with applications in memristor-based convolutional neural network
Cognitive Neurodynamics (2024)
-
Open-loop analog programmable electrochemical memory array
Nature Communications (2023)
-
Wearable in-sensor reservoir computing using optoelectronic polymers with through-space charge-transport characteristics for multi-task learning
Nature Communications (2023)
-
Monolithic three-dimensional integration of RRAM-based hybrid memory architecture for one-shot learning
Nature Communications (2023)