Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Autonomous functional movements in a tendon-driven limb via limited experience

Nature Machine Intelligence volume 1, pages 144–154 (2019)Cite this article

Subjects

A preprint version of the article is available at arXiv.

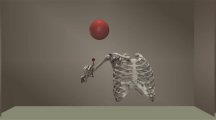
Abstract

Robots will become ubiquitously useful only when they require just a few attempts to teach themselves to perform different tasks, even with complex bodies and in dynamic environments. Vertebrates use sparse trial and error to learn multiple tasks, despite their intricate tendon-driven anatomies, which are particularly hard to control because they are simultaneously nonlinear, under-determined and over-determined. We demonstrate—in simulation and hardware—how a model-free, open-loop approach allows few-shot autonomous learning to produce effective movements in a three-tendon two-joint limb. We use a short period of motor babbling (to create an initial inverse map) followed by building functional habits by reinforcing high-reward behaviour and refinements of the inverse map in a movement’s neighbourhood. This biologically plausible algorithm, which we call G2P (general to particular), can potentially enable quick, robust and versatile adaptation in robots as well as shed light on the foundations of the enviable functional versatility of organisms.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: The G2P algorithm.
Fig. 2: A run of the G2P algorithm, in detail, for the reward-driven treadmill task.
Fig. 3: Planar robotic tendon-driven limb.
Fig. 4: Treadmill task results.
Fig. 5: A run of the G2P algorithm in detail for the tracking of free cyclical movements.
Fig. 6: Distribution of joint angles visited during motor babbling versus those used to produce a free cyclical movement in air.

Similar content being viewed by others

Data availability

The source code can be accessed at https://github.com/marjanin/Marjaninejad-et.-al.−2019-NMI.

All other data (run data for experiments as well as the 3D printing files) can be accessed at https://drive.google.com/drive/folders/1FO0QJ2fBsdYCJs-h1LH7Iwb-wa0VPDi-?usp=sharing

References

  1. Lowrey, K., Kolev, S., Dao, J., Rajeswaran, A. & Todorov, E. Reinforcement learning for non-prehensile manipulation: transfer from simulation to physical system. In Proc. 2018 IEEE International Conference on Simulation, Modeling, and Programming for Autonomous Robots (SIMPAR) 35–42 (IEEE, 2018).

  2. Andrychowicz, M. et al. Learning dexterous in-hand manipulation. Preprint at https://arxiv.org/abs/1808.00177 (2018).

  3. Kobayashi, H. & Ozawa, R. Adaptive neural network control of tendon-driven mechanisms with elastic tendons. Automatica 39, 1509–1519 (2003).

    Article  MathSciNet  Google Scholar 

  4. Nguyen-Tuong, D., Peters, J., Seeger, M. & Schölkopf, B. Learning inverse dynamics: a comparison. In Proc. European Symposium on Artificial Neural Networks 13–18 (2008).

  5. Osa, T., Peters, J. & Neumann, G. Hierarchical reinforcement learning of multiple grasping strategies with human instructions. Adv. Robot. 32, 955–968 (2018).

    Article  Google Scholar 

  6. Manoonpong, P., Geng, T., Kulvicius, T., Porr, B. & Wörgötter, F. Adaptive, fast walking in a biped robot under neuronal control and learning. PLoS Comput. Biol. 3, e134 (2007).

    Article  Google Scholar 

  7. Marques, H. G., Bharadwaj, A. & Iida, F. From spontaneous motor activity to coordinated behaviour: a developmental model. PLoS Comput. Biol. 10, e1003653 (2014).

    Article  Google Scholar 

  8. Gijsberts, A. & Metta, G. Real-time model learning using incremental sparse spectrum Gaussian process regression. Neural Netw. 41, 59–69 (2013).

    Article  Google Scholar 

  9. Della Santina, C., Lakatos, D., Bicchi, A. & Albu-Schäffer, A. Using nonlinear normal modes for execution of efficient cyclic motions in soft robots. Preprint at https://arxiv.org/abs/1806.08389 (2018).

  10. Bongard, J., Zykov, V. & Lipson, H. Resilient machines through continuous self-modeling. Science 314, 1118–1121 (2006).

    Article  Google Scholar 

  11. Krishnan, S. et al. SWIRL: A sequential windowed inverse reinforcement learning algorithm for robot tasks with delayed rewards. Int. J. Rob. Res. https://doi.org/10.1177/0278364918784350 (2018).

  12. James, S. et al. Sim-to-Real via Sim-to-Sim: Data-efficient Robotic Grasping via Randomized-to-Canonical AdaptationNetworks. Preprint at https://arxiv.org/abs/1812.07252 (2018).

  13. Takahashi, K., Ogata, T., Nakanishi, J., Cheng, G. & Sugano, S. Dynamic motion learning for multi-DOF flexible-joint robots using active–passive motor babbling through deep learning. Adv. Robot. 31, 1002–1015 (2017).

    Article  Google Scholar 

  14. Marco, A., Hennig, P., Bohg, J., Schaal, S. & Trimpe, S. Automatic LQR tuning based on Gaussian process global optimization. In 2016 IEEE International Conference on Robotics and Automation (ICRA) 270–277 (IEEE, 2016).

  15. Geijtenbeek, T., Van De Panne, M. & Van Der Stappen, A. F. Flexible muscle-based locomotion for bipedal creatures. ACM Trans. Graph. 32, 206 (2013).

    Article  Google Scholar 

  16. Kumar, V., Tassa, Y., Erez, T. & Todorov, E. Real-time behaviour synthesis for dynamic hand-manipulation. In Proc. 2014 IEEE International Conference on Robotics and Automation (ICRA) 6808–6815 (IEEE, 2014).

  17. Kumar, V., Gupta, A., Todorov, E. & Levine, S. Learning dexterous manipulation policies from experience and imitation. Preprint at https://arxiv.org/abs/1611.05095 (2016).

  18. Rombokas, E., Theodorou, E., Malhotra, M., Todorov, E. & Matsuoka, Y. Tendon-driven control of biomechanical and robotic systems: a path integral reinforcement learning approach. In Proc. 2012 IEEE International Conference on Robotics and Automation (ICRA) 208–214 (IEEE, 2012).

  19. Potkonjak, V., Svetozarevic, B., Jovanovic, K. & Holland, O. The puller–follower control of compliant and noncompliant antagonistic tendon drives in robotic systems. Int. J. Adv. Robot. Syst. 8, 69 (2011).

    Article  Google Scholar 

  20. Hunt, A., Szczecinski, N. & Quinn, R. Development and training of a neural controller for hind leg walking in a dog robot. Front. Neurorobot. 11, 18 (2017).

    Article  Google Scholar 

  21. Fazeli, N. et al. See, feel, act: hierarchical learning for complex manipulation skills with multisensory fusion. Sci. Robot. 4, eaav3123 (2019).

    Article  Google Scholar 

  22. Rasmussen, D., Voelker, A. & Eliasmith, C. A neural model of hierarchical reinforcement learning. PLoS One 12, e0180234 (2017).

    Article  Google Scholar 

  23. Parisi, S., Ramstedt, S. & Peters, J. Goal-driven dimensionality reduction for reinforcement learning. In Proc. 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 4634–4639 (IEEE, 2017).

  24. D’Souza, A., Vijayakumar, S. & Schaal, S. Learning inverse kinematics. Intell. Robots Syst. 1, 298–303 (2001).

    Article  Google Scholar 

  25. Bonarini, A., Lazaric, A. & Restelli, M. Incremental skill acquisition for self-motivated learning animats. In Proc. International Conference on Simulation of Adaptive Behavior 357–368 (Springer, 2006).

  26. Najjar, T. & Hasegawa, O. Self-organizing incremental neural network (SOINN) as a mechanism for motor babbling and sensory-motor learning in developmental robotics. In Proc. International Conference on Artificial Neural Networks 321–330 (Springer, 2013).

  27. Marjaninejad, A., Annigeri, R. & Valero-Cuevas, F. J. Model-free control of movement in a tendon-driven limb via a modified genetic algorithm. In 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC) (IEEE, 2018).

  28. Rajeswaran, A. et al. Learning complex dexterous manipulation with deep reinforcement learning and demonstrations. Preprint at https://arxiv.org/abs/1709.10087 (2017).

  29. Schulman, J., Levine, S., Abbeel, P., Jordan, M. & Moritz, P. Trust region policy optimization. In International Conference on Machine Learning 1889–1897 (PMLR, 2015).

  30. Mnih, V. et al. Human-level control through deep reinforcement learning. Nature 518, 529–533 (2015).

    Article  Google Scholar 

  31. Salimans, T., Ho, J., Chen, X., Sidor, S. & Sutskever, I. Evolution strategies as a scalable alternative to reinforcement learning. Preprint at https://arxiv.org/abs/1703.03864 (2017).

  32. Vinyals, O. et al. Starcraft II: a new challenge for reinforcement learning. Preprint at https://arxiv.org/abs/1708.04782 (2017).

  33. Metta, G. et al. The iCub humanoid robot: an open-systems platform for research in cognitive development. Neural Netw. 23, 1125–1134 (2010).

    Article  Google Scholar 

  34. Pathak, D., Agrawal, P., Efros, A. A. & Darrell, T. Curiosity-driven exploration by self-supervised prediction.Iin International Conference on Machine Learning (ICML) 2017, (2017).

  35. Luo, Q. et al. Design of a biomimetic control system for tendon-driven prosthetic hand. In 2018 IEEE International Conference on Cyborg and Bionic Systems (CBS) 528–531 (2018).

  36. Ravi, S. & Larochelle, H. Optimization as a model for few-shot learning. In Proc. ICLR (2016).

  37. Schaal, S. in Humanoid Robotics: A Reference. (eds Goswami, A. & Vadakkepat, P.) 1–9 (Springer, Dordrecht, 2018).

  38. Bohg, J. et al. Interactive perception: leveraging action in perception and perception in action. IEEE Trans. Robot. 33, 1273–1291 (2017).

    Article  Google Scholar 

  39. Ingram, T. G. J., Solomon, J. P., Westwood, D. A. & Boe, S. G. Movement related sensory feedback is not necessary for learning to execute a motor skill. Behav. Brain Res. 359, 135–142 (2019).

    Article  Google Scholar 

  40. Fine, M. S. & Thoroughman, K. A. Trial-by-trial transformation of error into sensorimotor adaptation changes with environmental dynamics. J. Neurophysiol. 98, 1392–1404 (2007).

    Article  Google Scholar 

  41. Adolph, K. E. et al. How do you learn to walk? Thousands of steps and dozens of falls per day. Psychol. Sci. 23, 1387–1394 (2012).

    Article  Google Scholar 

  42. Valero-Cuevas, F. J. Fundamentals of Neuromechanics 8 (Springer, New York, NY, 2015).

  43. Marjaninejad, A. & Valero-Cuevas, F. J. in Biomechanics of Anthropomorphic Systems (eds Venture, G., Laumond, J.-P. & Watier, B.) 7–34 (Springer, New York, NY, 2019).

  44. McAndrew, P. M., Wilken, J. M. & Dingwell, J. B. Dynamic stability of human walking in visually and mechanically destabilizing environments. J. Biomech. 44, 644–649 (2011).

    Article  Google Scholar 

  45. Jalaleddini, K. et al. Neuromorphic meets neuromechanics. Part II: The role of fusimotor drive. J. Neural Eng. 14, 025002 (2017).

    Article  Google Scholar 

  46. Loeb, G. E. Optimal isn’t good enough. Biol. Cybern. 106, 757–765 (2012).

    Article  Google Scholar 

  47. Collins, S. H., Wiggin, M. B. & Sawicki, G. S. Reducing the energy cost of human walking using an unpowered exoskeleton. Nature 522, 212–215 (2015).

    Article  Google Scholar 

  48. Kobayashi, T., Sekiyama, K., Hasegawa, Y., Aoyama, T. & Fukuda, T. Unified bipedal gait for autonomous transition between walking and running in pursuit of energy minimization. Rob. Auton. Syst. 103, 27–41 (2018).

    Article  Google Scholar 

  49. Finley, J. M. & Bastian, A. J. Associations between foot placement asymmetries and metabolic cost of transport in hemiparetic gait. Neurorehabil. Neural Repair 31, 168–177 (2017).

    Article  Google Scholar 

  50. Selinger, J. C., O’Connor, S. M., Wong, J. D. & Donelan, J. M. Humans can continuously optimize energetic cost during walking. Curr. Biol. 25, 2452–2456 (2015).

    Article  Google Scholar 

  51. Zhang, W., Gordon, A. M., Fu, Q. & Santello, M. Manipulation after object rotation reveals independent sensorimotor memory representations of digit positions and forces. J. Neurophysiol. 103, 2953–2964 (2010).

    Google Scholar 

  52. Wolpert, D. M. & Flanagan, J. R. Computations underlying sensorimotor learning. Curr. Opin. Neurobiol. 37, 7–11 (2016).

    Article  Google Scholar 

  53. Todorov, E. Optimality principles in sensorimotor control. Nat. Neurosci. 7, 907–915 (2004).

    Article  Google Scholar 

  54. Grillner, S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron 52, 751–766 (2006).

    Article  Google Scholar 

  55. Hebb, D. O. The Organization of Behavior: A Neuropsychological Theory (Wiley, New York, NY, 1949).

  56. Ijspeert, A. J., Nakanishi, J. & Schaal, S. in Advances in Neural Information Processing Systems Vol. 15 (eds Becker, S., Thrun, S. & Obermayer, K.) 1547–1554 (MIT Press, Cambridge, MA, 2003).

  57. Feirstein, D. S., Koryakovskiy, I., Kober, J. & Vallery, H. Reinforcement learning of potential fields to achieve limit-cycle walking. In Proc. 6th IFAC Workshop on Periodic Control System Vol. 49, 113–118 (Elsevier, 2016).

  58. http://ruina.tam.cornell.edu/research/topics/locomotion_and_robotics/ranger/ranger_paper/Reports/Ranger_Robot/control/simulator/doublependulum.html

Download references

Acknowledgements

The authors thank H. Zhao for support in designing and manufacturing the physical system as well as support in the analysis of the limb kinematics, S. Kamalakkannan for support in designing and implementing the data acquisition system, and Y. Kahsai for Figs. 1 and 2. Research reported in this publication was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health under award numbers R01 AR-050520 and R01 AR-052345 to F.J.V.-C. This work was also supported by Department of Defense CDMRP Grant MR150091 and Award W911NF1820264 from the DARPA-L2M programme to F.J.V.-C. The authors acknowledge additional support for A.M. for Provost and Research Enhancement Fellowships from the Graduate School of the University of Southern California and fellowships for D.U.-M. from the Consejo Nacional de Ciencia y Tecnología (Mexico) and for B.C. from the NSF Graduate Research Fellowship Program. The content of this endeavour is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health, the Department of Defense, The National Science Foundation nor the Consejo Nacional de Ciencia y Tecnología.

Author information

Authors and Affiliations

  1. Department of Biomedical Engineering, University of Southern California, Los Angeles, CA, USA

    Ali Marjaninejad, Darío Urbina-Meléndez & Francisco J. Valero-Cuevas

  2. Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, USA

    Ali Marjaninejad & Francisco J. Valero-Cuevas

  3. Department of Computer Science, University of Southern California, Los Angeles, CA, USA

    Brian A. Cohn & Francisco J. Valero-Cuevas

  4. Department of Aerospace & Mechanical Engineering, University of Southern California, Los Angeles, CA, USA

    Francisco J. Valero-Cuevas

  5. Division of Biokinesiology & Physical Therapy, University of Southern California, Los Angeles, CA, USA

    Francisco J. Valero-Cuevas

Authors
  1. Ali Marjaninejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Darío Urbina-Meléndez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Brian A. Cohn
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Francisco J. Valero-Cuevas
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed to the conception and design of the work and writing of the manuscript. A.M. led the development of the G2P algorithm, D.U.-M. led the construction of the robotic limb and B.A.C. led the data acquisition and analysis. F.J.V.-C. provided general direction for the project. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work. All persons designated as authors qualify for authorship, and all those who qualify for authorship are listed.

Corresponding author

Correspondence to Francisco J. Valero-Cuevas.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Materials and Methods, Supplementary Discussion, Supplementary Figures 1–7, Captions for Supplementary Videos 1,2

Supplementary Video 1

Video for Figs 4, 5a and 6

Supplementary Video 2

Video for additional experiments

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Marjaninejad, A., Urbina-Meléndez, D., Cohn, B.A. et al. Autonomous functional movements in a tendon-driven limb via limited experience. Nat Mach Intell 1, 144–154 (2019). https://doi.org/10.1038/s42256-019-0029-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s42256-019-0029-0

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing