Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Age-related loss of gene-to-gene transcriptional coordination among single cells

Nature Metabolism volume 2, pages 1305–1315 (2020)Cite this article

Subjects

Abstract

A long-standing model holds that stochastic aberrations of transcriptional regulation play a key role in the process of ageing. While transcriptional dysregulation is observed in many cell types in the form of increased cell-to-cell variability, its generality to all cell types remains doubted. Here, we propose a new approach for analysing transcriptional regulation in single-cell RNA sequencing data by focusing on the global coordination between the genes rather than the variability of individual genes or correlations between pairs of genes. Consistently, across very different organisms and cell types, we find a decrease in the gene-to-gene transcriptional coordination in ageing cells. In addition, we find that loss of gene-to-gene transcriptional coordination is associated with high mutational load of a specific, age-related signature and with radiation-induced DNA damage. These observations suggest a general, potentially universal, stochastic attribute of transcriptional dysregulation in ageing.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Loss of gene-to-gene coordination in ageing LT-HSCs.
Fig. 2: Ageing associated reduction of GCL in different tissues and cell types across various studies.
Fig. 3: Increased mutational load of signature S1 and high irradiation are associated with decreased gene-to-gene coordination.
Fig. 4: Cross-datasets pathway analysis reveals the characteristic ageing effect in LT-HSCs.

Data availability

All datasets analysed in this study are publicly available as described in Table 1, and the accession codes and references are provided in Supplementary Table 1.

Code availability

The custom MATLAB code for computing the GCL that was used in this study is available at https://github.com/guy531/gcl/blob/master/gcl.m.

References

  1. Moskalev, A. A. The role of DNA damage and repair in aging through the prism of Koch-like criteria. Ageing Res. Rev. 12, 661–684 (2013).

    Article  CAS  PubMed  Google Scholar 

  2. Benayoun, B. A., Pollina, E. A. & Brunet, A. Epigenetic regulation of ageing: linking environmental inputs to genomic stability. Nat. Rev. Mol. Cell Biol. 16, 593–610 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  3. Kirkwood, T. B. L. Understanding the odd science of aging. Cell 120, 437–447 (2005).

    Article  CAS  PubMed  Google Scholar 

  4. Aubert, G. & Lansdorp, P. M. Telomeres and aging. Physiol. Rev. 88, 557–579 (2008).

    Article  CAS  PubMed  Google Scholar 

  5. McHugh, D. & Gil, J. Senescence and aging: causes, consequences, and therapeutic avenues. J. Cell Biol. 217, 65–77 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  6. van Deursen, J. M. Senolytic therapies for healthy longevity. Science 364, 636–637 (2019).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  7. Vijg, J. Impact of genome instability on transcription regulation of aging and senescence. Mech. Ageing Dev. 125, 747–753 (2004).

    Article  CAS  PubMed  Google Scholar 

  8. López-Otín, C., Blasco, M. A., Partridge, L., Serrano, M. & Kroemer, G. The hallmarks of aging. Cell 153, 1194–1217 (2013).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  9. Booth, L. N. & Brunet, A. The aging epigenome. Mol. Cell 62, 728–744 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  10. Gems, D. & Partridge, L. Genetics of longevity in model organisms: debates and paradigm shifts. Annu. Rev. Physiol. 75, 621–644 (2013).

    Article  CAS  PubMed  Google Scholar 

  11. Vijg, J. & Dong, X. Pathogenic mechanisms of somatic mutation and genome mosaicism in aging. Cell 182, 12–23 (2020).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  12. Levsky, J. M. & Singer, R. H. Gene expression and the myth of the average cell. Trends Cell Biol. 13, 4–6 (2003).

    Article  CAS  PubMed  Google Scholar 

  13. Bahar, R. et al. Increased cell-to-cell variation in gene expression in ageing mouse heart. Nature 441, 1011–1014 (2006).

    Article  CAS  PubMed  Google Scholar 

  14. Busuttil, R., Bahar, R. & Vijg, J. Genome dynamics and transcriptional deregulation in aging. Neuroscience 145, 1341–1347 (2007).

    Article  CAS  PubMed  Google Scholar 

  15. Martinez-Jimenez, C. P. et al. Aging increases cell-to-cell transcriptional variability upon immune stimulation. Science 355, 1433–1436 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  16. Enge, M. et al. Single-cell analysis of human pancreas reveals transcriptional signature of aging and somatic mutation patterns. Cell 171, 321–330.e14 (2017).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  17. Ilias, A. et al. An atlas of the aging lung mapped by single cell transcriptomics and deep tissue proteomics. Nat. Commun. 10, 963 (2019).

    Article  CAS  Google Scholar 

  18. Wang, J. et al. A differentiation checkpoint limits hematopoietic stem cell self-renewal in response to DNA damage. Cell 148, 1001–1014 (2012).

    Article  CAS  PubMed  Google Scholar 

  19. Rossi, D. J. et al. Deficiencies in DNA damage repair limit the function of hematopoietic stem cells with age. Nature 447, 725–729 (2007).

    Article  CAS  PubMed  Google Scholar 

  20. Rossi, D. J. et al. Hematopoietic stem cell quiescence attenuates DNA damage response and permits DNA damage accumulation during aging. Cell Cycle 6, 2371–2376 (2007).

    Article  CAS  PubMed  Google Scholar 

  21. Rossi, J. et al. Stem cells and the pathways to aging and cancer. Cell 132, 681–696 (2008).

    Article  CAS  PubMed  Google Scholar 

  22. Warren, L. A. et al. Transcriptional instability is not a universal attribute of aging. Aging Cell 6, 775–782 (2007).

    Article  CAS  PubMed  Google Scholar 

  23. Zhang, Q. et al. Systems-level analysis of human aging genes shed new light of mechanisms of aging. Hum. Mol. Genet. 25, 2934–2947 (2016).

    CAS  PubMed  PubMed Central  Google Scholar 

  24. Southworth, LucindaK., Art, B. Owen & Stuart, K. Kim Aging mice show a decreasing correlation of gene expression within genetic modules. PLoS Genet. 5, e1000776 (2009).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  25. Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits (Chapman and Hall/CRC, 2006).

  26. McNabb, D. S., Xing, Y. & Guarente, L. Cloning of yeast HAP5: a novel subunit of a heterotrimeric complex required for CCAAT binding. Genes Dev. 9, 47–58 (1995).

    Article  CAS  PubMed  Google Scholar 

  27. Davidson, E. H. et al. A genomic regulatory network for development. Science 295, 1669–1678 (2002).

    Article  CAS  PubMed  Google Scholar 

  28. Shen-Orr, S., Milo, R., Mangan, S. & Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 31, 64–68 (2002).

    Article  CAS  PubMed  Google Scholar 

  29. Buchler, N. E., Gerland, U. & Hwa, T. On schemes of combinatorial transcription logic. Proc. Natl Acad. Sci. USA 100, 5136–5141 (2003).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  30. Székely, G. J. & Rizzo, M. L. The distance correlation t-test of the independence in high dimension. J. Multivar. Anal. 117, 193–213 (2013).

    Article  Google Scholar 

  31. Mann, M. et al. Heterogeneous responses of hematopoietic stem cells to inflammatory stimuli are altered with age. Cell Rep. 25, 2992–3005 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  32. Ogata, H. et al. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 27, 29–34 (1999).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  33. Kowalczyk, M. S. et al. Single-cell RNA-seq reveals changes in cell cycle and differentiation programs upon aging of hematopoietic stem cells. Genome Res. 25, 1860–1872 (2015).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  34. Grover, A. et al. Single-cell RNA sequencing reveals molecular and functional platelet bias of aged haematopoietic stem cells. Nat. Commun. 7, 11075 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  35. Yang, L. et al. Single-cell RNA-seq of esophageal squamous cell carcinoma cell line with fractionated irradiation reveals radioresistant gene expression patterns. BMC Genomics 20, 611 (2019).

    Article  PubMed  PubMed Central  CAS  Google Scholar 

  36. Kelley, R. in Systems Biology in Practice: Concepts, Implementation, and Application (eds Klipp, E. et al.) (Wiley-Blackwell, 2005).

  37. Ackers, G. et al. Quantitative model for gene regulation by lambda phage repressor. Proc. Natl Acad. Sci. USA 79, 1129 (1982).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  38. Karlebach, G. & Shamir, R. Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 9, 770–780 (2008).

    Article  CAS  PubMed  Google Scholar 

  39. Steelman, L. S. et al. Roles of the Raf/MEK/ERK and PI3K/PTEN/Akt/mTOR pathways in controlling growth and sensitivity to therapy-implications for cancer and aging. Aging 3, 192–222 (2011).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  40. Székely, G. J., Rizzo, M. L. & Bakirov, N. K. Measuring and testing dependence by correlation of distances. Ann. Stat. 35, 2769–2794 (2007).

    Article  Google Scholar 

  41. Lun, A. T. L., McCarthy, D. J. & Marioni, J. C. A step-by-step workflow for low-level analysis of single-cell RNA-seq data with Bioconductor. F1000 Res. 5, 2122 (2016).

    Google Scholar 

  42. Scialdon, A. et al. Computational assignment of cell-cycle stage from single-cell transcriptome data. Methods 85, 54–61 (2015).

    Article  CAS  Google Scholar 

  43. Durinck, S. et al. BioMart and Bioconductor: a powerful link between biological databases and microarray data analysis. Bioinformatics 21, 3439–3440 (2005).

    Article  CAS  PubMed  Google Scholar 

  44. Durinck, S., Spellman, P. T. & Huber, W. Mapping identifiers for the integration of genomic datasets with the R/Bioconductor package biomaRt. Nat. Protoc. 4, 1184–1191 (2009).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  45. Davie, K. et al. A single-cell transcriptome atlas of the aging Drosophila brain. Cell 174, 982–998.e20 (2018).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  46. Young, K. et al. Progressive alterations in multipotent hematopoietic progenitors underlie lymphoid cell loss in aging. J. Exp. Med. 213, 2259–2267 (2016).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

Download references

Acknowledgements

We thank M. Enge for sharing experimental data and for his helpful support. We also thank M.L. Rizzo, E. Eisenberg, Y. Brody, R. Cohen and S. Havlin for helpful discussions. Y.-Y.L. acknowledged grants from National Institutes of Health (R01AI141529, R01HD093761, UH3OD023268, U19AI095219 and U01HL089856). The project described was supported in part by award numbers R01 HL124233 and R01 HL147326 from the National Heart, Lung, and Blood Institute and the FDA Center for Tobacco Products (CTP). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the Food and Drug Administration. A.B. thanks the Azrieli Foundation for supporting this research.

Author information

Author notes

  1. These authors contributed equally: Orr Levy, Guy Amit.

Authors and Affiliations

  1. Department of Physics, Bar-Ilan University, Ramat-Gan, Israel

    Orr Levy, Guy Amit, Dana Vaknin & Amir Bashan

  2. The Mina and Everard Goodman Faculty of Life Science, Bar-Ilan University, Ramat-Gan, Israel

    Tom Snir, Sol Efroni & Haim Y. Cohen

  3. Channing Division of Network Medicine, Brigham and Women’s Hospital and Harvard Medical School, Boston, MA, USA

    Peter Castaldi & Yang-Yu Liu

  4. Division of Primary Care and General Medicine, Brigham and Women’s Hospital, Boston, MA, USA

    Peter Castaldi

Authors
  1. Orr Levy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guy Amit
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dana Vaknin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Tom Snir
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Sol Efroni
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Peter Castaldi
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Yang-Yu Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Haim Y. Cohen
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Amir Bashan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.B., O.L. and G.A. conceived and designed the project. O.L. and G.A. performed real data analysis, D.V. performed the simulations. T.S. performed the bioinformatics analysis of pathways. A.B., O.L., G.A., D.V., T.S., S.E., P.C., Y.-Y.L. and H.Y.C. analysed the results. A.B., O.L. and G.A. wrote the manuscript with contributions from all authors.

Corresponding author

Correspondence to Amir Bashan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Primary Handling Editor: Pooja Jha.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Illustration of global coordination level (GCL) for high-dimensional dependency analysis.

a, An example of a simple dependency form between two variables is given by \(x_2 = x_1^2\). The possible states are represented as points over the x1-x2 plane, where a disorder (random variable from a uniform distribution) is then added into each variable independently. For low disorder levels, the points lie on or very close to the 1D manifold (blue curve). As the disorder amplitude increases, the points lie farther from the manifold. For high disorder levels, the relationship between the variables is virtually indistinguishable from random noise, and the points fill the 2D embedding space. Correspondingly, the GCL decreases as the disorder level increases. The three blue circles represent the GCL values calculated for the three examples above. Note that the absolute GCL values are dependency-form-specific and are used to compare between entities. b, Similar to a for three variables, with a dependency given by \(x_3 = x_1^2 + x_2^2\), while a disorder term is then added into each variable independently. For low disorder the points lie on a 2D manifold, while for high disorder the points are farther from the manifold and fill the 3D embedding space. c, Like a and b but for ten variables. The dependency is given by \(x_N = \mathop {\sum }\limits_{i = 1}^{N - 1} x_i^2\) with N=10. In this case, the lower-dimensional manifold cannot be represented even after applying the standard dimensional reduction technique (PCA). Thus, the three cases of different disorder levels look similar in the reduced space. However, the differences are captured by the GCL analysis.

Extended Data Fig. 2 GCL captures effect of gene-to-gene dependency and functional relations.

(a, b) Schematic demonstration of the shuffling procedure. a, Gene expression of three individual cells are represented by different colors. b, Shuffled data across different cells, preserving the statistical properties of the individual genes, whilst removing the effects of the relationships between the genes, if any exists. c, GCL values of real data (yellow histogram) compared with shuffled data (red histogram). Since the effects of interrelations between the gene are effectively lost in the shuffled data, the GCL values are centered around zero. While are significantly higher in the real data. d, Visualization of the surrogate preparing process. Each pathway is composed of several genes with different mean expression values. We sort the genes by their mean expression values and for each gene belonging to the pathway (blue) we identify a subset of genes with similar expression values (pink). A surrogate expression profile is generated by selecting a random gene from each subset. This allows us to generate many surrogate pathways with similar expression values. e, The expression levels of the ‘T cell receptor signaling pathway’ are shown versus the mean values of the corresponding surrogate gene sets (n=20). The red area represents the range of expression values of the surrogate gene sets, demonstrating their similarity to the real pathway. f, GCL values of the real pathway (blue arrow) and the surrogate pathways (red histogram). Even though the expression profiles are very similar, the GCL of the real pathway is significantly higher than the surrogate pathway (P<0.05). This suggests that higher coordination is associated with real biological function. g, h, GCL values of pathways are compared with GCL values of compatible surrogate gene-sets, yielding a Z-score, by which the pathways are sorted in the figure. White, light-grey and dark-grey backgrounds mark pathways with Z-score>2, 1<Z-score<2 and Z-score<1, respectively. j, The lists of ‘high Z-score’ pathways (Z-score>1) in young LT-HSCs are compared across the three studies (colored areas in Venn diagrams). The number of pathways labeled as ‘high Z-score’ in all three datasets (marked with an arrow in the inset) is significantly higher compared with random permutations of the labeled pathways (see Methods section) (P<10−4). k, Same as j but for old cells (P<10−4). The total number of analyzed pathways is 170.

Extended Data Fig. 3 Pathways Z-score as a function of mean gene expression.

GCL values of pathways are compared with GCL values of matching surrogate gene-sets, yielding a Z-score for each KEGG pathway. In addition, for each pathway with a set Gof n annotated genes, we calculate the mean expression of the log-transformed TPMs, that is, \(\frac{1}{n}\mathop {\sum}\nolimits_{j \in G} {\log _2\left( {{\mathrm{TPM}}_{{\mathrm{i}},{\mathrm{j}}} + 1} \right)}\). Each pathway is represented as a point. a, young cells from Ref. 33, b, young cells from Ref. 31, c, young cells from Ref. 34, d, old cells from Ref. 33, e, old cells from Ref. 31, f, old cells from Ref. 34. Pathways with z-score>2 are marked with an X symbol. g–l, like a–f but for mean expression value. In all datasets we do not observe a correlation between the Z-score and the mean expression level or pathway size. m–o, Pathway size distribution by group association of aging (see Fig. 4). A two-tailed, unpaird t-test with unequal variances showed no significant differences between any group pathway size distribution (all p-values are larger than 0.1). We conclude therefore that there is no correlation between pathway size and aging effects of GCL on the pathways.

Extended Data Fig. 4 Cell-to-cell variability and Gene-to-gene coordination are independent measures.

We show here two examples of how cell-to-cell variability and gene-to-gene coordination (GCL) can be independently changed on simulated data. On the top box we analyze data of 3 dependent variables. a, The dependency between the three variables is shown (black line) along with 1000 simulated samples on it (blue dots). b, The data is shown on the 2-simplex after normalization along with the mean sample, indicated by the red cross sign. c, A manipulation on the data which increases the variability but does not affect the GCL value. Each point is stretched away from the mean point with a fixed distance whilst keeping all the samples normalized. This causes the variability to increase (since each point is further away from the mean point), but the variables are still completely dependent which ensures the GCL does not change. d, A manipulation on the data which decreases the GCL but does not affect the variability. Each point is moved towards or away from the mean point randomly. This does not affect the total distance from the mean point (which is the variability) but does break the dependency between the variables causing the GCL to decrease. e, and f, The variability and GCL of the three cases above, color coded according to the cases. It is clear that the variability and GCL can be independently manipulated. The variability was calculated using Euclidean distance of each point from the mean on the normalized space and the GCL was calculated using bootstrap method with 200 samples per bootstrap and 100 bootstraps. Bottom box, g and h: We show a similar analysis on simulated data based on Michaelis-Menten simulations of 400 genes and 200 samples (see Methods sec., Modelling of Gene Regulatory Networks). The GCL was calculated with bootstrap method, using 50 random cuts, 50 samples per bootstrap and 100 bootstraps. Here again it is clear that the two measures are independent from each other and are indicative of completely different properties of the data. Center line, median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; points, outliers.

Extended Data Fig. 5 Systematic analysis of cell-to-cell variability (1).

The cell-to-cell variability of each of the cohorts in Fig. 2 is evaluated using the measure presented by Ref. 15. Each point represents the change of variability in aging defined as \(log_2\frac{{{\it{var}}\left( {{\it{old}}} \right)}}{{{\it{var}}\left( {young} \right)}}\), where ‘var(young)’ and ‘var(old)’ represent the variance of a single gene in young and in old cells, respectively ST-HSCs from C57BL/6 mice (a) and DBA/2 mice (b) from Ref. 33 (c) from Ref. 31. LT-HSCs from C57BL/6 mice (d) and DBA/2 mice (e), MPP-HSCs from C57BL/6 mice (f) and DBA/2 mice (g) from Ref. 33, LT-HSCs (h) and MPP-HSCs (i) from C57BL/6 mice from Ref. 31, LT-HSCs from C57BL/6 mice from Ref. 34 (j) and MPP-HSCs from C57BL/6 mice from Ref. 46 (k), mouse immune CD4+ T cells, stimulated effector memory cells (l), stimulated naïve cells (m), unstimulated naïve cells (n) and unstimulated effector memory cells (o) from Ref. 15, Drosophila melanogaster Glia cells -, ‘Astrocyte-like’ (p), ‘Ensheathing’ (q) and Drosophila neurons - neurons of the optic lobes (‘Dm8.Tm5c’) (r) and antero-dorsal olfactory projection neurons (‘OPN.adPNandPN’) (s) from Ref. 45. There is no clear tendency of increased variability upon aging.

Extended Data Fig. 6 Systematic analysis of cell-to-cell variability (2).

The cell-to-cell variability of each of the cohorts in Fig. 2 is evaluated using the measure presented by Ref. 16. ST-HSCs from C57BL/6 mice (a) and DBA/2 mice (b) from Ref. 33 (c) from Ref. 31. LT-HSCs from C57BL/6 mice (d) and DBA/2 mice (e), MPP-HSCs from C57BL/6 mice (f) and DBA/2 mice (g) from Ref. 33, LT-HSCs (h) and MPP-HSCs (i) from C57BL/6 mice from Ref. 31, LT-HSCs from C57BL/6 mice from Ref. 34 (j) and MPP-HSCs from C57BL/6 mice from Ref. 46 (k), mouse immune CD4+ T cells, stimulated effector memory cells (l), stimulated naïve cells (m), unstimulated naïve cells (n) and unstimulated effector memory cells (o) from Ref. 15, Drosophila melanogaster Glia cells -, ‘Astrocyte-like’ (p), ‘Ensheathing’ (q) and Drosophila neurons - neurons of the optic lobes (‘Dm8.Tm5c’) (r) and antero-dorsal olfactory projection neurons (‘OPN.adPNandPN’) (s) from Ref. 45. There is no clear tendency of increased variability upon aging. Center line, median; box limits, upper and lower quartiles; whiskers, 1.5x interquartile range; points, outliers. *, P<10−10 using two-tailed, unpaired, unequal variance t-test; NS, P>10−3, adjusted for multiple comparisons by the Bonferroni procedure. The number of cells in each group is reported in Extended Data Table 1).

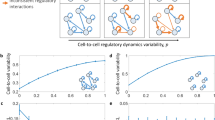
Extended Data Fig. 7 GCL decrease with damages accumulation in simulations of gene regulatory networks.

Synthetic gene-expression profiles were calculated for eight different generic mathematical models of gene regulatory networks (GRNs). For each generic model we generated cohorts of 200 cell profiles of 400 genes, where each cohort has a ‘base’ GRN dynamics. The expression profile of a cell in a cohort is set to be the steady state of an individual GRN model, which is produced by randomly changing p fraction of the base’s GRN weights (see Methods Sec.). a, Illustration of three individual models of regulatory networks with four different values of p (from left to right: 0, 0.33, 0.67, 1). Nodes represent genes and links represent regulatory interactions. In the left column (p=0) all three individual models have the same dynamics, represented by the blue links. As p increases, the weight of each interaction is randomly reassigned with probability p, in each model independently, represented by an orange link, leading to increased heterogeneity. b–i, Simulations were performed for eight different mathematical models of gene regulation: b, Only activating transcriptional regulations with Hill coefficient of 1. c, Only repression transcriptional regulations with Hill coefficient of 1. d, Both activation and repression with Hill coefficient of 1. e, Activation + repression + cooperativity of two co-activators with Hill coefficient of 1. f-i, same as b-e but with Hill coefficient of 2. For each model, the dynamics of each gene is represented by an ordinary differential rate equation. The GCL was calculated with the bootstrap method, using 20 random cuts. Data points and error bars represent mean and standard deviation over 5 realizations, respectively.

Extended Data Fig. 8 Standard deviation of GCL as a function of the number of division (M).

Analysis was done for young LTHSC from Ref. 12 with 113 cells and 2000 genes. We perform bootstrap analysis where each bootstrap realization had a random subset of 80% of the cells. The GCL STD is the standard deviations of the GCL calculated for each bootstrap (with 20 bootstrap realizations in total). The GCL STD stabilizes around 50 divisions. For analysis of the whole genome of the rest of the datasets we chose 50 divisions as well.

Supplementary information

Supplementary Information

Supplementary Notes 1–10, Figs. 1–7 and Table 1.

Reporting Summary

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Levy, O., Amit, G., Vaknin, D. et al. Age-related loss of gene-to-gene transcriptional coordination among single cells. Nat Metab 2, 1305–1315 (2020). https://doi.org/10.1038/s42255-020-00304-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s42255-020-00304-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing