Abstract
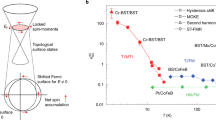
The importance of global band topology is unequivocally recognized in condensed matter physics, and new states of matter, such as topological insulators, have been discovered. Owing to their bulk band topology, 3D topological insulators possess a massless Dirac dispersion with spin–momentum locking at the surface. Although 3D topological insulators were originally proposed in time-reversal invariant systems, the onset of a spontaneous magnetization or, equivalently, a broken time-reversal symmetry leads to the formation of an exchange gap in the Dirac band dispersion. In such magnetic topological insulators, tuning of the Fermi level in the exchange gap results in the emergence of a quantum Hall effect at zero magnetic field, that is, of a quantum anomalous Hall effect. Here, we review the basic concepts of magnetic topological insulators and their experimental realization, together with the discovery and verification of their emergent properties. In particular, we discuss how the development of tailored materials through heterostructure engineering has made it possible to access the quantum anomalous Hall effect, the topological magnetoelectric effect, the physics related to the chiral edge states that appear in these materials and various spintronic phenomena. Further theoretical and experimental research on magnetic topological insulators will provide fertile ground for the development of new concepts for next-generation electronic devices for applications such as spintronics with low energy consumption, dissipationless topological electronics and topological quantum computation.
Key points
-
The chemical doping of topological insulators with transition metal elements induces a spontaneous magnetization that interacts with the topological surface state to open a mass gap at the Dirac point.
-
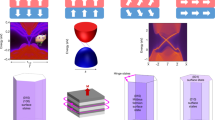
The precise tuning of the Fermi level at the mass gap enables the observation of the quantum anomalous Hall effect — a zero-magnetic-field quantum Hall effect arising in the presence of a spontaneous magnetization — which is further stabilized by heterostructure engineering.
-
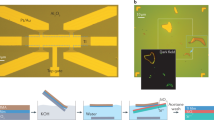
Chiral edge conduction associated with the quantum anomalous Hall effect is manipulated by magnetic domain walls, and the edge modes can be turned into chiral Majorana edge modes via proximity coupling with a superconductor.
-
Heterostructure engineering and terahertz measurements enable the observation of the quantized topological magnetoelectric effect.
-
The spin–momentum-locked conduction electrons in the surface state lead to versatile spintronic functionalities, such as an efficient generation of spin transfer torque, as a result of charge-to-spin conversion.
-
The further development of materials design and engineering will realize the quantum anomalous Hall effect at higher temperatures, the control of this state with external fields and exotic topological states of matter.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$99.00 per year
only $8.25 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout








Similar content being viewed by others
References
Stewart, G. R. Heavy-fermion systems. Rev. Mod. Phys. 56, 755–787 (1984).
Lee, P. A., Nagaosa, N. & Wen, X.-G. Doping a Mott insulator: physics of high-temperature superconductivity. Rev. Mod. Phys. 78, 17–85 (2006).
Fert, A. Nobel lecture: origin, development, and future of spintronics. Rev. Mod. Phys. 80, 1517–1530 (2008).
Tokura, Y. Critical features of colossal magnetoresistive manganites. Rep. Prog. Phys. 69, 797–851 (2006).
Dietl, T. & Ohno, H. Dilute ferromagnetic semiconductors: physics and spintronic structures. Rev. Mod. Phys. 86, 187–251 (2014).
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899–911 (2013).
Klitzing, Kv, Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494 (1980).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405 (1982).
Kohmoto, M. Topological invariant and the quantization of the Hall conductance. Ann. Phys. 160, 343 (1985).
Haldane, F. D. M. Model for a Quantum hall effect without Landau levels: condensed-matter realization of the "parity anomaly". Phys. Rev. Lett. 61, 2015 (1988).
Ohgushi, K., Murakami, S. & Nagaosa, N. Spin anisotropy and quantum Hall effect in the kagomé lattice: chiral spin state based on a ferromagnet. Phys. Rev. B 62, R6065 (2000).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539–1592 (2010).
Onoda, M. & Nagaosa, N. Quantized anomalous Hall effect in two-dimensional ferromagnets: quantum Hall effect in metals. Phys. Rev. Lett. 90, 206601 (2003).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Yu, R. et al. Quantized anomalous Hall effect in magnetic topological insulators. Science 329, 61–64 (2010).
Nomura, K. & Nagaosa, N. Surface-quantized anomalous Hall current and the magnetoelectric effect in magnetically disordered topological insulators. Phys. Rev. Lett. 106, 166802 (2011).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).
Kane, C. L. & Mele, E. J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 95, 226801 (2005).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Ando, Y. Topological insulator materials. J. Phys. Soc. Jpn. 82, 102001 (2013).
Cava, R. J., Ji, H., Fuccillo, M. K., Gibson, Q. D. & Hor, Y. S. Crystal structure and chemistry of topological insulators. J. Mater. Chem. C. 1, 3176–3189 (2013).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).
Murakami, S. Phase transition between the quantum spin Hall and insulator phases in 3D: emergence of a topological gapless phase. New J. Phys. 9, 356 (2007).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Hasan, M. Z., Xu, S. Y., Belopolski, I. & Huang, S. M. Discovery of Weyl fermion semimetals and topological Fermi arc states. Annu. Rev. Condens. Matter Phys. 8, 289–309 (2017).
Fang, Z. et al. The anomalous Hall effect and magnetic monopoles in momentum space. Science 302, 92–95 (2003).
Heremans, J. P., Cava, R. J. & Samarth, N. Tetradymites as thermoelectrics and topological insulators. Nat. Rev. Mater. 2, 17049 (2017).
Kou, X., Fan, Y., Lang, M., Upadhyaya, P. & Wang, K. L. Magnetic topological insulators and quantum anomalous hall effect. Sol. St. Commun. 215, 34–53 (2015).
Chang, C.-Z. & Li, M. Quantum anomalous Hall effect in time-reversal-symmetry breaking topological insulators. J. Phys. Condens. Matter 28, 123002 (2016).
Ke, H., Wang, Y. & Xue, Q.-K. Topological materials: quantum anomalous Hall system. Annu. Rev. Cond. Mat. Phys. 9, 329–344 (2018).
Biswas, R. R. & Balatsky, A. V. Impurity-induced states on the surface of three-dimensional topological insulators. Phys. Rev. B 81, 233405 (2010).
Rosenberg, G. & Franz, M. Surface magnetic ordering in topological insulators with bulk magnetic dopants. Phys. Rev. B 85, 195119 (2012).
Henk, J. et al. Complex spin texture in the pure and Mn-doped topological insulator Bi2Te3. Phys. Rev. Lett. 108, 206801 (2012).
Zhang, J.-M., Zhu, W., Zhang, Y., Xiao, D. & Yao, Y. Tailoring magnetic doping in the topological insulator Bi2Se3. Phys. Rev. Lett. 109, 266405 (2012).
Kacman, P. Spin interactions in diluted magnetic semiconductors and magnetic semiconductors. Semicond. Sci. Technol. 16, R25–R39 (2001).
Dietl, T., Ohno, H. & Matsukura, F. Hole-mediated ferromagnetism in tetrahedrally coordinated semiconductors. Phys. Rev. B 63, 195205 (2001).
Dietl, T. & Ohno, H. Ferromagnetic III-V and II-VI semiconductors. MRS Bull. 28, 714–719 (2003).
Liu, Q., Liu, C.-X., Xu, C., Qi, X.-L. & Zhang, S.-C. Magnetic impurities on the surface of a topological insulator. Phys. Rev. Lett. 102, 156603 (2009).
Abanin, D. A. & Pesin, D. A. Ordering of magnetic impurities and tunable electronic properties of topological insulators. Phys. Rev. Lett. 106, 136802 (2011).
Zhu, J.-J., Yao, D.-X., Zhang, S.-C. & Chang, K. Electrically controllable surface magnetism on the surface of topological insulators. Phys. Rev. Lett. 106, 097201 (2011).
Hor, Y. S. et al. Development of ferromagnetism in the doped topological insulator Bi2-xMnxTe3. Phys. Rev. B 81, 195203 (2010).
Checkelsky, J. G. et al. Dirac-fermion-mediated ferromagnetism in a topological insulator. Nat. Phys. 8, 729–733 (2012).
Sessi, P. et al. Signature of Dirac fermion-mediated magnetic order. Nat. Commun. 5, 5349 (2014).
Chang, C.-Z. et al. Thin films of magnetically doped topological insulator with carrier-independent long-range ferromagnetic order. Adv. Mater. 25, 1065–1070 (2013).
Li, M. et al. Experimental verification of the Van Vleck nature of long-range ferromagnetic order in the vanadium-doped three-dimensional topological insulator Sb2Te3. Phys. Rev. Lett. 114, 146802 (2015).
Kou, X. et al. Interplay between different magnetisms in Cr-doped topological insulators. ACSNano 7, 9205–9212 (2013).
Lee, I. et al. Imaging Dirac-mass disorder from magnetic dopant atoms in the ferromagnetic topological insulator Crx(Bi0.1Sb0.9)2-xTe3. Proc. Natl Acad. Sci. USA 112, 1316–1321 (2015).
Chen, Y. L. et al. Massive Dirac fermion on the surface of a magnetically doped topological insulator. Science 329, 659–662 (2010).
Wray, L. A. et al. A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nat. Phys. 7, 32–37 (2011).
Xu, S.-Y. et al. Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator. Nat. Phys. 8, 616–622 (2012).
Sessi, P. et al. Dual nature of magnetic dopants and competing trends in topological insulators. Nat. Commun. 7, 12027 (2016).
Krieger, J. A. et al. Spectroscopic perspective on the interplay between electronic and magnetic properties of magnetically doped topological insulators. Phys. Rev. B 96, 184402 (2017).
Chang, C.-Z. et al. High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator. Nat. Mater. 14, 473–477 (2015).
Wang, J., Lian, B., Zhang, H. & Zhang, S. C. Anomalous edge transport in the quantum anomalous Hall state. Phys. Rev. Lett. 111, 086803 (2013).
Kou, X. et al. Scale-invariant quantum anomalous Hall effect in magnetic topological insulators beyond the two-dimensional limit. Phys. Rev. Lett. 113, 137201 (2014).
Bestwick, A. J. et al. Precise quantization of the anomalous Hall effect near zero magnetic field. Phys. Rev. Lett. 114, 187201 (2015).
Chang, C.-Z. et al. Zero-field dissipationless chiral edge transport and the nature of dissipation in the quantum anomalous Hall state. Phys. Rev. Lett. 115, 057206 (2015).
Mogi, M. et al. Magnetic modulation doping in topological insulators toward higher-temperature quantum anomalous Hall effect. Appl. Phys. Lett. 107, 182401 (2015).
Ou, Y. et al. Enhancing the quantum anomalous Hall effect by magnetic codoping in a topological insulator. Adv. Mater. 30, 1703062 (2018).
Checkelsky, J. G. et al. Trajectory of the anomalous Hall effect towards the quantized state in a ferromagnetic topological insulator. Nat. Phys. 10, 731–736 (2014).
Kou, X. et al. Metal-to-insulator switching in quantum anomalous Hall states. Nat. Commun. 6, 8474 (2015).
Chang, C.-Z. et al. Observation of the quantum anomalous Hall insulator to Anderson insulator quantum phase transition and its scaling behavior. Phys. Rev. Lett. 117, 126802 (2016).
Kawamura, M. et al. Current-driven instability of the quantum anomalous Hall effect in ferromagnetic topological insulators. Phys. Rev. Lett. 119, 016803 (2017).
Fox, E. J. et al. Part-per-million quantization and current-induced breakdown of the quantum anomalous Hall effect. Phys. Rev. B 98, 075145 (2018).
Kawamura, M. et al. Topological quantum phase transition in magnetic topological insulator upon magnetization rotation. Phys. Rev. B 98, 140404 (2018).
Liu, C.-X., Qi, X.-L., Dai, X., Fang, Z. & Zhang, S.-C. Quantum anomalous Hall effect in Hg1−yMnyTe quantum wells. Phys. Rev. Lett. 101, 146802 (2008).
Jeckelmann, B. & Jeanneret, B. The quantum Hall effect as an electrical resistance standard. Rep. Prog. Phys. 64, 1603–1655 (2001).
Scherer, H. & Camarota, B. Quantum metrology triangle experiments: a status review. Meas. Sci. Technol. 23, 124010 (2012).
Gotz, M. et al. Precision measurement of the quantized anomalous Hall resistance at zero magnetic field. Appl. Phys. Lett. 112, 072102 (2018).
Kaneko, N. Review of quantum electrical standards and benefits and effects of the implementation of the ‘Revised SI’. IEEJ Trans. 12, 627–637 (2017).
Ribeiro-Palau, R. et al. Quantum Hall resistance standard in graphene devices under relaxed experimental conditions. Nat. Nanotechnol. 10, 965–972 (2015).
Upadhyaya, P. & Tserkovnyak, Y. Domain wall in a quantum anomalous Hall insulator as a magnetoelectric piston. Phys. Rev. B 94, 020411 (2016).
Liu, M. et al. Large discrete jumps observed in the transition between Chern states in a ferromagnetic topological insulator. Sci. Adv. 2, e1600167 (2016).
Yasuda, K. et al. Quantized chiral edge conduction on domain walls of a magnetic topological insulator. Science 358, 1311–1314 (2017).
Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 38, 9375–9389 (1988).
Rosen, I. T. et al. Chiral transport along magnetic domain walls in the quantum anomalous Hall effect. NPJ Quantum Mater. 2, 69 (2017).
Fu, L. & Kane, C. L. Superconducting proximity effect and majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Chiral topological superconductor from the quantum Hall state. Phys. Rev. B 82, 184516 (2010).
Wang, J., Zhou, Q., Lian, B. & Zhang, S.-C. Chiral topological superconductor and half-integer conductance plateau from quantum anomalous Hall plateau transition. Phys. Rev. B 92, 064520 (2015).
Majorana, E. Teoria simmetrica dell’elettrone e del positrone. Nuovo Cim. 14, 171–184 (1937).
Kitaev, A. Y. Anyons in an exactly solved model and beyond. Ann. Phys. 321, 2–111 (2006).
Wilczek, F. Majorana returns. Nat. Phys. 5, 614–618 (2009).
Alicea, J. New directions in the pursuit of Majorana fermions in solid state systems. Rep. Prog. Phys. 75, 076501 (2012).
He, Q. L. et al. Chiral Majorana fermion modes in a quantum anomalous Hall insulator–superconductor structure. Science 357, 294–299 (2017).
Wang, J., Lian, B. & Zhang, S.-C. Universal scaling of the quantum anomalous Hall plateau transition. Phys. Rev. B 89, 085106 (2014).
Feng, Y. et al. Observation of the zero Hall plateau in a quantum anomalous Hall insulator. Phys. Rev. Lett. 115, 126801 (2015).
Huang, Y., Setiawan, F. & Sau, J. D. Disorder-induced half-integer quantized conductance plateau in quantum anomalous Hall insulator-superconductor structures. Phys. Rev. B 97, 100501(R) (2018).
Ji, W. & Wen, X.-G. 1/2(e 2/h) conductance plateau without 1D chiral Majorana fermions. Phys. Rev. Lett. 120, 107002 (2018).
Lian, B., Wang, J., Sun, X.-Q., Vaezi, A. & Zhang, S.-C. Quantum phase transition of chiral Majorana fermions in the presence of disorder. Phys. Rev. B 97, 125408 (2018).
Lian, B., Sun, X.-Q., Vaezi, A., Qi, X.-L. & Zhang, S.-C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl Acad. Sci. USA 115, 10938–10942 (2018).
Qi, X. L., Hughes, T. L. & Zhang, S. C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Peccei, R. D. & Quinn, H. R. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 38, 1440 (1977).
Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Tokura, Y., Seki, S. & Nagaosa, N. Mulrtiferroics of spin origin. Rep. Prog. Phys. 77, 076501 (2014).
Freeman, A. J. & Schmid, H. Magnetoelectric interaction phenomena in crystals (Gordon and Breach Science Publishers London, 1975).
Kurumaji, T. et al. Optical magnetoelectric resonance in a polar magnet (Fe,Zn)2Mo3O8 with axion-type coupling. Phys. Rev. Lett. 119, 077206 (2017).
Tse, W.-K. & MacDonald, A. H. Giant magneto-optical Kerr effect and universal Faraday effect in thin-film topological insulators. Phys. Rev. Lett. 105, 057401 (2010).
Maciejko, J., Qi, X.-L., Drew, H. D. & Zhang, S.-C. Topological quantization in units of the fine structure constant. Phys. Rev. Lett. 105, 166803 (2010).
Okada, K. N. et al. Terahertz spectroscopy on Faraday and Kerr rotations in a quantum anomalous Hall state. Nat. Commun. 7, 12245 (2016).
Liang., W. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3D topological insulator. Science 354, 1124–1127 (2016).
Dziom, V. et al. Observation of the universal magnetoelectric effect in a 3D topological insulator. Nat. Commun. 8, 15197 (2017).
Armitage, N. P. & Wu, L. On the matter of topological insulators as magnetoelectrics. Preprint at https://arxiv.org/abs/1810.01233 (2018).
Morimoto, T., Furusaki, A. & Nagaosa, N. Topological magnetoelectric effects in thin films of topological insulators. Phys. Rev. B 92, 085113 (2015).
Wang, J., Lian, B., Qi, X.-L. & Zhang, S.-C. Quantized topological magnetoelectric effect of the zero-plateau quantum anomalous Hall state. Phys. Rev. B 92, 081107(R) (2015).
Mogi, M. et al. A magnetic heterostructure of topological insulators as a candidate for an axion insulator. Nat. Mater. 16, 516–521 (2017).
Mogi, M. et al. Tailoring tricolor structure of magnetic topological insulator for robust axion insulator. Sci. Adv. 3, eaao1669 (2017).
Xiao, D. et al. Realization of the axion insulator state in quantum anomalous Hall sandwich heterostructures. Phys. Rev. Lett. 120, 056801 (2018).
Edelstein, V. M. Spin polarization of conduction electrons induced by electric current in two-dimensional asymmetric electron systems. Solid State Commun. 73, 233 (1990).
Kondou, K. et al. Fermi-level-dependent charge-to-spin current conversion by Dirac surface states of topological insulators. Nat. Phys. 12, 1027–1031 (2016).
Mellnik, A. R. et al. Spin–transfer torque generated by a topological insulator. Nature 511, 449–451 (2014).
Wang, Y. et al. Topological surface states originated spin–orbit torques in Bi2Se3. Phys. Rev. Lett. 114, 257202 (2015).
Shiomi, Y. et al. Spin-electricity conversion induced by spin injection into topological insulators. Phys. Rev. Lett. 113, 196601 (2014).
Deorani, P. et al. Observation of inverse spin Hall effect in bismuth selenide. Phys. Rev. B 90, 094403 (2014).
Jamali, M. et al. Giant spin pumping and inverse spin Hall effect in the presence of surface and bulk spin–orbit coupling of topological insulator Bi2Se3. Nano Lett. 15, 7126–7132 (2015).
Mendes, J. B. S. et al. Dirac-surface-state-dominated spin to charge current conversion in the topological insulator (Bi0.22Sb0.78)2Te3 films at room temperature. Phys. Rev. B 96, 180415 (2017).
Wang, H. et al. Surface-state-dominated spin–charge current conversion in topological-insulator/ferromagnetic-insulator heterostructures. Phys. Rev. Lett. 117, 076601 (2016).
Liu, L. et al. Spin-polarized tunneling study of spin-momentum locking in topological insulators. Phys. Rev. B 91, 235437 (2015).
Fan, Y. et al. Magnetization switching through giant spin–orbit torque in a magnetically doped topological insulator heterostructure. Nat. Mater. 13, 699–704 (2014).
Yasuda, K. et al. Geometric Hall effects in topological insulator heterostructures. Nat. Phys. 12, 555–559 (2016).
Han, W., Otani, Y. & Maekawa, S. Quantum materials for spin and charge conversion. NPJ Quantum Mater. 3, 27 (2018).
Yabin, F. et al. Electric-field control of spin–orbit torque in a magnetically doped topological insulator. Nat. Nanotechol. 11, 352–359 (2016).
Jiang., Z. et al. Enhanced spin Seebeck effect signal due to spin-momentum locked topological surface states. Nat. Commun. 7, 11458 (2016).
Olejník, K., Novák, V., Wunderlich, J. & Jungwirth, T. Electrical detection of magnetization reversal without auxiliary magnets. Phys. Rev. B 91, 180402 (2015).
Avci, C. O. et al. Unidirectional spin Hall magnetoresistance in ferromagnet/normal metal bilayers. Nat. Phys. 11, 570–575 (2015).
Avci, C. O. et al. Magnetoresistance of heavy and light metal/ferromagnet bilayers. Appl. Phys. Lett. 107, 192405 (2015).
Yasuda, K. et al. Large unidirectional magnetoresistance in a magnetic topological insulator. Phys. Rev. Lett. 117, 127202 (2016).
Tokura, Y. & Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. Nat. Commun. 9, 3740 (2018).
Baibich, M. N. et al. Giant magnetoresistance of (001) Fe/(001) Cr magnetic superlattices. Phys. Rev. Lett. 61, 2472 (1988).
Binasch, G., Grünberg, P., Saurenbach, F. & ZinnEnhanced, W. magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 39, 4828 (1989).
Yoshimi, R. et al. Quantum Hall states stabilized in semi-magnetic bilayers of topological insulators. Nat. Commun. 6, 8530 (2015).
Ogawa, N. et al. Zero-bias photocurrent in ferromagnetic topological insulator. Nat. Commun. 7, 12246 (2016).
Grinberg, I. et al. Perovskite oxides for visible-light-absorbing ferroelectric and photovoltaic materials. Nature 503, 509–512 (2013).
Ogawa, N., Sotome, M., Kaneko, Y., Ogino, M. & Tokura, Y. Shift current in the ferroelectric semiconductor SbSI. Phys. Rev. B 96, 241203 (2017).
McIver, J. W., Hsieh, D., Steinberg, H., Jarillo-Herrero, P. & Gedik, N. Control over topological insulator photocurrents with light polarization. Nat. Nanotech. 7, 96–100 (2012).
Okada, K. N. et al. Enhanced photogalvanic current in topological insulators via Fermi energy tuning. Phys. Rev. B 93, 081403 (2016).
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Liu, C. et al. Dimensional crossover-induced topological Hall effect in a magnetic topological insulator. Phys. Rev. Lett. 119, 176809 (2017).
He, Q. L. et al. Exchange-biasing topological charges by antiferromagnetism. Nat. Commun. 9, 2767 (2018).
Miron, I. M. et al. Perpendicular switching of a single ferromagnetic layer induced by in-plane current injection. Nature 476, 189–193 (2011).
Liu, L., Lee, O. J., Gudmundsen, T. J., Ralph, D. C. & Buhrman, R. A. Current-induced switching of perpendicularly magnetized magnetic layers using spin torque from the spin Hall effect. Phys. Rev. Lett. 109, 096602 (2012).
Liu, L. et al. Spin-torque switching with the giant spin Hall effect of tantalum. Science 336, 555–558 (2012).
Pai, C. F. et al. Spin transfer torque devices utilizing the giant spin Hall effect of tungsten. Appl. Phys. Lett. 101, 122404 (2012).
Slonczewski, J. C. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mat. 159, L1–L7 (1996).
Ralph, D. C. & Stiles, M. D. Spin transfer torques. J. Magn. Magn. Mat. 230, 1190–1216 (2008).
Yasuda, K. et al. Current-nonlinear Hall effect and spin-orbit torque magnetization switching in a magnetic topological insulator. Phys. Rev. Lett. 119, 137204 (2017).
Gupta, S., Kanai, S., Matsukura, F. & Ohno, H. Magnetic and transport properties of Sb2Te3 doped with high concentration of Cr. Appl. Phys. Express 10, 103001 (2017).
Lv, Y. et al. Unidirectional spin-Hall and Rashba−Edelstein magnetoresistance in topological insulator-ferromagnet layer heterostructures. Nat. Commun. 9, 111 (2018).
Han, J. et al. Room-temperature spin–orbit torque switching induced by a topological insulator. Phys. Rev. Lett. 119, 077702 (2017).
Wang, Y. et al. Room temperature magnetization switching in topological insulator–ferromagnet heterostructures by spin–orbit torques. Nat. Commun. 8, 1364 (2017).
Khang, N. H. D., Ueda, Y. & Hai, P. N. A conductive topological insulator with colossal spin Hall effect for ultra-low power spin-orbit-torque switching. Nat. Mater. 17, 808–813 (2018).
DC, M. et al. Room-temperature perpendicular magnetization switching through giant spin-orbit torque from sputtered BixSe(1-x) topological insulator material. Nat. Mater. 17, 800–807 (2018).
Wei, P. et al. Exchange-coupling-induced symmetry breaking in topological insulators. Phys. Rev. Lett. 110, 186807 (2013).
Lee, C., Katmis, F., Jarillo-Herrero, P., Moodera, J. S. & Gedik, N. Direct measurement of proximity-induced magnetism at the interface between a topological insulator and a ferromagnet. Nat. Commun. 7, 12014 (2016).
Katmis, F. et al. A high-temperature ferromagnetic topological insulating phase by proximity coupling. Nature 533, 513–516 (2016).
Alegria, L. D. et al. Large anomalous Hall effect in ferromagnetic insulator-topological insulator heterostructures. Appl. Phys. Lett. 105, 053512 (2014).
Lang, M. et al. Proximity induced high-temperature magnetic order in topological insulator-ferrimagnetic insulator heterostructure. Nano Lett. 14, 3459–3465 (2014).
Jiang, Z. et al. Independent tuning of electronic properties and induced ferromagnetism in topological insulators with heterostructure approach. Nano Lett. 15, 5835–5840 (2015).
Tang, C. et al. Above 400-K robust perpendicular ferromagnetic phase in a topological insulator. Sci. Adv. 3, e1700307 (2017).
Otrokov, M. M. et al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects. 2D Mater. 4, 025082 (2017).
Zhang, D., Shi, M., Xing, D., Zhang, H. & Wang, J. Topological axion states in magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Preprint at https://arxiv.org/abs/1808.08014 (2018).
Li, J. et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials. Preprint at https://arxiv.org/abs/1808.08608 (2018).
Otrokov, M. M. et al. Prediction and observation of the first antiferromagnetic topological insulator. Preprint at https://arxiv.org/abs/1809.07389 (2018).
Gong, Y. et al. Experimental realization of an intrinsic magnetic topological insulator. Preprint at https://arxiv.org/abs/1809.07926 (2018).
Yeats, A. L. et al. Local optical control of ferromagnetism and chemical potential in a topological insulator. Proc. Natl Acad. Sci. USA 114, 10379–10383 (2017).
Mahoney, A. C. et al. Zero-field edge plasmons in a magnetic topological insulator. Nat. Commun. 8, 1836 (2017).
Fu, L. & Kane, C. L. Probing neutral Majorana fermion edge modes with charge transport. Phys. Rev. Lett. 102, 216403 (2009).
Akhmerov, A. R., Nilsson, J. & Beenakker, C. W. J. Electrically detected interferometry of Majorana fermions in a topological insulator. Phys. Rev. Lett. 102, 216404 (2009).
Schuffelgen, P. et al. Stencil lithography of superconducting contacts on MBE-grown topological insulator thin films. J. Cryst. Growth 477, 183–187 (2017).
He, Q. L. et al. Two-dimensional superconductivity at the interface of a Bi2Te3/FeTe heterostructure. Nat. Commun. 5, 4247 (2014).
Burkov, A. A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).
Balents, L. Viewpoint: Weyl electrons kiss. Physics 4, 36 (2011).
Armitage, N. P., Mele, E. J. & Vishwanath, A. Weyl and Dirac semimetals in three-dimensional solids. Rev. Mod. Phys. 90, 015001 (2018).
Jiang, G. et al. Quantum anomalous Hall multilayers grown by molecular beam epitaxy. Chin. Phys. Lett. 35, 076802 (2018).
Fang, C., Gilbert, M. J. & Bernevig, B. A. Large-Chern-number quantum anomalous Hall effect in thin-film topological crystalline insulators. Phys. Rev. Lett. 112, 046801 (2014).
Assaf, B. A. et al. Inducing magnetism onto the surface of a topological crystalline insulator. Phys. Rev. B 91, 195310 (2015).
Wang, F. et al. Chromium-induced ferromagnetism with perpendicular anisotropy in topological crystalline insulator SnTe (111) thin films. Phys. Rev. B 97, 115414 (2018).
Tang, E., Mei, J. W. & Wen, X. G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).
Sun, K., Gu, Z., Katsura, H. & Sarma, S. D. Nearly flatbands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).
Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).
Klinovaja, J., Tserkovnyak, Y. & Loss, D. Integer and fractional quantum anomalous Hall effect in a strip of stripes model. Phys. Rev. B 91, 085426 (2015).
Maciejko, J. & Fiete, G. A. Fractionalized topological insulators. Nat. Phys. 11, 385–388 (2015).
Acknowledgements
The authors thank R. Yoshimi, M. Mogi, M. Kawamura, N. Nagaosa, M. Kawasaki and T. Dietl for enlightening discussions on magnetic topological insulators. This research was supported in part by the Japan Society for the Promotion of Science (JSPS; no. 16J03476), the Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan (no. JP15H05853), and Core Research for Evolutional Science and Technology (CREST), Japanese Science and Technology (JST; no. JPMJCR16F1).
Author information
Authors and Affiliations
Contributions
All authors have read, discussed and contributed to the writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests statement
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Tokura, Y., Yasuda, K. & Tsukazaki, A. Magnetic topological insulators. Nat Rev Phys 1, 126–143 (2019). https://doi.org/10.1038/s42254-018-0011-5
Published:
Issue Date:
DOI: https://doi.org/10.1038/s42254-018-0011-5
This article is cited by
-
Atomic-scale magnetic doping of monolayer stanene by revealing Kondo effect from self-assembled Fe spin entities
npj Quantum Materials (2024)
-
Supercurrent mediated by helical edge modes in bilayer graphene
Nature Communications (2024)
-
Bipolarity of large anomalous Nernst effect in Weyl magnet-based alloy films
Nature Physics (2024)
-
Electrical switching of the edge current chirality in quantum anomalous Hall insulators
Nature Materials (2024)
-
Elastic, electronic, and optical properties of monolayer MnBi2Se4
Iranian Journal of Science (2024)