Electron-nuclear decoupling at a spin clock transition

Abstract

The ability to design quantum systems that decouple from environmental noise sources is highly desirable for development of quantum technologies with optimal coherence. The chemical tunability of electronic states in magnetic molecules combined with advanced electron spin resonance techniques provides excellent opportunities to address this problem. Indeed, so-called clock transitions have been shown to protect molecular spin qubits from magnetic noise, giving rise to significantly enhanced coherence. Here we conduct a spectroscopic and computational investigation of this physics, focusing on the role of the nuclear bath. Away from the clock transition, linear coupling to the nuclear degrees of freedom causes a modulation and decay of electronic coherence, as quantified via electron spin echo signals generated experimentally and in silico. Meanwhile, the effective hyperfine interaction vanishes at the clock transition, resulting in electron-nuclear decoupling and an absence of quantum information leakage to the nuclear bath, providing opportunities to characterize other decoherence sources.

Introduction

The synthetic tunability of molecular nanomagnets provides a versatile platform for exploring and potentially harnessing their unique physical attributes for the development of next-generation quantum technologies^1,2,3,4. In particular, the electronic spin associated with a magnetic molecule may serve as the computational basis for a quantum bit, or qubit. However, as with any such system, protection from environmental noise that causes decoherence is of critical importance, representing one of the main hurdles on the path toward practical applications. In an attempt to suppress one of the more stubborn sources of decoherence arising from electron-nuclear interactions, various synthetic strategies have been employed such as nuclear spin patterning^5,6 and the use of nuclear spin-free ligands^7,8. However, demonstration of long phase memory (coherence) times typically still requires extreme dilution in order to minimize electron spin–spin dephasing.

Rather than modifying the spin bath, an alternative approach involves exploiting so-called clock transitions⁹ at which the electron spin resonance (ESR) frequency is insensitive to the local magnetic induction and, therefore, does not couple to the fluctuating magnetic environment. Spin clock transitions occur at avoided level crossings associated with the Zeeman splitting of qubit basis states. This approach is well established in solid-state materials such as donor atoms in silicon^10,11 or defect states in various other host crystals^{12,13,14,15,16}. Our interest is in molecular systems, for which enhanced coherence was demonstrated at a clock transition for a [Ho(W₅O₁₈)₂]⁹⁻ molecule by Shiddiq et al.¹⁷. Subsequently, clock transitions have been studied in other molecular systems^{18,19,20,21,22} and the effects of structural distortions have been analyzed theoretically for several Ho^III and V^IV complexes²³.

Here we directly investigate electron-nuclear coupling in the vicinity of a clock transition by means of pulsed electron spin-echo measurements and numerical modelling. Away from the clock transition, dipolar hyperfine coupling to the nuclear bath results in periodic modulations of the electronic coherence—the so-called electron spin-echo envelope modulation (ESEEM) effect²⁴. This modulation vanishes at the clock transition. Theoretically, we consider a minimal model that can host a clock transition: an S = 1 spin subject to a relatively strong axial magnetic anisotropy, with an avoided Zeeman level crossing generated by a weaker transverse interaction (Fig. 1). We treat coupling to the nuclear bath explicitly to reproduce the ESEEM effect via quantum dynamics simulations. The parameters in our simplified S = 1 model are chosen to mimic the low energy physics of the [Ho(W₅O₁₈)₂]⁹⁻ molecule which, to the best of our knowledge, is the only system for which ESEEM has been characterized as a function of the applied magnetic field, B₀, in the vicinity of a clock transition. The simulations compare favorably with experiment, clearly demonstrating electron-nuclear decoupling at a spin clock transition. Although the experiments focus on [Ho(W₅O₁₈)₂]⁹⁻, our model applies quite generally for the coupling of an electronic spin to a finite nuclear bath. The combined study provides a microscopic view of the mechanism via which an electron spin qubit couples to nearby nuclei, in essence mediating leakage of quantum information to the nuclear bath.

Fig. 1: Simulated HoW₁₀ Zeeman diagram and ESR frequency.

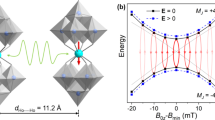
a Zeeman levels (solid blue lines) according to the Hamiltonian of Eq. (1), with the parameters given in the main text. An avoided crossing (a clock transition) between the two lowest-lying states (labeled m_S = ±1) is seen at ${B}_{0z}={B}_{\min }=23.6\,{\rm {mT}}$; the dashed lines denote the m_S = ±1 levels in the absence of an avoided crossing [i.e., E set to zero in Eq. (1)]. b ESR frequency, f (solid blue curve), corresponding to the transition between the m_S = ±1 states in (a), and the associated effective gyromagnetic ratio, ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}={\rm {d}}f/{\rm {d}}{B}_{0}$ (dashed red curve); the clock transition (CT) is indicated. Note that the ESR frequency couples linearly to B₀ far from the clock transition and quadratically at the clock transition, such that ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$ crosses through zero.

Results

Electron spin resonance measurements

Pulsed ESR, which is central to most spin-based quantum device implementations²⁵, is an extremely powerful technique enabling both sample characterization and quantum control. The simplest illustration involves the two-pulse Hahn echo sequence^24,26, where a coherent superposition of spin “up" and “down" states is first generated via a π/2 rotation on the Bloch sphere, and then the magnetization is allowed to evolve freely in the xy-plane; this evolution is later inverted via application of a π-pulse, ideally refocusing any dephasing that occurs due to static disorder, resulting in the emission of an electron spin-echo at time 2τ after the initial π/2 pulse (τ is the delay between pulses). A dynamic environment causes decoherence²⁷, which manifests as a decay of the electron spin-echo intensity upon increasing τ. Meanwhile, coherent interactions with nearby quantum systems, e.g., other electrons or atomic nuclei, can give rise to a modulation of the electron spin-echo intensity²⁴. In particular, ESEEM arises due to the excitation of formally forbidden nuclear transitions during the pulsed electron spin-echo sequence, through hyperfine coupling to the central electron spin. Here, “central” refers to spins that have been prepared in a prescribed coherent quantum state, e.g., via the application of a π/2 pulse. ESEEM may therefore be used to characterize this aspect of the environment, providing extremely sensitive fingerprints of electron-nuclear decoherence mechanisms.

In order to gain microscopic insights into electron-nuclear coupling in the vicinity of a clock transition, ESEEM measurements were performed on a Na₉[Ho_0.001Y_0.999(W₅O₁₈)₂]⋅nH₂O (hereon abbreviated HoW₁₀) single crystal, i.e., 0.1% HoW₁₀ doped into an isostructural non-magnetic YW₁₀ host crystal. Ho^III possesses a ground state spin–orbit coupled angular momentum, J = L + S = 8. The pseudo-axial coordination geometry imposed on the Ho^III ion results in a crystal field interaction that lifts the degeneracy of the 2J + 1 projection (m_J) states, giving rise to a singlet and a series of m_J ≈ ±i (i = 1–8) quasi-doublets, with the m_J = ±4 ground doublet lying ≈ 40 cm⁻¹ below the first excited crystal field states^28,29. A weak tetragonal crystal field interaction is effective in generating an avoided Zeeman level crossing between the m_J = ±4 basis states, thus giving rise to a 9.18 GHz clock transition^17,30. The hyperfine interaction involving the $I=\frac{7}{2}$ ¹⁶⁵Ho nuclear spin further splits the m_J = ±4 states into (2I + 1) = 8 pairs of m_I sub-levels, resulting in eight avoided-crossings, i.e., eight clock transitions, four on either side of zero applied field¹⁷. We focus here on the lowest field clock transition (at B_0z = 23.6 mT), which also gives the strongest ESEEM; note that, due to a small sample misalignment, this occurs at ${B}_{0}={B}_{\min }=25.5\,{\rm {mT}}$ in the present investigation (see the “Methods” section).

Electron spin-echo time traces recorded at a frequency of 9.18 GHz are shown in Fig. 2a for different detuning fields (${{\Delta }}B={B}_{0}-{B}_{\min }$) from the clock transition, revealing strong temporal modulations (ESEEM) at most detunings. The first thing to note is the variation in decay time (≡phase memory time, T_m) and modulation depth as a function of the detuning. In particular, a complete absence of ESEEM and the maximum T_m is observed at zero detuning, i.e., at the clock transition. Fast Fourier transforms (FFTs) of the time traces reveal three prominent peaks, highlighted by the red squares, green circles, and blue triangles in Fig. 2b. The associated ESEEM frequencies are plotted as a function B₀ in Fig. 2c; superimposed on the data are the 1st and 2nd harmonics of the bare proton Larmor frequency, ν_H = γ_HB₀, where γ_H = 42.577 MHz/T is the proton gyromagnetic ratio. The fact that the first two peaks (red squares and green circles) straddle the ν_H line and the third peak (blue triangles) lies on the 2ν_H line is a strong indication that the ESEEM is caused by dipolar coupling to protons. This is not surprising given the significant amount of water in the lattice of [HoW₁₀]⋅nH₂O (n ≈ 35 in fully solvated crystals). Indeed, a strong proton ESEEM effect is expected in this field range where the Ho–H dipolar coupling strength is comparable to the proton Larmor frequency (see below). By contrast, all other nuclei are predominantly non-magnetic, either due to low γ-values or a low abundance of magnetic isotopes.

Fig. 2: Experimental HoW₁₀ ESEEM spectra.

a Electron spin-echo decay curves recorded at 9.18 GHz and 5 K as a function of detuning, ${B}_{0}-{B}_{\min }$ (see labeling); the white dash curve is fit to a mono-exponential decay for zero detuning (${B}_{0}={B}_{\min }$), from which the optimum T_m = 8.43(6) μs is deduced. b FFTs of the decay curves in (a), presented in the same order; prominent peaks in the ESEEM spectra are marked with red squares, green circles, and blue triangles. c Plot of the FFT peak frequencies in (b) versus B₀, with error bars denoting ± s.d. (approximating each peak as a Gaussian); the dashed lines correspond to harmonics of the proton Larmor frequency (see legend), the data points are color/shape coded according to the same scheme as those in (b), and the vertical dashed red line marks the clock transition (CT).

A qualitative understanding of the ESEEM spectrum is obtained by first considering the simplest possible case of coupled $S=\frac{1}{2}$ and $I=\frac{1}{2}$ spins in the high-field limit in which ν_H > A, where A (=A_zz/h, A_zz is the z-component of the hyperfine tensor) quantifies the bare dipolar coupling strength in frequency units. ESEEM arises due to the excitation of formally forbidden zero- and double-quantum transitions that rotate coupled electron and nuclear spins³¹. The modulation results from combinations of the allowed (${\nu }_{{{{{{{{\rm{a}}}}}}}}}={\gamma }_{{{{{{{{\rm{e}}}}}}}}}{B}_{0}\pm \frac{1}{2}A$, γ_e is the electron gyromagnetic ratio) and formally forbidden (ν_f = γ_eB₀ ± ν_H) transition frequencies at $| {\nu }_{{{{{{{{\rm{a}}}}}}}}}^{\pm }-{\nu }_{{{{{{{{\rm{a}}}}}}}}}^{\mp }| =A$, $| {\nu }_{{{{{{{{\rm{f}}}}}}}}}^{+}-{\nu }_{{{{{{{{\rm{a}}}}}}}}}^{\pm }| =| {\nu }_{{{{{{{{\rm{f}}}}}}}}}^{-}-{\nu }_{{{{{{{{\rm{a}}}}}}}}}^{\pm }| ={\nu }_{{{{{{{{\rm{H}}}}}}}}}\pm \frac{1}{2}A$, and $| {\nu }_{{{{{{{{\rm{f}}}}}}}}}^{\pm }-{\nu }_{{{{{{{{\rm{f}}}}}}}}}^{\mp }| =2{\nu }_{{{{{{{{\rm{H}}}}}}}}}$³¹. One may then understand the lowest two frequencies in Fig. 2c (red squares and green circles) as being due to the hyperfine coupled proton frequencies, ${\nu }_{{{{{{{{\rm{H}}}}}}}}}\pm \frac{1}{2}{A}^{{{{{{{{\rm{eff}}}}}}}}}$, where A^eff is an effective coupling strength on account of the physics that emerges at the clock transition (A^eff is further renormalized for HoW₁₀ due to the fact that $S \,\ne\, \frac{1}{2}$). Right at the clock transition, A^eff → 0, which may be understood as being a consequence of the effective electron gyromagnetic ratio, ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$, crossing through zero at ${B}_{0}={B}_{\min }$ (${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}\propto {\rm {df}}/{\rm {d}}{B}_{0}$ or $\langle {\hat{S}}_{z}\rangle$, the z-component spin expectation value); this is illustrated in Fig. 1b, where the ESR (clock) frequency couples quadratically to B₀ at the avoided crossing (clock transition), in contrast to the usual linear coupling far from the clock transition. This is why the ordering of red squares and green circles switches at the clock transition, i.e., there is a smooth evolution of A^eff ($\propto {\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$) such that it switches signs at the clock transition. This implies that the effective dipolar coupling to protons vanishes right at the clock transition; hence the ESEEM effect also vanishes at the clock transition, as does the electron-nuclear decoherence, leading to the steep rise in T_m observed upon approaching the clock transition [=8.43(6) μs at the clock transition]¹⁷. Meanwhile, the ESEEM modulation depth grows with the detuning, ΔB (i.e., with ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$), away from the clock transition, as does the electron-nuclear contribution to the central spin decoherence, i.e., T_m decreases to ~1 μs far from the clock transition¹⁷.

The ESEEM effect is ultimately governed by the collective coupling of the Ho^III ion to the entire nuclear bath. However, the 1/r³ dependence of the dipolar interaction and large value of γ_H in comparison to other nuclei results in a spectrum that is dominated by nearby protons^32,33, the closest of which is ~4 Å from the central Ho^III ion³⁰. At this separation and in the linear Zeeman regime [ΔB > 300 mT, see Fig. 1b], the maximum Ho–H dipolar coupling strength, ${A}^{\max }\approx 3\,{\rm {MHz}}$ (= 2μ_oμ_Hoμ_H/4πhr³); this assumes m_J = ±4 for the ground state of Ho^III. The experimental results displayed in Fig. 2 remain very far from this linear regime, which is why the separation of the red squares and green circles (A^eff < 0.5 MHz) is well below the maximum. Meanwhile, ESEEM measurements far from the clock transitions are hampered by short phase memory times. Nevertheless, one would expect to observe strong ESEEM in proximity to most of the HoW₁₀ clock transitions due to the requirement that A^eff is of the same order as the proton Larmor frequency (see below), e.g., ν_H = 1.1 MHz at 25.5 mT. Indeed, ESEEM is also observed at the 2nd (ν_H = 3.3 MHz) and 3rd (ν_H = 5.4 MHz) clock transitions (see Supplementary Discussion). Although the effect is less pronounced, the same qualitative behavior is found, i.e., a vanishing of the ESEEM at each clock transition and harmonic content centered at ν_H and 2ν_H. Therefore, the enhanced coherence in the vicinity of the clock transitions provides a window through which to observe ESEEM, which ultimately vanishes right at the clock transitions because ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}\to 0$. We note that no modulation is discernible at the 4th clock transition (ν_H = 7.6 MHz), presumably because the effective dipolar coupling is just too weak in comparison to ν_H.

Numerical simulations

In order to gain microscopic understanding, we developed a simplified Hamiltonian for a central electron spin coupled to a finite proton spin bath. To preserve computational resources for the bath, we model the electronic system as an S = 1 spin with longitudinal and transverse anisotropy (Fig. 1a):

$${\hat{H}}_{{S}}=D[{\hat{S}}_{z}^{2}-\frac{1}{3}S(S+1)]+E({\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2})+{\gamma }_{{{{{{{{\rm{e}}}}}}}}}({B}_{0}-{B}_{\min }){\hat{S}}_{z}\,,$$

(1)

where the ${\hat{S}}_{j}$ are spin-1 generators of rotation about axis j, while D and E are the second-order axial and rhombic zero-field splitting (anisotropy) parameters, respectively. ${B}_{\min }$ is introduced to shift the clock transition away from B₀ = 0, mimicking the effect of the on-site hyperfine interaction with the ¹⁶⁵Ho nuclear spin; note that this field does not act on the proton bath. The eigenvectors of Eq. (1) at the clock transition (i.e., when ΔB = 0) are $\left\vert \pm \right\rangle =\frac{1}{\sqrt{2}}(\left\vert \uparrow \right\rangle \pm \left\vert \downarrow \right\rangle )$ and $\left\vert 0\right\rangle$, with energies $-\frac{1}{3}| D| \pm E$ and $+\frac{2}{3}| D|$, respectively. Here, $\left\vert \uparrow \right\rangle$, $\left\vert \downarrow \right\rangle$, and $\left\vert 0\right\rangle$ are the states with $\langle {\hat{S}}_{z}\rangle =\pm 1$ and $\langle {\hat{S}}_{z}\rangle =0$, respectively.

We set D = −45 GHz, ∣E∣ = 4.5 GHz and ${B}_{\min }=23.6\,{\rm {mT}}$ in order to mimic the actual low-energy electronic structure of HoW₁₀. These parameters ensure the same clock transition frequency, Δ = 2E = 9 GHz, the same curvature of the two lowest lying levels, and a sizeable separation to the $\left\vert 0\right\rangle$ state (Fig. 1). As an aside, because $\left\vert \pm \right\rangle$ are energetically well-separated from $\left\vert 0\right\rangle$ in the vicinity of the clock transition, we can project onto the two-dimensional subspace defined by the former, wherein,

$$\begin{array}{l}{\hat{S}}_{z}^{2}\to {\mathbb{1}}\,,\,\,{\hat{S}}_{z}\to {\sigma }_{x}\,,\,\,{\hat{S}}_{x}^{2}-{\hat{S}}_{y}^{2}\to {\sigma }_{z}\,,\,\,\{{\hat{S}}_{x},{\hat{S}}_{y}\}\to 2{\sigma }_{y},\\ {\hat{S}}_{x}\to 0\,,\,\,{\hat{S}}_{y}\to 0\,,\,\,\{{\hat{S}}_{y},{\hat{S}}_{z}\}\to 0\,,\,\,\{{\hat{S}}_{z},{\hat{S}}_{x}\}\to 0.\end{array}$$

(2)

Using this notation, the Hamiltonian reduces to ${\hat{H}}_{S}\to E{\sigma }_{z}+\gamma {{\Delta }}B{\sigma }_{x}$, which precisely maps onto a ‘fictitious’ spin-$\frac{1}{2}$ model subjected to an effective magnetic field in the xz-plane³⁴. The eigenvectors, which are quantized along the effective field direction, are still denoted $\left\vert \pm \right\rangle$, although these are no longer equally weighted mixtures of $\left\vert \uparrow \right\rangle$ and $\left\vert \downarrow \right\rangle$ upon detuning from the clock transition. Nevertheless, at the clock transition (ΔB = 0), one may visualize qubit operations within this subspace in terms of pure rotations around the jth axis of the Bloch sphere defined by $\left\vert \pm \right\rangle$, according to the Pauli matrices, σ_j; the corresponding spin-1 operators are then easily found from Eq. (2). This mapping is helpful in understanding the simulated Hahn-echo sequence (see the “Methods” section), as there is no simple analogy to the $S=\frac{1}{2}$ rotating frame for the actual S = 1 spin dynamics.

The nuclear spin bath, which ultimately causes decoherence and the observed ESEEM effect, is described by N protons coupled via dipolar interactions to the central S = 1 state

$${\hat{H}}_{SI}={\hat{S}}_{z}\mathop{\sum }\limits_{m=1}^{N}\left[{A}_{{{{{{{{\rm{sc}}}}}}}}}^{m}{\hat{I}}_{z}^{m}+{A}_{{{{{{{{\rm{psc}}}}}}}}}^{m}({\hat{I}}_{x}^{m}+{\hat{I}}_{y}^{m})\right].$$

(3)

Here, we employ secular (sc) and pseudosecular (psc) approximations with phenomenological couplings ${A}_{{{{{{{{\rm{sc}}}}}}}}}^{m}$ and ${A}_{{{{{{{{\rm{psc}}}}}}}}}^{m}$, respectively; the ${\hat{I}}_{j}^{m}$ are generators that rotate the spin of the mth proton around axis j. The pseudosecular interaction is often ignored due to averaging brought about by the mismatch in the proton Larmor and hyperfine frequencies. However, as previously discussed, this is not the case at the HoW₁₀ clock transitions. Indeed, the pseudosecular interaction turns out to be essential to the ESEEM effect because it is responsible for driving formally forbidden nuclear transitions during the Hahn echo sequence³¹. Meanwhile, the protons also undergo their own dynamics, independent of the central spin, according to

$${\hat{H}}_{I}=-\mathop{\sum}\limits_{m\ne n}{D}_{mn}(3\,{\cos }^{2}\,{\theta }_{mn}-1)[2{\hat{I}}_{z}^{m}{\hat{I}}_{z}^{n}-({\hat{I}}_{x}^{m}{\hat{I}}_{x}^{n}+{\hat{I}}_{y}^{m}{\hat{I}}_{y}^{n})]-{\gamma }_{{{{{{{{\rm{H}}}}}}}}}{B}_{0}\mathop{\sum }\limits_{m=1}^{N}{\hat{I}}_{z}^{m}.$$

(4)

That is, each proton in the bath undergoes Larmor precession at a bare frequency γ_HB₀, and couples to other protons via a dipolar interaction of strength D_mn (~10 kHz); θ_mn is the angle between B₀ and the vector joining protons m and n. Energy-conserving proton flip-flop processes, driven by the $({\hat{I}}_{x}^{m}{\hat{I}}_{x}^{n}+{\hat{I}}_{y}^{m}{\hat{I}}_{y}^{n})$ term, are central to the electron spin decoherence process^10,27,32,33. To simulate the ESEEM, we numerically recreate the two-pulse Hahn echo sequence in silico by performing a time evolution according to the total Hamiltonian, ${\hat{H}}_{{{{{{{{\rm{tot}}}}}}}}}={\hat{H}}_{S}+{\hat{H}}_{SI}+{\hat{H}}_{I}$ (see the “Methods” section).

As a warm-up, we first consider the simple case of a single proton (N = 1) coupled to the central S = 1 spin, with A = A_sc = 2A_psc = 1 MHz. Figure 3a–c displays FFTs of the Hahn echo simulations for several detuning fields [inset to (a) displays a representative time trace]. In analogy to the $S=\frac{1}{2}$ case, we associate the lowest frequency FFT peak, and the splitting of the peaks on either side of ν_H, with the effective hyperfine interaction strength, A^eff; the inset to Fig. 3b plots this frequency as a function of ${B}_{0}-{B}_{\min }$. As can clearly be seen, and in analogy with the experiments, A^eff → 0 at the clock transition; consequently, the modulation depth is also zero at zero detuning. Meanwhile, far from the clock transition, such that ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}| {B}_{0}-{B}_{\min }| \gg | E| /h$, A^eff → 2A; the factor of two is due to renormalization because S = 1 as opposed to $\frac{1}{2}$. Thus, in the high-field limit, FFT peaks occur at 2A, ν_H ± A, and 2ν_H. Superimposed on the data in the inset to Fig. 3b is a phenomenological fit that assumes ${A}^{{{{{{{{\rm{eff}}}}}}}}}\propto {\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$, deduced from df/dB₀ via Eq. (1). This confirms the idea that the variation in ${\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{{{{{{{{\rm{eff}}}}}}}}}$ (or $\langle {\hat{S}}_{z}\rangle$) in the vicinity of the clock transition governs the dipolar coupling of the central spin to the nearby proton. The final thing to note from the inset to Fig. 3a is the absence of decoherence, i.e., the peak electron spin-echo intensity does not decay. This is because the two-spin system executes perfectly coherent coupled dynamics, with no quantum phase leakage, i.e., there is no bath associated with this model.

Fig. 3: Simulated ESEEM spectra for N = 1.

FFTs of Hahn echo simulations for the simple case of a single $I=\frac{1}{2}$ proton coupled to a central S = 1 electron spin for different detunings, ${B}_{0}-{B}_{\min }$ = +5 mT (a), +20 mT (b), and +50 mT (c); see text for employed parameters. Several relevant frequencies are labeled in the FFT spectra. The inset to a shows a representative electron spin-echo intensity time trace. The inset to b plots A^eff deduced from the first FFT peak versus ${B}_{0}-{B}_{\min }$ (error bars corresponding to ± s.d. are considerably smaller than the data points and are not shown); the solid red curve is a simple fit that assumes A^eff ∝ df/dB₀ from Fig. 1b.

In order to better capture the physics associated with the spin bath, we extend the model to N = 7 nuclear spins with a distribution of dipolar couplings to the central spin (Fig. 4a), enabling simulations of the ESEEM on reasonable timescales whilst also capturing the emergence of decoherence; we set $\langle {A}_{{{{{{{{\rm{sc}}}}}}}}}^{m}\rangle =2\langle {A}_{{{{{{{{\rm{psc}}}}}}}}}^{m}\rangle =8$ MHz to best reproduce the experimental results (see the “Methods” section for further details). Time traces for several detunings on either side of the clock transition are displayed in Fig. 4b. As can be seen, the simulations qualitatively reproduce the experimental results in Fig. 2. A very clear ESEEM effect is observed with a modulation depth that increases with detuning, ΔB, while more-or-less vanishing right at the clock transition. The time traces also exhibit a very apparent decay in the coherence of the central spin dynamics, i.e., the finite spin bath model reproduces the experimentally observed decoherence of the central spin, including the maximum in T_m seen at the clock transition. Moreover, in spite of its simplicity, the simulated timescale associated with the decoherence is of the same order as the experiments. The only exception is at zero detuning, where the numerical decay is considerably flatter than the experiments. The residual decoherence observed at the clock transition in experiments is attributed to spin-lattice relaxation¹⁷, which is not included in our model; we comment on this further below. FFTs of the numerical time traces (Fig. 4c) are in excellent agreement with the experiment. Indeed, a plot of the center frequencies of the main FFT peaks as a function of detuning, ${B}_{0}-{B}_{\min }$ (Fig. 4d), reveals identical behavior to the experiments, i.e., a pair of peaks at ${\nu }_{{{{{{{{\rm{H}}}}}}}}}\pm \frac{1}{2}{A}^{{{{{{{{\rm{eff}}}}}}}}}$ and a higher frequency peak at ~2ν_H. Once again, it can be seen that A^eff → 0 at ${B}_{0}={B}_{\min }$, and increases with detuning from the clock transition.

Fig. 4: Simulated ESEEM spectra for N = 7.

a Schematic of the employed model consisting of a central S = 1 electron spin coupled to seven $I=\frac{1}{2}$ protons (see text for employed parameters). b Simulated ESEEM time traces as a function of the same detuning fields as Fig. 2 (see labeling). c FFTs of the time traces in (b), presented in the same order; prominent peaks are again marked with red squares, green circles, and blue triangles for direct comparison with Fig. 2. d Plot of the FFT peak frequencies in (c) as a function of B₀, with error bars denoting ± s.d. (approximating each peak as a Gaussian); the dashed lines correspond to harmonics of the proton Larmor frequency (see legend), the data points are color/shape coded according to the same scheme as those in (c), and the vertical dashed red line marks the clock transition (CT).

Discussion

The present experimental and theoretical investigation clearly demonstrates the effective decoupling of an electron spin qubit from the surrounding nuclear bath at a clock transition, going beyond previous studies that simply show evidence for enhanced coherence^17,30. In fact, the simulations reveal a pronounced enhancement in T_m at the clock transition, whereas the experiments on HoW₁₀ indicate that coherence is limited there by other factors. The primary culprit is spin-lattice (T₁) relaxation¹⁷. In particular, molecular vibrations that couple directly to the crystal field interaction(s) responsible for the clock transition (Fig. 1) may be expected to drive spin-lattice relaxation^30,35,36, an effect not included in our model. However, weak decoherence is observed even at the clock transition in the numerical simulations presented in Fig. 4. We attribute this to second-order coupling, ${{\rm {d}}}^{2}f/{\rm {d}}{B}_{0}^{2}={\gamma }_{{{{{{{{\rm{e}}}}}}}}}^{2}/{{\Delta }}$, i.e., df/dB₀ vanishes only precisely at the clock transition, and the HoW₁₀ qubit is therefore exposed to weak ¹H dipolar field fluctuations either side of ${B}_{\min }$. This suggests that electron-nuclear decoupling should improve upon increasing the clock transition frequency since the second-order coupling scales inversely with Δ.

Electron spin–spin interactions have also been omitted from our model since we consider only one central Ho^III ion. One may expect the diagonal part of this interaction (i.e., ${\hat{S}}_{z}^{m}{\hat{S}}_{z}^{n}$) to decouple at a clock transition in exactly the same way that the proton bath decouples in this study, provided that the interaction is not too strong. As noted above, perfect decoupling occurs only to first-order (df/dB₀ → 0) at the clock transition. However, second-order coupling should be weak if the spin–spin interaction strength is substantially weaker than the clock transition frequency (Δ = 2E)^10,22, as is the case for well-separated (>nm) qubits. Meanwhile, although one may safely ignore angular momentum conserving electron-nuclear dipolar flip-flop processes in the present work because of the vastly different clock transition (Δ) and proton Larmor (γ_HB₀) frequency scales, this is not the case for electron spin–spin interactions. Dipolar coupling within arrays of nominally identical qubits will cause decoherence due to flip-flop processes between resonant electron spins (Δ₁ = Δ₂) via the ${\hat{S}}_{x}^{m}{\hat{S}}_{x}^{n}+{\hat{S}}_{y}^{m}{\hat{S}}_{y}^{n}$ interaction^10,37. Correctly modeling this physics is more challenging, requiring a much larger bath with resonant and non-resonant qubits, due both to disorder (distributions in Δ) and a dynamic distribution of dipolar interactions within the ensemble. Such a model contains complex many-body physics that lies outside of the realm of the present investigation.

One may anticipate that future quantum devices based on molecular spins will feature controllable entangling interactions between individual qubits¹. Such control would enable the mitigation of resonant electron–electron spin flip-flop processes (or deliberate application of such two-qubit operations, when required). Likewise, quantum sensing applications involving single qubits are immune to this mode of decoherence. However, it is virtually impossible to remove all sources of magnetic noise, particularly nuclear spins, whilst maintaining the flexibility that molecular design principles allow. The present investigation, therefore, highlights the importance of clock transitions for suppressing electron-nuclear spin–spin decoherence. Moreover, one may expect these principles to apply quite generally to any type of clock transition. In this regard, hyperfine clock transitions show great promise due to weaker coupling to molecular vibrations²².

Methods

Experimental details

Since extensive discussions of sample preparation and handling, experimental setup and conditions, as well as the electronic properties that give rise to clock transitions in HoW₁₀ have been presented previously^17,28, only brief descriptions of essential details are given here. Single crystals of Na₉[Ho_0.001Y_0.999(W₅O₁₈)₂]⋅nH₂O were prepared according to literature methods³⁸. ESEEM measurements were performed using a commercial Bruker E680 X-band spectrometer equipped with a cylindrical TE₀₁₁ dielectric resonator (model ER 4118 X-MD5, with an unloaded center frequency of 9.75 GHz), which was overcoupled to increase bandwidth and, thus, allow measurements at frequencies down to 9.1 GHz^17,22. The sample temperature was controlled using an Oxford Instruments CF935 helium flow cryostat and ITC503 temperature controller.

All of the data presented in this study (Fig. 2) were obtained for a single crystal. However, similar ESEEM behavior has been observed in experiments performed on many other crystals of varying Ho^III concentration¹⁷. Although in situ rotation of the crystal about a single-axis is possible, the low symmetry HoW₁₀ structure²⁸ and the need for rapid sample loading to avoid degradation due to solvent loss resulted in an ~22.5° misalignment between the applied field and the molecular magnetic easy- (z-) axis. This simply leads to a re-scaling of the clock transition fields: in this study, the lowest field clock transition occurs at ${B}_{0}={B}_{\min }=25.5\,{\rm {mT}}$, which is equivalent to a longitudinal field, B_0z = 23.6 mT, where the z-direction defines the approximate HoW₁₀ four-fold symmetry axis. ESEEM results were derived from electron spin-echo decay curves generated using a standard two-pulse Hahn-echo sequence (π/2−τ−π−τ−echo) as a function of detuning from the clock transition field, ${B}_{\min }$. The frequency domain plots in Fig. 2b were obtained by performing FFTs of the time traces, which were zero-padded by twice the number of data points and further smoothed using a 5-point average.

The spin Hamiltonian of the HoW₁₀ molecule may be described in terms of a set of axial crystal field parameters, ${B}_{k}^{q}$ (k = 2, 4, 6, representing the rank of the associated crystal field operator, ${\hat{O}}_{k}^{q}$, and q = 0 the rotational order). Distortions away from the approximate D_4d point symmetry of the HoW₁₀ molecule engage the tetragonal crystal field interaction, ${B}_{4}^{4}{\hat{O}}_{4}^{4}\propto ({\hat{S}}_{+}^{4}+{\hat{S}}_{-}^{4})$²⁸, which is effective in generating avoided crossings between the eight hyperfine sub-level pairs associated with the m_J = ± 4 ground doublet, resulting in clock transitions at magnetic fields, ${B}_{\min }=\pm \!23.6$, ±70.9, ±118.1 and ±165.4 mT (for an applied field, B₀, parallel to the molecular z-axis)¹⁷. The W and O nuclei in the HoW₁₀ molecular core are predominantly non-magnetic, with the exception of ¹⁷O ($I=\frac{5}{2}$, γ = 5.77 MHz/T) and ¹⁸³W ($I=\frac{1}{2}$, γ = 1.77 MHz/T) with 0.04% and 14.3% natural abundance, respectively. Moreover, their associated γ-values, along with those of the more distant ²³Na and ⁸⁹Y nuclei (both 100% abundance) are considerably smaller than those of the proton. Consequently, one would not expect to see strong ESEEM from coupling to these other nuclei, i.e., the assignment of the observed ESEEM to protons is unambiguous.

Theoretical details

The two-pulse Hahn echo sequence was recreated in silico by performing a time evolution according to the total Hamiltonian, ${\hat{H}}_{{{{{{{{\rm{tot}}}}}}}}}={\hat{H}}_{S}+{\hat{H}}_{SI}+{\hat{H}}_{I}$³³. The initial density matrix at thermal equilibrium was defined in the lab frame as

$${\rho }_{{{{{{{{\rm{eq}}}}}}}}}=\frac{\exp (-\beta {\hat{H}}_{{{{{{{{\rm{tot}}}}}}}}})}{{{{{{{{\rm{Tr}}}}}}}}(\exp (-\beta {\hat{H}}_{{{{{{{{\rm{tot}}}}}}}}}))},$$

(5)

where β = h/k_BT and T = 5 K. Instantaneous π/2 and π pulses were performed according to the procedure described in the following paragraph. The density matrix was then allowed to evolve according to ${\hat{H}}_{{{{{{{{\rm{tot}}}}}}}}}$ for a time interval τ after each pulse. Finally, the echo intensity was evaluated by computing the expectation value of the z-component of the Ho^III magnetization in the lab frame, ${{{{{{{{\rm{Tr}}}}}}}}}_{I}(\rho {\hat{S}}_{z})$, with the trace taken over the nuclear states. Exact matrix diagonalization demands considerable computational resources. Therefore, in order to carry out these calculations on reasonable time scales, a number of compromises were necessary. Foremost among these was the limitation on the size of the nuclear spin bath to N = 7 protons. Meanwhile, based on a priori knowledge of the spin dynamics, we could also optimize the time step and duration of the simulations, i.e., the time step (100 ns) results in a frequency cut-off, which we set to well above the 2ν_H frequency seen in the experimental spectra (Fig. 2), and the duration (100 μs) was chosen to ensure an FFT resolution comparable to the experiments.

As discussed in the main text, the low energy $\left\vert \pm \right\rangle$ eigenvectors at the clock transition are not the usual $\left\vert \uparrow \right\rangle$ and $\left\vert \downarrow \right\rangle$ states relevant to the $S=\frac{1}{2}$ case; indeed, there is no simple rotating frame analogy that can easily be visualized in the case of the ‘real’ S = 1 system. One must therefore take care applying appropriate π/2 and π pulses in order to generate the echo. In fact, one may reduce the problem to the simple Bloch sphere picture via projection onto the two-dimensional $\left\vert \pm \right\rangle$ subspace according to Eq. (2), i.e., a ‘fictitious’ spin-$\frac{1}{2}$ subjected to an effective magnetic field in the xz-plane (${\hat{H}}_{S}\to E{\sigma }_{z}+{\gamma }_{{{{{{{{\rm{e}}}}}}}}}{{\Delta }}B{\sigma }_{x}$)³⁴. The appropriate pulses can then be implemented via rotations about any axis that is perpendicular to the effective field, ${\overrightarrow{B}}^{{{{{{{{\rm{eff}}}}}}}}}$ ($=\sqrt{{E}^{2}+{({\gamma }_{{{{{{{{\rm{e}}}}}}}}}{{\Delta }}B)}^{2}}$). Exactly at the clock transition (ΔB = 0), where ${\overrightarrow{B}}^{{{{{{{{\rm{eff}}}}}}}}}\parallel z$, this is easily achieved using either the pure σ_x or σ_y Pauli matrix, corresponding to the spin-1 operators ${\hat{S}}_{z}$ and $\{{\hat{S}}_{x},{\hat{S}}_{y}\}$, respectively. Away from the clock transition, ${\overrightarrow{B}}^{{{{{{{{\rm{eff}}}}}}}}}$ tilts towards x within the $\left\vert \pm \right\rangle$ subspace. We, therefore, employ a pure σ_y rotation, which does not depend on the orientation of ${\overrightarrow{B}}^{{{{{{{{\rm{eff}}}}}}}}}$, i.e., we implement pulses of the form $\exp [i\phi \{{\hat{S}}_{x},{\hat{S}}_{y}\}/2]$, where ϕ denotes the rotation angle in radians. Although the $\{{\hat{S}}_{x},{\hat{S}}_{y}\}$ operator has no direct correspondence with the microwave B₁ field employed in the experiments, it conveniently achieves the desired result. Moreover, it is formally equivalent to operating with ${\hat{S}}_{z}$ at the clock transition, which does correspond directly to the experimental parallel mode B₁ field. However, upon moving away from the clock transition, the ideal magnetic ${\hat{S}}_{z}$-pulse evolves with the applied field, B₀, as the eigenvectors acquire unequal $\left\vert \uparrow \right\rangle$ and $\left\vert \downarrow \right\rangle$ weights. Indeed, the durations of the π/2 and π pulses employed in the real experiments had to be optimized for each field step, something that could be avoided in the simulations by implementing pure σ_y rotations.

Additional subtleties of the calculations concern the precise details of the microscopic interactions. For example, in order to recreate a realistic proton bath, a distribution of electron-nuclear hyperfine coupling strengths, ${A}^{m}={A}_{{{{{{{{\rm{sc}}}}}}}}}^{m}=2{A}_{{{{{{{{\rm{psc}}}}}}}}}^{m}$ (m = 1 to N), was generated with random values in the range from 7 to 9 MHz such that 〈A〉 = 8 MHz. Likewise, the distribution of proton–proton dipolar interactions was implemented by fixing the coupling strength in Eq. (4), ${D}_{mn}={\mu }_{{{{{{{{\rm{o}}}}}}}}}{\mu }_{{{{{{{{\rm{H}}}}}}}}}^{2}/8\pi h{r}^{3}\approx 10$ kHz (≡1.8 Å distance), and randomizing the angle θ_mn. To compensate for the small size of the nuclear bath, the simulations were repeated 10 times for different A^m and θ_mn randomizations, then averaged; this approach is obviously vastly more efficient computationally compared to increasing the bath size by a factor of ten. Not only do these measures better mimic the real [HoW₁₀]⋅nH₂O system, they avoid the highly unphysical situation in which the seven protons are indistinguishable, with identical couplings to the central spin and to each other. The 8 MHz value for 〈A〉 was chosen so as to reproduce the effective hyperfine interaction seen in the experiments, i.e., the frequency splittings between the red squares and green circles in Figs. 2c and 4d. This corresponds to a Ho–¹H separation of ~2.9 Å, which is a little below the known closest distance (~4 Å), which we attribute to the fact that the model under-counts the number of nearby protons by about an order of magnitude, i.e., n = 35H₂O molecules, or 70 protons per Ho^III ion. Consequently, the smaller distance employed in the simulations effectively renormalizes the collective hyperfine coupling strength. Finally, the frequency-domain plots in Fig. 4c and d were obtained by first subtracting a stretched exponential background from the time traces (Fig. 4b), then performing FFTs of the residual ESEEM modulations; Fourier-transform filtering was then used to smooth the resulting frequency-domain plots.

In spite of the aforementioned simplifying assumptions, the employed model captures the essential physics associated with the ESEEM effect in the vicinity of a realistic clock transition. Moreover, the simulations reproduce the experimentally observed electron-nuclear decoherence. Approximate cluster correlation expansion (CCE) methods are able to consider a much larger and more realistic bath consisting of thousands of protons. Indeed, such studies applied to simple spin-$\frac{1}{2}$ qubits (with no clock transition) obtain essentially perfect quantitative agreement with experimental phase memory times³². However, they also reveal that decoherence is dominated by stochastic flip-flop processes associated with proton pairs that are relatively close (a few Å) to the central electron spin. As such, the exact quantum calculations considered here contain the same ingredients. It is therefore unsurprising that the obtained phase memory times agree with the experiment to within approximately a factor of two. Indeed, the N = 7 model enables the exploration of many other microscopic aspects of the bath that influence decoherence. We hope to explore this further in the future. We wish to emphasize, however, that it was not our original intent to quantitatively reproduce the decoherence, but rather to qualitatively reproduce the ESEEM effect in the vicinity of a clock transition, something that this investigation has achieved.