Introduction

Improving conversion efficiencies between photons and charges, phonons and charges1, spins and charges2, or triplet and singlet excitations3 is a central target of contemporary energy research. For example, the understanding of the conversion pathways in organic solar cells led to a more than ten-fold increase in power conversion efficiency (PCE)4,5,6,7,8,9,10,11,12,13,14,15, with current non-fullerene-acceptor-based devices having nearly 19 % PCE 16,17.

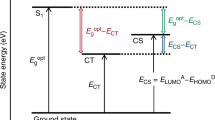
Organic solar cells are actively studied due to their low cost, environmental friendliness, and ease of processing. In these cells, strongly bound excitons dissociate into charge-transfer (CT) states at donor–acceptor interfaces, which subsequently dissociate into free charge carriers, detected as photocurrent5,18. Early optimization strategies targeted materials with small optical and large photovoltaic gaps, defined as the difference between the ionization energy (IE) of the donor and electron affinity (EA) of the acceptor, Γ = IED − EAA19. Small optical gaps helped to harvest a wider region of the solar spectrum, whereas larger photovoltaic gaps often correlated with larger open-circuit voltages, Voc. It was, however, soon realized that the abstraction of the density of states of a heterojunction to a single photovoltaic gap is an oversimplification. Accounting for the broadening of energy levels motivated additional optimization strategies20,21,22,23. Furthermore, detailed macroscopic models pointed out the importance of the charge-carrier mobility and non-geminate recombination coefficient, thus providing optimization criteria for the thickness of the active layer in order to achieve high short-circuit currents and fill factors24,25,26,27. A whole new era in organic photovoltaic research started with the development of low-bandgap non-fullerene acceptors (NFAs)11,12,13,14,15.

It was soon realized that long-range electrostatic interactions of a charge with surrounding molecular quadrupoles play a decisive role in defining the energetic landscape for electrons, holes and charge-transfer states28,29,30,31. The crystal field created by molecular quadrupoles contributes to the ionization energy (IE) and electron affinity (EA) of the organic film, and therefore to the open-circuit voltage of the solar cell28. This field also changes the energy offset between the charge-transfer and charge-separated states, favouring or disfavoring CT state dissociation29,31,32,33,34. It is unfortunate that the electrostatic effects, which favor efficient CT state dissociation also lead to a reduction of the photovoltaic gap, energy of the charge-transfer state, Ect, and hence smaller Voc. As a result, in order to optimize solar cell efficiency, one has to appropriately balance the electrostatic contributions to the energy profiles32,33.

In this paper, we use tailored material systems in order to disentangle the effects of morphology, molecular and device architecture on the microscopic energetics. In the first set of experiments, we study planar heterojunction solar cells. While the acceptor phase is always C60, the donor phase of these cells is a mixture of chemically similar compounds, ZnPc:F4ZnPc or ZnPc:F\({}_{4}^{* }\)ZnPc, isomers of which are shown in Fig. 1. Due to fluorination, the quadrupole component along the normal of the molecular plane, Q20 ≡ Qππ, differs significantly for all three compounds. This difference allows us to accurately tune the electrostatic field in the intermixed crystalline phase. As a result, IEs and EAs of such mixtures can be continuously tuned, while the crystalline morphology of the donor phase is preserved31,35. In the second set of experiments, an additional mixed donor:acceptor interlayer is deposited between the pure donor and acceptor layers. This interlayer is used to control the roughness of the donor–acceptor interface. We then show theoretically and prove experimentally that interfacial electrostatics can be used to tune the open-circuit voltage of an organic solar cell—by adjusting the roughness of the donor–acceptor interface. Moreover, we provide a detailed microscopic description of how Voc, Γ, and Ect depend on system composition, interface roughness, and energetic disorder.

Fig. 1: Chemical structures and electrostatic surface potentials illustrating their distinct electrostatic architecture.
figure 1

Isopotential surfaces at −0.5 V and +0.5 V are shown in blue and red, respectively. Note that for F4ZnPc, the material used is a mixture of different isomers, as the fluorine atoms can be in either of the two outer positions. IE0 and EA0 are gas-phase ionization energy and electron affinity, respectively, calculated at the B3LYP/6-311+g(d,p) level of theory. Q20 is the component of the quadrupole tensor in the direction normal to the molecular plane.

Full size image

Results

Ionization energy and photovoltaic gap

We begin by analyzing the density of states (DOS) of intermixed ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc co-crystals. In the absence of intermolecular interactions, the DOS of the binary mixture would only consist of two peaks corresponding to the ionization energies of ZnPc and F4ZnPc (or ZnPc and F\({}_{4}^{* }\)ZnPc) in the gas phase, IE0. The composition dependence of the IE and EA is thus given solely by the solid-state contribution Δh(c) for holes and Δe(c) for electrons, IE(c) = IE0 + Δh(c), EA(c) = EA0 + Δe(c), where c is the fraction of ZnPc in the mixture.

The microscopic mechanism responsible for this dependence is the long-range superposition of quadrupolar fields that act on the charge carrier31,35. ZnPc carries a net-negative out-of-π-plane quadrupole component, larger in magnitude than the corresponding negative quadrupole moment of F\({}_{4}^{* }\)ZnPc, whereas the corresponding quadrupole component of F4ZnPc is positive. In fact, this can be anticipated from the isopotential maps of the compounds, which are shown in Fig. 1. The long-range character of the charge-quadrupole interaction effectively results in a concentration-weighted average over both contributions, which can be used to tune ionization potential and electron affinity. This microscopic view is indeed supported by the good agreement between ionization energies measured by UPS31,35 and simulated using atomistically resolved models, as shown in Fig. 2.

Fig. 2: Crystalline morphologies and corresponding ionization potentials.
figure 2

a Model of a crystalline binary ZnPc:F4ZnPc thin film, with species represented by (semi-transparent) and gray molecules, with periodicity in the xy plane. Deeper red implies more F4ZnPc molecules in a column. b Dependence of the ionization energy (IE) on the fraction of ZnPc in the ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc systems, c.

Full size image

To relate this composition dependence of the energetics of holes in the mixtures to photovoltaic observables, we first consider its effect on the photovoltaic gap Γ(c) = IED(c) + EAA = Γ0 + Δh,D(c) + Δe,A. Here, Γ0 = IE0,D + EA0,A is the sum of the gas-phase IE of the donor and EA of the acceptor. Δe,A ≃ 0.95 eV for C60 denotes the solid-state correction to electron site energies in the acceptor component, as calculated from atomistic models. Note that we define the photovoltaic gap based on the mean of the low-energy Gaussian mode within the bimodal density of states of the mixed ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc systems. This low-energy contribution is due to the ZnPc component, and will eventually determine the chemical potential μh. The composition dependence of Γ(c) is therefore inherited directly from Δh,D(c). As a result, Γ(c) should display the same linear behavior in c as IED(c).

Electrostatic interfacial bias

To quantify the electrostatic heterogeneity of the donor–acceptor interface, we define an interfacial electrostatic bias for holes and electrons, \({B}_{h}={\Delta }_{h(A)}-{c}_{1}{\Delta }_{h,{D}_{1}}-{c}_{2}{\Delta }_{h,{D}_{2}}\), \({B}_{e}={c}_{1}{\Delta }_{e({D}_{1})}+{c}_{2}{\Delta }_{e({D}_{2})}-{\Delta }_{e,A}\), where Δh(A) is the solid-state contribution to the ionization energy of the donor molecule in the acceptor mesophase, i.e., when the donor molecule is completely surrounded (perfectly dispersed) by C60. Similarly, Δe(D) is this contribution to the electron affinity of the acceptor molecule placed in the donor mesophase. As the donor mesophase is a mixture of two compounds, we weigh the corresponding contributions of D1 and D2 by their respective concentrations in the mixture. In other words, if D1 is ZnPc then c1 = c and c2 = 1−c. In an ordered thin film, the solid-state contribution to the ionization energy and, therefore, the interfacial bias, are proportional to the Qπ−π component of the quadrupolar quadripolar tensor31,33. For the columnar molecular arrangement shown in Fig. 2, Qπ−π ≡ Q20 is the component of the tensor perpendicular to the conjugated core, as shown in Fig. 1.

Bh and Be quantify the electrostatic asymmetry of the interface by comparing the external contributions for holes and electrons on the donor and acceptor side of the interface. They are defined such that a positive interfacial bias pushes charge carriers away from the interface. To evaluate these quantities, we would need to explicitly simulate the donor–acceptor mixture. Instead, we approximate the corresponding solid-state contributions with their bulk values, Δh(A) ≈ Δh,A and Δe(D) ≈ Δe,D. This approximation is reasonable at the donor–acceptor interface, where donor (acceptor) molecules have mostly donor (acceptor) nearest neighbors, and where the long-range charge-quadrupole interactions dominate the solid-state contribution.

Since the solid-state contributions to the electron and hole on the donor side are linear in c, the interfacial bias also linearly depends on the composition, as shown in Fig. 3. Remarkably, for F4ZnPc, B becomes negative at c ≃ 0.3, which is also where the fill factor of the solar cell starts to deteriorate, see Table 1. This can be rationalized in that a negative B, i.e., a negative bias for charge push-out, leads to trap formation at donor/acceptor sites that protrudes into the opposite (acceptor/donor) domain. The electrostatic bias of the F\({}_{4}^{* }\)ZnPc system is always positive. This cell indeed performs much better than the F4ZnPc device.

Fig. 3: Interfacial bias potential.
figure 3

Dependence of the interfacial bias potential for electrons (blue curves, filled circles) and holes (red curves, open circles) on the composition of the donor layer, c, for the ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc systems as obtained through simulations. The bias potential has a linear dependence on c, inherited from the solid-state contributions Δh and Δe to electron and hole site energies.

Full size image
Table 1 Summary of the measurements for the ternary cells. For ZnPc:F\({}_{4}^{* }\)ZnPc/C60 and ZnPc:F4ZnPc/C60 as well as the planar junction cell with an interlayer we report short-circuit currents, Jsc, open-circuit voltages, Voc, fill factors, power conversion efficiencies (PCE), charge-transfer energies Ect and the corresponding fit parameters, as described in the “Methods” section.
Full size table

Charge-transfer states

We now evaluate the energies of interfacial CT states. Generally speaking, the energy of these states can be written as

$${E}_{{{{{{{{\rm{ct}}}}}}}}}(c)=\Gamma (c)-| {\Delta }_{eh}| +\chi (c,\rho ).$$
(1)

Here, ∣Δeh∣ is an effective binding energy that results from the electron-hole attraction reduced by dielectric solvation29,30,33,36. This binding energy can be assumed to be independent of composition, and amounts to 0.5 eV for the closest CT states in results obtained through simulations29,33. χ(c, ρ) is the interfacial electrostatic bias, as discussed below.

The ionization energy and electron affinity are impacted by the interfacial morphology at the nanoscale29,37. At a rough interface, donor molecules or domains can protrude into the acceptor phase. As a result, their gas-phase energy levels are dressed by the electrostatic field of the acceptor phase. This superposition of electrostatic fields in the donor and acceptor films across an intermixed region is triggered by the same long-range mechanism that gives rise to the composition dependence of site energies in the mixed donor phase.

The degree of interface roughness determines to what extent this bias actually impacts the CT energy of interfacial donor–acceptor pairs. In Supplementary Note 2 we quantify the amount by which Ect is raised (B > 0) or lowered (B < 0) by the bias for a rough interface of width h, which is shown in Fig. 4(a),

$$\chi (c,\rho )=\frac{1}{2}\left({B}_{e}(c)+{B}_{h}(c)\right)\frac{\rho }{1+\rho }.$$
(2)

In the limit where the corrugation period λ of the profile significantly exceeds both the depth h of the intermixed region, and the interlayer spacing δ, the degree of nanoscale roughness can be captured by a single parameter ρ = 2h/δ.

Fig. 4: Open-circuit voltage and charge-transfer state energy of a planar junction solar cell.
figure 4

a Model of a planar junction solar cell with a rough interface and co-deposited donor materials. Geometrical parameters of a rough interface: period, λ, width, h, and a minimal separation between the donor and acceptor molecules, δ. b Dependence of the open-circuit voltage (Voc, open symbols), and charge-transfer state energy (Ect, closed symbols) on the concentration c of ZnPc in the ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc solar cells. The experimentally measured slopes (black lines and symbols) are best reproduced for ρ = 1.

Full size image

To validate this relation, the measured composition dependence of Ect is shown in Fig. 4b. Experimental details are provided in the Methods section and Table 1. The slope is best fitted with ρ = 1, which corresponds roughly to two intermixed molecular layers. As we will see in the next section, the same roughness is required to fit the dependence of the open-circuit voltage on the composition of the donor. Moreover, we will also show that the interface roughness can be systematically varied in planar junction solar cells with an interlayer between the two phases.

Open-circuit voltage

With Γ and Ect at hand, the composition-dependent open-circuit voltage, Voc(c) = μe(c) − μh(c) is calculated by evaluating the chemical potentials μe(c) and μh(c) of electrons and holes, respectively:

$$e{V}_{{{{{{{{\rm{oc}}}}}}}}}(c)\simeq \Gamma (c)+\alpha {k}_{{{{{{{{\rm{B}}}}}}}}}T\ln \left[n(c)p(c)\right]-\beta {k}_{{{{{{{{\rm{B}}}}}}}}}T{\hat{\sigma }}^{2}(c),$$
(3)

where α ≈ 1 and β ≈ 1/2 are parameters with a weak dependence on charge density; \(\hat{\sigma }=\sigma /{k}_{{{{{{{{\rm{B}}}}}}}}}T\,\lesssim \,5\!-\!6\) is the effective disorder strength of the donor (energetic disorder in the acceptor is negligible in the case of C60), and n and p are the steady-state number densities (number of charges per number of available sites) of electrons and holes, respectively. The derivation is provided in Supplementary Note 1.

Evaluating n and p requires the simulation of the full dynamics of charge generation and recombination in a solar cell. Here, however, we are only interested in how the film composition affects Voc. We therefore define n0 and p0 as the charge-carrier densities that would follow from an effectively zero electron-hole binding energy of CT states, and assume n0 = p0 = 5 × 10−6, as was found to accurately describe the Voc under AM1.5g conditions of well-functioning systems with Bh, Be > 029. The steady-state charge-carrier densities can then be related to the charge push-out forces via a law of mass action, \(np={n}_{0}{p}_{0}\exp \left[-\frac{| {\Delta }_{eh}| -{\chi }_{e}(c,\rho )-{\chi }_{h}(c,\rho )}{{k}_{{{{{{{{\rm{B}}}}}}}}}T}\right]\) and the open-circuit voltage is obtained as

$$e{V}_{{{{{{{{\rm{oc}}}}}}}}}(c,\rho )\simeq \alpha {E}_{{{{{{{{\rm{ct}}}}}}}}}(c,\rho )+(1-\alpha )\Gamma (c)+\alpha {k}_{{{{{{{{\rm{B}}}}}}}}}T\ln [{n}_{0}{p}_{0}]-\beta {k}_{{{{{{{{\rm{B}}}}}}}}}T{\hat{\sigma }}^{2}(c),$$
(4)

where we have explicitly labeled the dependence on both composition c and roughness ρ. This relationship can finally be expressed in terms of the effective push-out energies χe + χh = χ simply via

$$e{V}_{{{{{{{{\rm{oc}}}}}}}}}(c,\rho )=e{V}_{{{{{{{{\rm{oc}}}}}}}}}(c,\rho =0)+\alpha \chi (c,\rho ).$$
(5)

Two important observations to be made here are as follows: first, as Ect(c, ρ = 0) + αΔχ(c, ρ) is the CT energy in the presence of charge push-out, the above relationship preserves correlations between the CT energy and Voc. Second, it adequately captures its low-temperature extrapolation, Voc → Ect for kBT → 0 (for α ≃ 1), in agreement with previous studies38,39.

The measured open-circuit voltages as a function of composition are shown in Fig. 4. Note that the red (Voc) and blue (Ect) lines are not fits but theoretical predictions based on the expressions for Ect(c) and Γ(c), Eqs. (1) and (5). The solid curves correspond to a surface roughness of ρ = 1, in which case the slope reproduces the experimental trends for both Voc and Ect. Note that here the increase in Voc is correlated with the decrease in Jsc. This anticorrelation is due to the reduction of the driving force required to convert excitons into chare transfer states, or transfer the hole from the acceptor to the donor32,33.

Of particular interest for solar-cell design is the correlation between the interfacial bias B and the open-circuit voltage. Due to symmetries of the electrostatic interaction sums for electrons and holes, the change of B and Γ with composition is anticorrelated: ΔB = − 2ΔΓ. Meanwhile, Δχ ≤ ΔB/2, as follows from Eq. (2). Two extremal situations can therefore be distinguished: (1) ρ ~ 0 (flat interface), where the change in open-circuit voltage follows precisely the change in photovoltaic gap, and (2) ρ ≫ 1 (rough interface), where the change in the photovoltaic gap may be completely compensated by the change in charge-carrier density, thus effecting an approximately constant Voc. In systems such as ZnPc/C60 with B > 0, interface roughness is therefore advantageous in that it enhances Voc, whereas it will be harmful in systems with B < 0, notably F4ZnPc/C60.

This conclusion can also be validated experimentally. To this end, we prepared planar heterojunction solar cells with an interlayer of mixed ZnPc:C60 (1:1). By changing the thickness h of this interlayer, we effectively modify the roughness ρ of the donor–acceptor interface (as indicated by in situ evaporation studies40), and thus the CT state energy:

$${E}_{{{{{{{{\rm{ct}}}}}}}}}(h)={E}_{{{{{{{{\rm{ct}}}}}}}},0}+\frac{{\chi }_{0}}{1+\frac{\delta }{h+{h}_{0}}}.$$
(6)

Ect,0 here denotes the CT state energy in the absence of any interface roughness, χ0 = (Be + Bh)/2 is the interfacial bias for the F4ZnPc/C60 system, δ is the center-of-mass distance between C60 and F4ZnPc in an edge-on orientation, and h0 is the interfacial roughness of the planar heterojunction with h = 0, i.e., without mixed interlayer. The experimentally measured Ect and Voc dependencies are shown in Fig. 5 (symbols) and are in excellent agreement with the trends suggested by Eqs. (6) and (3): This is illustrated by the fitted solid lines, which correspond to Ect,0 = 0.92 eV, χ0 = 0.27 eV and ρ = δ/h0 = 1. These are in turn very close to the simulated values (Ect,0 = 1.1 eV, χ0 = 0.48 eV), while the surface roughness estimated from the fit agrees well with the earlier observation that ρ ≃ 1 also yields the best agreement between simulated and experimental trends in the composition-dependent setting, shown in Fig. 4.

Fig. 5: Charge-transfer state energy and open-circuit voltage dependence on interfacial roughness.
figure 5

a Co-deposited layer of ZnPc:C60 sandwiched between pristine ZnPc and C60 layers. b Variation of the charge-transfer (CT) energy (Ect, blue curve and filled symbols) and open-circuit voltage (Voc, red curve and open symbols) with interface roughness, represented here by the interlayer thickness h. Dots are measurements performed on planar heterojunction cells with a ZnPc/ZnPc:C60/C60 architecture. Solid lines are fits to Eqs. (6) and (3), with fit parameters Ect,0 = 0.92 eV, χ0 = 0.27 eV, δ = 1.43 nm and h0 = 1.43 nm and the Ect − eVoc offset \(\alpha {k}_{{{{{{{{\rm{B}}}}}}}}}T\ln ({n}_{0}{p}_{0})=-0.66\,{{{{{{{\rm{eV}}}}}}}}\). These fitted parameters are in very good agreement with the values predicted by simulations, as well as the interface roughnesses extracted from the composition-dependent measurements in Fig. 4.

Full size image

Conclusions

To conclude, our model of a rough donor–acceptor interface accounts for the bending of the electrostatic potential and accurately captures the correlations between molecular architecture, film composition and open-circuit voltage. The linear dependence of the photovoltaic gap and charge-transfer state energies on composition is driven by the superposition of quadrupolar fields of ZnPc, F4ZnPc, and F\({}_{4}^{* }\)ZnPc. The same superposition creates a composition-dependent electrostatic bias at the donor–acceptor interface. A positive interfacial bias helps to split charge-transfer states and avoid non-geminate recombination. As, however, the change of the photovoltaic gap and electrostatic interfacial bias with composition are anticorrelated, ΔB ~ − 2ΔΓ, an increased bias reduces the open-circuit voltage: For a perfectly planar interface, the change in voltage follows precisely the change in photovoltaic gap. The reduction of the open-circuit voltage that follows from a large positive bias can be avoided at interfaces with nanoscale roughness. In ZnPc/C60 and F\({}_{4}^{* }\)ZnPc/C60 with B > 0, interface roughness is advantageous in that it recovers the Voc and suppresses charge recombination, whereas it is harmful in F4ZnPc/C60 with B < 0.

Methods

Simulations

The microscopic calculations were performed on atomistic models of mixed ZnPc:F4ZnPc and ZnPc:F\({}_{4}^{* }\)ZnPc films of 10 nm thickness. Each thin-film layer consists of 17 × 6 molecules in an edge-on orientation as suggested by X-ray diffraction studies41. The intermixing of the two species is performed randomly, with the concentration of ZnPc denoted by c.

To appropriately model long-range effects in the energy calculations, periodic boundary conditions are used in the plane of the film, without, however, replicating the molecular excitation, or its polarization cloud. Based on this long-range embedding approach37, we obtain the perturbative corrections Δh,D to hole (h) energy levels in the donor (D) film. The ionization energy (IE) results as IE = IE0 + Δh,D, where IE0 denotes the IE of the respective compound in the gas phase30. All calculations were performed using the VOTCA package42,43.

Sensitive EQEPV measurements

The measurements were performed according to previous works, reproduced here for completeness44.

The light of a quartz halogen lamp (50 W) is chopped at 140 Hz and coupled into a monochromator (Cornerstone 260 1/4m, Newport). The resulting monochromatic light is focused onto the organic solar cell (OSC), its current at short-circuit conditions is fed to a current pre-amplifier before it is analyzed with a lock-in amplifier (7280 DSP, Signal Recovery, Oak Ridge, USA). The time constant of the lock-in amplifier was chosen to be 1 s and the amplification of the pre-amplifier was increased to resolve low photocurrents. The EQEPV is determined by dividing the photocurrent of the OSC by the flux of incoming photons, which was obtained with a calibrated silicon (Si) and indium-gallium-arsenide (InGaAs) photodiode.

Electroluminescence measurements were obtained with an Andor SR393i-B spectrometer equipped with a cooled Si and cooled InGaAs detector array (DU420A-BR-DD and DU491A-1.7, UK). The spectral response of the setup was calibrated with a reference lamp (Oriel 63355). The emission spectrum of the OSCs was recorded at different injection currents, which correspond to applied voltages lower than or at least similar to the Voc of the device at 1 sun illumination.

The low-energy tail of the EQEPV spectrum is fitted with a Marcus equation38

$${{{{{{\rm{EQE}}}}}}}_{{{{{{{{\rm{PV}}}}}}}}}(E)=\frac{f}{E\sqrt{4\pi \lambda {k}_{{{{{{{{\rm{B}}}}}}}}}T}}\exp \left[\frac{-{({E}_{{{{{{{{\rm{ct}}}}}}}}}+\lambda -E)}^{2}}{4\lambda {k}_{{{{{{{{\rm{B}}}}}}}}}T}\right]$$
(7)

to obtain the charge-transfer state energy ECT, the relaxation energy λ, and the oscillator strength f.

In cases where Ect is close to the optical Eopt of the donor and accordingly no distinct CT state absorption is observed, Ect was obtained by fitting the high energy tail of the EL spectra38.

Device preparation

The devices were fabricated according to our previous work. The description is reproduced here for completeness45. All devices investigated in this work are constructed by a thermal evaporation vacuum system with a base pressure of less than 10−7 mbar. Before deposition, ITO substrates (Thin Film Devices Inc., USA) are cleaned for 15 min in different ultrasonic baths with NMP solvent, deionized water, and ethanol, followed by O2 plasma for 10 min. The organic materials are purified 1 or 2 times via thermal sublimation.

A first hole transporting layer is evaporated, consisting of 20 nm 9,9-bis[4-(N,N-bis-biphenyl-4-yl-amino)phenyl]-9H-fluorene (BPAPF) (Lumtec, Germany) doped at 10 wt% with NDP9 (Novaled, Germany). Subsequently, the active layer is evaporated. It comprises 10 nm of a blend of zinc-phthalocyanine (ZnPc) (ABCR, Germany) and tetrafluoro-zinc-phthalocyanine (F\({}_{4}^{* }\)ZnPc) (BASF, Germany) or F4ZnPc (synthesized by Dr. Beatrice Beyer, Fraunhofer FEP, Dresden) in varying ratios, from pure ZnPc to pure F\({}_{4}^{* }\)ZnPc or F4ZnPc (see main text for more information). An additional layer of ZnPc and Buckminster Fullerene (C60) (CreaPhys, Germany) in a 1:1 weight ratio is evaporated, the thickness is varied from 0 to 10 nm. Afterward a 40 nm C60 layer is evaporated. The devices are finalized with 8 nm of Bathophenanthroline (BPhen) (Lumtec, Germany), used as electron contact, and finished with 100 nm of Al. The devices are defined by the area overlap of the bottom and the top contact with an active area of 6.44 mm2. To avoid exposure to ambient conditions, the organic part of the device is covered by a small glass substrate, glued on top utilizing an epoxy resin (Nagase ChemteX Corp., Japan) cured by UV light. To hinder degradation, a moisture getter (Dynic Ltd., UK) is inserted between the top contact and the glass.

Current–voltage characteristics

Current–voltage characteristics are measured with a SMU (Keithley 2400) at standard testing conditions (16 S-150 V.3 Solar Light Co., USA) with a mismatch corrected light intensity and under dark conditions. All results are summarized in Table 1.