Introduction

Two-phase flow in porous media is important in a wide range of sectors, and holds applications in activities as diverse as food processing, management of underground water resources, sequestration of greenhouse gases or crude oil recovery. It is also crucial in everyday phenomena such as plant watering or making a cup of coffee. Owing to its broad impact but also to its complexity, it is a multidisciplinary subject that has been long investigated by physicists, geoscientists, hydrologists, chemists, biologists, and engineers. When one fluid displaces another immiscible fluid, the resulting structures in their distribution present various shapes and complexity1,2,3,4,5, that can be compact, ramified and fractal6,7. These structures are controlled by the forces, which actually drive the flow. These forces can for instance be viscous1,4,5,8,9,10, capillary1,9,10,11,12, gravitational13,14,15,16,17,18 or a combination of these19, and may depend on physical parameters such as the wetting properties of the solid-fluids system3 or changes in the local geometry of the porous medium20,21,22,23. In this work, we study the effect of the latter, that is, of the geometry of the solid matrix. In particular, we consider materials with an average gradient in their disordered porous structure. In nature, examples of such structured but disordered systems are graded geological bedding24, for instance formed in rivers of varying stream intensity or by turbidite deposition, which are of interest to hydrologists and petroleum geoscientists. After a first conjecture that correlated structures in the solid matrix could help prevent flow instabilities20, recent studies have considered the drainage of porous media presenting such gradients, first using regular matrices only displaying a structural gradient21, and then matrices that additionally hold some quenched disorder22. It has there been shown that the structural gradient could either stabilise or destabilise the drainage front. A generalised capillary number, taking into consideration the matrices’ structure, has then been introduced21 to predict the effective stability of the flow. It has also been proposed that, if significant enough, the structural gradient could mitigate the capillary fingering arising from the quenched disorder22.

We here follow a different theoretical approach based on percolation theory, and the generalisation of the recently reintroduced fluctuation number10 to describe the effect of the noise on the width of the invasion front. We show that the gradient in grain size has a similar effect on the flow of the fluids than that of gravity (or, alternatively, any other external field). We illustrate this equivalence with drainage experiments in 3D printed transparent matrices. This technique allows both an accurate control of the experimental models’ structure and quenched disorder and the visualisation of the fluids’ distribution when a non-wetting phase displaces a wetting one in the pore space. Finally, we support the proposed theory with invasion percolation simulations reproducing the experimental results and the predicted scaling law between the width of the invasion front and the fluctuation number.

Results

Porous model and experimental set-up

The experimental set-up and the 3D printed model for our drainage experiments are shown in Fig. 1. We describe, in the Methods section, the details of the set-up and the procedure we followed to print the model and run the flow experiments. This quasi two-dimensional porous matrix (of porosity ~70%) is composed of cylinders that are distributed in a monolayer using a Random Sequential Adsorption (RSA) algorithm25. The RSA parameters are the minimum distance between the cylinders, the cylinders’ diameter, the cylinders’ height and the dimensions of the desired porous system. In our case, the RSA parameters vary between the model’s inlet and outlet. The total size of the model is 140 × 140 mm2, with the cylinder diameter d varying linearly from 1 mm to 2 mm and the minimum cylinder separation varying from 0.4 mm to 0.8 mm, in order to preserve geometrical similarity along the model’s length. We thus design a model with a grain (cylinder) size gradient λ ~ 0.007 mm mm−1. The height of the cylinder was chosen to be 2 mm. The model is then mounted in a flow cell, and, as per Fig. 1, the whole set-up can be tilted by an angle θ for the flow to occur in a chosen effective gravity field \({g}_{0}\sin (\theta )\). Drainage experiments are then performed as described in the Methods section. A wetting water-glycerol solution, dyed with nigrosin, is displaced by air. The drainage is slow so that viscous forces are negligible, with a small capillary number Ca = μV/γ that is about 10−8, where V is the typical flow velocity, μ is the water-glycerol’s viscosity and γ is the surface tension at the fluid-fluid interface. Note that, in the case where viscous forces would not be negligible, the gradient designed in the model structure could actually be seen, in a Darcy description, as a permeability gradient. In our case, however, it is rather a gradient in capillary threshold.

Fig. 1: Experimental set-up.
figure 1

a Schematic cross-section of the experimental set-up. Two transparent PMMA plates (3 cm thick) are screwed together to close the 3D printed porous model with a gradient in grain and pore-throat sizes. Soft polymer layers (black layers) ensure good contacts between the PMMA plates and the model. The model is illuminated from below and pictures are taken from above. b, c Top-view pictures. Photographs of a non-wetting fluid (air) invading a wetting fluid (water-glycerol) in the square porous model of coordinate system (x,y). The side of the model is L = 140 mm. A pump is connected to the outlet and the inlet is open to air. The model can be tilted, leading to a capillary pressure gradient \(G=\Delta \rho \,{g}_{0}\,\sin (\theta )\) in the x direction, where g0 = 9.82 m s−2 and Δρ ~ 1200 kg m−3 is the difference of density between the wetting and non-wetting fluids. The full-extent width of the invasion front highlighted in c and, to better characterise the average front width, we will denote by η the standard deviation of the front position along x.

Full size image

Theory—gradient in pore throats and external fields

The requirement for invasion into one pore neck by the non-wetting fluid is that the capillary pressure p between the two fluids overcomes the capillary threshold value \({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}\) of this pore neck

$$p(x,y) \, > \,{\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}(x,y),$$
(1)

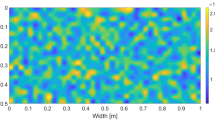
where x and y are the 2D coordinates for the pore neck position. In the case of our 3D printed model, the distribution in capillary pressure along the model is shown in Fig. 2. It is obtained from an approximation of Young-Laplace’s equation as \({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}(x,y)=\gamma \cos (\phi )(1/r+1/h)\), where r is the pore-throat radius, h is half the cylinders’ height and ϕ is the contact angle – measured within the defending phase – for the solid matrix and the two fluids at play.

Fig. 2: Statistical description of the porous model.
figure 2

a Probability density function \(\tilde{N}\) of \({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}(x,y)/{\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}\) in the six areas (denoted 1 to 6) defined in Fig. 1 on the 3D printed model. This distribution is conserved in our model and, around \({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}={p}_{{{{{{{{\rm{c}}}}}}}}}\) it scales approximately as \({({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}/{\hat{p}}_{{{{{{{{\rm{c}}}}}}}}})}^{-2}\), as highlighted by the dash-dotted line. Note: the average pore connectivity in our model being 3, we defined the percolation pressure \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}\) such that26,31\(\int\nolimits_{0}^{{\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}}N({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}})\,{{{{{{{\rm{d}}}}}}}}{\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}\approx 0.65\). b Evolution of the critical capillary pressure \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}\) along the model (crosses), arising from its intrinsic structure. The straight line shows a linear fit, which is a first-order approximation of \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}\) (the engineered gradient in the model was actually in grain size and not in percolation pressure). To this gradient, one can compute an equivalent model tilt (see Fig. 1): \({\theta }_{{{{{{{{\rm{eq}}}}}}}}}=\arcsin (-\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}/\Delta \rho \,{g}_{0})\). Here, θeq ~ 1.35 degrees.

Full size image

Assume that we have an external field that changes the capillary pressure linearly in the x direction. One such field is the gravitational field (e.g., controlled by θ in Fig. 1). Another one, if the flow is fast enough, is the viscous pressure drop inside the fluid being withdrawn. In the case discussed in the present manuscript, the flow rate is slow enough for this viscous effect to be negligible compared to that of the other forces at stake. We will, however, keep a general formalism so they may be included. If we write the gradient in capillary pressure from the external fields as G, this capillary pressure at a position (x, y) is

$$p(x,y)=p({x}_{0})+G\cdot (x-{x}_{0}),$$
(2)

where p(x0) is the capillary pressure at an arbitrary position x0. The condition for invasion can then be written as

$$p({x}_{0}) \, > \,{\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}(x,y)-G\cdot (x-{x}_{0})={p}_{{{{{{{{\rm{t}}}}}}}}}(x,y),$$
(3)

where we have introduced the modified thresholds pt. The system is now mapped onto a system without fields but where the thresholds are modified with the fields as a linear term in x. The capillary pressure p = p(x0) for this equivalent system is constant over the model. We now consider this modified system. The mapping between the occupation probability in percolation f and the capillary pressure p is given26 by

$$f(x)-{f}_{{{{{{{{\rm{c}}}}}}}}}=\int\nolimits_{{p}_{{{{{{{{\rm{c}}}}}}}}}(x)}^{p}N({p}_{{{{{{{{\rm{t}}}}}}}}},x){{{{{{{\rm{d}}}}}}}}{p}_{{{{{{{{\rm{t}}}}}}}}}$$
(4)

In this expression, fc is the critical occupation probability, pc is the critical percolation pressure and N is the normalised distribution in capillary pressure threshold. This distribution is a function of x due to the overall gradient in pore neck and to the external field. Truly, such mapping between occupation probability and pressure arises from the ordinary percolation theory rather than from invasion percolation with cluster trapping, which is typically at stake in draining porous materials (e.g., see Fig. 1c where trapped fluid clusters are visible). Both models have actually been pointed out to belong to different universality classes27, while, by contrast, invasion percolation without trapping shares the same class as ordinary percolation27. In this work, we are interested in the invasion front and its stability. By definition, trapped wetting clusters are not a part of this front, so that the different trapping rules do not affect its shape and statistical features but only the size of the trapped clusters that are left behind it. The standard tools of percolation theory should thus apply to describe the front. The match between the theory we now develop and the invasion percolation simulations with cluster trapping that we present in the next sections will confirm this hypothesis.

Let us now consider a stable invasion. In this case, a position x1 exists were the capillary pressure is equal to the critical capillary pressure such that

$$p={p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1}).$$
(5)

We can also Taylor expand N(pt, x) around the critical pc(x1) in Eq. (4) keeping only the lowest order in p − pc(x1) such that

$$f(x)-{f}_{{{{{{{{\rm{c}}}}}}}}}=N({p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1}),x)[{p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1})-{p}_{{{{{{{{\rm{c}}}}}}}}}(x)].$$
(6)

Expanding pc(x) to first order in x − x1

$${p}_{{{{{{{{\rm{c}}}}}}}}}(x)={p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1})+{\left.\frac{\partial {p}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right\vert }_{{x}_{1}}(x-{x}_{1}),$$
(7)

we get

$$f(x)-{f}_{{{{{{{{\rm{c}}}}}}}}}=-N({p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1}),x){\left.\frac{\partial {p}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right\vert }_{{x}_{1}}(x-{x}_{1}).$$
(8)

Now, ∂pc(x)/∂x will contain one term from the gradient in the critical capillary pressure \(\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)/\partial x\) of the porous medium plus the term G, which is due to the external linear field. This gives

$$f(x)-{f}_{{{{{{{{\rm{c}}}}}}}}}=aN({p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1}),x)\left({\left.G-\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right\vert }_{{x}_{1}}\right)\frac{x-{x}_{1}}{a}.$$
(9)

Here, we have introduced a as the typical length of a pore. We now choose x such that η = ∣x1 − x∣, where η is the width of the front. We here write η = x1 − x > 0, which corresponds to an invasion flow that progresses against the x direction if f(x) < fc. The opposite convention for x could have, of course, also been chosen. Furthermore, we use Sapoval’s assumption28, that η scales in the same way as the correlation length ξ in percolation, (ξ/a) ∝ ∣f − fc∣−ν, where ν is a critical exponent typically equal to 4/3 for 2D systems26. We obtain \((\eta /a)\propto {({f}_{{{{{{{{\rm{c}}}}}}}}}-f)}^{-\nu }\) and then, with Eq. (9), we find

$$\eta /a\propto {F}^{\frac{-\nu }{1+\nu }},$$
(10)

where the exponent β = ν/(1 + ν) is about 0.57. For a 3D system, β would be approximately 0.47, with ν ~ 0.8826. We call the quantity F the fluctuation number, which is given by

$$F(x)=a(x)N\left({p}_{{{{{{{{\rm{c}}}}}}}}}({x}_{1}),x\right)\left({\left.G-\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right\vert }_{{x}_{1}}\right).$$
(11)

F is a dimensionless number dictating the invasion process. It is a generalisation of the fluctuation number introduced by Måløy et al.10, Méheust et al.17 and Auradou et al.16. The quantity 1/N(pc, x) characterises the typical width of the capillary threshold fluctuations, and, in the scenario of interest in our experiments, \(a(G-\partial \hat{p}/\partial x)\) characterises the gravitational forces at the pore scale, corrected for the particular structure of the porous matrix. If the material disorder is important relatively to the gradient term, such a gradient becomes negligible at small scales (and reciprocally).

One can compare F to other dimensionless numbers usually used to predict flow patterns in porous materials. In our case, a relevant one would for instance be the Bond number29 \({{{{{{{\rm{Bo}}}}}}}} \sim {a}^{2}G/[\gamma \cos (\phi )]\), which compares the gravitational forces to the capillary ones. Previous works13,18 have proposed imbibition and drainage front widths to indeed scale as Bo−ν/(1+ν). Yet, and contrarily to F, the Bond number does not offer, a priori, any insight on the actual material disorder (e.g., N) or on an eventual structural trend (e.g., \(\partial \hat{p}/\partial x\)). We suggest that the Bond number could indeed sometimes help characterise the flow patterns in gravitational fields, because for regular enough geometries of the porous network (in particular without structural gradient), Bo does scale as F (see Supplementary Note 1). If one would, however, compare matrices with different distributions of disorder (N), such a direct scaling would fail. Furthermore, in the case where a matrix does hold a structural gradient, and where no external field applies (e.g., no gravity) the invasion can both be stable or unstable depending on the relative directions of the flow and the gradient, as we illustrate in the next sections. There, Bo is - by contrast - always null, and an accurate stability prediction based on this number only would then be impossible.

As shown in Fig. 2a, our model was designed so that the dimensionless distribution \(\tilde{N}({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}/{\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x))={\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)\cdot N({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}},x)\) is conserved along the x direction (i.e., it does not depend on x). Additionally, the pore throats in many media is to scale the same way as the size of the pores a. We can then write, as per the Young-Laplace law, \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)\propto \gamma \cos (\phi )/a(x)\). Note that, in case of 2D models such as ours, this last expression is only strictly valid if the height of the system is big enough respective to the pore size (i.e., h ≫ a), which in our model is correct for the smallest pores but is a brave assumption for the biggest ones for which h ~ a. This assumption, however, allows to rewrite Eqs. (10) and (11) as:

$$\eta \propto {\left[\frac{\tilde{N}(1)}{\gamma \cos (\phi )}\left(G-\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right)\right]}^{-\beta }\times {a}^{-2\beta +1}.$$
(12)

Here, the dependence in x1 of the gradient in percolation pressure has been removed, assuming a model where this pressure is perfectly linear in x (that is, a model where the first-order expansion leading to Eq. (7) is exact). The exponent − 2β + 1 is close to 0 so that the effect of the pore size a on the width of the front is small compared to that of the other terms.

This last expression is only a particular case of Eqs. (10) and (11), where the front width does not significantly evolve as the invasion progresses. In a more general porous material, the spatial distribution in pore size a(x) and/or in pore invasion threshold N(pc, x) would matter.

Experimental results

From Eqs. (10) and (11), we see that a negative gradient in the critical capillary pressure threshold will stabilise the front while a positive gradient will make it more unstable. In this sentence, the underlying convention is that the direction defining the gradient is opposing the general flow direction. This is illustrated in Fig. 3 that shows two drainage experiments in such configurations. In Fig. 3a we have a negative gradient in the critical capillary pressure threshold and the front is stabilised while in 3b the gradient is positive (the inlet and outlet having been swapped) and the front is unstable with a growing finger. In both cases the external (gravity) field is null. The stabilisation/destabilisation of the front is also reflected in the breakthrough time, which was about three times smaller in the case with the destabilising gradient (the externally imposed flow rate was the same for both experiments). Numerically analysing the images, we indeed measured that, in Fig. 3b, only 20% of the wetting phase is drained, while 65% is drained in Fig. 3a.

Fig. 3: Drainage experiments in a 3d printed quasi two-dimensional model.
figure 3

In each photograph, air has invaded the model from the top of the pictures, replacing a water-glycerol solution coloured with nigrosin. All sides of the models are of dimension L = 140 mm. In a, \(\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)/\partial x \, < \,0\), which corresponds to a decrease in `permeability' as the flow progresses (the air invades from the big pores to the small ones). The invasion is stable. In b, \(\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)/\partial x \, > \,0\), which corresponds to an increase in `permeability' with the flow progression and an unstable processes. In both cases, the model is horizontal (G = 0). c and d show the same experiments in a chosen destabilising or stabilising gravity field (respectively) with tilt angle − 2θeq (see Fig. 1 and 2). The stability of the flow is thus reversed.

Full size image

In Fig. 3c and d, we show the same experiments in a particular gravity field. The model is tilted with an angle \(-2{\theta }_{{{{{{{{\rm{eq}}}}}}}}}=-2\arcsin (\frac{-\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}/\Delta \rho {g}_{0})\) as explained in Fig. 2, which effectively inverses the sign of the \(\left(G-\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right)\) term in Eq. (11).

We should here restate that Eq. (11) only applies to the cases where the front is stable (i.e., to Fig. 3a and d) as front stability was an underlying hypothesis (to write Eq. (5)). As expected, for these two different experiments for which the fluctuation number F is the same, the features of the invasion front are very similar. In the case of unstable fronts, we suggest that, the fluctuation number could characterise the width of the invading fingers, rather than the width of the front. Indeed, in gravitational drainage experiments, such a finger width was indeed proposed15,30 to scale with the Bond number, with the same exponent β, which we have here considered. In the case of the drainage of a matrix with a structural gradient (that is of interest here), this hypothesis will be further verified with the help of invasion percolation simulations.

Invasion percolation simulations

Stabilising gradient

Fully validating Eq. (12) with experimental results remained a challenge. Indeed, because of the maximum size (~30 cm) of the models we could print, and because of the minimum distance between printed grains (a fraction of a millimetre) before they tended to unexpectedly merge, the range of gradient in capillary pressure that could be investigated was small. Owing to the theoretical scaling between such gradient and the front width (i.e., Eq. (12)), the range in obtainable η was even smaller. Therefore, to verify our theoretical framework, we ran a series of invasion percolation simulations with cluster trapping, known to represent well capillary invasion processes.

These simulations are performed on square lattices (indexed along x and y directions), which abide by the same conditions that underlie Eq. (12). At a given x, the distribution N in invasion threshold \({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}\) for a pixel is random and uniformly distributed. Similarly to Fig. 2 the mean values of these distributions follow an arbitrary gradient along x but the width of the distributions is such that \(\tilde{N}({p}_{{{{{{{{\rm{t}}}}}}}}}/\hat{{p}_{{{{{{{{\rm{c}}}}}}}}}})\) is conserved along this same direction. Additionally, the size a(x) of a pixel scales as \(1/\hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}(x)\). Here, because our matrices’ connectivity is 4, the percolation pressure \({\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}\) is such that26,31\(\int\nolimits_{0}^{{\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}}N({\hat{p}}_{{{{{{{{\rm{t}}}}}}}}})\,{{{{{{{\rm{d}}}}}}}}{\hat{p}}_{{{{{{{{\rm{t}}}}}}}}}=0.5\). More details on the simulations can be found in the Methods section and the numerical code is available on a public repository32.

We ran ten simulations in the stable invasion domain and without external field (\(\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x \, < \,0\) and G = 0), varying the gradient in percolation pressure, but also the average size of the pixel a in the model and the local width of the distribution in invasion threshold \(1/\tilde{N}(1)\). We thus covered four decades of \(\tilde{N}(1)\times \partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x \, < \,0\) and two decades of a. Additionally, we ran six simulations where a linear external field (G) modifies the local fluid pressure, in a way that the invasion remains stable (i.e., \(G-\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x \, > \,0\), although the respective sign of both terms may vary from one simulation to the other). For each simulation, we extracted the simulated front width η, once it reached a plateau after enough time steps. We defined this width as the standard deviation of the x coordinate of the front between the invading phase and the main cluster of the defending phase (see Fig. 4).

Fig. 4: Invasion percolation simulations—stabilising gradient.
figure 4

a to c: invasion percolation maps for the three simulations denoted in d, that have different stabilising gradient in invasion threshold. The invading non-wetting phase occupies the white pixels. The plain (red) line is the drainage front on which the width η is computed. Length are in an arbitrary unit, denoted a.u. d: Width of the front as a function of the pore size a, of the gradient \(\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x\), of the external field G and of the local distribution in capillary pressure \(\tilde{N}\) (logarithmic scales). Each data point was computed on an independent simulation. Crosses represent simulations with only a structural gradient in pore threshold (G = 0), whereas circles mark simulations also including an external field (G varying from −10−4 to +100 a.u. depending on the simulation). The grey plane is a fit of Eq. (12). The slopes of this plane along the two axes are given by −β and by 1 −2β, respectively, and both indicate β = 0.56 ± 0.02.

Full size image

Finally, with a least squares method, we fitted Eq. (12) to the obtained data in order to invert for the β exponent. This procedure provided a good fit of the simulated data with a coefficient of determination R2 ~ 0.998, and we found β ~ 0.56 ± 0.02, where the accuracy of the fit is computed by letting R2 vary by 5%. This value for β is satisfyingly close to our theoretical prediction for percolation theory (β = 0.57).

Destabilising gradient

We also ran similar simulations, but in the unstable case, that is, with \(G-\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x \, < \,0\). We varied the same parameters (i.e., \(\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x\), \(\tilde{N}\), a and G). In this unstable configuration, rather than characterising the width of a stable front, we characterised the average width W of the growing invasion finger. We defined such a width as W = A/l, where A is the area occupied by the finger (i.e., the area surrounded by the plain red lines in Fig. 5, in which the results are shown) and l is the length of the finger along the x direction. Comparing Figs. 4 and 5, one can notice how similar is the scaling of W and η. Although Eq. (12) was only formally derived for stable fronts, we then analogously write for the width of the fingers in the unstable scenario:

$$W\propto {\left[\frac{\tilde{N}(1)}{\gamma \cos (\phi )}\left(-G+\frac{\partial {\hat{p}}_{{{{{{{{\rm{c}}}}}}}}}(x)}{\partial x}\right)\right]}^{-\beta^{\prime} }\times {a}^{-2\beta^{\prime} +1},$$
(13)

when the same assumptions for the matrix structure than those underlying Eq. (12) are respected. Fitting this expression to our simulation results, we obtained a good match (R2 ~ 0.992) for \(\beta^{\prime} \sim 0.52\pm 0.05\). This value is close to the value of β. As previously mentioned, a similar scaling of W with respect to the Bond number (rather than to F) was reported in experimental observations of unstable drainage fingers growing in a gravitational field15,30,33. Our simulations suggest that, when possible, one should consider our defined fluctuation number instead.

Fig. 5: Invasion percolation simulations—destabilising gradient.
figure 5

a and b: Invasion percolation maps for the two simulations denoted in c, that have different destabilising gradient in invasion threshold. The invading non-wetting phase occupies the white pixels. The plain (red) line is the drainage front on which the width W is computed. Length are in arbitrary unit, denoted a.u.. c Width of the finger as a function of the pore size a, of the gradient \(\partial \hat{{p}_{{{{{{{{\rm{c}}}}}}}}}}/\partial x\), of the external field G, and of the local distribution in capillary pressure \(\tilde{N}\) (logarithmic scales). Each data point was computed on an independent simulation. Crosses represent simulations with only a structural gradient in pore threshold (G = 0), whereas circles mark simulations also including an external field, (G varying from −10−3 to −10−1 a.u. depending on the simulation). The grey plane is a fit of Eq. (13). The slopes of this plane along the two axes are given by \(-\beta^{\prime}\) and by \(1-2\beta^{\prime}\), respectively, and both indicate \(\beta^{\prime} =0.52\pm 0.05\).

Full size image

Note that, either for the stable or the unstable drainage case, the most general formalism that has been introduced in this article, for the scaling law of the flow patterns, is given by Eq. (10) rather than by Eq. (12) or Eq. (13). Figure 6 then displays the dependence of either η/a or W/a with the fluctuation number F in our numerical simulations, showing good agreement with the theory.

Fig. 6: Scaling of the flow patterns with the fluctuation number.
figure 6

Illustration of expression (10), which is here the most general formalism for the scaling of the size of the flow pattern with the fluctuation number, as defined by (11). The numerical results of Figs. 4 and 5 are shown (crosses and circles) and fitted with power laws (dotted line) for, respectively, the stable (a) and the unstable (b) drainage cases. Crosses represent simulations with only a structural gradient in pore threshold (G = 0), whereas circles mark simulations also including an external field.

Full size image

Conclusion

In this paper, we have discussed the importance of capillary fluctuations in porous media, as well as the characteristic length scales in two-phase flow patterns set by the competition between capillary fluctuations, external fields (e.g., gravitational or viscous ones) and a gradient in the matrix percolation pressure.

In the case of fluid fronts that are stabilised by these fields and porous media geometry, the fluctuation number F, which describes the scaling of the front width η, was introduced. There, the derived scaling exponents directly result from percolation theory. When considering a viscous and gravitational field, the theory describes well the scaling of the width of the fluid front and the final saturation of the fluid left behind the invasion front observed in laboratory experiments10. As shown here, it can also predict the stabilisation and destabilisation of the front width in such experiments depending on the sign of the spatial gradient in the critical capillary pressure. Truly, more experiments are needed to conduct a quantitative experimental investigation of the dependence of the scaling of the front width η when a structural gradient is present, the challenge being to obtain a permeability gradient varying over several decades in the laboratory. Standard invasion percolation simulations have, however, here underlined how reasonable the predicted scaling law is. In the case of a destabilised flow, these simulations also enabled us to infer a similar scaling law for the width of growing drainage fingers.

On a length scale smaller than η, the structure within the front is generally fractal, while on a length scale larger than η, it is homogeneous. The characteristic length scale η should thus be of primary importance in defining a relevant representative elementary volume (REV) for an average Darcy description of the two-phase flow problem34. We suggest that characterising the fluctuation number F, for instance from drilled core samples in geological contexts, would help in this prediction of the front width. Estimating the actual distribution in pore throats, needed to derive N, can indeed be achieved with various experimental techniques35,36. One could also characterise the relationship between the fluids’ pressures and saturations for systems with structural gradients, by extending the approach of Moura et al.31 and Ayaz et al.34. A good knowledge of this relationship is indeed relevant for reservoir geophysicists and hydrologists.

In these geological applications, one should also consider the usual repeating sequences of sediment layers with a gradient in permeability in a given direction. This is for instance often observed in fluvial or turbidite deposition24. There, if the gradient inside a single unit is stabilising, a change in layer would yet correspond to a local but brutal destabilising effect (and reciprocally). Predicting the flow behaviour over large distances would thus likely require to take into consideration the typical wave lengths of such layer repetitions, and compare them to the typical length scale η of the invading pattern. Such a study would be a natural continuation of the present work.

Methods

Experimental method

To generate our porous model, we have used a Formlabs Form 3L printer37, which employs a stereolithography 3D printing technology to produce objects in a transparent plastic material (Formlabs Clear Resin), composed of methacrylic acid esters and photoinitiators. This technique is based on the laser polymerisation of the resin. It allows to control the geometry of the porous network and in particular to fine-tune its grain and pore-throat distributions, for example by introducing a gradient in the pore sizes. In practice, cylinders are distributed in a monolayer using a Random Sequential Adsorption (RSA) algorithm25. The cylinders are printed within a frame (which is part of the total print) closing the sides and bottom of the porous medium so that only the top of the cylinders are not sealed. Pipe connectors are also included (i.e., printed) at the inlet and outlet of this frame to facilitate the connection of the model in the experimental set-up. The spatial resolution of the printed models is about 0.1 mm. All the RSA parameters are specified in the manuscript.

The model is mounted in a flow cell, which was constructed around the print, in a way that optimises the visualisation of the pores. The 3D printed model is inserted between two layers of a soft polymer (polyvinyl chloride, PVC-2mm thick) whose main role is to efficiently seal the top of each cylinder. Around these soft layers two 3-cm thick PMMA plates are screwed together to confine the flow. On the side, the model is closed by 3D printed walls. The tubular inlet and the outlet of the model feed large channels along the whole model width so that the boundary conditions are the same along this direction. Each layer is transparent and the flow cell lies on a white light box to allow a good quality imaging with a reflex camera.

The invading fluid is air and the defending one is a mixture of 20% water and 80% glycerol, where the percentages relate to the total mass. In this mixture a nigrosin dye has been added (4 g per litre of water) to create an imaging contrast between the air and the liquid. The coloured mixture is the wetting phase, with a contact angle to the solid resin of 60 ± 10∘ in presence of air (measured optically on several droplets). The wettability of the soft PVC plate sealing the top of the printed cylinders was inferred to be similar. With a syringe pump, the wetting liquid mixture is withdrawn at a constant flow rate from one of the two model’s ends while the air, connected to the atmospheric pressure of the laboratory, invades the model. We used a 0.3 ml/h flow rate.

Numerical method

The invasion percolation simulations are performed on square lattices (indexed along x and y directions), which abide by the same conditions that underlie Eq. (12). At the initial simulation stage, solely the first line of the matrix (the inlet) is invaded, so that the initial invasion front is a straight line. The pixels’ connectivity is four, so that a pixel is connected to its top, bottom, right and left neighbours. On the side of the matrix, pixels have only three neighbours, and, in the corners, only two. At each time step, one new pixel is invaded. This pixel is the neighbour of the invading phase that has the lowest invasion threshold and which is still connected to the matrix outlet (i.e., it is not trapped). The invasion front is recomputed after the invasion of each pixel and the simulation stops when the front reaches the last line of the matrix.