Synchronization induced by directed higher-order interactions

Abstract

Non-reciprocal interactions play a crucial role in many social and biological complex systems. While directionality has been thoroughly accounted for in networks with pairwise interactions, its effects in systems with higher-order interactions have not yet been explored as deserved. Here, we introduce the concept of M-directed hypergraphs, a general class of directed higher-order structures, which allows to investigate dynamical systems coupled through directed group interactions. As an application we study the synchronization of nonlinear oscillators on 1-directed hypergraphs, finding that directed higher-order interactions can destroy synchronization, but also stabilize otherwise unstable synchronized states.

Introduction

Network science is a powerful and effective tool in modeling natural and artificial systems with a discrete topology. The study of dynamical systems on networks has thus triggered the interest of scientists and has spread across disciplines, from physics and engineering, to social science and ecology^1,2,3. Network models rely on the hypothesis that the interactions between the units of a system are pairwise⁴. However this is only a first order approximation in many empirical systems, such as protein interaction networks^5,6, brain networks^7,8,9,10, social systems^11,12 and ecological networks^13,14,15, where group interactions are widespread and important. Recent years have thus witnessed an increasing research interest for more complex mathematical structures, such as simplicial complexes and hypergraphs^{4,16,17,18,19}, capable of encoding many-body interactions. These systems have been used to investigate various dynamical processes, such as epidemic and social contagion^20,21,22, random walks^23,24, synchronization^25,26, consensus^27,28 and Turing pattern formation²⁹, to name a few. However, the proposed formalism is not general enough to describe systems where the group interactions are intrinsically asymmetric. For instance, group pressure or bullying in social systems have an asymmetric nature, due to the fact that group interactions are addressed against one or more individuals but (often) not reciprocated³⁰. (Bio)chemical reactions are another typical example of higher-order directed processes, as, though some reactions can be reversible, there is often a privileged direction due to thermodynamics^5,31. Further examples come from the ecology of microbial communities, where a direct interaction between two species can be mediated by a third one^32,33.

Although including some form of directionality in higher-order structures is not entirely new^5,34, the few existing attempts to study the effects of directionality on dynamical processes all suffer from a series of limitations. For example, in the case of oriented hypergraphs, where the nodes of each hyperedge are partitioned into an input and an output set (not necessarily disjoint), because of the underlying assumptions, one ultimately gets symmetric operators (e.g., the adjacency or the Laplacian matrix) despite one would expect directed interactions to yield asymmetric ones^35,36,37. Furthermore, in the case of simplicial complexes^38,39,40,41 an orientation has been introduced with the purpose of defining (co-)homology operators, but is not associated to directionality, i.e., the Laplacian matrix is once again symmetric.

Here we introduce the framework of M-directed hypergraphs, which naturally leads to an asymmetric higher-order Laplacian and allows to study the dynamics of systems (e.g., nonlinear oscillators) with higher-order interactions, fully accounting for their directionality. In this article, we focus, in particular, on synchronization, a phenomenon of utmost importance in many natural and artificial networked systems⁴². In order to assess the stability of a synchronized state, we determine conditions under which a Master Stability Function (MSF) approach^43,44,45 can be generalized to such directed higher-order structures. As we will show in the following, the complex spectrum of the asymmetric Laplacian operator entering into the MSF has a strong impact on the system behavior. Indeed, we can determine cases where the presence of directionality in higher-order interactions can destabilize the complete synchronized state of the system, otherwise obtained with reciprocal, i.e., symmetric coupling. Analogously, we also find cases where the opposite behavior is observed, i.e., higher-order directionality is the main driver for the onset of synchronization.

Results

M-directed hypergraphs allow to model directionality in higher-order interactions

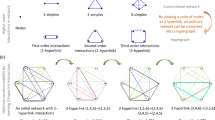
To introduce the framework we start by defining a 1-directed d-hyperedge as a set of (d + 1) nodes, d of which, the "source” nodes, "point” toward the remaining one. Let us observe that we used the notation where a d-hyperedge represents the interactions among d + 1 agents (this is similar to the notation adopted for simplicial complexes, where a d-simplex models the interactions of d + 1 agents, while, often, for hypergraphs a d-hyperedge accounts for the interactions among d agents¹⁸). In this way, an undirected d-hyperedge can be seen as the union of (d + 1) directed ones (see Fig. 1). Notice that this is a natural extension of the network framework, in which a pairwise undirected interaction can be decomposed into two directed interactions. A 1-directed d-hyperedge, where the source nodes j₁, j₂, … , j_d point toward node i, can be represented by an adjacency tensor A^(d) with the following property

$${A}_{i{j}_{1}\ldots {j}_{d}}^{(d)}=1\Rightarrow {A}_{i\pi (\,{j}_{1}\ldots {j}_{d})}^{(d)}=1,$$

(1)

where π( j₁ …, j_d) is any permutation of the indices j₁, …, j_d (Fig. 1). Observe that a generic permutation involving also index i does not necessarily imply a nonzero entry in the adjacency tensor, i.e., A^(d) is in general asymmetric. Note however that the (d − 1)-th rank tensors obtained by fixing the first index of A^(d) are symmetric. By 1-directed D-hypergraph we define a hypergraph formed by 1-directed d-hyperedges of any size d smaller or equal to D. Note that these definitions provide a formalization in terms of tensors of the concepts of B-arc and B-hypergraph introduced by Gallo et al.³⁴. Indeed, as it will be clear later on, our results strongly rely on the properties of such tensors.

Fig. 1: Elementary decomposition of undirected hyperedges.

An undirected 2-hyperedge can be seen as the composition of three directed hyperedges. In each of the three directed 2-hyperedges, the nodes acting as source of the interaction are interchangeable, i.e., switching them does not alter the nature of the interaction. Therefore, the adjacency tensors A⁽²⁾ is symmetric to a permutation of the indices corresponding to the source nodes.

Following the same reasoning, we can define an m-directed d-hyperedge, for some m ≤ d, as a set of (d + 1) nodes, a subset of which (formed by s = d + 1 − m units) points toward the remaining m ones. Resorting again to the adjacency tensor we can write

$${A}_{\pi ({i}_{1}\ldots {i}_{m})\pi ^{\prime} (\,{j}_{1}\ldots {j}_{s})}^{(d)}=1,$$

(2)

where π(i₁ … i_m) is any permutation of the indices i₁, …, i_m and $\pi ^{\prime} (\,{j}_{1}\ldots {j}_{s})$ is any permutation of the indices j₁, …, j_s. In analogy with the former case, a permutation where one or more of the indices i₁, …, i_m appear in a position other than the first m, may result in a zero entry of the adjacency tensor. By indicating with M the largest value of m, and with D the largest value of d, we can then define an M-directed D-hypergraph (or M-directed hypergraph of order D). The framework above can be straightforwardly extended to the case of weighted directed hypergraphs.

M-directed hypergraphs are applied to dynamical systems with asymmetric higher-order interactions

Let us now consider the dynamics of N identical units coupled through a 1-directed hypergraph of order D, with D ≥ 2. The equations governing the system can be written as

$${\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}={{{{{{{\bf{f}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}_{{{{{{{{\bf{i}}}}}}}}})+\mathop{\sum }\limits_{d=1}^{D}{\sigma }_{d}\mathop{\sum }\limits_{{j}_{1},\ldots ,{j}_{d}=1}^{N}{A}_{i{j}_{1}\ldots {j}_{d}}^{(d)}{{{{{{{{\bf{g}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},{{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}),$$

(3)

where ${{{{{{\bf{x}}}}}}}_{i}(t)\in {{\mathbb{R}}}^{m}$ is the state vector describing the dynamics of unit i, σ₁, … , σ_D > 0 are the coupling strengths, ${{{{{{{\bf{f}}}}}}}}:{{\mathbb{R}}}^{m}\to {{\mathbb{R}}}^{m}$ is a nonlinear function that describes the local dynamics, while ${{{{{{{{\bf{g}}}}}}}}}^{(d)}:{{\mathbb{R}}}^{m\times (d+1)}\to {{\mathbb{R}}}^{m}$, with d ∈ {1, …, D}, are nonlinear coupling functions encoding the (d + 1)-body interactions. Let us now assume that the coupling functions at each order d are diffusive-like

$${{{{{{{{\bf{g}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},{{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})={{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})-{{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{i}),$$

(4)

with ${{{{{{{{\bf{h}}}}}}}}}^{(d)}:{{\mathbb{R}}}^{m\times d}\to {{\mathbb{R}}}^{m}$, to ensure the existence of a synchronized (invariant) solution x^s = x₁ = ⋯ = x_N, i.e., the synchronization manifold. Diffusive coupling is common in many systems⁴⁶, being such assumption not particularly restrictive. However, it can be further relaxed to the milder requirement that the coupling functions are non-invasive, i.e., g^(d)(x, x, …, x) ≡ 0, ∀ d, which still guarantees the existence of the invariant solution⁴⁵. In addition, let us also assume that the coupling functions h^(d) satisfy the condition of natural coupling^45,47, namely

$${{{{{{{{\bf{h}}}}}}}}}^{(D)}({{{{{{{\bf{x}}}}}}}},\ldots ,{{{{{{{\bf{x}}}}}}}})=\cdots ={{{{{{{{\bf{h}}}}}}}}}^{(2)}({{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{x}}}}}}}})={{{{{{{{\bf{h}}}}}}}}}^{(1)}({{{{{{{\bf{x}}}}}}}}).$$

(5)

This second assumption turns out to be crucial to derive a Master Stability Equation (MSE) to characterize the synchronization (see Methods) and disentangle the effect of the directionality of the higher-order interactions on it.

For sake of definiteness, in the following we focus on the synchronization of identical oscillators coupled via 1-directed hypergraphs, whose adjacency tensors A^(d) respect the symmetry property (1). Let us thus denote by x^s(t) the synchronous state, which is solution of the decoupled systems ${\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}={{{{{{{\bf{f}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}_{i})$. From Eq. (4), it immediately follows that the former is also solution of the coupled system. To characterize the synchronization of the coupled system, a linear stability analysis can be performed. To this aim, we linearize Eqs. (3) around x^s(t), by considering small perturbations δx_i = x_i − x^s, and, since the time evolution of these variables determines the stability of the synchronous solution, we study their dynamics. In particular, it is convenient to introduce the stack vector $\delta {{{{{{{\bf{x}}}}}}}}={[\delta {{{{{{{{\bf{x}}}}}}}}}_{1}^{\top },\ldots ,\delta {{{{{{{{\bf{x}}}}}}}}}_{N}^{\top }]}^{\top }$, whose dynamical equation under the hypothesis of natural coupling can be derived with a series of steps detailed in Methods, obtaining

$$\delta \dot{{{{{{{{\bf{x}}}}}}}}}=\left[{{\mathbb{I}}}_{N}\otimes {{{{{{{\bf{JF}}}}}}}}-{{{{{{{\mathcal{M}}}}}}}}\otimes {{{{{{{\bf{JH}}}}}}}}\right]\delta {{{{{{{\bf{x}}}}}}}}$$

(6)

where JF (resp. JH), is the Jacobian matrix associated to the function f (resp. h⁽¹⁾), evaluated on the synchronous state x^s. Note that, because of the natural coupling (5), the Jacobians of h⁽¹⁾,… ,h^(D) evaluated on x^s are all equal, and this is key to write Eq. (6). In (6), the matrix ${{{{{{{\mathcal{M}}}}}}}}$ is given by

$${{{{{{{\mathcal{M}}}}}}}}={\sigma }_{1}{{{{{{{{\bf{L}}}}}}}}}^{(1)}+{\sigma }_{2}{{{{{{{{\bf{L}}}}}}}}}^{(2)}+...+{\sigma }_{D}{{{{{{{{\bf{L}}}}}}}}}^{(D)}.$$

(7)

where L^(d) is the generalized Laplacian matrix for the interactions of order d defined by

$${L}_{ij}^{(d)}=\left\{\begin{array}{ll}d!{k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)\hfill\quad &i=j\\ -(d-1)!{k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i,j)\quad &i\,\ne\, j,\end{array}\right.$$

(8)

with ${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)$ being the generalized d-in-degree of node i

$${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)=\frac{1}{d!}\mathop{\sum }\limits_{{j}_{1},..,{j}_{d}=1}^{N}{A}_{i{j}_{1}\ldots {j}_{d}}^{(d)},$$

(9)

namely the number of d-hyperedges pointing to node i, and ${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i,j)$ the generalized d-in-degree of a couple of nodes (i, j)

$${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i,j)=\frac{1}{(d-1)!}\mathop{\sum }\limits_{{k}_{1},...,{k}_{d-1}}^{N}{A}_{ij{k}_{1}\ldots {k}_{d-1}}^{(d)}.$$

(10)

The latter represents the number of d-hyperedges pointing to node i and having node j as one of the source nodes. Let us stress that, because the adjacency tensor A^(d) is asymmetric, the Laplacian matrix L^(d) is asymmetric as well. This matrix represents the generalization to the directed case of the Laplacian matrix introduced for undirected higher-order interactions^17,45.

As an equivalent formulation, we rewrite Eq. (6) as follows

$$\delta \dot{{{{{{{{\bf{x}}}}}}}}}=\left[{{\mathbb{I}}}_{N}\otimes {{{{{{{\bf{JF}}}}}}}}-{\sigma }_{1}\widetilde{{{{{{{{\mathcal{M}}}}}}}}}\otimes {{{{{{{\bf{JH}}}}}}}}\right]\delta {{{{{{{\bf{x}}}}}}}}$$

(11)

with $\widetilde{{{{{{{{\mathcal{M}}}}}}}}}$ given by

$$\widetilde{{{{{{{{\mathcal{M}}}}}}}}}={{{{{{{{\bf{L}}}}}}}}}^{(1)}+{r}_{2}{{{{{{{{\bf{L}}}}}}}}}^{(2)}+...+{r}_{D}{{{{{{{{\bf{L}}}}}}}}}^{(D)},$$

(12)

and where r_i = σ_i/σ₁, i = 2, …, D. Eq. (11) highlights the analogy between synchronization in directed hypergraphs with natural coupling functions and synchronization in networks. In facts, once fixed the parameters r_i, the equations governing the dynamics of the perturbations in a directed hypergraph are formally equivalent to those of a system with weighted, directed pairwise interactions among the units, coupling coefficient equal to σ₁, and a Laplacian matrix given by $\widetilde{{{{{{{{\mathcal{M}}}}}}}}}$. As both formulations (6) and (11) are equivalent, for convenience hereby we conclude the discussion on the analysis of the linearized system referring back to Eq. (6), while Eq. (11) will turn out useful in the numerical investigation, where, by fixing r_i, we can focus the analysis on the behavior as a function of σ₁.

Assuming for simplicity that ${{{{{{{\mathcal{M}}}}}}}}$ is diagonalizable, we can project Eq. (6) onto each of its eigenvectors, obtaining in this way N decoupled m-dimensional linear equations, parametrized by the corresponding eigenvalue, from which the following generic MSE can be written

$$\dot{{{{{{{{\boldsymbol{\xi }}}}}}}}}=[{{{{{{{\bf{JF}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}^{s})-(\alpha +{{{{{{{\rm{i}}}}}}}}\beta ){{{{{{{\bf{JH}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}^{s})]{{{{{{{\boldsymbol{\xi }}}}}}}}.$$

(13)

Note that, since the generalized Laplacian matrices are asymmetric, the effective matrix ${{{{{{{\mathcal{M}}}}}}}}$ will also be asymmetric, therefore it will have in general complex eigenvalues, motivating thus the use of the complex parameter α + iβ. From the MSE, the maximum Lyapunov exponent ${{{\Lambda }}}_{\max }$ can be calculated as a function of the complex parameter α + iβ. Stability requires that ${{{\Lambda }}}_{\max }(\alpha +{{{{{{{\rm{i}}}}}}}}\beta ) \, < \, 0$ where α + iβ is any non-zero eigenvalue of ${{{{{{{\mathcal{M}}}}}}}}$. The same condition on stability can be also found when ${{{{{{{\mathcal{M}}}}}}}}$ is not diagonalizable, provided to consider an approach analogous to that introduced in Nishikawa et al.⁴⁸ for networks of directed pairwise interactions and based on Jordan block decomposition in place of diagonalization. In such framework, the crucial step is to identify the matrix, which in our case is ${{{{{{{\mathcal{M}}}}}}}}$, that provides the eigenvalues to consider in checking the condition ${{{\Lambda }}}_{\max }(\alpha +{{{{{{{\rm{i}}}}}}}}\beta ) \, < \, 0$.

The linear stability analysis that leads to Eq. (13) can be carried out following steps similar to those performed in Gambuzza et al.⁴⁵ for undirected simplicial complexes. These steps can be straightforwardly generalized to deal with undirected hypergraphs. Instead, for directed hypergraphs the asymmetry of the adjacency tensors must be taken into account. In fact, in this case, the adjacency tensors are not symmetric with respect to all their indices. However, the property (1) still allows the derivation of generalized Laplacian matrices, extending the formalism presented in Gambuzza et al.⁴⁵. The interested reader can find the detailed calculations in Methods.

Despite the formal similarities of the equations for synchronization in hypergraphs and in simplicial complexes, we emphasize that in the two scenarios different dynamical behaviors can be obtained. For instance, due to the requirement that, given a simplex of order d, all the simplices of lower order included in it are present, the regions of synchronization are not identical in the two types of higher-order structures. An example of the different dynamics in the case of undirected interactions is provided in Supplementary Note 1, showing a larger region of synchronization for the simplicial complex.

A further important analysis would be to compare the dynamical behaviors of directed hypergraphs and simplicial complexes. However, at variance with hypergraphs, the introduction of directionality in simplicial complexes is disputable. In particular, a crucial aspect to solve is how to deal with the inclusion constraint, establishing whether and how it can be extended to the case of directed interactions. An attempt in this direction has been made for oriented simplicial complexes⁴⁰, where it is highlighted that a simplex and its boundary can have either concordant or opposite orientation. The definition and the study of directed simplicial complexes are beyond the purpose of the present paper, and thus left as future work.

Directed higher-order interactions can change stability behavior

Using the above introduced approach, we now illustrate the effect of higher-order directionality on synchronization by using a paradigmatic example of chaotic oscillator, i.e., the Rössler system⁴⁹. We consider a system of N coupled Rössler oscillators, whose parameters have been set to a = b = 0.2, and c = 9, so that the dynamics of the isolated system is chaotic. For sake of clarity we limited our analysis to 1-directed 2-hypergraphs, but of course its applicability goes beyond the considered case. The system of equations read

$$\left\{\begin{array}{l}{\dot{x}}_{i}=-{y}_{i}-{z}_{i}+{\sigma }_{1}\mathop{\sum }\limits_{j=1}^{N}{A}_{ij}^{(1)}\big({x}_{j}^{3}-{x}_{i}^{3}\big)+{\sigma }_{2}\mathop{\sum }\limits_{j,k=1}^{N}{A}_{ijk}^{(2)}\big({x}_{j}^{2}{x}_{k}-{x}_{i}^{3}\big)\quad \\ {\dot{y}}_{i}={x}_{i}+a{y}_{i}\hfill\quad \\ {\dot{z}}_{i}=b+{z}_{i}({x}_{i}-c),\hfill\quad \end{array}\right.$$

(14)

with i ∈ {1, …, N}. We remark that the coupling functions appearing in Eq. (14) are nonlinear and satisfy the natural coupling hypothesis.

We consider the system to be coupled through a directed weighted 2-hypergraph, whose asymmetry varies with a parameter p ∈ [0, 1], representing the relative weight of the directed hyperedges. The topology of the directed weighted 2-hypergraph is schematically illustrated in panel a of Fig. 2, for the case of a system with N = 8. When p = 0, a triplet of nodes interacts only through a single 1-directed 2-hyperedge. As p increases, so does the weight of the other two components (1-directed 2-hyperedges), up to p = 1, where an undirected hypergraph is recovered (see Methods for further details).

Fig. 2: Directionality induced (de)synchronization.

a The weighted hypergraph as a function of the parameter p, controlling the transition of the hyperedges from directed to undirected (the structure is schematically represented for N = 8 nodes). Each undirected 2-hyperedge can be seen as the combination of three directed hyperedges, two of which have a weight p ∈ [0, 1]. When p = 0, a triplet of nodes interacts only through a single directed hyperedge, whereas when p = 1, the hypergraph is symmetric. b Synchronization diagram in the plane (p, σ₁) for a system of Rössler oscillators with x-x cubic coupling, being σ₁ the coupling strength of the pairwise interactions. The white area indicates the region of stability, while the orange one the region where the synchronous solution is unstable. The horizontal dashed lines represent two values of σ₁ for which the system transits from a synchronized to an unsynchronized state as a function of p (green line), and the other way around (blue line). Panels c–f show the locus of eigenvalues of the effective Laplacian matrix ${{{{{{{\mathcal{M}}}}}}}}$ as a function of p, for a weighted hypergraph with N = 20 nodes at two different values of σ₁ (color coding is such that the directed case p = 0 is represented in yellow, and the symmetric one p = 1, in blue). In the background, the white area indicates the region identified by a negative Master Stability Function (MSF), the black line the boundary of this region, and the gray area the region where the MSF is positive. Panels d and f represent a zoom of the area close to the origin of panels c and e, respectively. Panels c and d show a setting where the symmetric topology drives the system unstable, whereas with a directed hypergraph the synchronization manifold results stable. Panels e and f display a case for which the symmetric topology admits a stable synchronization state, while the directed hypergraph triggers the instability. The coupling strength for panels c and d is set to σ₁ = 0.02, while for panels e and f to σ₁ = 0.007. In both cases we set the ratio r₂ = σ₂/σ₁ = 10, where σ₂ is the coupling strength of the three-body interactions.

To proceed with the analysis, first we calculate the MSF associated to system (14), by evaluating the maximum Lyapunov exponent, ${{{\Lambda }}}_{\max }(\alpha +{{{{{{{\rm{i}}}}}}}}\beta )$, as a function of α and β by means of the Wolf’s algorithm⁵⁰. For synchronization to be achieved, it is required that ${{{\Lambda }}}_{\max }(\alpha +{{{{{{{\rm{i}}}}}}}}\beta ) \, < \, 0$, where α + iβ is any non-zero eigenvalue of the matrix ${{{{{{{\mathcal{M}}}}}}}}$. Conversely, if there is at least a non-zero eigenvalue of ${{{{{{{\mathcal{M}}}}}}}}$ such that ${{{\Lambda }}}_{\max } \, > \, 0$, then synchronization is lost. To illustrate the effect of directionality on synchronization, we consider a directed weighted 2-hypergraph with structure as in Fig. 2a but N = 20 nodes, calculate the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ as a function of the asymmetry parameter p and the coupling strength σ₁, and check whether the stability condition is satisfied or not, in this way constructing a synchronization diagram in the plane (p, σ₁). Figure 2b shows this diagram for r₂ = σ₂/σ₁ = 10. The white area represents the values (p, σ₁) for which the system synchronizes, i.e., ${{{\Lambda }}}_{\max } \, < \, 0$ for every eigenvalue of ${{{{{{{\mathcal{M}}}}}}}}$, while the orange area depicts the region where the synchronous state is unstable, i.e., ${{{\Lambda }}}_{\max } \, > \, 0$ for at least one eigenvalue of ${{{{{{{\mathcal{M}}}}}}}}$. While there is a region where varying p at fixed values of σ₁ has no effect on synchronization, there are two other regions where this leads to a transition. In more detail, two different transitions can appear, an example of which is highlighted by the two horizontal dashed lines. For σ₁ = 0.02 the system synchronizes for small values of p, i.e, when the hypergraph is strongly directed, and loses synchronization for larger values of p, i.e., when the hypergraph becomes symmetric. Conversely, for σ₁ = 0.007 we find the opposite behavior, as synchronization is achieved by increasing p, while directed hyperedges hamper synchronization. The locus of the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ as a function of p and for two different values of σ₁, corresponding to the two types of transitions induced by directionality, is shown in the panels c–f of Fig. 2. Here, panels c and d refer to σ₁ = 0.02, while panels e and f to σ₁ = 0.007. Moreover, panels d and f show a zoom of the area close to the origin in panels c and e, respectively. In all these panels, the gray area represents the region where the MSF is positive, while the white area portrays the region of stability. Finally, the black line denotes the boundary value ${{{\Lambda }}}_{\max }(\alpha +{{{{{{{\rm{i}}}}}}}}\beta )=0$. We remark that the region of the complex plane for which ${{{\Lambda }}}_{\max }$ is negative is bounded, both along the real component, α, and the imaginary one, β. This suggests that either a large value of α, or a large value of β can lead to instability. In panels c and d, obtained for σ₁ = 0.02, we note that for large enough p the eigenvalues cross the boundary, thus leaving the stability region and inducing the desynchronization of the system. On the other hand, in panels e and f, which display the case σ₁ = 0.007, the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ leave the stability region for small values of p, namely in this case synchronization is observed for symmetric hyperedges, while directed hyperedges move the system in a region where the synchronous state is unstable.

To numerically validate this analysis, we monitor a synchronization error defined as follows:

$$E={\left\langle \sqrt{\frac{1}{N(N-1)}\mathop{\sum }\limits_{i,j = 1}^{N}\parallel {{{{{{{\bf{x}}}}}}}}-{{{{{{{{\bf{x}}}}}}}}}_{i}{\parallel }^{2}}\right\rangle }_{T}$$

(15)

where T is a sufficiently large window of time, after discarding the initial transient. In agreement with the analysis of the eigenvalues, for σ₁ = 0.02, E vanishes for p = 0, while for p = 1 it diverges. On the other hand, for σ₁ = 0.007, the synchronization error goes to zero for p = 1, while for p = 0 it again diverges after a transient. Overall, these results suggest that directionality can change the synchronization behavior of a system of coupled chaotic oscillators, either inducing synchronization in the system or desynchronizing it.

However, for a different choice of the coupling functions, a diverse synchronization behavior in relation to the structure of interactions may be obtained. For instance, if the coupling functions are ${{{{{{{{\bf{h}}}}}}}}}^{(1)}({{{{{{{{\bf{x}}}}}}}}}_{j})=[0,{y}_{j}^{3},0]$ and ${{{{{{{{\bf{h}}}}}}}}}^{(2)}({{{{{{{{\bf{x}}}}}}}}}_{j},{{{{{{{{\bf{x}}}}}}}}}_{k})=[0,{y}_{j}^{2}{y}_{k},0]$, then the resulting region of stability is unbounded, making impossible to desynchronize the system by turning the three-body interactions symmetric (Supplementary Note 2).

The results discussed so far refer to a specific example of connectivity between the oscillators. Since, once the oscillator dynamics and the coupling functions (hence the system MSF) are fixed, the main determinant for synchronization is the position of the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ with respect to the region of negative values of the MSF, understanding the effect of directionality in other structures requires the study of the spectrum of ${{{{{{{\mathcal{M}}}}}}}}$. As a systematic characterization of the spectrum as a function of the topological features of the structure is far from trivial, we limited our analysis to two random hypergraph generative models, obtained as higher-order generalization of random network models, namely the well-known Newman–Watts (NW) model and the Erdős–Rényi (ER) one. We have found that the impact of directionality on the eigenvalue position (and so ultimately on synchronization) strongly depends on the model adopted for generating the hypergraph, with the NW-like model showing a larger impact of directionality on the spreading of eigenvalues in the complex plane, when compared to the ER-like model (see Supplementary Note 3 for a detailed analysis of the two models).

Controlling for confounding factors

In the previous section, we have shown how directionality can induce either the synchronization of a system of coupled chaotic oscillators or its desynchronization. However, there may be confounding factors determining the change of the system behavior. In fact, the way in which 1-directed hypergraphs are made symmetric, namely by varying the parameter p, does not conserve the total strength of the interactions.

To determine whether the observed effects are truly due to directionality, we proceed with an alternative symmetrization method that keeps constant the total coupling strength. Starting from a 1-directed 2-hyperedge, we now add directed hyperedges in the two remaining directions with a weight q ∈ [0, 1/3], while simultaneously decreasing the strength of the initial one, setting the weight to 1 − 2q. In this way, for q = 0 we have a 1-directed 2-hyperedge with unitary weights, while for q = 1/3 we get an undirected 2-hyperedge with the same total weight, but having all hyperedges with weight equal to 1/3 (see Methods for further details). We notice that this symmetrization is analogous to that introduced by Asllani et al.⁵¹ for networks, where, starting from a directed link of weight 1, one obtains a symmetric link with the same total weight, as it is formed by two directed links, each of weight 1/2.

With this setup, we consider again a system of N = 20 Rössler oscillators coupled through the directed weighted 2-hypergraph discussed in the previous section. We then derive the synchronization diagram in the plane (q, σ₁). The diagram obtained for r₂ = σ₂/σ₁ = 0.7 is displayed in panel a of Fig. 3. Similarly to what observed with the previous symmetrization method, while there is a region where, for fixed σ₁, varying q does not affect synchronization, there are two areas where changing q leads to a transition in the synchronization behavior. For σ₁ = 0.195, highlighted in panel a of Fig. 3 as a green dashed line, the system synchronizes for small values of q, i.e, for a strongly directed hypergraph, whereas it desynchronizes for larger values of q, i.e., for a more symmetric structure. Inversely, for σ₁ = 0.03, displayed in panel a as a blue dashed line, we observe the opposite transition, as synchronization is achieved by increasing q, while directionality prevents system synchronization. The locus of the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ as a function of q and for the two different values of σ₁ is shown in the panels b–e of Fig. 3. In particular, panels b and c refer to σ₁ = 0.195, while panels d and e to σ₁ = 0.03. Panels c and e represent a zoom of the area close to the origin in panels b and d, respectively. In panels b and c, we observe that for large enough q the eigenvalues of ${{{{{{{\mathcal{M}}}}}}}}$ leave the stability region, thus inducing the desynchronization of the system. Conversely, in panels d and e, the eigenvalues leave the stability region for small values of q, meaning that synchronization is achieved for more symmetric hyperedges, while strongly directed hyperedges make the synchronization manifold unstable. In conclusion, these results confirm that directionality can change the synchronization behavior of a system of chaotic oscillators coupled through a 1-directed hypergraph, either inducing system synchronization or its desynchronization. In particular, by using the symmetrization method that preserves the total coupling strength of the interactions, we find that these transitions are due to directionality and not, or at least not only, to confounding factors.

Fig. 3: Directionality induced (de)synchronization with an alternative symmetrization method.

a Synchronization diagram in the plane (q, σ₁) for a system of Rössler oscillators with x-x cubic coupling. q is the symmetrization parameter, such that we have a directed hypergraph for q = 0, while we get an undirected sturcture for q = 1/3. σ₁ is the coupling strength of the pairwise interactions. The white area indicates the region of stability, while the orange one the region where synchronization is lost. The horizontal dashed lines represent two values of σ₁ for which the system transits from a synchronized to an unsynchronized state as a function of q (green line), and the other way around (blue line). Panels b–e display the locus of eigenvalues of the effective Laplacian matrix ${{{{{{{\mathcal{M}}}}}}}}$ as a function of q, for a hypergraph with N = 20 nodes at two different values of σ₁ (color coding is such that the directed case q = 0 is represented in yellow, and the symmetric one q = 1/3, in blue). In the background, the white area indicates the region where the Master Stability Function (MSF) is negative, the black line the boundary of this region, and the gray area the region with positive MSF. Panels c and e represent a zoom of the area close to the origin of panels b and d, respectively. Panels b and c display a setting where the symmetric topology drives the system unstable, starting from a directed hypergraph for which the synchronization manifold is stable. Panels d and e show a case for which the symmetric topology admits a stable synchronization state, while the directed hypergraph drives to instability. The coupling strength for panels b and c is fixed to σ₁ = 0.195, while for panels d and e to σ₁ = 0.03. In both cases we set the ratio r₂ = σ₂/σ₁ = 0.7, being σ₂ the coupling strength of the three-body interactions.

As discussed in the previous section, for a different choice of the coupling functions, namely ${{{{{{{{\bf{h}}}}}}}}}^{(1)}({{{{{{{{\bf{x}}}}}}}}}_{j})=[0,{y}_{j}^{3},0]$ and ${{{{{{{{\bf{h}}}}}}}}}^{(2)}({{{{{{{{\bf{x}}}}}}}}}_{j},{{{{{{{{\bf{x}}}}}}}}}_{k})=[0,{y}_{j}^{2}{y}_{k},0]$ the resulting region of stability is unbounded. In agreement with the results obtained with the first symmetrization method, turning symmetric the three-body interactions does not desynchronize the system. In this setting, it is only possible to induce desynchronization by making higher-order interactions asymmetric. This further case study is discussed in Supplementary Note 2.

Conclusion

In this paper we have introduced and described a tensor formalism to encode M-directed hypergraphs, which allows us to fully account for directionality in higher-order structures. We have then used such directed higher-order structure as substrate for coupled dynamical systems, and studied the ensuing synchronization behavior. We have shown that the latter can be analyzed by extending the Master Stability Function approach to the present framework for the particular case of 1-directed hypergraphs. We have numerically validated our theoretical results for a system of Rössler oscillators and observed that the stability of the synchronized state can be lost or gained as the asymmetry varies. Our results demonstrate that phenomena, previously observed in structures with pairwise interactions^{47,51,52,53,54,55}, also appear when directed higher-order interactions are considered.

For systems with pairwise interactions, there is a vast literature^56,57,58, showing how synchronization is actually enhanced in weighted graphs built using weighting procedures that ultimately result in determining asymmetric interactions in the network links. Few attempts have been already made to extend this study to higher-order topologies, in particular finding that structural symmetric hypergraphs can be optimally synchronizable⁵⁹. Here, however, we did not aim at using the directionality of the higher-order interactions to optimize the synchronizability of the structure, but focused on introducing the formalism to deal with directionality in higher-order interactions, in order to model systems where there is an evidence of such asymmetric and higher-order coupling, and analyze the effect of directionality on synchronization in these systems.

Our setting differs from the one recently proposed by Aguiar et al.⁶⁰. In fact, the asymmetry of the higher-order structure is here imposed only on the adjacency tensor, Eq. (1), and not directly on the higher-order coupling function as done in Aguiar et al.⁶⁰. Therefore, our formalism allows for a more general approach, as it leaves more freedom in the choice of the coupling functions. The framework and concepts here introduced pave the way to further studies on the effects of directionality in systems where empirical evidence of directed higher-order interactions has been found but not yet systematically investigated, as the proper mathematical setting for their description was lacking.

Methods

Linear stability analysis of 1-directed D-hypergraphs

Here we provide the full derivation of the Master Stability Equation (MSE), which allows to study the synchronization of a system of N identical oscillators coupled through a 1-directed D-hypergraph. Let us first write the equation describing the dynamics of the system, where, as we previously emphasized, the coupling term associated to the hyperedge provides a contribution only to the dynamics of the state vector of node i, i.e., x_i. This is different from the case of an undirected d-hyperedge where the higher-order coupling contributions appear in the derivatives of the state variables of all nodes of the hyperdege (see Fig. 4).

Fig. 4: From topology to dynamics: difference between the undirected and directed 1-hyperedge.

Panel a: the derivative of the state variables associated to each node i, j, k receives a contribution from the higher-order interaction. Panel b: only the derivative of x_i receives a contribution from the source nodes j and k, while the derivatives of the state variable of the source nodes, x_j and x_k, do not.

Taking into account the contributions from all the 1-directed d-hyperedges, d = 1, …, D, we eventually obtain

$${\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}={{{{{{{\bf{f}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}_{{{{{{{{\bf{i}}}}}}}}})+\mathop{\sum }\limits_{d=1}^{D}{\sigma }_{d}\mathop{\sum }\limits_{{j}_{1},\ldots ,{j}_{d}=1}^{N}{A}_{i{j}_{1}\ldots {j}_{d}}^{(d)}{{{{{{{{\bf{g}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},{{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})$$

(16)

where ${{{{{{{{\bf{x}}}}}}}}}_{i}(t)\in {{\mathbb{R}}}^{m}$ is the state vector describing the dynamics of unit i, σ₁, … , σ_D > 0 are the coupling strengths, ${{{{{{{\bf{f}}}}}}}}:{{\mathbb{R}}}^{m}\to {{\mathbb{R}}}^{m}$ describes the local dynamics, while ${{{{{{{{\bf{g}}}}}}}}}^{(d)}:{{\mathbb{R}}}^{m\times (d+1)}\to {{\mathbb{R}}}^{m}$, with d ∈ {1, …, D} are coupling functions ruling the (d + 1)-body interactions. Finally, ${A}_{i{j}_{1}\ldots {j}_{d}}^{(d)}$ are the entries of the adjacency tensors A^(d), with d ∈ {1, …, D}.

Let us now consider diffusive-like coupling functions at each order d

$${{{{{{{{\bf{g}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},{{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},{{{{{{{{\bf{x}}}}}}}}}_{{j}_{2}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})={{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})-{{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{i})$$

with

$${{{{{{{{\bf{h}}}}}}}}}^{(d)}:{{\mathbb{R}}}^{m\times d}\to {{\mathbb{R}}}^{m}$$

Note that this hypothesis on the form of coupling guarantees the existence of the synchronized solution x₁ = ⋯ = x_N = x^s. We remark that, in order to deal with an authentic multibody dynamics, we need to consider nonlinear coupling functions. Indeed, in the case of linear interactions, the three-body dynamical system can be reduced to a two-body dynamical system, by rescaling the adjacency matrix²⁷.

Equation (16) becomes then

$${\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}={{{{{{{\bf{f}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}_{{{{{{{{\bf{i}}}}}}}}})+\mathop{\sum }\limits_{d=1}^{D}{\sigma }_{d}\mathop{\sum }\limits_{{j}_{1},\ldots ,{j}_{d}=1}^{N}{A}_{i{j}_{1}\ldots {j}_{d}}^{(d)}({{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})-{{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{i},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{i}))$$

(17)

Let us now perturb the synchronous state x^s with a spatially inhomogeneous perturbation, meaning that ∀ i ∈ {1, …, N} we have x_i = x^s + δx_i. Substituting into Eq. (17) and expanding up to the first order we obtain

$$\delta {\dot{{{{{{{{\bf{x}}}}}}}}}}_{i}= \frac{\partial {{{{{{{\bf{f}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}_{i})}{\partial {{{{{{{{\bf{x}}}}}}}}}_{i}}\bigg|_{{{{{{{{{\bf{x}}}}}}}}}^{s}}\delta {{{{{{{{\bf{x}}}}}}}}}_{i}+\\ -\mathop{\sum }\limits_{d=1}^{D}{\sigma }_{d}\mathop{\sum }\limits_{{j}_{1},\ldots ,{j}_{d}=1}^{N}{T}_{i{j}_{1}\ldots {j}_{d}}\mathop{\sum }\limits_{\ell =1}^{d}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{\ell }}}\bigg|_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}\delta {{{{{{{{\bf{x}}}}}}}}}_{{j}_{\ell }},$$

where

$${T}_{i{j}_{1}}=\; {k}_{{{{{{{{\rm{in}}}}}}}}}^{(1)}(i){\delta }_{i{j}_{1}}-{A}_{i{j}_{1}}^{(1)}\,,\\ {T}_{i{j}_{1}{j}_{2}}=\; 2{k}_{{{{{{{{\rm{in}}}}}}}}}^{(2)}(i){\delta }_{i{j}_{1}{j}_{2}}-{A}_{i{j}_{1}{j}_{2}}^{(2)}\,,\\ \quad\quad\ldots ,\\ {T}_{i{j}_{1}{j}_{2}\ldots {j}_{D}}=\; D!{k}_{{{{{{{{\rm{in}}}}}}}}}^{(D)}(i){\delta }_{i{j}_{1}{j}_{2}\ldots {j}_{D}}-{A}_{i{j}_{1}{j}_{2}\ldots {j}_{D}}^{(D)},$$

being ${\delta }_{i{j}_{1}{j}_{2}\ldots {j}_{D}}$ the generalized multi-indexes Kronecker-δ, and the d-in-degree ${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)$ of node i is here defined as

$${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)=\frac{1}{d!}\mathop{\sum }\limits_{{j}_{1},..,{j}_{d}=1}^{N}{A}_{i{j}_{1}\ldots {j}_{d}}^{(d)},$$

which represents the number of hyperedges of order d pointing to node i.

Let us now consider the terms relative to the d-body interactions

$$\begin{array}{l}\mathop{\sum }\limits_{{j}_{1}=1}^{N}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}}}\bigg|_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}\delta {{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}}\mathop{\sum }\limits_{{j}_{2}=1}^{N}\cdots \mathop{\sum }\limits_{{j}_{d}=1}^{N}{T}_{i{j}_{1}\ldots {j}_{d}}+\ldots \\ +\mathop{\sum }\limits_{{j}_{d}=1}^{N}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}}\bigg|_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}\delta {{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}\mathop{\sum }\limits_{{j}_{1}=1}^{N}\cdots \mathop{\sum }\limits_{{j}_{d-1}=1}^{N}{T}_{i{j}_{1}\ldots {j}_{d}}.\end{array}$$

By defining

$${k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i,j)=\frac{1}{(d-1)!}\mathop{\sum }\limits_{{k}_{1},...,{k}_{d-1}}^{N}{A}_{ij{k}_{1}\ldots {k}_{d-1}}^{(d)},$$

which represents the number of hyperedges of order d pointing to node i and having node j as one of the source nodes, and by observing that, given the property of symmetry of 1-directed hypergraphs, we have

$${T}_{i{j}_{1}\ldots {j}_{d}}={T}_{i\pi (\,{j}_{1}\ldots {j}_{d})},$$

(18)

for any permutation π of the indexes j_1,…,j_d, we can write

$$\begin{array}{l}\mathop{\sum }\limits_{{j}_{1}=1}^{N}{L}_{i{j}_{1}}^{(d)}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}}}\bigg|_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}\delta {{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}}+\cdots +\mathop{\sum }\limits_{{j}_{d}=1}^{N}{L}_{i{j}_{d}}^{(d)}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}}{| }_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}\delta {{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}\\ =\mathop{\sum }\limits_{j=1}^{N}{L}_{ij}^{(d)}\left(\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}}}{| }_{({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s})}+\cdots +\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}}}\bigg|_{\big({{{{{{{{\bf{x}}}}}}}}}^{s},\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{s}\big)}\right)\delta {{{{{{{{\bf{x}}}}}}}}}_{j},\end{array}$$

where to lighten the notation we removed the explicit dependence of h^(d) on $({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})$, and we have defined the generalized Laplacian matrix for the interaction of order d as

$${L}_{ij}^{(d)}=\left\{\begin{array}{ll}d!{k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i)\hfill\quad &i=j\\ -(d-1)!{k}_{{{{{{{{\rm{in}}}}}}}}}^{(d)}(i,j)\quad &i\,\ne\, j\end{array}\right..$$

(19)

It is worth noting that the generalized Laplacian matrices defined above may not be symmetric, hence in general they have complex spectra.

Finally, by denoting

$${{{{{{{{\bf{JH}}}}}}}}}^{(d)}:=\mathop{\sum }\limits_{\ell =1}^{d}\frac{\partial {{{{{{{{\bf{h}}}}}}}}}^{(d)}({{{{{{{{\bf{x}}}}}}}}}_{{j}_{1}},\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{{j}_{d}})}{\partial {{{{{{{{\bf{x}}}}}}}}}_{{j}_{\ell }}}{| }_{({{{{{{{{\bf{x}}}}}}}}}^{* },\ldots ,{{{{{{{{\bf{x}}}}}}}}}^{* })},$$

and by defining the vector ${{{{{{{\bf{x}}}}}}}}={[{{{{{{{{\bf{x}}}}}}}}}_{1}^{\top },\ldots ,{{{{{{{{\bf{x}}}}}}}}}_{N}^{\top }]}^{\top }$, we can rewrite the linearized dynamics in a more compact form, namely

$$\delta \dot{{{{{{{{\bf{x}}}}}}}}}=\left[{{\mathbb{I}}}_{N}\otimes {{{{{{{\bf{JF}}}}}}}}-\mathop{\sum }\limits_{d=1}^{D}{\sigma }_{d}{{{{{{{{\bf{L}}}}}}}}}^{(d)}\otimes {{{{{{{{\bf{JH}}}}}}}}}^{(d)}\right]\delta {{{{{{{\bf{x}}}}}}}}$$

(20)

We here assume the hypothesis of natural coupling

$${{{{{{{{\bf{h}}}}}}}}}^{(D)}({{{{{{{\bf{x}}}}}}}},\ldots ,{{{{{{{\bf{x}}}}}}}})=\cdots ={{{{{{{{\bf{h}}}}}}}}}^{(2)}({{{{{{{\bf{x}}}}}}}},{{{{{{{\bf{x}}}}}}}})={{{{{{{{\bf{h}}}}}}}}}^{(1)}({{{{{{{\bf{x}}}}}}}}),\quad \,\forall {{{{{{{\bf{x}}}}}}}}\in {{\mathbb{R}}}^{m}$$

which leads to

$${{{{{{{{\bf{JH}}}}}}}}}^{(D)}=\cdots ={{{{{{{{\bf{JH}}}}}}}}}^{(2)}={{{{{{{{\bf{JH}}}}}}}}}^{(1)}={{{{{{{\bf{JH}}}}}}}}.$$

Under such hypothesis, we can define the matrix

$${{{{{{{\mathcal{M}}}}}}}}={\sigma }_{1}{{{{{{{{\bf{L}}}}}}}}}^{(1)}+{\sigma }_{2}{{{{{{{{\bf{L}}}}}}}}}^{(2)}+\cdots+{\sigma }_{D}{{{{{{{{\bf{L}}}}}}}}}^{(D)},$$

allowing us to write the following MSE describing the dynamics of the perturbation

$$\delta \dot{{{{{{{{\bf{x}}}}}}}}}=\left[{{\mathbb{I}}}_{N}\otimes {{{{{{{\bf{JF}}}}}}}}-{{{{{{{\mathcal{M}}}}}}}}\otimes {{{{{{{\bf{JH}}}}}}}}\right]\delta {{{{{{{\bf{x}}}}}}}}$$

(21)

Assuming that matrix ${{{{{{{\mathcal{M}}}}}}}}$ is diagonalizable, we can construct a basis made by the eigenvectors v₁, …, v_N of this matrix, and then project Eq. (21) onto each eigenvector, obtaining a system of N decoupled linear equations. In more detail, by defining the new variable ${{{{{{{\boldsymbol{\eta }}}}}}}}=({{{{{{{{\bf{V}}}}}}}}}^{-1}\otimes {{\mathbb{I}}}_{m}){{{{{{{\bf{\delta x}}}}}}}}$, where V = [v₁, …, v_N], we can rewrite Eq. (21) as

$${\dot{{{{{{{{\boldsymbol{\eta }}}}}}}}}}_{i}=[{{{{{{{\bf{JF}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}^{s})-{\lambda }_{i}{{{{{{{\bf{JH}}}}}}}}({{{{{{{{\bf{x}}}}}}}}}^{s})]{{{{{{{{\boldsymbol{\eta }}}}}}}}}_{i}$$

(22)

with i ∈ {1, …, N} and where λ₁, λ₂, …, λ_N are the eigenvalues of the matrix ${{{{{{{\mathcal{M}}}}}}}}$. The equation for i = 1 corresponds to λ₁ = 0, representing the linearized motion along the synchronous state x^s(t). The other equations describe instead the motion transverse to x^s(t). As these equations, except for the eigenvalue λ₁, have the same form, by considering the generic complex parameter α + iβ, we finally arrive to the MSE in (13).

Construction of weighted 1-directed 2-hypergraphs

We describe here how to construct the 1-directed hypergraph we have analyzed in Results and give further details about its tensor representation and the resulting generalized Laplacian matrices.

To construct the hypergraph, we start from an undirected ring network of N nodes, where N is even. We consider a consecutive labeling, so that each node i is connected to nodes i − 1 and i + 1. We then add N/2 2-hyperedges, namely containing 3 nodes, connecting nodes (1, 2, 3), (3, 4, 5), … , (N − 1, N, 1). For the first method of symmetrization, for each triple of nodes (i, i + 1, i + 2), we set ${A}_{i+2,i,i+1}^{(2)}={A}_{i+2,i+1,i}^{(2)}=1$, ${A}_{i,i+1,i+2}^{(2)}={A}_{i,i+2,i+1}^{(2)}=p$ and ${A}_{i+1,i+2,i}^{(2)}={A}_{i+1,i,i+2}^{(2)}=p$, where p ∈ [0, 1]. In this way we encode the information that nodes i and i + 1 point toward node i + 2 with strength 1, and we allow a weaker directed interaction from (i + 1, i + 2) toward i and from (i, i + 2) toward i + 1. As p increases, so does the weight of the other two directions, until we recover an undirected hypergraph for p = 1. Observe that this symmetrization does not preserve the total coupling strength of the hyperedges. A graphical representation of the symmetrization is provided in Fig. 5.

Fig. 5: Symmetrization of a 1-directed 2-hyperedge via the increase of the weight p of the hyperdeges associated to the other directions.

Starting from a fully directed hyperedge (p = 0), the strength of the couplings in the other directions grows until all directions of interaction have the same weight (p = 1).

For what concerns the second method of symmetrization, for each triple of nodes (i, i + 1, i + 2), we set ${A}_{i+2,i,i+1}^{(2)}={A}_{i+2,i+1,i}^{(2)}=1-2q$, ${A}_{i,i+1,i+2}^{(2)}={A}_{i,i+2,i+1}^{(2)}=q$ and ${A}_{i+1,i+2,i}^{(2)}={A}_{i+1,i,i+2}^{(2)}=q$, where q ∈ [0, 1/3]. As q increases, so does the weight of the hyperedges in the other two directions, until we recover an undirected hypergraph for q = 1/3. This second method of symmetrization preserves the total coupling strength of the hyperedges, thus allowing to control for confounding factors (see also Results). Figure 6 displays a graphical representation of the second symmetrization considered.

Fig. 6: Symmetrization of a 1-directed 2-hyperedge while preserving the total coupling strength.

Starting from a fully directed hyperedge, as the strength of the couplings, q, in the other directions grows, the weight of the initial directed hyperedge decreases until all directions of interaction have the same weight (q = 1/3).

Let us now explicitly characterize the hypergraph of 6 nodes displayed in Fig. 7 by writing its adjacency tensors and the corresponding Laplacians. First, the adjacency matrix A⁽¹⁾, which encodes the standard pairwise interactions, is given by

$${{{{{{{{\bf{A}}}}}}}}}^{(1)}=\left(\begin{array}{cccccc}0&1&0&0&0&1\\ 1&0&1&0&0&0\\ 0&1&0&1&0&0\\ 0&0&1&0&1&0\\ 0&0&0&1&0&1\\ 1&0&0&0&1&0\end{array}\right).$$

(23)

Fig. 7: An example of a weighted 1-directed hypegraph with N = 6 nodes.

The arrow indicates the node to which the 1-directed hyperedge points when the symmetrization parameter p (or q) is equal to zero. The different colors of the hyperedges are used to distinguish them.

From A⁽¹⁾, we can evaluate the Laplacian matrix for the two-body interactions, namely

$$\begin{array}{c}{{{{{{{{\bf{L}}}}}}}}}^{(1)}=\left(\begin{array}{cccccc}2&-1&0&0&0&-1\\ -1&2&-1&0&0&0\\ 0&-1&2&-1&0&0\\ 0&0&-1&2&-1&0\\ 0&0&0&-1&2&-1\\ -1&0&0&0&-1&2\end{array}\right),\end{array}$$

(24)

For the first method of symmetrization, the adjacency tensor A⁽²⁾(p), which instead describes the three-body interactions, is

$$\begin{array}{c}{{{{{{{{\bf{A}}}}}}}}}^{(2)}(p)=\big(\big\{{A}_{1jk}^{(2)}\big\},\ldots ,\big\{{A}_{6jk}^{(2)}\big\}\big)=\\ \left(\left(\begin{array}{cccccc}0&0&0&0&0&0\\ 0&0&p&0&0&0\\ 0&p&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&1\\ 0&0&0&0&1&0\end{array}\right),\left(\begin{array}{cccccc}0&0&p&0&0&0\\ 0&0&0&0&0&0\\ p&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right),\left(\begin{array}{cccccc}0&1&0&0&0&0\\ 1&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&p&0\\ 0&0&0&p&0&0\\ 0&0&0&0&0&0\end{array}\right),\right.\\ \left.\left(\begin{array}{cccccc}0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&p&0\\ 0&0&0&0&0&0\\ 0&0&p&0&0&0\\ 0&0&0&0&0&0\end{array}\right),\left(\begin{array}{cccccc}0&0&0&0&0&p\\ 0&0&0&0&0&0\\ 0&0&0&1&0&0\\ 0&0&1&0&0&0\\ 0&0&0&0&0&0\\ p&0&0&0&0&0\end{array}\right),\left(\begin{array}{cccccc}0&0&0&0&p&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ p&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right)\right).\end{array}$$

(25)

We remark that, while the adjacency matrix A⁽¹⁾ is symmetric, the adjacency tensor A⁽²⁾(p) is not, as, for example, A₁₂₃ ≠ A₃₁₂ for p ≠ 1. However, one can see that the tensor becomes symmetric (${A}_{ijk}^{(2)}=1\Rightarrow {A}_{\pi (ijk)}^{(2)}=1$, with π a generic permutation of indices) when p = 1. Furthermore, we note that the matrices resulting from fixing the first index of the tensor, given the property in Eq. (1), are symmetric for any value of p.

Given A⁽²⁾(p), it is possible to calculate the generalized in-degrees of the nodes (see Eq. (9) for the definition) and the generalized in-degrees of the node couples (Eq. (10)). Hence, we can evaluate the generalized Laplacian matrix for the three-body interactions (Eq. (8)). We have

$${{{{{{{{\bf{L}}}}}}}}}^{(2)}(p)=\left(\begin{array}{cccccc}2(1+p)&-p&-p&0&-1&-1\\ -p&2p&-p&0&0&0\\ -1&-1&2(1+p)&-p&-p&0\\ 0&0&-p&2p&-p&0\\ -p&0&-1&-1&2(1+p)&-p\\ -p&0&0&0&-p&2p\end{array}\right).$$

(26)

Since the adjacency tensor A⁽²⁾(p) is asymmetric, consequently L⁽²⁾(p) is also asymmetric. Consistently, when p = 1, which corresponds to the case of an undirected hypergraph, the Laplacian matrix becomes symmetric.

For the second method of symmetrization for three-body interactions, the adjacency tensor A⁽²⁾(q) is given by

$$\begin{array}{c}{{{{{{{{\bf{A}}}}}}}}}^{(2)}(q)=\big(\big\{{A}_{1jk}^{(2)}\big\},\ldots ,\big\{{A}_{6jk}^{(2)}\big\}\big)=\\ \left(\left(\begin{array}{cccccc}0&0&0&0&0&0\\ 0&0&q&0&0&0\\ 0&q&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&1-2q\\ 0&0&0&0&1-2q&0\end{array}\right),\left(\begin{array}{cccccc}0&0&q&0&0&0\\ 0&0&0&0&0&0\\ q&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right),\right.\\ \left(\begin{array}{cccccc}0&1-2q&0&0&0&0\\ 1-2q&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&q&0\\ 0&0&0&q&0&0\\ 0&0&0&0&0&0\end{array}\right),\left(\begin{array}{cccccc}0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&q&0\\ 0&0&0&0&0&0\\ 0&0&q&0&0&0\\ 0&0&0&0&0&0\end{array}\right),\\ \left.\left(\begin{array}{cccccc}0&0&0&0&0&q\\ 0&0&0&0&0&0\\ 0&0&0&1-2q&0&0\\ 0&0&1-2q&0&0&0\\ 0&0&0&0&0&0\\ q&0&0&0&0&0\end{array}\right),\left(\begin{array}{cccccc}0&0&0&0&q&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ 0&0&0&0&0&0\\ q&0&0&0&0&0\\ 0&0&0&0&0&0\end{array}\right)\right),\end{array}$$

(27)

which, similarly to A⁽²⁾(p) is in general asymmetric. From A⁽²⁾(q) we can evaluate the generalized Laplacian L⁽²⁾(q), which has the following expression

$${{{{{{{{\bf{L}}}}}}}}}^{(2)}(q)=\left(\begin{array}{cccccc}2(1-q)&-q&-q&0&-(1-2q)&-(1-2q)\\ -q&2q&-q&0&0&0\\ -(1-2q)&-(1-2q)&2(1-q)&-q&-q&0\\ 0&0&-q&2q&-q&0\\ -q&0&-(1-2q)&-(1-2q)&2(1-q)&-q\\ -q&0&0&0&-q&2q\end{array}\right).$$

As the adjacency tensor A⁽²⁾(q) is asymmetric, so the generalized Laplacian matrix L⁽²⁾(q) is asymmetric. Nonetheless, when q = 1/3, corresponding to the case of an undirected hypergraph, L⁽²⁾(q) becomes symmetric.